质点运动学(二)
合集下载
第二章 质点运动学总结
z A· Δ S r1 o x
下页 返回 结束 Δr
t 0
dr ds
r2
· B
y
元位移的大小
元路程
上页
第二章 质点运动学
§2.2
速度与加速度
§2.2.1 平均速度与瞬时速度 §2.2.2 平均加速度与瞬时加速度
上页
下页
返回
结束
第二章 质点运动学
§2.2.1 平均速度与瞬时速度
1.平均速度 r (t t ) r (t ) r 定义 v t t __ r 相 同 v 是矢量 , 方向与 __ r 大小为 v t 平均速率 P Q r r ( t t )
地面系
o
日心系
上页
Y
结束
X
下页
地心系
返回
第二章 质点运动学
选取不同的参考系，描写物 体运动的规律是不同的。
选择合适的参考系， 建立恰当的坐标系，
月亮 地球 以地球为参照系
以太阳为参考系
以方便确定物体的运动性质； 以定量描述物体的运动；
提出准确的物理模型， 以突出问题中最基本的运动规律。 讨论：刻舟求剑的启示？
x a( sin ) a(t sint ) y a(1 cos ) a(1 cost )
思考：圆内的一点和圆外的一点？
x a b sin y a b cos
上页
下页
返回
结束
第二章 质点运动学
§2.1.2 位移
1. 位移——位置矢量的增量 位移——是由初位置引向末位置的矢量，
r (t )
O
s v 0 s为路程 t
v 不能反映位移变化相对 于时间的不均匀性 .
下页 返回 结束 Δr
t 0
dr ds
r2
· B
y
元位移的大小
元路程
上页
第二章 质点运动学
§2.2
速度与加速度
§2.2.1 平均速度与瞬时速度 §2.2.2 平均加速度与瞬时加速度
上页
下页
返回
结束
第二章 质点运动学
§2.2.1 平均速度与瞬时速度
1.平均速度 r (t t ) r (t ) r 定义 v t t __ r 相 同 v 是矢量 , 方向与 __ r 大小为 v t 平均速率 P Q r r ( t t )
地面系
o
日心系
上页
Y
结束
X
下页
地心系
返回
第二章 质点运动学
选取不同的参考系，描写物 体运动的规律是不同的。
选择合适的参考系， 建立恰当的坐标系，
月亮 地球 以地球为参照系
以太阳为参考系
以方便确定物体的运动性质； 以定量描述物体的运动；
提出准确的物理模型， 以突出问题中最基本的运动规律。 讨论：刻舟求剑的启示？
x a( sin ) a(t sint ) y a(1 cos ) a(1 cost )
思考：圆内的一点和圆外的一点？
x a b sin y a b cos
上页
下页
返回
结束
第二章 质点运动学
§2.1.2 位移
1. 位移——位置矢量的增量 位移——是由初位置引向末位置的矢量，
r (t )
O
s v 0 s为路程 t
v 不能反映位移变化相对 于时间的不均匀性 .
物理 质点运动学(2)
t2
t1
t
dx vdt
x2
x1
dx vdt
t1
t2
1
3.几种特殊的直线运动
⒈匀速直线运动
⒉匀变速直线运动
a 恒量,
a 0, v v0 , x x0 vt .
v v0 at (1)
1 2 x x0 v0 t at 2 (2)
v v0 2a( x x0 )
2 0
射程 y
根据轨迹方程的极值条件， 求得最大射高为： v
v0
v sin h 2g
2 0 2
g Ov 0y
0x
v
h H
x
1
抛体运动分类： 自由落体：v0=0 平抛： v0 0 0 v 上（下）抛： 0 0 2 斜抛： v 0 0 ,0
1
习题册P1-
习题5
提示
灯距地面高度为h1，一个人身高为h2，在灯下以 匀速率v沿水平直线行走，如图所示。试计算他的头 顶在地上的影子M点沿地面移动的速度大小 关键：寻找运动方程(利用几何关系等） 找出人和M点位置关系式
1
一、 抛体运动
在空中所做的运动称抛体运动。
1-5抛体运动
抛体运动： 从地面上某点向空中抛出的物体
dx( t ) d r 2 ( t ) h2 vx dt dt
v0
h
x
r(t )
dr( t ) v 0 r 2 h2 dt
r
x( t ) h x( t )
2
2
x(t t ) x (t )
方向：水平向左（即负号表示沿x轴负方向）
1
加速度为
2 质点运动学-2
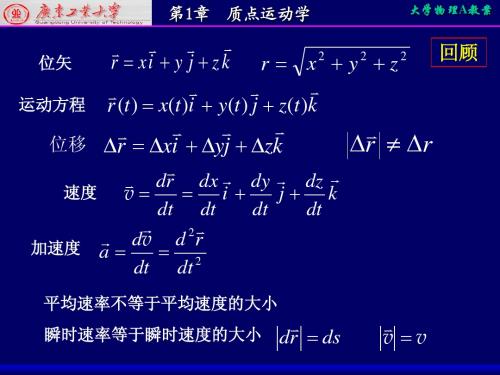
方向如图所
v
3 an g cos 30 g 2
0
a
A
g
300 an
v 2 3v an 3 g
2
2
第1章
质点运动学
大学物理A教案
4、圆周运动
(1) 圆周运动的角量描述 角位置 ： 角运动方程 (t)： R
B
s
A
质点所在的位矢 r 与x轴正 向的夹角,单位是弧度 rad。 角位移 : 规定：逆时针转向为正, 角速度
,加速度
kx
v v0 e
证： a dv dv dx v dv kv 2
dt dx dt
dx
dv kdx v
两边积分：
x dv v0 v k 0 dx v
v ln kx v0
v v0 e
kx
第1章
质点运动学
大学物理A教案
§1-3 自然坐标系中的速度和加速度
dt
dv a c dt
（2）
v (b ct ) an R R
2
2
a an
b R t c c
当子弹从枪口射出时，椰子刚好从树上由静止自由下 落. 试说明为什么子弹总可以射中椰子[忽略空气阻力]?
5、抛体运动
抛体运动的特点：加速度 a 为常量，为重力加速度。
抛体运动的运动学特征：
dr dx dy dz 速度 v i j k dt dt dt dt 2 加速度 a dv d r dt dt 2
平均速率不等于平均速度的大小 瞬时速率等于瞬时速度的大小
dr ds
v v
第1章
第二章 质点运动学
第二章 质点运动学运动学的任务是描述随时间的推移物体位置变化(运动)的规律,不涉及物体间相互作用与运动的关系。
§2.1 质点的运动学方程一、质点的位置矢量和运动学方程 要描述某质点在空间的位置，可以在参考系上先建立一个空间直角坐标系xyz o -，从坐标原点向该质点引一条有向线段，用r表示。
1、 位置矢量定义：自参考点（原点o ）引向质点P 所在位置的矢量。
质点位矢在直角坐标系中的表示：k z j y i x r++=ˆˆk j i,ˆ,ˆ分别为沿x 轴，y 轴，z 轴正方向的单位矢量，z y x ,,称为质点的位置坐标，质点的一组位置坐标就对应于一个位置矢量，也就对应质点一空间位置。
位矢的大小： 222z y x r r ++==位矢的方向（用方向余弦表示）：rzr y r x ===γβαcos ,cos ,cos 1cos cos cos 222=++γβα γβα,,分别为位矢与x 轴，y 轴，z 轴正方向的夹角。
2、质点的运动学方程由于质点的运动的不同时刻，位矢不同，则有：)(t r r= 即为质点的运动学方程，它给出了任意时刻质点的位置。
方程在直角坐标系中的正交分解式：k t z j t y i t x t r)()()()(++=质点运动学方程的标量形式为： )(),(),(t z z t y y t x x === 3、质点的运动轨迹质点运动时位矢端点描出的曲线，称质点运动轨迹。
由运动学方程消去t 得： 0),,(=z y x f[例] 一质点的运动学方程为：j t r i t R rsin cos +=，求其轨迹。
解：由已知，tR y t R x sin cos == ，则轨迹方程：222R y x =+，圆心在原点。
二、质点的位移和路程1、位移：描述质点在一定时间间隔内位置变动的物理量，用r∆表示。
)()(t r t t r r-∆+=∆位移在直角坐标中的正交分解式： k t z j t y i t x t r t t r r)()()()()(∆+∆+∆=-∆+=∆注意：质点的位移是矢量，其大小 12r r r r -=∆≠∆2、路程：描述质点在一定时间间隔内在其轨迹上经过路径的长度，用l ∆表示。
第二章质点运动学(2)
F
F
t1
t2 t
例 质量M=3t的重锤，从高度h=1.5m处自由落 到受锻压的工件上，工件发生形变。如果作用 的时间 (1) =0.1s， (2) =0.01s 。试求锤对工件 的平均冲力。 解法一利用动量定理，取竖 直向上为正。
( N Mg ) Mv Mv0
初状态动量为 M 2 gh ， 末状态动量为 0。
第二章 质点动力学
（2） 动量守恒定律 火箭运动 质心运动定律
2-3 冲量‧动量定理
1、冲量
dp 把牛顿第二定律的微分形式 F dt 改写为 F d t d p
考虑一过程，力对质点的作用时间从t1 — t2， t2 p2 两端积分 Fdt dp p 2 p1 mv2 mv1
mi ri
d vi mi d vc dt ac dt mi
由牛顿第二定律得
mi ai
m
i
m1a1 m2 a2 mn an
d v1 m1 F1 f12 f13 f1n dt d v2 m2 F2 f 21 f 23 f 2 n dt d vn mn Fn f n 2 f n 3 f n ( n 1) dt
x g v x g 2 gx 3x g 所以桌面受的压力 N N 3x g
2
例 2 一柔软链条长为 l ，单位长度的质量为。 链条放在桌上，桌上有一小孔，链条一端由小孔稍 伸下，其余部分堆在小孔周围。由于某种扰动，链 条因自身重量开始落下。求链条下落速度与落下距 离之间的关系。设链与各处的摩擦均略去不计，且 认为链条软得可以自由伸开。 解 以竖直悬挂的链条 m2 和桌面上的链条为一系统, O 建立如图坐标。 则 F m1 g yg 动量定理 m1
大学物理习题册及解答_第二版_第一章_质点的运动
如果质点在原点处的速度为零，试求其在任意位置的速度
为
．
a
d
dt
d
dx
dx dt
d
dx
d adx (3 6x2 )dx
d
x (3 6x2 )dx
0
0
6x 4x3
2．一质点沿半径为R的圆周运动，其路程S随时间t变化的规律为：
(S I)S，式bt中b0、.5cct为2 大于零的常数，且b2>R c．
Δt
2 1
“-”表示平均速度 方向沿x轴负向。
dx
(2) 第2秒末的瞬时速度 v 10t 9t 2 16m/s
dt
t2
(3) 由2秒末的加速度 a dv 10 18t 26m/s2
dt
t2
2.一质点在Oxy平面上运动，运动方程为x=3t, y=3t2-5(SI), 求(1)质 点运动的轨道方程,并画出轨道曲线;(2)t1=0s和t2=120s时质点的 的速度、加速度。
与其速度矢量恰好垂直；(4) 在什么时刻电子离原点最近．
4 质点作曲线运动， 表示位置矢量， 表示速度， 表示加速度，
S表示路程，at表示切向加速度，下列表达式中，
(1) d a
dt
(3) dS
dt
(2) dr
(4)
ddtr
dt
at
（A）只有(1)、(4)是对的．
（B） 只有(2)、(4)是对的．
（C）只有(2)是对的．
（D） 只有(3)是对的．
, ay
dvy dt
dv 2dt, dv 36t 2dt
x
y
dv vx
0
x
t
0
2 dt
质点运动学第二课
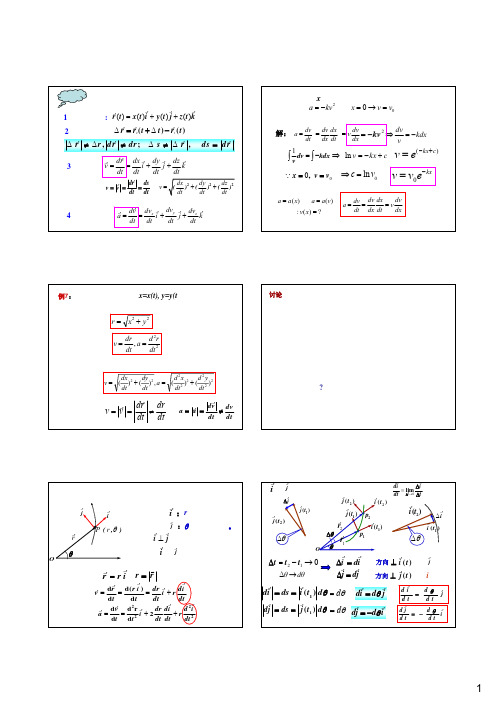
r r dv dvx r dv y r dvz r a= = i+ j+ k dt dt dt dt
求 : v( x) = ?
dv dv dv dx = =v dt dx dt dx
例7：质点的运动方程为 x=x(t), y=y(t），计算物体
讨论
的速度和加速度的大小。有两种做法哪种正确 解一：先求出
dv = aτ dt
j
r v0
o
θ
2.微分 d v / d t 是否有变化？
r r dv r r r a= = at + an = g dt
r
r an α
r g
r aτ
r i
思考题1 质点沿固定的圆形轨道运动， 若速率 v 均匀 增加，at 、an、a 以及加速度与速度间的夹角 中哪些量随时间变化？
a n = Rω 2 = v2 R dv aτ = Rα = dt
d 2r 2 a r = 2 − rω 2 = −Rω dt a = ( Rω 2 )2 + ( Rα )2 aθ = rα + 2 v r ω = Rα
· O
r n
τ
r
法向加速度——速度方向变化 切向加速度——速度大小变化
（1）质点的速度 速度总是沿轨道切线方向 r r ds v = vτ v = dt （2）质点的加速度
（ρ为轨道曲线P点的曲率半径）
( ∆t → 0, ρ ≈ ρ ′, ds = ρ ⋅ dθ )
dv dt
v2
r r r dv r v 2 r a = aτ + an = τ + n ρ dt
r aτ v
r a
ρ
r an
dv r v 2 r r r r a = aτ + a n = n τ + dt ρ
第2章质点运动学2
=
d 2rr dt 2
= axir + a y rj
a = ar =
a2 x
+
a2 y
两种表示法下加速度
lim ar =
∆t →0
∆vr ∆t
的大小相同吗？
= anern + at ert
a = ar =
a2 n
+
a2 t
a = dv , a = v2
t dt n ρ
16
课堂讨论
ar = anern + atert
*法向加速度: 由速度方向的变化带来得的加速度
大小:
方向
an :
= ern
arn
= v2
ρ
= vω = ρω2
ρ：曲率半径。
垂直于速度,指向曲线的凹侧。
*切向加速度：由速度大小的变化带来的加速度。
大小:
方向:
at
ert
=
art
= dv dt
= ρβ
切线方向,与该点速度同向或反向.
圆周运动的加速度：ρ=R； at = Rβ ;
=dβrt × rr + ωv ×d(ωrt × rr)
切向at 法向an
20
抛体运动
例: 设质点在XOY铅垂平面内作无阻力抛体运动。
试求: 质点的速度与时间t的关系和质点的运动方程.
解: 建立坐标系
y
⎪⎪⎧a x
=
dv x dt
=0
⎨ ⎪⎪⎩a y
=
dv y dt
=
−g
vr0
由初始条件：o α
t = t0;
v(t) = v2 + v2
x
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
v2 a an n R
匀速圆周运动的加速度是法向加速度，由于速度方向变化而产生。 （1） 变速圆周运动中的加速度 质点作变速圆周运动，速度的大小和方向都发生变化，都产生加速度。 t1 时刻运动到 M 点，速度为 v1 ， t 2 时刻运动到 N 点，速度为 v2 ， v v2 v1
质点作变速圆周运动时，其加速度可分为切向和法向加速度。法向加速度：
dv v2 an n —由速度的方向发生变化产生；切向加速度： a —由速度的大小 dt R
发生变化产生。
v2 2 a 的大小： a a n a2 R
a a 的方向： cos1 n a
dv a b, dt
v 2 v0 bt an R R
2
2 a a2 a n b 2
v0 bt4
R2
一质点沿 X 轴运动，其加速度 a=4t,已知 t=0 时，质点位于 x0 10m 处，初 速度 v0 0, 试求其位置和时间的关系式。 解：
（四）圆周运动（4）角加速度
d t dt
lim v t dv t 0 a dv adt dv adt v v0 at v0 0 dt 2、圆周运动中的加速度 r t 1 2 dr v dr v dt dr v dt r r0 v0 t （1）匀速圆周运动中的加速度 at r0 0 dt 2 v2 a an n R （二）匀变速直线运动 三）抛体运动 1、圆周运动的角量描述 1 2 12 （1）角坐标 r v0 t gt v0 ti gt j （1） 1、平抛运动 （2）角位移 2 2 1 （3）角速度 2、斜抛运动 r v0 t gt 2 2
d 旋定则来判断它的方向。 （4）角加速度 ， lim 。 dt t 0 t
第 3 页 共 9 页
Hei long jiang Institute of Science and Technology
2、圆周运动中的加速度 （1）匀速圆周运动中的加速度 质点作匀速圆周运动，速度的大小不变，速度的方向发生变化，产生加速度， t1 时刻运动到 M 点，速度为 v1 ， t 2 时刻运动到 N 点，
v 2 dv a an a n dt
3、角量与线量的关系 （1） ds Rd ds d R R （2） v dt dt
第 7 页 共 9 页
Hei long jiang Institute of Science and Technology
v 速度为 v2 ， v1 v2 v ， v v2 v1 ， a lim ， t 0 t
v a lim t 0 t
由图可知，
v MN v MN v v R R
a lim
t 0
MN v v v2 lim ， a 方向为 n 的方向。 t R R t 0 R
（2）变速圆周运动中的加速度
v 2 dv a a n a n R dt
（3） a
dv d R R dt dt
（3）一般曲线运动
二质点运动学的两类问题 111、已知：运动方程 r r (t ) 或 (t ) ，求速度 或角速度，加速度或角加速度。 —求导 2、 已知加速度和初始条件， 求速度或运动方程。 —积分
课的类型
掌握描述质点圆周运动参量： 角速 教学目的 度、角加速度、切向及法向加速度。 讲授
赵凯华《新概念物理教程—力学》 张三慧《大学物理学—力学》 马文蔚《物理学》 郭奕玲《物理学史》 程守洙《普通物理学》 戴剑峰《物理发展与科技进步》
教学手段
参考教材
作业布置
大学物理标准化作业 2
教学重点
掌握描述质点运动的角速度、 角 加速度、 切向及法向加速度的概念 ； 教学难点 掌握质点运动学的两类问题的计算 方法，掌握适量运算变标量。
教
1.4 圆周运动
学
基
本
内
容
备注栏
回顾：匀变速运动（ a 恒量 ）
dv dr , v 若已知初始条件： v v0 , r r0 ，根据公式： a dt dt v t dv a dv adt dv adt v v0 at v0 0 dt r t 1 dr v dr v dt dr v dt r r0 v0 t at 2 r0 0 dt 2
v a lim , v v v n ，其中 v 是速度的大小变化产生，所以 t 0 t
v v2 v1 v ， vn 是 速 度 的 方 向 发 生 变 化 产 生 。
v v n v v n a lim lim t t lim t t 0 t 0 t 0 vn v 2 n 其中 a n lim R t 0 t
第 1 页 共 9 页
Hei long jiang Institute of Science and Technology 课堂互动 本节课的匀变速直线运动和抛体运动部分内容，对于学生不是陌生的内容，所以可采取提问 的形式提出来，从而引出运动的叠加原理。 例题精选 例 1： 《大学物理疑难点剖析与能力培养》第 8 页
2 3 t 10 3 一艘正在沿直线行驶电艇，在发动机关闭后，其加速度与速度方向相反，大
小与速度平方成正比，即 dv / dt kv 2 ，式中可 k 为正的常数，试证明电艇在关闭 发动机后又行驶 x 距离时的速度。 v v0 e kx 其中 v0 是发动机关闭时的速度。 解
a dv dv dx dv v kv 2 dt dx dt dx
切向及法向加速度两物理量的 理解及计算；质点运动学的两类问 题的计算方法。
教
重点突出
学
基
本
设
计
圆周运动中的加速度是本节课的重点。在讲述时应突出切向加速度和法向加速度产生的原 因，使学生理解两加速度的意义。 难点突破 对切向加速度和法向加速度的理解和质点运动学的两类问题是本节的难点。为帮助学生理解两 加速度的意义可举例，如 a 0, an 0 ； a 0, an 0 ； a 0, an 0 ； a 0, an 0 ，质点各作 何种运动。对于质点运动学的两类问题，可采取归纳总结和举例的方法来突破这一难点。 原则上讲应用描述质点运动的四个矢量可以描述一切质点的一切运动，但实际 教学导入 上限于数学知识的限制。 只能描述一些简单的基本的具有对称性的运动。 直线、 圆周和抛体运动。 双语教学 抛体运动 projectile motion,匀加速运动 uniformly accelerated motion, 匀加速直线运动 uniformly accelerated rectilinear motion, 角速度 angular velocity, 角加速度 angular acceleration, 切向加速度 Tangential acceleration,法向加速度 normal acceleration.
Hei long jiang Institute of Science and Technology
2008 春季大学物理教案
授课次序：02； 授课日期： 2 月 27 日
教
教学课题 大纲要求 教学方法 质点运动学（二）学基本 Nhomakorabea指
标
新知识课 通过本课使学生学会用角量描 述质点运动大学物理；掌握质点运 动学的两类问题。 动画——相对运动
所以 所以
v
v0
x dv kdx , 0 v
ln
v kx v0
v v0 e kx
第 6 页 共 9 页
Hei long jiang Institute of Science and Technology
拟
一、圆周运动
(一)匀变速运动（ a 恒量 ）
板
书
设
计（提纲）
《物理.工程.创新》教材——抛体理论在体育运动中的应用：如体育运动中的跳高、跳远、投篮、 标枪等项目。抛体理论可定量描述初速度、抛射角等因素对运动成绩的影响，从而找出取得最加 成绩的途径。以标枪为例：运用抛体理论分析如何分得更高更远？
第 2 页 共 9 页
Hei long jiang Institute of Science and Technology
运动的叠加原理——运动的合成与分解 几个简单而彼此独立的运动可以叠加成一较为复杂的运动；同样，一个较为 复杂的运动可以看成由几个简单的彼此独立运动的叠加。 1.4.1 圆周运动 当质点作圆周运动时，用角量描述更形象、直观，更能体现出运动的特点。 1、圆周运动的角量描述 （1）角坐标 ——标量 矢径与 x 正向的夹角。规 （ t 时刻质点运动到 M 点， 定逆时针转动方向为正——右手定则） 。 （2）角位移 t t 时刻质点运动到 N 点，则 t 时间内质点的角 位移为 （3）角速度 d 角速度是一个矢量，用右手螺 lim dt t 0 t
a dv 4t , dt
dv 4tdt
第 5 页 共 9 页
Hei long jiang Institute of Science and Technology
dv 4tdt,
0 0
v
t
v 2t 2
v
dx 2t 2 dt x
x
10
dx 2t 2 dt
0
t
应用举例
1 一质点沿半径为 R 的圆周运动， 其路程随时间的变化规律为 s v 0 t bt 2 ， 0 v 2 和 b 都是正的常量。求 t 时刻质点的加速度的大小。