江苏省建湖县高作中学2009—2010年八年级数学下学期一元一次不等式抽测考试(无答案)
(好题)初中数学八年级数学下册第二单元《一元一次不等式和一元一次不等式组》测试(含答案解析)(1)

一、选择题1.已知a b >,下列不等式中,不成立的是( )A .44a b +>+B .33a b ->- C.22a b> D .22a b ->-2.不等式组123x x -≤⎧⎨-<⎩的解集是( ) A .1x ≥- B .1x <- C .15x -≤<D .1x ≤-或5x < 3.如果m n >,则下列各式不成立的是( )A .22m n +>+B .22m n ->-C .22m n >D .22m n -<- 4.如图,已知AB 是线段MN 上的两点,MN =12,MA =3,MB >3,以A 为中心顺时针旋转点M ,以点B 为中心顺时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,当△ABC 为直角三角形时AB 的长是( )A .3B .5C .4或5D .3或51 5.若关于x 的不等式组5335x x x a -+⎧⎨⎩><无解,则a 的取值范围为( ) A .a <4 B .a=4C .a≤4D .a≥4 6.如果关于x 的不等式组2243(2)x m x x -⎧≥⎪⎨⎪-≤-⎩的解集为x≥1,且关于x 的方程(1)23m x x --=-有非负整数解,则所有符合条件的整数m 的值有( )个. A .2个 B .3个 C .4个 D .5个7.运行程序如图所示,规定:从“输入一个值x ”到“结果是否26>”为一次程序操作,如果程序操作进行了1次后就停止,则x 最小整数值取多少( )A .7B .8C .9D .108.运行程序如图所示,规定从“输入一个值x ”到“结果是否95>”为一次程序操作,如果程序操作进行了两次才停止,那么x 的取值范围是()A .23x >B .2347x <≤C .1123x ≤<D .47x ≤ 9.不等式组13x x ≤⎧⎨>-⎩的解集在数轴上表示正确的是( ) A . B .C .D .10.己知关于x 的不等式组0320x a x ->⎧⎨->⎩的整数解共有6个,则a 的取值范围是( ) A .54a -<<- B .4a C .54a -≤<- D .352a -<< 11.下列不等式变形中,一定正确的是( )A .若ac>bc ,则a>bB .若a>b ,则ac>bcC .若ac²>bc²,则a>bD .若a>0,b>0,且11a b >,则a>b 12.不 等式112x >-的解集是( ) A .12x >- B .2x >- C .2x <- D .12x <- 二、填空题13.如图,函数y x =和4y ax =+的图象交于点()2,2,A 则不等式4x ax <+的解集为_____________________.14.过点()5,2-的一条直线与x 轴、y 轴分别相交于点A ,B ,且与直线312y x =-+平行,则在线段AB 上,横、纵坐标都是整数的点坐标是______.15.若不等式组30x a x >⎧⎨-≤⎩只有三个正整数解,则a 的取值范围为__________. 16.现用甲、乙两种运输车将46吨救灾物资运往灾区,甲种车每辆载重5吨,乙种车每辆载重4吨,安排车辆不超过10辆,则甲种运输车至少需要安排 ________辆. 17.点()3,1m m --在第四象限,则m 的取值范围是_______.18.如图,直线y kx b =+交坐标轴于,A B 两点,则不等式0kx b +>的解是__________.19.一次函数 y 1=kx +b 与 y 2=x +a 的图象如图所示,则下列结论:①k <0;②a <0,b <0;③当 x =3 时,y 1=y 2;④不等式 kx +b >x +a 的解集是 x <3,其中正确的结论有_______.(只填序号)20.已知关于x 的不等式(2)50m n x m n -+->的解集1x <,则关于x 的不等式mx n >的解集是__________.三、解答题21.在近期“抗疫”期间,某药店销售A 、B 两种型号的口罩,已知销售80只A 型和45只B 型的利润为21元,销售40只A 型和60只B 型的利润为18元.(1)求每只A 型口罩和B 型口罩的销售利润;(2)该药店计划一次购进两种型号的口罩共2000只,其中B 型口罩的进货量不少于A 型口罩的进货量且不超过它的3倍,则该药店购进A 型、B 型口罩各多少只,才能使销售总利润最大?22.某企业准备购买一批爱心物资捐赠给学校.经了解,若购买洗手液300瓶和口罩200包,则共需6000元;若购买洗手液500瓶和口罩300包,则共需9500元.(1)问:每瓶洗手液和每包口罩的价格各是多少元?(2)现计划购买洗手液和口罩,若购买这两种物资的总费用不超过11500元,洗手液瓶数和口罩的包数之和为1000,且洗手液的瓶数不大于口罩包数的3倍.设购买洗手液m 瓶,购买这两种物资的总费用为W 元,请写出W (元)与m (瓶)之间的函数关系式,并求出W 的最小值.23.今年,“地摊经济”成为了社会关注的热门话题.小明从市场得知如下信息:甲商品乙商品进价(元/件)355售价(元/件)458x件,甲、乙商品全部销售完后获得利润为y元.(1)求出y与x之间的函数关系式;(2)小明用不超过2000元资金一次性购进甲,乙两种商品,求x的取值范围;(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于632.5元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大.24.某校运动会需购买,A B两种奖品,A单价是12元/件,B单价是15元/件,已知购买A种奖品x(件)与购买B奖品y件)之间的函数关系如图所示.(1)求y与x之间的函数关系式;(2)学校计划购买,A B两种奖品的总费用不超过1290元,且A种奖品的数量不大于B种奖品数量的3倍.设购买,A B两种奖品的总费用为w元,请你设计购买,A B两种奖品的方案,怎样购买才能使费用最少,w的最小值是多少?25.解下列不等式(组):(1)2132x x-≤;(2)把它的解集表示在数轴上.3(2)41213x xxx--≤⎧⎪+⎨>-⎪⎩26.某商家欲购进甲、乙两种抗疫用品共180件,其进价和售价如表:甲乙进价(元/件)1435售价(元/件)2043、乙两种用品应分别购进多少件?(请用二元一次方程组求解)(2)若商家计划投入资金少于5040元,且销售完这批抗疫用品后获利不少于1314元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据不等式的性质逐个判断即可.【详解】解:A .不等式a b >两边都加上4,不等号的方向不变,即44a b +>+,原变形成立,故此选项不符合题意;B .不等式a b >两边都减去3,不等号的方向不变,即33a b ->-,原变形成立,故此选项不符合题意;C .不等式a b >两边都除以2,不等号的方向不变,即22a b >,原变形成立,故此选项不符合题意; D .不等式a b >两边都乘以2-,不等号的方程改变,即22a b -<-,原变形不成立,故此选项符合题意;故选:D .【点睛】本题考查了不等式的性质,能熟记不等式的性质的内容是解此题的关键,注意:①不等式的性质1:不等式的两边都加(或减)同一个数或式子,不等号的方向不变;:②不等式的性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;③不等式的性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.2.C解析:C【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分,即可得到答案.【详解】解:∵123x x -≤⎧⎨-<⎩, ∴15x x ≥-⎧⎨<⎩, ∴15x -≤<;故选:C .【点睛】本题考查了解一元一次不等式组,解题的关键是熟练掌握解不等式组的方法进行解题. 3.B解析:B【分析】根据不等式的性质解答.【详解】A 、在不等式m >n 的两边同时加上2,不等式仍成立,即m+2>n+2,故本选项不符合题意.B 、在不等式m >n 的两边同时乘以-1然后再加上2,不等式号方向改变,即2-m <2-n ,故本选项符合题意.C 、在不等式m >n 的两边同时除以2,不等式仍成立,即22m n >,故本选项不符合题意. D 、在不等式m >n 的两边同时乘以-2,不等式号方向改变,即-2m <-2n ,故本选项不符合题意.故选:B .【点睛】本题主要考查了不等式的性质,在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.4.C解析:C【分析】设AB =x ,则BC =9-x ,根据三角形两边之和大于第三边,得到x 的取值范围,再利用分类讨论思想,根据勾股定理列方程,计算解答.【详解】解:∵在△ABC 中,AC =AM =3,设AB =x ,BC =9-x ,由三角形两边之和大于第三边得:3939x x x x +-⎧⎨+-⎩>>, 解得3<x <6,①AC 为斜边,则32=x 2+(9-x )2,即x 2-9x +36=0,方程无解,即AC 为斜边不成立,②若AB 为斜边,则x 2=(9-x )2+32,解得x =5,满足3<x <6,③若BC 为斜边,则(9-x )2=32+x 2,解得x =4,满足3<x <6,∴x =5或x =4;故选C .【点睛】本题考查三角形的三边关系,勾股定理等,分类讨论和方程思想是解答的关键. 5.C解析:C【解析】解:5335x x x a -+⎧⎨⎩>①<②,由①得:x >4.∵不等式组无解,∴a ≤4.故选C . 点睛:本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解). 6.A解析:A【分析】表示出不等式组的解集,由已知解集确定出m 的范围,表示出方程的解,由方程的解为非负整数,确定出整数m 的值即可.【详解】解:不等式组整理得:41≥+⎧⎨≥⎩x m x , ∵不等式组的解集为x ≥1,∴m +4≤1,即m ≤-3,方程去分母得:m -1+x =3x -6, 解得:5+2=m x , ∵方程有非负整数解,∴50m +≥,且5+m 能被2整除,∴-53m ≤≤-,∴当m=-5时,符合题意,当m=-3时,符合题意,则符合条件的整数m 的值有2个,故选:A .【点睛】本题考查一元一次不等式组的整数解,熟练掌握不等式组的解法是解本题的关键. 7.D解析:D【分析】根据程序操作进行了1次后就停止,即可得出关于x 的一元一次不等式,解之即可得出x 的取值范围,再取其中最小的整数值即可得出结论.【详解】依题意,得:3126x ->,解得:9x >.∵x 为整数,∴x 的最小值为10.故选:D .【点睛】本题考查了一元一次不等式的应用,找准等量关系,正确列出一元一次不等式是解题的关键.8.B解析:B【分析】根据运行程序,第一次运算结果小于等于95,第二次运算结果大于95列出不等式组,然后求解即可.【详解】解:由题意得,()2195221195x x +≤⎧⎪⎨++⎪⎩①>② 解不等式①得,47x ≤,解不等式②得,23x >,∴2347x ≤<,故选:B .【点睛】本题考查了一元一次不等式组的应用,读懂题目信息,理解运行程序并列出不等式组是解题的关键.9.A解析:A【分析】在数轴上表示解集时,一要找准起点,二要找准方向,三要区别实心点与空心圈.【详解】解:不等式组13x x ≤⎧⎨>-⎩的解集在数轴上表示为: ;故选A .【点睛】本题考查了一元一次不等式组的解集在数轴上的表示方法,掌握一元一次不等式组的解集在数轴上的表示方法是解题的关键.10.C解析:C【分析】先解出不等式组的解,然后确定x 的取值范围,根据整数解的个数可知a 的取值.【详解】由不等式组可得: 1.5a x <<.因为有6个整数解,可以知道x 可取-4,-3,-2,-1,0,1,因此54a -≤<-.故选:C .【点睛】本题考查了不等式组中不等式的未知字母的取值,解答此题要先求出不等式组的解集,求不等式组的解集要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.第II 卷(非选择题)请点击修改第II 卷的文字说明11.C解析:C【分析】根据不等式的基本性质分别进行判定即可得出答案.【详解】A .当c <0,不等号的方向改变.故此选项错误;B .当c=0时,符号为等号,故此选项错误;C .不等式两边乘(或除以)同一个正数,不等号的方向不变,正确;D .不等式的两边都乘以或除以同一个正数,不等号的方向不变,错误.故选:C .【点睛】本题考查了不等式的性质,注意不等式的两边都乘以或除以同一个负数,不等号的方向改变.12.B解析:B【分析】根据解一元一次不等式基本步骤系数化为1可得.【详解】解:两边都乘以2,得:x>-2,故选:B .【点睛】本题考查了解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.二、填空题13.【分析】先利用A 点坐标然后观察函数图得到当x <2时y=x 的图象都在直线的下方由此得到不等式x <ax+4的解集【详解】解:A (23)观察函数图得到:当x <2时y=x 的图象都在直线的下方不等式x <ax+解析:2x <【分析】先利用A 点坐标,然后观察函数图得到当x <2 时,y=x 的图象都在直线4y ax =+的下方,由此得到不等式x <ax+4的解集.【详解】 解: A (2,3),观察函数图得到:当x <2 时,y=x 的图象都在直线4y ax =+的下方,∴ 不等式x <ax+4的解集x <2.故答案为:2x <.【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.理解好上面原理是解题的关键.14.(14)(31)【分析】依据与直线平行设出直线AB 的解析式;代入点(5-2)即可求得b 然后求出与x 轴的交点横坐标列举符合条件的x 的取值依次代入即可【详解】解:∵过点(5-2)的一条直线与直线平行设直解析:(1,4),(3,1).【分析】 依据与直线312y x =-+平行设出直线AB 的解析式32y x b =-+;代入点(5,-2)即可求得b ,然后求出与x 轴的交点横坐标,列举符合条件的x 的取值,依次代入即可.【详解】 解:∵过点(5,-2)的一条直线与直线312y x =-+平行,设直线AB 为32y x b =-+; 把(5,-2)代入32y x b =-+;得-2=152b -+ 解得:b=112∴直线AB 的解析式为31122y x =-+ 令y=0,得:311022x =-+ 解得:x=113∴0<x <113的整数为:1、2、3; 把x 等于1、2、3分别代入解析式得4、52、1; ∴在线段AB 上,横、纵坐标都是整数的点的坐标是(1,4),(3,1).故答案为:(1,4),(3,1).【点睛】本题考查了待定系数法求解析式以及直线上点的情况,列举出符合条件的x 的值是本题的关键.15.【分析】先确定不等式组的整数解再求出的取值范围即可【详解】∵不等式组只有三个正整数解∴故答案为:【点睛】本题考查了解不等式组的整数解的问题掌握解不等式组的整数解的方法是解题的关键解析:01a ≤<【分析】先确定不等式组的整数解,再求出a 的取值范围即可.【详解】30x a x >⎧⎨-≤⎩ 30x -≤3x ≤∵不等式组只有三个正整数解∴01a ≤<故答案为:01a ≤<.【点睛】本题考查了解不等式组的整数解的问题,掌握解不等式组的整数解的方法是解题的关键. 16.6【解析】设甲种运输车共运输x 吨则乙种运输车共运输(46-x )吨根据题意得≤10解不等式得:则故甲种运输车辆至少需要6辆故答案:6解析:6【解析】设甲种运输车共运输x 吨,则乙种运输车共运输(46-x )吨.根据题意,得x 4654x -+≤10.解不等式得:45(46)200,30x x x +-≤≥,则65x ≥ ,故甲种运输车辆至少需要6辆. 故答案:6. 17.【分析】根据点()在第四象限列出关于m 的不等式组解之可得【详解】∵点()在第四象限∴解得故答案为:【点睛】本题考查了已知点所在的象限求参数以及求一元一次不等式组的解集正确求出每一个不等式解是基础熟知解析:1m <【分析】根据点(3m -,1m -)在第四象限列出关于m 的不等式组,解之可得.【详解】∵点(3m -,1m -)在第四象限,∴3010m m ->⎧⎨-<⎩, 解得1m <,故答案为:1m <.【点睛】本题考查了已知点所在的象限求参数以及求一元一次不等式组的解集,正确求出每一个不等式解是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.18.【分析】看在x 轴上方的函数图象所对应的自变量的取值即可【详解】由图象可以看出x 轴上方的函数图象所对应自变量的取值为故不等式的解集是故答案为:【点睛】本题考查了一次函数与一元一次不等式的关系:从函数的 解析:2x >-【分析】看在x 轴上方的函数图象所对应的自变量的取值即可.【详解】由图象可以看出,x 轴上方的函数图象所对应自变量的取值为2x >-,故不等式0kx b +>的解集是2x >-.故答案为:2x >-.【点睛】本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.19.①③④【分析】仔细观察图象①k 的正负看函数图象从左向右成何趋势即可;②ab 看y2=x+ay1=kx+b 与y 轴的交点坐标;③看两函数图象的交点横坐标;④以两条直线的交点为分界哪个函数图象在上面则哪个函解析:①③④【分析】仔细观察图象,①k 的正负看函数图象从左向右成何趋势即可;②a,b 看y 2=x +a , y 1=kx +b 与y 轴的交点坐标;③看两函数图象的交点横坐标;④以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大.【详解】解:① y 1=kx +b 的图象从左向右呈下降趋势,∴k<0正确;② y 2=x +a 与y 轴的交点在负半轴上, ∴a<0,另一条直线与y 轴交于正半轴,所以b>0,故②错误;③两函数图象的交点横坐标为3,∴当x=3时, y 1=y 2 ,故③正确;④当x <3时, y 1>y 2 ,故④正确;故正确的判断是①③④.故答案为: ①③④.【点睛】此题主要考查了一次函数的图象,考查学生的分析能力和读图能力,一次函数y=kx+b 的图象有四种情况:①当k>0,b>0,函数y=kx+b 的图象经过第一、二、三象限;②当k>0,b <0,函数y=kx+b 的图象经过第一、三、四象限;③当k <0,b>0,函数y=kx+b 的图象经过第一、二、四象限;④当k <0,b <0,函数y=kx+b 的图象经过第二、三、四象限.20.【分析】根据不等式和解集间的关系可知时化简可得mn 的关系由此可解不等式【详解】解:由题意得时即化简得且不等式的解集变号了说明等量代换可得不等式即为由不等式基本性质可得故答案为【点睛】本题考查了不等式 解析:12x <【分析】根据不等式和解集间的关系可知1x =时,(2)50m n x m n -+-=,化简可得m,n 的关系,由此可解不等式mx n >.【详解】解:由题意得1x =时,(2)50m n x m n -+-=,即250m n m n -+-=,化简得2m n =,且不等式的解集变号了,说明20m n -<,等量代换可得 40,30,0n n n n -<<<,不等式mx n >即为2nx n >,由不等式基本性质可得12x <. 故答案为12x <【点睛】本题考查了不等式,熟练掌握不等式的性质及不等式与解集间的关系是解题的关键. 三、解答题21.(1)每只A 型口罩销售利润为0.15元,每只B 型口罩销售利润为0.2元;(2)药店购进A 型口罩500只、B 型口罩1500只,才能使销售总利润最大.【分析】(1)设每只A 型口罩销售利润为a 元,每只B 型口罩销售利润为b 元,根据“销售80只A型和45只B 型的利润为21元,销售40只A 型和60只B 型的利润为180元”列方程组解答即可;(2)根据题意即可得出y 关于x 的函数关系式;再根据题意列不等式得出x 的取值范围,再结合一次函数的性质解答即可.【详解】解:(1)设每只A 型口罩销售利润为a 元,每只B 型口罩销售利润为b 元,根据题意得:804521406018a b a b +=⎧⎨+=⎩, 解得0.150.2a b =⎧⎨=⎩, 答:每只A 型口罩销售利润为0.15元,每只B 型口罩销售利润为0.2元;(2)设购进A 型口罩x 只,这2000只口罩的销售总利润为y 元.根据题意得,y=0.15x+0.2(2000-x ),即y=-0.05x+400;根据题意得,200020003x x x x-≥⎧⎨-≤⎩,解得500≤x≤1000, ∴y=-0.05x+400(500≤x≤1000);∵k=-0.05<0;∴y 随x 的增大而减小,∵x 为正整数,∴当x=500时,y 取最大值,则2000-x=1500,即药店购进A 型口罩500只、B 型口罩1500只,才能使销售总利润最大.【点睛】本题主要考查了一次函数的应用,二元一次方程组及一元一次不等式的应用,解题的关键是根据一次函数x 值的增大而确定y 值的增减情况.22.(1)每瓶洗手液和每包口罩的价格分别为10元、15元;(2)W =﹣5m +15000,W 的最小值是11250.【分析】(1)根据题意,可以列出相应的二元一次方程组,从而可以求得每瓶洗手液和每包口罩的价格各是多少元;(2)根据题意可以写出W (元)与m (瓶)之间的函数关系式,并求出W 的最小值.【详解】解:(1)设每瓶洗手液和每包口罩的价格分别为a 元、b 元,30020060005003009500a b a b +=⎧⎨+=⎩, 解得1015a b =⎧⎨=⎩, 答:每瓶洗手液和每包口罩的价格分别为10元、15元;(2)由题意可得,W=10m+15(1000﹣m)=﹣5m+15000,∴W随m的增大而减小,∵购买这两种物资的总费用不超过11500元,洗手液瓶数和口罩的包数之和为1000,且洗手液的瓶数不大于口罩包数的3倍,∴515000115003(1000)mm m-+≤⎧⎨≤-⎩,解得700≤m≤750,∴当m=750时,W取得最小值,此时W=11250,答:W(元)与m(瓶)之间的函数关系式是W=﹣5m+15000,W的最小值是11250.【点睛】本题考查一次函数的应用、二元一次方程组的应用、一元一次不等式组的应用,解答本题的关键是明确题意,利用一次函数的性质和不等式的性质解答.23.(1)y=7x+300;(2)0≤x≤50;(3)甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件;当甲商品进50件,乙商品进50件时,利润有最大值.【分析】(1)分别求出甲、乙商品的利润,根据y=甲商品利润+乙商品利润即可得解析式;(2)由用不超过2000元资金一次性购进甲,乙两种商品,列出不等式组,即可求解;(3)由获得的利润不少于632.5元,列出不等式可求x的范围,根据一次函数的性质即可得答案.【详解】(1)∵购进甲、乙商品共100件进行销售,小明购进甲商品x件,∴甲商品利润为(45-35)x=10x,乙商品利润为(100-x)(8-5)=300-3x,∵甲、乙商品全部销售完后获得利润为y元,∴y=10x+(300-3x)=7x+300.(2)∵用不超过2000元资金一次性购进甲,乙两种商品,∴35x+5(100﹣x)≤2000,∴x≤50,又∵x≥0,∴0≤x≤50;(3)∵甲,乙商品全部销售完后获得的利润不少于632.5元,∴7x+300≥632.5,∴x≥47.5,由(2)可得0≤x≤50,∴47.5≤x≤50,∵x为整数,∴x=48,49,50,∴进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件;∵y =7x+300,7>0,∴y 随x 的增大而增大,∴当x =50时,y 有最大利润.∴当甲商品进50件,乙商品进50件,利润有最大值.【点睛】本题考查一元一次不等式的应用及一次函数的应用,理解题意,正确列出不等式并熟练掌握一次函数的性质是解题关键.24.(1)100=-+y x ;(2)购买A 种奖品75件,B 种奖品25件,能使总费用最少为1275元【分析】(1)根据题意,由待定系数法,即可求出一次函数的解析式;(2)根据总费用=两种奖品的费用之和表示出w 与x 的关系式,并由条件建立不等式组求出x 的取值范围,由一次函数的性质就可以求出结论.【详解】解:设y kx b =+,则20806040k n k b +=⎧⎨+=⎩解得:1100k b =-⎧⎨=⎩100y x ∴=-+;()2解:由题意得()121510031500W x x x =+-+=-+()3150012903100x x x -+≤⎧∴⎨≤-+⎩解得:7075x ≤≤31500w x =-+,30k ∴=-<,w ∴随x 的增大而减小,75x ∴=时,1275w =最小,当75x =时,25y =;即应购买A 种奖品75件,B 种奖品25件,才能使总费用最少为1275元.【点睛】本题考查了一次函数的性质的运用,待定系数法求解析式,一元一次不等式组的运用,解答时求出一次函数的解析式是关键.25.(1)2x ≤;(2)1≤x <4,数轴见详解.【分析】(1)通过去分母,移项,合并同类项,未知数系数化为1,即可求解;(2)通过去分母,移项,合并同类项,未知数系数化为1,分别求出两个不等式的解,进而即可求解,然后再数轴上表示不等式组的解,即可.【详解】(1)2132x x -≤, 2(21)3x x -≤,423x x -≤,432x x -≤,2x ≤;(2)3(2)41213x x x x --≤⎧⎪⎨+>-⎪⎩①② 由①得:x≥1,由②得:x <4,∴不等式组的解为:1≤x <4,在数轴上表示如下:【点睛】本题主要考查解一元一次不等式(组),熟练掌握解一元一次不等式的基本步骤,是解题的关键.26.(1)甲种商品购进100件,乙种商品购进80件;(2)方案一:甲种商品购进61件,乙种商品购进119件.方案二:甲种商品购进62件,乙种商品购进118件.方案三:甲种商品购进63件,乙种商品购进117件.获利最大的是方案一:甲种商品购进61件,乙种商品购进119件.【分析】(1)等量关系为:甲件数+乙件数=180;甲总利润+乙总利润=1240.(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量<5040;甲总利润+乙总利润≥1314.【详解】解:(1)(1)设甲种商品应购进x 件,乙种商品应购进y 件.根据题意得:180681240x y x y +=⎧⎨+=⎩. 解得:10080x y =⎧⎨=⎩. 答:甲种商品购进100件,乙种商品购进80件.(2)设甲种商品购进a 件,则乙种商品购进(180)a -件.根据题意得1435(180)504068(180)1314a aa a+-<⎧⎨+-≥⎩解不等式组得6063a<.a为非负整数,a∴取61,62,63180a∴-相应取119,118,117方案一:甲种商品购进61件,乙种商品购进119件,此时利润为:66181191318⨯+⨯=元;方案二:甲种商品购进62件,乙种商品购进118件,此时利润为:66281181316⨯+⨯=元;方案三:甲种商品购进63件,乙种商品购进117件,此时利润为:66281181314⨯+⨯=元;所以,有三种购货方案,其中获利最大的是方案一:甲种商品购进61件,乙种商品购进119件.【点睛】本题考查了二元一次方程组的应用及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.。
(好题)初中数学八年级数学下册第二单元《一元一次不等式和一元一次不等式组》测试卷(含答案解析)(1)

一、选择题1.下列不等式组的解集,在数轴上表示为如图所示的是()A.1020xx->⎧⎨+≤⎩B.1020xx+>⎧⎨+≤⎩C.1020xx+>⎧⎨-≤⎩D.1020xx-≤⎧⎨+<⎩2.三角形的两边长分别是4和11,第三边长为34m+,则m的取值范围在数轴上表示正确的是()A .B .C .D .3.若不等式组11233x xx m+⎧<+⎪⎨⎪>⎩有解,则m的取值范围为()A.1m B.1m<C.1m D.3m<4.如图,已知AB是线段MN上的两点,MN=12,MA=3,MB>3,以A为中心顺时针旋转点M,以点B为中心顺时针旋转点N,使M、N两点重合成一点C,构成△ABC,当△ABC为直角三角形时AB的长是()A.3 B.5 C.4或5 D.3或515.若关于x的不等式组5335x xx a-+⎧⎨⎩><无解,则a的取值范围为()A.a<4 B.a=4 C.a≤4D.a≥46.如果a<b,那么下列不等式中一定成立的是()A.a2<ab B.ab<b2C.a2<b2D.a﹣2b<﹣b 7.下列各式中正确的是()A.若a b>,则11a b-<-B.若a b>,则22a b>C.若a b>,且0c≠,则ac bc>D.若||||a bc c>,则a b>8.若关于x的不等式721x mx-<⎧⎨-≤⎩的整数解共有4个,则m的取值范围是()A.68m<<B.67≤<m C.67m≤≤D.67m<≤9.某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往青岛,这列货车可挂,A B 两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节A 型货厢,甲种货物25吨和乙种货物35吨可装满一节B 型货厢,按此要求安排,A B 两种货厢的节数,有几种运输方案( )A .1种B .2种C .3种D .4种10.如图是一次函数1y kx b =+与2y x a =+的图象,则不等式kx b x a ++<的解集是( )A .0x >B .0x <C .3x >D .3x <11.如果a b >,可知下面哪个不等式一定成立( )A .a b ->-B .11a b <C .2a b b +>D .2a ab >12.不等式组111x x -<⎧⎨≥-⎩的解集在数轴上表示正确的是( ) A . B . C . D .二、填空题13.由ac bc >得到a b <的条件是:c ______0(填“>”“<”或“=”).14.关于x 的不等式组3222553x x x m +⎧+⎪⎪⎨+⎪<+⎪⎩有且只有4个整数解,则常数m 的取值范围是_____.15.若关于x 、y 的二元一次方程组23242x y a x y a+=-⎧⎨+=+⎩的解满足1x y +<,则a 的取值范围为________.16.如图,直线y =x+2与直线y =ax+c 相交于点P(m ,3).则关于x 的不等式x+2≥ax+c 的不等式的解为_____.17.不等式组112251x x ⎧-≤⎪⎨⎪+>⎩的最大整数解是__________.18.在一次知识竞赛中,有25道抢答题,答对一题得4分,答错或不答每题扣2分,成绩不低于60分就可获奖.那么获奖至少要答对___________道题.19.已知一次函数y kx b =+的图像如图所示,则关于x 的不等式320kx b ->的解集为_____.20.若方程组3133x y a x y +=+⎧⎨+=⎩的解x 、y 满足 3y x -<,则a 的取值范围为_________. 三、解答题21.某数学兴趣小组开展了一次活动,过程如下:设()090BAC θθ∠=︒<<︒,小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.活动一:如图甲所示,从点1A 开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,12A A 为第1根小棒.数学思考:(1)小棒能无限摆下去吗?答:______;(填“能”或“不能”)(2)若112231AA A A A A ===,则θ=______度;活动二:如图乙所示,从点1A 开始,用等长的小棒依次向右摆放,其中12A A 为第1根小棒,且121A A AA =.数学思考:(3)若已经向右摆放了3根小棒,则1θ=______,2θ=______,3θ=______(用含θ的式子表示);(4)若只能摆放4根小棒,求θ的范围.22.某校运动会需购买,A B 两种奖品,A 单价是12元/件,B 单价是15元/件,已知购买A 种奖品x (件)与购买B 奖品y 件)之间的函数关系如图所示.(1)求y 与x 之间的函数关系式;(2)学校计划购买,A B 两种奖品的总费用不超过1290元,且A 种奖品的数量不大于B 种奖品数量的3倍.设购买,A B 两种奖品的总费用为w 元,请你设计购买,A B 两种奖品的方案,怎样购买才能使费用最少,w 的最小值是多少?23.某水果店购买某种水果的进价为18元/千克,在销售过程中有10%的水果损耗,该水果店以a元/千克的标价出售该种水果.(1)为避免亏本,求a的最小值.(2)若该水果店以标价销售了70%的该种水果,在扣除10%损耗后,剩下的20%水果按10元/千克的价格售完.为确保销售该种水果所得的利润率不低于20%,求a的最小值.24.解关于x的不等式组:2311 23xxx x<+⎧⎪⎨<+⎪⎩25.如图,在平面直角坐标系xOy中,直线124:33l y x=-+与x轴交于点A,直线2:2l y x b=+与x轴交于点B,且与直线1l交于点(1,)C m-.(1)求m和b的值;(2)求ABC的面积;(3)若将直线2l向下平移(0)t t>个单位长度后,所得到的直线与直线1l的交点在第一象限,直接写出t的取值范围.26.某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.(2)哪种方案更省钱?并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】由数轴可得表示的解集为12x -<≤,把各个选项求出解集,即可解答.【详解】数轴表示的解集为12x -<≤.解不等式组1020x x ->⎧⎨+≤⎩,得:12x x >⎧⎨≤-⎩,解集为空集,故A 不符合题意. 解不等式组1020x x +>⎧⎨+≤⎩,得:12x x >-⎧⎨≤-⎩,解集为空集,故B 不符合题意. 解不等式组1020x x +>⎧⎨-≤⎩,得:12x x >-⎧⎨≤⎩,解集为12x -<≤,故C 符合题意. 解不等式组1020x x -≤⎧⎨+<⎩,得:12x x ≤⎧⎨<-⎩,解集为2x <-,故D 不符合题意. 故选C .【点睛】本题考查在数轴上表示不等式的解集以及解不等式组,解决本题的关键是求出不等式组的解集.2.A解析:A【分析】已知两边的长,第三边应该大于任意两边的差,而小于任意两边的和,列不等式进行求解后再进行判断即可.【详解】解:根据三角形的三边关系,得11-4<3+4m <11+4,解得1<m <3.故选:A .【点睛】此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.3.B解析:B【分析】不等式组整理后,利用有解的条件确定出m 的范围即可.【详解】不等式组整理得:33x x m<⎧⎨>⎩, 由不等式组有解,得到3m <3,解得:m <1.故选:B .【点睛】本题考查了解一元一次不等式组,熟练掌握不等式组的解法是解本题的关键.4.C解析:C【分析】设AB =x ,则BC =9-x ,根据三角形两边之和大于第三边,得到x 的取值范围,再利用分类讨论思想,根据勾股定理列方程,计算解答.【详解】解:∵在△ABC 中,AC =AM =3,设AB =x ,BC =9-x ,由三角形两边之和大于第三边得:3939x x x x +-⎧⎨+-⎩>>, 解得3<x <6,①AC 为斜边,则32=x 2+(9-x )2,即x 2-9x +36=0,方程无解,即AC 为斜边不成立,②若AB 为斜边,则x 2=(9-x )2+32,解得x =5,满足3<x <6,③若BC 为斜边,则(9-x )2=32+x 2,解得x =4,满足3<x <6,∴x =5或x =4;故选C .【点睛】本题考查三角形的三边关系,勾股定理等,分类讨论和方程思想是解答的关键.5.C解析:C【解析】解:5335x xx a-+⎧⎨⎩>①<②,由①得:x>4.∵不等式组无解,∴a≤4.故选C.点睛:本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).6.D解析:D【分析】利用不等式的基本性质逐一进行分析即可.【详解】A、a<b两边同时乘以a,应说明a>0才得a2<ab,故此选项错误;B、a<b两边同时乘以b,应说明b>0才得ab<b2,故此选项错误;C、a<b两边同时乘以相同的数,故此选项错误;D、a<b两边同时减2b,不等号的方向不变可得a−2b<−b,故此选项正确;故选D.【点睛】此题主要考查了不等式的基本性质,关键是要注意不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变.7.D解析:D【分析】根据不等式的性质,可得答案.【详解】A、不等式的两边都减1,不等号的方向不变,故A错误;B、当a<0时,不等式两边乘负数,不等号的方向改变,故B错误;C、当c<0时,ac<bc,故C错误;D、不等式两边乘(或除以)同一个正数,不等号的方向不变,故D正确;故选:D.【点睛】本题考查了不等式的基本性质.不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.8.D解析:D【分析】首先确定不等式组的解集,先利用含m 的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于m 的不等式,从而求出m 的范围.【详解】解不等式0721x m x -<⎧⎨-≤⎩①②,由①式得,x m <,由②式得3x ≥,即故m 的取值范围是67m <≤,故选D .【点睛】本题考查不等式组的整数解问题,利用数轴就能直观的理解题意,列出关于m 的不等式组,再借助数轴做出正确的取舍.9.C解析:C【分析】设用A 型货厢x 节,B 型货厢()50x -节,根据题意列不等式组求解,求出x 的范围,看有几种方案.【详解】解:设用A 型货厢x 节,B 型货厢()50x -节,根据题意列式:()()35255015301535501150x x x x ⎧+-≥⎪⎨+-≥⎪⎩,解得2830x ≤≤, 因为x 只能取整数,所以x 可以取28,29,30,对应的()50x -是22,21,20,有三种方案.故选:C .【点睛】本题考查一元一次不等式组的应用,解题的关键是根据题意列出不等式组求解,需要注意结果要符合实际情况.10.C解析:C【分析】根据函数图象可以直接判断本题的答案.【详解】解:结合图象,当3x >时,函数1y kx b =+在函数2y x a =+的下方,即不等式kx b x a ++<的解集是3x >;故选:C .【点睛】本题考查了一次函数与一元一次不等式:从函数图象的角度看,一元一次不等式的解集就是确定直线=+y kx b 在另一条直线(或者x 轴)上(或下)方部分所有点的横坐标的集合;这是数形结合的典型考查.11.C解析:C【分析】由基本不等式a >b ,根据不等式的性质,逐一判断.【详解】解:A 、∵a >b ,∴-a <-b ,故本选项不符合题意;B 、∵a >b ,∴当a 与b 同号时有11a b <,当a 与b 异号时,有11a b>, 故本选项不符合题意;C 、∵a >b ,∴a+b >2b ,故本选项符合题意;D 、∵a >b ,且a >0时,∴a 2>ab ,故本选项不符合题意;故选:C .【点睛】本题考查了不等式的性质.不等式的基本性质: (1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.12.B解析:B【分析】先根据不等式组求出解集,然后在数轴上准确的表示出来即可.【详解】111x x -<⎧⎨-⎩①② 由不等式①组得,x<2∴不等式组的解集为:21x x ⎧⎨≥-⎩<其解集表示在数轴上为,故选B .【点睛】 此题主要考查不等式组的解法及在数轴上表示不等式组的解集.不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.二、填空题13.【分析】根据不等式的性质两边同时除以c (c<0)即可得到【详解】根据不等式的性质:由得到的条件是:c<0故答案为:<【点睛】此题考查不等式的性质:不等式的性质1:不等式两边加减同一个数(或式子)不等解析:<【分析】根据不等式的性质,两边同时除以c (c<0)即可得到.【详解】根据不等式的性质:由ac bc >得到a b <的条件是:c<0,故答案为:<.【点睛】此题考查不等式的性质:不等式的性质1:不等式两边加减同一个数(或式子),不等号的方向不变;不等式的性质2:不等式两边乘(或除)同一个正数,不等号的方向不变;不等式的性质3:不等式的两边乘(或除以)同一个负数,不等号的方向改变.14.【分析】首先利用不等式的基本性质解不等式组再从不等式的解集中找出适合条件的整数解再确定字母的取值范围即可【详解】解:解①得:解②得:∴不等式组的解集为:∵不等式组只有4个整数解即不等式组只有4个整数 解析:423m -<≤- 【分析】首先利用不等式的基本性质解不等式组,再从不等式的解集中找出适合条件的整数解,再确定字母的取值范围即可.【详解】解:3222553x x x m +⎧+⎪⎪⎨+⎪<+⎪⎩①② 解①得:1x ≥-,解②得:3102m x +<, ∴不等式组的解集为:31012m x +-≤<, ∵不等式组只有4个整数解,即不等式组只有4个整数解为﹣1、0、1、2, 则有310232m +<≤, 解得:423m -<≤-, 故答案为:423m -<≤-【点睛】本题考查不等式组的解法及整数解的确定.解不等式要用到不等式的性质:(1)不等式的两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式的两边乘(或除以)同一个负数,不等号的方向改变.15.【分析】直接把两个方程相加得到然后结合即可求出a 的取值范围【详解】解:直接把两个方程相加得:∴∵∴∴故答案为:【点睛】本题考查了解二元一次方程组以及解一元一次不等式解题的关键是掌握运算法则正确得到 解析:4a.【分析】直接把两个方程相加,得到337x y a +=+,然后结合1x y +<,即可求出a 的取值范围.【详解】 解:23242x y a x y a +=-⎧⎨+=+⎩, 直接把两个方程相加,得:337x y a +=+,∴73a x y ++=, ∵1x y +<, ∴713a +<,∴4a .故答案为:4a.【点睛】 本题考查了解二元一次方程组,以及解一元一次不等式,解题的关键是掌握运算法则,正确得到73a x y ++=. 16.x≥1【分析】将点P 的坐标代入直线y =x+2解出m 的值即得出点P 的坐标数形结合将不等式x+2≥ax+c 的解集转化为直线y =x+2与直线y =ax+c 的交点以及直线y =x+2图像在直线y =ax+c 图像上解析:x≥1【分析】将点P 的坐标代入直线y =x +2,解出m 的值,即得出点P 的坐标,数形结合,将不等式x +2≥ax +c 的解集转化为直线y =x +2与直线y =ax +c 的交点以及直线y =x +2图像在直线y =ax +c 图像上方部分x 的范围即可.【详解】把P (m ,3)代入y =x +2得:m +2=3,解得:m =1,∴P (1,3),∵x ≥1时,x +2≥ax +c ,∴关于x 的不等式x +2≥ax +c 的不等式的解为x ≥1.故答案为:x ≥1.【点睛】本题主要考查一次函数与不等式的关系,将不等式的解集转化为一次函数的图像问题是解题关键.17.【分析】先解不等式组再求整数解的最大值【详解】解不等式①得解不等式②得故不等式组的解集是所以整数解是:-101最大是1故答案为【点睛】考核知识点:求不等式组的最大整数值解不等式组是关键解析:1x =【分析】先解不等式组,再求整数解的最大值.【详解】112251x x ⎧-≤⎪⎨⎪+>⎩①②解不等式①,得32x ≤ 解不等式②,得2x >-故不等式组的解集是3 22x-<≤所以整数解是:-1,0,1最大是1故答案为1x=【点睛】考核知识点:求不等式组的最大整数值.解不等式组是关键.18.19【分析】设答对x道题可以获奖则答错或不答(25-x)道题根据成绩=4×答对的题目数-2×答错或不答的题目数即可得出关于x的一元一次不等式解之取其中的最小整数值即可得出结论【详解】解:设答对x道题解析:19【分析】设答对x道题可以获奖,则答错或不答(25-x)道题,根据成绩=4×答对的题目数-2×答错或不答的题目数,即可得出关于x的一元一次不等式,解之取其中的最小整数值即可得出结论.【详解】解:设答对x道题可以获奖,则答错或不答(25-x)道题,依题意,得:4x-2(25-x)≥60,解得:x≥553,又x为整数,故x的最小为19,故答案为:19.【点睛】题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.19.【分析】根据函数的图象可知k<0且x=-6时y=0把(-60)代入y=kx+b得出k与b之间的关系式再利用一元一次不等式解法得出答案【详解】解:∵一次函数y=kx+b的图象过(-60)∴0=-6k+解析:4x<【分析】根据函数的图象可知,k<0且x=-6时,y=0,把(-6,0)代入y=kx+b,得出k与b之间的关系式,再利用一元一次不等式解法得出答案.【详解】解:∵一次函数y=kx+b的图象过(-6,0),∴0=-6k+b,∴b=6k,∴3kx-2b=3kx-12k>0,∵函数图象经过第二、三、四象限,∴k <0,∴x-4<0,解得:x <4.故答案为:x <4.【点睛】本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.20.a >-4【分析】先把两式相减求出y−x 的值再代入中得到关于a 的不等式进而求出a 的取值范围即可【详解】由②-①得:2y−2x =2−a ∵则∴2−a <6∴a >-4故答案是:a >-4【点睛】本题考查的是解二解析:a >-4【分析】先把两式相减求出y−x 的值,再代入 3y x -<中得到关于a 的不等式,进而求出a 的取值范围,即可.【详解】3133x y a x y +=+⎧⎨+=⎩①②, 由②-①得:2y−2x =2−a ,∵ 3y x -<,则2 26y x -<,∴2−a <6,∴a >-4,故答案是:a >-4.【点睛】本题考查的是解二元一次方程组及一元一次不等式,解答此题的关键是把a 当作常数表示出y−x 的值,再得到关于a 的不等式.三、解答题21.(1)能;(2)22.5︒;(3)2θ;3θ;4θ;(4)1822.5θ︒≤︒<【分析】(1)因为角的两条边为两条射线,没有长度限制,所以小棒可以无限摆下去; (2)根据直角三角形的性质、三角形外角的性质和等腰三角形的性质,即可推出; (3)根据三角形外角的性质、等腰三角形的性质即可推出12132A A A θθ=∠=,即可推出,同理即可推出2θ,3θ;(4)根据(3)的结论,和三角形外角的性质,即可推出不等式,解不等式即可.【详解】(1)∵角的两边为两条射线,没有长度限制,∴小棒可以无限摆下去;(2)∵112231AA A A A A ===,1223A A A A ⊥,∴12AA A 为等腰三角形,145a ∠=︒, ∴1122.52a θ=∠=︒; (3)∵1212334A A AA A A A A ===,,∴12132312A A A A A A θθ=∠=∠=,∴223123A A A θθθθθ=∠+=+=,∴324334A A A θθθθθ=∠+=+=;(4)∵根据三角形内角和定理和等腰三角形的性质,∴590490θθ≥︒⎧⎨︒⎩,< 解得,1822.5θ︒≤︒<.【点睛】本题考查了射线的性质、等腰三角形的性质、解一元一次不等式组,解题的关键在于找到等量关系,求相关角的度数.22.(1)100=-+y x ;(2)购买A 种奖品75件,B 种奖品25件,能使总费用最少为1275元【分析】(1)根据题意,由待定系数法,即可求出一次函数的解析式;(2)根据总费用=两种奖品的费用之和表示出w 与x 的关系式,并由条件建立不等式组求出x 的取值范围,由一次函数的性质就可以求出结论.【详解】解:设y kx b =+,则20806040k n k b +=⎧⎨+=⎩解得:1100k b =-⎧⎨=⎩ 100y x ∴=-+;()2解:由题意得()121510031500W x x x =+-+=-+()3150012903100x x x -+≤⎧∴⎨≤-+⎩解得:7075x ≤≤31500w x =-+,30k ∴=-<,w ∴随x 的增大而减小,75x ∴=时,1275w =最小,当75x =时,25y =;即应购买A 种奖品75件,B 种奖品25件,才能使总费用最少为1275元.【点睛】本题考查了一次函数的性质的运用,待定系数法求解析式,一元一次不等式组的运用,解答时求出一次函数的解析式是关键.23.(1)a 的最小值为20;(2)28a ≥.【分析】(1)根据只能售出所进商品的110%-,且销售额大于等于进价即可列出不等式,求解即可;(2)根据70%按照标价a 元/千克出售,20%水果按10元/千克出售,且销售额应该大于等于(120%)18+⨯列出不等式求解即可.【详解】解:(1)由题意得:(110%)18a -≥,解得20a ≥,即a 的最小值为20;(2)由题意得:70%20%10(120%)18a ⋅+⨯≥+⨯,解得28a ≥.【点睛】本题考查一元一次不等式的应用.熟记商品销售时所用的常用公式是解题关键.注意本题与销售了多少千克无关.24.16x -<<【分析】分别解两个不等式,取公共解集即可.【详解】解: 231123x x x x <+⎧⎪⎨<+⎪⎩①② 解不等式①,移项得:231x x -<,合并同类项得:1x -<,系数化为1得:1x >-,解不等式②得,去分母得:326x x <+,移项合并得:6x <,所以该不等式组的解集为:16x -<<【点睛】本题考查解不等式组.掌握取不等式解集的口诀“同大取大,同小取小,大小小大取中间,大大小小是无解”是解题关键.25.(1)m=2,b=4;(2)4;(3)83<t<8 【分析】(1)先把(1,)C m -代入124:33l y x =-+,求出m 的值,再把点C 的坐标代入2:2l y x b =+即可求出b 的值;(2)先求出点A 和点B 的坐标,然后根据三角形的面积公式求解即可;(3)设出平移后的解析式,然后分别把点D 和点A 的坐标代入即可解答.【详解】解:(1)把(1,)C m -代入124:33l y x =-+,得()241233m =-⨯-+=,把(1,2)C -代入2:2l y x b =+,得22b =-+,∴b=4;(2)当24033x -+=时,解得x=2,∴A(2,0);当240x +=时,解得x=-2,∴B(-2,0);∴AB=4,∴ABC 的面积=1142422y AB C ⋅=⨯⨯=;(3)设平移后的解析式为24y x t =+-,当x=0时,2440333y =-⨯+=,∴D(0,43),把D(0,43)代入24y x t =+-,得4043t =+-,∴t=83;把A(2,0)代入24y x t =+-,得044t =+-,∴t=8;∴t 的取值范围83<t<8.【点睛】本题考查了一次函数的交点,一次函数与坐标轴的交点,一次函数的平移,利用函数图象解不等式,以及三角形的面积公式等知识,熟练掌握各知识点是解答本题的关键. 26.(1)有3种购买方案:第一种是购买3台A 型污水处理设备,7台B 型污水处理设备;第二种是购买4台A 型污水处理设备,6台B 型污水处理设备;第三种是购买5台A 型污水处理设备,5台B 型污水处理设备;(2)购买3台A 型污水处理设备,7台B 型污水处理设备更省钱【分析】(1)设购买污水处理设备A 型号x 台,则购买B 型号(10﹣x )台,由不等量关系购买A 型号的费用+购买B 型号的费用≤136;A 型号每月处理的污水总量+B 型号每月处理的污水总量≥2150,列出不等式组,然后找出最合适的方案即可.(2)计算出每一方案的花费,通过比较即可得到答案.【详解】设购买污水处理设备A 型号x 台,则购买B 型号(10﹣x )台,根据题意,得1512(10)136250200(10)2150x x x x +-≤⎧⎨+-≥⎩, 解这个不等式组,得:1353x ≤≤.∵x 是整数,∴x=3或x=4或x=5.当x=3时,10﹣x=7;当x=4时,10﹣x=6;当x=5时,10-x=5.答:有3种购买方案:第一种是购买3台A型污水处理设备,7台B型污水处理设备;第二种是购买4台A型污水处理设备,6台B型污水处理设备;第三种是购买5台A型污水处理设备,5台B型污水处理设备;(2)当x=3时,购买资金为15×3+12×7=129(万元),当x=4时,购买资金为15×4+12×6=132(万元),当x=5时,购买资金为15×5+12×5=135(万元).因为135>132>129,所以应购污水处理设备A型号3台,B型号7台.答:购买3台A型污水处理设备,7台B型污水处理设备更省钱.【点睛】此题考查方案类不等式组的实际应用,有理数的混合运算,正确理解题意,根据题意列得不等式组是解题的关键.。
(必考题)初中数学八年级数学下册第二单元《一元一次不等式和一元一次不等式组》检测题(答案解析)(1)

一、选择题1.若点(4,12)--A a a 在第三象限,则a 的取值范围是( ).A.142a << B .12a > C .4a < D .4a > 2.关于函数3y x =-,下列说法正确的是( )A .在 y 轴上的截距是3B .它不经过第四象限C .当x≥3时,y≤0D .图象向下平移4个单位长度得到7y x =-的图象3.如果m n >,则下列各式不成立的是( )A .22m n +>+B .22m n ->-C .22m n >D .22m n -<- 4.如图,已知AB 是线段MN 上的两点,MN =12,MA =3,MB >3,以A 为中心顺时针旋转点M ,以点B 为中心顺时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,当△ABC 为直角三角形时AB 的长是( )A .3B .5C .4或5D .3或51 5.下列各式中正确的是( )A .若a b >,则11a b -<-B .若a b >,则22a b >C .若a b >,且0c ≠,则ac bc >D .若||||a b c c >,则a b > 6.若关于x 的不等式组0722x m x -<⎧⎨-≤⎩的整数解共有3个,则m 的取值范围是( ) A .5<m <6 B .5<m ≤6C .5≤m ≤6D .6<m ≤7 7.爆破员要爆破一座旧桥,根据爆破情况,安全距离是70米(人员要撤到70米及以外的地方).已知人员撤离速度是7米/秒,导火索燃烧速度是10.3厘米/秒,为了确保安全,这次爆破的导火索至少为( )A .100厘米B .101厘米C .102厘米D .103厘米8.已知不等式组1113x a x -<-⎧⎪-⎨≤⎪⎩的解集如图所示(原点没标出,数轴单位长度为1),则a 的值为( )A .﹣1B .0C .1D .29.不等式组111x x -<⎧⎨≥-⎩的解集在数轴上表示正确的是( ) A . B . C . D .10.如果不等式组5x x m <⎧⎨>⎩有解,那么m 的取值范围是( ) A .m >5 B .m≥5 C .m <5 D .m≤811.如图,在平面直角坐标系中,正比例函数2y x =的图像与直线y kx b =+交于()1,2--A .直线y kx b =+,还经过点()2,0-.则不等式20x kx b <+<的解集为( )A .2x <-B .20x -<<C .21x -<<-D .10x -<< 12.已知a 、b 为有理数,且a<0,b>0,a >b ,则( ).A .a<-b<b<-aB .-b<a<b<-aC .-a<b<-b<aD .-b<b<-a<a二、填空题13.若不等式00x b x a -<⎧⎨+>⎩的解集为23x <<,则a ,b 的值分别为_______________. 14.若关于x 、y 的二元一次方程组23224x y m x y +=-+⎧⎨+=⎩的解满足32x y +>-,则满足条件的m 的取值范围是____________.15.方程组24x y k x y +=⎧⎨-=⎩的解满足1x >,1y <,k 的取值范围是:__________. 16.已知:a 、b 、c 是三个非负数,并且满足326a b c ++=,231a b c +-=,设37m a b c =+-,设s 为m 的最大值.则s 的值为__________.17.某次知识竞赛共有20道题,每一题答对得8分,答错或不答都扣4分,小红的得分要超过80分,她至少要答对_______道.18.若不等式12x x -<的解都能使关于x 的一次不等式()11a x a -<+成立,则a 的取值范围是________.19.一次函数y =kx +b (k≠0)的图象如图所示,则一元一次不等式﹣kx +2k +b >0的解集为_____.20.如图,直线y =ax +b 和y =kx +2与x 铀分别交于点A (﹣2,0),点B (2.8,0).则020ax b kx +>⎧⎨+<⎩的解集为_____.三、解答题21.现对x ,y 定义一种新的运算T ,规定:(,)++=+ax by c T x y x y (其中a ,b ,c 为常数,且0abc ≠).例如:10(1,0)10⨯+⨯+==++a b c T a c . 已知(3,1)2,(2,3) 2.8,(1,1)3-===T T T .(1)求a ,b ,c 的值;(2)求关于m 的不等式组(4,54)3,(2,32)1T m m T m m -<⎧⎨->⎩的整数解. 22.已知用2辆A 型车和1辆B 型车装满货物一次可运货11吨;用3辆A 型车和2辆B 型车装满货物一次可运货19吨,某物流公司现有50吨货物,计划同时租用A 型车a 辆,B 型车b 辆,一次运转,且恰好每辆车都装满货物.根据以上信息,解答下列问题:(1)1辆A 型车和1辆B 型车都装满货物一次可分别运货多少吨?(2)请你帮该物流公司设计,有几种租车方案?(3)若A 型车每辆需租金100元/次,B 型车每辆需租金120元次,请选出最省钱的租车方案,并求出最少租车费.23.抗击新型冠状肺炎疫情期间,84消毒液和酒精都是重要的防护物资.某药房根据实际需要采购了一批84消毒液和酒精,共花费11500元,84消毒液和酒精的进价和售价如下: 84消毒液 酒精进价(元/瓶) 25 20售价(元/瓶) 4028 6100元,则84消毒液和酒精各销售了多少瓶?(2)随着疫情的发展,该药房打算再次采购一批84消毒液和酒精,第二次采购仍以原价购进84消毒液和酒精,购进84消毒液的数量不变,而购进酒精的数量是第一次采购数量的2倍,84消毒液按原价出售,而酒精打折让利出售.若该药房将84消毒液和酒精全部销售完,要使第二次的销售获利不少于4900元,则每瓶酒精最多打几折?24.已知不等式组54312133x x x x +>+⎧⎪⎨+≥⎪⎩. (1)解这个不等式组,并把它的解集在数轴上表示出来.(2)若a 是这个不等式组的最小整数解,求2(2)a -的值.25.如图,平面直角坐标系中,点O 为坐标原点,直线AB 分别与x 轴、y 轴交于点A (5,0)、B (0,5),动点P 的坐标为(a ,1a -).(1)求直线AB 的函数表达式;(2)连接AP ,若直线AP 将△AOB 的面积分成相等的两部分,求此时P 点的坐标. (3)若动点P 在△AOB 的内部(不包括边缘),求a 的取值范围;26.某商店销售10台A 型和20台B 型电脑的利润为4000元,销售20台A 型和10台B 型电脑的利润为3500元.(1)求每台A 型电脑和B 型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共100台,其中B 型电脑的进货量不超过A 型电脑的2倍,设购进A 型电脑x 台,这100台电脑的销售总利润为y 元;①求y 关于x 的函数关系式;②该商店购进A 型、B 型电脑各多少台,才能使销售总利润最大?(3)实际进货时,厂家对A 型电脑出厂价下调(0100)m m <<元,且限定商店最多购进A 型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】结合题意,根据点的坐标、象限的性质,列一元一次不等式组并求解,即可得到答案.【详解】∵点(4,12)--A a a 在第三象限∴40a -<且120a -<∴4a <且12a > ∴142a << 故选:A .【点睛】 本题考查了直角坐标系和一元一次不等式组的知识;解题的关键是熟练掌握坐标、象限、一元一次不等式组的性质,从而完成求解.2.D解析:D【分析】令x=0,得到的y 值就是在y 轴上的截距;根据k ,b 判定图像的分布;根基自变量的范围计算函数的范围;根据平移规律确定即可.【详解】令x=0,得y= -3,∴函数在y 轴上的截距为-3,∴选项A 错误;∵3y x =-,∴函数分布在第一,第三,第四象限,∴选项B 错误;∵x≥3,∴x-3≥0,∴y≥0,∴选项C 错误;∵3y x =-,∴图象向下平移4个单位长度得到7y x =-的图象,∴选项D 正确;故选D .【点睛】本题考查了一次函数的性质,图像分布,平移规律,截距的定义,熟练掌握性质,规律是解题的关键.3.B解析:B【分析】根据不等式的性质解答.【详解】A 、在不等式m >n 的两边同时加上2,不等式仍成立,即m+2>n+2,故本选项不符合题意.B 、在不等式m >n 的两边同时乘以-1然后再加上2,不等式号方向改变,即2-m <2-n ,故本选项符合题意.C 、在不等式m >n 的两边同时除以2,不等式仍成立,即22m n >,故本选项不符合题意. D 、在不等式m >n 的两边同时乘以-2,不等式号方向改变,即-2m <-2n ,故本选项不符合题意.故选:B .【点睛】本题主要考查了不等式的性质,在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.4.C解析:C【分析】设AB =x ,则BC =9-x ,根据三角形两边之和大于第三边,得到x 的取值范围,再利用分类讨论思想,根据勾股定理列方程,计算解答.【详解】解:∵在△ABC 中,AC =AM =3,设AB =x ,BC =9-x ,由三角形两边之和大于第三边得:3939x x x x+-⎧⎨+-⎩>>, 解得3<x <6,①AC 为斜边,则32=x 2+(9-x )2,即x 2-9x +36=0,方程无解,即AC 为斜边不成立,②若AB 为斜边,则x 2=(9-x )2+32,解得x =5,满足3<x <6,③若BC为斜边,则(9-x)2=32+x2,解得x=4,满足3<x<6,∴x=5或x=4;故选C.【点睛】本题考查三角形的三边关系,勾股定理等,分类讨论和方程思想是解答的关键.5.D解析:D【分析】根据不等式的性质,可得答案.【详解】A、不等式的两边都减1,不等号的方向不变,故A错误;B、当a<0时,不等式两边乘负数,不等号的方向改变,故B错误;C、当c<0时,ac<bc,故C错误;D、不等式两边乘(或除以)同一个正数,不等号的方向不变,故D正确;故选:D.【点睛】本题考查了不等式的基本性质.不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.6.B解析:B【分析】分别求出不等式组中不等式的解集,利用取解集的方法表示出不等式组的解集,根据解集中整数解有3个,即可得到m的范围.【详解】解不等式x﹣m<0,得:x<m,解不等式7﹣2x≤2,得:x≥52,因为不等式组有解,所以不等式组的解集为52≤x<m,因为不等式组的整数解有3个,所以不等式组的整数解为3、4、5,所以5<m≤6.故选:B.【点睛】此题考查了一元一次不等式组的整数解,表示出不等式组的解集,根据题意找出整数解是解本题的关键.7.D解析:D【分析】设这次爆破的导火索需要xcm 才能确保安全,安全距离是70米(人员要撤到70米以外),根据人员速度是7米/秒,导火索的燃烧速度是10.3厘米/秒,列不等式求解即可.【详解】设这次爆破的导火索为x 厘米才能确保安全.根据安全距离是70米(人员要撤到70米及以外的地方),可列不等式:77010.3x ⨯≥ 解得:103x ≥故选:D【点睛】本题考查一元一次不等式的应用,关键是理解导火索燃尽时人撤离的距离要大于等于70米. 8.D解析:D【分析】首先解不等式组,求得其解集,又由数轴知该不等式组有3个整数解即可得到关于a 的方程,解方程即可求得a 的值.【详解】解:∵1113x a x -<-⎧⎪-⎨≤⎪⎩, 解不等式1x a -<-得:1x a <-, 解不等式113x -≤得:2x ≥-, ∴不等式组的解集为:21x a -≤<-,由数轴知该不等式组有3个整数解,所以这3个整数解为-2、-1、0,则11a -=,解得:2a =,故选:D .【点睛】本题考查了一元一次不等式组的整数解,以及在数轴上表示不等式的解集,熟练掌握运算法则是解本题的关键.9.B解析:B【分析】先根据不等式组求出解集,然后在数轴上准确的表示出来即可.【详解】111x x -<⎧⎨-⎩①② 由不等式①组得,x<2∴不等式组的解集为:21x x ⎧⎨≥-⎩< 其解集表示在数轴上为, 故选B .【点睛】此题主要考查不等式组的解法及在数轴上表示不等式组的解集.不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.10.C解析:C【解析】∵不等式组有解, ∴m <5.故选C .【方法点睛】本题主要考查的是不等式的解集,依据口诀列出不等式是解题的关键. 11.C解析:C【分析】根据图象知正比例函数y=2x 和一次函数y=kx+b 的图象的交点,即可得出不等式2x <kx+b 的解集,根据一次函数y=kx+b 的图象与x 轴的交点坐标即可得出不等式kx+b <0的解集是x >-2,即可得出答案.【详解】由图象可知:正比例函数y=2x 和一次函数y=kx+b 的图象的交点是A (-1,-2), ∴不等式2x <kx+b 的解集是x <-1,∵一次函数y=kx+b 的图象与x 轴的交点坐标是B (-2,0),∴不等式kx+b <0的解集是x >-2,∴不等式2x <kx+b <0的解集是-2<x <-1,故选:C .【点睛】本题考查一次函数和一元一次不等式的应用,主要考查学生的观察图形的能力和理解能力.12.A解析:A【分析】根据绝对值和不等式的性质,经计算,即可得到答案.【详解】∵a<0,b>0∴0a ->,0b -< ∴a a =-,b b =,a a <-,b b >- ∵a b >∴a b ->∴a b <-∴a b b a <-<<-故选:A .【点睛】本题考查了绝对值和不等式的知识;解题的关键是熟练掌握不等式和绝对值的性质,从而完成求解.二、填空题13.【分析】由于不等式组有解则解不等式组得到-a <x <b 然后与2<x <3进行对比即可确定a 和b 的值【详解】解:∵不等式组的解集为2<x <3而解不等式组得-a <x <b ∴-a=2b=3即a=-2b=3故答案解析:2a =-、3b =【分析】由于不等式组00x b x a -<⎧⎨+>⎩有解,则解不等式组得到-a <x <b ,然后与2<x <3进行对比即可确定a 和b 的值.【详解】解:∵不等式组00x b x a -<⎧⎨+>⎩的解集为2<x <3, 而解不等式组00x b x a -<⎧⎨+>⎩得-a <x <b , ∴-a=2,b=3,即a=-2,b=3.故答案为:2a =-、3b =.【点睛】本题考查了不等式的解集,掌握不等式的性质是解题的关键.14.【分析】先将m 看做常数解方程组求出再代入可得关于m 的不等式解之可得答案【详解】①-②得:将代入②得:∵∴+∴故答案为:【点睛】本题主要考查了解二元一次方程组和解一元一次不等式熟练掌握运算法则是解本题 解析:72m <【分析】先将m 看做常数解方程组求出2x m =-、2y m =+,再代入32x y +>-可得关于m 的不等式,解之可得答案.【详解】 23224x y m x y +=-+⎧⎨+=⎩①② ①2⨯-②得:2x m =-,将2x m =-代入②得:2y m =+, ∵32x y +>-, ∴2m - +322m +>-, ∴72m <. 故答案为:72m <. 【点睛】本题主要考查了解二元一次方程组和解一元一次不等式,熟练掌握运算法则是解本题的关键.注意:不等式两边都乘以或除以同一个负数不等号方向要改变.15.【分析】先求出方程组的解再得出关于k 的不等式组求出不等式组的解集即可【详解】解:解方程组得:∵关于xy 的方程组的解满足∴解得:-1<k <3故答案为-1<k <3【点睛】本题考查了解二元一次方程组和解一解析:13k -<<【分析】先求出方程组的解,再得出关于k 的不等式组,求出不等式组的解集即可.【详解】解:解方程组得:22x k y k +⎧⎨-⎩==, ∵关于xy 的方程组24x y k x y +⎧⎨-⎩==的解满足1x >,1y <,∴2121k k +⎧⎨-⎩><, 解得:-1<k <3,故答案为-1<k <3.【点睛】本题考查了解二元一次方程组和解一元一次不等式组,能得出关于k 的不等式组是解此题的关键.16.【分析】根据题意先把看作已知数分别用表示出和让列式求出的取值范围再求得用表示的形式结合的取值范围即可求得的值【详解】解:3a+2b+c=62a+b-3c=1解得a=7c-4b=9-11c ;∵a≥0b 解析:611-【分析】根据题意先把c 看作已知数,分别用c 表示出a 和b ,让0a ≥,0b ≥列式求出c 的取值范围,再求得m 用c 表示的形式,结合c 的取值范围即可求得s 的值.【详解】解:3a+2b+c=6,2a+b-3c=1,解得a=7c-4,b=9-11c ;∵a≥0、b≥0,∴7c-4≥0,9-11c≥0, ∴49711c ≤≤. ∵m=3a+b-7c=3c-3,∴m 随c 的增大而增大, ∵911c ≤. ∴当c 取最大值911,m 有最大值, ∴m 的最大值为s=3×911-3=611-. 故答案为:611-. 【点睛】 本题考查解三元一次方程组以及解不等式组,把c 看作已知数,分别用c 表示a 和b 是解答本题的关键.17.14【分析】设她答案了x 道题根据得分超过80列不等式进行求解即可【详解】设她答案了x 道题则有8x-4(20-x)>80解得:x>因为x 是整数所以x≥14且x 为整数所以她至少要答对14道题故答案为:1解析:14【分析】设她答案了x 道题,根据得分超过80列不等式进行求解即可.【详解】设她答案了x 道题,则有8x-4(20-x)>80,解得:x>1133, 因为x 是整数, 所以x≥14且x 为整数,所以她至少要答对14道题,故答案为:14.【点睛】本题考查了一元一次不等式的应用,弄清题意,找准不等式关系列出不等式是解题的关键.18.【分析】求出不等式的解求出不等式的解集得出关于a 的不等式求出a 即可【详解】解:解不等式可得∵不等式的解都能使不等式成立∴∴解得故答案为:【点睛】本题考查解一元一次不等式不等式的性质等知识点能根据已知 解析:113a ≤< 【分析】 求出不等式12x x -<的解,求出不等式()11a x a -<+的解集,得出关于a 的不等式,求出a 即可.【详解】 解:解不等式12x x -<可得2x >-, ∵不等式12x x -<的解都能使不等式()11a x a -<+成立, ∴10a -<,11a x a +>-, ∴121a a +≤--, 解得113a ≤<, 故答案为:113a ≤<. 【点睛】本题考查解一元一次不等式,不等式的性质等知识点,能根据已知得到关于a 的不等式是解此题的关键..19.x <4【分析】根据函数图象可以得到一次函数y =kx +b (k≠0)的图象交x 轴于点(﹣20)y 随x 的增大而增大从而可以得到k 和b 的关系k >0然后即可得到不等式﹣kx +2k +b >0的解集【详解】解:由图解析:x <4【分析】根据函数图象可以得到一次函数y =kx +b (k≠0)的图象交x 轴于点(﹣2,0),y 随x 的增大而增大,从而可以得到k 和b 的关系,k >0,然后即可得到不等式﹣kx +2k +b >0的解集.【详解】解:由图象可得,一次函数y =kx +b (k≠0)的图象交x 轴于点(﹣2,0),y 随x 的增大而增大, ∴﹣2k +b =0,k >0,∴b =2k ,∴不等式﹣kx +2k +b >0可以化为:﹣kx +2k +2k >0,解得:x <4,故答案为:x <4.【点睛】本题考查一次函数与一元一次不等式、一次函数的图象,解答本题的关键是明确题意,利用数形结合的思想解答解答.20.x >28【分析】根据题意和函数图象分别得到不等式和不等式的解集再取公共部分即可求解【详解】解:由图象得直线y =ax+b 中y 随x 的增大而增大与x 铀交于点A (﹣20)∴不等式解集为x >-2由图象得直线y解析:x >2.8【分析】根据题意和函数图象分别得到不等式0ax b +>和不等式20kx +<的解集,再取公共部分即可求解.【详解】解:由图象得直线y =ax +b 中y 随x 的增大而增大,与x 铀交于点A (﹣2,0), ∴不等式0ax b +>解集为x >-2,由图象得直线y =kx +2中y 随x 的增大而减小,与x 铀交于点B (2.8,0),∴不等式20kx +<解集为x >2.8,∴020ax b kx +>⎧⎨+<⎩的解集为x >2.8. 故答案为:x >2.8【点睛】本题考查了一次函数和一元一次不等式的关系,明确题意,利用数形结合的思想分别求出两个不等式的解集是解题关键.三、解答题21.(1)231abc=⎧⎪=⎨⎪=⎩;(2)关于m的不等式组(4,54)3(2,32)3T m mT m m-<⎧⎨->⎩的整数解有1,2,3.【分析】(1)由题意易得3231232.82311311a b ca b ca b c⨯-+⎧=⎪-⎪⨯+⨯+⎪=⎨+⎪⨯+⨯+⎪=⎪+⎩,然后求解即可;(2)由题意,得243(54)135223(32)113m mm m⨯+-+⎧<⎪⎪⎨⨯+-+⎪>⎪⎩,则有大于14且小于72的整数有1,2,3,然后问题可求解.【详解】解:(1)由题意,得3231232.82311311a b ca b ca b c⨯-+⎧=⎪-⎪⨯+⨯+⎪=⎨+⎪⨯+⨯+⎪=⎪+⎩,整理,得34 23146a b ca b ca b c-+=⎧⎪++=⎨⎪++=⎩,解得231abc=⎧⎪=⎨⎪=⎩;(2)由题意,得243(54)135223(32)113m mm m⨯+-+⎧<⎪⎪⎨⨯+-+⎪>⎪⎩,解得17 42 <<m,∵大于14且小于72的整数有1,2,3,∴关于m 的不等式组()()4,5432,323T m m T m m ⎧-<⎪⎨->⎪⎩的整数解有1,2,3. 【点睛】 本题主要考查一元一次不等式的应用,熟练掌握一元一次不等式的应用是解题的关键. 22.(1)1辆A 型车和1辆B 型车一次分别可以运货3吨,5吨;(2)4种;(3)当租用A 型车0辆,B 型车10辆时,租车费最少为1200元.【分析】(1)设1辆A 型车和1辆B 型车一次分别可以运货x 吨,y 吨,根据题意列出方程组,求出方程组的解得到x 与y 的值,即可确定出所求;(2)根据某物流公司现有50吨货物,计划同时租用A 型车a 辆,B 型车b 辆,列出方程,确定出a 的范围,根据a 为整数,确定出a 的值即可确定出具体租车方案. (3)根据几个租车方案得出租车费即可.【详解】解:(1)设1辆A 型车和1辆B 型车一次分别可以运货x 吨,y 吨,根据题意得:2113219x y x y +=⎧⎨+=⎩, 解得:35x y =⎧⎨=⎩, 则1辆A 型车和1辆B 型车一次分别可以运货3吨,5吨; (2)某物流公司现有50吨货物,计划同时租用A 型车a 辆,B 型车b 辆, 3550a b ∴+=, 则有050305a a b ⎧⎪-⎨=⎪⎩, 解得:20163a , a 为整数,0a ∴=,1,2,⋯,10,11,12,13,14,15,16. 50331055a b a -==-为整数, 0a ∴=,5,10,15,0a ∴=,10b =,5a =,7b =;10a =,4b =;15a =,1b =,∴满足条件的租车方案一共有4种,0a =,10b =,5a =,7b =;10a =,4b =;15a =,1b =;(3)A 型车每辆需租金100元/次,B 型车每辆需租金120元/次,当0a =,10b =,租车费用为:1000101201200W =⨯+⨯=元; 当5a =,7b =,租车费用为:100571201340W =⨯+⨯=元;当10a =,4b =,租车费用为:1001041201480W =⨯+⨯=元;当15a =,1b =,租车费用为:1001511201620W =⨯+⨯=元,∴当租用A 型车0辆,B 型车10辆时,租车费最少.【点睛】此题考查了一次不等式组的应用,二元一次方程的应用,以及二元一次方程组的应用,弄清题意是解本题的关键.23.(1)销售84消毒液300瓶,酒精200瓶;(2)每瓶酒精最多打7.5折.【分析】(1)设84消毒液和酒精各销售了x ,y 瓶,根据“销售完这批84消毒液和酒精后共获利6100元”列出二元一次方程组,即可求解;(2)设酒精打m 折,根据第二次的销售获利不少于4900元,列出不等式,即可得到答案.【详解】解:(1)设84消毒液和酒精各销售了x ,y 瓶,根据题意得:252011500(4025)(2820)6100x y x y +=⎧⎨-+-=⎩,解得:300200x y =⎧⎨=⎩, 答:销售84消毒液300瓶,酒精200瓶;(2)设酒精打m 折, 由题意得:3004020022830025200220490010m ⨯+⨯⨯⨯-⨯-⨯⨯≥, 解得:m≥7.5,答:每瓶酒精最多打7.5折.【点睛】本题主要考查二元一次方程组及一元一次不等式的实际应用,根据数量关系,列出方程组和不等式,是解题的关键.24.(1)312-<≤x ,见解析;(2)3 【分析】(1)解不等式组,表示即可;(2)根据(1)求出最小整数,代入计算即可;【详解】 (1)54312133x x x x +>+⎧⎪⎨+≥⎪⎩, 由5431+>+x x 得32x >-, 由2133+≥x x ,解得1x ≤, ∴不等式组的解集为312-<≤x ;(2)由(1)可知1a =-, ∴2(2)23a a -=-=;【点睛】本题主要考查了一元一次不等式组的求解,结合代数式求值是解题的关键.25.(1)5y x =-+;(2)74,33P ⎛⎫⎪⎝⎭ ;(3)1 3.a << 【分析】(1)设AB 的解析式为:,y kx b =+ 把()()5,0,0,5A B 代入解析式,利用待定系数法列方程组,解方程组即可得到答案;(2)如图,取OB 的中点,M 则50,,2M ⎛⎫ ⎪⎝⎭由直线AP 将△AOB 的面积分成相等的两部分,则AP 一定经过OB 的中点,M 所以先求解AM 的解析式,再把P 的坐标代入解析式,解方程即可得到答案;(3)先说明(),1P a a - 在函数1y x =-的图像上,由动点P 在△AOB 的内部(不包括边缘),可得P 在第一象限,且在函数5y x =-+的图像的下方,再列不等式组01015a a a a >⎧⎪->⎨⎪-<-+⎩,再解不等式组可得答案. 【详解】(1)解:设AB 的解析式为:,y kx b =+把()()5,0,0,5A B 代入解析式:50,5k b b +=⎧⎨=⎩ 解得:1,5k b =-⎧⎨=⎩ 所以AB 的解析式为: 5.y x =-+(2)如图,取OB 的中点,M50,,2M ⎛⎫∴ ⎪⎝⎭直线AP 将△AOB 的面积分成相等的两部分,AP ∴一定经过OB 的中点,M设直线AM 为:,y mx n =+50,52m n n +=⎧⎪∴⎨=⎪⎩ 解得:12,52m n ⎧=-⎪⎪⎨⎪=⎪⎩ 所以直线AM 为15,22y x =-+ (),1P a a -在直线AM 上,151,22a a ∴-=-+ 解得:7,3a = 7411,33a ∴-=-= 74,.33P ⎛⎫∴ ⎪⎝⎭(3)(),1,P a a -1x a y a =⎧∴⎨=-⎩①② 把①代入②得:1,y x =-P ∴在函数1y x =-的图像上,动点P 在△AOB 的内部(不包括边缘),P ∴在第一象限,且在函数5y x =-+的图像的下方,01015a a a a >⎧⎪∴->⎨⎪-<-+⎩由1a ->0可得:a >1,由1a -<5a -+可得:a <3,所以a 的取值范围为:1 3.a <<【点睛】本题考查的是利用待定系数法求解一次函数的解析式,三角形的中线的性质,一次函数与不等式组的联系,掌握以上知识是解题的关键.26.(1)每台A 型电脑的销售利润为100元,每台B 型电脑的销售利润为150元;(2)①150********y x x ⎛⎫=-+≥ ⎪⎝⎭,,②商店购进A 型电脑34台,B 型电脑66台,才能使销售总利润最大;(3)①当050m <<时,商店购进34台A 型电脑和66台B 型电脑才能获得最大利润;②当50m =时,商店购进A 型电脑数量满足133703x ≤≤的整数时,均获得最大利润;③当50 <m < 100时,商店购进70台A 型电脑和30台B 型电脑才能获得最大利润.【分析】(1)设每台A 型加湿器和B 型加湿器的销售利润分别为a 元,b 元,然后根据题意列出二元一次方程组解答即可;(2)①据题意得即可确定y 关于x 的函数关系式,利用A 型利润与B 型利润即可求出总利润y 与x 的关系,并确定x 的范围即可;②根据一次函数的增减性,解答即可;(3)根据题意列出函数数关系式,分以下三种情况①0<m<50,②m=50,③ 50 <m < 100时,m-50 >0结合函数的性质,进行求解即可.【详解】(1)设每台A 型电脑的销售利润为a 元,每台B 型电脑的销售利润为b 元,根据题意得:1020400020103500a b a b +=⎧⎨+=⎩解得=100150a b ⎧⎨=⎩答:每台A 型电脑的销售利润为100元,每台B 型电脑的销售利润为150元; (2)①设购进A 型电脑x 台,每台A 型电脑的销售利润为100元,A 型电脑销售利润为100x 元,每台B 型电脑的销售利润为150元,B 型电脑销售利润为()150100x -元()100150100y x x =+-,即这100台电脑的销售总利润为:5015000y x =-+;1002x x -≤,解得1333x ≥. 150********y x x ⎛⎫=-+≥ ⎪⎝⎭, ②5015000y x =-+中,k=500-<,y ∴随x 的增大而减小. x 为正整数,1333x ≥ ∴当34x =时,y 取得最大值,此时10066x -=.答:商店购进A 型电脑34台,B 型电脑66台,才能使销售总利润最大;(3)根据题意得()()100150100y m x x =++-,即()5015000y m x =-+,其中133703x ≤≤.①当050m <<时,k=500m -<,y ∴随x 的增大而减小,∴当34x =时,y 取得最大值, 即商店购进34台A 型电脑和66台B 型电脑才能获得最大利润;②当50m =时,k=500m -=,15000y ∴=,即商店购进A 型电脑数量满足133703x ≤≤的整数时,均获得最大利润; ③当50 <m < 100时,k=500m ->,y ∴随x 的增大而增大.∴当70x =时,y 取得最大值.即商店购进70台A 型电脑和30台B 型电脑才能获得最大利润.【点睛】 本题主要考查了一次函数的应用,二元一次方程组及一元一次不等式的应用,掌握一次函数的增减性是解答本题的关键.。
(好题)初中数学八年级数学下册第二单元《一元一次不等式和一元一次不等式组》测试卷(包含答案解析)

一、选择题1.若点(4,12)--A a a 在第三象限,则a 的取值范围是( ).A .142a << B .12a >C .4a <D .4a >2.三角形的两边长分别是4和11,第三边长为34m +,则m 的取值范围在数轴上表示正确的是( ) A . B . C .D .3.不等式组10840x x -⎧⎨-≤⎩>的解集在数轴上表示为 ( ).A .B .C .D .4.在平面直角坐标系中,若点()3,1B m m -+在第二象限,则m 的取值范围为( ) A .13m -<<B .3m >C .1m <-D .1m >-5.不等式组()()303129x x x -≥⎧⎨->+⎩的解集为( )A .3x <-B .3x >-C .3x ≥D .3x ≤6.若不等式组010a x x ->⎧⎨+>⎩无解,则a 的取值范围是( )A .a≤-1B .a≥-1C .a<-1D .a>-17.下列不等式说法中,不正确的是( ) A .若,2x y y >>,则2x > B .若x y >,则22x y -<- C .若x y >,则22x y >D .若x y >,则2222x y --<--8.不等式-3<a≤1的解集在数轴上表示正确的是( ) A . B . C .D .9.如图是一次函数1y kx b =+与2y x a =+的图象,则不等式kx b x a ++<的解集是( )A .0x >B .0x <C .3x >D .3x <10.已知x=2是不等式()()5320x ax a --+≤的解,且x=1不是这个不等式的解,则实数a 的取值范围是( ) A .a >1B .a≤2C .1<a≤2D .1≤a≤211.下列不等式变形中,一定正确的是( )A .若ac>bc ,则a>bB .若a>b ,则ac>bcC .若ac²>bc²,则a>bD .若a>0,b>0,且11a b>,则a>b 12.已知点()1,23P a a +-在第四象限,则a 的取值范围是( ) A .1a <-B .312a -<<C .312a -<< D .32a >二、填空题13.“鼠去牛来辞旧岁,龙飞凤舞庆明时.”在新年的钟声敲响之际,南开中学初2022级举行了元旦晚会.在晚会前,一、二、三班都组织购买了 A 、B 、C 三类糖果.已知一班分别购买 A 、B 、C 三类糖果各3千克、2千克、5千克,二班分别购买A 、B 、C 三类糖果各 2千克、1千克、4千克,且一班和二班购买糖果的总金额比值为3∶2.若三类糖果单价和为108元,且各单价是低于50元/千克的整数,A 与C 单价差大于25元.则三班分别购买A 、B 、C 三类糖果各2千克、3千克、4千克的总金额为______元. 14.如果三角形两条边分别为3和5,则周长L 的取值范围是________ 15.过点()5,2-的一条直线与x 轴、y 轴分别相交于点A ,B ,且与直线312y x =-+平行,则在线段AB 上,横、纵坐标都是整数的点坐标是______. 16.不等式2x+9>3(x+4)的最大整数解是_____. 17.如图,函数2y x =和y ax b =+的图象相交于点(),3Am ,则关于x 的不等式2x ax b >+的解集为________.18.已知关于x 的不等式0123x a x ->⎧⎨->-⎩只有五个整数解,则实数a 的取值范围是__________.19.一张试卷共20道题,做对一题得5分,做错或不做一题扣1分,小明做了全部试题,若要成绩优秀(注:70分及以上成绩为优秀),那么小明至少要做_________道题.20.若方程组3133x y a x y +=+⎧⎨+=⎩的解x 、y 满足 3y x -<,则a 的取值范围为_________.三、解答题21.在同一平面直角坐标系内画出一次函数14y x =-+和225y x =-的图象,根据图象回答下列问题: (1)求出方程组425y x y x =-+⎧⎨=-⎩的解;(2)当x 取何值时,12y y >?当x 取何值时,10y >且20y <?22.在初中阶段的函数学习中,我们知道由含有未知数x 和y 的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数;同时知道任何一个以x 为未知数的一元一次不等式都可以变形为0ax b +≥或0(0)ax b a +≤≠的形式,因此我们可以用画一次函数图象的方法得到方程组的解或不等式的解集.(1)在给出的平面直角坐标系中,直接画出函数2y x =-+的图象;(2)如图,直线(0,0)y kx b k b =+>>与2y x =-+相交于点(1,)m -,根据图象直接写出关于x 的方程2kx b x +=-+的解;(3)根据图象直接写出不等式2kx b x +≤-+的解集.23.解不等式组:533(1)21352x x x x +>-⎧⎪⎨-≥-⎪⎩①②,并写出它的所有非负整数解.24.某校运动会需购买,A B 两种奖品,A 单价是12元/件,B 单价是15元/件,已知购买A 种奖品x (件)与购买B 奖品y 件)之间的函数关系如图所示.(1)求y 与x 之间的函数关系式;(2)学校计划购买,A B 两种奖品的总费用不超过1290元,且A 种奖品的数量不大于B 种奖品数量的3倍.设购买,A B 两种奖品的总费用为w 元,请你设计购买,A B 两种奖品的方案,怎样购买才能使费用最少,w 的最小值是多少?25.某厂贷款8万元购进一台机器生产商品.已知商品的成本每个8元,成品后售价是每个15元,应付税款和损耗总费用是销售额的20%.若每个月能生产销售1000个该商品,问至少几个月后能赚回这台机器的贷款?26.某商家欲购进甲、乙两种抗疫用品共180件,其进价和售价如表:、乙两种用品应分别购进多少件?(请用二元一次方程组求解)(2)若商家计划投入资金少于5040元,且销售完这批抗疫用品后获利不少于1314元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】结合题意,根据点的坐标、象限的性质,列一元一次不等式组并求解,即可得到答案. 【详解】∵点(4,12)--A a a 在第三象限 ∴40a -<且120a -< ∴4a <且12a >∴142a << 故选:A . 【点睛】本题考查了直角坐标系和一元一次不等式组的知识;解题的关键是熟练掌握坐标、象限、一元一次不等式组的性质,从而完成求解.2.A解析:A 【分析】已知两边的长,第三边应该大于任意两边的差,而小于任意两边的和,列不等式进行求解后再进行判断即可. 【详解】解:根据三角形的三边关系,得 11-4<3+4m <11+4, 解得1<m <3.故选:A . 【点睛】此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.3.A解析:A 【分析】解不等式组,看解集表示是否正确即可. 【详解】解:10840x x -⎧⎨-≤⎩>①②解不等式①得,1x >, 解不等式②得,2x ≥, 不等式组的解集为:2x ≥. 故选:A . 【点睛】本题考查了一元一次不等式组的解法及在数轴上表示解集,解题关键是熟练的运用解不等式组的方法进行计算.4.A解析:A 【分析】点在第二象限的条件是:横坐标是负数,纵坐标是正数,可得m-3<0,m+1>0,求不等式组的解即可. 【详解】解:∵点()3,1B m m -+在第二象限, ∴可得到3010m m -<⎧⎨+>⎩,解得m 的取值范围为13m -<<. 故答案为:13m -<<. 【点睛】此题主要考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).5.A解析:A 【分析】先解每一个不等式,再求不等式组的解集. 【详解】解:()()303129x x x -≥⎧⎪⎨->+⎪⎩①②,解不等式①得,x ≤3, 解不等式②得,x <-3, ∴不等式组的解集为x <-3, 故选A 【点睛】本题考查了解一元一次不等式组,先解每一个不等式,再求它们解集的公共部分即可求出不等式组的解集.6.A解析:A 【分析】要求出a 的值,首先分别求出这两个不等式解,最后根据不等式组无解的情况来确定a 的值. 【详解】解:010a x x ->⎧⎨+>⎩①② 解不等式①,得 x<a ,解不等式②,得 x>-1∵原不等式组无解, ∴a≤-1 故答案为:A . 【点睛】本题考查了解一元一次不等式组,关键是知道不等式组的解集是由这两个不等式的解集的公共部分构成的,题目无解说明这两个不等式的解集没有公共部分这是关键.7.B解析:B 【分析】根据不等式的基本性质,逐项判断即可. 【详解】 解:∵,2x y y >> ∴2x >,∴选项A 不符合题意; ∵x y >, ∴22x y ->-, ∴选项B 符合题意;∵x y >, ∴22x y >, ∴选项C 不符合题意; ∵x y >, ∴22x y -<-, ∴2222x y --<-- ∴选项D 不符合题意. 故选:B . 【点睛】此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.8.A解析:A 【分析】根据在数轴上表示不等式解集的方法求解即可. 【详解】 解:∵-3<a≤1,∴1处是实心原点,且折线向左. 故选:A . 【点睛】本题考查了在数轴上表示不等式的解集,掌握“小于向左,大于向右”是解题的关键.9.C解析:C 【分析】根据函数图象可以直接判断本题的答案. 【详解】解:结合图象,当3x >时,函数1y kx b =+在函数2y x a =+的下方, 即不等式kx b x a ++<的解集是3x >; 故选:C . 【点睛】本题考查了一次函数与一元一次不等式:从函数图象的角度看,一元一次不等式的解集就是确定直线=+y kx b 在另一条直线(或者x 轴)上(或下)方部分所有点的横坐标的集合;这是数形结合的典型考查.10.C解析:C∵x=2是不等式(x−5)(ax−3a+2)⩽0的解,∴(2−5)(2a−3a+2)⩽0,解得:a ⩽2, ∵x=1不是这个不等式的解,∴(1−5)(a−3a+2)>0,解得:a>1, ∴1<a ⩽2, 故选C.11.C解析:C 【分析】根据不等式的基本性质分别进行判定即可得出答案. 【详解】A .当c <0,不等号的方向改变.故此选项错误;B .当c=0时,符号为等号,故此选项错误;C .不等式两边乘(或除以)同一个正数,不等号的方向不变,正确;D .不等式的两边都乘以或除以同一个正数,不等号的方向不变,错误. 故选:C . 【点睛】本题考查了不等式的性质,注意不等式的两边都乘以或除以同一个负数,不等号的方向改变.12.B解析:B 【分析】根据第四象限内点的横坐标是正数,纵坐标是负数列不等式组求解即可. 【详解】∵点P (1a +,23a -)在第四象限, ∴10230a a +>⎧⎨-<⎩,∴a 的取值范围是312a -<<. 故选:B . 【点睛】本题考查了各象限内点的坐标的符号特征以及解不等式组,记住各象限内点的坐标的符号是解决的关键.二、填空题13.296【分析】可设A 单价x 元B 单价y 元由三类糖果单价和为108元得C 单价;再由一班和二班购买糖果的总金额比值为3∶2可得xy 的关系式再由A 与C 单价差大于25元可得一元一次不等式根据各单价是低于50元解析:296可设A 单价x 元,B 单价y 元,由三类糖果单价和为108元得C 单价;再由一班和二班购买糖果的总金额比值为3∶2,可得x 、y 的关系式,再由A 与C 单价差大于25元,可得一元一次不等式,根据各单价是低于50元/千克的整数求出符合题意的解即可 【详解】解:设A 单价x 元,B 单价y 元三类糖果单价和为108元得C 单价为(108-x-y )元 又一班和二班购买糖果的总金额比值为3∶2可得:325(108)324(108)2x y x y x y x y ++--=++--整理可得:2x+3y=216①又A 与C 单价差大于25元,即x-(108-x-y )>25 整理可得:2x+y>133,将①中的2x 代入可得:y<41.5 又A 、B 、C 三类糖果单价是低于50元/千克的整数,故: 若y=41,代入①得x=46.5,不符合题意 若y=40,代入①得x=48,符合题意 若y=39,代入①得x=49.5,不符合题意 若y=38,代入①得x=51,不符合题意y 越小,x 越大,故后面x 的结果均大于50,不符合题意 故x=48,y=40,108-x-y=20 由上可知:A 类糖果的单价是48元B 类糖果的单价是40元C 类糖果的单价是20元故分别购买A 、B 、C 三类糖果各2千克、3千克、4千克的总金额为: 48×2+40×3+20×4=296(元) 故答案为:296 【点睛】本题考查一元一次不等式的解法,利用条件建立一元一次不等式并结合题意准确得到A 、B 、C 三类糖果的单价是解本题的关键14.10<L<16【分析】根据三角形的三边关系确定第三边的取值范围再根据不等式的性质求出答案【详解】设第三边长为x ∵有两条边分别为3和5∴5-3<x<5+3解得2<x<8∴2+3+5<x+3+5<8+3解析:10<L<16 【分析】根据三角形的三边关系确定第三边的取值范围,再根据不等式的性质求出答案. 【详解】 设第三边长为x , ∵有两条边分别为3和5,∴5-3<x<5+3,解得2<x<8,∴2+3+5<x+3+5<8+3+5,∵周长L=x+3+5,∴10<L<16,故答案为: 10<L<16.【点睛】此题考查三角形三边关系,不等式的性质,熟记三角形的三边关系确定出第三条边长是解题的关键.15.(14)(31)【分析】依据与直线平行设出直线AB的解析式;代入点(5-2)即可求得b然后求出与x轴的交点横坐标列举符合条件的x的取值依次代入即可【详解】解:∵过点(5-2)的一条直线与直线平行设直解析:(1,4),(3,1).【分析】依据与直线312y x=-+平行设出直线AB的解析式32y x b=-+;代入点(5,-2)即可求得b,然后求出与x轴的交点横坐标,列举符合条件的x的取值,依次代入即可.【详解】解:∵过点(5,-2)的一条直线与直线312y x=-+平行,设直线AB为32y x b=-+;把(5,-2)代入32y x b=-+;得-2=152b-+解得:b=11 2∴直线AB的解析式为31122 y x=-+令y=0,得:311 022x=-+解得:x=11 3∴0<x<113的整数为:1、2、3;把x等于1、2、3分别代入解析式得4、52、1;∴在线段AB上,横、纵坐标都是整数的点的坐标是(1,4),(3,1).故答案为:(1,4),(3,1).【点睛】本题考查了待定系数法求解析式以及直线上点的情况,列举出符合条件的x的值是本题的关键.16.-4【分析】先求出不等式的解集在其解集范围内找出符合条件的x的最大整数解即可【详解】解:去括号移项得2x﹣3x>12﹣9合并同类项得﹣x>3系数化为1得x<﹣3∴x的最大整数解是﹣4故答案为:﹣4【解析:-4【分析】先求出不等式的解集,在其解集范围内找出符合条件的x的最大整数解即可.【详解】解:去括号、移项得,2x﹣3x>12﹣9,合并同类项得,﹣x>3,系数化为1得,x<﹣3,∴x的最大整数解是﹣4.故答案为:﹣4.【点睛】考核知识点:解不等式.运用不等式基本性质是关键.17.【分析】先将点A的坐标代入正比例函数中求得m的值再结合图象得出不等式的解集即可【详解】∵函数y=2x经过点A(m3)∴2m=3解得:m=由图象得当时的图象位于图象上方∴关于x的不等式2x>ax+b的解析:32 x>【分析】先将点A的坐标代入正比例函数中求得m的值,再结合图象得出不等式的解集即可.【详解】∵函数y=2x经过点A(m,3),∴2m=3,解得:m=32,由图象得,当32x>时,2y x=的图象位于y ax b=+图象上方,∴关于x的不等式2x>ax+b的解集为32x>.故答案为:32 x>.【点睛】本题考查了一次函数与一次不等式的关系,属于简单题,熟悉一次函数的图象和性质是解题关键.18.【分析】此题需要首先解不等式根据解的情况确定a的取值范围特别是要注意不等号中等号的取舍【详解】解不等式x-a>0得:x>a解不等式1-2x>-3得:x<2∴不等式组的解集是a<x<2∵只有五个整数解解析:43a -≤<-【分析】此题需要首先解不等式,根据解的情况确定a 的取值范围.特别是要注意不等号中等号的取舍.【详解】解不等式x -a >0,得:x >a ,解不等式1-2x >-3,得:x <2,∴不等式组的解集是a < x <2,∵只有五个整数解,∴整数解是1,0,-1,-2,-3∴-4≤a <-3,故答案为:-4≤a <-3.【点睛】此题考查了一元一次不等式组的解法.解题中要注意分析不等式组的解集的确定,含参数问题需要特别注意取等号时的情况.19.15【分析】设小明做对x 道题则做错或不做(20−x )道题根据总分=5×做对题目数−1×做错或不做题目数结合总分不少于70分即可得出关于x 的一元一次不等式解之即可得出x 的取值范围再取其中的最小整数值即解析:15【分析】设小明做对x 道题,则做错或不做(20−x )道题,根据总分=5×做对题目数−1×做错或不做题目数,结合总分不少于70分,即可得出关于x 的一元一次不等式,解之即可得出x 的取值范围,再取其中的最小整数值即可得出结论.【详解】解:设小明做对x 道题,则做错或不做(20−x )道题,依题意,得:5x−(20−x )≥70,解得:x≥15,∴小明至少要做对15道题.故答案为:15.【点睛】本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.20.a >-4【分析】先把两式相减求出y−x 的值再代入中得到关于a 的不等式进而求出a 的取值范围即可【详解】由②-①得:2y−2x =2−a ∵则∴2−a <6∴a >-4故答案是:a >-4【点睛】本题考查的是解二解析:a >-4【分析】先把两式相减求出y−x 的值,再代入 3y x -<中得到关于a 的不等式,进而求出a 的取值范围,即可.【详解】3133x y a x y +=+⎧⎨+=⎩①②, 由②-①得:2y−2x =2−a ,∵ 3y x -<,则2 26y x -<,∴2−a <6,∴a >-4,故答案是:a >-4.【点睛】本题考查的是解二元一次方程组及一元一次不等式,解答此题的关键是把a 当作常数表示出y−x 的值,再得到关于a 的不等式.三、解答题21.(1)31x y =⎧⎨=⎩;(2)当3x <时,12y y >,当 2.5x <时,10y >且20y < 【分析】(1)根据题意画出一次函数y 1=-x+4和y 2=2x-5的图象,根据两图象的交点即可得出方程组425y x y x =-+⎧⎨=-⎩的解; (2)根据函数图象可直接得出结论.【详解】解:(1)如图所示:一次函数14y x =-+和225y x =-的图象相交于点(3,1)∴方程组425y x y x =-+⎧⎨=-⎩的解为31x y =⎧⎨=⎩; (2)由图可知,当3x <时,12y y >当 2.5x <时,10y >且20y <;本题考查的是一次函数与一元一次方程组,一次函数与一元一次不等式,能根据题意画出函数图象,利用数形结合求解是解答此题的关键.22.(1)见解析;(2)1x =-;(3)1x ≤-【分析】(1)求出2y x =-+ 与x 轴、y 轴的交点,连接两点的直线即为2y x =-+的图象; (2)y kx b =+与2y x =-+相交于(-1,m),即两函数交点的横坐标即为方程的解; (3)观察图象,求出x 的取值范围即可;【详解】(1)∵2y x =-+,∴ (0,2)和(2,0)两点在2y x =-+上;∴如图所示(图中下降趋势直线为画图答案)(2)∵y kx b =+与2y x =-+相交于(-1,m),∴2kx b x +=-+ 的解为:1x =-;(3)观察图象,当y kx b =+的图象在2y x =-+的下方时,∴2kx b x +≤-+,即:1x ≤-.【点睛】本题考查了一次函数的交点问题、一次函数的图象的性质以及根据两直线交点求不等式的解集,正确掌握图象的性质是解题的关键;23.不等式的解集为:934x -<≤,非负整数解有:0、1、2. 【分析】先解不等式①,再解不等式②,将两个不等式的解取交集,得到的公共解集就是不等式组的解集,然后在不等式解集的范围内找到非负整数解.解:由①得3x >-由②得94x ≤ 原不等式的解集为:934x -<≤非负整数解有:0、1、2.【点睛】这道题考察的是一元一次不等式组的解法.解题的关键确定不等式组的解集,记住顺口溜:大大取大,小小取小,大小小大中间找,小小大大解不了.24.(1)100=-+y x ;(2)购买A 种奖品75件,B 种奖品25件,能使总费用最少为1275元【分析】(1)根据题意,由待定系数法,即可求出一次函数的解析式;(2)根据总费用=两种奖品的费用之和表示出w 与x 的关系式,并由条件建立不等式组求出x 的取值范围,由一次函数的性质就可以求出结论.【详解】解:设y kx b =+,则20806040k n k b +=⎧⎨+=⎩解得:1100k b =-⎧⎨=⎩100y x ∴=-+;()2解:由题意得()121510031500W x x x =+-+=-+()3150012903100x x x -+≤⎧∴⎨≤-+⎩解得:7075x ≤≤31500w x =-+,30k ∴=-<,w ∴随x 的增大而减小,75x ∴=时,1275w =最小,当75x =时,25y =;即应购买A 种奖品75件,B 种奖品25件,才能使总费用最少为1275元.【点睛】本题考查了一次函数的性质的运用,待定系数法求解析式,一元一次不等式组的运用,解答时求出一次函数的解析式是关键.25.20设x 个月后能赚回这台机器的贷款,根据总利润=单个利润×每月销售数量×月份数结合总利润不低于贷款数,即可得出关于x 的一元一次不等式,解出不等式取其中最小值即可得出结论.【详解】解:设至少x 个月后能赚回这台机器的贷款则()1581520%100080000x --⨯⨯≥解得:20x ≥答:至少20个月后能赚回这台机器的贷款.【点睛】本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.26.(1)甲种商品购进100件,乙种商品购进80件;(2)方案一:甲种商品购进61件,乙种商品购进119件.方案二:甲种商品购进62件,乙种商品购进118件.方案三:甲种商品购进63件,乙种商品购进117件.获利最大的是方案一:甲种商品购进61件,乙种商品购进119件.【分析】(1)等量关系为:甲件数+乙件数=180;甲总利润+乙总利润=1240.(2)设出所需未知数,甲进价×甲数量+乙进价×乙数量<5040;甲总利润+乙总利润≥1314.【详解】解:(1)(1)设甲种商品应购进x 件,乙种商品应购进y 件.根据题意得:180681240x y x y +=⎧⎨+=⎩. 解得:10080x y =⎧⎨=⎩. 答:甲种商品购进100件,乙种商品购进80件.(2)设甲种商品购进a 件,则乙种商品购进(180)a -件.根据题意得1435(180)504068(180)1314a a a a +-<⎧⎨+-≥⎩解不等式组得6063a <. a 为非负整数,a ∴取61,62,63180a ∴-相应取119,118,117方案一:甲种商品购进61件,乙种商品购进119件,此时利润为:66181191318⨯+⨯=元;方案二:甲种商品购进62件,乙种商品购进118件,此时利润为:66281181316⨯+⨯=元;方案三:甲种商品购进63件,乙种商品购进117件,此时利润为:66281181314⨯+⨯=元;所以,有三种购货方案,其中获利最大的是方案一:甲种商品购进61件,乙种商品购进【点睛】本题考查了二元一次方程组的应用及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.。
(好题)初中数学八年级数学下册第二单元《一元一次不等式和一元一次不等式组》测试(有答案解析)
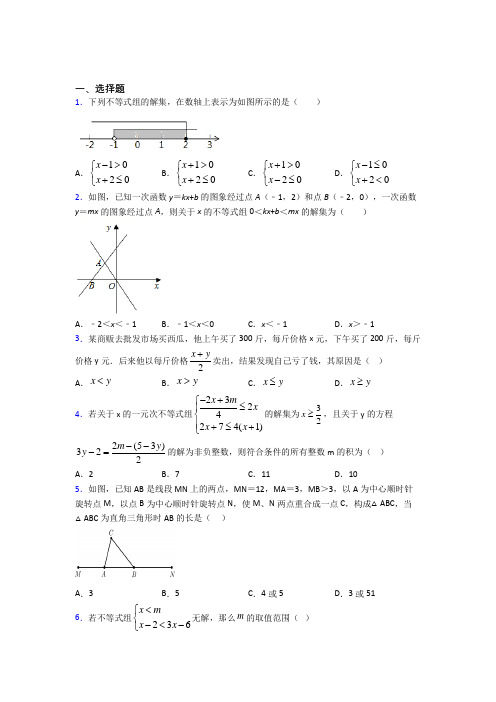
一、选择题1.下列不等式组的解集,在数轴上表示为如图所示的是( )A .1020x x ->⎧⎨+≤⎩B .1020x x +>⎧⎨+≤⎩C .1020x x +>⎧⎨-≤⎩D .1020x x -≤⎧⎨+<⎩2.如图,已知一次函数y =kx +b 的图象经过点A (﹣1,2)和点B (﹣2,0),一次函数y =mx 的图象经过点A ,则关于x 的不等式组0<kx +b <mx 的解集为( )A .﹣2<x <﹣1B .﹣1<x <0C .x <﹣1D .x >﹣1 3.某商贩去批发市场买西瓜,他上午买了300斤,每斤价格x 元,下午买了200斤,每斤价格y 元.后来他以每斤价格2xy +卖出,结果发现自己亏了钱,其原因是( ) A .x y < B .x y > C .x y ≤ D .x y ≥4.若关于x 的一元次不等式组2324274(1)x m x x x -+⎧≤⎪⎨⎪+≤+⎩的解集为32x ≥,且关于y 的方程2(53)322m y y ---=的解为非负整数,则符合条件的所有整数m 的积为( ) A .2 B .7 C .11 D .105.如图,已知AB 是线段MN 上的两点,MN =12,MA =3,MB >3,以A 为中心顺时针旋转点M ,以点B 为中心顺时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,当△ABC 为直角三角形时AB 的长是( )A .3B .5C .4或5D .3或516.若不等式组236x m x x <⎧⎨-<-⎩无解,那么m 的取值范围( )A .2m ≤B .2m ≥C .2m <D .2m > 7.关于x 的方程3a x -=的解是非负数,那么a 满足的条件是( )A .3a >B .3a ≤C .3a <D .3a ≥ 8.不等式-3<a≤1的解集在数轴上表示正确的是( )A .B .C .D .9.直线1y x =+与2y x a =-+的交点在第一象限,则a 的取值可以是( )A .1-B .3C .1D .010.如图,一次函数1y ax b 与一次函数24y kx =+的图象交点()1,3P ,则下列说法正确的个数是( )①1x =是方程3ax b +=的一个解; ②方程组4y ax b y kx =+⎧⎨=+⎩的解是31x y =⎧⎨=⎩;③不等式4ax b kx +>+的解集是1x >; ④不等式44ax b kx +<+<的解集是01x <<.A .1B .2C .3D .411.若关于x 的不等式组0721x m x -⎧⎨-≤⎩<的整数解有且仅有3个,则实数m 的取值范围是( ) A .56m ≤<.B .56m <<C .56m ≤≤D .56m <≤ 12.在方程组2122x y m x y +=-⎧⎨+=⎩中,若未知数x y ,满足0x y ->,则m 的取值范围是( ) A .1m >- B .1m <- C .1m ≥- D .1m ≤-二、填空题13.“鼠去牛来辞旧岁,龙飞凤舞庆明时.”在新年的钟声敲响之际,南开中学初2022级举行了元旦晚会.在晚会前,一、二、三班都组织购买了 A 、B 、C 三类糖果.已知一班分别购买 A 、B 、C 三类糖果各3千克、2千克、5千克,二班分别购买A 、B 、C 三类糖果各 2千克、1千克、4千克,且一班和二班购买糖果的总金额比值为3∶2.若三类糖果单价和为108元,且各单价是低于50元/千克的整数,A 与C 单价差大于25元.则三班分别购买A 、B 、C 三类糖果各2千克、3千克、4千克的总金额为______元.14.若不等式(6)6m x m ->-,两边同除以(6)m -,得1x <,则m 的取值范围为__. 15.小张同学在解一元一次不等式时,发现一个不等式右边的数被墨迹污染看不清了,所看到的部分不等式是13x -<■,他查看练习本后的答案知道这个不等式的解是2x >,则被污染的数是__________.16.如图,已知一次函数y kx b =+的图象如图所示,①方程0kx b +=的解为_______;②关于x 的不等式0kx b ->的解集为_______.17.若关于x 的不等式组0521x m x -<⎧⎨-≤⎩的整数解有且只有4个,则m 的取值范围是:__________.18.不等式组210322x x x ->⎧⎨<+⎩的整数解为_____. 19.一次函数 y 1=kx +b 与 y 2=x +a 的图象如图所示,则下列结论:①k <0;②a <0,b <0;③当 x =3 时,y 1=y 2;④不等式 kx +b >x +a 的解集是 x <3,其中正确的结论有_______.(只填序号)20.一次函数y =kx +b ,(k ,b 为常数)的图象如图所示,则关于x 的不等式kx +2b <0的解集是_____.三、解答题21.某社区计划对面积为3600m 2的区域进行绿化,经投标,由甲,乙两个工程队来完成,已知甲队5天能完成绿化的面积等于乙队10天完成绿化的面积,甲队3天能完成绿化的面积比乙队5天能完成绿化面积多60m 2.(1)求甲、乙两工程队每天能完成绿化的面积;(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,要使这次绿化的总费用不超过32万元,则至少应安排乙工程队绿化多少天?22.2020年以来,新冠肺炎疫情肆虐全球,感染人数不断攀升,口罩瞬间成为需求最为迫切的防疫物资.为了缓解供需矛盾,在中央的号召下,许多企业纷纷跨界转行生产口罩.我县某工厂接到订单任务,要求用7天时间生产A 、B 两种型号的口罩,共不少于5.8万只,其中A 型口罩只数不少于B 型口罩.该厂的生产能力是:每天只能生产一种口罩,如果2天生产A 型口罩,3天生产B 型口罩,一共可以生产4.6万只;如果3天生产A 型口罩,2天生产B 型口罩,一共可以生产4.4万只,并且生产一只A 型口罩可获利0.5元,生产一只B 型口罩可获利0.3元.(1)试求出该厂的生产能力,即每天能生产A 型口罩或B 型口罩多少万只?(2)在完成订单任务的前提下,应怎样安排生产A 型口罩和B 型口罩的天数,才能使获得的总利润最大,最大利润是多少万元?23.如图,ABC 中,8,6AC BC AB ===,现有两点,M N 分别从点A 点B 同时出发,沿三角形的边运动,已知点M 的速度为每秒1个单位长度,点N 的运度为每秒2个单位长度,当点M 到达B 点时,,M N 同时停止运动,设运动时间为t 秒.(1)当03t ≤≤时,AM = ,AN = ;(用含t 的代数式表示)(2)当点,M N 在边BC 上运动时,是否存在某个时刻,使得12AMN ABC S S =△△成立,若成立,请求出此时点M 运动的时间;若不成立请说明理由.(3)当点,M N 在同一直线上运动时,求运动时间t 的取值范围.24.某数学兴趣小组开展了一次活动,过程如下:设()090BAC θθ∠=︒<<︒,小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.活动一:如图甲所示,从点1A 开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,12A A 为第1根小棒.数学思考:(1)小棒能无限摆下去吗?答:______;(填“能”或“不能”)(2)若112231AA A A A A ===,则θ=______度;活动二:如图乙所示,从点1A 开始,用等长的小棒依次向右摆放,其中12A A 为第1根小棒,且121A A AA =.数学思考:(3)若已经向右摆放了3根小棒,则1θ=______,2θ=______,3θ=______(用含θ的式子表示);(4)若只能摆放4根小棒,求θ的范围.25.解不等式组253(2)13212x x x x +≤+⎧⎪⎨+-≤⎪⎩, 并把不等式组的解集在数轴上表示出来,写出不等式组的非负整数解.26.新年将至,小开计划购进部分年货进行销售;若购进40副春联和30对窗花共需410元;购进60副春联和80对窗花共需720元.(1)求每副春联、每对窗花的进价各是多少元;(2)小开计划购进春联、窗花共300件进行销售,进价不超过1400元,且全部销售完后总利润不低于1000元.已知小开将春联和窗花的售价分别定为15元和6元.设批发春联a 副,总利润为W 元.写出W (元)与a (副)的函数关系式,并求最大总利润W 的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】由数轴可得表示的解集为12x -<≤,把各个选项求出解集,即可解答.【详解】数轴表示的解集为12x -<≤.解不等式组1020x x ->⎧⎨+≤⎩,得:12x x >⎧⎨≤-⎩,解集为空集,故A 不符合题意. 解不等式组1020x x +>⎧⎨+≤⎩,得:12x x >-⎧⎨≤-⎩,解集为空集,故B 不符合题意. 解不等式组1020x x +>⎧⎨-≤⎩,得:12x x >-⎧⎨≤⎩,解集为12x -<≤,故C 符合题意. 解不等式组1020x x -≤⎧⎨+<⎩,得:12x x ≤⎧⎨<-⎩,解集为2x <-,故D 不符合题意. 故选C .【点睛】本题考查在数轴上表示不等式的解集以及解不等式组,解决本题的关键是求出不等式组的解集.2.A解析:A【分析】利用函数图象,写出在x 轴上方且函数y=kx+b 的函数值小于函数y=mx 的函数值对应的自变量的范围即可.【详解】解:当x >﹣2时,y =kx +b >0;当x <﹣1时,kx +b <mx ,所以不等式组0<kx +b <mx 的解集为﹣2<x <﹣1.故选:A .【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.3.B解析:B【分析】题目中的不等关系是:买西瓜每斤平均价>卖黄瓜每斤平均价.【详解】 解:根据题意得,他买西瓜每斤平均价是300200500x y +, 以每斤2x y +元的价格卖完后,结果发现自己赔了钱, 则300200500x y +>2x y +, 解之得,x >y .所以赔钱的原因是x >y .故选:B .【点睛】本题考查了一元一次不等式的应用,解决问题的关键是读懂题意,找到关键描述语,列出不等式.4.D解析:D【分析】不等式组整理后,根据已知解集确定出m 的范围,由方程有非负整数解,确定出m 的值,求出之积即可.【详解】 不等式组整理得:31032x m x ⎧≥⎪⎪⎨⎪≥⎪⎩, 由解集为32x ≥,得到33102m ≤,即5m ≤, 方程去分母得:64253y m y -=-+,即213m y -=, 由y 为非负整数,得213m k -=(k 为非负整数), 整理得:3152k m +=≤, 解得:0k ≤≤3, ∴0k =或1或2或3,∴12m =(舍去)或2或72(舍去)或5, ∴2m =或5, ∴符合条件的所有整数m 的积为2510⨯=,故选:D .【点睛】本题考查了解一元一次方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.5.C解析:C【分析】设AB =x ,则BC =9-x ,根据三角形两边之和大于第三边,得到x 的取值范围,再利用分类讨论思想,根据勾股定理列方程,计算解答.【详解】解:∵在△ABC 中,AC =AM =3,设AB =x ,BC =9-x ,由三角形两边之和大于第三边得:3939x x x x +-⎧⎨+-⎩>>, 解得3<x <6,①AC 为斜边,则32=x 2+(9-x )2,即x 2-9x +36=0,方程无解,即AC 为斜边不成立,②若AB 为斜边,则x 2=(9-x )2+32,解得x =5,满足3<x <6,③若BC 为斜边,则(9-x )2=32+x 2,解得x =4,满足3<x <6,∴x =5或x =4;故选C .【点睛】本题考查三角形的三边关系,勾股定理等,分类讨论和方程思想是解答的关键. 6.A解析:A【分析】先求出每个不等式的解集,再根据不等式组解集的求法和不等式组无解的条件,即可得到m 的取值范围.【详解】解:236x m x x <⎧⎨-<-⎩①② 由①得,x <m ,由②得,x >2,又因为不等式组无解,所以根据“大大小小解不了”原则,m≤2.故选:A.【点睛】本题考查了不等式组的求法,求不等式组的解集,要根据以下原则:同大取较大,同小较小,小大大小中间找,大大小小解不了.7.D解析:D【分析】求出方程的解,根据已知得出a-3≥0,求出即可.【详解】解:解方程a-x=3得:x=a-3,∵方程的解是非负数,∴a-3≥0,解得:a≥3,故选:D.【点睛】本题考查了一元一次方程的解,解一元一次不等式,解一元一次方程的应用,关键是得出一个关于a的不等式.8.A解析:A【分析】根据在数轴上表示不等式解集的方法求解即可.【详解】解:∵-3<a≤1,∴1处是实心原点,且折线向左.故选:A.【点睛】本题考查了在数轴上表示不等式的解集,掌握“小于向左,大于向右”是解题的关键.9.B解析:B【分析】联立两直线解析式,解关于x、y的二元一次方程组,然后根据交点在第一象限,横坐标是正数,纵坐标是正数,列出不等式组求解即可.【详解】联立12y xy x a=+⎧⎨=-+⎩,解得:1323a x a y -⎧=⎪⎪⎨+⎪=⎪⎩, ∵交点在第一象限, ∴103203a a -⎧>⎪⎪⎨+⎪>⎪⎩, 解得:1a >.只有3a =符合要求.故选:B .【点睛】本题考查了两直线相交的问题,第一象限内点的横坐标是正数,纵坐标是正数,以及一元一次不等式组的解法,把a 看作常数表示出x 、y 是解题的关键.10.C解析:C【分析】根据函数图象上点的特征和方程及不等式的关系可以直接作出判断.【详解】解:①如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则点(1,3)P 位于直线1y ax b 上,所以1x =是方程3ax b +=的一个解,故①说法正确. ②如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则方程组4y ax b y kx =+⎧⎨=+⎩的解是13x y =⎧⎨=⎩,故②说法错误. ③如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则不等式4ax b kx +>+的解集是1x >,故③说法正确. ④如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,且直线24y kx =+与y 轴的交点是(0,4),则不等式44ax b kx +<+<的解集是01x <<,故④说法正确.综上所述,说法正确的个数是3,故选:C .【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y kx b =+的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y kx b =+在x 轴上(或下)方部分所有的点的横坐标所构成的集合.11.D【分析】分别求出不等式组中不等式的解集,利用取解集的方法表示出不等式组的解集,根据解集中整数解有3个,即可得到m 的范围.【详解】解不等式0x m -<,得:x m <,解不等式721x -≤,得:3x ≥,则不等式组的解集为3x m ≤<,∵不等式组的整数解有且仅有3个,∴不等式组的整数解为3、4、5,则56m <≤.故答案为:D .【点睛】本题考查了一元一次不等式组的整数解,表示出不等式组的解集,根据题意找出整数解是解本题的关键.12.B解析:B【分析】将方程组中两方程相减,便可得到关于x y -的方程,再根据0x y ->,即可求出m 的取值范围.【详解】2122x y m x y +=-⎧⎨+=⎩①②, ①-②得,()()()2212x y x y m +-+=--,即1x y m -=--,∵0x y ->,∴10m -->,解得:1m <-,故选:B .【点睛】本题考查了解二元一次方程组和解一元一次不等式,要注意0x y ->,则解出x ,y 关于m 的式子,最终求出m 的取值范围.二、填空题13.296【分析】可设A 单价x 元B 单价y 元由三类糖果单价和为108元得C 单价;再由一班和二班购买糖果的总金额比值为3∶2可得xy 的关系式再由A 与C 单价差大于25元可得一元一次不等式根据各单价是低于50元【分析】可设A 单价x 元,B 单价y 元,由三类糖果单价和为108元得C 单价;再由一班和二班购买糖果的总金额比值为3∶2,可得x 、y 的关系式,再由A 与C 单价差大于25元,可得一元一次不等式,根据各单价是低于50元/千克的整数求出符合题意的解即可【详解】解:设A 单价x 元,B 单价y 元三类糖果单价和为108元得C 单价为(108-x-y )元又一班和二班购买糖果的总金额比值为3∶2可得:325(108)324(108)2x y x y x y x y ++--=++-- 整理可得:2x+3y=216①又A 与C 单价差大于25元,即x-(108-x-y )>25整理可得:2x+y>133,将①中的2x 代入可得:y<41.5又A 、B 、C 三类糖果单价是低于50元/千克的整数,故:若y=41,代入①得x=46.5,不符合题意若y=40,代入①得x=48,符合题意若y=39,代入①得x=49.5,不符合题意若y=38,代入①得x=51,不符合题意y 越小,x 越大,故后面x 的结果均大于50,不符合题意故x=48,y=40,108-x-y=20由上可知:A 类糖果的单价是48元B 类糖果的单价是40元C 类糖果的单价是20元故分别购买A 、B 、C 三类糖果各2千克、3千克、4千克的总金额为:48×2+40×3+20×4=296(元)故答案为:296【点睛】本题考查一元一次不等式的解法,利用条件建立一元一次不等式并结合题意准确得到A 、B 、C 三类糖果的单价是解本题的关键14.【分析】由不等式的基本性质知m-6<0据此可得答案【详解】解:若不等式两边同除以得则解得故答案为:【点睛】本题考查了解一元一次不等式解题的关键是掌握不等式的基本性质解析:6m <【分析】由不等式的基本性质知m-6<0,据此可得答案.【详解】解:若不等式(6)6m x m ->-,两边同除以(6)m -,得1x <,则60m -<,解得6m <,故答案为:6m <.【点睛】本题考查了解一元一次不等式,解题的关键是掌握不等式的基本性质.15.−5【分析】设被污染的数为a 表示出不等式的解集根据已知解集确定出a 的值即可【详解】解:设被污染的数为a 不等式为1−3x <a 解得:x >由已知解集为x >2得到=2解得:a =−5故答案为:−5【点睛】此题解析:−5【分析】设被污染的数为a ,表示出不等式的解集,根据已知解集确定出a 的值即可.【详解】解:设被污染的数为a ,不等式为1−3x <a .解得:x >1-3a , 由已知解集为x >2,得到1-3a =2, 解得:a =−5,故答案为:−5【点睛】此题考查了不等式的解集,熟练掌握运算法则是解本题的关键.16.【分析】根据图象可知一次函数y=kx+b 的图象过点(-60)即当x=-6时y=0由此得出关于x 的方程kx+b=0的解和关于的不等式的解集【详解】解:根据图象可知:∵一次函数y=kx+b 的图象过点(-解析:6x =- 6x <-【分析】根据图象可知,一次函数y=kx+b 的图象过点(-6,0),即当x=-6时,y=0,由此得出关于x 的方程kx+b=0的解和关于x 的不等式0kx b ->的解集.【详解】解:根据图象可知:∵一次函数y=kx+b 的图象过点(-6,0)∴关于x 的方程kx+b=0的解是x=-6;关于x 的不等式0kx b ->的解集为:6x <-.故答案为:6x =-;6x <-.【点睛】本题考查了一次函数与一元一次方程及一元一次不等式的关系,利用数形结合是解题的关键.17.【分析】先解不等式组得到解集为:<此时的整数解有且只有4个结合数轴分析可得到的取值范围【详解】解:由①得:<由②得:所以不等式组的解集为:<不等式组的整数解有且只有4个如图不等式组的整数解为<故答案 解析:56m <≤【分析】先解不等式组,得到解集为:2x ≤<m ,此时的整数解有且只有4个,结合数轴分析可得到m 的取值范围.【详解】解:0521x m x -<⎧⎨-≤⎩①②由①得:x <m ,由②得:24,x -≤-2,x ∴≥所以不等式组的解集为:2x ≤<m ,不等式组的整数解有且只有4个,如图,不等式组的整数解为2,3,4,5,5∴< 6.m ≤故答案为:56m <≤.【点睛】本题考查的是不等式组的整数解问题,掌握利用数轴分析得出不等式组中字母的取值范围是解题的关键.18.1【分析】分别求出不等式组中两不等式的解集找出两解集的公共部分即可【详解】解:由①得:x >由②得:x <2∴不等式组的解集为<x <2则不等式组的整数解为1故答案为1【点睛】考查了一元一次不等式组的整数 解析:1【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.【详解】解:210322x x x ->⎧⎨<+⎩①②, 由①得:x >12, 由②得:x <2,∴不等式组的解集为1<x<2,2则不等式组的整数解为1,故答案为1【点睛】考查了一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.19.①③④【分析】仔细观察图象①k的正负看函数图象从左向右成何趋势即可;②ab看y2=x+ay1=kx+b与y轴的交点坐标;③看两函数图象的交点横坐标;④以两条直线的交点为分界哪个函数图象在上面则哪个函解析:①③④【分析】仔细观察图象,①k的正负看函数图象从左向右成何趋势即可;②a,b看y2=x+a, y1=kx+b与y轴的交点坐标;③看两函数图象的交点横坐标;④以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大.【详解】解:① y 1=kx+b的图象从左向右呈下降趋势,∴k<0正确;②y2=x+a与y轴的交点在负半轴上, ∴a<0,另一条直线与y轴交于正半轴,所以b>0,故②错误;③两函数图象的交点横坐标为3,∴当x=3时, y1=y2 ,故③正确;④当x<3时, y1>y2 ,故④正确;故正确的判断是①③④.故答案为: ①③④.【点睛】此题主要考查了一次函数的图象,考查学生的分析能力和读图能力,一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;③当k<0,b>0,函数y=kx+b的图象经过第一、二、四象限;④当k<0,b<0,函数y=kx+b的图象经过第二、三、四象限.20.x>6【分析】由题意可以用k表示b于是题中不等式变为含有参数k的不等式然后由一次函数图象可以得知k<0最后根据不等式的性质可以得到解答【详解】解:把(30)代入y=kx+b得3k+b=0∴b=﹣3k解析:x>6【分析】由题意可以用k表示b,于是题中不等式变为含有参数k的不等式,然后由一次函数图象可以得知k<0,最后根据不等式的性质可以得到解答.【详解】解:把(3,0)代入y=kx+b得,3k+b=0,∴b=﹣3k,∵kx+2b<0,∴kx<6k,由图象可知k<0,∴x>6,故答案为x>6.【点睛】本题考查一次函数与不等式的综合应用,熟练掌握一次函数的图象与性质、不等式的基本性质是解题关键.三、解答题21.(1)甲工程队每天能完成绿化的面积为120m2,乙工程队每天能完成绿化的面积为60m2;(2)至少应安排乙工程队绿化40天.【分析】(1)设乙工程队每天能完成绿化的面积为xm2,则甲工程队每天能完成绿化的面积为2xm2,根据甲队3天能完成绿化的面积比乙队5天能完成绿化面积多50m2,即可得出关于x的一元一次方程,解之即可得出结论;(2)设安排乙工程队绿化m天,则安排甲工程队绿化360060120m-天,根据总费用=每日绿化的费用×绿化时间结合这次绿化的总费用不超过32万元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.【详解】解:(1)设乙工程队每天能完成绿化的面积为xm2,则甲工程队每天能完成绿化的面积为2xm2,依题意,得:3×2x﹣5x=60,解得:x=60,∴2x=120.答:甲工程队每天能完成绿化的面积为120m2,乙工程队每天能完成绿化的面积为60m2.(2)设安排乙工程队绿化m天,则安排甲工程队绿化360060120m-天,依题意,得:1.2×360060120m-+0.5m≤32,解得:m≥40.答:至少应安排乙工程队绿化40天.【点睛】本题考查了一元一次方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)根据各数量之间的关系,正确列出一元一次不等式.22.(1)该厂每天能生产A 型口罩0.8万只或B 型口罩1万只;(2)当安排生产A 型口罩6天、B 型口罩1天,获得2.7万元的最大总利润【分析】(1)设该厂每天能生产A 型口罩x 万只或B 型口罩y 万只,由2天生产A 型口罩,3天生产B 型口罩,一共可以生产4.6万只;如果3天生产A 型口罩,2天生产B 型口罩,一共可以生产4.4万只,列出方程组,即可求解;(2)由总利润=A 型口罩的利润+B 型口罩的利润,列出一次函数关系式,由不等式组和一次函数的性质可求解.【详解】解:(1)设该厂每天能生产A 型口罩x 万只或B 型口罩y 万只.根据题意,得23 4.632 4.4x y x y +=⎧⎨+=⎩, 解得0.81x y =⎧⎨=⎩, 答:该厂每天能生产A 型口罩0.8万只或B 型口罩1万只.(2)设该厂应安排生产A 型口罩m 天,则生产B 型口罩(7)m -天.根据题意,得()0.870.87 5.8m m m m ≥-⎧⎨+-≥⎩, 解得3569m ≤≤, 设获得的总利润为w 万元, 根据题意得:0.50.80.31(7)0.1 2.1w m m m =⨯+⨯⨯-=+,∵0.10m =>,∴w 随m 的增大而增大.∴当m =6时,w 取最大值,最大值为0.16 2.1 2.7⨯+=(万元).答:当安排生产A 型口罩6天、B 型口罩1天,获得2.7万元的最大总利润.【点睛】本题主要考查二元一次方程组的应用以及一次函数的应用,根据工作效率×工作时间=工作总量即可列出(1)问的方程;第二问根据总利润=单件利润×数量列出关系式,求解即可.属于基础类应用题.23.(1)t ,62t -;(2)存在,10秒;(3)37t ≤≤或811t ≤≤【分析】(1)先由运动得出AM=t ,BN=2t ,继而得出AN ,即可得出结论;(2)当点M ,N 在边BC 上运动时,AM=t-8,CN=2t-6-8,即可得到MN=t-6,根据题意知12MN BC =,列出方程即可求解; (3)根据运动的时间、速度和距离即可求得运动时间t 的取值范围.【详解】(1)∵6÷2=3,∴当 0≤t≤3 时,点N 在AB 上运动(包括端点),∵运动时间为t 秒.∴AM=t ,BN=2t ,∴AN=6-2t ,故答案为:t ,6-2t ;(2)存在.理由如下:当M N 、在边BC 上运动时,8672t +>=,点N 在边BC 上, 881t >=,点M 在边BC 上, ∴点N 在点M 前面,此时,CM=t-8,CN=2t-14, ∵12AMN ABC S S ∆∆=, ∴12MN BC =, 则1(214)(8)82t t ---=⨯, 解得:10t = 所以,当点M N 、在边BC 上运动,10t =秒时,12AMN ABCS S ∆∆=; (3)①当点M N 、同在AC 上时,∵68AB AC ==,,点N 的速度为2, ∴当66822t +≤≤即37t ≤≤时,点N 在AC 上, 又∵点M 的速度为1,∴当18t ≤≤时,点M 在AC 上, ∴当37t ≤≤时,点M N 、同在AC 上;②当点M N 、同在BC 上时,∵68AB AC ==,,点N 的速度为2,∴当6868822t +++≤≤即711t ≤≤时,点N 在BC 上, 又∵点M 的速度为1. ∴当88811t +≤≤即816t ≤≤时,点M 在BC 上, ∴当811t ≤≤时,点M N 、同在AC 上; 综上所述,当37t ≤≤与811t ≤≤时,点M N 、在同一直线上运动.【点睛】本题考查了一元一次方程在几何中的应用,一元一次不等式在几何中的应用等,解题的关键是理解题意,学会用方程的思想思考问题.24.(1)能;(2)22.5︒;(3)2θ;3θ;4θ;(4)1822.5θ︒≤︒<【分析】(1)因为角的两条边为两条射线,没有长度限制,所以小棒可以无限摆下去; (2)根据直角三角形的性质、三角形外角的性质和等腰三角形的性质,即可推出; (3)根据三角形外角的性质、等腰三角形的性质即可推出12132A A A θθ=∠=,即可推出,同理即可推出2θ,3θ;(4)根据(3)的结论,和三角形外角的性质,即可推出不等式,解不等式即可.【详解】(1)∵角的两边为两条射线,没有长度限制,∴小棒可以无限摆下去;(2)∵112231AA A A A A ===,1223A A A A ⊥,∴12AA A 为等腰三角形,145a ∠=︒, ∴1122.52a θ=∠=︒; (3)∵1212334A A AA A A A A ===,,∴12132312A A A A A A θθ=∠=∠=,∴223123A A A θθθθθ=∠+=+=,∴324334A A A θθθθθ=∠+=+=;(4)∵根据三角形内角和定理和等腰三角形的性质,∴590490θθ≥︒⎧⎨︒⎩,< 解得,1822.5θ︒≤︒<.【点睛】本题考查了射线的性质、等腰三角形的性质、解一元一次不等式组,解题的关键在于找到等量关系,求相关角的度数.25.﹣1≤x ≤3,非负整数解为3,2,1,0.【分析】分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可,再找出解集范围内的非负整数即可.【详解】解:()253213212x x x x ⎧+≤+⎪⎨+-≤⎪⎩,①.②, 由①得:x ≥﹣1,由②得:x ≤3,不等式组的解集为:﹣1≤x ≤3.在数轴上表示为:.∴不等式组的非负整数解,3,2,1,0.【点睛】此题主要考查了解一元一次不等式(组),解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解.26.(1)每副春联的进价是8元,每对窗花的进价是3元;(2)W=4a+900, 1300元.【分析】(1)设每副春联、每对窗花的进价分别是x 元、y 元,根据40副春联和30对窗花共需410元,购进60副春联和80对窗花共需720元,列出二元一次方程组,解方程组即可; (2)根据利润=(售价-进价)×数量可以得出W 与a 的函数关系式,根据总利润和总进价的条件列出不等式组,解不等式组求出a 的取值范围,然后根据一次函数的增减性质,即可得到最大利润.【详解】解:(1)设每副春联、每对窗花的进价分别是x 元、y 元,40304106080720x y x y +=⎧⎨+=⎩, 解得83x y =⎧⎨=⎩, 答:每副春联的进价是8元,每对窗花的进价是3元.(2)总利润W=(15-8)a+(6-3)(300-a)=4a+900,由题意得83(300)140049001000a a a +-≤⎧⎨+≥⎩解得,25100a ≤≤,∵在W=4a+900中,W 随a 的增大而增大,∴当a=100时,W 取得最大值,此时W=1300.答:W 与a 的函数关系式是W=4a+900,最大总利润1300元.【点睛】本题考查一次函数的应用、二元一次方程组的应用、一元一次不等式组的应用,解答本题的关键是明确题意,利用一次函数的性质和不等式的性质解答.。
(必考题)初中数学八年级数学下册第二单元《一元一次不等式和一元一次不等式组》检测(含答案解析)

一、选择题1.点P 坐标为(m +1,m -2),则点P 不可能在( )A .第一象限B .第二象限C .第三象限D .第四象限 2.某商贩去批发市场买西瓜,他上午买了300斤,每斤价格x 元,下午买了200斤,每斤价格y 元.后来他以每斤价格2xy +卖出,结果发现自己亏了钱,其原因是( ) A .x y < B .x y > C .x y ≤ D .x y ≥3.如果m n >,则下列各式不成立的是( ) A .22m n +>+ B .22m n ->- C .22m n > D .22m n -<-4.若关于x 的不等式组5335x x x a -+⎧⎨⎩><无解,则a 的取值范围为( ) A .a <4 B .a=4 C .a≤4 D .a≥45.直线11:l y k x b =+与直线22:l y k x =在同一平面直角坐标系中的图象如图所示,关于x 的不等式21k x k x b >+的解集为( )A .-1x >B .1x <-C .2x <-D .无法确定6.关于x 的不等式620x x a -≤⎧⎨≤⎩有解,则a 的取值范围是( ) A .a <3 B .a≤3 C .a≥3 D .a >37.已知关于x 的不等式组1021x x x a -⎧<⎪⎨⎪+>⎩有且只有一个整数解,则a 的取值范围是( )A .11a -<≤B .11a -≤<C .31a -<≤-D .31a -≤<- 8.如图是一次函数1y kx b =+与2y x a =+的图象,则不等式kx b x a ++<的解集是( )A .0x >B .0x <C .3x >D .3x < 9.不等式组23x x ≥-⎧⎨<⎩的整数解的个数是( ) A .4个B .5个C .6个D .无数个 10.如果不等式组5x x m <⎧⎨>⎩有解,那么m 的取值范围是( ) A .m >5B .m≥5C .m <5D .m≤8 11.已知a ,b 均为实数,且a ﹣1>b ﹣1,下列不等式中一定成立的是( )A .a <bB .3a <3bC .﹣a >﹣bD .a ﹣2>b ﹣2 12.若关于x 的不等式组31421232()4x x m x ++⎧->⎪⎨⎪-≥⎩无解,则m 的取值范围为( ) A .9m ≤ B .9m ≥ C .5m ≥ D .5m ≤-二、填空题13.若关于x 、y 的二元一次方程组23242x y a x y a +=-⎧⎨+=+⎩的解满足1x y +<,则a 的取值范围为________.14.不等式组63024x x x -⎧⎨<+⎩的解集是__. 15.若不等式00x b x a -<⎧⎨+>⎩的解集为23x <<,则a ,b 的值分别为_______________. 16.关于x 的不等式132x a x -≤⎧⎨-<⎩有5个整数解,则a 的取值范围是______. 17.已知:a 、b 、c 是三个非负数,并且满足326a b c ++=,231a b c +-=,设37m a b c =+-,设s 为m 的最大值.则s 的值为__________.18.某同学设计了一个程序:对输入的正整数x ,首先进行奇偶识别,然后进行对应的计算,如下图所示.如果按1,2,3…的顺序依次逐个输入正整数x ,则首次输出大于100的y 的值是__________.19.不等式2(53)3(12)x x x +≤--的解集为_____.20.若方程组3133x y a x y +=+⎧⎨+=⎩的解x 、y 满足 3y x -<,则a 的取值范围为_________. 三、解答题21.阅读下列材料,解答下面的问题:我们知道方程2312x y +=有无数个解,但在实际生活中我们往往只需求出其正整数解. 例:由2312x y +=,得1222433x y x -==-(x ,y 为正整数).要使243y x =-为正整数,则23x 为正整数,由2,3互质,可知x 为3的倍数,从而把3x =,代入243y x =-,得2y =.所以2312x y +=的正整数解为32x y =⎧⎨=⎩, 问题: (1)请你直接写出方程36x y -=的一组正整数解:__________.(2)若123x -为自然数,则满足条件的x 的正整数值有( )A .5个;B .6个;C .7个;D .8个 (3)七年级某班为了奖励学生学习的进步,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费48元,问有几种购买方案?写出购买方案.22.为发展校园足球运动,某城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)求每套队服和每个足球的价格是多少元;(2)若城区四校联合购买100套队服和()10a a >个足球,请用含a 的式子分别表示出到甲商场和乙商场购买装备所花费用;(3)在(2)的条件下,计算a 为何值时,两家商场所花费用相同;(4)在(3)的条件下,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?(直接写出方案)23.如图,在平面直角坐标系xOy 中,直线124:33l y x =-+与x 轴交于点A ,直线2:2l y x b =+与x 轴交于点B ,且与直线1l 交于点(1,)C m -.(1)求m 和b 的值;(2)求ABC 的面积;(3)若将直线2l 向下平移(0)t t 个单位长度后,所得到的直线与直线1l 的交点在第一象限,直接写出t 的取值范围.24.某商家欲购进甲、乙两种抗疫用品共180件,其进价和售价如表:甲 乙 进价(元/件)14 35 售价(元/件) 20 43、乙两种用品应分别购进多少件?(请用二元一次方程组求解)(2)若商家计划投入资金少于5040元,且销售完这批抗疫用品后获利不少于1314元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.25.近两年,重庆市奉节县紧紧围绕“村有骨干产业、户有致富门路”的发展思路,大力实施农产品产业扶贫项目,实现助农增收其中“乡坛子”什锦套菜礼盒、奉节脐橙10km 装广受好评,单价分别为100元/盒和60元/盒.(1)某公司大力响应扶贫政策,准备用不低于15000元购买什锦套菜礼盒、奉节脐橙共200盒,则至少购入什锦套菜礼盒多少盒?(2)2021年春节将至,该公司准备再次购入以上两种产品作为员工新春福利.恰逢“学习强国”重庆学习平台开展“党员直播带货、‘渝’你抗疫助农”扶贫农产品公益直播活动.直播中,什锦套菜礼盒以原价8折销售,该公司购买数量在(1)问最少数量的基础上增加了5%2m ;奉节脐橙售价比原价降低了815m 元,购买数量在(1)问奉节脐橙最多数量的基础上增加了40%.该公司在直播间下单后实际花费比(1)问中最低花费增加2350元,求m 的值.26.解不等式组32,121.25x x x x <+⎧⎪⎨++≥⎪⎩①②并把解集在数轴上表示出来.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】根据各象限坐标的符号及不等式的解集求解 .【详解】解:A 、当m>2时,m+1与m-2都大于0,P 在第一象限,所以A 不符合题意; B 、若P 在第二象限,则有m+1<0、m-2>0,即m<-1与m>2同时成立,但这是不可能是的,所以B 符合题意;C 、当m<-1时,m+1与m-2都小于0,P 在第三象限,所以C 不符合题意;D 、当-1<m<2时,m+1>0,m-2<0,P 在第四象限,所以D 不符合题意;故选B .【点睛】本题考查直角坐标系各象限点坐标符号与不等式的综合应用,根据不等式的解集确定点的坐标符号并最终确定点所在象限是解题关键.2.B解析:B【分析】题目中的不等关系是:买西瓜每斤平均价>卖黄瓜每斤平均价.【详解】 解:根据题意得,他买西瓜每斤平均价是300200500x y +, 以每斤2x y +元的价格卖完后,结果发现自己赔了钱, 则300200500x y +>2x y +, 解之得,x >y .所以赔钱的原因是x >y .故选:B .【点睛】本题考查了一元一次不等式的应用,解决问题的关键是读懂题意,找到关键描述语,列出不等式.3.B解析:B【分析】根据不等式的性质解答.【详解】A 、在不等式m >n 的两边同时加上2,不等式仍成立,即m+2>n+2,故本选项不符合题意.B 、在不等式m >n 的两边同时乘以-1然后再加上2,不等式号方向改变,即2-m <2-n ,故本选项符合题意.C 、在不等式m >n 的两边同时除以2,不等式仍成立,即22m n >,故本选项不符合题意. D 、在不等式m >n 的两边同时乘以-2,不等式号方向改变,即-2m <-2n ,故本选项不符合题意.故选:B .【点睛】本题主要考查了不等式的性质,在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.4.C解析:C【解析】解:5335x x x a -+⎧⎨⎩>①<②,由①得:x >4.∵不等式组无解,∴a ≤4.故选C . 点睛:本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解). 5.B解析:B【分析】由图象可知,当1x =-时,两个函数的函数值是相等的,再根据函数的增减性可以判断出不等式21k x k x b >+解集.【详解】两条直线的交点坐标为(-1,3),且当 x<−1 时,直线2l 在直线1l 的上方,∴不等式21k x k x b >+的解集为: x<−1故选:B.【点睛】本题考察借助一次函数的图象解一元一次不等式,两个图象的“交点”是两个函数值大小关系的“分界点”,在“分界点”处函数值的大小发生了改变.6.C解析:C【分析】解不等式6-2x ≤0,再根据不等式组有解求出a 的取值范围即可.【详解】解不等式6-2x ≤0,得:x ≥3,∵不等式组有解,∴a ≥3.故选:C .【点睛】本题主要考查根据不等式组的解判断未知参数的范围,熟练掌握不等式组的解法是解题关键.7.D解析:D【分析】首先解每个不等式,然后根据不等式组的整数解的个数,确定整数解,从而确定a 的范围.【详解】 解:1021x x x a -⎧<⎪⎨⎪+>⎩①② 解①得1x <且0x ≠,解②得12a x ->. 若不等式组只有1个整数解,则整数解是1-.1212a -∴-≤<- 所以31a -≤<-,故选:D .【点睛】此题考查的是一元一次不等式组的解法和一元一次不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了. 8.C解析:C【分析】根据函数图象可以直接判断本题的答案.【详解】解:结合图象,当3x >时,函数1y kx b =+在函数2y x a =+的下方,即不等式kx b x a ++<的解集是3x >;故选:C .【点睛】本题考查了一次函数与一元一次不等式:从函数图象的角度看,一元一次不等式的解集就是确定直线=+y kx b 在另一条直线(或者x 轴)上(或下)方部分所有点的横坐标的集合;这是数形结合的典型考查.9.B解析:B【分析】本题首先求解该不等式组公共解集,继而在解集内确定整数解.【详解】由已知得:23x -≤<,该范围内包含5个整数解:2-,1-,0,1,2.故选:B .【点睛】本题考查求不等式的整数解,解题关键在于确定公共解集,其次确定答案时要确保不重不漏.10.C解析:C【解析】∵不等式组有解, ∴m <5.故选C .【方法点睛】本题主要考查的是不等式的解集,依据口诀列出不等式是解题的关键. 11.D解析:D【分析】根据不等式的性质进行判断.【详解】解:因为a ,b 均为实数,且a ﹣1>b ﹣1,可得a >b ,所以3a >3b ,﹣a <﹣b ,a ﹣2>b ﹣2,故选D .【点睛】本题考查了不等式的性质,掌握在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.12.A解析:A【分析】先求出两个不等式的解集,再根据不等式组无解列出关于m 的不等式求解即可.【详解】 解不等式3142123x x ++->,得:7x >, 解不等式()24m x -≥,得:2x m ≤-,∵不等式组无解,∴27m -≤,则9m ≤,故选:A .【点睛】本题主要考查了解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.二、填空题13.【分析】直接把两个方程相加得到然后结合即可求出a 的取值范围【详解】解:直接把两个方程相加得:∴∵∴∴故答案为:【点睛】本题考查了解二元一次方程组以及解一元一次不等式解题的关键是掌握运算法则正确得到 解析:4a. 【分析】直接把两个方程相加,得到337x y a +=+,然后结合1x y +<,即可求出a 的取值范围.【详解】解:23242x y a x y a+=-⎧⎨+=+⎩, 直接把两个方程相加,得:337x y a +=+, ∴73a x y ++=, ∵1x y +<, ∴713a +<, ∴4a .故答案为:4a.【点睛】本题考查了解二元一次方程组,以及解一元一次不等式,解题的关键是掌握运算法则,正确得到73a x y ++=. 14.【分析】分别解两个不等式得到和x <4然后根据同大取大同小取小大于小的小于大的取中间小于小的大于大的无解确定不等式组的解集【详解】解:解不等式得:解不等式得:则不等式组的解集为故答案为【点睛】本题考查 解析:2x【分析】分别解两个不等式得到2x 和x <4,然后根据同大取大,同小取小,大于小的小于大的取中间,小于小的大于大的无解确定不等式组的解集.【详解】解:解不等式630x -,得:2x ,解不等式24x x <+,得:4x <,则不等式组的解集为2x ,故答案为2x .【点睛】本题考查了解一元一次不等式组:求解出两个不等式的解集,然后按照“同大取大,同小取小,大于小的小于大的取中间,小于小的大于大的无解”确定不等式组的解集. 15.【分析】由于不等式组有解则解不等式组得到-a <x <b 然后与2<x <3进行对比即可确定a 和b 的值【详解】解:∵不等式组的解集为2<x <3而解不等式组得-a <x <b ∴-a=2b=3即a=-2b=3故答案解析:2a =-、3b =【分析】由于不等式组00x b x a -<⎧⎨+>⎩有解,则解不等式组得到-a <x <b ,然后与2<x <3进行对比即可确定a 和b 的值.【详解】解:∵不等式组00x b x a -<⎧⎨+>⎩的解集为2<x <3, 而解不等式组00x b x a -<⎧⎨+>⎩得-a <x <b , ∴-a=2,b=3, 即a=-2,b=3.故答案为:2a =-、3b =.【点睛】本题考查了不等式的解集,掌握不等式的性质是解题的关键.16.【分析】首先解每个不等式两个不等式的解集的公共部分就是不等式组的解集确定整数解据此即可写出a 的范围【详解】解:解不等式①得;解不等式②得:则不等式的解集为∵不等式有5个整数解∴一定是01234∴即故 解析:12a ≤<【分析】首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,确定整数解,据此即可写出a 的范围.【详解】解:132x a x -≤⎧⎨-<⎩①②, 解不等式①得,4x ≤;解不等式②得:2x a >-,则不等式的解集为24a x -<≤,∵不等式132x a x -≤⎧⎨-<⎩有5个整数解, ∴一定是0,1,2,3,4. ∴120a ,即12a ≤<, 故答案为:12a ≤<.【点睛】此题考查的是一元一次不等式组的解法,根据x 的取值范围,得出x 的整数解,然后代入方程即可解出a 的值.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.17.【分析】根据题意先把看作已知数分别用表示出和让列式求出的取值范围再求得用表示的形式结合的取值范围即可求得的值【详解】解:3a+2b+c=62a+b-3c=1解得a=7c-4b=9-11c ;∵a≥0b 解析:611-【分析】根据题意先把c 看作已知数,分别用c 表示出a 和b ,让0a ≥,0b ≥列式求出c 的取值范围,再求得m 用c 表示的形式,结合c 的取值范围即可求得s 的值.【详解】解:3a+2b+c=6,2a+b-3c=1,解得a=7c-4,b=9-11c ;∵a≥0、b≥0,∴7c-4≥0,9-11c≥0, ∴49711c ≤≤. ∵m=3a+b-7c=3c-3,∴m 随c 的增大而增大,∵911c≤.∴当c取最大值911,m有最大值,∴m的最大值为s=3×911-3=611-.故答案为:6 11 -.【点睛】本题考查解三元一次方程组以及解不等式组,把c看作已知数,分别用c表示a和b是解答本题的关键.18.101【分析】根据图示可知此题需要分两种情况讨论:①假设输入正整数x 为偶数时由题意得:;②假设输入的正整数x为奇数时由题意得:5x-23>100分别解出不等式的解集再确定x的值【详解】解:①假设输入解析:101【分析】根据图示可知此题需要分两种情况讨论:①假设输入正整数x为偶数时,由题意得:1891002x;②假设输入的正整数x为奇数时,由题意得:5x-23>100,分别解出不等式的解集,再确定x的值.【详解】解:①假设输入正整数x为偶数时,由题意得:189100 2x,解得:x>22,∵x为偶数,∴x=24,当x=24时,对应的y=12489101 2;②假设输入的正整数x为奇数时,由题意得:5x-23>100,解得:x>24.6,∵x为奇数,∴x=25,当x=25时,对应的y=5×25-23=102;∵24<25,∴首次大于100时对应的x=24,y=101,故答案为:101.【点睛】此题主要考查了一元一次不等式的应用,关键是看懂题意与图示,根据题目中的条件列出不等式,注意要分两种情况进行计算.19.【分析】利用不等式的基本性质先将不等式去括号然后移项合并同类项把系数化为1得到x的取值范围【详解】去括号得10x+6≤x−3+6x移项合并同类项得3x≤−9解得x≤−3故答案为:x≤−3【点睛】解不解析:3x ≤-【分析】利用不等式的基本性质,先将不等式去括号,然后移项合并同类项,把系数化为1,得到x 的取值范围.【详解】去括号得,10x +6≤x−3+6x ,移项合并同类项得,3x≤−9,解得,x≤−3.故答案为:x≤−3【点睛】解不等式应依据不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.特别是在系数化为1这一个过程中要注意不等号的方向的变化.20.a >-4【分析】先把两式相减求出y−x 的值再代入中得到关于a 的不等式进而求出a 的取值范围即可【详解】由②-①得:2y−2x =2−a ∵则∴2−a <6∴a >-4故答案是:a >-4【点睛】本题考查的是解二解析:a >-4【分析】先把两式相减求出y−x 的值,再代入 3y x -<中得到关于a 的不等式,进而求出a 的取值范围,即可.【详解】3133x y a x y +=+⎧⎨+=⎩①②, 由②-①得:2y−2x =2−a ,∵ 3y x -<,则2 26y x -<,∴2−a <6,∴a >-4,故答案是:a >-4.【点睛】本题考查的是解二元一次方程组及一元一次不等式,解答此题的关键是把a 当作常数表示出y−x 的值,再得到关于a 的不等式.三、解答题21.(1)33x y =⎧⎨=⎩;(2)B ;(3)三种,方案见解析 【分析】(1)求方程3x-y=6的正整数解,可给定x 一个正整数值,计算y 的值,如果y 的值也是正整数,那么就是原方程的一组正整数解.(2)参照例题的解题思路进行解答;(3)设购买单价为3元的笔记本m 本,单价为5元的钢笔n 支.则根据题意得:3m+5n=48,其中m 、n 均为自然数.求该二元一次方程的正整数解即可.【详解】解:(1)由3x-y=6,得y=3x-6,要使y 是正整数,则3x-6是正整数,所以需要x >2,故当x=3时,y=3,所以3x-y=6的一组正整数解可以是:33x y =⎧⎨=⎩, 故答案是:33x y =⎧⎨=⎩; (2)若123x -为自然数,则满足条件的x 的正整数值有4,5,6,7,9,15共6个, 故答案是:B ;(3)设购买单价为3元的笔记本m 本,单价为5元的钢笔n 支.则根据题意得:3m+5n=48,其中m 、n 均为自然数.于是有:n=4835m -, 则有483050m m -⎧>⎪⎨⎪>⎩, 解得:0<m <16.由于n=4835m -为正整数,则48-3m 为正整数,且为5的倍数. ∴当m=1时,n=9;当m=6时,n=6,当m=11时,n=3. 答:有三种购买方案:即购买单价为3元的笔记本1本,单价为5元的钢笔9支; 或购买单价为3元的笔记本6本,单价为5元的钢笔6支;或购买单价为3元的笔记本11本,单价为5元的钢笔3支.【点睛】本题考查了二元一次方程的应用,解题关键是要读懂题目给出的已知条件,根据条件求解.注意笔记本和钢笔是整体,所有不可能出现小数和负数,这也就说要求的是正整数. 22.(1)150元;100元;(2)甲商场()10014000a + ,乙商场()8015000a +元;(3)50a =;(4)当50a =时,两家花费一样;当1050a <<时,到甲处购买更合算;当50a 时,到乙处购买更合算【分析】(1)设每个足球的定价是x 元,则每套队服是()50x +元,根据“两套队服与三个足球的费用相等”得出等量关系,列出一元一次方程,求解即可;(2)根据甲商场和乙商场的方案列出式子即可;(3)令100140008015000,a a ++=解方程即可;(4)列出不等式分别求解即可.【详解】解:(1)设每个足球的定价是x 元,则每套队服是()50x +元.根据题意得()2503x x +=解得100,50150x x +==. 答:每套队服150元,每个足球100元.(2)到甲商场购买所花的费用为:()1001001501001001400010a a ⎛⎫⨯+-=+ ⎪⎝⎭元; 到乙商场购买所花的费用为:()100150+100808015000a a ⨯⨯%=+元;(3)由100140008015000,a a ++=得:50a =,所以:当50a =时,两家花费一样。
(必考题)初中数学八年级数学下册第二单元《一元一次不等式和一元一次不等式组》检测题(包含答案解析)4

一、选择题1.不等式组211x x ≥-⎧⎨>-⎩的解集是( )A .1x >-B .12x >-C .21x ≥- D .112x -<≤- 2.在平面直角坐标系中,将点A (m -1,n +2)先向右平移3个单位,再向上平移2个单位,得到点A ′.若点A ′位于第二象限,则m 、n 的取值范围分别是( ) A .m <0,n >0 B .m <0,n <-2 C .m <-2,n >-4 D .m <1,n >-23.如果a >b ,那么下列不等式不成立...的是( ) A .0a b ->B .33a b ->-C .1133a b >D .33a b ->-4.关于x 的方程3a x -=的解是非负数,那么a 满足的条件是( ) A .3a >B .3a ≤C .3a <D .3a ≥5.若关于x 的不等式0721x m x -<⎧⎨-≤⎩的整数解共有4个,则m 的取值范围是( )A .68m <<B .67≤<mC .67m ≤≤D .67m <≤6.已知关于x 的不等式组1021x x x a -⎧<⎪⎨⎪+>⎩有且只有一个整数解,则a 的取值范围是( )A .11a -<≤B .11a -≤<C .31a -<≤-D .31a -≤<-7.不等式-3<a≤1的解集在数轴上表示正确的是( ) A . B . C .D .8.运行程序如图所示,规定从“输入一个值x ”到“结果是否95>”为一次程序操作,如果程序操作进行了两次才停止,那么x 的取值范围是()A .23x >B .2347x <≤C .1123x ≤<D .47x ≤9.不等式组23x x ≥-⎧⎨<⎩的整数解的个数是( )A .4个B .5个C .6个D .无数个10.己知关于x ,y 的二元一次方程ax b y +=,下表列出了当x 分别取值时对应的y 值.则关于x 的不等式0ax b --<的解集为( )x… -2 -1 0 1 2 3 … y …321-1-2…A .x <1B .x >1C .x <0D .x >011.如图,一次函数1y ax b 与一次函数24y kx =+的图象交点()1,3P ,则下列说法正确的个数是( )①1x =是方程3ax b +=的一个解; ②方程组4y ax b y kx =+⎧⎨=+⎩的解是31x y =⎧⎨=⎩;③不等式4ax b kx +>+的解集是1x >; ④不等式44ax b kx +<+<的解集是01x <<.A .1B .2C .3D .412.已知不等式()33a x a -<-的解集是1x >-,则a 的取值范围是( ) A .3a >B .3a ≥C .3a <D .3a ≤二、填空题13.关于x 的不等式组3222553x x x m +⎧+⎪⎪⎨+⎪<+⎪⎩有且只有4个整数解,则常数m 的取值范围是_____.14.如图,函数y x =和4y ax =+的图象交于点()2,2,A 则不等式4x ax <+的解集为_____________________.15.若不等式组0122x a x x +≥⎧⎨->-⎩恰有四个整数解,则a 的取值范围是_________.16.如图,已知一次函数y=kx+b 的图象与正比例函数y=mx 的图象相交于点P (﹣3,2),则关于x 的不等式mx ﹣b≥kx 的解集为_____.17.已知:a 、b 、c 是三个非负数,并且满足326a b c ++=,231a b c +-=,设37m a b c =+-,设s 为m 的最大值.则s 的值为__________.18.如图,一次函数2y x m =-+与26y ax =+的图象相交于点()2,3P -,则关于x 的不等式26x m ax -+>+的解集为__________.19.若关于x 的不等式2x ﹣a ≥3的解集如图所示,则常数a =_____.20.若方程组3133x y a x y +=+⎧⎨+=⎩的解x 、y 满足 3y x -<,则a 的取值范围为_________.三、解答题21.现对x ,y 定义一种新的运算T ,规定:(,)++=+ax by cT x y x y(其中a ,b ,c 为常数,且0abc ≠).例如:10(1,0)10⨯+⨯+==++a b cT a c .已知(3,1)2,(2,3) 2.8,(1,1)3-===T T T .(1)求a ,b ,c 的值; (2)求关于m 的不等式组(4,54)3,(2,32)1T m m T m m -<⎧⎨->⎩的整数解.22.某数学兴趣小组开展了一次活动,过程如下:设()090BAC θθ∠=︒<<︒,小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上. 活动一:如图甲所示,从点1A 开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,12A A 为第1根小棒.数学思考:(1)小棒能无限摆下去吗?答:______;(填“能”或“不能”) (2)若112231AA A A A A ===,则θ=______度; 活动二:如图乙所示,从点1A 开始,用等长的小棒依次向右摆放,其中12A A 为第1根小棒,且121A A AA =.数学思考:(3)若已经向右摆放了3根小棒,则1θ=______,2θ=______,3θ=______(用含θ的式子表示);(4)若只能摆放4根小棒,求θ的范围.23.为发展校园足球运动,某城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折. (1)求每套队服和每个足球的价格是多少元;(2)若城区四校联合购买100套队服和()10a a >个足球,请用含a 的式子分别表示出到甲商场和乙商场购买装备所花费用;(3)在(2)的条件下,计算a 为何值时,两家商场所花费用相同;(4)在(3)的条件下,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?(直接写出方案)24.某厂贷款8万元购进一台机器生产商品.已知商品的成本每个8元,成品后售价是每个15元,应付税款和损耗总费用是销售额的20%.若每个月能生产销售1000个该商品,问至少几个月后能赚回这台机器的贷款?25.某水果店购买某种水果的进价为18元/千克,在销售过程中有10%的水果损耗,该水果店以a 元/千克的标价出售该种水果. (1)为避免亏本,求a 的最小值.(2)若该水果店以标价销售了70%的该种水果,在扣除10%损耗后,剩下的20%水果按10元/千克的价格售完.为确保销售该种水果所得的利润率不低于20%,求a 的最小值. 26.2020年新冠肺炎疫情在全球蔓延,全球疫情大考面前,中国始终同各国安危与共、风雨同舟,时至5月,中国已经向150多个国家和国际组织提供医疗物资援助.某次援助,我国组织20架飞机装运口罩、消毒剂、防护服三种医疗物资共120吨,按计划20架飞机都要装运,每架飞机只能装运同一种医疗物资,且必须装满.根据如下表提供的信息,解答以下问题:(2)若此次物资运费为W 元,求W 与x 之间的函数关系式;(3)如果装运每种医疗物资的飞机都不少于4架,那么怎样安排运送物资,方能使此次物资运费最少,最少运费为多少元?【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】先求出2x≥-1的解集,再确定不等式组的解集即可. 【详解】解:211x x ≥-⎧⎨>-⎩①②解不等式①得,21x ≥-, 解不等式②得,x>-1,∴不等式组的解集为:21x ≥-故选:C . 【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.2.C解析:C 【分析】根据点的平移规律可得向右平移3个单位,再向上平移2个单位得到(m-1+3,n+2+2),再根据第二象限内点的坐标符号可得. 【详解】点A (m-1,n+2)先向右平移3个单位,再向上平移2个单位得到点A′(m+2,n+4), ∵点A′位于第二象限, ∴2040m n +<⎧⎨+>⎩解得:m <-2,n >-4, 故选C . 【点睛】此题主要考查了坐标与图形变化-平移,关键是横坐标,右移加,左移减;纵坐标,上移加,下移减.3.D解析:D 【分析】根据不等式的基本性质逐项判断即可得. 【详解】A 、0a b ->,成立;B 、不等式的两边同减去3,不改变不等号的方向,即33a b ->-,成立;C 、不等式的两边同乘以正数13,不改变不等号的方向,即1133a b >,成立;D 、不等式的两边同乘以负数3-,改变不等号的方向,即33a b -<-,不成立; 故选:D . 【点睛】本题考查了不等式的基本性质,熟练掌握不等式的基本性质是解题关键.4.D解析:D 【分析】求出方程的解,根据已知得出a-3≥0,求出即可. 【详解】解:解方程a-x=3得:x=a-3,∵方程的解是非负数, ∴a-3≥0, 解得:a≥3, 故选:D . 【点睛】本题考查了一元一次方程的解,解一元一次不等式,解一元一次方程的应用,关键是得出一个关于a 的不等式.5.D解析:D 【分析】首先确定不等式组的解集,先利用含m 的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于m 的不等式,从而求出m 的范围. 【详解】 解不等式0721x m x -<⎧⎨-≤⎩①②,由①式得,x m <,由②式得3x ≥,即故m 的取值范围是67m <≤,故选D . 【点睛】本题考查不等式组的整数解问题,利用数轴就能直观的理解题意,列出关于m 的不等式组,再借助数轴做出正确的取舍.6.D解析:D 【分析】首先解每个不等式,然后根据不等式组的整数解的个数,确定整数解,从而确定a 的范围. 【详解】解:1021x x x a -⎧<⎪⎨⎪+>⎩①②解①得1x <且0x ≠, 解②得12a x ->. 若不等式组只有1个整数解,则整数解是1-.1212a -∴-≤<-所以31a -≤<-, 故选:D . 【点睛】此题考查的是一元一次不等式组的解法和一元一次不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.7.A解析:A 【分析】根据在数轴上表示不等式解集的方法求解即可. 【详解】 解:∵-3<a≤1,∴1处是实心原点,且折线向左. 故选:A . 【点睛】本题考查了在数轴上表示不等式的解集,掌握“小于向左,大于向右”是解题的关键.8.B解析:B 【分析】根据运行程序,第一次运算结果小于等于95,第二次运算结果大于95列出不等式组,然后求解即可. 【详解】解:由题意得,()2195221195x x +≤⎧⎪⎨++⎪⎩①>②解不等式①得,47x ≤, 解不等式②得,23x >, ∴2347x ≤<, 故选:B . 【点睛】本题考查了一元一次不等式组的应用,读懂题目信息,理解运行程序并列出不等式组是解题的关键.9.B解析:B 【分析】本题首先求解该不等式组公共解集,继而在解集内确定整数解. 【详解】由已知得:23x -≤<,该范围内包含5个整数解:2-,1-,0,1,2. 故选:B .【点睛】本题考查求不等式的整数解,解题关键在于确定公共解集,其次确定答案时要确保不重不漏.10.A解析:A 【分析】将x=0、y=1和x=1、y=0代入ax+b=y 得到关于a 、b 的方程组,解之得出a 、b 的值,从而得到关于x 的不等式,解之可得答案. 【详解】解:根据题意,得:1b a b =⎧⎨+=⎩,解得a=-1,b=1,则不等式-ax-b <0为x-1<0, 解得x <1, 故选:A . 【点睛】本题考查了解一元一次不等式,解题的关键是根据题意列出关于x 的不等式,并熟练掌握解一元一次不等式的步骤和依据.11.C解析:C 【分析】根据函数图象上点的特征和方程及不等式的关系可以直接作出判断. 【详解】解:①如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则点(1,3)P 位于直线1y ax b 上,所以1x =是方程3ax b +=的一个解,故①说法正确.②如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则方程组4y ax b y kx =+⎧⎨=+⎩的解是13x y =⎧⎨=⎩,故②说法错误. ③如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,则不等式4ax b kx +>+的解集是1x >,故③说法正确.④如图所示,一次函数1y ax b 与一次函数24y kx =+的图象交于点(1,3)P ,且直线24y kx =+与y 轴的交点是(0,4),则不等式44ax b kx +<+<的解集是01x <<,故④说法正确.综上所述,说法正确的个数是3, 故选:C . 【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y kx b=+的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y kx b =+在x 轴上(或下)方部分所有的点的横坐标所构成的集合.12.C解析:C 【分析】根据已知解集得到a-3为负数,即可确定出a 的范围. 【详解】解:不等式(a-3)x <3-a 的解集为x >-1, ∴a-3<0, 解得a <3. 故选:C . 【点睛】本题考查不等式的解集,熟练掌握不等式的基本性质是解题关键.二、填空题13.【分析】首先利用不等式的基本性质解不等式组再从不等式的解集中找出适合条件的整数解再确定字母的取值范围即可【详解】解:解①得:解②得:∴不等式组的解集为:∵不等式组只有4个整数解即不等式组只有4个整数解析:423m -<≤-【分析】首先利用不等式的基本性质解不等式组,再从不等式的解集中找出适合条件的整数解,再确定字母的取值范围即可. 【详解】解:3222553x x x m +⎧+⎪⎪⎨+⎪<+⎪⎩①②解①得:1x ≥-, 解②得:3102m x +<, ∴不等式组的解集为:31012m x +-≤<, ∵不等式组只有4个整数解,即不等式组只有4个整数解为﹣1、0、1、2, 则有310232m +<≤,解得:423m -<≤-, 故答案为:423m -<≤-【点睛】本题考查不等式组的解法及整数解的确定.解不等式要用到不等式的性质:(1)不等式的两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式的两边乘(或除以)同一个负数,不等号的方向改变.14.【分析】先利用A 点坐标然后观察函数图得到当x <2时y=x 的图象都在直线的下方由此得到不等式x <ax+4的解集【详解】解:A (23)观察函数图得到:当x <2时y=x 的图象都在直线的下方不等式x <ax+解析:2x <【分析】先利用A 点坐标,然后观察函数图得到当x <2 时,y=x 的图象都在直线4y ax =+的下方,由此得到不等式x <ax+4的解集.【详解】 解: A (2,3),观察函数图得到:当x <2 时,y=x 的图象都在直线4y ax =+的下方,∴ 不等式x <ax+4的解集x <2.故答案为:2x <.【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.理解好上面原理是解题的关键.15.3≤a <4【分析】求出每个不等式的解集根据找不等式组解集的规律找出不等式组的解集根据已知不等式组有四个整数解得出不等式组-4<-a≤-3求出不等式的解集即可得答案【详解】解不等式①得:x≥-a 解不等解析:3≤a <4【分析】求出每个不等式的解集,根据找不等式组解集的规律找出不等式组的解集,根据已知不等式组有四个整数解得出不等式组-4<-a≤-3,求出不等式的解集即可得答案.【详解】0122x a x x +≥⎧⎨->-⎩①② 解不等式①得:x≥-a ,解不等式②x <1,∴不等式组得解集为-a≤x <1,∵不等式组恰有四个整数解,∴-4<-a≤-3,解得:3≤a <4,故答案为:3≤a <4【点睛】本题考查了解一元一次不等式(组),不等式组的整数解,能根据不等式组的解集得出关于a 的不等式组是解题关键.16.x≥﹣3【分析】根据图象得出P 点横坐标为﹣3观察函数图象得在P 点右侧y=mx 的函数在y=kx+b 的函数图象上方由此得到不等式mx ﹣b≥kx 的解集为x≥﹣3【详解】由图象可知:P 点横坐标为﹣3当x≥﹣解析:x ≥﹣3【分析】根据图象得出P 点横坐标为﹣3,观察函数图象得在P 点右侧,y=mx 的函数在y=kx+b 的函数图象上方,由此得到不等式mx ﹣b≥kx 的解集为x≥﹣3.【详解】由图象可知:P 点横坐标为﹣3,当x≥﹣3时,y=mx 的函数在y=kx+b 的函数图象上方,即mx ﹣b≥kx ,所以关于x 的不等式mx ﹣b≥kx 的解集是x≥﹣3.故答案为:x≥﹣3【点睛】本题主要考查对一次函数与一元一次不等式的理解和掌握,能根据图象得出当x≥﹣3时mx ﹣b≥kx 是解此题的关键.17.【分析】根据题意先把看作已知数分别用表示出和让列式求出的取值范围再求得用表示的形式结合的取值范围即可求得的值【详解】解:3a+2b+c=62a+b-3c=1解得a=7c-4b=9-11c ;∵a≥0b 解析:611-【分析】根据题意先把c 看作已知数,分别用c 表示出a 和b ,让0a ≥,0b ≥列式求出c 的取值范围,再求得m 用c 表示的形式,结合c 的取值范围即可求得s 的值.【详解】解:3a+2b+c=6,2a+b-3c=1,解得a=7c-4,b=9-11c ;∵a ≥0、b≥0,∴7c-4≥0,9-11c≥0,∴49711c ≤≤. ∵m=3a+b-7c=3c-3,∴m 随c 的增大而增大, ∵911c ≤. ∴当c 取最大值911,m 有最大值, ∴m 的最大值为s=3×911-3=611-. 故答案为:611-. 【点睛】 本题考查解三元一次方程组以及解不等式组,把c 看作已知数,分别用c 表示a 和b 是解答本题的关键.18.【分析】观察函数图象根据两函数图象的上下位置关系即可找出关于x 的不等式的解集【详解】解:观察函数图象可知:当x<-2时一次函数y1=-2x+m 的图象在y2=ax+6的图象的上方∴关于x 的不等式的解集解析:2x <-【分析】观察函数图象,根据两函数图象的上下位置关系即可找出关于x 的不等式26x m ax -+>+的解集.【详解】解:观察函数图象可知:当x<-2时,一次函数y 1=-2x+m 的图象在y 2=ax+6的图象的上方, ∴关于x 的不等式26x m ax -+>+的解集是x<-2.故答案为:2x <-.【点睛】本题考查了一次函数与一元一次不等式,根据两函数图象的上下位置关系找出不等式的解集是解题的关键.19.-5【分析】先根据数轴上不等式解集的表示方法求出此不等式的解集再求出所给不等式的解集与已知解集相比较即可求出a 的值【详解】解:由数轴上关于x 的不等式的解集可知x≥﹣1解不等式:2x ﹣a≥3解得:x≥解析:-5【分析】先根据数轴上不等式解集的表示方法求出此不等式的解集,再求出所给不等式的解集与已知解集相比较即可求出a 的值.【详解】解:由数轴上关于x 的不等式的解集可知x≥﹣1,解不等式:2x ﹣a≥3,解得:x≥3+2a , 故3+2a =﹣1, 解得:a =﹣5.故答案为:﹣5.【点睛】本题考查在数轴上表示一元一次不等式的解集,熟知实心圆点与空心圆点的区别是解题关键.20.a >-4【分析】先把两式相减求出y−x 的值再代入中得到关于a 的不等式进而求出a 的取值范围即可【详解】由②-①得:2y−2x =2−a ∵则∴2−a <6∴a >-4故答案是:a >-4【点睛】本题考查的是解二解析:a >-4【分析】先把两式相减求出y−x 的值,再代入 3y x -<中得到关于a 的不等式,进而求出a 的取值范围,即可.【详解】3133x y a x y +=+⎧⎨+=⎩①②, 由②-①得:2y−2x =2−a ,∵ 3y x -<,则2 26y x -<,∴2−a <6,∴a >-4,故答案是:a >-4.【点睛】本题考查的是解二元一次方程组及一元一次不等式,解答此题的关键是把a 当作常数表示出y−x 的值,再得到关于a 的不等式.三、解答题21.(1)231a b c =⎧⎪=⎨⎪=⎩;(2)关于m 的不等式组(4,54)3(2,32)3T m m T m m -<⎧⎨->⎩的整数解有1,2,3. 【分析】(1)由题意易得323123 2.82311311a b c a b c a b c ⨯-+⎧=⎪-⎪⨯+⨯+⎪=⎨+⎪⨯+⨯+⎪=⎪+⎩,然后求解即可; (2)由题意,得243(54)135223(32)113m m m m ⨯+-+⎧<⎪⎪⎨⨯+-+⎪>⎪⎩,则有大于14且小于72的整数有1,2,3,然后问题可求解.【详解】解:(1)由题意,得323123 2.82311311a b c a b c a b c ⨯-+⎧=⎪-⎪⨯+⨯+⎪=⎨+⎪⨯+⨯+⎪=⎪+⎩, 整理,得3423146a b c a b c a b c -+=⎧⎪++=⎨⎪++=⎩, 解得231a b c =⎧⎪=⎨⎪=⎩; (2)由题意,得243(54)135223(32)113m m m m ⨯+-+⎧<⎪⎪⎨⨯+-+⎪>⎪⎩, 解得1742<<m , ∵大于14且小于72的整数有1,2,3, ∴关于m 的不等式组()()4,5432,323T m m T m m ⎧-<⎪⎨->⎪⎩的整数解有1,2,3. 【点睛】本题主要考查一元一次不等式的应用,熟练掌握一元一次不等式的应用是解题的关键. 22.(1)能;(2)22.5︒;(3)2θ;3θ;4θ;(4)1822.5θ︒≤︒<【分析】(1)因为角的两条边为两条射线,没有长度限制,所以小棒可以无限摆下去; (2)根据直角三角形的性质、三角形外角的性质和等腰三角形的性质,即可推出; (3)根据三角形外角的性质、等腰三角形的性质即可推出12132A A A θθ=∠=,即可推出,同理即可推出2θ,3θ;(4)根据(3)的结论,和三角形外角的性质,即可推出不等式,解不等式即可.【详解】(1)∵角的两边为两条射线,没有长度限制,∴小棒可以无限摆下去;(2)∵112231AA A A A A ===,1223A A A A ⊥,∴12AA A 为等腰三角形,145a ∠=︒, ∴1122.52a θ=∠=︒; (3)∵1212334A A AA A A A A ===,,∴12132312A A A A A A θθ=∠=∠=,∴223123A A A θθθθθ=∠+=+=,∴324334A A A θθθθθ=∠+=+=;(4)∵根据三角形内角和定理和等腰三角形的性质,∴590490θθ≥︒⎧⎨︒⎩,< 解得,1822.5θ︒≤︒<.【点睛】本题考查了射线的性质、等腰三角形的性质、解一元一次不等式组,解题的关键在于找到等量关系,求相关角的度数.23.(1)150元;100元;(2)甲商场()10014000a + ,乙商场()8015000a +元;(3)50a =;(4)当50a =时,两家花费一样;当1050a <<时,到甲处购买更合算;当50a 时,到乙处购买更合算【分析】(1)设每个足球的定价是x 元,则每套队服是()50x +元,根据“两套队服与三个足球的费用相等”得出等量关系,列出一元一次方程,求解即可;(2)根据甲商场和乙商场的方案列出式子即可;(3)令100140008015000,a a ++=解方程即可;(4)列出不等式分别求解即可.【详解】解:(1)设每个足球的定价是x 元,则每套队服是()50x +元.根据题意得()2503x x +=解得100,50150x x +==. 答:每套队服150元,每个足球100元.(2)到甲商场购买所花的费用为:()1001001501001001400010a a ⎛⎫⨯+-=+ ⎪⎝⎭元; 到乙商场购买所花的费用为:()100150+100808015000a a ⨯⨯%=+元;(3)由100140008015000,a a ++=得:50a =,所以:当50a =时,两家花费一样。
(好题)初中数学八年级数学下册第二单元《一元一次不等式和一元一次不等式组》检测题(答案解析)

一、选择题1.定义[x]为不超过x 的最大整数,如[3.5]=3,[0.5]=0,[﹣2.5]=﹣3.对于任意实数,下列式子中错误的是( )A .[x]=x (x 为整数)B .0≤x ﹣[x]< 1C .[n+x]=n+[x](n 为整数)D .[x+y]≤[x]+[y] 2.关于函数3y x =-,下列说法正确的是( ) A .在 y 轴上的截距是3B .它不经过第四象限C .当x≥3时,y≤0D .图象向下平移4个单位长度得到7y x =-的图象3.不等式组()()303129x x x -≥⎧⎨->+⎩的解集为( ) A .3x <- B .3x >- C .3x ≥ D .3x ≤4.若不等式组11233x x x m+⎧<+⎪⎨⎪>⎩有解,则m 的取值范围为( )A .1mB .1m <C .1mD .3m < 5.如果m n >,则下列各式不成立的是( )A .22m n +>+B .22m n ->-C .22m n >D .22m n -<- 6.如果a <b ,那么下列不等式中一定成立的是( )A .a 2<abB .ab <b 2C .a 2<b 2D .a ﹣2b <﹣b7.若不等式组010a x x ->⎧⎨+>⎩无解,则a 的取值范围是( ) A .a≤-1 B .a≥-1 C .a<-1 D .a>-18.直线11:l y k x b =+与直线22:l y k x =在同一平面直角坐标系中的图象如图所示,关于x 的不等式21k x k x b >+的解集为( )A .-1x >B .1x <-C .2x <-D .无法确定9.关于x 的不等式620x x a -≤⎧⎨≤⎩有解,则a 的取值范围是( ) A .a <3 B .a≤3 C .a≥3 D .a >310.爆破员要爆破一座旧桥,根据爆破情况,安全距离是70米(人员要撤到70米及以外的地方).已知人员撤离速度是7米/秒,导火索燃烧速度是10.3厘米/秒,为了确保安全,这次爆破的导火索至少为( )A .100厘米B .101厘米C .102厘米D .103厘米 11.已知a <b ,下列变形正确的是( )A .a ﹣3>b ﹣3B .2a <2bC .﹣5a <﹣5bD .﹣2a +1<﹣2b +1 12.不等式组23x x ≥-⎧⎨<⎩的整数解的个数是( ) A .4个 B .5个 C .6个 D .无数个二、填空题13.不等式组63024x x x -⎧⎨<+⎩的解集是__. 14.如图,一次函数y kx b =+的图象经过()2,0A 和()0,1B -,则关于x 的不等式0kx b +≥的解集为______.15.如图,函数y x =和4y ax =+的图象交于点()2,2,A 则不等式4x ax <+的解集为_____________________.16.过点()5,2-的一条直线与x 轴、y 轴分别相交于点A ,B ,且与直线312y x =-+平行,则在线段AB 上,横、纵坐标都是整数的点坐标是______. 17.若关于x 的不等式组0521x m x -<⎧⎨-≤⎩的整数解有且只有4个,则m 的取值范围是:__________.18.已知一次函数y ax b =+的图象如图,根据图中信息请写出不等式0ax b +≥的解集为___________.19.在平面直角坐标系中,点A (0,4),B (-2,0),C (a ,-a ),△ABC 的面积小于10,则a 的取值范围是__________________.20.一次函数y =kx +b ,(k ,b 为常数)的图象如图所示,则关于x 的不等式kx +2b <0的解集是_____.三、解答题21.某校七年级(6)班对半学期考试成绩优秀的学生进行奖励,颁发奖品,班主任安排生活委员到某文具店购买甲、乙两种奖品,若买甲种奖品20个,乙种奖品10个,共用110元,买甲种奖品30个比买乙种奖品20个少花10元.(1)求甲、乙两种奖品的单价各是多少元;(2)因奖品数量的需要和班费的限制,现要求本次购买甲种奖品的数量是乙种奖品的数量的2倍还少10个,而且购买这两种奖品的总金额不低于280元且不超过320元,请问有哪几种购买方案?哪种方案最省钱?22.在同一平面直角坐标系内画出一次函数14y x =-+和225y x =-的图象,根据图象回答下列问题:(1)求出方程组425y x y x =-+⎧⎨=-⎩的解; (2)当x 取何值时,12y y >?当x 取何值时,10y >且20y <?23.设一次函数()11y m x =-,()21y n x =+(m ,n 是常数,且m≠0,m≠n ,n>0) (1)当m=3,n=2时,①求函数y 1,y 2图象的交点坐标.②若y 1>y 2,求自变量x 的取值范围.(2)在0<x<1的范围内,有且只有部分函数值满足y 1>y 2,求证:m+n<0.24.解下列一元一次不等式组.23253x x x +≤⎧⎪+⎨>⎪⎩ 25.已知直线y kx b =+经过点()5,0A ,()1,4B .(1)求直线AB 的解析式;(2)若直线24y x =-与直线AB 相交于点C ,求点C 的坐标;(3)根据图像,写出关于x 的不等式24x kx b -<+的解集.26.某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A 、B 两种型号的污水处理设备共10台,具体情况如下表:经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.A 型B 型 价格(万元/)15 12 月污水处理能力(吨/月) 250 200(2)哪种方案更省钱?并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据“定义[x]为不超过x 的最大整数”进行计算.【详解】解:A 、∵[x]为不超过x 的最大整数,∴当x 是整数时,[x]=x ,成立;B 、∵[x]为不超过x 的最大整数,∴0≤x -[x]<1,成立;C 、[n+x]=n+[x](n 为整数),成立;D 、例如,[-5.4-3.2]=[-8.6]=-9,[-5.4]+[-3.2]=-6+(-4)=-10,∵-9>-10,∴[-5.4-3.2]>[-5.4]+[-3.2],∴[x+y]≤[x]+[y]不成立,故选:D .【点睛】本题考查了一元一次不等式组的应用,解决本题的关键是理解新定义,新定义解题是近几年高考常考的题型.2.D解析:D【分析】令x=0,得到的y 值就是在y 轴上的截距;根据k ,b 判定图像的分布;根基自变量的范围计算函数的范围;根据平移规律确定即可.【详解】令x=0,得y= -3,∴函数在y 轴上的截距为-3,∴选项A 错误;∵3y x =-,∴函数分布在第一,第三,第四象限,∴选项B 错误;∵x≥3,∴x-3≥0,∴y≥0,∴选项C 错误;∵3y x =-,∴图象向下平移4个单位长度得到7y x =-的图象,∴选项D 正确;故选D .【点睛】本题考查了一次函数的性质,图像分布,平移规律,截距的定义,熟练掌握性质,规律是解题的关键.3.A解析:A【分析】先解每一个不等式,再求不等式组的解集.【详解】解:()()303129x x x -≥⎧⎪⎨->+⎪⎩①②, 解不等式①得,x ≤3,解不等式②得,x <-3,∴不等式组的解集为x <-3,故选A【点睛】本题考查了解一元一次不等式组,先解每一个不等式,再求它们解集的公共部分即可求出不等式组的解集.4.B解析:B【分析】不等式组整理后,利用有解的条件确定出m 的范围即可.【详解】不等式组整理得:33x x m<⎧⎨>⎩, 由不等式组有解,得到3m <3,解得:m <1.故选:B .【点睛】本题考查了解一元一次不等式组,熟练掌握不等式组的解法是解本题的关键.5.B解析:B【分析】根据不等式的性质解答.【详解】A 、在不等式m >n 的两边同时加上2,不等式仍成立,即m+2>n+2,故本选项不符合题意.B 、在不等式m >n 的两边同时乘以-1然后再加上2,不等式号方向改变,即2-m <2-n ,故本选项符合题意.C 、在不等式m >n 的两边同时除以2,不等式仍成立,即22m n >,故本选项不符合题意. D 、在不等式m >n 的两边同时乘以-2,不等式号方向改变,即-2m <-2n ,故本选项不符合题意.故选:B .【点睛】本题主要考查了不等式的性质,在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.6.D解析:D【分析】利用不等式的基本性质逐一进行分析即可.【详解】A 、a <b 两边同时乘以a ,应说明a >0才得a 2<ab ,故此选项错误;B 、a <b 两边同时乘以b ,应说明b >0才得ab <b 2,故此选项错误;C 、a <b 两边同时乘以相同的数,故此选项错误;D 、a <b 两边同时减2b ,不等号的方向不变可得a−2b <−b ,故此选项正确;故选D .【点睛】此题主要考查了不等式的基本性质,关键是要注意不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变.7.A解析:A【分析】要求出a 的值,首先分别求出这两个不等式解,最后根据不等式组无解的情况来确定a 的值.【详解】解:010a x x ->⎧⎨+>⎩①②解不等式①,得x<a ,解不等式②,得x>-1∵原不等式组无解,∴a≤-1故答案为:A .【点睛】本题考查了解一元一次不等式组,关键是知道不等式组的解集是由这两个不等式的解集的公共部分构成的,题目无解说明这两个不等式的解集没有公共部分这是关键.8.B解析:B【分析】由图象可知,当1x =-时,两个函数的函数值是相等的,再根据函数的增减性可以判断出不等式21k x k x b >+解集.【详解】两条直线的交点坐标为(-1,3),且当 x<−1 时,直线2l 在直线1l 的上方,∴不等式21k x k x b >+的解集为: x<−1故选:B.【点睛】本题考察借助一次函数的图象解一元一次不等式,两个图象的“交点”是两个函数值大小关系的“分界点”,在“分界点”处函数值的大小发生了改变.9.C解析:C【分析】解不等式6-2x ≤0,再根据不等式组有解求出a 的取值范围即可.【详解】解不等式6-2x ≤0,得:x ≥3,∵不等式组有解,∴a ≥3.故选:C .【点睛】本题主要考查根据不等式组的解判断未知参数的范围,熟练掌握不等式组的解法是解题关键.10.D解析:D【分析】设这次爆破的导火索需要xcm 才能确保安全,安全距离是70米(人员要撤到70米以外),根据人员速度是7米/秒,导火索的燃烧速度是10.3厘米/秒,列不等式求解即可.【详解】设这次爆破的导火索为x 厘米才能确保安全.根据安全距离是70米(人员要撤到70米及以外的地方),可列不等式:77010.3x ⨯≥ 解得:103x ≥故选:D【点睛】本题考查一元一次不等式的应用,关键是理解导火索燃尽时人撤离的距离要大于等于70米. 11.B解析:B【分析】运用不等式的基本性质求解即可.【详解】由a <b ,可得:a ﹣3<b ﹣3,2a <2b ,﹣5a >﹣5b ,﹣2a+1>﹣2b+1,故选B .【点睛】本题主要考查了不等式的性质,解题的关键是注意不等号的开口方向.12.B解析:B【分析】本题首先求解该不等式组公共解集,继而在解集内确定整数解.【详解】由已知得:23x -≤<,该范围内包含5个整数解:2-,1-,0,1,2.故选:B .【点睛】本题考查求不等式的整数解,解题关键在于确定公共解集,其次确定答案时要确保不重不漏.二、填空题13.【分析】分别解两个不等式得到和x <4然后根据同大取大同小取小大于小的小于大的取中间小于小的大于大的无解确定不等式组的解集【详解】解:解不等式得:解不等式得:则不等式组的解集为故答案为【点睛】本题考查 解析:2x【分析】分别解两个不等式得到2x 和x <4,然后根据同大取大,同小取小,大于小的小于大的取中间,小于小的大于大的无解确定不等式组的解集.【详解】解:解不等式630x -,得:2x ,解不等式24x x <+,得:4x <,则不等式组的解集为2x ,故答案为2x .【点睛】本题考查了解一元一次不等式组:求解出两个不等式的解集,然后按照“同大取大,同小取小,大于小的小于大的取中间,小于小的大于大的无解”确定不等式组的解集. 14.x≥2【分析】根据一次函数的性质及与一元一次不等式的关系即可直接得出答案【详解】∵一次函数图象经过一三象限∴y 随x 的增大而增大∵一次函数y =kx+b 的图象经过A (20)B (0﹣1)两点∴x≥2时y≥解析:x≥2【分析】根据一次函数的性质及与一元一次不等式的关系即可直接得出答案.【详解】∵一次函数图象经过一、三象限,∴y 随x 的增大而增大,∵一次函数y =k x +b 的图象经过A (2,0)、B (0,﹣1)两点,∴x≥2时,y≥0,即kx+b≥0,故答案为:x≥2【点睛】本题主要考查一次函数和一元一次不等式的知识点,解答本题的关键是进行数形结合,此题比较简单.15.【分析】先利用A 点坐标然后观察函数图得到当x <2时y=x 的图象都在直线的下方由此得到不等式x <ax+4的解集【详解】解:A (23)观察函数图得到:当x <2时y=x 的图象都在直线的下方不等式x <ax+解析:2x <【分析】先利用A 点坐标,然后观察函数图得到当x <2 时,y=x 的图象都在直线4y ax =+的下方,由此得到不等式x <ax+4的解集.【详解】 解: A (2,3),观察函数图得到:当x <2 时,y=x 的图象都在直线4y ax =+的下方,∴ 不等式x <ax+4的解集x <2.故答案为:2x <.【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.理解好上面原理是解题的关键.16.(14)(31)【分析】依据与直线平行设出直线AB 的解析式;代入点(5-2)即可求得b 然后求出与x 轴的交点横坐标列举符合条件的x 的取值依次代入即可【详解】解:∵过点(5-2)的一条直线与直线平行设直解析:(1,4),(3,1).【分析】 依据与直线312y x =-+平行设出直线AB 的解析式32y x b =-+;代入点(5,-2)即可求得b ,然后求出与x 轴的交点横坐标,列举符合条件的x 的取值,依次代入即可.【详解】 解:∵过点(5,-2)的一条直线与直线312y x =-+平行,设直线AB 为32y x b =-+; 把(5,-2)代入32y x b =-+;得-2=152b -+ 解得:b=112∴直线AB 的解析式为31122y x =-+ 令y=0,得:311022x =-+ 解得:x=113 ∴0<x <113的整数为:1、2、3; 把x 等于1、2、3分别代入解析式得4、52、1; ∴在线段AB 上,横、纵坐标都是整数的点的坐标是(1,4),(3,1).故答案为:(1,4),(3,1).【点睛】本题考查了待定系数法求解析式以及直线上点的情况,列举出符合条件的x 的值是本题的关键.17.【分析】先解不等式组得到解集为:<此时的整数解有且只有4个结合数轴分析可得到的取值范围【详解】解:由①得:<由②得:所以不等式组的解集为:<不等式组的整数解有且只有4个如图不等式组的整数解为<故答案 解析:56m <≤【分析】先解不等式组,得到解集为:2x ≤<m ,此时的整数解有且只有4个,结合数轴分析可得到m 的取值范围.解:0521x m x -<⎧⎨-≤⎩①② 由①得:x <m ,由②得:24,x -≤-2,x ∴≥所以不等式组的解集为:2x ≤<m ,不等式组的整数解有且只有4个,如图,不等式组的整数解为2,3,4,5,5∴< 6.m ≤故答案为:56m <≤.【点睛】本题考查的是不等式组的整数解问题,掌握利用数轴分析得出不等式组中字母的取值范围是解题的关键.18.【分析】观察函数图形得到当x ≥-1时一次函数y=ax+b 的函数值不小于0即ax+b≥0【详解】解:根据题意得当x≥-1时ax+b≥0即不等式ax+b≥0的解集为x≥-1故答案为:x≥-1【点睛】本题解析:1x ≥-【分析】观察函数图形得到当x≥-1时,一次函数y=ax+b 的函数值不小于0,即ax+b≥0.【详解】解:根据题意得当x≥-1时,ax+b≥0,即不等式ax+b≥0的解集为x≥-1.故答案为:x≥-1.【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.19.且【分析】根据AB 坐标利用待定系数法可求出直线AB 的解析式根据点C 坐标可得点C 在直线y=-x 上即在直线OC 上联立ABOC 解析式可得交点坐标分a=0a >0<a <0a <四种情况画出图形分别用a 表示出△A 解析:1423a -<<且4-3a ≠根据A、B坐标,利用待定系数法可求出直线AB的解析式,根据点C坐标可得点C在直线y=-x上,即在直线OC上,联立AB、OC解析式可得交点坐标,分a=0,a>0,43-<a<0、a<43-四种情况,画出图形,分别用a表示出△ABC的面积,根据△ABC的面积小于10列不等式求出a的取值范围即可得答案.【详解】设直线AB的解析式为y=kx+b,∵A(0,4),B(-2,0),∴OA=4,OB=2,∵点A、B在直线AB上,∴204k bk-+=⎧⎨=⎩,解得:24 kb=⎧⎨=⎩,∴直线AB的解析式为y=2x+4,①当a=0时,点C(0,0),与原点重合,S△ABC=12OA·OB=4<10,∴a=0符合题意,②如图,当a>0时,点C(a,-a)在第四象限,连接OC,∴S△ABC=S△ABO+S△AOC+S△BOC=12×2×4+12×4a+12×2a=4+3a,∵△ABC的面积小于10,∴4+3a<10,解得a<2,∴0<a<2,∵点C(a,-a),∴点C在直线y=-x上,即在直线OC上,联立直线AB与直线OC的解析式得24 y xy x=+⎧⎨=-⎩,解得:4343 xy⎧=-⎪⎪⎨⎪=⎪⎩,∴直线AB与直线OC的交点坐标为(43-,43),∴a≠43-,②如图,当43-<a<0时,点C在△ABO的内部,∴S△ABC<S△ABO<10,∴43-<a<0符合题意,③如图,当a<43-时,点C(a,-a)在第二象限,且在△ABO的外部,连接OC,∴S△ABC=S△AOC+S△BOC-S△ABO=12×4(-a)+12×2(-a)-12×2×4 =3a-4,∵△ABC 的面积小于10,∴-3a-4<10,解得:a >143-, ∴143-<a <43-,综上所述:a 的取值范围是143-<a <2,且a≠43-. 故答案为:143-<a <2,且a≠43- 【点睛】 本题考查一次函数的交点问题及三角形的面积,熟练掌握待定系数法求一次函数解析式、利用图形正确表示出△ABC 的面积并灵活运用分类讨论的思想是解题关键.20.x >6【分析】由题意可以用k 表示b 于是题中不等式变为含有参数k 的不等式然后由一次函数图象可以得知k<0最后根据不等式的性质可以得到解答【详解】解:把(30)代入y =kx+b 得3k+b =0∴b =﹣3k解析:x >6【分析】由题意可以用k 表示b ,于是题中不等式变为含有参数k 的不等式,然后由一次函数图象可以得知k<0,最后根据不等式的性质可以得到解答.【详解】解:把(3,0)代入y =kx +b 得,3k +b =0,∴b =﹣3k ,∵kx +2b <0,∴kx <6k, 由图象可知k <0,∴x >6,故答案为x >6.【点睛】本题考查一次函数与不等式的综合应用,熟练掌握一次函数的图象与性质、不等式的基本性质是解题关键.三、解答题21.(1)甲种奖品的单价为3元,乙种奖品的单价是5元;(2)方案①购买乙种奖品29个,购买甲种奖品48个最省钱.【分析】(1)设甲种奖品的单价是x 元,一种奖品的单价是y 元,然后依据买甲种奖品20个,乙种奖品10个,共用110元,买甲种奖品30个比买乙种奖品20个少花10元列方程组求解即可;(2)设购买乙种奖品的数量为a 个,则购买甲种奖品的数量为(2a-10)个,然后依据总费用在280元到320元之间列不等式组求解即可.【详解】解:(1)设甲种奖品的单价是x 元,一种奖品的单价是y 元.根据题意得:2010110302010x y x y +=⎧⎨-=-⎩, 解得:x=3,y=5.答:甲种奖品的单价为3元,乙种奖品的单价是5元.(2)设购买乙种奖品的数量为a 个,则购买甲种奖品的数量为(2a -10)个.根据题意得3(210)52803(210)5320a a a a -+≥⎧⎨-+≤⎩解得:2928311111a ≤≤. ∵a 只能取正整数,∴a =29,30,31.∴有3中购买方案. 方案①:购买乙种奖品29个,购买甲种奖品48个;方案②:购买乙种奖品30个,购买甲种奖品50个;方案③:购买乙种奖品31个,购买甲种奖品52个.方案①最省钱.∵3×48+5×29=289元;3×50+5×30=3009元;3×52+5×31=311元,∴方案①最省钱.【点睛】本题主要考查的是二元一次方程组和一元一次不等式组的应用,根据列出方程组和不等式组是解题的关键.22.(1)31x y =⎧⎨=⎩;(2)当3x <时,12y y >,当 2.5x <时,10y >且20y < 【分析】(1)根据题意画出一次函数y 1=-x+4和y 2=2x-5的图象,根据两图象的交点即可得出方程组425y x y x =-+⎧⎨=-⎩的解; (2)根据函数图象可直接得出结论.【详解】解:(1)如图所示:一次函数14y x =-+和225y x =-的图象相交于点(3,1)∴方程组425y x y x =-+⎧⎨=-⎩的解为31x y =⎧⎨=⎩; (2)由图可知,当3x <时,12y y >当 2.5x <时,10y >且20y <;【点睛】本题考查的是一次函数与一元一次方程组,一次函数与一元一次不等式,能根据题意画出函数图象,利用数形结合求解是解答此题的关键.23.(1)①(5,12);②x>5;(2)见解析.【分析】(1)①将m=3、n=2代入两个一次函数,然后联立解二元一次方程组即可; ②根据题意列不等式求解即可;(2)先确定两函数与y 轴的交点坐标以及所多顶点,然后再根据x 的取值范围即可解答.【详解】解:(1)当m=3,n=2时,133y x =-,222y x =+①联立3322y x y x =-⎧⎨=+⎩,解得512x y =⎧⎨=⎩ ∴交点坐标为(5,12);②y 1>y 2则3322x x >-+解得x>5;(2)∵()11y m x =-与y 轴交点为(0,m -),1y 过定点(1,0),()21y n x =+与y 轴交点为(0,n ),同时2y 过定点(-1,0),∵在0<x<1的范围内,有且只有部分函数值满足y 1>y 2∴根据图像得到m ->n 即m+n<0.【点睛】本题属于一次函数的综合题,主要考查了一次函数的性质、解二元一次方程组、解不等式,考查知识点较多,灵活应用相关知识成为解答本题的关键.24.1x ≤【分析】先求出不等式的解集,再求出不等式组的解集即可.【详解】解:23253x x x +≤⎧⎪⎨+>⎪⎩①② 由①得1x ≤,由②得5x <,所以原不等式组的解是1x ≤.【点睛】本题考查了解一元一次不等式组,不等式的解等知识点,求出不等式或不等式组的解集是解此题关键.25.(1)y =-x +5;(2)点C 的坐标(3,2);(3)3x <【分析】(1)利用待定系数法求解;(2)联立方程组524y x y x =-+⎧⎨=-⎩,解得方程组的解即可得到答案; (3)不等式24x kx b -<+的解集即直线y=2x-4的图象在直线y=kx+b 的下方,依据图象直接得到答案.【详解】解:(1)设一次函数的解析式为y =kx +b ,∵一次函数的图象经过点A (5,0)和B (1,4)两点.∴504k b k b +=⎧⎨+=⎩解得-15k b =⎧⎨=⎩∴一次函数的表达式为y =-x +5;(2)联立方程组524y x y x =-+⎧⎨=-⎩, 解得32x y =⎧⎨=⎩, ∴点C 的坐标(3,2);(3)不等式24x kx b -<+的解集为:3x <.【点睛】此题考查待定系数法求函数解析式,一次函数与二元一次方程组及一次函数与不等式的关系,掌握一次函数的基础知识是解题的关键.26.(1)有3种购买方案:第一种是购买3台A 型污水处理设备,7台B 型污水处理设备;第二种是购买4台A 型污水处理设备,6台B 型污水处理设备;第三种是购买5台A 型污水处理设备,5台B 型污水处理设备;(2)购买3台A 型污水处理设备,7台B 型污水处理设备更省钱【分析】(1)设购买污水处理设备A 型号x 台,则购买B 型号(10﹣x )台,由不等量关系购买A 型号的费用+购买B 型号的费用≤136;A 型号每月处理的污水总量+B 型号每月处理的污水总量≥2150,列出不等式组,然后找出最合适的方案即可.(2)计算出每一方案的花费,通过比较即可得到答案.【详解】设购买污水处理设备A 型号x 台,则购买B 型号(10﹣x )台,根据题意,得1512(10)136250200(10)2150x x x x +-≤⎧⎨+-≥⎩, 解这个不等式组,得:1353x ≤≤.∵x 是整数,∴x=3或x=4或x=5.当x=3时,10﹣x=7;当x=4时,10﹣x=6;当x=5时,10-x=5.答:有3种购买方案:第一种是购买3台A 型污水处理设备,7台B 型污水处理设备;第二种是购买4台A型污水处理设备,6台B型污水处理设备;第三种是购买5台A型污水处理设备,5台B型污水处理设备;(2)当x=3时,购买资金为15×3+12×7=129(万元),当x=4时,购买资金为15×4+12×6=132(万元),当x=5时,购买资金为15×5+12×5=135(万元).因为135>132>129,所以应购污水处理设备A型号3台,B型号7台.答:购买3台A型污水处理设备,7台B型污水处理设备更省钱.【点睛】此题考查方案类不等式组的实际应用,有理数的混合运算,正确理解题意,根据题意列得不等式组是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009—2010学年八年级数学第二学期抽测考试
一元一次不等式
一、选择与填空 ( 满分48分,第1—7
题,每题3分,第7—14题,每题3分)
1.如图 ,数轴上A ,B ,C 三点表示的数分别为a ,b ,c ,则它们的大小关系( )
(A ) a >b >c (B ) b >c >a (C ) c >a >b (D ) b >a >c
2.根据图1和图2所示,对a b c ,,三种物体的重量判断不正确的是( ) (A )
a c <
(B )B .a b <
(C )a c >
(D )b c <
3. 若x >y ,则下列不等式中成立的是 ( ) (A ) x+a < y+b (B )ax <by (C )a 2x >b 2y (D )a-x <a-y
4. 不等式260x ->的解集在数轴上表示正确的是 ( )
5. 如图,在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为
( )
(A )x <4 (B )x <2 (C )2<x <4 (D )x >2
6. 关于x 的不等式2x -a ≤-1的解集如图所示,则a 的取值是 ( )
(A )0 (B )-3 (C )-2 (D )-1
7.不等式组2
21
x x -⎧⎨
-<⎩≤的整数解共有( )
A .3个
B .4个
C .5个
D .6个
8.若不等式组0,
122x a x x +⎧⎨->-⎩
≥有解,则a 的取值范围是( )
(A)a >-1 (B)a ≥-1 (C)a ≤1 (D)a <1
9. x 与5的差不小于3,用不等式表示为 . . 10 . 关于x 的方程x kx 21=-的解为正实数,则k 的取值范围是 . 11. 当x 时,式子3x -5的值大于5x +3的值.
(A ) (B ) (C ) (D )
( 第6题)
( 第1题)
图1
图2
( 第2题) ( 第5题)
12. 解集在数轴上表示为如图所示的不等式组是 . 13. 三个连续正整数的和不大于12.这样的正整数有 组.
14.已知不等式:①1x >,②4x >,③2x <,④21x ->-,从这四个不等式中取两个,构成正整数解是2的不等式组是 .
二、求解与应用(满分20分,第15题12分, 第16题8分)
15.解不等式(组) :
(1) 解不等式:5x –12≤2(4x -3)
(2)解不等式组3(1)54121
23x x x x +>+⎧⎪
⎨--⎪⎩
①≤ ②,并将解集在数轴上表示出来.
16. 有个两位数,其十位数比个位数字大2,这个两位数在50和70之间,你能求出这个两位数吗?
三、生活与数学(满分20分,每题10分)
17. 某次知识竞赛共有20道题,每题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少要对多少道题?
18.开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本
共48件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不少于钢笔数,共有多少种购买方案?请你一一写出.
四、操作与探究(满分12分)
19. 从2008年12月1日起,国家开始实施家电下乡计划,国家按照农民购买家电金额的13%予以政策补贴,某商场计划购进A、B两种型号的彩电共100台,已知该商场所筹购买的资
金不少于222000元,但不超过222800元,国家规定这两种型号彩电的进价和售价如下表:
(1)农民购买哪种型号的彩电获得的政府补贴要多些?请说明理由;
(2)该商场购进这两种型号的彩电共有哪些方案?其中哪种购进方案获得的利润最大?请说明理由.(注:利润=售价-进价)。
