江苏省启东中学高一数学第一学期第三次月考试题-苏教版
江苏省启东中学高一数学上学期第一次月考试题(创新班,

江苏省启东中学2016~2017学年度创新班高一阶段考试 数学试卷 2016.9.20一、填空题:本题共14小题,每小题5分,共70分.请把答案填写在答题..纸.相应位置上...... 1.不等式223x x -<的解集为 .2.在ABC ∆中,已知3AB =,2BC =,60B ︒∠=,则AC = . 3.已知等比数列{}n a 的各项都是正数,且41016a a =,则8a = .4.ABC ∆的三边长分别为a ,b ,c ,若cos cos sin b C c B a A +=,则ABC ∆的形状为 . 5.方程3sin 1cos2x x =+在区间[]02π, 上的解集为 .6.在数列{}n a 中,12a =,*11(N )n n a a n +=-∈,n S 为数列的前n 项和,则2015201620172S S S -+的值为 .7.函数()=(3sin cos )(3cos sin )f x x x x x +-的最小正周期是 .8.若x ,y 满足错误!未找到引用源。
2030x y x y x -≤⎧⎪+≤⎨⎪≥⎩,,,则2x y +的最大值为 .9.已知正数a ,b 满足3ab a b =++,则a b +的最小值为 .10.已知数列{}n a 是以3为公差的等差数列,n S 是其前n 项和,若10S 是数列{}n S 中的唯一最小项,则数列{}n a 的首项1a 的取值范围是 .11.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若223a b bc -=,sin 23sin C B =,则角A = .12.各项均为正数的等比数列{}n a 中,若1a ≥1,2a ≤2,3a ≥3,则4a 的取值范围是 .13.已知函数27()1x ax a f x x +++=+,R a ∈,若对于任意的*N x ∈,()f x ≥4恒成立,则a 的取值范围是 . 14.无穷数列{}n a 由k 个不同的数组成,n S 为{}n a 的前n 项和.若对任意*N n ∈,{}23n S ∈, ,则k 的最大值为 .二、解答题:本大题共6小题,共计90分,请在答题..纸.指定区域....内作答.解答时应写出文字说明、 证明过程或演算步骤. 15.(本小题满分14分)在ABC ∆中,2222a c b ac +=+.⑴求B ∠的大小;⑵求2cos cos A C +的最大值.16.(本小题满分14分) 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知tan tan 2(tan tan )cos cos A BA B B A+=+.⑴证明:2a b c +=;⑵求cos C 的最小值.17.(本小题满分14分)对于实数π(0)2x ∈, ,2214()=9sin 9cos f x x x+. ⑴若()f x ≥t 恒成立,求t 的最大值M ;⑵在⑴的条件下,求不等式2|2|x x M +-+≥3的解集.18.(本小题满分16分)已知数列{}n a 的前n 项和238n S n n =+,{}n b 是等差数列,且1n n n a b b +=+.⑴求数列{}n b 的通项公式;⑵令1(1)(2)n n n nn a c b ++=+,求数列{}n c 的前n 项和n T .19.(本小题满分16分)请用多种方法证明不等式:(用一种方法得8分,两种方法得14分,三种方法得16分.)已知a ,(0)b ∈+∞, ,证明:b a +≥a b +.20.(本小题满分16分)设A是由有限个正整数组成的集合,若存在两个集合B,C满足:①B C=∅I;②B C AU;③B的元素之和等于C的元素之和,则称集合A“可均分”.=⑴证明:集合{}A=, , , , , , ,“可均分”;12345678⑵证明:集合{}, , ,“可均分”;LA=+++2015120152201593⑶求出所有的正整数k,使得{}, , ,“可均分”.L=+++A k20151201522015。
南通市启东中学2022-2023学年高三上学期第一次月考数学试题含解析

江苏省启东中学2022-2023学年度高三第一学期第一次月考一、单选题(本大题共8小题,共40.0分.)1.已知集合{}1,2A =,{}220B x x mx =+-=,若{}1A B ⋂=,则B =()A.{}1,3 B.{}1 C.{}1,2- D.{}1,1,2-2.若1i z =-+,设zzω=,则ω=()A.12B.1C.32D.23.牛顿曾经提出了常温环境下的温度冷却模型:()100ektθθθθ-=-+,其中为时间(单位:min ),0θ为环境温度,1θ为物体初始温度,θ为冷却后温度),假设在室内温度为20C o 的情况下,一桶咖啡由100C 降低到60C 需要20min .则k 的值为()A.ln 220B.ln 320 C.ln 210-D.ln 310-4.已知平面α和平面β不重合,直线m 和n 不重合,则//αβ的一个充分条件是().A .,m n αβ⊂⊂且//m nB.,m n αβ⊂⊂且//,//m n βαC.//,//m n αβ且//m nD.,m n αβ⊥⊥且//m n5.设()f x 是定义在实数集R 上的函数,且满足()()11f x f x +=-,()()22f x f x +=--,则()f x 是()A.偶函数,又是周期函数B.偶函数,但不是周期函数C.奇函数,又是周期函数D.奇函数,但不是周期函数6.若()1tan022θθπ=<<,则sin 2θ的值为()A.2425B.1516 C.1516-D.2425-7.在ABC 中,120BAC ∠=,AD 为BAC ∠的平分线,2AB AC =,则ABAD=()A.2B.C.3D.8.已知 2.12.2a =, 2.22.1b =, 2.12.1c =,则()A.a c b<< B.c b a<< C.b c a<< D.c a b<<二、多选题(本大题共4小题,共20.0分.在每小题有多项符合题目要求)9.函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象如图所示,则()A.2ω= B.6π=ϕC.对任意的x 都有()512f x f π⎛⎫≥⎪⎝⎭D.()f x 在区间[],ππ-上的零点之和为3π10.已知,D E 是 ABC 边BC 的三等分点,点P 在线段DE 上,若AP xAB yAC =+,则xy 的值可以是()A.19B.29C.14D.1311.公比为q 的等比数列{}n a ,其前n 项和为n S ,前n 项积为n T ,满足11a >,202120221a a ⋅>,20212022101a a -<-.则下列结论正确的是()A.01q <<B.202120231a a ⋅>C.n S 的最大值为2023S D.n T 的最大值为2021T 12.已知定义域为R 的函数()f x 的图象连续不断,且R x ∀∈,()()24f x f x x +-=,当()0,x ∈+∞时,()4f x x '<,若()()221682f m f m m m +--≤++,则实数m 的取值可以为()A.-1B.13-C.12D.1三、填空题(本大题共4小题,共20.0分)13.已知数列{}n a 满足()121n n a a n n N +++=+∈,1=1a ,则数列{}n a 的通项公式为___________.14.如图,△ABC 的外接圆的圆心为O ,AB =2,AC =3,7BC =AO BC ⋅=________.15.三棱锥P ABC -中,2PA AB PB AC ====,22CP =D 是侧棱PB 的中点,且7CD =则三棱锥P ABC -的外接球O 的表面积___________.16.不等式220x x ax a ---<的解集中只存在两个整数,则正数a 的取值范围是___________.四、解答题(本大题共6小题,共70.0分.解答应写出文字说明,证明过程或演算步骤)17.已知函数()243xf x x a-=-,a R ∈.(1)若()y f x =在()()1,1f 处的切线斜率为5-,求a 的值;(2)若()f x 在1x =-处取得极值,求()f x 在[]22-,上的最大值.18.如图所示,在梯形ABCD 中,//AB CD ,2BAD π∠=,点E 是AD 上一点,2=4DE AE =,2cos cos cos BC BEC BE EBC CE ECB ∠=∠+∠.(1)求BEC ∠的大小;(2)若BCE 的面积S 为BC .19.如图,在四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,1AA ⊥平面ABCD ,122AA AB ==,点M 在1DD 上,且1B D ⊥平面ACM.(1)求1DMDD 的值;(2)求二面角D AC M --的正弦值.20.已知各项都为正数的数列{}n a 的前n 项和为n S ,且对任意的*n ∈N ,都有22(n n n pS a pa =+其中0p >,且p 为常数),记数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和为nH (1)求数列{}n a 的通项公式及n H (2)当=2p 时,将数列1n a ⎧⎫⎨⎬⎩⎭的前4项抽去其中一项后,剩下三项按原来的顺序恰为等比数列{}n b 的前3项,记{}n b 的前m 项和为m T ,若存在*N m ∈,使得对任意*n ∈N ,总有m n T H λ<+恒成立,求实数λ的取值范围21.已知椭圆2222:1(0)x y a b a b Γ+=>>的离心率为2,点A ,B ,C 分别为Γ的上,左,右顶点,且||4BC =.(1)求Γ的标准方程;(2)点D 为线段AB 上异于端点的动点,过点D 作与直线AC 平行的直线交Γ于点P ,Q ,求||||PD QD ⋅的最大值.22.已知函数()e xf x x x =-.(Ⅰ)讨论()f x 的单调性;(Ⅱ)证明:当0x >时,()ln 1f x x -≥.2022-2023学年度江苏省启东中学高三第一学期第一次月考一、单选题(本大题共8小题,共40.0分.在每小题列出的选项中,选出符合题目的一项)1.已知集合{}1,2A =,{}220B x x mx =+-=,若{}1A B ⋂=,则B =()A.{}1,3 B.{}1 C.{}1,2- D.{}1,1,2-【答案】C 【解析】【分析】分析可知1B ∈,根据根与系数的关系求出m 的值,进而可求得集合B .【详解】因为{}1A B ⋂=,所以1B ∈,把1x =代入220x mx +-=得1m =,所以{}{}2201,2B x x x =+-==-,故选:C.2.若1i z =-+,设zzω=,则ω=()A.12B.1C.32D.2【答案】B 【解析】【分析】利用复数的除法化简复数ω,利用复数的模长公式可求得结果.【详解】()()()21i 1i i 1i 1i 1i z z ω----====-+-+--,所以1ω=.故选:B.3.牛顿曾经提出了常温环境下的温度冷却模型:()100e kt θθθθ-=-+,其中为时间(单位:min ),0θ为环境温度,1θ为物体初始温度,θ为冷却后温度),假设在室内温度为20C o 的情况下,一桶咖啡由100C 降低到60C 需要20min .则k 的值为()A.ln 220B.ln 320C.ln 210-D.ln 310-【答案】A 【解析】【分析】把020θ=,1100θ=,60θ=,20t =代入()100e kt θθθθ-=-+可求得实数k 的值.【详解】由题意,把020θ=,1100θ=,60θ=,20t =代入()100e kt θθθθ-=-+中得2080e 2060k -+=,可得201e 2k -=,所以,20ln 2k -=-,因此,ln 220k =.故选:A.4.已知平面α和平面β不重合,直线m 和n 不重合,则//αβ的一个充分条件是().A.,m n αβ⊂⊂且//m n B.,m n αβ⊂⊂且//,//m n βαC.//,//m n αβ且//m nD.,m n αβ⊥⊥且//m n【答案】D 【解析】【分析】根据空间中直线、平面的平行关系进行逐项判断即可.【详解】A .若,m n αβ⊂⊂且//m n ,此时α和β可以相交或平行,故错误;B .若,m n αβ⊂⊂且//,//m n βα,此时α和β可以相交或平行,故错误;C .若//,//m n αβ且//m n ,此时α和β可以相交或平行,故错误;D .若,mn αβ⊥⊥且//m n ,则有m β⊥,两个不同平面和同一直线垂直,则两平面平行,所以//αβ,故正确;故选:D.5.设()f x 是定义在实数集R 上的函数,且满足()()11f x f x +=-,()()22f x f x +=--,则()f x 是()A.偶函数,又是周期函数B.偶函数,但不是周期函数C.奇函数,又是周期函数D.奇函数,但不是周期函数【答案】C 【解析】【分析】利用题中条件推导出()()4f x f x =+,()()f x f x -=-,即可得出结论.【详解】因为()()11f x f x +=-,()()22f x f x +=--,所以()()()()()()()211112f x f x f x f x f x -=+-=--==-+,所以()()()24f x f x f x +=-+=-,故()()4f x f x =+,所以()f x 周期为4,因为()()()()()()()42222f x f x f x f x f x -=-=+-=---=-,所以()f x 是奇函数.故选:C.6.若()1tan022θθπ=<<,则sin 2θ的值为()A.2425 B.1516 C.1516- D.2425-【答案】A 【解析】【分析】根据正切的倍角公式,求得tan θ,再利用正弦的倍角公式将sin 2θ转化为齐次式,结合同角三角函数关系即可求得结果.【详解】因为22tan42tan 31tan 2θθθ==-,又2222sin cos 2tan 24sin 2sin cos tan 125θθθθθθθ===+.故选:A .7.在ABC中,120BAC∠= ,AD 为BAC∠的平分线,2AB AC=,则ABAD=()A.2B.C.3D.【答案】C 【解析】【分析】利用ABC ABD ACD S S S =+ ,得到AB和AD大小关系,即可得到结果.【详解】ABC ABD ACD S S S =+ ,且120BAC ∠= ,AD 为BAC ∠的平分线,∴1211sin sin sin 232323AB AC AB AD AC AD πππ⋅⋅⋅=⋅⋅⋅+⋅⋅⋅,即AB AC AB AD AC AD⋅=⋅+⋅,(*)2AB AC =,∴(*)式可化为:1322AB AD =,即3AB AD=.故选:C.8.已知2.12.2a =, 2.22.1b =, 2.12.1c =,则()A.a c b<< B.c b a<< C.b c a<< D.c a b<<【答案】B 【解析】【分析】利用幂函数的单调性可得出a 、c的大小关系,利用指数函数的单调性可得出b 、c 的大小关系,构造函数()ln xf x x=,利用函数()f x 在()0,e 上的单调性可得出a 、b 的大小关系,即可得出结论.【详解】因为2.1 2.12.2 2.1>, 2.2 2.12.1 2.1>,即a c >,b c >,构造函数()ln x f x x =,则()21ln xf x x-'=,当0e x <<时,()0f x '>,故函数()f x 在()0,e 上为增函数,因为0 2.1 2.2e <<<,则()()2.1 2.2f f <,即ln 2.1ln 2.22.1 2.2<,可得2.2ln 2.1 2.1ln 2.2<,即2.2 2.1ln 2.1ln 2.2<,故 2.2 2.12.1 2.2<,因此c b a <<.故选:B.二、多选题(本大题共4小题,共20.0分.在每小题有多项符合题目要求)9.函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象如图所示,则()A.2ω= B.6π=ϕ C.对任意的x 都有()512f x f π⎛⎫≥⎪⎝⎭D.()f x 在区间[],ππ-上的零点之和为3π【答案】AB 解析】【分析】利用图象求得函数)f x 的解析式,可判断AB 选项的正误;计算512f π⎛⎫⎪⎝⎭的值,可判断C 选项的正误;利用正弦型函数的对称性可判断D 选项的正误.【详解】由题图可知函数()f x 的最小正周期为4113126T πππ⎛⎫=-=⎪⎝⎭,则22πωπ==,所以,()()sin 2f x x ϕ=+,把,16π⎛⎫ ⎪⎝⎭代入得1sin 3πϕ⎛⎫=+ ⎪⎝⎭,则()232k k Z ππϕπ+=+∈,得()26k k Z πϕπ=+∈,2πϕ< ,6πϕ∴=,则AB 选项均正确;()sin 26f x x π⎛⎫+ ⎝=⎪⎭,当512x π=时,()0f x =,不满足对任意的x 都有()512f x f π⎛⎫≥ ⎪⎝⎭,C 错误;[],x ππ∈- ,11132,666x πππ⎡⎤∴+∈-⎢⎥⎣⎦,则()f x 共有4个零点,不妨设为a 、b 、c 、d ,且ab c d<<<,则222662ab πππ⎛⎫+++=⨯- ⎪⎝⎭,3222662c d πππ+++=⨯,两式相加,整理得422223ab c d π+++=,故()f x 的所有零点之和为23a b c d π+++=,D 错误,故选:AB.10.已知,D E 是 ABC 边BC 的三等分点,点P 在线段DE 上,若AP xAB yAC =+,则xy 的值可以是()A.19B.29C.14D.13【答案】BC 【解析】【分析】根据平面向量共线定理的推论,求得1x y +=以及,x y 的取值范围,将xy 转化为关于x 的二次函数,求其值域,即可结合选项进行选择.【详解】因为,D E 是BC 边的三等分点,点P 在线段DE 上,若AP xAB yAC =+ ,可得1x y +=,12,,33x y ⎡⎤∈⎢⎥⎣⎦,故()2211124xy x x x x x ⎛⎫=-=-=--+⎪⎝⎭,当12x =时,xy 取最大值14,当13x =或23x =时,x 取最小值29.故选:BC .11.公比为q 的等比数列{}n a ,其前n 项和为n S ,前n 项积为n T ,满足11a >,202120221a a ⋅>,20212022101a a -<-.则下列结论正确的是()A.01q << B.202120231a a ⋅>C.n S 的最大值为2023S D.n T 的最大值为2021T 【答案】AD 【解析】【分析】推导出0q >,20211a >,202201a <<,可判断A 选项的正误;利用等比中项的性质可判断B 选项的正误;由数列{}n a 为正项等比数列可判断C 选项的正误;由20211a >,202201a <<可判断D 选项的正误.【详解】若0q <,则22021202220210a a a q =<不合乎题意,所以,0q >,故数列{}n a 为正项等比数列,11a >Q ,202120221a a ⋅>,20212022101a a -<-,20211a ∴>,202201a <<,所以01q <<,故A 正确;22021202320221a a a ⋅=<,故B 错误;11a >Q ,01q <<,所以,数列{}n a 为各项为正的递减数列,所以,n S 无最大值,故C 错误;又20211a >,202201a <<,所以,2021T 是数列{}n T 中的最大项,故D 正确.故选:AD.12.已知定义域为R 的函数()f x 的图象连续不断,且R x ∀∈,()()24f x f x x +-=,当()0,x ∈+∞时,()4f x x '<,若()()221682f m f m m m +--≤++,则实数m 的取值可以为()A.-1B.13-C.12D.1【答案】BCD 【解析】【分析】利用已知条件得到()()()2222f x x f x x ⎡⎤-=----⎣⎦,构造函数()()22g x f x x =-,利用已知条件得到函数()g x 为奇函数且函数()g x 在()0,∞+上单调递减,可得函数()g x 在R 上单调递减,所给的不等式转化为()()21g m g m +≤-,利用单调性求解即可.【详解】依题意可得:()()24f x f x x +-=,故()()()2222f x x f x x ⎡⎤-=----⎣⎦,令()()22g x f x x =-,则()()g x g x =--,所以函数()g x 为奇函数,()()4g x f x x ''=-,因为当()0,x ∈+∞时,()4f x x '<,即当()0,x ∈+∞时,()()40g x f x x ''=-<,故()g x 在()0,∞+上单调递减,由()g x 为奇函数可知,()g x 在R 上单调递减,因为()()221682f m f m m m +--≤++,故()()()()22212212f m m f m m +-⋅+≤--⋅-,即()()21g m g m +≤-,故21m m +≥-,故13m ≥-,故实数m 的取值范围为1,3⎡⎫-+∞⎪⎢⎣⎭.由选项可知:BCD 正确;故选:BCD.三、填空题(本大题共4小题,共20.0分)13.已知数列{}n a 满足()121n n a a n n N +++=+∈,1=1a ,则数列{}n a 的通项公式为___________.【答案】=n a n 【解析】【分析】把n 变为1n -,得到()121121n n a a n n -+=-+=-,和原式相减得到112n n a a +--=,得到奇数项成等差,偶数项也成等差,公差为2,即可得解.【详解】当2n ≥时,由题得()121121n n a a n n -+=-+=-,联立()1+1+=21+1=21+=2+1n n n n a a n n a a n ---⎧⎨⎩得,112n n a a +--=,所以奇数项成等差,偶数项也成等差,公差为2,由1=1a 得当n 为奇数时,=n a n ,当=1n 时,由()121n n a a n n N +++=+∈得22a =,所以当n 为偶数时,=n a n ,从而=n a n .故答案为:=n a n .14.如图,△ABC 的外接圆的圆心为O ,AB =2,AC =3,BC =AO BC ⋅=________.【答案】52【解析】【详解】因为BC AC AB=- AO BC ⋅= 0()00A AC AB A AC A AB⋅-=⋅-⋅,根据向量数量积的几何意义得:35003232122A AC A AB AE AF ⋅-⋅=-=⨯-⨯= .15.三棱锥P ABC -中,2PA AB PB AC ====,CP =,点D 是侧棱PB 的中点,且CD =P ABC -的外接球O 的表面积___________.【答案】283π##283π【解析】【分析】推导出AC ⊥平面PAB ,利用正弦定理计算出PAB △的外接圆半径r ,可得出三棱锥P ABC -的外接球半径为R =,利用球体的表面积公式可求得结果.【详解】如下图所示:圆柱12O O 的底面圆直径为2r ,母线长为h ,则12O O 的中点O 到圆柱底面圆上每点的距离都相等,则O 为圆柱12O O 的外接球球心,且有2R =.本题中,依题意,由2PA AC ==,CP =,得AP AC ⊥.连接AD ,由点D 是PB 的中点且2PA AB PB ===,则AD PB ⊥,且AD ==,又CD=2AC =,则222CD AC AD =+,可知AD AC ⊥,又AP AD A ⋂=,所以AC ⊥平面PAB .可将三棱锥CPAB -置于圆柱12O O 中,且PAB △的外接圆为圆2O ,圆2O 的半径为2sin 603AB r==,所以,三棱锥CPAB -的外接球的直径为23R ==,则3R =,故三棱锥P ABC -的外接球的表面积23428S R ππ==.故答案为:283π.16.不等式220x x ax a ---<的解集中只存在两个整数,则正数a 的取值范围是___________.【答案】10,2⎛⎤⎥⎝⎦【解析】【分析】画出22y x x=-与()1=+y a x 的图象,数形结合,找出临界状态从而得到a 的取值范围即可.【详解】220x x ax a ---<,则22x x ax a -<+,分别画出22y x x=-与()1=+y a x 的图象,因为只存在两个整数x ,使得不等式成立,故而从图象上看,只需22y x x=-上有两个横坐标为整数的点在()1y a x =+的下方.数形结合可知:当1x =时,22y x x=-过点()1,1A ,此处为临界状态.此时直线()1y a x =+的斜率12a =,故而要满足题意,只需12a ≤.满足不等式解集的整数为0x =或2x =.又a >,故a 的取值范围为10,2⎛⎤ ⎝⎦.故答案为:10,2⎛⎤ ⎥⎝⎦.四、解答题(本大题共6小题,共70.0分.解答应写出文字说明,证明过程或演算步骤)17.已知函数()243xf x x a-=-,a R ∈.(1)若()y f x =在()()1,1f 处的切线斜率为5-,求a 的值;(2)若()f x 在1x =-处取得极值,求()f x 在[]22-,上的最大值.【答案】(1)0a=或75a =(2)32【解析】【分析】(1)由已知可得出()15f '=-,即可解得实数a 的值;(2)由已知可得()10f '-=,求得实数a 的值,然后利用导数分析函数()f x 在区间[]22-,上的单调性,即可求得函数()f x 在区间[]22-,上的最大值.【小问1详解】解:因为()243xf x x a-=-,则()()()()()2222223243383x a x x x x af x xa xa -----+'==--,因为()y f x =在()()1,1f 处的切线斜率为5-,所以()()235151a f a -'==--,整理得2570a a -=,解得0a =或75a =.【小问2详解】解:因为()f x 在1x =-处取得极值,即()()2311101a f a +'-==-,解得113a =-,所以()243113xf x x -=+,则()2223811113x x f x x --'=⎛⎫+ ⎪⎝⎭,令()0f x '=,解得1113x =,21x =-,所以当()2,1x ∈--时,()0f x '>,()f x 单调递增,当()1,2x ∈-时,()0f x '<,()f x 单调递减,()()max 312f x f =-=.18.如图所示,在梯形ABCD 中,//AB CD ,2BAD π∠=,点E 是AD 上一点,2=4DE AE =,2cos cos cos BC BEC BE EBC CE ECB ∠=∠+∠.(1)求BEC ∠的大小;(2)若BCE 的面积S为BC .【答案】(1)∠BEC =3π;(2)B C =.【解析】【分析】(1)利用余弦定理将角化为边,从而可得1cos 2BEC ∠=,故可求其大小.(2)设AEB α∠=,由解直角三角形可得,BE CE ,根据面积可求α的值,利用余弦定理可求BC 的长.【详解】(1)∵2cos cos cos BC BEC BE EBC CE ECB∠=∠+∠2222222•2•BE C BE BC CE CE BC BE BE BC CE E BCBC+-+-⋅⋅=+=∴1cos 2BEC ∠=,而BEC ∠为三角形内角,故3BEC π∠=.(2)设AEB α∠=,则23DECπα∠=-,其中203πα<<,∵DE =2AE =4,∴2cos cos AE BE αα==,422cos()cos()33CE DE ππαα=--=,∵△BCE的面积1sin 223cos cos()3S BE CE ππαα=⋅⋅=-22=2sin(2)16πα==--,∴由已知得2sin(21)6πα=--,∴sin 216πα⎛⎫-= ⎪⎝⎭,因为72666πππα-<-<,故262ππα-=,即3πα=,此时24cos BE α==,482cos()3CE πα==-,∴在△BCE 中,由余弦定理得:2222cos 48BC BE CE BE CE BEC +⨯∠=-=,∴B C =.19.如图,在四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,1AA ⊥平面ABCD ,122AA AB ==,点M在1DD 上,且1B D ⊥平面ACM.(1)求1DM DD 的值;(2)求二面角D AC M --的正弦值.【答案】(1)14(2)3【解析】【分析】(1)以点A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立空间直角坐标系,设()0,1,M a ,利用空间向量法可得出关于a 的等式,求出a 的值,即可得出结果;(2)利用空间向量法结合同角三角函数的基本关系可求得结果.【小问1详解】解:因为在四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,1AA ⊥平面ABCD ,以点A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 、y 、z轴建立如下图所示的空间直角坐标系,因为122AA AB ==,故可设()0,1,M a ,其中02a ≤≤,则()11,0,2B 、()0,1,0D 、()C ,所以()1,1,0AC = ,()0,1,AM a =,()11,1,2B D =-- ,设平面ACM 的一个法向量为(),,m x y z = ,则有00m AC m AM ⎧⋅=⎨⋅=⎩,即00x y y az +=⎧⎨+=⎩,取x a =,得(),,1m a a =-,因为1B D ⊥平面ACM,所以1//B D m,即1112a a -==--,解得12a =,所以12DM =,114DM DD =.【小问2详解】易知平面ACD 的一个法向量为()0,0,1n =,设二面角D AC M --的大小θ为,而11,,122m ⎛⎫=- ⎪⎝⎭,cos ,3m n m n m n ⋅<>==⋅,则sin3θ=.20.已知各项都为正数的数列{}n a 的前n 项和为n S ,且对任意的*n ∈N ,都有22(n n n pS a pa =+其中0p >,且p 为常数),记数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和为n H (1)求数列{}n a 的通项公式及nH (2)当=2p 时,将数列1n a ⎧⎫⎨⎬⎩⎭的前4项抽去其中一项后,剩下三项按原来的顺序恰为等比数列{}n b 的前3项,记{}n b 的前m 项和为m T ,若存在*N m ∈,使得对任意*n ∈N ,总有m n T H λ<+恒成立,求实数λ的取值范围【答案】(1)n a np =,21n n H p n =⋅+(2)()0,+∞.【解析】【分析】(1)利用11,=1=,2n n n S n a S S n --≥⎧⎨⎩,求出10n n a a p --=>,得到数列{}n a 是等差数列,求出通项公式和n S ,利用裂项相消法求解n H ;(2)当=2p 时,2n a n =,可得1234111111112468a a a a ====,,,,只有111248,,成等比数列,利用等比数列的通项公式和前n 项和公式可得n b 、.n T 再利用m T 及n H 的单调性即可.【小问1详解】当=1n 时,21112paa pa =+,10a > ,12p a p ∴=+,解得1a p =.当2n ≥时,由22n n n pS a pa =+,21112n n n pS a pa ---=+,两式相减得:22112nn n n n paa pa a pa --=+-+(),化为()()110n n n n a a a a p --+--=,*N n ∀∈ ,都有0n a >,10n n a a p -∴-=>,∴数列{}n a 是等差数列,1n a p n p np∴=+-=(),222222n n p np n n pS p ++∴==(),12111n S p n n ∴=-+(),1211121111112231n n H S S S p n n ⎡⎤∴=++⋯+=-+-+⋯+-⎢⎥+⎣⎦()(2121.11np n p n =-=⋅++()即21nn na np H p n ==⋅+,.【小问2详解】当=2p 时,2n a n =,1234111111112468a a a a ∴====,,,,只有111248,,成等比数列,∴数列{}n b 的首项112b =,公比12q =,1111222n nn b -∴=⋅=()(.11112211212n n n T ⎡⎤-⎢⎥⎣⎦==--(().112mm T =- ()是关于m 的单调递增数列,112m T ∴≤<.又2211nn nH n n =⋅=++因为()()11102121n n n n H H n n n n ++=-=>++++-,所以1n n H n =+的最小值为112H =,存在*N m ∈,使对任意*n ∈N ,总有m n T H λ<+恒成立,故只需()()min min m n T H λ<+11022λ∴>-=,故实数λ的取值范围是()0,+∞.21.已知椭圆2222:1(0)x y a b a b Γ+=>>的离心率为2,点A ,B ,C 分别为Γ的上,左,右顶点,且||4BC =.(1)求Γ的标准方程;(2)点D 为线段AB 上异于端点的动点,过点D 作与直线AC 平行的直线交Γ于点P ,Q ,求||||PD QD ⋅的最大值.【答案】(1)2214x y +=(2)54【解析】【分析】(1)由题可得2a =,根据离心率即可求出;(2)求出直线AB 的方程,设出直线l 的方程12y x λ=-+,与椭圆联立,得出11λ-<<,联立两直线表示出D 坐标,表示出||||PD QD ⋅即可求出最值.【小问1详解】由题意得:2||4aBC ==,解得2a =.又因为2c e a ==,所以c =2221b a c =-=.所求Γ的标准方程为2214x y +=.【小问2详解】可得(0,1),(2,0),(2,0)A B C -,则12AC k =-,直线AB 的方程为:220x y -+=,设直线l 的方程为12y x λ=-+.联立方程组221214y x x y λ⎧=-+⎪⎪⎨⎪+=⎪⎩,消y ,得221442x x λ⎛⎫+-+=⎪⎝⎭,整理得:222220x x λλ-+-=①由l 与线段AB 有公共点,得11λ-<<,联立方程组12220y x x y λ⎧=-+⎪⎨⎪-+=⎩,解得D 的坐标为11,2λλ+⎛⎫- ⎪⎝⎭,设()()1122,,,P x y Q x y ,由①知12212222x x x x λλ+=⎧⎨=-⎩②又12||(1),||(1)PD QD λλ=--=--所以()212125||||(1)(1)4PD QD x x x x λλ⋅=--++-③②代入③,得25||||1,(1,1)4PD QD λλ⋅=-∈-所以当0λ=时,||||PD QD ⋅有最大值54.22.已知函数()e x f x x x =-.(Ⅰ)讨论()f x 的单调性;(Ⅱ)证明:当0x >时,()ln 1f x x -≥.【答案】(Ⅰ)()f x 在(),0-∞上单调递减,在()0,∞+上单调递增;(Ⅱ)证明见解析.【解析】【分析】(Ⅰ)求出导函数()'f x ,由()'f x 的正负确定()f x 的单调区间;(Ⅱ)不等式变形为()ln e ln 1x x x x +-+≥,令ln t x x =+,又变为e 1t t -≥.引入新函数()e t u t t =-,由导数求得最小值可证明不等式成立.【详解】(Ⅰ)由题意得()()1e 1x f x x =+-',设()()1e x g x x =+,则()()2e x g x x '=+,当1x ≤-时,()0g x ≤,当1x >-时,()0g x '>,()g x 单调递增,又因为()01g =,所以当0x <时,()1g x <,即()0f x '<,当0x >时,()1g x >,即()0f x '>因此()f x 在(),0-∞上单调递减,在()0,∞+上单调递增.(Ⅱ)要证()ln 1f x x -≥,即证e ln 1x x x x --≥,即证()ln e ln 1x x x x +-+≥,令ln t x x =+,易知R t ∈,待证不等式转化为e 1t t -≥.设()e t u t t =-,则()e 1t u t '=-,当0t<时,()0u t '<,当0t >时,()0u t '>,故()u t 在(),0-∞上单调递减,在()0,∞+上单调递增.所以()()01u t u ≥=,原命题得证.。
江苏省启东中学高三上学期第一次月考数学(理)试题Word版含答案
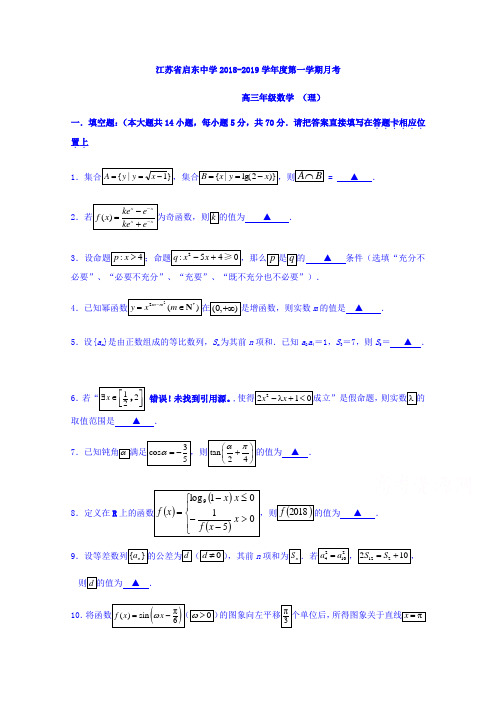
(1)求区域Ⅱ的总面积;
(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y万元. 试问当 为多少时,年总收入最大?
(3)若函数 存在极大值,且极大值点为1,证明: .
江苏省启东中学2018-2019学年度第一学期月考
高三年级数学答案
答题卷上只有第18题需要附图,其余按模式搞就行了
1. 2. 3.充分不必要4.1 5. 6. 7.
8. 9. 10. 11. 12. 13. 14.
15.解: 或
16.解:(1)在△ABC中,因为 , , ,
则 的值为▲.
10.将函数 ( )的图象向左平移 个单位后,所得图象关于直线
对称,则 的最小值为▲.
11.已知函数 , ,则 的解集是▲.
12.若向量 满足 , ,且对一切实数 , 恒成立,则向量 的夹角的大小为▲.
13.在斜三角形ABC中,若 ,则sinC的最大值为▲.
14.已知函数 , ( 为自然对数的底数),若函数
③若 ,则 时, ,
当 时, 的最小值为 ;
当 时, 的最小值为 .
因为 , ,所以 的最小值为 .14分
综上所述: ………………………………16分
20.解(1)当 ,函数 在 上单调递增;
当 ,函数 在 上单调递减,在 上单调递增;
当 ,函数 在 上单调递增,在 上单调递减.……………4分
(2) 若对任意 , 恒成立,求实数 的取值范围;
江苏省启东中学2018-2019学年高三上学期第三次月考试卷数学含答案

江苏省启东中学2018-2019学年高三上学期第三次月考试卷数学含答案 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 函数f (x )=1﹣xlnx 的零点所在区间是( )A .(0,)B .(,1)C .(1,2)D .(2,3)2. 已知全集I={1,2,3,4,5,6},A={1,2,3,4},B={3,4,5,6},那么∁I (A ∩B )等于( ) A .{3,4} B .{1,2,5,6} C .{1,2,3,4,5,6} D .∅3. 复数z=(其中i 是虚数单位),则z 的共轭复数=( )A .﹣iB .﹣﹣iC . +iD .﹣ +i4. 如图,1111D C B A ABCD -为正方体,下面结论:① //BD 平面11D CB ;② BD AC ⊥1;③ ⊥1AC 平面11D CB .其中正确结论的个数是( )A .B .C .D .5. 单位正方体(棱长为1)被切去一部分,剩下部分几何体的三视图如图所示,则( )A .该几何体体积为B .该几何体体积可能为C .该几何体表面积应为+D .该几何体唯一6. 设集合M={1,2},N={a 2},则“a=1”是“N ⊆M ”的( ) A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件7. 若动点),(),(2211y x B y x A 、分别在直线: 011=-+y x 和2l :01=-+y x 上移动,则AB 中点M 所在直线方程为( )A .06=--y xB .06=++y xC .06=+-y xD .06=-+y x 8. 数列1,3,6,10,…的一个通项公式是( )A .21n a n n =-+B .(1)2n n n a -=C .(1)2n n n a += D .21n a n =+ 9. 已知等差数列{}n a 的前项和为n S ,且120a =-,在区间()3,5内任取一个实数作为数列{}n a的公差,则n S 的最小值仅为6S 的概率为( ) A .15 B .16 C .314 D .1310.若某程序框图如图所示,则该程序运行后输出的值是( ) A.7B.8C. 9D. 10【命题意图】本题考查阅读程序框图,理解程序框图的功能,本质是循环语句循环终止的条件.1110y -+=的倾斜角为( )A .150B .120C .60D .3012.已知f (x )=m •2x +x 2+nx ,若{x|f (x )=0}={x|f (f (x ))=0}≠∅,则m+n 的取值范围为( ) A .(0,4) B .[0,4) C .(0,5] D .[0,5]二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.已知函数y=f (x ),x ∈I ,若存在x 0∈I ,使得f (x 0)=x 0,则称x 0为函数y=f (x )的不动点;若存在x 0∈I ,使得f (f (x 0))=x 0,则称x 0为函数y=f (x )的稳定点.则下列结论中正确的是 .(填上所有正确结论的序号)①﹣,1是函数g (x )=2x 2﹣1有两个不动点;②若x 0为函数y=f (x )的不动点,则x 0必为函数y=f (x )的稳定点; ③若x 0为函数y=f (x )的稳定点,则x 0必为函数y=f (x )的不动点; ④函数g (x )=2x 2﹣1共有三个稳定点;⑤若函数y=f (x )在定义域I 上单调递增,则它的不动点与稳定点是完全相同.14.幂函数1222)33)(+-+-=m m xm m x f (在区间()+∞,0上是增函数,则=m . 15.函数1()lg(1)1f x x x=++-的定义域是 ▲ .16.定义在R 上的函数)(x f 满足:1)(')(>+x f x f ,4)0(=f ,则不等式3)(+>x x e x f e (其中为自然对数的底数)的解集为 .三、解答题(本大共6小题,共70分。
江苏省启东中学高一数学月考试卷答案

江苏省启东中学高一数学月考试卷答案1、72、32π 3、10 4、007515或 5、 -n+3 6、156 7、直角三角形 8、3 9、1 10、338≤<d 11、 ③ 12、 3 13、⎪⎩⎪⎨⎧>+≤+)21()24()21()32(22k k k k ππ 14、2002 15.8616.解(1)由(3)23n n m S ma m -+=+,得11(3)23,n n m S ma m ++-+=+两式相减,得1(3)2,(3)n n m a ma m ++=≠-12,3n n a m a m +∴=+ {}n a ∴是等比数列. 111111112(2)1,(),2,3233()22311133.311{}131121,333.2n n n n n n n n n n n n n m b a q f m n N n m b b f b b b b b b b b b n n b b n ------====∈≥+==⋅++=⇒-=∴-+∴=+==+由且时,得是为首项为公差的等差数列,故有 17.(1)0120;(2)10;(3)23 18.解:(1)依题意,10,1001091212==+=a a a a 故,…………………………2分当109,21+=≥-n n S a n 时 ① 又1091+=+n n S a ②…………………………………4分②-①整理得:}{,101n nn a a a 故=+为等比数列,且n a q a a n n n n =∴==-log ,1011 *1}{lg ,1)1(lg lg N n a n n a a n n n ∈=-+=-∴+即是等差数列.…………………6分(2)由(1)知,)1(1321211(3+++⋅+⋅=n n T n ………………………………8分133)1113121211(3+-=+-++-+-=n n n ……………………………………10分,23≥∴n T 依题意有,61),5(41232<<-->m m m 解得 故所求最大正整数m 的值为5.……………………………………………………15分19.解:(1)为了计算前三项321,,a a a 的值,只要在递推式1,)1(2≥-+=n a S n n n 中,对n 取特殊值1,2,3n =,就可以消除解题目标与题设条件之间的差异.由111121,1;a S a a ==-=得由2122222(1),0;a a S a a +==+-=得由31233332(1), 2.a a a S a a ++==+-=得……………………………6分(2)为了求出通项公式,应先消除条件式中的n S .事实上当2≥n 时,有,)1(2)(211n n n n n n a a S S a -⨯+-=-=--即有 ,)1(2211---⨯+=n n n a a从而 ,)1(22221----⨯+=n n n a a32322(1),n n n a a ---=+⨯-…….2212-=a a接下来,逐步迭代就有122111)1(2)1(2)1(22-----⨯++-⨯+-⨯+=n n n n n a a ].)1(2[323])2(1[2)1(2)]2()2()2[()1(21211211--------+=----=-++-+--+=n n n n n n n n n经验证a 1也满足上式,故知 .1],)1(2[3212≥-+=--n a n n n 其实,将关系式1122(1)n n n a a --=+⨯-和课本习题1n n a ca d -=+作联系,容易想到:这种差异的消除,只要对1122(1)n n n a a --=+⨯-的两边同除以(1)n -,便得1122(1)(1)n n n n a a --=-⋅---. 令,(1)n n na b =-就有122n n b b -=--,于是 1222()33n n b b -+=-+, 这说明数列23n b ⎧⎫+⎨⎬⎩⎭是等比数列,公比2,q =- 首项11b =-,从而,得 111221()(2)()(2)333n n n b b --+=+⋅-=-⋅-, 即121()(2)(1)33n n n a -+=-⋅--,故有.1],)1(2[3212≥-+=--n a n n n 20.解:(1)设}{n a 的公差为d ,由题意0>d ,且⎩⎨⎧=++=+28)2)(3(52111d a d a d a 2分 11,2a d ==,数列}{n a 的通项公式为12-=n a n ………………4分(2)由题意)11()11)(11(12121n n a ++++≤ 对*N n ∈均成立 …5分 记)11()11)(11(121)(21n a a a n n F ++++= 则1)1(2)1(21)1(4)1(2)32)(12(22)()1(2=++>-++=+++=+n n n n n n n n F n F ()0F n > ,∴(1)()F n F n +>,∴()F n 随n 增大而增大 ……8分 ∴()F n 的最小值为332)1(=F∴a ≤a 的最大值为332 …………………9分 (3)12-=n a n∴在数列}{n b 中,m a 及其前面所有项之和为22)222()]12(531[212-+=++++-++++-m m m m …11分 21562211200811222210112102=-+<<=-+ ,即11102008a a <<12分又10a 在数列}{n b 中的项数为:521221108=++++ … 14分且244388611222008⨯==-, 所以存在正整数964443521=+=m 使得2008=m S。
江苏省启东中学2022-2023学年高三上学期第一次月考数学试卷(含答案)

2022-2023学年度江苏省启东中学高三第一学期第一次月考一、单选题(本大题共8小题,共40.0分。
在每小题列出的选项中,选出符合题目的一项)1.已知集合A={1,2},B={x|x2+mx−2=0},若A∩B={1},则B=( )A. {1,3}B. {1}C. {1,−2}D. {−1,1,2}2.若z=−1+i,设ω=zz,则|ω|=( )A. 12B. 1 C. 32D. 23.牛顿曾经提出了常温环境下的温度冷却模型:θ=(θ1−θ0)e−kt+θ0,其中t为时间(单位:min),θ0为环境温度,θ1为物体初始温度,θ为冷却后温度),假设在室内温度为20℃的情况下,一桶咖啡由100℃降低到60℃需要20min,则k的值为( )A. ln220B. ln320C. −ln210D. −ln3104.已知平面α和平面β不重合,直线m和n不重合,则α//β的一个充分条件是( )A. m⊂α,n⊂β且m//nB. m⊂α,n⊂β且m//β,n//αC. m⊥α,n⊥β且m//nD. m//α,n//β且m//n5.设f(x)是定义在实数集R上的函数,且满足f(1+x)=f(1−x),f(2+x)=−f(2−x),则f(x)是( )A. 奇函数,又是周期函数B. 奇函数,但不是周期函数C. 偶函数,又是周期函数D. 偶函数,但不是周期函数6.若tanθ2=12(0<θ<π),则sin2θ的值为( )A. 2425B. 1516C. −1516D. −24257.在△ABC中,∠BAC=120∘,AD为∠BAC的平分线,|AB|=2|AC|,则|AB||AD|=( )A. 2B. √3C. 3D. 2√38.已知a=2.22.1,b=2.12.2,c=2.12.1,则( )A. a<c<bB. c<b<aC. b<c<aD. c<a<b二、多选题(本大题共4小题,共20.0分。
江苏省启东市高一数学上学期期初考试试题

2021-2021学年度第一学期期初考试高一数学试卷【总分值160分考试时间120分钟】一、填空题:本大题共14小题,每题5分,共70分.1.不等式x 3 x 2 7的解为.2.分解因式:(2x23x 1)222x233x 1=.13.函数f(x)=x+1+2-x的定义域是;4.化简:〔式中字母都是正数〕(36a9)2·(63a9)2=__________.5.f(x)=3x-b(2≤x≤4,b为常数)的图象过点(2,1),那么f(x)的值域为________.6.不等式16x1的解为.x17.假定对于x的方程x2+x+a=0的一个根大于1、另一个根小于1,那么实数a的取值范围为.8.会合M {2,3,5},且M中起码有一个奇数,那么这样的会合共有________个.9.假定会合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},且B A,那么m的取值范围为.ax-110.会合A=x x-a<0,且2∈A,3A,那么实数a的取值范围是________.11.f〔x+1〕=x3+1,那么f〔x〕;x x312.函数f(x)=x3+x,对随意的m∈[-2,2],f(mx-2)+f(x)<0恒建立,那么x的取值范围为____________.13.函数ya x(a0,a1)在区间[1,1]上的最大值与最小值的差是1,那么实数a的值为.14.函数f(x)的定义域为D,假定知足①f(x)在D内是单一函数,②存在[a,,使f(x)在[a,b]上的值域为[a,b],那么y=f(x)叫做闭函数,现有f(x)=x+2+k是闭函数,那么k的取值范围是________.二、解答题:本大题共6小题,共90分.解允许写出文字说明、证明过程或演算步骤.〔本题总分值14分〕x1、x2是一元二次方程4kx24kx k10的两个实数根.〔1〕能否存在实数k,使(2x1x2)(x12x2)3建立?假定存在,求出k的值;假定不存在,请说2明原因.〔2〕求使x1x22的值为整数的实数k的整数值.x2x1〔本题总分值14分〕会合A={x|x2-1=0},B={x|x2-2ax+b=0},假定A∪B=A,务实数a,b知足的条件.17.〔本题总分值15分〕5x +4(1)求函数f (x )=2x +41-x 的值域;(2)求函数f (x )=x -2的值域.(3) 函数f (x )=x 2-2x -3,x ∈(-1,4]的值域.18.〔本题总分值15分〕某工厂生产一种机器的固定本钱为5000元,且每生产100台需要增添投入2500元,对销售市场进行检查后得悉,市场对此产品的需求量为每年500台,销售收入函数为:H(x)1=500x -2(1) x 2,此中x 是产品售出的数目,且 0≤x ≤500. (2)假定x 为年产量,y 为收益,求y =f(x)的分析式;当年产量为什么值时,工厂的年收益最大,其最大值是多少?〔本题总分值16分〕函数f(x)ax b是定义在 1,1上的奇函数,且f(1) 2.1 x 22 51〕确立函数f(x)的分析式;2〕用定义证明f(x)在1,1上是增函数;〔3〕解不等式 f(t 1) f(t) 0.20.〔本题总分值16分〕11 3函数f(x)=a x-1+2 x(a>0 且a ≠1).(1) 求函数f(x)的定义域;(2)议论函数f(x)的奇偶性;(3) 求a 的取值范围,使f(x)>0在定义域上恒建立.2021年江苏省启东中学高一年级开学考试数学答案答案:4x32. 答案: x(2x 3)(x 3)(2x 3){x |x ≥-1且x ≠2}a 2. [1,9]3x1或x5a2 6 {m|m ≤3} 13,2∪(2,3] f 〔x 〕=x 3-3x12. 2-2, 313. 15 15a2或a2914. -,-2415.答案:〔1〕由k ≠0和△≥0k <0,∵x 1x 21,x 1x 2k14k∴(2x 1x 2)(x 1 2x 2) 2(x 1 x 2)29x 1x 2k93,∴k9 ,而k <0,∴不存在。
江苏省南通市启东中学高一数学上学期第一次月考试卷(含解析)

2015-2016学年江苏省南通市启东中学高一(上)第一次月考数学试卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在相应位置上.1.若集合A={x|﹣1<x<3},B={x|2<x<4},则集合A∩B=.2.已知A={﹣1,3,m},集合B={3,4},若B⊆A,则实数m= .3.函数y=定义域.(区间表示)4.若f(1﹣x)=x2,则f(1)= .5.若集合A={1,2,3},B={1,3,4},则A∪B的真子集个数为.6.函数的单调增区间为.7.给定映射f:(x,y)→(x+2y,2x﹣y),则映射f下的对应元素为(3,1),则它原来的元素为.8.若函数的定义域和值域都是[1,b],则b的值为.9.若集合A={x|kx2+4x+4=0},x∈R中只有一个元素,则实数k的值为.10.函数f(x)=1﹣的最大值是.11.若函数y=的定义域为R,则实数a的取值范围.12.函数f(x)是定义在(﹣1,1)上的奇函数,且它为单调增函数,若f(1﹣a)+f(1﹣a2)>0,则a的取值范围是.13.函数f(x)是偶函数,当x∈[0,2]时,f(x)=x﹣1,则不等式f(x)>0在[﹣2,2]上的解集为.(用区间表示)14.对于实数a和b,定义运算*:,设f(x)=(2x﹣1)*(x ﹣1),若直线y=m与函数y=f(x)恰有三个不同的交点,则m的取值范围.二、解答题(本大题6小题,共90分.解答时应写出文字说明,证明过程或演算步骤)15.已知集合A={x|x2=1},B={x|ax=1}.若B⊆A,求实数a的值.16.已知函数f(x)的定义域为D,若存在x0∈D,使等式f(x0)=x0成立,则称x=x0为函数f(x)的不动点,若x=±1均为函数f(x)=的不动点.(1)求a,b的值.(2)求证:f(x)是奇函数.17.“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v(单位:千克/年)是养殖密度x (单位:尾/立方米)的函数.当x不超过4(尾/立方米)时,v的值为2(千克/年);当4≤x≤20时,v是x的一次函数;当x达到20(尾/立方米)时,因缺氧等原因,v的值为0(千克/年).(1)当0<x≤20时,求函数v(x)的表达式;(2)当养殖密度x为多大时,鱼的年生长量(单位:千克/立方米)f(x)=x•v(x)可以达到最大,并求出最大值.18.已知集合A={x|x2﹣2x﹣8<0},B={x|x2+2x﹣3>0},C={x|x2﹣3ax+2a2<0}试求实数a 的取值范围使C⊆A∩B.19.已知二次函数f(x)=x2﹣4x﹣4在闭区间[t,t+2](t∈R)上的最大值记为g(t),求g(t)的表达式,并求出g(t)的最小值.20.已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=2,任取a,b∈[﹣1,1],a+b≠0,都有>0成立.(1)证明函数f(x)在[﹣1,1]上是单调增函数.(2)解不等式f(x)<f(x2).(3)若对任意x∈[﹣1,1],函数f(x)≤2m2﹣2am+3对所有的a∈[0,]恒成立,求m 的取值范围.2015-2016学年江苏省南通市启东中学高一(上)第一次月考数学试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在相应位置上.1.若集合A={x|﹣1<x<3},B={x|2<x<4},则集合A∩B={x|2<x<3} .【考点】交集及其运算.【专题】集合.【分析】由A与B,求出两集合的交集即可.【解答】解:∵A={x|﹣1<x<3},B={x|2<x<4},∴A∩B={x|2<x<3}.故答案为:{x|2<x<3}【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.已知A={﹣1,3,m},集合B={3,4},若B⊆A,则实数m= 4 .【考点】集合的包含关系判断及应用.【专题】计算题.【分析】先由B⊆A知,集合B是集合A的子集,然后利用集合子集的定义得集合A必定含有4求出m即可.【解答】解:已知A={﹣1,3,m},集合B={3,4},若B⊆A,即集合B是集合A的子集.则实数m=4.故填:4.【点评】本题主要考查了集合的关系,属于求集合中元素的基础题,也是高考常会考的题型.3.函数y=定义域(﹣2,﹣1)∪(﹣1,+∞).(区间表示)【考点】函数的定义域及其求法.【专题】函数的性质及应用.【分析】根据函数成立的条件,即可求出函数的定义域.【解答】解:要使函数f(x)有意义,则,即,解得x>﹣2且x≠﹣1,即函数的定义域为(﹣2,﹣1)∪(﹣1,+∞),故答案为:(﹣2,﹣1)∪(﹣1,+∞)【点评】本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.4.若f(1﹣x)=x2,则f(1)= 0 .【考点】函数的值.【专题】函数的性质及应用.【分析】根据函数的解析式,进行转化即可.【解答】解:∵f(1﹣x)=x2,∴f(1)=f(1﹣0)=02=0,故答案为:0【点评】本题主要考查函数值的计算,比较基础.5.若集合A={1,2,3},B={1,3,4},则A∪B的真子集个数为15 .【考点】并集及其运算.【专题】集合.【分析】由A与B,求出两集合的并集,找出并集的真子集个数即可.【解答】解:∵A={1,2,3},B={1,3,4},∴A∪B={1,2,3,4},则A∪B的真子集个数为24﹣1=15.故答案为:15【点评】此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.6.函数的单调增区间为[,1)和(1,+∞).【考点】复合函数的单调性.【专题】函数的性质及应用.【分析】利用换元法结合复合函数单调性之间的关系进行求解即可.【解答】解:由x(1﹣x)≠0得x≠0且x≠1,即函数的定义域为{x|x≠0且x≠1},设t=x(1﹣x)=﹣x2+x,对称轴为x=,则函数等价y=,由t=x(1﹣x)>0得0<x<1,此时y=为减函数,要求函数f(x)的单调递增区间,则求函数t=x(1﹣x)在0<x<1上的递减区间,∵当≤x<1时,函数t=x(1﹣x)单调递减,此时函数f(x)的单调递增区间为[,1).由t=x(1﹣x)<0得x>1或x<0,此时y=为减函数,要求函数f(x)的单调递增区间,则求函数t=x(1﹣x)在x>1或x<0的递减区间,∵当x>1时,函数t=x(1﹣x)单调递减,此时函数f(x)的单调递增区间为(1,+∞).∴函数的单调递增区间为[,1)和(1,+∞).故答案为:[,1)和(1,+∞).【点评】本题主要考查函数单调区间的求解,利用换元法,结合复合函数单调性之间的关系是解决本题的关键.注意要对分母进行讨论.7.给定映射f:(x,y)→(x+2y,2x﹣y),则映射f下的对应元素为(3,1),则它原来的元素为(1,1).【考点】映射.【专题】函数的性质及应用.【分析】本题已知映射f的对应法则和映射的象,可列出参数x、y相应的关系式,解方程组求出原象,得到本题题结论.【解答】解:∵映射f:(x,y)→(x+2y,2x﹣y),映射f下的对应元素为(3,1),∴,∴.∴(3,1)原来的元素为(1,1).【点评】本题考查的是映射的对应关系,要正确理解概念,本题运算不大,属于容易题.8.若函数的定义域和值域都是[1,b],则b的值为 3 .【考点】函数的值域;函数的定义域及其求法.【专题】计算题.【分析】先根据f(x)在[1,b]上为增函数,当x=1时,f(x)=1,当x=b时,f(x)=(b ﹣1)2+1=b,可得然后把b代入即可得出答案.【解答】解:∵函数的定义域和值域都是[1,b],且f(x)在[1,b]上为增函数,∴当x=1时,f(x)=1,当x=b时,f(x)=(b﹣1)2+1=b,解得:b=3或b=1(舍去),∴b的值为3,故答案为:3.【点评】本题考查了函数的值域及函数的定义域的求法,属于基础题,关键是根据f(x)在[1,b]上的单调性求解.9.若集合A={x|kx2+4x+4=0},x∈R中只有一个元素,则实数k的值为0或1 .【考点】集合关系中的参数取值问题.【专题】计算题.【分析】集合A表示的是方程的解;讨论当二次项系数为0时是一次方程满足题意;再讨论二次项系数非0时,令判别式等于0即可.【解答】解:当k=0时,A={x|4x+4=0}={﹣1}满足题意当k≠0时,要集合A仅含一个元素需满足△=16﹣16k=0解得k=1故k的值为0;1故答案为:0或1【点评】本题考查解决二次型方程的根的个数问题时需考虑二次项系数为0的情况、考虑判别式的情况.10.函数f(x)=1﹣的最大值是 1 .【考点】函数的值域.【专题】计算题;函数的性质及应用.【分析】由观察法可直接得到函数的最大值.【解答】解:∵≥0,∴1﹣≤1,即函数f(x)=1﹣的最大值是1.故答案为:1.【点评】本题考查了函数的最大值的求法,本题用到了观察法,属于基础题.11.若函数y=的定义域为R,则实数a的取值范围[0,).【考点】函数的定义域及其求法.【专题】函数的性质及应用.【分析】由题意得不等式组,解出即可.【解答】解:由题意得:,解得:0≤a<,故答案为:[0,).【点评】本题考查了二次函数,二次根式的性质,是一道基础题.12.函数f(x)是定义在(﹣1,1)上的奇函数,且它为单调增函数,若f(1﹣a)+f(1﹣a2)>0,则a的取值范围是0<a<1 .【考点】奇偶性与单调性的综合.【专题】计算题;函数的性质及应用.【分析】将不等式进行转化,利用函数的单调性和奇偶性,即可得到结论.【解答】解:∵f(x)为奇函数,∴f(1﹣a)+f(1﹣a2)>0可化为f(1﹣a)>﹣f(1﹣a2)=f(a2﹣1),又f(x)在定义域(﹣1,1)上递增,∴﹣1<a2﹣1<1﹣a<1,解得0<a<1.∴a的取值范围为:0<a<1.故答案为:0<a<1.【点评】本题考查函数的奇偶性、单调性的综合应用,考查抽象不等式的求解,考查学生的转化能力.综合考查函数的性质.13.函数f(x)是偶函数,当x∈[0,2]时,f(x)=x﹣1,则不等式f(x)>0在[﹣2,2]上的解集为[﹣2,﹣1)∪(1,2] .(用区间表示)【考点】函数奇偶性的性质;函数单调性的性质.【专题】函数的性质及应用.【分析】先求出当x∈[0,2]时,解集为(1,2],再由函数的奇偶性求出当x∈[﹣2,0]时,解集为(1,2],即可求出不等式f(x)>0在[﹣2,2]上的解集.【解答】解:当x∈[0,2]时,f(x)=x﹣1>0,即有x>1,解集为(1,2],函数f(x)是偶函数,所以图象是对称的,当x∈[﹣2,0]时,解集为[﹣2,﹣1),综上所述,不等式f(x)>0在[﹣2,2]上的解集为[﹣2,﹣1)∪(1,2],故答案为:解集为[﹣2,﹣1)∪(1,2].【点评】本题主要考察了函数奇偶性的性质,属于基础题.14.对于实数a和b,定义运算*:,设f(x)=(2x﹣1)*(x﹣1),若直线y=m与函数y=f(x)恰有三个不同的交点,则m的取值范围(0,).【考点】根的存在性及根的个数判断.【专题】计算题;作图题;函数的性质及应用.【分析】化简f(x)=,作函数f(x)的图象,利用数形结合的方法求解.【解答】解:当x≤0时,2x﹣1≤x﹣1,f(x)=(2x﹣1)*(x﹣1)=(2x﹣1)2﹣(2x﹣1)(x﹣1)=(2x﹣1)x,当x>0时,2x﹣1>x﹣1,f(x)=(2x﹣1)*(x﹣1)=﹣x(x﹣1),故f(x)=,作函数f(x)=的图象如下,结合图象可知,m的取值范围为(0,);故答案为:(0,).【点评】本题考查了数形结合的思想的应用及分段函数的化简与运算.二、解答题(本大题6小题,共90分.解答时应写出文字说明,证明过程或演算步骤)15.已知集合A={x|x2=1},B={x|ax=1}.若B⊆A,求实数a的值.【考点】集合关系中的参数取值问题.【专题】计算题;分类讨论.【分析】已知B⊆A,分两种情况:①B=∅,②B≠∅,然后再根据子集的定义进行求解;【解答】解:显然集合A={﹣1,1},对于集合B={x|ax=1},当a=0时,集合B=∅,满足B⊆A,即a=0;当a≠0时,集合,而B⊆A,则,或,得a=﹣1,或a=1,综上得:实数a的值为﹣1,0,或1.【点评】此题主要考查子集的定义及其性质,此题还用到分类讨论的思想,注意B=∅,这种情况不能漏掉;16.已知函数f(x)的定义域为D,若存在x0∈D,使等式f(x0)=x0成立,则称x=x0为函数f(x)的不动点,若x=±1均为函数f(x)=的不动点.(1)求a,b的值.(2)求证:f(x)是奇函数.【考点】函数奇偶性的判断.【专题】函数的性质及应用.【分析】(1)直接利用定义把条件转化为f(﹣1)=﹣1,f(1)=1联立即可求a,b的值及f(x)的表达式;(2)根据奇函数的定义进行证明.【解答】解:(1)有题意可得:解得:;(2)由(1)知,,故f(x)=,定义域是R,设任意x,则,f(﹣x)==﹣=﹣f(x),故函数f(x)是奇函数.【点评】本题考查的知识点是函数解析式的求法,函数的奇偶性,属于基础题.17.“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v(单位:千克/年)是养殖密度x (单位:尾/立方米)的函数.当x不超过4(尾/立方米)时,v的值为2(千克/年);当4≤x≤20时,v是x的一次函数;当x达到20(尾/立方米)时,因缺氧等原因,v的值为0(千克/年).(1)当0<x≤20时,求函数v(x)的表达式;(2)当养殖密度x为多大时,鱼的年生长量(单位:千克/立方米)f(x)=x•v(x)可以达到最大,并求出最大值.【考点】函数模型的选择与应用.【专题】应用题;综合题.【分析】(1)由题意:当0<x≤4时,v(x)=2.当4<x≤20时,设v(x)=ax+b,v(x)=ax+b在[4,20]是减函数,由已知得,能求出函数v(x).(2)依题意并由(1),得f(x)=,当0≤x≤4时,f(x)为增函数,由此能求出f max(x)=f(4),由此能求出结果.【解答】解:(1)由题意:当0<x≤4时,v(x)=2.…当4<x≤20时,设v(x)=ax+b,显然v(x)=ax+b在[4,20]是减函数,由已知得,解得…故函数v(x)=…(2)依题意并由(1),得f(x)=,…当0≤x≤4时,f(x)为增函数,故f max(x)=f(4)=4×2=8.…当4≤x≤20时,f(x)=﹣=﹣=﹣+,f max(x)=f(10)=12.5.…所以,当0<x≤20时,f(x)的最大值为12.5.当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为12.5千克/立方米.…【点评】本题考查函数表达式的求法,考查函数最大值的求法及其应用,解题时要认真审题,注意函数有生产生活中的实际应用.18.已知集合A={x|x2﹣2x﹣8<0},B={x|x2+2x﹣3>0},C={x|x2﹣3ax+2a2<0}试求实数a 的取值范围使C⊆A∩B.【考点】一元二次不等式的解法;集合关系中的参数取值问题.【专题】计算题.【分析】先求出集合A与集合B,从而求出A∩B,讨论a的正负,根据条件C⊆A∩B建立不等关系,解之即可.【解答】解:依题意得:A={x|﹣2<x<4},B={x|x>1或x<﹣3,}∴A∩B={x|1<x<4}(1)当a=0时,C=Φ,符合C⊆A∩B;(2)当a>0时,C={x|a<x<2a},要使C⊆A∩B,则,解得:1≤a≤2;(3)当a<0时,C={x|2a<x<a},∵a<0,C∩(A∩B)=Φ,∴a<0不符合题设.∴综合上述得:1≤a≤2或a=0.【点评】本题主要考查了一元二次不等式的解法,以及集合关系中的参数取值问题,同时考查了分类讨论的数学思想,属于中档题.19.已知二次函数f(x)=x2﹣4x﹣4在闭区间[t,t+2](t∈R)上的最大值记为g(t),求g(t)的表达式,并求出g(t)的最小值.【考点】二次函数在闭区间上的最值.【专题】函数的性质及应用.【分析】首先不二次函数的一般式转化成顶点式,进一步求出对称轴方程,根据轴固定和区间不固定进行分类讨论,然后确定函数的单调性,进一步求出最大值和最小值.【解答】解:二次函数f(x)=x2﹣4x﹣4=(x﹣2)2﹣8开口方向向上,对称轴方程:x=2,当2<,即t>1时,x=t+2距离对称轴的距离比x=t的距离远,所以,当x=t+2时,g(t)=t2﹣8;当2≥,即t≤1时,x=t+2距离对称轴的距离比x=t的距离近,所以,当x=t时,g(t)=t2﹣4t﹣4;综上可得,g(t)=当t≤1时,t=0时,g(t)取小值﹣8,当t>1时,t=2时,g(t)取小值﹣8,所以g(t)的最小值为﹣8【点评】本题考查的知识点:二次函数一般式与顶点式的转换,对称轴方程,二次函数轴固定与区间不固定之间的讨论,求二次函数的最值.20.已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=2,任取a,b∈[﹣1,1],a+b≠0,都有>0成立.(1)证明函数f(x)在[﹣1,1]上是单调增函数.(2)解不等式f(x)<f(x2).(3)若对任意x∈[﹣1,1],函数f(x)≤2m2﹣2am+3对所有的a∈[0,]恒成立,求m 的取值范围.【考点】函数恒成立问题;函数单调性的判断与证明;函数单调性的性质.【专题】计算题.【分析】(1)根据函数的奇偶性及已知不等式可得差的符号,由单调性的定义可作出判断;(2)根据函数的奇偶性、单调性可去掉不等式中的符号“f”,转化为具体不等式可求,注意函数定义域;(3)对所有x[﹣1,1],f(x)≤2m2﹣2am+3成立,等价于f(x)max≤2m2﹣2am+3,由单调性易求f(x)max,从而可化为关于a的一次函数,利用一次函数的性质可得关于m的不等式组.【解答】解:(1)证明:任取x1、x2∈[﹣1,1],且x1<x2,又f(x)是奇函数,于是f(x1)﹣f(x2)=f(x1)+f(﹣x2)=.据已知>0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).∴f(x)在[﹣1,1]上是增函数.(2)f(x)<f(x2),由函数单调性性质知,x<x2,而﹣1≤x≤1,﹣1≤x2≤1故不等式的解集为{x|﹣1≤x<0}.(3)对所有x[﹣1,1],f(x)≤2m2﹣2am+3成立,等价于f(x)max≤2m2﹣2am+3,由f(x)在[﹣1,1]上的单调递增知,f(x)max=f(1)=2,所以2≤2m2﹣2am+3,即0≤2m2﹣2am+1,又对a∈[0,]恒成立,则有,解得m≤或m≥1,故实数m的取值范围为m≤或m≥1.【点评】本题主要考查函数的单调性和奇偶性的综合运用,考查恒成立问题.考查转化思想,在解题时要利用好单调性和奇偶性的定义.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省启东中学高一数学第一学期第三次月考试题-苏教版
(指数、对数、指数函数、对数函数,考试时间:120分钟)
一、选择题(每小题5分,共60分)
1.329
8log log 的值是( )
A .32
B .1
C .2
3 D .2 2.化简)25lg 22(lg 25log 5
+的结果是( ) A .lg 51 B .lg5 C .lg 25
1 D .lg 25 3.设a,b,c 都是正数,且3a =4b =6c ,那么( )
A .c 1=a 1+b 1
B .c 2=a 2+b 1
C .c 1=a 2+b 2
D .c 2=a 1+b
2 4.满足方程log 2x ·log x 7=log 27的正数x 为( )
A .7
B .2
C .7或2
D .x ≠1的正数
5.已知x=31log 131log 1
5121+,则x 的值属于区间( )
A .(-2,-1)
B .(1,2)
C .(-3,-2)
D .(2,3)
6.当a>1时,在同一坐标系中,函数y=a -x 与y=log a x 的图象是( )
7.已知y=log a (2-ax)在[0,1]上是关于x 的减函数,则a 的取值范围是( )
A .(0,1)
B .(1,2)
C .(0,2)
D .[)+∞,2
8.当函数f(x)=2-|x -1|-m 的图象与x 轴有交点时,实数m 的取值范围是( )
A .-1≤m <0
B .0≤m ≤1
C .0<m ≤1
D .m ≥1
9.若0<a<b<1,则下列各式成立的是( )
A .log a b>1
B .log a b<0
C .log a b<-1
D .0<log a b<1
10.已知1<x<d ,令a=2)(log x d ,b=2log x d ,c=2)(log log x d d ,则( )
A .a<b<c
B .a<c<b
C .c<a<b
D .c<b<a
11.若a ∈(0,1),则方程a x =|log a x|的解的个数为( )
A .0
B .1
C .2
D .3
12.已知2lg(x -2y)=lgx+lgy ,则y
x 的值为( ) A .1 B .4 C .1或4 D .
41或4 二、填空题(每小题4分,共16分)
13.如果lg 2x+(lg3+lg5)lgx+lg3·lg5=0的两根为α、β,则αβ=___________。
14.函数y=log a [1-(2
1)x ],x ∈(0,1),0<a<1的值域是____________。
15.方程33
131=++-x x
的解是____________。
16.函数f(x)=a x (a>0,a ≠1)在区间[1,2]上的最大值比最小值大
2a ,则a 的值为_____。
三、解答题
17.(本题满分12分)已知lg12=a, lg72=b ,不查求lg1.8。
18.(本题满分12分)已知关于x 的方程2a 2(x
-1)-7·a x -
1+3=0有一个根是2,求a 的值和方程其余的根。
19.(本题满分12分)求y=f(x)=a x -1(a>1)的反函数f -1(x),并证明2f -1(x)≥f -1(2x)。
20.(本题满分12分)给定函数f(x)=log a |log a x|(a>0,且a ≠1),当f(x)>0时,求x 的取值范围。
21.(本题满分12分)若关于x 的方程(lgax )(lgax 2)=4的所有解都大于1,求参数a 的取值范围。
22.(本题满分14分)若a,b 为不等于1的正数,且a<b ,试比较log a
b
1,log a b ,log b b 1的大小。
高一数学第一学期第三次月考解答
一、选择题
1.A 2. B 3. B 4.D 5.D 6.A 7.C 8.C 9.D 10.C 11.C 12.B
二、填空题
13.151 14. (log a 21,+∞) 15.x=-1 16. a=21或2
3 三、解答题
17.解:12=22×3,72=22×32 (……2')
∵lg12=a ,∴2lg2+lg3=a , (1) (……4')
∵lg72=b ,∴3lg2+2lg3=b (2) (……6')
解(1)、(2)得lg2=2a -b,lg3=2b -3a (……9')
于是有lg1.8=lg18-1=lg2+2lg3-1=3b -4a -1 (……12')
18.解:将x=2代入原方程,得2a 2-7a+3=0,解得a=
21,或a=3 (……3') 当a=21时,原方程为2(21)2x -2-7(2
1)x -1+3=0, 解得x 1=2,x 2=1+21log 3 (……6')
当a=3时,原方程为2·32x -2-7·3x -
1+3=0, 解得x 1=2,x 2=1-log 32 (……12')
19.解:由y=a x -1,得x=log a (y+1)(y>-1) (……3')
故f -
1(x)=log a (x+1)(x>-1) (……6') 证:f -
1(2x)=log a (2x+1) (x>-2
1),2f -1(x)=log a (x+1)2 (……9') ∵(x+1)2=x 2+2x+1≥2x+1>0 (x>-21),又∵a>1,∴log a (x+1)2≥log a (2x+1) 即2f -1(x)≥f -
1(2x) (……12') 20.解:当a>1时,log a |log a x| >0,|log a x| >1 (……3')
∴log a x>1,或log a x<-1,得x>a ,或0<x<a
1;(……6') 当0<a<1时,由log a |log a x| >0,0<|log a x| <1 (……9') ∴-1<log a x<1,得a<x<a
1,且x ≠1 (……12') 21.解:原方程化为2lg 2x+3lgalgx+lg 2a -4=0 (……3' )
由于 x>1,故关于lgx 的方程应有lgx>0,(……6' )
△=9lg 2a -8(lg 2a -4)≥0
∴ -
23lga>0 (……9')
2
1(lg 2a -4)>0 →lga<-2 → 0<a<
100
1 (……12') 22.解:(1)当1<a<b 时,因为log a b 1< log a a 1, log b b
1=-1,log a b>0, ∴log a b 1< log b b
1< log a b (……3') (2)当0<a<b<1时,因为0> log a b 1> log a a 1=-1,log b b
1=-1, ∴log b b 1< log a b
1< log a b (……6') (3)当0<a< 1< b 时,且b>a 1时,因为log a b< log a a 1=-1,log b b
1=-1, log a b 1>log a a=1,∴log a b< log b b 1< log a b
1 (……9') (4)当0<a< 1< b ,且b=a 1时,log a b= log b b 1< log a b
1 (……12') (5)当0<a< 1< b ,且b<a 1时,log b b 1< log a b< log a b 1 (……14')。
