13.9 安培环路定理
安培环路定理
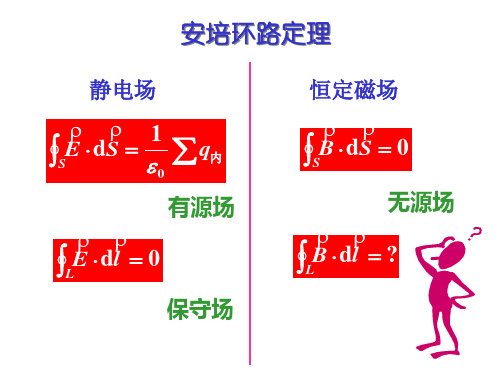
静电场
1
E dS
S
0
q内有源场Fra bibliotekLE dl 0
保守场
恒定磁场
SB dS 0
无源场
LB dl ?
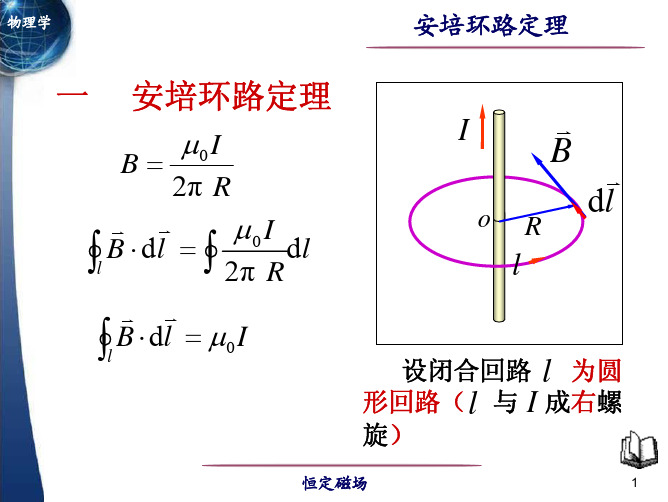
一、 安培环路定理
以无限长直电流的磁场为例说明
1、圆形积分回路
选在垂直于长直载流导线的平面内,以导线与平面
交点o为圆心,半径为 r 的圆周路径 L,其指向与电流
成右旋关系。
练习:如图,流出纸面的电流为 2I ,流进纸面的电 流为 I ,则下述各式中那一个是正确的?
( A)
B• L1
dl
2
0I
(C )
B • dl
L3
0I
(B)
B• L2
dl
0I
( D)
B • dl
L4
0I
2I •
L1 I
L2
L3
L4
(D)
二、安培环路定理的应用
B • dl 0 Ii
...............
B
I
2)选取回路
作矩形安培环路,如图 规定:顺时针绕向为正
M
NB
++++++++++++
P
LO
N O p M
l B d l M B d l N B d l O B d l P B d l
B MN 利用安培环路定理求 B
B MN 0nMNI
B 0nI
方向可由右手螺旋法定。 无限长直螺线管内为均匀磁场
3、求螺线环内的磁感应强度
已知:I 、N、R1、R2
N——导线总匝数
4,安培环路定理 位移电流
dq0 dΦe = ε0 Ic = = Id dt dt
麦克斯韦把这种电流称为位移电流 记作 麦克斯韦把这种电流称为位移电流,记作 d 位移电流 记作I
I = ∫ j ⋅ dS
S
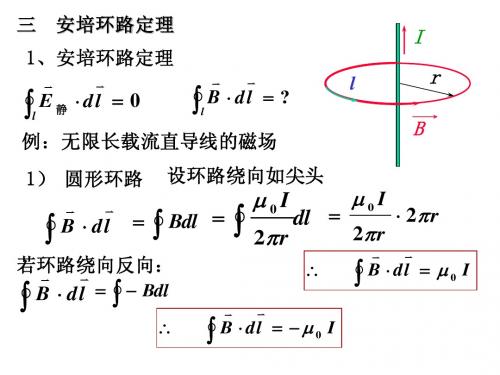
三
安培环路定理
I
1、安培环路定理
∫ E静 ⋅ dl = 0
l
∫ B ⋅ dl = ?
l
l
r B
例:无限长载流直导线的磁场 1) 圆形环路 设环路绕向如尖头
µ0I µ0I ⋅ 2πr dl = = ∫ Bdl = ∫ 2πr ∫ B ⋅ dl 2πr
∴
若环路绕向反向: 若环路绕向反向:
B ⋅ dl = ∫ − Bdl ∫
l 0
l
则有: c.若有数个电流(不一定为直电流) c.若有数个电流(不一定为直电流)穿过环路 则有: 若有数个电流
= ∫ ( B1 + B2 + ⋯) ⋅ dl
∫ B ⋅ dl
叠加原理
=
I1 l
I2
I3
= Σ ∫ Bi ⋅dl = µ 0 ΣI i
[安培环路定理]磁感应强度沿任意闭合路径一周的线积分 安培环路定理]磁感应强度沿任意闭合路径一周的线积分 任意 等于穿过闭合路径所包围面积的电流代数和的µ 等于穿过闭合路径所包围面积的电流代数和的µ0倍。
dI
R r
r〈 R
B ⋅ dl = ∫ Bdl = B ⋅ 2πr ∫ = µ 0 ∑ I i内 =0
i
dB’ dB
dB合
dI’
∴ B内 = 0
r〉 R
安培环路定理
安培环路定理
二
安培环路定理的应用举例
例1 求载流螺绕环内的磁场 解 (1) 对称性分析:环内 B 线为同心 圆,环外 B 为零.
d
R
恒定磁场
7
物理学
安培环路定理
(2)选回路
∫l B ⋅ d l = 2π RB = μ0 NI
B=
μ0 NI
2π R
令 L = 2 πR
d
B = μ0 NI L
R
当 2R >> d 时,螺绕环内可视为均匀场 .
l
恒定磁场
l
B = B1 + B2 + B3
∫ B ⋅ d l = μ (I
0
2
− I3 )
I1
I2
I3
推广: 安培环路定理
l
∫ B ⋅ dl
恒定磁场
= μ0 ∑ Ii
i =1
n
4
物理学
安培环路定理
安培环路定理
∫ B ⋅ dl
= μ0 ∑ Ii
i =1
n
在真空的恒定磁场中,磁感强度 B 沿任一闭合路径的积分的值,等于 μ 0 乘以 该闭合路径所穿过的各电流的代数和. 注意 电流 I 正负的规定 : I 与 L 成右螺 旋时,I 为正;反之为负.
恒定磁场
5
物理学
安培环路定理
∫ B⋅dl = μ (−I − I )
L 0 1 2
= −μ0 I1 + I2) (
问(1) 是否与回路 L B 外电流有关?
I1
I1
L
I2 I 3
I1
(2)若 ∫LB ⋅ d l = 0 ,是否回路 L 上各处 B = 0 ?是否回路 L 内无电流穿过?
安培环路定理

安培环路定理安培环路定理的严格证明(缩略图)在稳恒磁场中,磁场强度H沿任何闭合路径的线积分,等于这闭合路径所包围的各个电流之代数和。
这个结论称为安培环路定理(Ampere circuital theorem)。
安培环路定理可以由毕奥-萨伐尔定律导出。
它反映了稳恒磁场的磁感应线和载流导线相互套连的性质。
目录按照安培环路定理,环路所包围电流之正负应服从右手螺旋法则。
安培环路定理应用如果闭合路径l包围着两个流向相反的电流I1和I2(如左图所示),这在下式中,按图中选定的闭合路径l 的绕行方向,B矢量沿此闭合路径的环流为如果闭合路径l包围的电流等值反向(如右图所示),或者环路中并没有包围电流,则:安培环路定理的证明(严格证明,大图见参考资料的链接)编辑本段安培环路定理的证明(不完全证明)以长直载流导线产生的磁场为例,证明安培环路定理的正确性。
安培环路定理应用在长直载流导线的周围作三个不同位置,且不同形状的环路,可以证明对磁场中这三个环路,安培环路定理均成立。
取对称环路包围电流在垂直于长直载流导线的平面内,以载流导线为圆心作一条半径为r 的圆形环路l,则在这圆周上任一点的磁感强度H的大小为其方向与圆周相切.取环路的绕行方向为逆时针方向,取线元矢量dl,则H与dl间的夹角,H沿这一环路 l 的环流为式中积分是环路的周长。
于是上式可写成为从上式看到,H沿此圆形环路的环流只与闭合环路所包围的电流I 有关,而与环路的大小、形状无关。
取任意环路包围电流在垂直于长直载流导线的平面内,环绕载流直导线作一条如下图所示的任意环路l,取环路的绕行方向为逆时针方向。
在环路上任取一段线元dl,载流直导线在线元dl处的磁感强度B大小为H与dl的夹角为,则H对dl的线积分为直导线中心向线元的张角为,则有,所以有可见,H对dl的线积分与到直导线的距离无关。
那么B对整个环路的环流值为上述计算再次说明H的环流值与环路的大小、形状无关。
取任意环路不包围电流在垂直于长直载流导线的平面内,在载流直导线的外侧作一条如下图所示的任安培环路定理应用意环路l,取环路的绕行方向为逆时针方向。
安培环路定理

安培环路定理
安培环路定理,又称为安培定理或安培第二定理,是电磁学中的一条重要定理,描述了由电流所产生的磁场的性质。
它是由法国物理学家安德烈-玛丽·安培在19世纪初提出的。
安培环路定理是基于麦克斯韦方程组中的一个方程,可以用来计算磁场的强度。
根据该定理,通过电流所形成的磁场的磁感应强度H,沿着任意封闭曲线所围成的面积S的总磁通量Φ,与该封闭曲线所围成的电流之间的关系为:
∮H·dl = ∫∫S B·dS = Φ
其中,H是磁场的强度,dl是沿着闭合曲线的微元路径元素,B是磁感应强度,dS是平面面元素,Φ是通过该曲线所围成的面积的磁通量。
安培环路定理本质上是一个积分方程,可以通过对曲线的路径和曲面的选择来灵活地应用。
根据闭合曲线的选择不同,可以得到更方便的计算磁场的方法。
通常情况下,选择封闭曲线为简单的几何形状,例如圆形、矩形或直线,可以大大简化计算的过程。
安培环路定理的应用广泛,可以用于解决与电流所产生的磁场相关的问题。
例如,在电磁铁中,可以利用安培环路定理计算铁芯的磁场分布;在电感器中,可以通过该定理计算电感量。
此外,还可以利用安培环路定理推导出其他电磁学中的重要定理,如磁场的叠加定理和比奥-萨伐尔定律等。
综上所述,安培环路定理是电磁学中的一条基本定理,描述了电流所产生的磁场的性质。
通过应用安培环路定理,可以方便地计算出磁场的强度和分布,解决各种与电流和磁场相关的问题,为电磁学的研究和应用提供了重要的理论基础。
稳恒磁场--安培环路定理

方程。它表明磁场是涡旋场(非保守场)。
2)正确理解定理中各量的含义
B 空间所有(环路内外)电流共同产生
L 在磁场中任取的一闭合线
Ii内环路所包围的电流的代数和
i
讨论
B dl 0 Ii内
环B 沿路该外回的路电的流积对L 分空(间B任 的一环点i 流的)B无有贡贡献献。,而对
解:电流均匀分布,则电流密度为
II J S πR2
根据电流分布的柱对称性,取过 场点的圆作为安培环路
l B dl B2πr
由安环定理有 2πrB 0 Ii
i
IR
B Jr
2πrB 0 Ii
i
解得
μ0 Ii
B i 2πr
若场点在圆柱内,即 r < R
3)对一些具有对称分布的电流的磁感强度可 利用安培环路定理方便地计算。
B dl
l
μ0
Ii内 对比
i
1n
S
E dS
ε0
qi内
i 1
二、安培环路定理的应用
1、分析对称性
2、选取积分回路——安培环路
3、计算 B dl l
4、计算
I i内
5、应用定理求出 B
r
B
2πr
r <R
B
μ0
J
r
B
场的分布为
2
r > R B μ0 I
2πr (令 R 0 ,即长直载流导线)
OR
r
求长为l的一段的磁通量: 建坐标如图,
在任意坐标 r 处 宽为dr的面积 元的磁通量为
安培环路定理课件

电磁感应的概念
电磁感应是指因磁通量变化而引起感应电动势的现象,它是 能量转换的一种形式。
电磁感应在安培环路定理中扮演着重要的角色,它可以解释 磁场和电流之间的相互作用和变化规律。
03
CATALOGUE
安培环路定理的证明
证明方法一:利用积分
总结词
通过在闭合曲线上的积分,我们可以证明安培环路定理。
实验二:电磁力测量
总结词
电磁力测量是研究安培环路定理的重要实验,通过测量通电导线在磁场中所受的力,可 以验证安培环路定理的推论。
详细描述
该实验采用电磁力测量仪和不同大小的电流源,通过测量通电导线在磁场中所受的力, 可以验证安培环路定理的推论。在实验过程中,需要注意保持电流的稳定和避免空气阻
力的影响。
安培环路定理的应用场景
要点一
总结词
安培环路定理的应用场景广泛,包括电力工程、电子设备 、磁力设备和科学研究等。
要点二
详细描述
在电力工程中,安培环路定理可以用于计算电流产生的磁 场,从而设计合适的磁路和电磁铁。在电子设备中,安培 环路定理可以用于分析电磁干扰和射频干扰等问题。在磁 力设备中,安培环路定理可以用于设计磁力控制器和磁力 泵等装置。此外,安培环路定理也是科学研究的重要工具 ,可以用于研究电磁场和电磁波等物理现象。
有节点电流的求和。
基尔霍夫定律的应用
03
基尔霍夫定律在电路理论、电子工程、电力工程等领域都有广
泛的应用。
06
CATALOGUE
安培环路定理实验及解析
实验一:磁场分布测量
总结词
磁场分布测量是研究安培环路定理的基础实 验,通过测量不同电流下磁场的分布情况, 可以验证安培环路定理的正确性。
安培环路定理

(1)管内:取L矩形回路 abcda
边在轴上,两边与轴平行,另
aP b
两个边垂直于轴。
LB dl Bab ab Bcd cd Bab ab
e
Q
f
0I 0nI ab
d
c
∞
B内 onI 其方向与电流满足右手螺旋.
(2)管外 :
取回路efbae同理可证,无限长直螺线管外任一点的磁场为
A(rQ )
0I 2
ln
r Q
r P
A(rP )
A(rQ
)
0I 2
ln
r Q
r
-I
r P
P
两式相加,得:
A(rP )
A(rQ )
0I 2
ln
rQ rP
rP rQ
0I 2
ln
rP rP
A(rP )
A(rQ )
0I 2
ln
r P
r P
若选Q点的矢势为零,则
A(rP )
0I 2
ln
r P
r P
例2.一无限长载流圆柱导体,半径为R, 电流I均匀分布
ldr
0I 2
l
ln
rQ r
A(rP ) A(rQ )
0I 2
ln
rQ rP
+I
Q
若选Q点的矢势为零,则
A(rp
)
0I 2
ln
rQ rP
r P
注意:若选Q点在无穷远处或导线
上,磁矢势将无意义.
讨论:两根平行的载流直导线,电流大 小相等方向相反,求磁矢势.
选Q点在两直线电流之间垂线的中点处.
A(rP )
B dS 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r 1
推广到一般情况
I3
电流分布
∫
说明: 说明:
L
B ⋅ dl = µ o ∑ I内
I1> 0
I2< 0
1)安培环路定理只适用于稳恒 ) 电流(闭合或伸展到∞ 电流(闭合或伸展到∞); 2) I 流向与 绕向成右手 ) 内 流向与L绕向成右手 关系时I 为正, 关系时 内为正, I内 流向与 绕向成左手 流向与L绕向成左手 关系时为负; 关系时为负; 3)环路上各点的磁场为所有 ) 电流的贡献; 电流的贡献; 4) 磁场是有旋场 )
I
n
I
B = µ0nI
管外场强仍为零。 管外场强仍为零。
7 第13章 电流和磁场
求无限大平面电流的磁场。 例3 求无限大平面电流的磁场。
?
解 平板上下两侧的磁场平行于 平板,且垂直于平板电流, 平板,且垂直于平板电流, 又是面对称的。 又是面对称的。 取回路,环量为 取回路,
I
B
b
P
a
d
B'
∫ B⋅dl = ∫
L
I
B = µ0N / 2πr I
0
若螺绕环的截面很小, 若螺绕环的截面很小,
N B = µ0 I = µ nI 内 0 2π r
若在外部再做一个环路, 若在外部再做一个环路,可得
r =r
N
o
R 1
h
R2
r
dr
∑Ii =0
螺绕环内的磁通量为
B =0 外
R 2
1
S
Φm = ∫ B⋅ dS = ∫R
R 1
§13.9 安培环路定理
静电场: 静电场 磁 场:
I
∫ ∫ B⋅dl =?
L
L
E⋅dl =0 静电场是保守场
L
r
一、磁场的安培环路定理
以无限长载流直导线为例
P
B=
µ0I
2π r
∫
1
L
B⋅ dl = ∫ Bcosθdl = ∫L
µ0I
2πr
rdϕ
I
L
= µ0I
L
r dϕ
r′ B
dl
θ
磁场的环流与环路中所包围的电流有关。 磁场的环流与环路中所包围的电流有关。
3
L
d l
ˆ n
I1 > 0 L S
I2 < 0
—— 电流是磁场涡旋的轴心
第13章 电流和磁场
安培环路定律
∫LB⋅dl =µ0∑Ii内
恒定电流的磁场中, 恒定电流的磁场中,磁感应强度沿一闭合路径 L 的线积 分等于路径 L 包围的电流强度的代数和的 µ0 倍。
二、安培环路定理的应用
R
求无限长圆柱面电流的磁场分布。 例1 求无限长圆柱面电流的磁场分布。 系统有轴对称性, 解 系统有轴对称性, 圆周上各点的 B 相同 时过圆柱面外P r > R 时过圆柱面外 点做一圆周
第13章 电流和磁场
环路方向反向
−µ0I ∫L B⋅dl = ∫L 2πr rdϕ
=−µ0I
µ0I
2π 2 r
I L
r dϕ
B 2
r′ B
θ
环路中不包围电流
dl
θ1
d1 l
B= 1
µ0I
2π 1 r
B = 2
对一对线元来说
I
r θ2 2
Idϕ
B 1
B ⋅ dl + B ⋅ dl 1 2
dl2
L = Bdl cosθ1 + B dl cosθ2 1 2 µ0Irdϕ µ0Ir2dϕ 若环路不包围电流, 若环路不包围电流, 1 = − =0 则磁场环流为零。 则磁场环流为零。 2πr 2πr 1 2
6
R 2
µ0N I
2π r
hdr =
µ0hN I
R ln 2 2π R 1
第13章 电流和磁场
思考
截面形状任意的密绕长直螺线管内外的磁场 截面形状任意的密绕长直螺线管内外的磁场 长直螺线管内 如何? 如何? (书P274 思考题 8.11) )
答:
螺线管的每圈电流都圆电流 叠加而成,故从电流分布来 叠加而成 故从电流分布来 看,截面形状任意的密绕长 直螺线管可看成无数大大小 小的圆截面螺线管叠加而成。 小的圆截面螺线管叠加而成。 所以管内仍是均匀场
b a
ab
B⋅ dl +∫ B⋅ dl
cd
= B∫ dl +B∫ dl = µ0abI
c
d
c
x
B = µ0I /2
推广: 推广:有厚度的无限大平面电流 • 在外部 • 在内部
8
d
j
B = µ0 jd /2 B = µ0 jx
j 为线电流密度
第13章 电流和磁场
o
R
r
I J= π 2 R
2
r <R
r
I
L
2
B2π = µ0 jπr r
5
B=
第13章 电流和磁场
2π R
µ0Ir
求螺绕环电流的磁场分布及环内的磁通量。 例2 求螺绕环电流的磁场分布及环内的磁通量。 在螺绕环内部做一个环路, 解 在螺绕环内部做一个环路,
∫ Bcosθdl = B⋅2πr= µ NI
r
I
Lห้องสมุดไป่ตู้
∫
4
Bcosθdl = B∫ dl = B2π = µ0I r L L
第13章 电流和磁场
B=
µ0I
2π r
(r > R)
Bm =
µ0I
2πR
r <R
L
时在圆柱面内做一圆周 时在圆柱面内做一圆周 圆柱面
∫ Bcosθdl = B2πr = 0
B=0
(r < R)
推论: 推论:无限长圆柱体载流直导线 的磁场分布 电流密度
