【三维设计】北京联合大学附中2014年高考数学一轮复习 空间几何体单元训练 新人教A版
北京联合大学附中高考数学一轮复习 不等式单元训练 新人教A版

北京联合大学附中三维设计2014年高考数学一轮复习单元训练:不等式本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.不等式2252xx x -->的解集是( )A .{}51x x x ≥≤-或 B .{}51x x x ><-或 C .{}15x x -<<D .{}15x x -≤≤【答案】B 2.不等式1ax x a >-⎧⎨+>⎩的解集不是空集,则实数a 的取值范围是( )A .(0,)+∞B .(1,)+∞C .(1,)-+∞D .(,1)-∞-【答案】C3.若n<0,m>0,且m+n>0,则下列不等式中成立的是( )A .-n<m <n<-mB .-m<n<-n<mC .-n<-m<n<mD .-n<n<m<-m 【答案】B4.若0<<a b ,则下列不等式①ab b a <+;②|;|||b a >③ba 11<;④2>+b a a b 中,正确的不等式有( ) A .1个 B .2个 C .3个D .4个【答案】C5.若b a >,则下列各式正确的是( )A . 22b a >B . b a ->-22C . b a 22->-D . 22->-b a【答案】D6.如果0a b <<,那么( )A .0a b ->B .ac bc <C .11a b> D .22a b<【答案】C7.不等式2x x >的解集是( )A .(),0-∞ B . ()0,1C .()1,+∞D .()(),01,-∞⋃+∞【答案】D8.若b a b a >是任意实数,且、,则下列不等式成立的是( ) A .22b a >B .1<a bC .0)lg(>-b aD .ba )31()31(< 【答案】D9.若a ,b ,c ∈R ,a >b ,则下列不等式成立的是( )A .b a 11<B .a 2>b 2C .22+1+1a b c c > D .a|c|>b|c| 【答案】C 10.在R 上定义运算⊙:a ⊙b =ab +2a +b ,则满足x ⊙(x -2)<0的实数x 的取值范围为( )A .(0,2)B .(-2,1)C .(-∞,-2)∪(1,+∞)D .(-1,2) 【答案】B11.设x R ∈,则不等式4212>-x的解集是( )A .{}Rx x x ∈±≠,3B .{}33<<-x xC .{}22<<-x xD .{}33-<>x x x 或【答案】D12.目标函数y x z +=2,变量y x ,满足⎪⎩⎪⎨⎧≥<+≤+-12553034x y x y x ,则有( )A .3,12min max ==z zB .z z ,3min =无最大值C .,12max=z z 无最小值D .z 既无最大值,也无最小值【答案】B第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.已知关于x 的不等式25x x k -+->的解集为R ,则实数k 的范围是 . 【答案】k<314.已知函数()f x =21010x x x ⎧+≥⎨<⎩,则满足不等式2(1)(2)f x f x ->的x 的范围是____________. 【答案】(21)- 15.若关于x 的不等式-21x 2+2x>ax 的解集为{x|0<x<2},则实数a 的值为____________。
【三维设计】2014届高考数学一轮复习 (基础知识+高频考点+解题训练)空间几何体的表面积和体积教学案
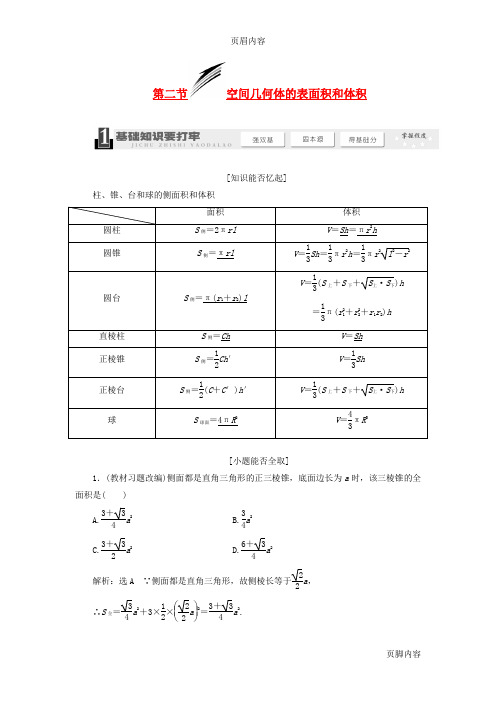
页眉内容第二节空间几何体的表面积和体积[知识能否忆起]柱、锥、台和球的侧面积和体积[小题能否全取]1.(教材习题改编)侧面都是直角三角形的正三棱锥,底面边长为a时,该三棱锥的全面积是( )A.3+34a2 B.34a2C.3+32a2 D.6+34a2解析:选A ∵侧面都是直角三角形,故侧棱长等于22a,∴S全=34a2+3×12×⎝⎛⎭⎪⎫22a2=3+34a2.2.已知正四棱锥的侧棱与底面的边长都为32,则这个四棱锥的外接球的表面积为( )A .12πB .36πC .72πD .108π解析:选B 依题意得,该正四棱锥的底面对角线长为32×2=6,高为22-⎝ ⎛⎭⎪⎫12×62=3,因此底面中心到各顶点的距离均等于3,所以该四棱锥的外接球的球心为底面正方形的中心,其外接球的半径为3,所以其外接球的表面积等于4π×32=36π.3.某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为5的等腰三角形,侧视图是一个底边长为6,高为5的等腰三角形,则该几何体的体积为( )A .24B .80C .64D .240解析:选B 结合题意知该几何体是四棱锥,棱锥底面是长和宽分别为8和6的矩形,棱锥的高是5,可由锥体的体积公式得V =13×8×6×5=80.4.(教材习题改编)表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________.解析:设圆锥的母线为l ,圆锥底面半径为r , 则πrl +πr 2=3π,πl =2πr . 解得r =1,即直径为2. 答案:25.某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是________.解析:由三视图可知此几何体的表面积分为两部分:底面积即俯视图的面积,为23;侧面积为一个完整的圆锥的侧面积,且圆锥的母线长为2,底面半径为1,所以侧面积为2π.两部分加起来即为几何体的表面积,为2(π+3).答案:2(π+3)1.几何体的侧面积和全面积:几何体侧面积是指(各个)侧面面积之和,而全面积是侧面积与所有底面积之和.对侧面积公式的记忆,最好结合几何体的侧面展开图来进行.2.求体积时应注意的几点:(1)求一些不规则几何体的体积常用割补的方法转化成已知体积公式的几何体进行解决.(2)与三视图有关的体积问题注意几何体还原的准确性及数据的准确性. 3.求组合体的表面积时注意几何体的衔接部分的处理.典题导入[例1] (2012·安徽高考)某几何体的三视图如图所示,该几何体的表面积是________.[自主解答] 由几何体的三视图可知,该几何体是底面为直角梯形的直四棱柱(如图所示).在四边形ABCD 中,作DE ⊥AB ,垂足为E ,则DE =4,AE =3,则AD =5. 所以其表面积为2×12×(2+5)×4+2×4+4×5+4×5+4×4=92.[答案] 92由题悟法1.以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.2.多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理. 3.旋转体的表面积问题注意其侧面展开图的应用.以题试法1.(2012·河南模拟)如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为32,且一个内角为60°的菱形,俯视图为正方形,那么该饰物的表面积为( )A. 3 B .2 3 C .4 3 D .4解析:选D 依题意得,该饰物是由两个完全相同的正四棱锥对接而成,正四棱锥的底面边长和侧面上的高均等于菱形的边长,因此该饰物的表面积为8×⎝ ⎛⎭⎪⎫12×1×1=4.典题导入[例2] (1)(2012·广东高考)某几何体的三视图如图所示,它的体积为( )A .72πB .48πC .30πD .24π(2)(2012·山东高考)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E 为线段B 1C 上的一点,则三棱锥A -DED 1的体积为________.[自主解答] (1)由三视图知,该几何体是由圆锥和半球组合而成的,直观图如图所示,圆锥的底面半径为3,高为4,半球的半径为3.V =V 半球+V 圆锥=12·43π·33+13·π·32·4=30π.(2)VA -DED 1=VE -ADD 1=13×S △ADD 1×CD =13×12×1=16.[答案] (1)C (2)16本例(1)中几何体的三视图若变为:其体积为________.解析:由三视图还原几何体知,该几何体为圆柱与圆锥的组合体,其体积V =V 圆柱-V 圆锥=π×32×4-13π×32×4=24π.答案:24π由题悟法1.计算柱、锥、台体的体积,关键是根据条件找出相应的底面面积和高,应注意充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解.2.注意求体积的一些特殊方法:分割法、补体法、转化法等,它们是解决一些不规则几何体体积计算常用的方法,应熟练掌握.3.等积变换法:利用三棱锥的任一个面可作为三棱锥的底面.①求体积时,可选择容易计算的方式来计算;②利用“等积法”可求“点到面的距离”.以题试法2.(1)(2012·长春调研)四棱锥P -ABCD 的底面ABCD 为正方形,且PD 垂直于底面ABCD ,N 为PB 中点,则三棱锥P -ANC 与四棱锥P -ABCD 的体积比为( )A .1∶2B .1∶3C .1∶4D .1∶8解析:选C 设正方形ABCD 面积为S ,PD =h ,则体积比为13Sh -13·12S ·12h -13·12Sh 13Sh =14.(2012·浙江模拟)如图,是某几何体的三视图,则这个几何体的体积是( )A .32B .24C .8D.323解析:选B 此几何体是高为2的棱柱,底面四边形可切割成为一个边长为3的正方形和2个直角边分别为3,1的直角三角形,其底面积S =9+2×12×3×1=12,所以几何体体积V =12×2=24.典题导入[例3] (2012·新课标全国卷)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( )A.26B.36C.23D.22[自主解答] 由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍. 在三棱锥O -ABC 中,其棱长都是1,如图所示,S △ABC =34×AB 2=34, 高OD =12-⎝⎛⎭⎪⎫332=63, ∴V S -ABC =2V O -ABC =2×13×34×63=26.[答案] A由题悟法1.解决与球有关的“切”、“接”问题,一般要过球心及多面体中的特殊点或过线作截面,把空间问题转化为平面问题,从而寻找几何体各元素之间的关系.2.记住几个常用的结论:(1)正方体的棱长为a ,球的半径为R , ①正方体的外接球,则2R =3a ; ②正方体的内切球,则2R =a ; ③球与正方体的各棱相切,则2R =2a .(2)长方体的同一顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2. (3)正四面体的外接球与内切球的半径之比为1∶3.以题试法3.(1)(2012·琼州模拟)一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接球的表面积为( )A .23π B.8π3 C .4 3D.16π3(2)(2012·潍坊模拟)如图所示,已知球O 的面上有四点A 、B 、C 、D ,DA ⊥平面ABC ,AB ⊥BC ,DA =AB =BC =2,则球O 的体积等于________.解析:(1)由三视图可知几何体的直观图如图所示. 其中侧面DBC ⊥底面ABC ,取BC 的中点O 1,连接AO 1,DO 1知DO 1⊥底面ABC 且DO 1=3,AO 1=1,BO 1=O 1C =1.在Rt △ABO 1和Rt △ACO 1中,AB =AC =2, 又∵BC =2,∴∠BAC =90°.∴BC 为底面ABC 外接圆的直径,O 1为圆心, 又∵DO 1⊥底面ABC ,∴球心在DO 1上, 即△BCD 的外接圆为球大圆,设球半径为R , 则(3-R )2+12=R 2,∴R =23. ∴S 球=4πR 2=4π×⎝ ⎛⎭⎪⎫232=16π3.(2)如图,以DA ,AB ,BC 为棱长构造正方体,设正方体的外接球球O 的半径为R ,则正方体的体对角线长即为球O 的直径,所以|CD |=22+22+22=2R ,所以R =62. 故球O 的体积V =4πR33=6π.答案:(1)D (2)6π1.(2012·北京西城模拟)某几何体的三视图如图所示,该几何体的体积是( )A .8 B.83 C .4D.43解析:选D 将三视图还原,直观图如图所示,可以看出,这是一个底面为正方形(对角线长为2),高为2的四棱锥,其体积V =13S 正方形ABCD ×PA =13×12×2×2×2=43.2.(2012·山西模拟)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且AB =3,BC =2,则棱锥O -ABCD 的体积为( )A.51 B .351 C .251D .651解析:选A 依题意得,球心O 在底面ABCD 上的射影是矩形ABCD 的中心,因此棱锥O-ABCD 的高等于42-⎝ ⎛⎭⎪⎫1232+222=512,所以棱锥O -ABCD 的体积等于13×(3×2)×512=51.3.(2012·马鞍山二模)如图是一个几何体的三视图,则它的表面积为( )A .4π B.154π C .5πD.174π 解析:选D 由三视图可知该几何体是半径为1的球被挖出了18部分得到的几何体,故表面积为78·4π·12+3·14·π·12=174π. 4.(2012·济南模拟)用若干个大小相同,棱长为1的正方体摆成一个立体模型,其三视图如图所示,则此立体模型的表面积为( )A .24B .23C .22D .21解析:选C 这个空间几何体是由两部分组成的,下半部分为四个小正方体,上半部分为一个小正方体,结合直观图可知,该立体模型的表面积为22.5. (2012·江西高考)若一个几何体的三视图如下图所示,则此几何体的体积为( )A.112B .5 C.92D .4解析:选D 由三视图可知,所求几何体是一个底面为六边形,高为1的直棱柱,因此只需求出底面积即可.由俯视图和主视图可知,底面面积为1×2+2×12×2×1=4,所以该几何体的体积为4×1=4.6.如图,正方体ABCD -A ′B ′C ′D ′的棱长为4,动点E ,F 在棱AB 上,且EF =2,动点Q 在棱D ′C ′上,则三棱锥A ′-EFQ 的体积( )A .与点E ,F 位置有关B .与点Q 位置有关C .与点E ,F ,Q 位置都有关D .与点E ,F ,Q 位置均无关,是定值解析:选D 因为V A ′-EFQ =V Q -A ′EF =13×⎝ ⎛⎭⎪⎫12×2×4×4=163,故三棱锥A ′-EFQ 的体积与点E ,F ,Q 的位置均无关,是定值.7.(2012·湖州模拟)如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是________.解析:由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V =13×1×1×22=26. 答案:268.(2012·上海高考)若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的体积为________.解析:因为半圆的面积为2π,所以半圆的半径为2,圆锥的母线长为2.底面圆的周长为2π,所以底面圆的半径为1,所以圆锥的高为3,体积为33π.答案:33π 9.(2013·郑州模拟)在三棱锥A -BCD 中,AB =CD =6,AC =BD =AD =BC =5,则该三棱锥的外接球的表面积为________.解析:依题意得,该三棱锥的三组对棱分别相等,因此可将该三棱锥补形成一个长方体,设该长方体的长、宽、高分别为a 、b 、c ,且其外接球的半径为R ,则⎩⎪⎨⎪⎧a 2+b 2=62,b 2+c 2=52,c 2+a 2=52,得a 2+b 2+c 2=43,即(2R )2=a 2+b 2+c 2=43,易知R 即为该三棱锥的外接球的半径,所以该三棱锥的外接球的表面积为4πR 2=43π.答案:43π10.(2012·江西八校模拟)如图,把边长为2的正六边形ABCDEF 沿对角线BE 折起,使AC = 6.(1)求证:面ABEF ⊥平面BCDE ; (2)求五面体ABCDEF 的体积.解:设原正六边形中,AC ∩BE =O ,DF ∩BE =O ′,由正六边形的几何性质可知OA =OC =3,AC ⊥BE ,DF ⊥BE .(1)证明:在五面体ABCDE 中,OA 2+OC 2=6=AC 2, ∴OA ⊥OC ,又OA ⊥OB ,∴OA ⊥平面BCDE .∵OA ⊂平面ABEF , ∴平面ABEF ⊥平面BCDE .(2)由BE ⊥OA ,BE ⊥OC 知BE ⊥平面AOC ,同理BE ⊥平面FO ′D ,∴平面AOC ∥平面FO ′D ,故AOC -FO ′D 是侧棱长(高)为2的直三棱柱,且三棱锥B -AOC 和E -FO ′D 为大小相同的三棱锥,∴V ABCDEF =2V B -AOC +V AOC -FO ′D=2×13×12×(3)2×1+12×(3)2×2=4.11.(2012·大同质检)如图,在四棱锥P -ABCD 中,底面是直角梯形ABCD ,其中AD ⊥AB ,CD ∥AB ,AB =4,CD =2,侧面PAD 是边长为2的等边三角形,且与底面ABCD 垂直,E 为PA 的中点.(1)求证:DE ∥平面PBC ; (2)求三棱锥A -PBC 的体积.解:(1)证明:如图,取AB 的中点F ,连接DF ,EF .在直角梯形ABCD 中,CD ∥AB ,且AB =4,CD =2,所以BF 綊CD . 所以四边形BCDF 为平行四边形. 所以DF ∥BC .在△PAB 中,PE =EA ,AF =FB ,所以EF ∥PB . 又因为DF ∩EF =F ,PB ∩BC =B , 所以平面DEF ∥平面PBC .因为DE ⊂平面DEF ,所以DE ∥平面PBC . (2)取AD 的中点O ,连接PO . 在△PAD 中,PA =PD =AD =2, 所以PO ⊥AD ,PO = 3.又因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD , 所以PO ⊥平面ABCD .在直角梯形ABCD 中,CD ∥AB ,且AB =4,AD =2,AB ⊥AD ,所以S △ABC =12×AB ×AD =12×4×2=4.故三棱锥A -PBC 的体积V A -PBC =V P -ABC =13×S △ABC ×PO =13×4×3=433.12.(2012·湖南师大附中月考)一个空间几何体的三视图及部分数据如图所示,其正视图、俯视图均为矩形,侧视图为直角三角形.(1)请画出该几何体的直观图,并求出它的体积; (2)证明:A 1C ⊥平面AB 1C 1.解:(1)几何体的直观图如图所示,四边形BB 1C 1C 是矩形,BB 1=CC 1=3,BC =B 1C 1=1,四边形AA 1C 1C 是边长为3的正方形,且平面AA 1C 1C 垂直于底面BB 1C 1C ,故该几何体是直三棱柱,其体积V =S △ABC ·BB 1=12×1×3×3=32.(2)证明:由(1)知平面AA 1C 1C ⊥平面BB 1C 1C 且B 1C 1⊥CC 1, 所以B 1C 1⊥平面ACC 1A 1.所以B 1C 1⊥A 1C . 因为四边形ACC 1A 1为正方形,所以A 1C ⊥AC 1. 而B 1C 1∩AC 1=C 1,所以A 1C ⊥平面AB 1C 1.1.(2012·潍坊模拟)已知矩形ABCD 的面积为8,当矩形ABCD 周长最小时,沿对角线AC 把△ACD 折起,则三棱锥D -ABC 的外接球表面积等于( )A .8πB .16πC .482πD .不确定的实数解析:选B 设矩形长为x ,宽为y ,周长P =2(x +y )≥4xy =82,当且仅当x =y =22时,周长有最小值.此时正方形ABCD 沿AC 折起,∵OA =OB =OC =OD ,三棱锥D -ABC 的四个顶点都在以O 为球心,以2为半径的球上,此球表面积为4π×22=16π.2.(2012·江苏高考)如图,在长方体ABCD -A 1B 1C 1D 1中,AB=AD =3 cm ,AA 1=2 cm ,则四棱锥A -BB 1D 1D 的体积为________cm 3.解析:由题意得VA -BB 1D 1D =23VABD -A 1B 1D 1=23×12×3×3×2=6.答案:63.(2013·深圳模拟)如图,平行四边形ABCD 中,AB ⊥BD ,AB =2,BD =2,沿BD 将△BCD 折起,使二面角A -BD -C 是大小为锐角α的二面角,设C 在平面ABD 上的射影为O .(1)当α为何值时,三棱锥C -OAD 的体积最大?最大值为多少? (2)当AD ⊥BC 时,求α的大小. 解:(1)由题知CO ⊥平面ABD ,∴CO ⊥BD , 又BD ⊥CD ,CO ∩CD =C ,∴BD ⊥平面COD . ∴BD ⊥OD .∴∠ODC =α.V C -AOD =13S △AOD ·OC =13×12·OD ·BD ·OC=26·OD ·OC =26·CD ·cos α·CD ·sin α =23·sin 2α≤23, 当且仅当sin 2α=1,即α=45°时取等号. ∴当α=45°时,三棱锥C -OAD 的体积最大,最大值为23.(2)连接OB ,∵CO ⊥平面ABD ,∴CO ⊥AD ,又AD ⊥BC , ∴AD ⊥平面BOC . ∴AD ⊥OB .∴∠OBD +∠ADB =90°.故∠OBD =∠DAB ,又∠ABD =∠BDO =90°, ∴Rt △ABD ∽Rt △BDO . ∴OD BD =BD AB.∴OD =BD 2AB=222=1,在Rt △COD 中,cos α=OD CD =12,得α=60°.1.两球O 1和O 2在棱长为1的正方体ABCD -A 1B 1C 1D 1的内部,且互相外切,若球O 1与过点A 的正方体的三个面相切,球O 2与过点C 1的正方体的三个面相切,则球O 1和O 2的表面积之和的最小值为( )A .(6-33)πB .(8-43)πC .(6+33)πD .(8+43)π解析:选A 设球O 1、球O 2的半径分别为r 1、r 2, 则3r 1+r 1+3r 2+r 2=3,r 1+r 2=3-32,从而4π(r 21+r 22)≥4π·r 1+r 222=(6-33)π.2.已知某球半径为R ,则该球内接长方体的表面积的最大值是( ) A .8R 2B .6R 2C .4R 2D .2R 2解析:选A 设球内接长方体的长、宽、高分别为a 、b 、c ,则a 2+b 2+c 2=(2R )2,所以S 表=2(ab +bc +ac )≤2(a 2+b 2+c 2)=8R 2,当且仅当a =b =c =233R 时,等号成立.3.右图是一个几何体的三视图(侧视图中的弧线是半圆),则该几何体的表面积是( )A .20+3πB .24+3πC .20+4πD .24+4π解析:选 A 根据几何体的三视图可知,该几何体是一个正方体和一个半圆柱的组合体,其中,正方体的棱长为2,半圆柱的底面半径为1,母线长为2.故该几何体的表面积为4×5+2×π+2×12π=20+3π.4.(2012·湖北高考)我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V ,求其直径d 的一个近似公式d ≈ 3169V .人们还用过一些类似的近似公式,根据π=3.141 59…判断,下列近似公式中最精确的一个是( )A .d ≈ 3169VB .d ≈ 32V C .d ≈ 3300157VD .d ≈ 32111V解析:选D ∵V =43πR 3,∴2R =d = 36V π,考虑到2R 与标准值最接近,通过计算得6π-169≈0.132 08,6π-2≈-0.090 1,6π-300157≈-0.001 0,6π-2111≈0.000 8,因此最接近的为D 选项.5.(2012·上海高考)如图,AD 与BC 是四面体ABCD 中互相垂直的棱,BC =2.若AD =2c ,且AB +BD =AC +CD =2a ,其中a ,c 为常数,则四面体ABCD的体积的最大值是________.解析:如图过点B 在平面BAD 中作BE ⊥AD ,垂足为E ,连接CE ,因为BC ⊥AD ,所以AD ⊥平面BCE .所以四面体ABCD 的体积为13S △BCE ·AD .当△BCE 的面积最大时,体积最大.因为AB +BD =AC +CD =2a ,所以点B ,C在一个椭圆上运动,由椭圆知识可知当AB =BD =AC =CD =a 时,BE =CE=a 2-c 2为最大值,此时截面△BCE 面积最大,为12×2a 2-c 2-1=a 2-c 2-1,此时四面体ABCD 的体积最大,最大值为13S △BCE ·AD =2c 3·a 2-c 2-1.答案:23c a 2-c 2-1。
北京联合大学附中高考数学一轮复习 计数原理单元训练

北京联合大学附中三维设计2014年高考数学一轮复习单元训练:计数原理本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若},6,5,4,3,2,1{)2,1,0(},1010|{,0122∈=+⨯+⨯=∈i a a a a x x n m i 其中并且606=+n m ,则实数对(m ,n )表示平面上不同点的个数为( )A .32个B .30个C .62个D .60个【答案】D2.设{a n }是等差数列,从{a 1,a 2,a 3,··· ,a 20}中任取3个不同的数,使这三个数仍成等差数列,则这样不同的等差数列最多有( )A .90个B .120个C .160个D .180个【答案】D3.()82x -展开式中不含..4x 项的系数的和为( )A .1-B . 0C . 1D . 2【答案】B4.将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中.若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有( ) A. 12种 B.18种 C. 36种 D. 48种【答案】B5.在8)1)(1(+-x x 的展开式中5x 的系数是( )A .−14B .14C .−28D .28 【答案】B6.在集合中任取一个偶数和一个奇数构成以原点为起点的向量.从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为,其中面积不超过...的平行四边形的个数为,则( )A .B .C .D .【答案】B7.从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加,星期六有两人参加,星期日有一人参加,则不同的选派方法共有( )A .120种B .96种C .60种D .48种【答案】C8.有5名同学被安排在周一至周五值日,已知同学甲只能值周一或周二,那么5名同学值日顺序的编排方案共有( )A .24种B .48种C .96种D .120种【答案】B9.10)1(-x 的展开式中的第6项是( ) A . 6610x CB . 6610x C - C . 5510x C - D . 5510x C 【答案】C10.5个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有( )A .33AB .523533A A A -C .334AD .2311323233A A A A A +【答案】B11.从4名男生和3名女生中选出3人参加某个座谈会,若这3中必须既有男生又有女生,则不同的选法共有( )种.A .60B .35C .34D .30【答案】D12.某团支部进行换届选举,从甲、乙、丙、丁四人中选出三人分别担任书记、副书记、组织委员,规定上届任职的甲、乙、丙三人不能连任原职,则不同的任职方案有( )A .10B .11C .12D .13【答案】B第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.将数字1,2,3,4,5填入标号为1,2,3,4,5的五个方格里,每格填一个数字,则每个方格的标号与所填的数字恰有两个相同的不同的填法有 种 【答案】2014.523()x x +的展开式的常数项为 【答案】1515.现有7件互不相同的产品,其中有4件次品,3件正品,每次从中任取一件测试,直到4件次品全被测出为止,则第三件次品恰好在第4次被测出的所有检测方法有_____种.【答案】108016.某地教育部门欲派5名工作人员到3所学校进行地震安全教育,每所学校至少1人,至多派2人,则不同的安排方案共有 种。
北京科技大学附中三维设计2014年高考数学一轮复习空间几何体

北京科技大学附中三维设计2014年高考数学一轮复习:空间几何体本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知平面α外的直线b 垂直于α内的二条直线,有以下结论:○1b 一定不垂直于α;○2b 可能垂直于平面α;○3b 一定不平行于平面α,其中正确的结论有( ) A .0个 B .1个C .2个D .3个【答案】B2.△ABC 的BC 边上的高线为AD ,BD=a ,CD=b ,将△ABC 沿AD 折成大小为θ的二面角B-AD-C ,若ba=θcos ,则三棱锥A-BCD 的侧面三角形ABC 是( ) A .锐角三角形 B .钝角三角形C .直角三角形D .形状与a 、b 的值有关的三角形【答案】C3.正方体的棱长为4,在正方体内放八个半径为1的球,再在这八个球中间放一个小球,则小球的半径为( )A .1B .2C .12D .1【答案】A4.已知一几何体的三视图如图,主视图和左视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何形体可能是( )①矩形;②有三个面为直角三角形,有一个面为等腰三角形的四面体;③每个面都是直角三角形的四面体.A .①②③B .②③C .①③D .①②【答案】A5.如图是某一几何体的三视图,则这个几何体的体积为( )A.4 B.8 C.16 D.20 【答案】A6.圆锥的侧面展形图是( )A.三角形B.长方形C.圆D.扇形【答案】D7.若=(2x,1,3),=(1, -2y,9),如果与为共线向量,则( )A. x=1,y=1 B. x=12,y=-12C. x=16,y=-32D. x=-16,y=32【答案】C8.给出下列命题:①底面多边形内接于一个圆的棱锥的侧棱长相等;②棱台的各侧棱不一定相交于一点;③如果不在同一平面内的两个相似的直角三角形的对应边互相平行,则连结它们的对应顶点所围成的多面体是三棱台;④圆台上底圆周上任一点与下底圆周上任一点的连线都是圆台的母线.其中正确的个数为( )A.3 B.2 C.1 D.0【答案】C9.下图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是( )个A.8个B.7个C.6个D.5个【答案】D10.已知空间四边形ABCD,M、G分别是BC、CD的中点,连结AM、AG、MG,则−→−AB+1()2BD BC+等于( )A.−→−AG B.−→−CG C.−→−BC D.21−→−BC【答案】A11.已知直线l⊥平面α,直线m⊂平面β,下面三个命题( )①α∥β⇒l ⊥m ;②α⊥β⇒l ∥m ;③l ∥m⇒α⊥β. 则真命题的个数为A . 0B . 1C . 2D . 3【答案】C12.正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( )A .75°B .60°C .45°D .30°【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.下面是关于四棱柱的四个命题( )①若有两个侧面垂直于底面,则该四棱柱是直四棱柱②若四个过相对侧棱的截面则该四棱柱是直四棱柱都垂直于底面, ③若四个侧面两两全等,则该四棱柱是直四棱柱④若四棱柱的两条对角线两两相等,则该四棱柱是直四棱柱 其中,真命题的编号为 【答案】②④ 14.给出下列命题: ①已知函数f (x)=21()sin 21xx x a ⋅-+-(a 为常数),且f (lglog 81000)=3,则f (lglg2)=-3; ②若函数f (x)=lg(x 2+ax-a)的值域是R ,则a ∈(-4, 0);③关于x 的方程1()lg 2xa =有非负实数根,则实数a 的取值范围是(1, 10);④如图,三棱柱ABC —A 1B 1C 1中,E 、F 分别是AB ,AC 的中点,平面EB 1C 1F 将三棱柱分成几何体AEF —AB 1C 1和B 1C 1—EFCB 两部分,其体积分别为V 1,V 2,则V 1:V 2=7:5。
【VIP专享】《三维设计》2014届高考数学理科一轮复习教师备选作业第七章 第一节 空间几何体的结构特征及三

EFGHB1C1 后得到的几何体,其中 E为线段 A1B1 上异于 B1 的点,F 为线段
BB1 上异于 B1 的点,且 EH∥A1D1,则下列结论中不正确的是
A.EH∥FG
B.四边形 EFGH 是矩形
C.Ω 是棱柱
D.Ω 是棱台
5.右 图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱
柱,其正视图、俯视图如右图;②存在四棱柱,其正视图、俯视图如右图;③
可得这个几何体的体积是 3 cm3,则正视图中的 h 等于________cm.
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2014届北京体育大学附中高考数学一轮复习单元训练:《空间几何体》

空间几何体本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.某几何体的正视图和侧视图均为如图所示,则在下图的四个图中可以作为该几何体的俯视图的是( )A.(1),(3)B.(1),(3),(4)C.(1),(2),(3)D.(1),(2),(3),(4)【答案】A2.设有四个命题:①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.其中假命题的序号是( )A.①B.②③C.①②③D.③④【答案】C3.一个简单几何体的主视图,左视图如图所示,则其俯视图不可能为①长方形;②直角三角形;③圆;④椭圆.其中正确的是A.①B.②C.③D.④【答案】C4.如图,能推断这个几何体可能是三棱台的是( )A.A1B1=2,AB=3,B1C1=3,BC=4B .A 1B l =1,AB =2,B lC l =1.5,BC =3,A 1C 1=2,AC =3 C .A l B l =1,AB =2,B 1C l =1.5,BC =3,A l C l =2,AC =4D .AB =A 1B 1,BC =B 1C 1,CA =C 1A 1 【答案】C5.已知三角形的三边分别为c b a ,,,内切圆的半径为r ,则三角形的面积为;四面体的四个面的面积分别为4321,,,s s s s ,内切球的半径为R 。
类比三角形的面积可得四面体的体积为( )ABC D .R s s s s V )(4321+++=【答案】B6.长度分别为1,a ,a ,a ,a ,a 的线段能成为同一个四面体的6条棱的充要条件是( )A .30<<a B .20<<aC .33>a D .333<<a 【答案】C7.下列命题中,正确的是( )A .直线l ⊥平面α,平面β∥直线l ,则α⊥βB .平面α⊥β,直线m ⊥β,则m ∥αC .直线l 是平面α的一条斜线,且l ⊂β,则α与β必不垂直D .一个平面内的两条直线与另一个平面内的两条直线分别平行,则这两个平面平行 【答案】A8.如图,一个空间几何体正视图与侧视图为全等的等边三角形,俯视图为一个半径为1的圆,那么这个几何体的全面积为( )A .πB .3πC .2πD .π+3【答案】B9.如图,平面四边形ABCD 中,1===CD AD AB ,CD BD BD ⊥=,2,将其沿对角线BD 折成四面体BCD A -',使平面⊥BD A '平面BCD ,若四面体BCD A -'顶点在同一个球面上,则该球的体积为( )A . π23B . π3C . π32 D . π2【答案】A10.a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b 或a ∩b 或a,b 异面②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b.其中正确命题的个数有( ) A . 0个 B . 1个 C .2个 D . 3个 【答案】C11.下图是一个几何体的三视图,则该几何体的体积为( )A . 6B . 8C . 16D . 24【答案】D12.以正方体1111ABCD A B C D -的顶点D 为坐标原点O ,如图建立空间直角坐标系,则与1DB 共线的向量的坐标可以是( )A .(1,B .(1, 1,C .D . 1)【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.一个几何体的三视图如图所示,则该几何体为 。
【三维设计】北京联合大学附中2014年高考数学一轮复习 选考内容单元训练 新人教A版

北京联合大学附中三维设计2014年高考数学一轮复习单元训练:选考内容本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图:AB 是⊙O 的直径,M 是⊙O 上一点,MN ⊥AB ,垂足为N ,P 和Q 分别是AM 和BM 上一点,(不与端点重合),如果∠MNP=∠MNQ ,下面结论:①1=∠2;②∠P+∠Q=180°;③∠MQN=∠PMN ;④PM=QM ;⑤ 2MN PN QN =∙。
其中正确的是( )A .①③B .①③⑤C .④⑤D .①②⑤ 【答案】B2.高为8的圆台内有一个半径为2 的球O 1,球心O 1在圆台的轴上,球O 1与圆台的上底面、侧面都相切,圆台内可再放入一个半径为3的球O 2,使得球O 2与球O 1、圆台的下底面及侧面都只有一个公共点,除球O 2,圆台内最多还能放入半径为3的球的个数是( )O 3O 4HO 2C332O 2O 1HA . 1B . 2C . 3D . 4【答案】B 3.不等式||012x x>-的解集是( ) A . )21,(-∞B .)21,0()0,( -∞C .),21(+∞D . )21,0( 【答案】B4.参数方程为1()2x t t t y ⎧=+⎪⎨⎪=⎩为参数表示的曲线是( )A .一条直线B .两条直线C .一条射线D .两条射线【答案】D5.极坐标方程sin 2cos ρθθ=+所表示的曲线是( ) A .直线 B . 圆C . 双曲线D . 抛物线【答案】B 6.已知⎪⎭⎫⎝⎛-3,5πM ,下列所给出的不能表示点的坐标的是( ) A .⎪⎭⎫⎝⎛-3,5π B .⎪⎭⎫ ⎝⎛34,5π C .⎪⎭⎫ ⎝⎛-32,5π D .⎪⎭⎫ ⎝⎛--35,5π 【答案】A7.直角坐标)2,2(-化为极坐标可以是( )A . )4,22(πB . )43,22(π C . )45,22(πD . )47,22(π【答案】D8.若一个变换所对应的矩阵是1002-⎛⎫ ⎪⎝⎭,则抛物线24y x =-在这个变换下所得到的曲线的方程是( )A .24y x = B .2y x = C .216y x =- D .216y x = 【答案】D9.极坐标方程(1)()0(0)ρθπρ--=≥表示的图形是( )A.两个圆B. 两条直线 C .一个圆和一条射线 D .一条直线和一条射线【答案】C10.在极坐标中点 2,3π⎛⎫⎪⎝⎭到圆2cos ρθ= 的圆心的距离为( ) A .2B .C .D .【答案】D11.如图,已知AB 是⊙O 的弦,AC 切⊙O 于点A ,∠BAC=60°,则∠ADB 的度数为( )A . 60°B . 120°C .140°D .150°【答案】B12.设,,a b c R +∈,且1a b c ++=,若111(1)(1)(1)M a b c=---,则必有( )A .108M ≤< B .118M ≤< C .18M ≤< D .8M ≥【答案】D第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.已知圆的直径13AB cm =,C 为圆上一点,CD AB ⊥,垂足为D ,且6CD cm =,则AD =____________cm . 【答案】4或914.已知曲线22()2x pt t p y pt ⎧=⎨=⎩为参数,为正常数上的两点,M N 对应的参数分别为12,t t 和,120t t +=且,那么MN =____________。
【三维设计】2014届高考数学一轮(基础知识高频考点解题

第二节同角三角函数的根本关系与诱导公式[ 知识能否忆起 ]1.同角三角函数的根本关系式(1 平方关系: sin2α+cos2α=1(α∈R.(2 商数关系: tan α=.2.六组诱导公式角2kπ+α(k∈Zπ +α-απ-α-α+α函数正弦sin_α-sin_α-sin_αsin_αcos_αcos_α余弦cos_α-cos_αcos_α-cos_αsin_α-sin_α正切tan_ αtan_α-tan_α-tan_α对于角“±α〞(k∈Z 的三角函数记忆口诀“奇变偶不变,符号看象限〞,“奇变偶不变〞是指“当 k 为奇数时,正弦变余弦,余弦变正弦;当 k 为偶数时,函数名不变〞.“符号看象限〞是指“在α的三角函数值前面加上当α为锐角时,原函数值的符号〞.[ 小题能否全取 ]1.sin 585°的值为 (A.- B.C.- D.解析:选 A sin 585 °= sin(360 °+225°=s in 225°= sin(180°+45°=- sin 45°=-.2.(教材习题改编 sin( π+θ=-cos(2π-θ,|θ|< ,那么θ等于 (A.- B.-C. D.解析:选 D∵sin(π+θ=-cos(2π-θ,∴- sin θ=-cos θ,∴ tan θ= .∵|θ|< ,∴θ= .3. tan θ= 2,那么= (A.2 B.- 2C.0 D.解析:选 B原式====- 2.4. (教材习题改编如果sin( +πA =,那么c os 的值是 ________.解析:∵ sin( π+ A =,∴- sin A = .∴c os=- sin A =.答案:5.α是第二象限角,tan α=-,那么cos α= ________.解析:由题意知cos α<0,又 sin 2α+cos2α=1,tan α==- .∴ cos α=- .答案:-应用诱导公式时应注意的问题(1 利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步骤:去负号—脱周期—化锐角.特别注意函数名称和符号确实定.(2 在利用同角三角函数的平方关系时,假设开方,要特别注意判断符号.(3 注意求值与化简后的结果要尽可能有理化、整式化.同角三角函数的根本关系式典题导入[例 1](1(2021 江·西高考假设tan θ+= 4,那么 sin 2θ=(A. B.C. D.(2 sin(3π+α=2sin,那么= ________.[自主解答]+=,(1∵ tan θ4∴+=4,∴=4,即=4,∴sin 2θ=.(2 法一:由 sin(3π+α=2sin 得 tan α=2.原式===- .法二:由得 sin α= 2cos α.原式==- .[答案] (1D (2-在(2 的条件下, sin2α+sin 2α= ________.解析:原式= sin2α+2sin αcos α=== .答案:由题悟法1.利用 sin2α+cos2α=1 可以实现角α的正弦、余弦的互化,利用= tan α可以实现角α的弦切互化.2.应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用 (sin α±cos α2=1±2sin αcos α,可以知一求二 (参阅本节题型技法点拨.3.注意公式逆用及变形应用:1= sin2α+ cos2α, sin2α=1- cos2α, cos2α= 1- sin2α.以题试法1. (1(2021 长·沙模拟假设角α的终边落在第三象限,那么+的值为( A.3 B.- 3C.1 D.- 1(2 sin α= 2sin β, tan α= 3tan β,那么 cos α= ________.解析: (1 由角α的终边落在第三象限得sin α<0, cos α<0,故原式=+=+=-1- 2=- 3.(2∵ sin α= 2sin β, tan α= 3tan β,∴sin2α= 4sin2β,①tan2α= 9tan2β,②由①÷②得: 9cos2α= 4cos2β,③①+③得: sin2α+ 9cos2α=4,∵c os2α+ sin2α= 1,∴cos2α=,即 cos α=±.答案: (1B(2 ±三角函数的诱导公式典题导入[例 2](1= ________.(2 A=+ (k∈Z,那么 A 的值构成的集合是(A . {1 ,- 1,2,- 2}B. { - 1,1}C. {2 ,- 2} D .{1 ,- 1,0,2,- 2}[自主解答 ] (1 原式====-=-·=- 1.(2 当 k 为偶数时, A=+= 2;k 为奇数时, A=-=- 2.[答案 ] (1- 1(2C由题悟法利用诱导公式化简求值时的原那么(1 “负化正〞,运用-α的诱导公式将任意负角的三角函数化为任意正角的三角函数.(2 “大化小〞,利用 k·360 °+α(k∈Z的诱导公式将大于 360 °的角的三角函数化为 0°到360 °的三角函数.(3 “小化锐〞,将大于90°的角化为0°到 90°的角的三角函数.(4 “锐求值〞,得到 0°到 90°的三角函数后,假设是特殊角直接求得,假设是非特殊角可由计算器求得.以题试法2. (1(2021 滨·州模拟sin 600 +°tan 240 的°值等于 (A.- B.C.-D. +(2 f(x= asin( xπ+α+ bcos( xπ-β,其中α,β, a, b 均为非零实数,假设f(2 012=- 1,那么 f(2 013 等于 ________.解析: (1sin 600°+ tan 240°= sin(720 °- 120°+ tan(180 °+ 60°=- sin 120°+ tan 60°=-+=.(2 由诱导公式知f(2 012 = asin α+bcos β=- 1,∴f(2 013 = asin( π+α+bcos( π-β=- (asin α+ bcos β= 1.答案: (1B (21诱导公式在三角形中的应用典题导入[例 3]在△ABC中,假设sin(2-πA=-sin(π-B,cos A=-cos (π-B,求△ABC的三个内角.[自主解答 ]由得sin A =sin B , cos A= cos B 两式平方相加得2cos2A = 1,即 cos A =或 cos A=- .(1 当 cos A=时, cos B=,又角 A 、 B 是三角形的内角,∴A =, B =,∴C=π- (A + B = .(2 当 cos A=-时, cos B=-,又角 A 、B 是三角形的内角,∴A=,B=,不合题意.综上知, A=, B=, C= .由题悟法1.诱导公式在三角形中经常使用,常用的角的变形有: A + B =π- C,2A + 2B = 2π-2C,++=等,于是可得sin(A + B = sin C, cos= sin 等;2.求角时,通常是先求出该角的某一个三角函数值,再结合其范围,确定该角的大小.以题试法3.在三角形ABC 中,(1 求证: cos2+ cos2= 1;(2 假设 cossintan (C-π <0,求证:三角形ABC 为钝角三角形.证明: (1 在△ ABC 中, A+B=π- C,那么=-,所以 cos= cos= sin,故 cos2+ cos2= 1.(2 假设 cossintan (C-π <0,那么(- sin A(-cos Btan C<0,即 sin Acos Btan C<0,∵在△ ABC 中, 0<A<π,0< B<π,0<C<π,∴s in A>0 ,或∴B 为钝角或 C 为钝角,故△ ABC 为钝角三角形.1. sin(θ+π <0, cos(θ-π >0,那么以下不等关系中必定成立的是( A . sin θ<0,cos θ>0B. sin θ>0, cos θ<0C. sin θ>0,cos θ>0 D . sin θ<0 , cos θ<0解析:选 B sin(θ+π<0,∴- sin θ<0, sin θ>0.∵c os(θ-π>0,∴- cos θ>0.∴ cos θ<0.2. (2021 ·徽名校模拟安tan x= 2,那么 sin2x+ 1= (A.0 B.C. D.解析:选 B sin2x+ 1=== .3. (2021 ·西高考假设=,那么江tan 2α= (A.- B.C.- D.解析:选 B∵ ==,∴ tanα=-3.∴tan 2α== .4. (2021 ·博模拟淄sin 2α=-,α∈,那么 sin α+cos α=( A.- B.C.- D.解析:选 B(sin α+cos α2= 1+ 2sin αcos α=1+ sin 2α=,又α∈, sin α+ cos α>0,所以 sin α+cos α=.5. cos=,且 |φ|<,那么 tan φ= (A.- B.C.- D.解析:选 D cos= sin φ=,又|φ|<,那么 cos φ=,所以 tan φ= .6. 2tan α·sin α= 3,-<α< 0,那么 sin α= (A.B .-C.D.-解析:选 B由2tanα·sinα=3得,=3,即 2cos2α+ 3cos α- 2= 0,又-<α< 0,解得 cos α= (cos α=- 2 舍去,故 sin α=- .7. cos- sin 的值是 ________.解析:原式= cos+ sin = cos+ sin= .答案:8.假设= 2,那么 sin( θ- 5π sin= ________.解析:由= 2,得sin θ+ cos θ= 2(sin θ- cos θ,两边平方得:1+ 2sin θcos θ=4(1- 2sin θcos θ,故 sin θcos θ=,∴sin(θ- 5πsin= sin θcos θ= .答案:9. (2021 ·山模拟中cos=,那么 sin= ________.解析: sin= sin=- sin =- cos=- .答案:-10.求值: sin(- 1 200 ·°cos 1 290 +°cos(-1 020 °·sin( - 1 050 +°tan 945 . °解:原式=- sin 1 200 ·°cos 1 290 +° cos 1 020 °·(- sin 1 050 +°tan 945 °=- sin 120 ·°cos 210 °+ cos 300 °·(- sin 330 °+ tan 225 °=(- sin 60 ·°(- cos 30 °+ cos 60 °·sin 30 +°tan 45 °=×+×+ 1= 2.11. cos( π+α=-,且α是第四象限角,计算:(1sin(2 -πα;(2(n∈Z.解:∵ cos(π+α=-,∴-cos α=-, cos α=.又∵ α是第四象限角,∴s in α=-=- .(1sin(2π-α= sin [2π+(-α]= sin(-α=-sinα=;(2=====-=- 4.12.(2021 ·信阳模拟角α的终边经过点 P.(1 求 sin的α值;(2 求·的值.解:(1∵ |OP|=1,∴点 P 在单位圆上.由正弦函数的定义得sinα=-.(2 原式=·==,由余弦函数的定义得cos α=.故所求式子的值为 . 1.=-,那么的值是 (A.B .-C.2 D.- 2解析:选 A由于·==-1,故=.2.假设角α的终边上有一点P(- 4, a,且 sinα· cos=,那么α a的值为(A.4 B.±4C.- 4 或- D.解析:选 C依题意可知角α的终边在第三象限,点P(- 4,a 在其终边上且sinα· cos=α易得 tan α=或,那么a=- 4 或- .3. A 、 B、 C 是三角形的内角,sin A ,- cos A 是方程 x2- x+ 2a=0 的两根.(1求角 A;(2 假设=- 3,求 tan B.解: (1 由可得,sin A -cos A =1.①又 sin2A + cos2A= 1,所以 sin2A +(sin A - 12= 1,即 4sin2A - 2sin A = 0,得 sin A = 0(舍去或 sin A =,那么 A=或,将 A =或代入①知 A =时不成立,故 A=.(2 由=- 3,得 sin2B - sin Bcos B - 2cos2B= 0,∵c os B ≠0,∴ tan2B -tan B- 2=0,∴tan B = 2 或 tan B=- 1.∵tan B =- 1 使 cos2B- sin2B= 0,舍去,故 tan B = 2.1. sin= m,那么 cos 等于 (A . mB .- mC.D.-解析:选 A∵sin=m,∴cos= sin= m.2.求证: sinθ+(1tan+θcos=θ+.证明:左边= sinθ+cosθ=s in +θ+ cos θ+=+=+=+=右边.3. sin( -πα- cos( π+α= .求以下各式的值:(1sin α- cos α;(2sin3+ cos3.解:由 sin( π-α- cos(π+α=,得 sin α+ cos α=,①将①两边平方,得1+ 2sin α·cos α=,故 2sin α·cos α=- .又<α<π,∴ sin α>0, cos α<0.(1(sin α- cos α2= 1- 2sin α·cos α= 1-=,∴ sin α- cos α= .(2sin3+ cos3=cos3α-sin3α= (cos α- sin α(cos2α+ cos α·sin α+sin2α=-×=- .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B.四边开 EFGH 是矩形 D. 是棱台
【答案】D 12.M 是空间直角坐标系 Oxyz 中任一点(异于 O) ,若直线 OM 与 xOy 平面,yoz 平面,zox 2 2 2 平面所成的角的余弦值分别为 p, q, r,则 p +q +r =( ) 1 A. B.1 4 C. 2 【答案】C 第Ⅱ卷(非选择题 共 90 分) 二、填空题 (本大题共 4 个小题,每小题 5 分,共 20 分,把正确答案填在题中横线上) 13.等腰梯形 ABCD 中,上底 CD 1 ,腰 AD CB 2 ,下底 AB 3 ,以下底所在直 线为 x 轴,则由斜二测画法画出的直观图 ABC D 的面积为__________ __ 【答案】 D.
BD BP 3 PD 3 2 3 3 ,∴ AD a .∴ DE AD sin60 ,∴ PD a . a ,又∵ DA PA1 2 AA1 5 5 5 5 PD 3 ,∴ P AC B 的大小为 PED 60 . DE
∴ tanPED
【法二】以 A 为原点, AB 为 x 轴,过 A 点与 AB 垂直的直线为 y 轴, AA1 为 z 轴,建立空间
北京联合大学附中三维设计 2014 年高考数学一轮复习单元训练:空 间几何体
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分 150 分.考试时间 120 分钟. 第Ⅰ卷(选择题 共 60 分) 一、选择题 (本大题 共 12 个小题,每小题 5 分,共 60 分,在每小题给出的四个选项中, 只有一项是符合题目要求的 ) 1. 与正方体
21.如图,已知三棱锥 P—ABC 中,AP⊥PC, AC⊥BC,M 为 AB 中点,D 为 PB 中点, 且△PMB 为正三角形. (1)求证:DM∥平面 APC; (2)求证:平面 ABC⊥平面 APC; (3)若 BC=4,AB=20,求三棱锥 D-BCM 的体积.
A.
1 3
B.1 2C.3 2D.1【答案】B 4.用斜二测画法画一个水平放置的平面 图形为如下图的一个正方形,则原来图形的形状是 ( )
【答案】A 5.一个正方体的顶点都在球面上,它的棱长为2cm,则球的表面积是( ) 2 2 2 2 A.8 cm B.12 cm C.16 cm D.20 cm 【答案】D
a 2,
3a .∴ m 是平面 ,0 0 2
mn 1 PAC 的一个法向量.又平面 ABC 的一个法向量为 n 0,0,1 . cos m, n ,∴二 mn 2
面角 P AC B 的大小是 60 .
【答案】 (1 )证明: E、F 分别是A1B、A1C的中点, EF ∥ BC ,
又EF 平面ABC, BC 平面ABC,所以EF ∥ 平面ABC
2 直三棱柱ABC A1 B1C1, BB1 平面A1 B1C1, BB1 A1 D,
又A1 D B1C , A1 D 平面BB1C1C, 而A1 D 平面A1 FD, 平面A1 FD 平面BB1C1C.
2 2
、
3 2
、
6 2
,则三棱锥 A BCD 的外接球的表面积为( C. 6
)
B. 6
D. 4 6
10.对于三条不同的直线 a、b、c,与三个不同的平面 a 、 、 ,有下述四个命题: ① // , b b // ; ③ c a , c b, a , b c ; 其中正确的有( A.①③ 【答案】D ) B.②③ C.②④ D.①④ ② a ⊥ , a a ④ a⊥ a ,b⊥ a a ∥b;
∴
6
∴ BD 3 .
∴ AD // 平面 CEF . (3)由(2)知 AD // EF , AD ED ,且 ED BD BE 1 ∴ F 到 AD 的距离等于 E 到 AD 的距离,为 1. ∴ S FAD
1 3 . 3 1 2 2
CE 平面 ABD
a 3a 直角坐标系 A xyz ,如图所示,设 P x,0, z ,则 B a ,0,0 、 A1 0,0, a 、 C , . 2 2 ,0 1 a a 3a (Ⅰ)由 CP AB 0 得 x , ,z a,0,0 0 ,即 x a 0 ,∴ x a ,即 P 2 2 2 2
(1)求证: AD 平面 BCE ; (2)求证: AD // 平面 CEF ; (3) 求三棱锥 A CFD 的体积. 【答案】 (1)依题意: AD BD
2 , BC 6
RtABD 中, AB 2 3 , AD 3
BF BE 2 . BA BD 3 ∴ AD // EF AD 在平面 CEF 外
8.将正三棱柱截去三个角(如图 1 所示 A,B,C 分别是 △GHI 三边的中点)得到几何体 如图 2,则该几何体按图 2 所示方向的侧视图(或称左视图)为( )
【答案】A 9.在三棱锥 A BCD 中,侧棱 AB、AC、AD 两两垂直, ABC 、 ACD 、 ADB 的面积 分别为 A. 2 【答案】C
∴ B1 D1 (2, 2, 0), AP (1,1, 2) ∴ B1 D1 AP 0 ,
又 AB 2, PA
6 , ∴ PE 2
∴ P (1,1,4)
即 PA B1 D1 .
(2)设平面 PAD 的法向量是 m ( x, y , z ) ,
3
该球表面积为
.
【答案】 12 三、解答题 (本大题共 6 个小题,共 70 分,解答应 写出文字说明,证明过程或演算步骤) 17.如图,P—ABCD 是 正四棱锥, ABCD A1B1C1D1 是正方体,其中 AB 2, PA
6
(1)求证: PA B1 D1 ; (2)求平面 PAD 与平面 BDD1 B1 所成的锐二面角 的余弦值; 【答案】以 A1 B1 为 x 轴, A1 D1 为 y 轴, A1 A 为 z 轴建立空间直角坐标系 (1)证明:设 E 是 BD 的中点, P—ABCD 是正四棱锥, ∴ PE ABCD
AD (0, 2, 0), AP (1,1, 2)
4
∴ y 0, x 2 z 0
取 z 1 得 m (2, 0,1) ,
又平面 BDD1 B1 的法向量是 n (1,1, 0)
mn 10 ∴ cos m, n 5 m n
5
为 A1 B 的中点,也即 A1 P : PB 1 时, PC AB .
2a 3a ,0, . (Ⅱ)当 A1 P : PB 2 : 3 时, P 点的坐标是 5 5
取 m 3, 3, 2 .则
2a 3a m AP 3, 3, 2 ,0, 0 , m AC 3, 3, 2 5 5
11.如图,若 是长方体
ABCD A1B1C1D1 被平面 EFGH 截去几何体 EFGHB1C1 后得到 A1 B1 上异于 B1 的点, F 为线段 BB1 上异于 B1 的点,且
)
的几何体,其中 E 为线段
EH / / A1 D1 ,则下列结论中不正确的是(
2
A. EH / / FG C. 是棱柱
19. 如图:C 、D 是以 AB 为直径的圆上两点,AB 2 AD 2 3 ,AC BC ,F 是 AB 上一点, 且 AF 已知 CE
1 将圆沿直径 AB 折起, 使点 C 在平面 ABD 的射影 E 在 BD 上, AB , 3
2.
∴ CE AD CE 平面 ABD BD CE E ∴ AD 平面 BCE . (2) RtBCE 中, CE ∴ BE 2
之当 A1 P : PB 1 时, 取 AB 的中点 D , 连接 CD 、 ∴ CD AB . PD .∵ ABC 为正三角形, 由于 P 为 A1 B 的中点时,PD // A1 A ∵ A1 A 平面 ABC , ∴ PD 平面 ABC , ∴ PC AB . (Ⅱ)当 A1 P : PB 2 : 3 时,作 P 在 AB 上的射影 D . 则 PD 底面 ABC .作 D 在 AC 上的 射影 E ,连结 PE ,则 PE AC .∴ DEP 为二面角 P AC B 的平面角.又∵ PD // AA1 , ∴
9 4
2 2
1 4 r l
14.设圆锥的母线长 为 l,底面半径为 r,满足条件“它的一个内接圆柱的侧面积等于圆锥侧 面积的 ”的情况有且只有一种,则 【答案】
3 2
.
15.如图是一个空间几何体的三视图,则该几何体外接球的表面积是
;
【答案】 8 16.四棱锥 P ABCD 的三视图如右图所示,四棱锥 P ABCD 的五个顶点都在一个球面 上, E 、 F 分别是棱 AB 、 CD 的中点,直线 EF 被球面所截 得的 线段长为 2 2 ,则
ABCD A1B1C1D1 的三条棱 AB 、CC1 、A1 D1 所在直线的距离相等的点(
)
A.有且只有 1 个 B.有且只有 2 个 C.有且只有 3 个 D.有无数个 【答案】D 2.下列命题正确的是( ) A.有两个面平行,其余各面都是四边形的几何体叫棱柱。 B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱。 C.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行 的几何体叫棱柱。 D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台。 【答案】C 3.一个棱锥的三视图如图所示,则它的体积为( )
