初二数学几何证明初步练习题含答案
初中数学几何证明经典试题(含答案)
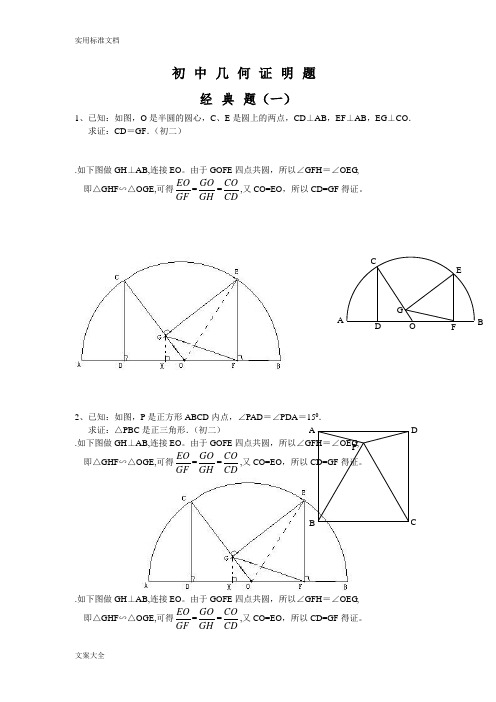
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明试题(含答案)
第 6 页 共 15 页
4.如下图连接 AC 并取其中点 Q,连接 QN 和 QM,所以可得∠QMF=∠F,∠QNM=∠
DEN 和∠QMN=∠QNM,从而得出∠DEN=∠F。
经 典 题(二)
1.(1)延长 AD 到 F 连 BF,做 OG⊥AF,
又∠F=∠ACB=∠BHD, 可得 BH=BF,从而可得 HD=DF, 又 AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM
BE AD
= ,即 AD•BC=BE•AC,
①
BC AC
又∠ACB=∠DCE,可得△ABC∽△DEC,既得
AB = DE ,即 AB•CD=DE•AC,
②
AC DC
由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证。
第 11 页 共 15 页
4.过 D 作 AQ⊥AE
(2)连接 OB,OC,既得∠BOC=1200,
从而可得∠BOM=600, 所以可得 OB=2OM=AH=AO, 得证。
第 7 页 共 15 页
3.作 OF⊥CD,OG⊥BE,连接 OP,OA,OF,AF,OG,AG,OQ。 由于 AD = AC = CD = 2FD = FD , AB AE BE 2BG BG
(2)过 P 点作 BC 的平行线交 AB,AC 与点 D,F。
由于∠APD>∠ATP=∠ADP,
推出 AD>AP
①
又 BP+DP>BP
②
和 PF+FC>PC
③
又 DF=AF
④
由①②③④可得:最大 L< 2 ;
初中数学几何证明经典题含答案
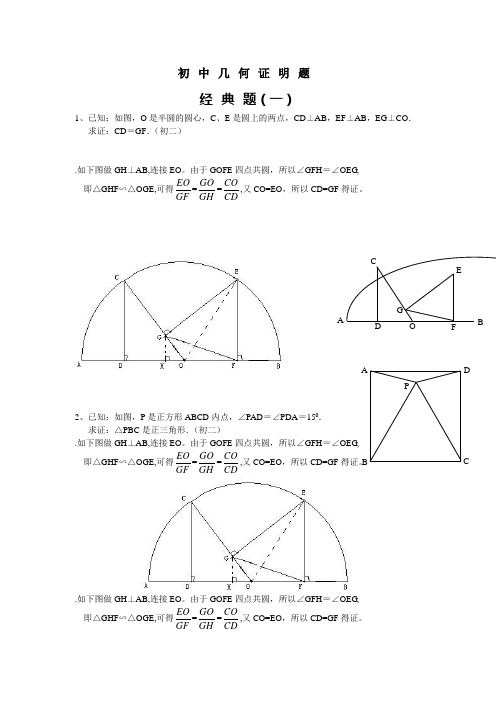
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 AN FE CDMB· A DHEM CBOF2、设MN 是圆O 外始终线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、假如上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的间隔 等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 及CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 及CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACBPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
中考复习初中数学几何证明经典试题(含答案)
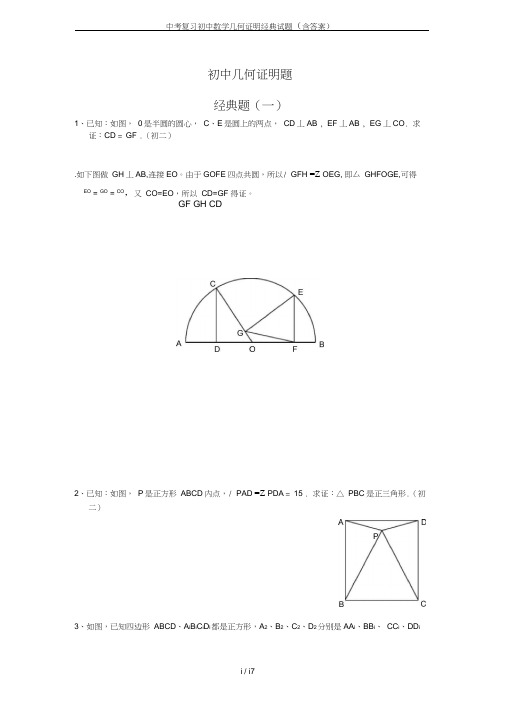
初中几何证明题经典题(一)1、已知:如图,0是半圆的圆心,C、E是圆上的两点,CD丄AB , EF丄AB , EG丄CO. 求证:CD = GF .(初二).如下图做GH丄AB,连接EO。
由于GOFE四点共圆,所以/ GFH =Z OEG, 即厶GHFOGE,可得EO = GO = CO,又CO=EO,所以CD=GF 得证。
GF GH CD2、已知:如图,P是正方形ABCD内点,/ PAD =Z PDA = 15°. 求证:△ PBC是正三角形.(初二)3、如图,已知四边形ABCD、A i B i C i D i都是正方形,A2、B2、C2、D2分别是AA i、BB i、CC i、DD i的中点.及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP = AQ .(初二)3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN P 、Q .4、 1、求证:四边形 A 2B 2C 2D 2是正方形.(初二)已知: 求证: 如图,在四边形 的延长线交 / DEN = Z△ ABC 中, MN F .ABCD 中,AD = BC , M 、N 分别是 AB 、CD 的中点,AD 、BC 于E 、F .经典题(二)已知: (1) 求证:AH = 20M ;(2) 若/ BAC = 60°,求证:H 为垂心 (各边高线的交点),0为外心,且 0M 丄BC 于M . AH = A0 .(初二)2、设MN 是圆O 外一直线,过O 作OA 丄MN 于A ,自A 引圆的两条直线,交圆于DCGN求证:AP = AQ .(初二)ECAM NP4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于 AB 的一半.(初二)经典题(二)1、如图,四边形 ABCD 为正方形, 求证:CE = CF .(初二)2、如图,四边形 ABCD 为正方形,DE // AC ,且CE = CA ,直线EC 交DA 延长线于F . 求证:AE = AF .(初二)DE // AC , AE = AC , AE 与 CD 相交于 F .FEAD1、设P 是边长为1的正△ ABC 内任一点,4、如图,PC 切圆0于C , AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于3、设ABCD 为圆内接凸四边形,求证: AB • CD + AD • BC = AC • BD .(初三)B 、D .求证: AB = DC , BC = AD .(初三)1、已知:△ ABC 是正三角形,P 是三角形内一点 求:/ APB 的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/求证:/ PAB = Z PCB .(初二)4、平行四边形 ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证:/ DPA =Z DPC .(初二)AO DB EFC求证:4、如图,△ ABC 中,/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点,/ DCA = 30°, / EBA = 20°,求/ BED 的度数. LiB C经典题(一)1•如下图做GH丄AB,连接E0。
初二数学 几何证明初步经典练习题 含答案

几何证明初步练习题1、三角形的内角和定理:三角形的内角和等于180°.推理过程:○1 作CM ∥AB ,则∠A= ,∠B= ,∵∠ACB +∠1+∠2=1800( ,∴∠A+∠B+∠ACB=1800. ○2 作MN ∥BC ,则∠2= ,∠3= ,∵∠1+∠2+∠3=1800,∴∠BAC+∠B+∠C=1800. 2.求证:在一个三角形中,至少有一个内角大于或者等于60°。
3、.如图,在△ABC 中,∠C >∠B,求证:AB >AC 。
4. 已知,如图,AE5. 已知:如图,EF ∥AD ,∠1 =∠2. 求证:∠AGD +∠BAC = 180°.反证法经典例题6.求证:两条直线相交有且只有一个交点.7.如图,在平面内,AB 是L 的斜线,CD 是L 的垂线。
求证:AB 与CD 必定相交。
8.2一.角平分线--轴对称9、已知在ΔABC 中,E为BC的中点,AD 平分BAC ∠,BD ⊥AD 于D .AB =9,AC=13求DE的长第9题图 第10题图 第11题图分析:延长BD交AC于F.可得ΔABD ≌ΔAFD .则BD =DF .又BE =EC ,即D E为ΔBCF 的中位线.∴DE=12FC=12(AC-AB)=2. 10、已知在ΔABC 中,108A ∠=,AB =AC ,BD 平分ABC ∠.求证:BC =AB +CD . 分析:在BC上截取BE=BA,连接DE.可得ΔBAD ≌ΔBED .由已知可得:18ABD DBE ∠=∠=,108A BED ∠=∠=,36C ABC ∠=∠=.∴72DEC EDC ∠=∠=,∴CD=CE ,∴BC =AB +CD .11、如图,ΔABC 中,E是BC 边上的中点,DE ⊥BC 于E ,交BAC ∠的平分线AD 于D ,过D 作DM ⊥AB 于M,作DN ⊥AC 于N .求证:BM =CN .分析:连接DB 与DC .∵DE 垂直平分BC ,∴DB =DC .易证ΔAMD ≌ΔAND .∴有DM =DN .∴ΔBMD ≌ΔCND (HL).∴BM =CN .二、旋转12、如图,已知在正方形ABCD 中,E在BC 上,F在DC 上,BE +DF=EF .求证:45EAF ∠=. C B ADE F D A B C B A E D NM B D A C分析:将ΔADF 绕A顺时针旋转90得ABG .∴GAB FAD ∠=∠.易证ΔAGE ≌ΔAFE .∴ 1452FAE GAE FAG ∠=∠=∠= 13、如图,点E 在ΔABC 外部,D 在边BC 上,DE 交AC 于F .若123∠=∠=∠,AC=AE.求证:ΔABC ≌ΔADE .分析:若ΔABC ≌ΔADE ,则ΔADE 可视为ΔABC 绕A逆时针旋转1∠所得.则有B ADE ∠=∠.∵12B ADE ∠+∠=∠+∠,且12∠=∠.∴B ADE ∠=∠.又∵13∠=∠.∴BAC DAE ∠=∠.再∵AC=AE.∴ΔABC ≌ΔADE .14、如图,点E为正方形ABCD的边CD上一点,点F为CB的延长线上的一点,且EA⊥AF.求证:DE=BF.分析:将ΔABF 视为ΔADE 绕A顺时针旋转90即可.∵90FAB BAE EAD BAE ∠+∠=∠+∠=.∴FBA EDA ∠=∠. 又∵90FBA EDA ∠=∠=,AB=AD.∴ΔABF ≌ΔADE .(ASA)∴DE=DF. 平移第14题图 第15题图 第16题图 第17题图三、平移15、如图,在梯形ABCD 中,BD ⊥AC ,AC =8,BD =15.求梯形ABCD 的中位线长. 分析:延长DC到E使得CE=AB.连接BE.可得ACEB .可视为将AC平移到BE.AB平移到CE.由勾股定理可得DE=17.∴梯形ABCD中位线长为8.5.16、已知在ΔABC 中,AB =AC ,D 为AB 上一点,E为AC 延长线一点,且BD =CE .求证:DM =EM 分析:作DF∥AC交BC于F.易证DF=BD=CE.则DF可视为CE平移所得.∴四边形DCEF为DCEF .∴DM=EM.线段中点的常见技巧 --倍长四、倍长17、已知,AD为ABC 的中线.求证:AB+AC>2AD.分析:延长AD到E使得AE=2AD.连接BE易证ΔBDE ≌ΔCDA .∴BE=AC.∴AB+AC>2AD.18、如图,AD 为ΔABC 的角平分线且BD =CD .求证:AB =AC . 分析:延长AD到E使得AD=ED.易证ΔABD ≌ΔECD .∴EC=AB. ∵BAD CAD ∠=∠.∴E CAD ∠=∠.∴AC=EC=AB. 19、已知在等边三角形ABC中,D和E分别为BC与AC上的点,且AE=CD.连接AD与BE交于点P,作BQ⊥AD于Q.求证:BP=2PQ.分析:延长PD到F使得FQ=PQ.在等边三角形ABC中AB=BC=AC,60ABD C ∠=∠=.又∵AE=CD,∴BD=CE.∴ΔABD ≌ΔBCE .∴CBE BAD ∠=∠.∴60BPQ PBA PAB PBA DBP ∠=∠+∠=∠+∠=.易证ΔBPQ ≌ΔBFQ .得BP=BF,又60BPD ∠=.∴ΔBPF 为等边三角形.∴BP=2PQ.中位线五、中位线、中线:20、已知在梯形ABCD 中,AD ∥BC ,E和F分别为BD 与AC 的中点, 求证:1()2EF BC AD =-. 分析:取DC中点G,连接EG与FG.则EG为ΔBCD 中位线,FG为ΔACD 的中位线. ∴EG∥=12BC ,FG ∥=12AD .∵AD ∥BC .∴过一点G有且只有一条直线平行于已知直线BC,即E、F、G共线.∴1()2EF BC AD =-. 直角三角形斜边上的中线等于斜边的一半21、已知,在ABCD 中BD AB 21=.E为OA的中点,F为OD中点,G为BC中点. 求证:EF=EG.分析:连接BE .∵BD AB 21=,AE=O E.∴BE⊥CE,∵BG=CG. ∴BD EG 21=.又EF为ΔAOD 的中位线.∴AD EF 21=.∴EF=EG. 22、在ΔABC 中,AD是高,CE是中线,DC=BE,DG⊥CE于G.求证:(1)CG=EG.(2)2B BCE ∠=∠.分析:(1)连接DE.则有DE=BE=DC.∴Rt ΔCDG ≌Rt ΔEDG (HL).∴EG=CG.∵DE=BE.∴B BDE DEC BCE ∠=∠=∠+∠.∵DE=CD.∴DEC BCE ∠=∠.∴2B BCE ∠=∠.几何证明初步测验题(1)一、选择题(每空3 分,共36 分)1、使两个直角三角形全等的条件是( )A 、一组锐角对应相等B 、两组锐角分别对应相等C 、一组直角边对应相等D 、两组直角边分别对应相等2、如图,已知AB ∥CD ,∠A =50°,∠C =∠E .则∠C =( )A .20°B .25°C .30°D .40°第2题图 第4题图 第6题图 第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中( )A .有两个角是直角B .有两个角是钝角C .有两个角是锐角D .一个角是钝角,一个角是直角4、如图,直线AB 、CD 相交于点O ,∠BOE=90°,OF 平分∠AOE ,∠1=15°30’,则下列结论不正确的是( ) A D B E F OC B E F ED G AA.∠2=45° B.∠1=∠3 C.∠AOD+∠1=180° D.∠EOD=75°30’5、下列说法中,正确的个数为()①三角形的三条高都在三角形内,且都相交于一点②三角形的中线都是过三角形的某一个顶点,且平分对边的直线③在△ABC中,若∠A=12∠B=13∠C,则△ABC是直角三角形④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18A.1个 B.2个 C.3个 D.4个6、如图,在AB=AC的△ABC中,D是BC边上任意一点,DF⊥AC于F,E在AB边上,使ED⊥BC于D,∠AED=155°,则∠EDF等于()A、50°B、65°C、70°D、75°7、如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm8、如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A. B.9、如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.小明认为:若MN = EF,则MN⊥EF;小亮认为: 若MN⊥EF,则MN = EF.你认为()A.仅小明对 B.仅小亮对 C.两人都对 D.两人都对第9题图第10题图第11题图第12题图10、如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,•则四个结论正确的是().①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A.全部正确; B.仅①和②正确; C.仅②③正确; D.仅①和③正确11、如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是()①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A.1 B.2 C.3 D.412、如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为()A.13B.12C.23D.不能确定二、填空题(每空3 分,共15 分)13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。
初二数学----几何证明初步经典练习题(含答案) (2)

几何证明初步练习题1、三角形的内角和定理:三角形的内角和等于180°.推理过程:○1 作CM ∥AB ,则∠A= ,∠B= ,∵∠ACB +∠1+∠2=1800( ,∴∠A+∠B+∠ACB=1800.○2 作MN ∥BC ,则∠2= ,∠3= ,∵∠1+∠2+∠3=1800,∴∠BAC+∠B+∠C=1800. 2.求证:在一个三角形中,至少有一个内角大于或者等于60°。
3、.如图,在△ABC 中,∠C >∠B,求证:AB >AC 。
的垂线。
9∴,AB ,BD .求证:=AB18∠,A ∠,∴BC =11DM ⊥∴有DM =DN .∴ΔBMD ≌ΔCND (HL).∴BM =CN .二、旋转12、如图,已知在正方形ABCD 中,E在BC 上,F在DC 上,BE +DF =EF .求证:45EAF ∠=.分析:将ΔADF 绕A顺时针旋转90得ABG .∴GA B F A D ∠=∠.易证ΔAGE ≌ΔAFE .∴ 1452FAE GAE FAG ∠=∠=∠=13、如图,点E 在ΔABC 外部,D 在边BC 上,DE 交AC 于F .若123∠=∠=∠,AC=AE.求证:ΔABC ≌ΔADE .B分析:若ΔABC ≌ΔADE ,则ΔADE 可视为ΔABC 绕A逆时针旋转1∠所得.则有B ADE ∠=∠.∵12B ADE ∠+∠=∠+∠,且12∠=∠.∴B ADE ∠=∠.又∵13∠=∠.∴BAC DAE ∠=∠.再∵AC=AE.∴ΔABC ≌ΔADE .14、如图,点E为正方形ABCD的边CD上一点,点F为CB的延长线上的一点,且EA⊥AF.求证:DE=BF.分析:将ΔABF 视为ΔADE 绕A顺时针旋转90即可.∵90FAB BAE EAD BAE ∠+∠=∠+∠=.∴FBA EDA ∠=∠.又∵90FBA EDA ∠=∠=,AB=AD.∴ΔABF ≌ΔADE .(ASA)∴DE=DF.平移第14题图 第15题图 第16题图 第17题图 ACEB .可视为将AC平移到BE.AB平移到CE.由勾股定理可得DE=17.∴梯形ABCD中位线长为8.5.16CE .DCEF .四、倍长 17ABC 的中线.求证:AB+分析:延长AD到E使得AE=2AD.连接BE易证Δ18、如图,19、60∠.又∵AE=CD,∴BD=CE.∴Δ∴BAD .∴.易证Δ.∴Δ为等边三角形.分析:取DC中点G,连接EG与FG.则EG为ΔBCD 中位线,FG为ΔACD 的中位线.∴EG∥=12BC ,FG ∥=12AD .∵AD ∥BC .∴过一点G有且只有一条直线平行于已知直线BC,即E、F、G共线.∴1()2EF BC AD =-.直角三角形斜边上的中线等于斜边的一半21、已知,在ABCD 中BD AB 21=.E为OA的中点,F为OD中点,G为BC中点. 求证:EF=EG. 分析:连接BE .∵BD AB 21=,AE=O E.∴BE⊥CE,∵BG=CG. ∴BD EG1=.又EF为ΔAOD 的中位线.∴AD EF 1=.∴EF=EG. 分析: A .20???????3、A .4OF 平分∠AOE A ?③在△ABC 中,若∠A=12∠B=13∠C ,则△ABC 是直角三角形 ?④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18A .1个B .2个C .3个??D .4个6、如图,在AB=AC 的△ABC 中,D 是BC 边上任意一点,DF ⊥AC 于F ,E 在AB 边上,使ED ⊥BC 于D ,∠AED=155°,则∠EDF 等于(?? )A 、50°?B 、65°???C 、70°??D 、75°?7、如图,已知△ABC 是等腰直角三角形,∠A=90°,BD 是∠ABC 的平分线,DE ⊥BC 于E ,若BC=10cm ,则△DEC 的周长为(?? )A .8cm????????B .10cm??????????C .12cm ?????????D .14cm8、如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为(??? )A. ? ???B.?????C.5???? ??D.49、如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.小明认为:若MN = EF,则MN⊥EF;小亮认为: 若MN⊥EF,则MN = EF.你认为(??? )A.仅小明对?? B.仅小亮对? C.两人都对? D.两人都对??第9题图第10题图第11题图第12题图10、如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,•则四个结论正确的是(? ).①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A.全部正确;?????????????? B.仅①和②正确; C.仅②③正确;?????????? ?D.仅①和③正确11)④=3:4:5????1216、?对于同一平面内的三条直线、、,给出下列五个论断:①∥∥;③⊥;④∥;_____. 17CDE19和等边第19题图第20题图第21题图第22题图20如果ABC三点不在一条直线上,那么AE=DC和BF=BG是否仍然成立明。
初中数学几何证明经典试题(含答案)
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、 E 是圆上的两点,CD⊥ AB,EF⊥ AB, EG⊥ CO.求证: CD= GF.(初二)CEGA BD O F2、已知:如图,P 是正方形ABCD内点,∠ PAD=∠ PDA= 150.求证:△ PBC是正三角形.(初二)A DPB C3、如图,已知四边形ABCD、 A1B1C1D1都是正方形, A2、 B2、 C2、 D2分别是AA1、BB1、 CC1、 DD1的中点.A DA2D2求证:四边形 A B C D 是正方形.(初二)A12222D1B1C1B22CB C4、已知:如图,在四边形ABCD中, AD= BC,M、N 分别是 AB、CD的中点, AD、BC的延伸线FEN C交 MN于 E、 F.求证:∠ DEN=∠ F.经典题(二)1、已知:△ ABC中, H 为垂心(各边高线的交点), O为外心,且 OM⊥ BC于M.( 1)求证: AH=2OM;A( 2)若∠ BAC= 600,求证: AH= AO.(初二)O·H EB M D C2、设 MN是圆 O外向来线,过 O作 OA⊥ MN于 A,自 A引圆的两条直线,交圆于B、C及D、E,直线 EB及 CD分别交 MN于 P、 Q.GE求证: AP= AQ.(初二)O·CB DMP A Q N3、假如上题把直线MN由圆外平移至圆内,则由此可得以下命题:设 MN是圆 O的弦,过 MN的中点 A 任作两弦 BC、DE,设 CD、 EB分别交 MN于 P、 Q.求证: AP=AQ.(初二)CEA M Q·P N·O B D4、如图,分别以△ABC的 AC和 BC为一边,在△ ABC的外侧作正方形ACDE和正方形 CBFG,点 P是 EF的中点.求证:点P 到边 AB的距离等于AB的一半.(初二)DGCEPFA Q B经典题(三)1、如图,四边形ABCD为正方形, DE∥AC, AE=AC, AE与 CD订交于 F.求证: CE=CF.(初二)AB2、如图,四边形ABCD为正方形, DE∥AC,且 CE= CA,直线 EC交 DA延伸线于求证: AE= AF.(初二)DF ECF.F A DB C3、设 P 是正方形ABCD一边 BC上的任一点,PF⊥ AP, CF均分∠ DCE.求证: PA= PF.(初二)AE DFBP C E4、如图, PC切圆 O于 C,AC为圆的直径, PEF为圆的割线, AE、AF 与直线 PO订交于 B、D.求证: AB= DC, BC= AD.(初三)AB O DPEFC经典题(四)A1、已知:△ ABC是正三角形, P 是三角形内一点,PA=3, PB= 4, PC= 5.P 求:∠ APB的度数.(初二)B C2、设 P 是平行四边形ABCD内部的一点,且∠PBA=∠ PDA.求证:∠ PAB=∠ PCB.(初二)A DPB C3、设 ABCD为圆内接凸四边形,求证:AB· CD+AD· BC=AC· BD.(初三)ADB C4、平行四边形ABCD中,设 E、 F 分别是 BC、 AB上的一点, AE 与 CF订交于 P,且AE= CF.求证:∠ DPA=∠ DPC.(初二)A DFPB E C经典难题(五)A1、设 P 是边长为 1 的正△ ABC内任一点, L= PA+ PB+ PC,PB C求证:≤ L<2.2、已知: P 是边长为 1 的正方形ABCD内的一点,求PA+ PB+ PC的最小值.A DPCB3、 P 为正方形ABCD内的一点,而且PA= a, PB= 2a, PC= 3a,求正方形的边长.A DPCB4、如图,△ ABC中,∠ ABC=∠ ACB= 800, D、 E 分别是 AB、 AC上的点,∠ DCA= 300,∠ EBAAE= 200,求∠ BED的度数.经典题(一)1.以下列图做 GH⊥ AB,连结 EO。
青岛版八年级上册数学第5章 几何证明初步 含答案
青岛版八年级上册数学第5章几何证明初步含答案一、单选题(共15题,共计45分)1、用反证法证明:“一个三角形中至多有一个角不小于90°”时,应假设( )A.一个三角形中至少有两个角不小于 90°B.一个三角形中至多有一个角不小于 90°C.一个三角形中至少有一个角不小于 90°D.一个三角形中没有一个角不小于 90°2、如图,在△ABC中,∠C=70º,沿图中虚线截去∠C,则∠1+∠2=()A.360ºB.250ºC.180ºD.140º3、如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件序号为( )A.①②B.①③C.①④D.③④4、三角形中,最大角α的取值范围是()A.0º<α<90ºB.60º<α<90ºC.60º<α<180ºD.60º≤α<90º5、平面内有两两不重合的直线和,已知,则的位置关系是()A.互相平行B.可能平行,可能不平行C.互相垂直D.可能垂直,可能不垂直6、已知等腰三角形的一个底角为40°,则这个等腰三角形的顶角为()A.40°B.100°C.40°或100°D.50°或70°7、下列命题是真命题的是()A.相等的角是对顶角B.在同一平面内,如果,,则C.内错角相等D.如果,,则8、如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=()A.25°B.35°C.55°D.65°9、①两点之间线段最短;②同旁内角互补;③若 AC=BC,则点 C 是线段AB 的中点;④经过一点有且只有一条直线与这条直线平行,其中正确的说法有( )A.1 个B.2 个C.3 个D.4 个10、如图,在▱OABC中C(2,0),AC⊥OC,反比例函数y= (k>0)在第一象限内的图象过点A,且与BC交于点D,点D的横坐标为3,连接AD,△ABD的面积为,则k的值为()A.4B.5C.D.11、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中正确的结论的个数是()A.2个B.3个C.4个D.5个12、如图,已知a∥b,点A在直线a上,点B,C在直线b上,若∠1=125°,∠2=50°,则∠3为()A.55°B.65°C.70°D.75°13、如图所示,在中,,于,,则线段的长是()A.3B.4C.8D.114、如图是琳琳6个装好糖果的礼包盒,每盒上面的数字代表这盒礼包实际装有的糖果数量.她把其中的5盒送给好朋友小芬和小红,自己留下1盒.已知送的都是整盒,包装没拆过,送给小芬的糖果数量是小红的2倍,则琳琳自己留下的这盒有糖果()A.15粒B.18粒C.20粒D.21粒15、若等腰三角形中有一个角等于50°,则其它两个角的度数为()。
青岛版八年级上册数学第5章 几何证明初步含答案
青岛版八年级上册数学第5章几何证明初步含答案一、单选题(共15题,共计45分)1、为了从500只外形相同的鸡蛋中找到唯一的一只双黄蛋,检查员将这些鸡蛋按1-500的顺序排成一列,第一次先从中取出序号为单数的蛋,发现其中没有双黄蛋,他将剩下的蛋的原来位置上又按1-250编号(即原来的2号变为1号,原来的4号变成2号,…,原来的500号变成250号)。
又从中取出新序号为单数的蛋进行检查,任没有发现双黄蛋,……,如此下去,检查到最后的一个是双黄蛋,问这只双黄蛋最初的序号是()A.48B.250C.256D.5002、已知三角形ABC的三个内角满足关系∠B+∠C=3∠A,则此三角形( ).A.一定有一个内角为45°B.一定有一个内角为60°C.一定是直角三角形D.一定是钝角三角形3、如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=()A.10°B.20°C.30°D.40°4、如图,把一块含45°角的三角板的直角顶点靠在长尺(两边a∥b)的一边b上,若∠1=30°,则三角板的斜边与长尺的另一边a的夹角∠2的度数为()A.10°B.15°C.30°D.35°5、如图所示,点E在AC的延长线上,下列条件中不能判断BD∥AE的是()A.∠D=∠DCEB.∠D+∠ACD=180°C.∠1=∠2D.∠3=∠46、在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,满足下列条件的△ABC 不是直角三角形的是()A.∠A∶∠B∶∠C = 1∶1∶2B.a∶b∶c =1∶1∶C.D.∠A+∠B=2∠C7、如图,把一个三角形纸片ABC的三个顶角向内折叠之后(3个顶点不重合),那么图中的度数和是()A. B. C. D.8、如图,将矩形纸带ABCD,沿EF折叠后,C、D两点分别落在C′、D′的位置,经测量得∠EFB=65°,则∠AED′的度数是()A.65°B.55°C.50°D.25°9、如图,点D在BA的延长线上,AE∥BC.若∠DAC=100°,∠B=65°,则∠ACB 的度数为()A.65°B.35°C.30°D.40°10、如图,在△ABC中,过顶点A的直线DE∥BC,∠ABC、∠ACB的平分线分别交DE于点E、D,若AC=3,AB=4,则DE的长为()A.6B.7C.8D.911、如图,BE,CF是△ABC的角平分线,∠ABC=80°,∠ACB=60°,EB,CF相交于D,则∠CDE的度数是()A.130°B.70°C.80°D.75°12、如图,在中,,的外角,则的度数是()A.30°B.45°C.60°D.75°13、如图,已知∠1=∠2=∠3=55º,则∠4=()A.135ºB.125ºC.110ºD.无法确定14、如图,直线a、b被直线c所截,现给出下列四个条件:(1)∠1=∠5;(2)∠4=∠7,(3)∠2+∠3=180°;(4)∠1=∠7;其中能判定a∥b的条件的序号是()A.(1),(2)B.(2),(3)C.(1),(4)D.(3),(4)15、小颖在做下面的数学作业时,因钢笔漏墨水,不小心将部分字迹污损了,作业过程如下(涂黑部分即为污损部分):如图,OP平分∠AOB,MN∥OB,试说明:OM=MN.理由:因为OP平分∠AOB,所以■,又因为MN∥OB,所以■,故∠1=∠3,所以OM=MN.小颖思考:污损部分应分别是以下四项中的两项:①∠1=∠2;②∠2=∠3;③∠3=∠4;④∠1=∠4.那么她补出来的部分应是( )A.①④B.②③C.①②D.③④二、填空题(共10题,共计30分)16、如图,若,,则________.17、将一张矩行纸片按图中方式折叠,若∠1 =50°,则∠2为________度.18、如图,AD是△ABC的高,BE是△ABC的内角平分线,BE、AD相交于点F,已知∠BAD=40°,则∠BFD=________°.19、在△ABC中,∠A﹣∠B=10°,,则∠C=________20、如图,EF⊥AB于点F,CD⊥AB于点D,E是AC上一点,∠1=∠2,则图中互相平行的直线有________ 对.21、按要求完成下列证明如图,AB∥CD,CB∥DE,求证:∠B+∠D=180°.证明:∵AB∥CD,∴∠B=________(________).∵CB∥DE,∴∠C+________=180°(________).∴∠B+∠D=180°.22、完成推理过程如图,AB∥DC,AE⊥BD,CF⊥BD,BF=DE.求证:AE=CF.证明∵AB∥DC,∴∠1=________.∵AE⊥BD,CF⊥BD,∴∠AEB=________∵BF=DE,∴BF﹣EF=DE﹣EF∴________=________.∴△ABE≌△CDF________.∴AE=CF________23、阅读下面解答过程,并填空或填理由.已知如下图,点E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H,∠A=∠D,∠1=∠2.试说明:∠B=∠C.解:∵∠1=∠2(已知)∠2=∠3(________)∴∠3=∠1(等量代换)∴AF∥DE(________)∴∠4=∠D(________)又∵∠A=∠D(已知)∴∠A=∠4(等量代换)∴AB∥CD(________)∴∠B=∠C(________).24、如图,一个正方形和两个等边三角形的位置如图所示,若∠2=52°,则∠1+∠3=________°.25、平行四边形ABCD中,∠ABC的平分线将AD边分成的两部分的长分别为2和3,则平行四边形ABCD的周长是________.三、解答题(共5题,共计25分)26、如图,,,,求、的度数.27、如图,已知在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD相交于D,试说明∠A=2∠D的理由.28、如图,已知∠A=∠F,∠C=∠E,求证:BE∥CD.29、已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数.30、在平面上有三条直线a,b,c,它们之间有哪几种可能的位置关系?你能画出来吗?参考答案一、单选题(共15题,共计45分)1、C2、A3、A4、B5、C6、D7、C8、C9、B10、B11、B12、A13、B14、C15、C二、填空题(共10题,共计30分)17、18、19、20、21、22、23、24、三、解答题(共5题,共计25分)26、27、29、。
初中数学-几何证明经典试题(含答案)
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)AP C DB A F GC EB O D3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)D 2C 2 B 2 A 2D 1 C 1 B 1 C BD A A 14、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.F3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)D4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)经典题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.APCBACBP D A CBPD4中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠=200,求∠BED的度数.参考答案经典题(一)1.如下图做GH⊥AB,连接EO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明初步练习题1、三角形的内角和定理:三角形的内角和等于180°.推理过程:○1 作CM ∥AB ,则∠A= ,∠B= ,∵∠ACB +∠1+∠2=1800( ,∴∠A+∠B+∠ACB=1800. ○2 作MN ∥BC ,则∠2= ,∠3= ,∵∠1+∠2+∠3=1800,∴∠BAC+∠B+∠C=1800. 2.求证:在一个三角形中,至少有一个内角大于或者等于60°。
3、.如图,在△ABC 中,∠C >∠B,求证:AB >AC 。
4. 已知,如图,AE5. 已知:如图,EF ∥AD ,∠1 =∠2. 求证:∠AGD +∠BAC = 180°.反证法经典例题6.求证:两条直线相交有且只有一个交点.7.如图,在平面内,AB 是L 的斜线,CD 是L 的垂线。
求证:AB 与CD 必定相交。
8.2一.角平分线--轴对称9、已知在ΔABC 中,E为BC的中点,AD 平分BAC ∠,BD ⊥AD 于D .AB =9,AC=13求DE的长第9题图 第10题图 第11题图分析:延长BD交AC于F.可得ΔABD ≌ΔAFD .则BD =DF .又BE =EC ,即D E为ΔBCF 的中位线.∴DE=12FC=12(AC-AB)=2. 10、已知在ΔABC 中,108A ∠=,AB =AC ,分ABC ∠.求证:BD 平BC =AB +CD . 分析:在BC上截取BE=BA,连接DE.可得ΔBAD ≌ΔBED .由已知可得:18ABD DBE ∠=∠=,108A BED ∠=∠=,36C ABC ∠=∠=.∴72DEC EDC ∠=∠=,∴CD =CE ,∴BC =AB +CD .11、如图,ΔABC 中,E是BC 边上的中点,DE ⊥BC 于E ,交BAC ∠的平分线AD 于D ,过D 作DM ⊥AB 于M,作DN ⊥AC 于N .求证:BM =CN .分析:连接DB 与DC .∵DE 垂直平分BC ,∴DB =DC .易证ΔAMD ≌ΔAND .∴有DM =DN .∴ΔBMD ≌ΔCND (HL).∴BM =CN .二、旋转12、如图,已知在正方形ABCD 中,E在BC 上,F在DC 上,BE +DF =EF .求证:45EAF ∠=. 分析:将ΔADF 绕A顺时针旋转90得ABG .∴GAB FAD ∠=∠.易证ΔAGE ≌ΔAFE .∴ 1452FAE GAE FAG ∠=∠=∠=13、如图,点E 在ΔABC 外部,D 在边BC 上,DE 交AC 于F .若123∠=∠=∠,AC=AE.求证:ΔABC ≌ΔADE . C B A D E F D A B C B A E DN M B D A C213ED B A分析:若ΔABC ≌ΔADE ,则ΔADE 可视为ΔABC 绕A逆时针旋转1∠所得.则有B ADE ∠=∠.∵12B ADE ∠+∠=∠+∠,且12∠=∠.∴B ADE ∠=∠.又∵13∠=∠.∴BAC DAE ∠=∠.再∵AC=AE.∴ΔABC ≌ΔADE .14、如图,点E为正方形ABCD的边CD上一点,点F为CB的延长线上的一点,且EA⊥AF.求证:DE=BF.分析:将ΔABF 视为ΔADE 绕A顺时针旋转90即可.∵90FAB BAE EAD BAE ∠+∠=∠+∠=.∴FBA EDA ∠=∠.又∵90FBA EDA ∠=∠=,AB=AD.∴ΔABF ≌ΔADE .(ASA)∴DE=DF. 平移第14题图 第15题图 第16题图 第17题图三、平移15、如图,在梯形ABCD 中,BD ⊥AC ,AC =8,BD =15.求梯形ABCD 的中位线长. 接BE.可得ACEB .可分析:延长DC到E使得CE=AB.连视为将AC平移到BE.AB平移到CE.由勾股定理可得DE=17.∴梯形ABCD中位线长为8.5. 16、已知在ΔABC 中,AB =AC ,D 为AB 上一点,E为AC 延长线一点,且BD =CE .求证:DM =EM 分析:作DF∥AC交BC于F.易证DF=BD=CE.则DF可视为CE平移所得.∴四边形DCEF为DCEF .∴DM=EM.线段中点的常见技巧 --倍长四、倍长17、已知,AD为ABC 的中线.求证:AB+AC>2AD.分析:延长AD到E使得AE=2AD.连接BE易证ΔBDE ≌ΔCDA .∴BE=AC.∴AB+AC>2AD.18、如图,AD 为ΔABC 的角平分线且BD =CD .求证:AB =AC .分析:延长AD到E使得AD=ED.易证ΔABD ≌ΔECD .∴EC=AB.∵BAD CAD ∠=∠.∴E CAD ∠=∠.∴AC=EC=AB.19、已知在等边三角形ABC中,D和E分别为BC与AC上的点,且AE=CD.连接AD与BE交于点P,作BQ⊥AD于Q.求证:BP=2PQ.分析:延长PD到F使得FQ=PQ.在等边三角形ABC中AB=BC=AC,60ABD C ∠=∠=.又∵AE=CD,∴BD=CE.∴ΔABD ≌ΔBCE .∴CBE BAD ∠=∠.∴60BPQ PBA PAB PBA DBP ∠=∠+∠=∠+∠=.易证ΔBPQ ≌ΔBFQ .得BP=BF,又60BPD ∠=.∴ΔBPF 为等边三角形.∴BP=2PQ.中位线五、中位线、中线:20、已知在梯形ABCD 中,AD ∥BC ,E和F分别为BD 与AC 的中点, 求证:1()2EF BC AD =-.分析:取DC中点G,连接EG与FG.则EG为ΔBCD 中位线,FG为ΔACD 的中位线. ∴EG∥=12BC ,FG ∥=12AD .∵AD ∥BC .∴过一点G有且只有一条直线平行于已知直线BC,即E、F、G共线.∴1()2EF BC AD =-.直角三角形斜边上的中线等于斜边的一半21、已知,在ABCD 中BD AB 21=.E为OA的中点,F为OD中点,G为BC中点. 求证:EF=EG. 分析:连接BE .∵BD AB 21=,AE=O E.∴BE⊥CE,∵BG=CG. ∴BD EG 21=.又EF为ΔAOD 的中位线.∴AD EF 21=.∴EF=EG. 22、在ΔABC 中,AD是高,CE是中线,DC=BE,DG⊥CE于G. 求证:(1)CG=EG.(2)2B BCE ∠=∠. 分析:(1)连接DE.则有DE=BE=DC.∴Rt ΔCDG ≌Rt ΔEDG (HL).∴EG=CG.∵DE=BE.∴B BDE DEC BCE ∠=∠=∠+∠.∵DE=CD.∴DEC BCE ∠=∠.∴2B BCE ∠=∠.几何证明初步测验题(1)一、选择题(每空3 分,共36 分)1、使两个直角三角形全等的条件是( )A 、一组锐角对应相等B 、两组锐角分别对应相等C 、一组直角边对应相等D 、两组直角边分别对应相等2、如图,已知AB ∥CD ,∠A =50°,∠C =∠E .则∠C =( )A .20°B .25°C .30°D .40°第2题图 第4题图 第6题图 第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中( )A .有两个角是直角B .有两个角是钝角C .有两个角是锐角D .一个角是钝角,一个角是直角4、如图,直线AB 、CD 相交于点O ,∠BOE=90°,OF 平分∠AOE ,∠1=15°30’,则下列结论不正确的是( )A .∠2=45°B .∠1=∠3C .∠AOD+∠1=180°D .∠EOD=75°30’5、下列说法中,正确的个数为( )①三角形的三条高都在三角形内,且都相交于一点②三角形的中线都是过三角形的某一个顶点,且平分对边的直线③在△ABC 中,若∠A=12∠B=13∠C ,则△ABC 是直角三角形 ④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18A .1个B .2个C .3个D .4个 O C BE F E D G A6、如图,在AB=AC的△ABC中,D是BC边上任意一点,DF⊥AC于F,E在AB边上,使ED⊥BC于D,∠AED=155°,则∠EDF等于()A、50°B、65°C、70°D、75°7、如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm8、如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A. B.9、如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.小明认为:若MN = EF,则MN⊥EF;小亮认为: 若MN⊥EF,则MN = EF.你认为()A.仅小明对 B.仅小亮对 C.两人都对 D.两人都对第9题图第10题图第11题图第12题图10、如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,•则四个结论正确的是().①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A.全部正确; B.仅①和②正确; C.仅②③正确; D.仅①和③正确11、如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是()①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A.1 B.2 C.3 D.412、如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为()A.13B.12C.23D.不能确定二、填空题(每空3 分,共15 分)13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。
14、请写出“等腰三角形的两个底角相等”的逆命题:15、如图,已知∠1=∠2,请你添加一个条件:___________,使△ABD≌△ACD。
16、对于同一平面内的三条直线、、,给出下列五个论断:①∥;②∥;③⊥;④∥;⑤⊥.以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题:_____.17、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC 和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:① AD=BE;② PQ∥AE;③ AP=BQ;④ DE=DP;⑤∠AOB=60°.恒成立的结论有______________(把你认为正确的序号都填上).三、计算、简答题18、已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,E、F分别为垂足.求证:AD垂直平分EF.19、如图7,已知A、B、C在一条直线上,分别以AB、BC为边在AC同侧作等边三角形ABD和等边三角形BCE,AE交BD于点F,DC交BE于点G。
