初二几何证明题
初二几何证明题(完整版)
初二几何证明题初二几何证明题..bf=e=bd== ∠bdf=∠bfdf=be d== ∠df ∠fd== ∠bdf+∠df ∠bfd+∠fd== ∠bd ∠bf矛盾,从而假设不成立所以ab=a。
2、两地角的平分线相等，为等腰三角形作三角形ab,d,be为角,b的角平分线，交于ab,be.两平分线交点为o连结de,即de平行b，所以三角形do与ob相似。
有dod=eoeb,又eb=d所以do=eo,三角形ob为等腰又角ode=ob=oed=ob又因为be和d是叫平分线，所以容易得出角=角b，即ab为等腰。
第三篇：初二几何证明题28.（本小题满分10分）如图，在矩形abd中，ab=8，ad=6，点p、q分别是ab边和d边上的动点，点p从点a向点b运动，点q从点向点d运动，且保持ap-q。
设ap=x（1）当pq∥ad时，求x的值；（2）当线段pq的垂直平分线与b边相交时，求x的取值范围；（3）当线段pq的垂直平分线与b相交时，设交点为e，连接ep、eq，设△epq的面积为s，求s关于x的函数关系式，并写出s的取值范围。
21．（本小题满分9分）如图，直线?x?m与双曲线?（1）求m及k的值； k相交于a（2，1）、b两点． x??x?m,?（2）不解关于x、的方程组?直接写出点b的坐标； k?,?x?（3）直线2x?4m经过点b吗？请说明理由．（第21题）28．（201X江苏淮安，28，12分）如题28图，在平面直角坐标系中，点a坐标为，点b坐标为，点为ob的中点，点d从点o出发，沿△oab的三边按逆时针方向以2个单位长度／秒的速度运动一周．点坐标是)，当点d运动8.5秒时所在位置的坐标是，)；设点d运动的时间为t秒，试用含t的代数式表示△od的面积s,并指出t为何值时，s最大；点e在线段ab上以同样速度由点a向点b运动，如题28图，若点e与点d同时出发，问在运动5秒钟内，以点d，a，e为顶点的三角形何时与△od相似：题28图题28图（10江苏南京）21.（7分）如图，四边形abd的对角线a、bd相较于点o，△ab≌△bad。
(完整版)初中几何证明题五大经典(含答案)
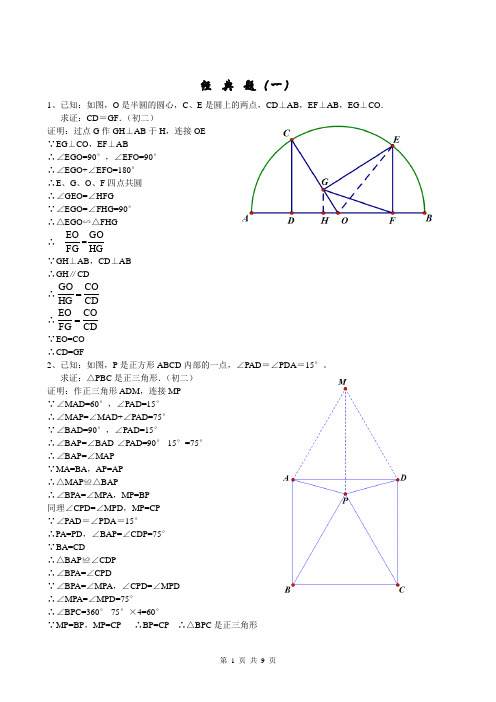
经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）证明：过点G 作GH ⊥AB 于H ，连接OE ∵EG ⊥CO ，EF ⊥AB∴∠EGO=90°，∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ，CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知：如图，P 是正方形ABCD 内部的一点，∠PAD ＝∠PDA ＝15°。
求证：△PBC 是正三角形．（初二） 证明：作正三角形ADM ，连接MP ∵∠MAD=60°，∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°，∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ，AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ，MP=BP 同理∠CPD=∠MPD ，MP=CP ∵∠PAD ＝∠PDA ＝15°∴PA=PD ，∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ，∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ，MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN于E 、F ．求证：∠DEN ＝∠F ．证明:连接AC ，取AC 的中点G ,连接NG 、MG ∵CN=DN ，CG=DG ∴GN ∥AD ，GN=21AD ∴∠DEN=∠GNM ∵AM=BM ，AG=CG ∴GM ∥BC ，GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ． （1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二） 证明：（1）延长AD 交圆于F ，连接BF ，过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ，BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH ）=2GD 又AD ⊥BC ，OM ⊥BC ，OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM （2）连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ，OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由（1）知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线，过O 作OA ⊥MN 于A ，自A 引圆的两条割线交圆O 于B 、C 及D 、E ，连接CD 并延长交MN 于Q ，连接EB 并延长交MN 于P. 求证：AP ＝AQ ．证明：作点E 关于AG 的对称点F ，连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ，PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）证明：作OF ⊥CD 于F ，OG ⊥BE 于G ，连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ，∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN ， ∴OA ⊥MN 又OG ⊥BE ，∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°，OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ，点O 是DF 的中点，OP ⊥BC求证：BC=2OP （初二）证明：分别过F 、A 、D 作直线BC 的垂线，垂足分别是L 、M 、N ∵OF=OD ，DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ． 求证：CE ＝CF ．（初二）证明：连接BD 交AC 于O 。
初二数学 几何证明初步经典练习题 含答案
几何证明初步练习题1、三角形的内角和定理：三角形的内角和等于180°．推理过程：○1 作CM ∥AB ，则∠A= ，∠B= ，∵∠ACB +∠1+∠2=1800（ ，∴∠A+∠B+∠ACB=1800． ○2 作MN ∥BC ，则∠2= ，∠3= ，∵∠1+∠2+∠3=1800，∴∠BAC+∠B+∠C=1800． 2．求证：在一个三角形中，至少有一个内角大于或者等于60°。
3、.如图，在△ABC 中，∠C ＞∠B,求证：AB ＞AC 。
4. 已知，如图，AE5. 已知：如图，EF ∥AD ，∠1 =∠2. 求证：∠AGD ＋∠BAC = 180°.反证法经典例题6.求证:两条直线相交有且只有一个交点.7.如图，在平面内，AB 是L 的斜线，CD 是L 的垂线。
求证：AB 与CD 必定相交。
8.2一．角平分线－－轴对称9、已知在ΔABC 中，Ｅ为ＢＣ的中点，AD 平分BAC ∠，BD ⊥AD 于D ．AB ＝9，ＡＣ＝13求ＤＥ的长第9题图 第10题图 第11题图分析：延长ＢＤ交ＡＣ于Ｆ．可得ΔABD ≌ΔAFD ．则BD ＝DF ．又BE ＝EC ，即D Ｅ为ΔBCF 的中位线．∴DE=12FC=12(AC-AB)=2． 10、已知在ΔABC 中，108A ∠=，AB ＝AC ，BD 平分ABC ∠．求证：BC ＝AB ＋CD ． 分析：在ＢＣ上截取ＢＥ＝ＢＡ，连接ＤＥ．可得ΔBAD ≌ΔBED ．由已知可得：18ABD DBE ∠=∠=，108A BED ∠=∠=，36C ABC ∠=∠=．∴72DEC EDC ∠=∠=，∴CD＝CE ，∴BC ＝AB ＋CD ．11、如图，ΔABC 中，Ｅ是BC 边上的中点，DE ⊥BC 于E ，交BAC ∠的平分线AD 于D ，过D 作DM ⊥AB 于Ｍ，作DN ⊥ＡC 于N ．求证：BM ＝CN ．分析：连接DB 与DC ．∵DE 垂直平分BC ，∴DB ＝DC ．易证ΔAMD ≌ΔAND ．∴有DM ＝DN ．∴ΔBMD ≌ΔCND （ＨＬ）．∴BM ＝CN ．二、旋转12、如图，已知在正方形ABCD 中，Ｅ在BC 上，Ｆ在DC 上，BE ＋DF＝EF ．求证：45EAF ∠=． C B ADE F D A B C B A E D NM B D A C分析：将ΔADF 绕Ａ顺时针旋转90得ABG ．∴GAB FAD ∠=∠．易证ΔAGE ≌ΔAFE ．∴ 1452FAE GAE FAG ∠=∠=∠= 13、如图，点E 在ΔABC 外部，D 在边BC 上，DE 交AC 于F ．若123∠=∠=∠，ＡＣ＝ＡＥ．求证：ΔABC ≌ΔADE ．分析：若ΔABC ≌ΔADE ，则ΔADE 可视为ΔABC 绕Ａ逆时针旋转1∠所得．则有B ADE ∠=∠．∵12B ADE ∠+∠=∠+∠，且12∠=∠．∴B ADE ∠=∠．又∵13∠=∠．∴BAC DAE ∠=∠．再∵ＡＣ＝ＡＥ．∴ΔABC ≌ΔADE ．14、如图，点Ｅ为正方形ＡＢＣＤ的边ＣＤ上一点，点Ｆ为ＣＢ的延长线上的一点，且ＥＡ⊥ＡＦ．求证：ＤＥ＝ＢＦ．分析：将ΔABF 视为ΔADE 绕Ａ顺时针旋转90即可．∵90FAB BAE EAD BAE ∠+∠=∠+∠=．∴FBA EDA ∠=∠． 又∵90FBA EDA ∠=∠=，ＡＢ＝ＡＤ．∴ΔABF ≌ΔADE ．（ＡＳＡ）∴ＤＥ＝ＤＦ． 平移第14题图 第15题图 第16题图 第17题图三、平移15、如图，在梯形ABCD 中，BD ⊥AC ，AC ＝８，BD ＝１５．求梯形ABCD 的中位线长． 分析：延长ＤＣ到Ｅ使得ＣＥ＝ＡＢ．连接ＢＥ．可得ACEB ．可视为将ＡＣ平移到ＢＥ．ＡＢ平移到ＣＥ．由勾股定理可得ＤＥ＝１７．∴梯形ＡＢＣＤ中位线长为８．５．16、已知在ΔABC 中，AB ＝AC ，D 为AB 上一点，Ｅ为AC 延长线一点，且BD ＝CE ．求证：DM ＝EM 分析：作ＤＦ∥ＡＣ交ＢＣ于Ｆ．易证ＤＦ＝ＢＤ＝ＣＥ．则ＤＦ可视为ＣＥ平移所得．∴四边形ＤＣＥＦ为DCEF ．∴ＤＭ＝ＥＭ．线段中点的常见技巧 --倍长四、倍长17、已知，ＡＤ为ABC 的中线．求证：ＡＢ＋ＡＣ>２ＡＤ．分析：延长ＡＤ到Ｅ使得ＡＥ＝２ＡＤ．连接ＢＥ易证ΔBDE ≌ΔCDA ．∴ＢＥ＝ＡＣ．∴ＡＢ＋ＡＣ>２ＡＤ．18、如图，AD 为ΔABC 的角平分线且BD ＝CD ．求证：AB ＝AC ． 分析：延长ＡＤ到Ｅ使得ＡＤ＝ＥＤ．易证ΔABD ≌ΔECD ．∴ＥＣ＝ＡＢ． ∵BAD CAD ∠=∠．∴E CAD ∠=∠．∴ＡＣ＝ＥＣ＝ＡＢ． 19、已知在等边三角形ＡＢＣ中，Ｄ和Ｅ分别为ＢＣ与ＡＣ上的点，且ＡＥ＝ＣＤ．连接ＡＤ与ＢＥ交于点Ｐ，作ＢＱ⊥ＡＤ于Ｑ．求证：ＢＰ＝２ＰＱ．分析：延长ＰＤ到Ｆ使得ＦＱ＝ＰＱ．在等边三角形ＡＢＣ中ＡＢ＝ＢＣ＝ＡＣ，60ABD C ∠=∠=．又∵ＡＥ＝ＣＤ，∴ＢＤ＝ＣＥ．∴ΔABD ≌ΔBCE ．∴CBE BAD ∠=∠．∴60BPQ PBA PAB PBA DBP ∠=∠+∠=∠+∠=．易证ΔBPQ ≌ΔBFQ ．得ＢＰ＝ＢＦ，又60BPD ∠=．∴ΔBPF 为等边三角形．∴ＢＰ＝２ＰＱ．中位线五、中位线、中线：20、已知在梯形ABCD 中，AD ∥BC ，Ｅ和Ｆ分别为BD 与AC 的中点, 求证：1()2EF BC AD =-． 分析：取ＤＣ中点Ｇ，连接ＥＧ与ＦＧ．则ＥＧ为ΔBCD 中位线，ＦＧ为ΔACD 的中位线． ∴ＥＧ∥＝12BC ，FG ∥＝12AD ．∵AD ∥BC ．∴过一点Ｇ有且只有一条直线平行于已知直线ＢＣ，即Ｅ、Ｆ、Ｇ共线．∴1()2EF BC AD =-． 直角三角形斜边上的中线等于斜边的一半21、已知，在ABCD 中BD AB 21=．Ｅ为ＯＡ的中点，Ｆ为ＯＤ中点，Ｇ为ＢＣ中点． 求证：ＥＦ＝ＥＧ．分析：连接ＢE ．∵BD AB 21=，ＡＥ＝O Ｅ．∴ＢＥ⊥ＣＥ，∵ＢＧ＝ＣＧ． ∴BD EG 21=．又ＥＦ为ΔAOD 的中位线．∴AD EF 21=．∴ＥＦ＝ＥＧ． 22、在ΔABC 中，ＡＤ是高，ＣＥ是中线，ＤＣ＝ＢＥ，ＤＧ⊥ＣＥ于Ｇ．求证：（１）ＣＧ＝ＥＧ．（２）2B BCE ∠=∠．分析：（１）连接ＤＥ．则有ＤＥ＝ＢＥ＝ＤＣ．∴Rt ΔCDG ≌Rt ΔEDG （ＨＬ）．∴ＥＧ＝ＣＧ．∵ＤＥ＝ＢＥ．∴B BDE DEC BCE ∠=∠=∠+∠．∵ＤＥ＝ＣＤ．∴DEC BCE ∠=∠．∴2B BCE ∠=∠．几何证明初步测验题（1）一、选择题（每空3 分，共36 分）1、使两个直角三角形全等的条件是（ ）A 、一组锐角对应相等B 、两组锐角分别对应相等C 、一组直角边对应相等D 、两组直角边分别对应相等2、如图，已知AB ∥CD ，∠A ＝50°，∠C ＝∠E ．则∠C ＝（ ）A ．20°B ．25°C ．30°D ．40°第2题图 第4题图 第6题图 第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”，应先假设这个三角形中（ ）A ．有两个角是直角B ．有两个角是钝角C ．有两个角是锐角D ．一个角是钝角，一个角是直角4、如图，直线AB 、CD 相交于点O ，∠BOE=90°，OF 平分∠AOE ，∠1=15°30’，则下列结论不正确的是( ) A D B E F OC B E F ED G AA．∠2=45° B．∠1=∠3 C．∠AOD+∠1=180° D．∠EOD=75°30’5、下列说法中，正确的个数为（）①三角形的三条高都在三角形内，且都相交于一点②三角形的中线都是过三角形的某一个顶点，且平分对边的直线③在△ABC中，若∠A=12∠B=13∠C，则△ABC是直角三角形④一个三角形的两边长分别是8和10，那么它的最短边的取值范围是2<b<18A．1个 B．2个 C．3个 D．4个6、如图，在AB=AC的△ABC中，D是BC边上任意一点，DF⊥AC于F，E在AB边上，使ED⊥BC于D，∠AED=155°，则∠EDF等于（）A、50°B、65°C、70°D、75°7、如图，已知△ABC是等腰直角三角形，∠A=90°，BD是∠ABC的平分线，DE⊥BC于E，若BC=10cm，则△DEC的周长为（）A．8cm B．10cm C．12cm D．14cm8、如图，已知△ABC中，∠ABC=45°，AC=4，H是高AD和BE的交点，则线段BH的长度为（）A. B.9、如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分别在边AB、CD、AD、BC上．小明认为：若MN = EF，则MN⊥EF；小亮认为: 若MN⊥EF，则MN = EF．你认为（）A．仅小明对 B．仅小亮对 C．两人都对 D．两人都对第9题图第10题图第11题图第12题图10、如图，△ABC为等边三角形，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，•则四个结论正确的是（）．①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A．全部正确; B．仅①和②正确; C．仅②③正确; D．仅①和③正确11、如图，△ABC中，CD⊥AB于D，一定能确定△ABC为直角三角形的条件的个数是（）①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A．1 B．2 C．3 D．412、如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为（）A．13B．12C．23D．不能确定二、填空题（每空3 分，共15 分）13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。
初二数学几何证明题（5篇可选）
初二数学几何证明题（5篇可选）第一篇：初二数学几何证明题1.在△ABC中，AB=AC，D在AB上，E在AC的延长线上，且BD=CE，线段DE交BC于点F，说明：DF=EF。
2.已知：在正方形ABCD中，M是AB的中点，E是AB延长线上的一点，MN垂直DM于点M，且交∠CBE的平分线于点N.（1）求证：MD＝MN.（2）若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变，则（1）的结论还成立吗？如果成立，请证明，如果不成立，请说明理由。
3.。
如图，点E,F分别是菱形ABCD的边CD和CB延长线上的点，且DE=BF，求证∠E=∠F。
4，如图，在△ABC中，D,E,F,分别为边AB,BC,CA,的中点，求证四边形DECF为平行四边形。
5.如图，在菱形ABCD中，∠DAB=60度，过点C作CE垂直AC 且与AB的延长线交与点E，求证四边形AECD是等腰梯形？6.如图，已知平行四边形ABCD中，对角线AC,BD，相交与点0，E是BD延长线上的点，且三角形ACE是等边三角形。
1.求证四边形ABCD是菱形。
2.若∠AED=2∠EAD，求证四边形ABCD是正方形。
7.已知正方形ABCD中，角EAF=45度，F点在CD边上，E点在BC边上。
求证：EF=BE+DF第二篇：初二几何证明题1如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DCCF．（1）求证：D是BC的中点；（2）如果AB=ACADCF的形状，并证明你的结论AEB第三篇：初二几何证明题初二几何证明题1.已知：如图，在△ABC中，AD⊥BC，垂足为D，BE⊥AC，垂足为E。
M为AB中点，联结ME,MD、ED求证：角EMD=2角DAC证明：∵M为AB边的中点，AD⊥BC，BE⊥AC，∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图，已知四边形ABCD中，AD=BC,E、F分别是AB、CD中点，AD、BC的延长线与EF的延长线交于点H、D求证：∠AHE=∠BGE证明：连接AC，作EM‖AD交AC于M，连接MF.如下图：∵E是CD的中点，且EM‖AD，∴EM=1/2AD，M是AC的中点，又因为F是AB的中点∴MF‖BC，且MF=1/2BC.∵AD=BC，∴EM=MF，三角形MEF为等腰三角形，即∠MEF=∠MFE.∵EM‖AH，∴∠MEF=∠AHF ∵FM‖BG，∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题，并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。
八年级上数学几何证明练习题(17题)
C A B C DE P 图 ⑴八年级数学（上）几何证明练习题1、 已知：在⊿ABC 中，∠A=900，AB=AC ，在BC 上任取一点P ，作PQ ∥AB 交AC 于Q ，作PR∥CA 交BA 于R ，D 是BC 的中点，求证：⊿RDQ 是等腰直角三角形。
B2、 已知：在⊿ABC 中，∠A=900，AB=AC ，D 是AC 的中点，AE ⊥BD ，AE 延长线交BC 于F ，求证：∠ADB=∠FDC 。
3、 已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ，求证：MA ⊥NA 。
4、已知：如图(1)，在△ABC 中，BP 、CP 分别平分∠ABC 和∠ACB ，DE 过点P 交AB 于D ，交AC 于E ，且DE ∥BC ．求证：DE －DB=EC ．5、在Rt △ABC 中，AB ＝AC ，∠BAC =90°，O 为BC 的中点。
(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明)；(2)如果点M 、N 分别在线段AB 、AC 上移动，在移动中保持AN ＝BM ，请判断△OMN 的形状，并证明你的结论。
6、如图，△ABC 为等边三角形，延长BC 到D ，延长BA 到E ，AE=BD ， 连结EC 、ED ，求证：CE=DE7、如图，等腰三角形ABC 中，AB ＝AC ，∠A ＝90°，BD 平分∠ABC ，DE ⊥BC 且BC ＝10，求△DCE 的周长。
8．如图所示，已知AD 是∠BAC 的平分线，EF 垂直平分AD 交BC 的延长线于点F ，交AD 于点E ，连接AF ，求证：∠B=∠CAF 。
A B COM N9．如图所示，AD 是∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，垂足分别为E ，F ，连接EF ，EF 与AD 交于点G ，求证：AD 垂直平分EF 。
C10．如图所示，已知点D 是等边三角形ABC 的边BC 延长线上的一点，∠EBC=∠DAC ，CE ∥AB 。
(完整版)初中经典几何证明练习题集(含答案解析),推荐文档
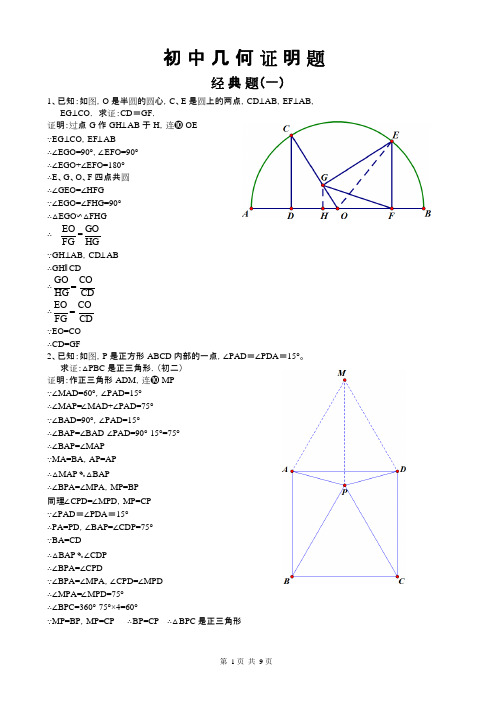
初 中 几 何 证 明 题经 典 题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．证明：过点 G 作 GH ⊥AB 于 H ，连➓ OE ∵EG ⊥CO ，EF ⊥AB ∴∠EGO=90°，∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴EO = GOFG HG∵GH ⊥AB ，CD ⊥AB ∴GH ∥CD∴GO = COHG CD ∴ EO = CO FG CD∵EO=CO ∴CD=GF2、已知：如图，P 是正方形 ABCD 内部的一点，∠PAD ＝∠PDA ＝15°。
求证：△PBC 是正三角形．（初二） 证明：作正三角形 ADM ，连➓ MP ∵∠MAD=60°，∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°，∠PAD=15° ∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ，AP=AP ∴△MAP ➴△BAP ∴∠BPA=∠MPA ，MP=BP 同理∠CPD=∠MPD ，MP=CP ∵∠PAD ＝∠PDA ＝15° ∴PA=PD ，∠BAP=∠CDP=75° ∵BA=CD∴△BAP ➴∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ，∠CPD=∠MPD ∴∠MPA=∠MPD=75° ∴∠BPC=360°-75°×4=60°∵MP=BP ，MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知：如图，在四边形 ABCD 中，AD ＝BC ，M 、N 分别是 AB 、CD 的中点，AD 、BC 的延长线交 MN 于E 、F ．求证：∠DEN ＝∠F ．证明:连➓ AC ，取 AC 的中点 G,连➓ NG 、MG ∵CN=DN ，CG=DG ∴GN ∥AD ，GN= 1AD2∴∠DEN=∠GNM ∵AM=BM ，AG=CG ∴GM ∥BC ，GM= 1 BC2∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经 典 题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且 OM ⊥BC 于 M ． （1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）证明：（1）延长 AD 交圆于 F ，连➓ BF ，过点 O 作 OG ⊥AD 于 G ∵OG ⊥AF ∴AG=FG ⌒ ⌒ AB AB ∵ =∴∠F=∠ACB又 AD ⊥BC ，BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又 AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH ）=2GD 又 AD ⊥BC ，OM ⊥BC ，OG ⊥AD ∴四边形 OMDG 是矩形 ∴OM=GD ∴AH=2OM （2）连➓ OB 、OC ∵∠BAC=60∴∠BOC=120° ∵OB=OC ，OM ⊥BC∴∠BOM= 1∠BOC=60°∴∠OBM=30°2∴BO=2OM由（1）知 AH=2OM ∴AH=BO=AO2、设 MN 是圆 O 外一条直线，过 O 作 OA ⊥MN 于 A ，自 A 引圆的两条割线交圆 O 于 B 、C 及 D 、E ，连➓ CD 并延长交 MN 于 Q ，连➓ EB 并延长交 MN 于 P. 求证：AP ＝AQ ．证明：作点 E 关于 AG 的对称点 F ，连➓ AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ，PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ3、设 MN 是圆 O 的弦，过 MN 的中点 A 任作两弦 BC 、DE ，设 CD 、EB 分别交 MN 于 P 、Q ． 求证：AP ＝AQ ．（初二）证明：作 OF ⊥CD 于 F ，OG ⊥BE 于 G ，连➓ OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ，∠E=∠C ∴△ABE ∽△ADC ∴AB = BE = 2BG =BGAD DC 2FD DF∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN ， ∴OA ⊥MN又 OG ⊥BE ，∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°，OA=OA ∴△OAQ ➴△OAP ∴AP=AQ4、如图,分别以△ABC 的 AB 和 AC 为一边,在△ABC 的外侧作正方形 ABFG 和正方形 ACDE ，点 O 是 DF 的中点，OP ⊥BC求证：BC=2OP （初二）证明：分别过 F 、A 、D 作直线 BC 的垂线，垂足分别是 L 、M 、N ∵OF=OD ，DN ∥OP ∥FL ∴PN=PL∴OP 是✲形 DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB ∴△BFL ➴△ABM ∴FL=BM同理△AMC ➴△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经 典 题（三）1、如图，四边形 ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与 CD 相交于 F ． 求证：CE ＝CF ．（初二）证明：连➓ BD 交 AC 于 O 。
初二数学几何证明题
1.在△ABC中，AB=AC，D在AB上，E在AC的延长线上，且BD=CE，线段DE交BC 于点F，说明：DF=EF。
2.已知：在正方形ABCD中，M是AB的中点，E是AB延长线上的一点，MN垂直DM于点M，且交∠CBE的平分线于点N.
（1）求证：MD＝MN.
（2）若将上述条件中的“M是AB的中点”改为“M是AB上任意一点”其余条件不变，则（1）的结论还成立吗？如果成立，请证明，如果不成立，请说明理由。
3.。
如图，点E,F分别是菱形ABCD的边CD和CB延长线上的点，且DE=BF，求证∠E=∠F。
4，如图，在△ABC中，D,E,F,分别为边AB,BC,CA,的中点，求证四边形DECF为平行四边形。
5.如图，在菱形ABCD中，∠DAB=60度，过点C作CE垂直AC且与AB的延长线交与点E，求证四边形AECD是等腰梯形？
6.如图，已知平行四边形ABCD中，对角线AC,BD，相交与点0，E是BD延长线上的点，且三角形ACE是等边三角形。
1.求证四边形ABCD是菱形。
2.若∠AED=2∠EAD，求证四边形ABCD是正方形。
7.已知正方形ABCD中，角EAF=45度，F点在CD边上，E点在BC边上。
求证：EF=BE+DF。
（完整版）八年级几何证明题集锦及解答值得收藏
（完整版）八年级几何证明题集锦及解答值得收藏八年级几何全等证明题归纳1.如图，梯形ABCD中，AD∥BC，∠DCB=45°，BD⊥CD．过点C作CE⊥AB 于E，交对角线BD于F，点G为BC中点，连接EG、AF．求证：CF=AB+AF．证明：在线段CF上截取CH=BA，连接DH，∵BD⊥CD，BE⊥CE，∴∠EBF+∠EFB=90°，∠DFC+∠DCF=90°，∵∠EFB=∠DFC，∴∠EBF=∠DCF，∵DB=CD，BA=CH，∴△ABD≌△HCD，∴AD=DH，∠ADB=∠HDC，∵AD∥BC，∴∠ADB=∠DBC=45°，∴∠HDC=45°，∴∠HDB=∠BDC—∠HDC=45°，∴∠ADB=∠HDB，∵AD=HD，DF=DF，∴△ADF≌△HDF，∴AF=HF，∴CF=CH+HF=AB+AF，∴CF=AB+AF．2.如图，ABCD为正方形，E为BC边上一点，且AE=DE，AE与对角线BD交于点F，连接CF，交ED于点G．判断CF与ED的位置关系，并说明理由．解：垂直．理由：∵四边形ABCD为正方形，∴∠ABD=∠CBD，AB=BC，∵BF=BF，∴△ABF≌△CBF，∴∠BAF=∠BCF，∵在RT△ABE和△DCE中，AE=DE，AB=DC，∴RT△ABE≌△DCE，∴∠BAE=∠CDE，∴∠BCF=∠CDE，∵∠CDE+∠DEC=90°，∴∠BCF+∠DEC=90°，∴DE⊥CF．3.如图，在直角梯形ABCD中，AD∥BC，∠A＝90o，AB＝AD，DE⊥CD交AB于E，DF平分∠CDE交BC于F，连接EF．证DA明：CF＝EF解：EB F C过D作DG⊥BC于G．由已知可得四边形ABGD为正方形，∵DE⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG，∴∠ADE=∠GDC．又∵∠A=∠DGC且AD=GD，∴△ADE≌△GDC，∴DE=DC且AE=GC．在△EDF和△CDF中∠EDF=∠CDF，DE=DC，DF为公共边，∴△EDF ≌△CDF，∴EF=CF4.已知：在⊿ABC中，∠A=900，AB=AC，D是AC的中点，AE⊥BD，AE延长线交BC于F，求证：∠ADB=∠FDC。
初二几何证明题(精选多篇)
初二几何证明题(精选多篇)第一篇：初二几何证明题1如图，在△abc中，d是bc边上的一点，e是ad的中点，过点a作bc的平行线交be的延长线于f，且af=dccf．（1）求证：d是bc的中点；（2）如果ab=acadcf 的形状，并证明你的结论aeb第二篇：初二几何证明题初二几何证明题1.已知：如图，在△abc中，ad⊥bc，垂足为d，be⊥ac，垂足为e。
m为ab中点，联结me,md、ed求证：角emd=2角dac证明：∵m为ab边的中点，ad⊥bc，be⊥ac，∴md=me=ma=mb(斜边上的中线=斜边的一半)∴△med为等腰三角形∵me=ma∴∠mae=∠mea∴∠bme=2∠mae∵md=ma∴∠mad=∠mda,∴∠bmd=2∠mad,∵∠emd=∠bme-∠bmd=2∠mae-2∠mad=2∠dac2.如图，已知四边形abcd中，ad=bc,e、f分别是ab、cd中点，ad、bc的延长线与ef的延长线交于点h、d求证：∠ahe=∠bge证明：连接ac，作em‖ad交ac于m，连接mf.如下图：∵e是cd的中点，且em‖ad，∴em=1/2ad，m是ac的中点，又因为f是ab的中点∴mf‖bc，且mf=1/2bc.∵ad=bc，∴em=mf，三角形mef为等腰三角形，即∠mef=∠mfe.∵em‖ah，∴∠mef=∠ahf∵fm‖bg，∴∠mfe=∠bgf∴∠ahf=∠bgf.3.写出“等腰三角形两底角的平分线相等”的逆命题，并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知bd平分∠abc,ce平分∠acb,bd=ce,求证:ab=ac证明:bd平分∠abc==>be/ae=bc/ac==>be/ab=bc/(bc+ac)==>be=ab*bc/(bc+ac)同理:cd=ac*bc/(bc+ab)假设ab≠ac,不妨设ab>ac.....(*)ab>ac==>bc+acac*bc==>ab*ab/(bc+ac)>ac*bc/(bc+ab)==>be>cdab>ac==>∠acb>∠abc∠bec=∠a+∠acb/2,∠bdc=∠a+∠abc/2==>∠bec>∠bdc过b作ce平行线,过c作ab平行线,交于f,连df则becf为平行四边形==>∠bfc=∠bec>∠bdc (1)bf=ce=bd==>∠bdf=∠bfdcf=be>cd==>∠cdf>∠cfd==>∠bdf+∠cdf>∠bfd+∠cfd==>∠bdc>∠bfc (2)(1)(2)矛盾,从而假设(*)不成立所以ab=ac。
初二上几何证明题100题专题训练
初二上几何证明题100题专题训练3.如图, OP 平分∠ AOB, 且 OA=OB( 1)写出图中三对你认为全等的三角形( 注：不添加任何辅助线) ；(2)从( 1)中任选一个结论停止证明.5. 如图,在△ ABC中 , AB=AD=DC∠BAD=28 ,求∠ B和∠C的度数.6. 如图 , B 、D 、 E 在同一直线上, A B=AC,AD=AE, 求证: BD=CE.7. 写出下列命题的抗命题 ，并断定抗命题的真假. 如果是真命题 ，请给予证明； ? 如果是假命题 ，请举反例说明.命题：有双方上的高相等的三角形是等腰三角形.8. 如图 ,在△ ABC中,∠ ACB=9ω , D 是 AC 上的一点 , 且 AD=BC; DE□AC于 D, ∠EAB=9@ .求证: AB=AE.9. 如图 , 等边△ ABO中 , 点 P 在△ ABQ内 ,点 Q 在△ ABC外 , B, P,Q 三点在一条直线上 ,且∠ ABP∠ACQ BP=CQ,问△ APQ是什么形状的三角形?试证明你的结论.1. 如图 , 已知△ EAB≌△ DCE, AB, EC分别是两个三角形的最长边 ,∠ A=∠C= 35° ,∠ CDE= 100° , ∠ DEB= 10° ,求∠ AEC的度数 .2. 如图,点 E 、 A 、B 、 F 在同一条直线上 ,AD 与 BC 交于点 O,已知∠ CAE=∠DBF,AC=BD求证:∠ C=∠D4. 已知: 如图, AB= AC,DB= DC, AD 的延长线交 BC 于点 E,求证: BE= EC.10. 如图, △ ABC中,∠ C=90° , AB的中垂线 DE交 AB于 E, 交 BC于 D,若 AB=13, AC=5, 则△ ACD的周长为多少?11.如图所示, AC⊥BC, AD⊥BD, AD= BC, CE⊥AB, DF⊥AB,垂足分别是 E , F , 求证: CE= DF.12. 如图 ,已知△ ABC中, ∠ ACB= 90° , AC= BC, BE⊥CE, 垂足为E, AD⊥CE,垂足为D.(1) 断定直线 BE与 AD的位置关系是 ;BE与 AD之间的间隔是线段的长；(2) 若 AD= 6 cm, BE=2 cm,求 BE与 AD之间的间隔及 AB的长.13. 如图,已知△ ABQ △ ADE均为等边三角形 ,点 D是 BC延长线上一点 , 保持 CE,求证: BD=CE证:? BG3AD15. 如图 ,四边形 ABCD中,∠ DAB=∠ BCD=90° , M为 BD 中点 , N 为 AC中点 , 求证: MNL AC.16、已知: 如图所示 , 在△ ABC中,∠ ABC=45° , CD⊥AB于点 D, BE平分∠ ABC,且 BE⊥AC于点 E,与 CD相交于点 F , H是BC边的中点,毗连 DH与 BE相交于点G. ( 1)求证: BF=AC; ( 2)求证: DG=DF.18. 如图所示 ,在△ ABC中 , AB=AC, BD⊥AC于点 D,CE⊥AB于点 E, BD, CE 相交于 F.求证: AF 平分∠ BAC.19. 如 图 所 示 , △ ABC≌ △ ADE, 且 ∠ CAD=10° , ∠ B=∠ D=25° , ∠ EAB=120 , 求 ∠DFB和∠DGB的度数.20. 已知:如图,在△ ABC中 , AB=AC, 点 D 在边 BC 上, DE⊥AB, DF⊥ AC, 且 DE=DF,求证:△ ABD≌△ ACD( 1)求证:△ BDE是等腰三角形(2)若 ∠A=36° ,求∠ ADE的度数 .17. 如图 , 点 B, D 在射线 AM 上 ,点 C,上 , 且 AB=BC=CD=D,E已知∠ EDM=84 ,求∠ A的度数. E 在射线 AN21. 如图, 一张直角三角形的纸片 ABC, 两直角边 AC=6cm, BC=8cm 现将直角边 AC 沿直线 AD 折叠 ，使它落在斜边AB ,且 AC 与 AE 重合, 求 CD 的长.22. 已知: 如图, 在△ ABC中 , AB=AC, BD 平分∠ABC, E是底边 BC 的延长线上的一点且 CD=CE.23. 如图,在△ ABC中,AB=CB,∠ABC= ,AB 延长线上一点,点 E 在 BC 边上且 BE=BD, 保持 AE DE DC.25. 已知: 如图,在 ABC 中, CABC , 点 D 为边 AC 上的一个动点 , 延长 AB 至 E, 使 BE=CD, 保持 DE, 交 BC 于点P.( 1) DP 与 PE 相等吗?请说明来由 .说明来由)26. 如图, C 为线段 BD 上一点(不与点 B, D 重合) ,在 BD 同侧分别作正三角形 ABC 和正三角形 CDE, AD 与 BE 交于一点 F , AD 与 CE 交于点 H, BE 与 AC 交于点 G.(1)求证: BE=AD;(2)求∠ AFG的度数;( 3)求证: CG=CH27. 已知:如图 , 在△ ABC中 , CD⊥AB, CD=BD BF平分∠ DBC, 与 CD, AC 分别交与点 E 、 点 F , 且 DA=DE H 是 BC 边的中点 , 保持 DH 与 BE 相交于点 G. ( 1)求证:△ EBD≌△ ACD;(2)求证:点 G 在∠DCB的平分线上(3)试探索 CF 、 GF 和 BG 之间的等量关系 ，并证明你的结论28. 如图 ,在在△ ABC 中, AB=CB,∠ ABC=90° , F 为 AB 延长线上一单, 点 E 在 BC 上,且 AE=CF.(1)求证: Rt ABERt CBF(2)若∠ CAE=30° ,求∠ ACF的度数(1) 求证 : AE=CD;(2)若∠ CAE=30 ,求∠ BDC的度数.24. 如图,在□ABC中,点 D 在 AC 边上, DB=BC, 点 E 是CD 的中点,点 F 是 AB 的中点 ，则可以得到结论： [EF 12AB ],请说明来由 .29. 如图,△ ACD和△ BCE都是等腰直角三角形,∠ ACD∠BCE90° , AE交 DC于 F , BD分别交 CE, AE于点 G H 试猜测线段 AE和 BD数量关系 ,并说明来由 .30. 如图,在△ ABC中 , AB= AC, AD和 BE是高 , 它们相交于点 H,且 AE= BE.求证: AH = 2BD.A31. 如图,在 ABC中, B32, C48,AD BC于点D,AE平分 BAC32. 如图所示 , 在△ ABC中 ,已知点 D, E, F 分别是 BC, AD, CE的中点 , 且[S ABC]=4,则SBEF的值为多少 .33. 如图, ABC中,ACB90 ,CDBA于D,AE平分DDBAC交CD于E,交BC于，求证：CEF是等腰三角形.34. 如图,在四边形 ABCD中, Dq|AB, BD 平分∠ ADC, ∠ADC=60 ,过点 B作BE⊥DC, 过点 A作AF⊥BD, 垂足分4 BEF的形状,并说明来由 .35. 如图,已知Rt△ ABC≌Rt△ ADE, ∠ABG∠ADE 90° , BC与 DE相交于点 F , 毗连 CD, EB(1) 图中还有几对全等三角形，请你一一罗列； (不必证明)(2) 如图2, 当点回在AC 延长线时, 求证: APO 12ACB BAC ; (3) 如图 3,当点在边 AC 所示位置时 ,请直接写出 APO 与ACB,BAC 之间的数量关系式.(2) 求证 : CF= EF36. 在ABC 中,BO 平分ABC,点向为直线AC 上一动点, PO BO 于点.(1) 如图 1,,当□ABC 40。
初二上几何证明题100题专题训练
C A B C DE P 图 ⑴八年级上册几何题专题训练100题1、 已知：在⊿ABC 中，∠A=900，AB=AC ，在BC 上任取一点P ，作PQ ∥AB 交AC 于Q ，作PR ∥CA 交BA 于R ，D 是BC的中点，求证：⊿RDQ 是等腰直角三角形。
B2、 已知：在⊿ABC 中，∠A=900，AB=AC ，D 是AC 的中点，AE ⊥BD ，AE 延长线交BC 于F ，求证：∠ADB=∠FDC 。
3、 已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ，求证：MA ⊥NA 。
4、已知：如图(1)，在△ABC 中，BP 、CP 分别平分∠ABC 和∠ACB ，DE 过点P 交AB 于D ，交AC 于E ，且DE ∥BC ．求证：DE －DB=EC ．5、在Rt△ABC中，AB＝AC，∠BAC=90°，O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明)；(2)如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。
6、如图，△ABC为等边三角形，延长BC到D，延长BA到E，AE=BD，连结EC、ED，求证：CE=DE7、如图，等腰三角形ABC中，AB＝AC，∠A＝90°，BD平分∠ABC，DE⊥BC且BC＝10，求△DCE的周长。
8. 如图，已知△EAB≌△DCE，AB，EC分别是两个三角形的最长边，∠A＝∠C＝35°，∠CDE＝100°，∠DEB＝10°，求∠AEC的度数．ABCOMNOEDCB 9. 如图,点E、A、B、F在同一条直线上,AD与BC交于点O, 已知∠CAE=∠DBF,AC=BD.求证：∠C=∠D10.如图，OP平分∠AOB，且OA=OB．（1）写出图中三对你认为全等的三角形（注：不添加任何辅助线）；（2）从（1）中任选一个结论进行证明．11. 已知：如图，AB＝AC，DB＝DC，AD的延长线交BC于点E，求证：BE＝EC。
(完整版)八年级几何证明题集锦及解答值得收藏
八年级几何全等证明题归纳1.如图，梯形ABCD中，AD∥BC，∠DCB=45°，BD⊥CD．过点C作CE⊥AB 于E，交对角线BD于F，点G为BC中点，连接EG、AF．求证：CF=AB+AF．证明：在线段CF上截取CH=BA，连接DH，∵BD⊥CD，BE⊥CE，∴∠EBF+∠EFB=90°，∠DFC+∠DCF=90°，∵∠EFB=∠DFC，∴∠EBF=∠DCF，∵DB=CD，BA=CH，∴△ABD≌△HCD，∴AD=DH，∠ADB=∠HDC，∵AD∥BC，∴∠ADB=∠DBC=45°，∴∠HDC=45°，∴∠HDB=∠BDC—∠HDC=45°，∴∠ADB=∠HDB，∵AD=HD，DF=DF，∴△ADF≌△HDF，∴AF=HF，∴CF=CH+HF=AB+AF，∴CF=AB+AF．2.如图，ABCD为正方形，E为BC边上一点，且AE=DE，AE与对角线BD交于点F，连接CF，交ED于点G．判断CF与ED的位置关系，并说明理由．解：垂直．理由：∵四边形ABCD为正方形，∴∠ABD=∠CBD，AB=BC，∵BF=BF，∴△ABF≌△CBF，∴∠BAF=∠BCF，∵在RT△ABE和△DCE中，AE=DE，AB=DC，∴RT△ABE≌△DCE，∴∠BAE=∠CDE，∴∠BCF=∠CDE，∵∠CDE+∠DEC=90°，∴∠BCF+∠DEC=90°，∴DE⊥CF．3.如图，在直角梯形ABCD中，AD∥BC，∠A＝90º，AB＝AD，DE⊥CD交AB于E，DF平分∠CDE交BC于F，连接EF．证DA明：CF＝EF解：EB F C过D作DG⊥BC于G．由已知可得四边形ABGD为正方形，∵DE⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG，∴∠ADE=∠GDC．又∵∠A=∠DGC且AD=GD，∴△ADE≌△GDC，∴DE=DC且AE=GC．在△EDF和△CDF中∠EDF=∠CDF，DE=DC，DF为公共边，∴△EDF ≌△CDF，∴EF=CF4.已知：在⊿ABC中，∠A=900，AB=AC，D是AC的中点，AE⊥BD，AE延长线交BC于F，求证：∠ADB=∠FDC。
初二上几何证明题100题专业题材训练
八年级上册几何题专题训练100题1、已知：在△ABC 中，ZA=90°,AB=AC,在BC上任取一点P,作PQ//AB交AC于Q,作PR//CA交BA于R,D是BC的中点，求证：△RDQ是等腰直角三角形。
2、已知：在△ABC 中，ZA=90°,AB=AC,D是AC 的中点，AE工BD,AE延长线交BC于F,求证：ZADB=ZFDC。
3、已知：在△ABC 中BD 、CE是高，在BD 、CE或其延长线上分别截取BM=AC 、CN=AB,求证：MA上NA。
4、已知：如图(1),在△ABC 中，BP 、CP分别平分ZABC和ZACB,DE过点P交AB于D,交AC于E,且DE//BC .求证：DE - DB=EC .5、在Rt△ABC 中，AB=AC,ZBAC=90°,0为BC 的中点。
(1)写出点0到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);(2)如果点M、N分别在线段AB、AC上移动，在移动中保持AN=BM,请判断△OMN的形状，并证明你的结论。
6、如图，△ABC为等边三角形，延长BC到D,延长BA到E,AE=BD,连结EC 、ED,求证：CE=DE7、如图，等腰三角形ABC 中，AB=AC,ZA=90°,BD平分ZABC,DE工BC且BC=10,求△DCE 的周长。
8. 如图，已知△EAB丝△DCE,AB,EC分别是两个三角形的最长边，ZA=ZC=35°,ZCDE=100°,ZDEB=10°, 求ZAEC的度数.9. 如图，点E 、A 、B 、F在同一条直线上，AD与BC交于点0, 已知ZCAE=ZDBF,AC=BD.求证：ZC=ZD10.如图，OP平分ZAOB,且0A=0B.(1)写出图中三对你认为全等的三角形(注；不添加任何辅助线);(2)从(1)中任选一个结论进行证明.11. 已知：如图，AB=AC,DB=DC,AD 的延长线交BC于点E,求证；BE=EC。
初中经典几何证明练习题(含答案)
（2）若∠BAC＝600，求证：AH＝AO．（初二）
证明：（1）延长AD交圆于F，连接BF，过点O作OG⊥AD于G
∵OG⊥AF
∴AG=FG
∵ =
∴∠F=∠ACB
又AD⊥BC，BE⊥AC
∴∠BHD+∠DBH=90°
∠ACB+∠DBH=90°
∴∠ACB=∠BHD
∴∠F=∠BHD
又∠GAE=∠GAF∴∠PAG+∠GAE=∠QAG+∠GAF
即∠PAE=∠QAF
∵E、F、C、D四点共圆
∴∠AEF+∠FCQ=180°
∵EF⊥AG，PQ⊥AG
∴EF∥PQ
∴∠PAF=∠AFE
∵AF=AE
∴∠AFE=∠AEF
∴∠AEF=∠PAF
∵∠PAF+∠QAF=180°
∴∠FCQ=∠QAF
∴F、C、A、Q四点共圆
则△BPQ是正三角形
∴∠BQP=60°，PQ=PB=3
在△PQC中，PQ=4，CQ=AP=3，PC=5
∴△PQC是直角三角形
∴∠PQC=90°
∴∠BQC=∠BQP+∠PQC=60°+90°=150°
∴∠APB=∠BQC=150°
2、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．
求证：∠PAB＝∠PCB．（初二）
∴∠AFQ=∠ACQ
又∠AEP=∠ACQ
∴∠AFQ=∠AEP
3、设MN是圆O的弦，过MN的中点A任作两弦BC、DE，设CD、EB分别交MN于P、Q．
求证：AP＝AQ．（初二）
证明：作OF⊥CD于F，OG⊥BE于G，连接OP、OQ、OA、AF、AG
初中经典几何证明练习题集(含答案解析)
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．证明：过点G 作GH ⊥AB 于H ，连接OE ∵EG ⊥CO ，EF ⊥AB∴∠EGO=90°，∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ，CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知：如图，P 是正方形ABCD 内部的一点，∠PAD ＝∠PDA ＝15°。
求证：△PBC 是正三角形．（初二） 证明：作正三角形ADM ，连接MP ∵∠MAD=60°，∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°，∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ，AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ，MP=BP 同理∠CPD=∠MPD ，MP=CP ∵∠PAD ＝∠PDA ＝15°∴PA=PD ，∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ，∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ，MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ． 求证：∠DEN ＝∠F ．证明:连接AC ，取AC 的中点G,连接NG 、MG ∵CN=DN ，CG=DG ∴GN ∥AD ，GN=21AD ∴∠DEN=∠GNM ∵AM=BM ，AG=CG ∴GM ∥BC ，GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ． （1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二） 证明：（1）延长AD 交圆于F ，连接BF ，过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ，BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH ）=2GD 又AD ⊥BC ，OM ⊥BC ，OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM （2）连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ，OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由（1）知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线，过O 作OA ⊥MN 于A ，自A 引圆的两条割线交圆O 于B 、C 及D 、E ，连接CD 并延长交MN 于Q ，连接EB 并延长交MN 于P. 求证：AP ＝AQ ．证明：作点E 关于AG 的对称点F ，连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ，PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）证明：作OF ⊥CD 于F ，OG ⊥BE 于G ，连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ，∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN ， ∴OA ⊥MN 又OG ⊥BE ，∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°，OA=OA ∴△OAQ ≌△OAP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ，点O 是DF 的中点，OP ⊥BC求证：BC=2OP （初二）证明：分别过F 、A 、D 作直线BC 的垂线，垂足分别是L 、M 、N ∵OF=OD ，DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ． 求证：CE ＝CF ．（初二）证明：连接BD 交AC 于O 。
经典初二数学几何证明题
A DB C E最新中考数学几何证明（平行四边形，菱形矩形正方形）经典1．（本题10分）如图，已知： ABCD 中，BCD ∠的平分线CE 交边AD 于E ，ABC∠的平分线BG 交CE 于F ，交AD 于G ．求证：AE DG =．2．在正方形ABCD 中，AC 为对角线，E 为AC 上一点，连接EB 、ED ． （1）求证：△BEC ≌△DEC ；（2）延长BE 交AD 于F ，当∠BED =120°时，求∠EFD 的度数．3.（本小题满分5分）如图，在△ABC 中，点D 、E 分别在边AC 、AB 上，BD=CE ，∠DBC=∠求证：AB=AC 。
4.（本小题满分7分）如图，在△ABC 中，AB=AC ，D 为BC 中点，四边形ABDE 是平行四边形。
是矩形。
5．(10分)在□ABCD 中，AC 是一条对角线，∠B ＝∠CAD ，延长BC 至点接DE ．(1)求证：四边形ABED 是等腰梯形．(2)若AB ＝AD ＝4，求梯形ABED 的面积． 6、（本小题7分）如图，点A 、E 、B 、D 在同一条直线上，AE=DB ，AC=DF ，AC ∥DF. 请探索BC 与EF 有怎样的位置关系？并说明理由。
7.如图，已知BE ⊥AD ，CF ⊥AD ，且BE ＝CF ．（1） 请你判断AD 是△ABC 的中线还是角平分线？请证明你的结论．（2）连接BF 、CE ，若四边形BFCE 是菱形，则△ABC 添加一个条件 ▲8．（广东广州，18，9分）如图5，在等腰梯形ABCD 中，AD ∥BC ．求证：∠A ＋∠C ＝180°10.如图，C 是线段AB 的中点，CD 平分∠ACE ，CE 平分∠BCD ，CD=CE ．(1)求证：△ACD≌△BCE；(2)若∠D=50°，求∠B 的度数． 11．(本题6分)如图，在△ABC 中，D 是BC 边上的点（不与B ，C 重合），F ，E 分别是AD 及其延长线上的点，CF ∥BE. 请你添加一个条件，使△BDE ≌△CDF (不再添加其它线段，不再标注或使用其他字母)，并给出证明．（1）你添加的条件是： ▲ ；（2）证明：.12.（8分）如图，请在下列四个关系中，选出两个恰当．．．．的关系作为条件，推出四边形ABCD 是平行四边形，并予以证明．（写出一种即可）B A CBD FE(第11题)B CDE F A 关系：①AD ∥BC ，②CD AB =，③C A ∠=∠，④︒=∠+∠180C B ． 已知：在四边形ABCD 中， ， ； 求证：四边形ABCD 是平行四边形． 13．(本题满分9分)将三角形纸片ABC (AB ＞AC )沿过点A 的直线折叠，使得AC 落在AB 边上，折痕为AD ，展平纸片，如图(1)；再次折叠该三角形纸片，使得点A 与点D 重合，折痕为EF ，再次展平后连接DE 、DF ，如图2，证明：四边形AEDF 是菱形．14．如图10，已知ABC ADE Rt △≌Rt △，90ABC ADE ∠=∠=°，BC 与DE 相交于点F ，连接CD ，EB ．（1）图中还有几对全等三角形，请你一一列举. （2）求证：.CFEF =15．（本小题满分8分） 如图，已知：点B 、F 、C 、E 在一条直线上，FB =CE ，AC =DF ．能否由上面的已知条件证明AB ∥ED ？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件．．．．．．．，添加到已知条件中，使AB ∥ED 成立，并给出证明． 供选择的三个条件（请从其中选择一个）： ①AB =ED ； ②BC =EF ； ③∠ACB =∠DFE ． 16．(6分)已知：正方形ABCD 中，E 、F 分别是边CD 、DA 上的点，且CE =DF ，AE 与BF 交于点M ． （1）求证：△ABF ≌△DAE ；（2）找出图中与△ABM 相似的所有三角形（不添加任何辅助线）．17．(6分)如图，在△ABC 中，BC ＞AC ，点D 在BC 上，且DC ＝AC ，∠ACB 的平分线CF 交AD 于点F ．点E 是AB 的中点，连接EF ．(1)求证：EF ∥BC ；(2)若△ABD 的面积是6，求四边形BDFE 的面积．18．（本小题满分8分）如图，四边形ABCD 的对角线AC 、DB 相交于点O ，现给出如下三个条件：AB DC AC DB OBC OCB ==∠=∠①②③.（1）请你再增加一个．．条件：________，使得四边形ABCD 为矩形（不添加其它字母和辅助线，只填一个即可，不必证明）；（2）请你从①②③中选择两个条件________（用序号表示，只填一种AB CD(1) (2)A B DC C DB F A E图10 ABDEFC（第15题）A EB F CDA G EB CF D 情况），使得AOB DOC △≌△，并加以证明.19．如图，在直角梯形ABCD 中，AD ∥BC ，∠A ＝90º，AB ＝AD ＝6，DE ⊥CD 交AB 于E ，DF 平分∠CDE 交BC 于F ，连接EF ． (1)证明：CF ＝EF ； (2)当tan ∠ADE ＝ 13时，求EF 的长．20．(10分)如图，在□ABCD 中，E 、F 分别是边AB 、CD的中点，AG ∥BD 交CB 的延长线于点G ． (1)求证：△ADE ∽≌△CBF ；(2)若四边形BEDF 是菱形，则四边形AGBD 是什么特 殊四边形？请说明你的理由．21．（本题满分8分）如图，在ABCD 中，点E 、F 是对角线AC 上两点，且CF AE =．求证：FDE EBF =∠．22.（8分）如图，四边形ABCD 是矩形，∠EDC=∠CAB ， ∠DEC=90°。
(完整版)初中数学几何证明经典试题(含答案)
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ； （2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）E经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ． 求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）D经典难题（五）1、 设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ， 求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．APCBACBPDEDCB AA CBPD经典题（一）1.如下图做GH⊥AB,连接EO。
初中经典几何证明练习题(含答案)
初中几何证明题【1】经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．证明：过点G 作GH ⊥AB 于H ，连接OE ∵EG ⊥CO ，EF ⊥AB∴∠EGO=90°，∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG∴FG EO =HG GO∵GH ⊥AB ，CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CD COFG EO = ∵EO=CO ∴CD=GF2、已知：如图，P 是正方形ABCD 内部的一点，∠PAD ＝∠PDA ＝15°。
求证：△PBC 是正三角形．（初二） 证明：作正三角形ADM ，连接MP ∵∠MAD=60°，∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°，∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ，AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ，MP=BP 同理∠CPD=∠MPD ，MP=CP ∵∠PAD ＝∠PDA ＝15°∴PA=PD ，∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ，∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ，MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ． 求证：∠DEN ＝∠F ．证明:连接AC ，取AC 的中点G,连接NG 、MG ∵CN=DN ，CG=DG∴GN ∥AD ，GN=21AD∴∠DEN=∠GNM ∵AM=BM ，AG=CG∴GM ∥BC ，GM=21BC∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ． （1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）证明：（1）延长AD 交圆于F ，连接BF ，过点O 作OG ⊥AD 于G∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ，BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH ）=2GD 又AD ⊥BC ，OM ⊥BC ，OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM （2）连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ，OM ⊥BC∴∠BOM=21∠BOC=60°∴∠OBM=30°∴BO=2OM由（1）知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线，过O 作OA ⊥MN 于A ，自A 引圆的两条割线交圆O 于B 、C 及D 、E ，连接CD 并延长交MN 于Q ，连接EB 并延长交MN 于P. 求证：AP ＝AQ ．证明：作点E 关于AG 的对称点F ，连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ，PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）证明：作OF ⊥CD 于F ，OG ⊥BE 于G ，连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ，∠E=∠C ∴△ABE ∽△ADC∴DF BGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN ， ∴OA ⊥MN 又OG ⊥BE ，∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ又∠OAQ=∠OAP=90°，OA=OA ∴△OAQ ≌△OAP ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ，点O 是DF 的中点，OP ⊥BC 求证：BC=2OP （初二）证明：分别过F 、A 、D 作直线BC 的垂线，垂足分别是L 、M 、N ∵OF=OD ，DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ． 求证：CE ＝CF ．（初二）证明：连接BD 交AC 于O 。
八年级几何证明题集锦及解答值得收藏
For personal use only in study and research; not for commercial use八年级几何全等证明题归纳1.如图，梯形ABCD中，AD∥BC，∠DCB=45°，BD⊥CD．过点C作CE⊥AB 于E，交对角线BD于F，点G为BC中点，连接EG、AF．求证：CF=AB+AF．证明：在线段CF上截取CH=BA，连接DH，∵BD⊥CD，BE⊥CE，∴∠EBF+∠EFB=90°，∠DFC+∠DCF=90°，∵∠EFB=∠DFC，∴∠EBF=∠DCF，∵DB=CD，BA=CH，∴△ABD≌△HCD，∴AD=DH，∠ADB=∠HDC，∵AD∥BC，∴∠ADB=∠DBC=45°，∴∠HDC=45°，∴∠HDB=∠BDC—∠HDC=45°，∴∠ADB=∠HDB，∵AD=HD，DF=DF，∴△ADF≌△HDF，∴AF=HF，∴CF=CH+HF=AB+AF，∴CF=AB+AF．2.如图，ABCD为正方形，E为BC边上一点，且AE=DE，AE与对角线BD交于点F，连接CF，交ED于点G．判断CF与ED的位置关系，并说明理由．解：垂直．理由：∵四边形ABCD为正方形，∴∠ABD=∠CBD，AB=BC，∵BF=BF，∴△ABF≌△CBF，∴∠BAF=∠BCF，∵在RT△ABE和△DCE中，AE=DE，AB=DC，∴RT△ABE≌△DCE，∴∠BAE=∠CDE ，∴∠BCF=∠CDE ，∵∠CDE+∠DEC=90°，∴∠BCF+∠DEC=90°，∴DE ⊥CF ．3.如图，在直角梯形ABCD 中，AD ∥BC ，∠A ＝90º，AB ＝AD ，DE ⊥CD 交AB 于E ，DF 平分∠CDE 交BC 于F ，连接EF ．证明：CF ＝EF解：过D 作DG ⊥BC 于G ．由已知可得四边形ABGD 为正方形， ∵DE ⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG ，∴∠ADE=∠GDC ．又∵∠A=∠DGC 且AD=GD ，∴△ADE ≌△GDC ，∴DE=DC 且AE=GC ．在△EDF 和△CDF 中∠EDF=∠CDF ，DE=DC ，DF 为公共边，∴△EDF≌△CDF ，∴EF=CF4.已知：在⊿ABC 中，∠A=900，A EB F CDAB=AC，D是AC的中点，AE⊥BD，AE延长线交BC于F，求证：∠ADB=∠FDC。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
28.（本小题满分10分）
如图，在矩形ABCD 中，AB=8，AD=6，点P 、Q 分别是AB 边和CD 边上的动点，点P 从点A 向点B 运动，点Q 从点C 向点D 运动，且保持AP-CQ 。
设AP=x （1）当PQ ∥AD 时，求x 的值；
（2）当线段PQ 的垂直平分线与BC 边相交时，求x 的取值范围；
（3）当线段PQ 的垂直平分线与BC 相交时，设交点为E ，连接EP 、EQ ，设△EPQ 的面积为S ，求S 关于x 的函数关系式，并写出S 的取值范围。
21．（本小题满分9分）
如图，直线y x m =+与双曲线k
y x
=相交于A （2，1）、B 两点． （1）求m 及k 的值；
（2）不解关于x 、y 的方程组,
,y x m k
y x =+⎧⎪
⎨=⎪⎩
直接写出点B 的坐标； （3）直线24y x m =-+经过点B 吗？请说明理由．
A B
O
x
y （第21题）
2 1 2
3 －3 －1 －2 1
3 －3
－1
－2
28．（2010江苏淮安，28，12分）如题28(a)图，在平面直角坐标系中，点A坐标为(12，0)，点B坐标为(6，8)，点C为OB的中点，点D从点O出发，沿△OAB的三边按逆时针方向以2个单位长度／秒的速度运动一周．
(1)点C坐标是( ，)，当点D运动8.5秒时所在位置的坐标是( ，)；
(2)设点D运动的时间为t秒，试用含t的代数式表示△OCD的面积S,并指出t为何值
时，S最大；
(3)点E在线段AB上以同样速度由点A向点B运动，如题28(b)图，若点E与点D同时
出发，问在运动5秒钟内，以点D，A，E为顶点的三角形何时与△OCD相似(只考虑以点A．O为对应顶点的情况)：
题28(a)图题28(b)图
（10江苏南京）21.（7分）如图，四边形ABCD的对角线AC、BD相较于点O，△ABC≌△BAD。
求证：（1）OA=OB；（2）AB∥CD.
（10江苏南京）28.（8分）如图，正方形ABCD的边长是2，M是AD的中点，点E从点A
出发，沿AB运动到点B停止，连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC 于点G，连结EG、FG。
（1）设AE=x时，△EGF的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；
（2）P是MG的中点，请直接写出点P的运动路线的长。
23．(本题8分)如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上， CE ∥BF，连接BE、CF．
(1)求证：△BDF≌△CDE；
(2)若AB=AC，求证：四边形BFCE是菱形．
27．(本题8分)如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点M处，点C落在点N处，MN与CD交于点P，连接EP．
(1)如图②，若M为AD边的中点，
①,△AEM的周长=_____cm；
②求证：EP=AE+DP；
(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．
27．（本题满分12分）如图1所示，在直角梯形ABCD中，AD∥BC，AB⊥BC，∠DCB=75º，以CD为一边的等边△DCE的另一顶点E在腰AB上．
（1）求∠AED的度数；
（2）求证：AB=BC；
（3）如图2所示，若F为线段CD上一点，∠FBC=30º．
求DF
FC的值．
A
B C
D
E
F
图2
A
B C
D
E
图1。