几何证明题集-R10-2
初三几何证明练习题和答案

初三几何证明练习题和答案几何证明是初中数学中的重要内容,通过练习不同类型的几何证明题,可以帮助学生理解并掌握几何证明的基本方法与技巧。
本文将为大家提供一些初三几何证明的练习题和答案,希望对同学们的学习有所帮助。
1. 题目:已知ABCD是平行四边形,证明∠ABC + ∠ADC = 180°。
证明:解:连接AC,根据平行四边形的性质可知∠ADC = ∠ACB,所以要证明∠ABC + ∠ADC = 180°,只需证明∠ABC + ∠ACB = 180°。
由角的内外(对顶、同旁)定理可知∠ACB + ∠ABC = 180°,即∠ABC + ∠ACB = 180°。
所以,∠ABC + ∠ADC = 180°得证。
2. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = 5cm,BC= 12cm,证明AB = 13cm。
证明:解:根据勾股定理可得AB² = AC² + BC²。
代入已知条件,即可得AB² = 5² + 12² = 25 + 144 = 169。
开方可得AB = 13cm。
所以,AB = 13cm得证。
3. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = BC,证明∠ABC = 45°。
证明:解:连接AB,根据等腰直角三角形的性质可知∠ACB = ∠CAB。
所以,∠ABC = 180° - ∠ACB - ∠CAB = 180° - ∠ACB - ∠ACB = 180° - 2∠ACB。
由于∠ACB = 90°,代入得∠ABC = 180° - 2 × 90° = 0°。
所以,∠ABC = 0°,即∠ABC = 45°得证。
4. 题目:已知ABCD是一个平行四边形,E为AD的中点,证明BE平分∠CBD。
数学几何证明专项练习题

数学几何证明专项练习题1. 已知三角形ABC中,角A等于60度,边AB等于AC,求证:三角形ABC是等边三角形。
2. 若四边形ABCD是平行四边形,且角A等于90度,求证:四边形ABCD是矩形。
3. 已知线段AB和线段CD相交于点O,且AO等于CO,BO等于DO,求证:AB平行于CD。
4. 在三角形ABC中,若角BAC等于角BCA,且AB等于AC,求证:三角形ABC是等腰三角形。
5. 已知直角三角形ABC中,角C等于90度,且AB是斜边,求证:AB的平方等于AC的平方加BC的平方。
6. 若线段DE是三角形ABC的中线,且D是AB的中点,E是AC的中点,求证:DE平行于BC且DE等于BC的一半。
7. 已知圆心O的半径为r,点P在圆上,求证:OP等于r。
8. 在三角形ABC中,若角A等于角B,且AC等于BC,求证:三角形ABC是等腰三角形。
9. 若点P在直线AB上,且AP等于PB,求证:P是AB的中点。
10. 已知三角形ABC中,角A等于角C,且AB等于AC,求证:三角形ABC是等腰三角形。
11. 若四边形ABCD是梯形,且AB平行于CD,求证:角A加角D等于180度。
12. 在三角形ABC中,若角A等于角B等于角C,求证:三角形ABC是等边三角形。
13. 已知线段AB和线段CD相交于点O,且AO等于CO,BO等于DO,求证:AB等于CD。
14. 若三角形ABC中,角A等于90度,且AB等于AC,求证:三角形ABC是等腰直角三角形。
15. 在三角形ABC中,若AB等于AC,且角B等于角C,求证:三角形ABC是等腰三角形。
16. 已知圆心O的半径为r,点P在圆上,且OP垂直于圆的切线,求证:OP等于r。
17. 若线段DE是三角形ABC的高,且D是BC的中点,求证:DE垂直于BC。
18. 在三角形ABC中,若角A等于角B,且AB等于AC,求证:三角形ABC是等腰三角形。
19. 已知线段AB和线段CD相交于点O,且AO等于CO,BO等于DO,求证:AB垂直于CD。
高考数学几何证明题型题库

高考数学几何证明题型题库题目一:平行四边形性质的证明证明:平行四边形的对角线互相平分解析:首先,我们知道平行四边形的对角线是互相等长的。
因此,我们可以将平行四边形ABCD的对角线AC和BD相交于点O。
现在,我们需要证明AC和BD互相平分。
证明过程如下:1. 过点O分别作直线DE和FG分别平行于AB和CD,DE和FG 与AC交于点E和G,分别与BD交于点F和H。
2. 由于ABCD为平行四边形,所以AB∥CD,而DE∥AB,所以DE∥CD。
同理,FG∥CD。
3. 由平行线的性质可知,∠DAO = ∠OCD,而∠OAC = ∠OCB,所以∠EAO = ∠FDO。
4. 又因为平行四边形的对角线等长,所以AO = CO,BO = DO。
根据等边三角形的性质可知,AO = EO,DO = FO。
5. 综上所述,AO = EO = CO,BO = FO = DO,即AC和BD互相平分。
题目二:三角形角平分线的性质的证明证明:三角形内角的角平分线互相相交于同一点,且与对边相交点构成的线段等长。
解析:给定三角形ABC,角A的角平分线与BC相交于点D,角B的角平分线与AC相交于点E,角C的角平分线与AB相交于点F。
我们需要证明角平分线AD、BE和CF相交于同一点,且AD = BD = CD。
证明过程如下:1. 过点A分别作直线DE和DF分别平分∠BAC和∠BDC,DE与BC交于点E,DF与BC交于点F。
2. 由于∠BAF和∠BDF是角B的平分线,所以∠BAF = ∠FAD = α,∠BDF = ∠FDC = β。
3. 将直线DE延长与直线AB相交于点G,直线DF延长与直线BC相交于点H。
4. 在△ABG和△DFH中,根据内角和定理可得∠ABG + ∠BAG = 180°,∠DHG + ∠FDH = 180°。
5. ∠ABG和∠BDF互补,∠BAG和∠FDH互补,所以∠FAD +∠FDC = ∠BAF + ∠BDF = 180°。
(完整版)精选初中数学几何证明经典试题(含答案)
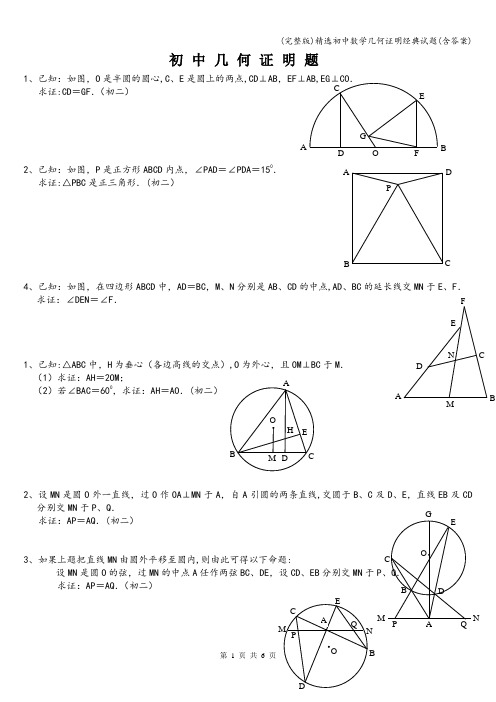
初中几何证明题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 求证:AP =AQ .(初二)APCDB AFGCEB O D NF 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC,且CE =CA,直线EC求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 求证:PA =PF .(初二)4、如图,PC 切圆O于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)D经典题(一)1。
初中数学几何证明试题(含答案)
第 6 页 共 15 页
4.如下图连接 AC 并取其中点 Q,连接 QN 和 QM,所以可得∠QMF=∠F,∠QNM=∠
DEN 和∠QMN=∠QNM,从而得出∠DEN=∠F。
经 典 题(二)
1.(1)延长 AD 到 F 连 BF,做 OG⊥AF,
又∠F=∠ACB=∠BHD, 可得 BH=BF,从而可得 HD=DF, 又 AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM
BE AD
= ,即 AD•BC=BE•AC,
①
BC AC
又∠ACB=∠DCE,可得△ABC∽△DEC,既得
AB = DE ,即 AB•CD=DE•AC,
②
AC DC
由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证。
第 11 页 共 15 页
4.过 D 作 AQ⊥AE
(2)连接 OB,OC,既得∠BOC=1200,
从而可得∠BOM=600, 所以可得 OB=2OM=AH=AO, 得证。
第 7 页 共 15 页
3.作 OF⊥CD,OG⊥BE,连接 OP,OA,OF,AF,OG,AG,OQ。 由于 AD = AC = CD = 2FD = FD , AB AE BE 2BG BG
(2)过 P 点作 BC 的平行线交 AB,AC 与点 D,F。
由于∠APD>∠ATP=∠ADP,
推出 AD>AP
①
又 BP+DP>BP
②
和 PF+FC>PC
③
又 DF=AF
④
由①②③④可得:最大 L< 2 ;
八年级几何证明题集锦及解答值得收藏

For personal use only in study and research; not for commercial use八年级几何全等证明题归纳1.如图,梯形ABCD中,AD∥BC,∠DCB=45°,BD⊥CD.过点C作CE⊥AB 于E,交对角线BD于F,点G为BC中点,连接EG、AF.求证:CF=AB+AF.证明:在线段CF上截取CH=BA,连接DH,∵BD⊥CD,BE⊥CE,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°,∵∠EFB=∠DFC,∴∠EBF=∠DCF,∵DB=CD,BA=CH,∴△ABD≌△HCD,∴AD=DH,∠ADB=∠HDC,∵AD∥BC,∴∠ADB=∠DBC=45°,∴∠HDC=45°,∴∠HDB=∠BDC—∠HDC=45°,∴∠ADB=∠HDB,∵AD=HD,DF=DF,∴△ADF≌△HDF,∴AF=HF,∴CF=CH+HF=AB+AF,∴CF=AB+AF.2.如图,ABCD为正方形,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.解:垂直.理由:∵四边形ABCD为正方形,∴∠ABD=∠CBD,AB=BC,∵BF=BF,∴△ABF≌△CBF,∴∠BAF=∠BCF,∵在RT△ABE和△DCE中,AE=DE,AB=DC,∴RT△ABE≌△DCE,∴∠BAE=∠CDE ,∴∠BCF=∠CDE ,∵∠CDE+∠DEC=90°,∴∠BCF+∠DEC=90°,∴DE ⊥CF .3.如图,在直角梯形ABCD 中,AD ∥BC ,∠A =90º,AB =AD ,DE ⊥CD 交AB 于E ,DF 平分∠CDE 交BC 于F ,连接EF .证明:CF =EF解:过D 作DG ⊥BC 于G .由已知可得四边形ABGD 为正方形, ∵DE ⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG ,∴∠ADE=∠GDC .又∵∠A=∠DGC 且AD=GD ,∴△ADE ≌△GDC ,∴DE=DC 且AE=GC .在△EDF 和△CDF 中∠EDF=∠CDF ,DE=DC ,DF 为公共边,∴△EDF≌△CDF ,∴EF=CF4.已知:在⊿ABC 中,∠A=900,A EB F CDAB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB=∠FDC。
初二几何证明题(完整版)

初二几何证明题初二几何证明题..bf=e=bd== ∠bdf=∠bfdf=be d== ∠df ∠fd== ∠bdf+∠df ∠bfd+∠fd== ∠bd ∠bf矛盾,从而假设不成立所以ab=a。
2、两地角的平分线相等,为等腰三角形作三角形ab,d,be为角,b的角平分线,交于ab,be.两平分线交点为o连结de,即de平行b,所以三角形do与ob相似。
有dod=eoeb,又eb=d所以do=eo,三角形ob为等腰又角ode=ob=oed=ob又因为be和d是叫平分线,所以容易得出角=角b,即ab为等腰。
第三篇:初二几何证明题28.(本小题满分10分)如图,在矩形abd中,ab=8,ad=6,点p、q分别是ab边和d边上的动点,点p从点a向点b运动,点q从点向点d运动,且保持ap-q。
设ap=x(1)当pq∥ad时,求x的值;(2)当线段pq的垂直平分线与b边相交时,求x的取值范围;(3)当线段pq的垂直平分线与b相交时,设交点为e,连接ep、eq,设△epq的面积为s,求s关于x的函数关系式,并写出s的取值范围。
21.(本小题满分9分)如图,直线?x?m与双曲线?(1)求m及k的值; k相交于a(2,1)、b两点. x??x?m,?(2)不解关于x、的方程组?直接写出点b的坐标; k?,?x?(3)直线2x?4m经过点b吗?请说明理由.(第21题)28.(201X江苏淮安,28,12分)如题28图,在平面直角坐标系中,点a坐标为,点b坐标为,点为ob的中点,点d从点o出发,沿△oab的三边按逆时针方向以2个单位长度/秒的速度运动一周.点坐标是),当点d运动8.5秒时所在位置的坐标是,);设点d运动的时间为t秒,试用含t的代数式表示△od的面积s,并指出t为何值时,s最大;点e在线段ab上以同样速度由点a向点b运动,如题28图,若点e与点d同时出发,问在运动5秒钟内,以点d,a,e为顶点的三角形何时与△od相似:题28图题28图(10江苏南京)21.(7分)如图,四边形abd的对角线a、bd相较于点o,△ab≌△bad。
几何证明题十道

几何证明题十道1. 证明等腰三角形两边相等假设三角形ABC是等腰三角形,即AB=AC。
连接线段BC,延长AC至D,使得AD=BC。
则有三角形ABD和ABC是全等的,因为它们有AA条件(两个角相等,一个对边相等)。
因此,BD=AB,又因为AB=AC,所以BD=AC,即等腰三角形两边相等。
2. 证明垂直平分线上的点到两侧线段距离相等假设线段AB是一条线段,CD是它的垂直平分线,且P是CD上的一点。
连接PA和PB。
则有三角形PAC和PBC是全等的,因为它们有SAS条件(两个角相等,一个边相等)。
因此,PA=PB,即点P到线段AB的距离相等。
3. 证明三角形内角和为180度以三角形ABC为例。
连接线段AC和BC。
则有三角形ABC 和三角形ACB有一个公共角ABC,因此三角形ABC和三角形ACB的对边之和AB+BC相等。
又因为角ACB和角ABC 互补,所以它们的和为180度。
因此,三角形ABC的内角和为180度。
4. 证明平行直线的交角相等设有两条平行线L1和L2,分别与第三线L3相交于点A和点B。
连接线段AB。
则由三角形ABA'和ABB'的角度之和为180度,可以得出角A'AB=角B'BA。
由平行线的定义,可知角A'AB=角BAC,角B'BA=角CBA。
因此,角BAC=角CBA,即平行直线的交角相等。
5. 证明垂线段上的点到直线的距离最短假设有一条直线L和一条点A到直线L的垂线段BC。
连接线段AB和AC。
则有三角形ABC和三角形ACD的角度之和为180度,可以得出角ACD=90度。
因此,直线L和线段BC垂直,且BC是直线L上离点A最近的点。
因此,垂线段上的点到直线的距离最短。
6. 证明平行四边形对角线互相平分假设ABCD是一个平行四边形,AC和BD是它的对角线。
连接线段AD和BC。
则由三角形ABD和三角形ACD的角度之和为180度,可以得出角BAC=角CDA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
217 1kAA、。又作一平面2,使它们相距
2kAA
①。
(1)完备性:在探求已知:111POkAA,222KOkAA
1122,PP。 (2)纯粹性:在平面1上任取一点1P,连1APD,1BPC。
AB,
ABCD作AA于A,11PO于1O,则11PO1RAA。
又111:POAAkDC()DCAB, :()()DCDCABDCDCAB,因而DCDC。 由此可见,1P合条件即平面1上任一点合条件。 同理可证得平面2上任一点2P合条件。 由(1)、(2)所证得:1P点的轨迹是一平面1,2P点的轨迹是平面2。 讨论:若ABCD,则2P点无轨迹。在理论上,2在无穷远处。 注:若是ABCD,则题解中1P与2P性质应互换。 4.45 设形状和大小固定的三角形的顶点在一平面上变动,底边在另一给定平行
平面上变动,求重心的轨迹。 探求:平面平面,A, A点到平面的距离AA一定(就是与的距离)。 设AGBCM(G为重心)则:1:3MGMA,因此G点到平面的距离GG 13AA(定长)。
由此可见,G点的轨迹很可能是一平行平面、的平面,平面与的距离等于平面、
间的距离 13。
证明:在平面、之间,作一平面且距离为3
d,d是与的距离。
(1)完备性:AA作于A,GGG于。 :1:3MGMA,:1:3GGAA。
①若2k是负值,则表示2P与A在的异则。
题图 4-45 218
因此33AAdGG,G平面。 (2)纯粹性:设BCa,CAb,ABc。
在平面上任取一点G,过G在平面上任一线段BC,使13GBGCa。在平面 上求一点A,使23BAC,23CAb。连AGM,ABB,
ACC,则BMC、、共线,BCBC
。
13BGGCa,
12BMMCa。
又::1:3MGMAGGAA, G为ABC的重心。
再2BCBMa,32CAACb,32ABABc, G是合条件的ABC的重心。 因此平面,上任取一点符合条件。 综合(1)、(2)得:G点的轨迹就是一平面。 讨论:设ABC的BC边上高为h,与相距d,(1)若h≥d,则轨迹是一平面; (2)hd,则无轨迹。
注:假若题中不限定哪一边为底,则G的轨迹一般可能是三个平面。 4.46 求形状和大小固定的三角形的顶点的轨迹,已知它的底在一定平面上变
动,重心在与之平行的另一定平面上变动。 题设:点G是形状和大小固定的ABC的重心,平面、是两定平行平面,BC在上变动,G在上变动。 探求:连AGBCI,作AAA于,GGG于。设平面、相距为d,则GGd(定长)。
::1:3GGAAIGIA, 33AAGGd(定长)。
题图 4-46 219
由此可见,A点的轨迹可能是与在同一侧且平行于的一平面,在相距为3d。 证明:(1)完备性:在探求中已知A平面。 (2)纯粹性:在平面上任取一点0A,作0()AAB与的交线B,球
0()AAC与的交线C,又作一线段00BC,使00BCBC且0BB
,0CC。
000ABC则≌ABC,又易得00AB0C的重心0G
在平面上,由此可见,平面上任取
一点0A符合条件。
根据(1)、(2)知,A点的轨迹是平面 讨论:设G到BC的距离为h。 (1)若h≥d,则轨迹是一平面;
(2)若hd,则无轨迹。
注:如题中不限定哪一边为底,则A点的轨迹一般可能是三个平行平面。 4.47 由直径为d的定球面上的定点A任引一弦AP,并在其延长线上取点M使
APAMd,求点M的轨迹。 探求:设定球为()2dO,连()2dAOOB球,则
ABd。 2:APAMAB,因此AP::ABABAM。
PABBAM, PABBAM∽。 因而90MBABPA。 MBBA。 由此可知:M点的轨迹也许就是垂直AB于B的一平面。 证明:(1)完备性:在探求中,已见M平面。 (2)纯粹性:在平面上任取一点M,连MA交球()
2d
O于P,又连BPBM、,则
ABBM(AB,AM得),90APB。 在PAB和BAM中有90MBABPA,PABBAM。 因此PABBAM∽。 ::APABABAM故22APAMABd,因知M点满足条件。 由(1)、(2)得,M点的轨迹就是平面。
题图 4-47 220
4.48 在已知平面上求动点的轨迹,使该点到平面外两定点的连线与这平面成等角。 题设:AB、是平面外两定点,AAa
于A,BB于B,P是上的动点且满足APABPB。 求:P点的轨迹。 探求:APABPB,AAP 90BBP,
AAPBBP∽。 因此::PAPBAABBk常数。 此时由平面几何轨迹定理可知:P的轨迹很可能就是在平面上至两定点AB距离成定比k的动点轨迹u。 证明:(1)完备性:在探求中已知::PAPBk。 Pu。 (2)纯粹性:在u上任取一点P,连PAPAPBPB、、、,则:PAPBR,即
::PAPBAABB。 90AAPBBP又,
AAPBBP∽,因而APABPB。 P点符合条件。 由(1)、(2)知,P点的轨迹是u。 讨论:(1)当AB时,轨迹是u; (2)当AB时,轨迹是一点。
注:u的作法:(1)若AABB则u就是以AB的定比内外分点连线为直径的阿氏圆。(2)若AABB,则u就是AB,的中垂线。 4.49 在空间给定两点AB、及正数r,试求满足下列条件之一的点M的轨迹:
(1)MArMB;
(2)MArMB。
探求:我们分三种情形来分析:1r和1r。 ①当1r时
题图 4-48 题图 4-49-1 221
1MArMB时,M点的轨迹是AB的中垂面, 当1MArMMB,点的轨迹就是平面的A所以的一侧。 当1MArMB,M点的轨迹就是平面的B所以的一侧。 证明:(略) ②当1r时
首先看一下,MArMB时,M点的轨迹是什么。由平面几何中间波罗尼斯轨迹定理知:M在过AB的任一平面上的轨迹是以AB的比为r的内外分点CD、连线为直径的圆()OR,由此可想见M点的轨迹应该是球()OR。 现在我们已经知道当MArMB时,M点的轨迹是球()OK。 当MArMB时,容易得知:M点的轨
迹就是球()OR将空间分成内外两部分中的A所在的这一部分。 当MArMB时,容易得知M点的轨迹就是球面将空间分成内外两部分中的B所在的这一部分。 证明:(1)当MArMB时,(题图4-49-3和题图4-49-4)。
题图 4-49-2 题图 4-49-3 题图 4-49-4 222
①完备性:在AB上求两点C、D使CAMACBMB,DAMADBMB,则由阿波罗尼斯轨迹可知:M在以CD,为直径的球O()R上, MArMB,CADACBDB,
CACACBCB,DADADBDB
。
因此,C在线段AC内,D在BD延长线(若1r或1r)。 CD与A在线段DC内或CD与A在CD线段外因而球'O(R)与A在球()OR内或外(1r或1r)。 又M球()OR, 故M与A在球()OR内或外(11rr或)。 ②纯粹性:为了证明的方便,改设1r,如果1r时能证得,那么仿此可证得
1r时也成立。 在球()OR内任取一点M。连MAMB、,显然MArMB;假若MAMBr,则可得M
在球()OR外。故只有MArMB,因此得球()OR内任一点M是符合条件。 同理可证得当1r时,球()OR外任一点。符合条件。 总结①、②两步证明,得M点的轨迹是球面()OR将空间分成的内、外两部分中A所在的这一部分。 (2)当MArMB时(题图4-49-1和题图4-49-2)仿(1)可证得M的轨迹是球
面()OR将空间分成的内外两部分中,B所在的这一部分。 4.50 试求所设两个或三个球成相等视角的点的轨迹。
题设:P是一动点,它对所设二球1122()()OROR、或三球1O12233()()()ROROR、、视角相等。 求:P点的轨迹。 探求:我们先分析对二个球视角相等的点的情形。设11APB22APB,
112222
APBAPB。
