各年级学霸解答世界上最难简单几何题都未算出答案

初中数学几何题(超难)及答案分析-七年级几何题超难

1、已知：如图，O 是半圆的圆心, 求证：CD= GF .（初三）2、已知：如图，P 是正方形 ABCD 内点, ∠ PAD =∠ PDA = 15°.求证：△ PBC 是正三角形.（初二）4、已知：如图，在四边形 ABCD 中，AD = BC , M 、N 分别是 AB 、CD 的中点，AD 、BCMN 于 E 、F . 求证：∠ DEN = ∠ F .5、已知：△ ABC 中，H 为垂心（各边高线的交点）（1）求证：AH = 2OM ;（2）若∠ BAC = 60°,求证：AH = AO .（初三）几何经典难题HE3、如图，已知四边形 ABCD 、A I B I C I D I 都是正方形，A 2、B 2、C ?、D ?分别是AA 1>BB 1、 CC 1∖ DD I的中点.求证：四边形 A 2B 2C 2D 2是正方形.的延长线交BC（初二）,O 为外心，且OM 丄BC 于M .6、设MN 是圆O 外一直线，过 O 作OA 丄MN 于A ,自A 引圆的两条直线，交圆于 B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证：AP = AQ .（初三）7、如果上题把直线 MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过 MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .8如图，分别以厶 ABC 的AC 和BC 为一边，在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ,点P是EF 的中点. 求证：点P 到边AB 的距离等于AB 的一半.（初二）求证：AP = AQ .（初三）GN9、如图，四边形 ABCD 为正方形, 求证：CE = CF .（初二）11、设P 是正方形 ABCD 一边BC 上的任求证：PA = PF .（初二）12、如图，PC 切圆O 于C , AC 为圆的直径,证：AB = DC , BC = AD .（初三）求证: AE = AF .（初二）An10、如图，四边形 ABCD 为正方形, AF 与直线PO 相交于B 、D .求DE //AC ,DE //ACEPEF 为圆的割线,AE、13、已知：△ ABC 是正三角形，P 是三角形内一点, 求：∠APB 的度数.（初二）15、设ABCD 为圆内接凸四边形，求证： AB ∙ CD + AD ∙ BC = AC ∙ BD .（初三）16、平行四边形 ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ,且AE = CF .求证：∠ DPA =∠ DPC .（初二）14、设P 是平行四边形 ABCD 内部的一点，且∠ 求证：∠ PAB = ∠ PCB .（初二） PBA = ∠PDA .17、设P 是边长为1的正△ ABC 内任一点, L = PA + PB + PC ,求证:'≤ L V 2.18、已知：P是边长为1的正方形ABCD内的一点，求PA + PB + PC的最小值.19、P为正方形ABCD内的一点，并且PA = a, PB= 2a, PC = 3a,求正方形的边长.AD20、如图，△ ABC 中，∠ ABC =∠ ACB = 80°,=20°,求∠ BED的度数.D、E 分别是AB、AC 上的点，∠ DCA = 300,∠ EBA解答1•如下图做GH丄AB,连接E0。

初中数学几何题(超难)及答案分析-七年级几何题超难之欧阳学创编

几何经典难题1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初三）2、已知：如图，P 是正方形ABCD 内点， ∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二） 4、已知：如图，在四边形ABCD分别是AB 、CD 的中点，AD 于E 、F ．求证：∠DEN ＝∠F ．5、已知：△ABC 中，H 为垂心（各边高线的交点），O为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；AP CDBAFG CE BODD 2C 2B 2 A 2D 1C 1B 1CBDAA 1B（2）若∠BAC＝600，求证：AH＝AO．（初三）6、设MN是圆O外一直线，过O A引圆的两条直线，交圆于B、C CD分别交MN于P、Q．求证：AP＝AQ．（初三）7、如果上题把直线MN以下命题：设MN是圆O的弦，过BC、DE，设CD、EB分别交求证：AP＝AQ．（初三8、如图，分别以△ABC的AC和的外侧作正方形ACDE和正方形中点．求证：点P到边AB的距离等于9、如图，四边形ABCDAE与CD相交于F．求证：CE＝CF10、如图，四边形CA，直线EC交求证：AE＝AF11、设PAP，CF平分∠AE 17＋PC 18PA＋19、P且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．20、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300BED 的度数．解答1.如下图做GH ⊥AB,连接EO 以∠GFH ＝∠OEG,即△GHF ∽△OGE,可得EO GF =GOGH=CD=GF 得证。

初中数学几何题(超难)及答案分析

几何经典难题1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初三）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．5、已知：△ABC 中，H 为垂心（各边高线的交点）（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初三）A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初三）7、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初三）8、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．N9、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）10、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．11、设P 是正方形ABCD 一边BC求证：PA ＝PF ．（初二）12、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）E E P13、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）14、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）15、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）16、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．17、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．AP C B PA D CB CB D AFPDECBA18、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．19、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．20、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．CCD解答1.如下图做GH ⊥AB,连接EO 。

初中最难几何题

初中最难几何题引言几何学是数学中的一个重要分支，它研究空间和形状的性质。

在初中阶段，学生开始接触几何学的基本概念和定理，逐渐掌握几何图形的性质和相关计算方法。

然而，有些几何题目对初中生来说可能会显得比较困难。

本文将介绍一些初中阶段最难的几何题目，并对其解题思路进行详细解析。

1. 三角形面积计算问题三角形面积计算是几何学中的基本问题之一，通常使用面积公式S=1/2×底边长×高来求解。

然而，有些题目会给出一些条件，使得计算面积变得相对困难。

题目示例：在平面直角坐标系中，已知三角形的三个顶点坐标分别为A（0，0），B（3，0），C（0，4），求三角形ABC的面积。

解题思路：通过给出的三个顶点坐标，我们可以确定三角形ABC的边长。

首先，计算AB的长度，使用勾股定理可以得到AB=3。

同样地，计算AC和BC的长度分别为AC=4和BC=5。

接下来，我们可以使用海伦公式来计算三角形ABC的面积。

海伦公式是一个计算三角形面积的公式，它可以通过三角形的边长来计算。

海伦公式的表达式为：S=√p(p−a)(p−b)(p−c)其中，p为三角形的半周长，a，b，c分别为三角形的三边长。

对于本题，我们可以计算半周长p=（AB+AC+BC）/2=（3+4+5）/2=6。

代入海伦公式，可以得到S=6。

因此，三角形ABC的面积为6平方单位。

2. 圆的面积和周长问题圆是几何学中的一个重要概念，它由一个中心点和半径组成。

计算圆的面积和周长是初中阶段的基本问题之一。

然而，有些题目给出的条件较为复杂，使得计算圆的面积和周长变得困难。

题目示例：已知一个圆的周长为10π，求其面积。

解题思路：首先，我们知道圆的周长公式为C=2πr，其中C为周长，r为半径。

根据题目给出的条件，我们可以得到2πr=10π，即r=5。

接下来，我们可以使用圆的面积公式S=πr²来计算圆的面积。

代入半径r=5，可以得到S=π×5²=25π。

平面几何经典难的题目及解答

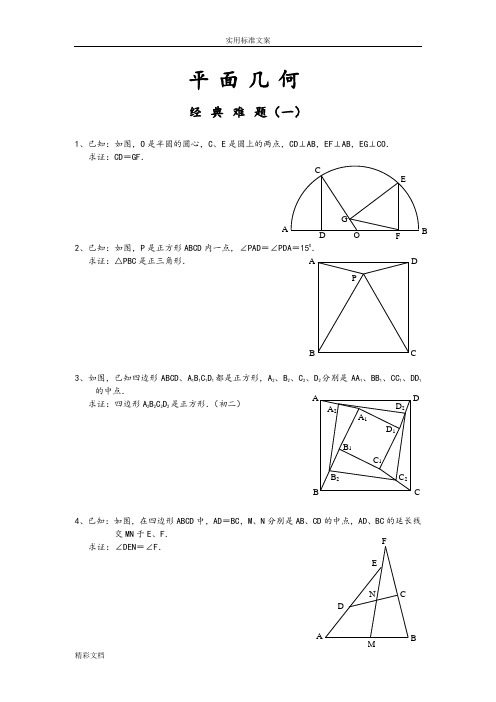
平面几何经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．2、已知：如图，P 是正方形ABCD 内一点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A PC D B AFG C EBOD D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF经典难题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．4、平行四边形ABCD 中，设E 、F分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC＝200，求∠BED 的度数．经典难题解答:经典难题（一）1.如下图做GH⊥AB,连接EO。

初中最难几何题

初中最难几何题初中数学中的几何题是许多学生感到头疼的难题。

它们需要学生掌握几何图形的性质和运用相关定理解决问题。

在初中阶段，有几个几何题目被普遍认为是较为困难的。

本文将介绍初中数学中的一些最难的几何题目，并探讨解题的思路和方法。

一、三角形内角和问题在初中数学中，三角形内角和问题是一个经典的难题。

根据欧几里得几何知识，三角形的三个内角和等于180度。

然而，要求学生证明这一定理并解决相关问题却并不容易。

为了解决这个问题，学生需要灵活运用几何知识和相关定理，例如直角三角形的特性以及同位角等概念。

二、相似三角形问题相似三角形也是初中数学中的难点之一。

相似三角形的性质包括对应角相等和对应边成比例。

学生需要找出相似三角形的特点，并利用这些特点解决相关问题。

解决相似三角形问题的关键在于观察和分析图形，并将观察到的规律应用到具体问题中。

三、圆的性质问题圆的性质问题是初中数学中的另一个难点，尤其是与切线和弦的关系。

学生需要掌握切线与半径的垂直关系以及弦的性质，进而解决与圆相关的几何问题。

这需要学生的观察力和逻辑思维能力，同时需要运用到直角三角形和相似三角形等知识。

四、平行线与角关系问题平行线与角关系是初中几何中的经典难题。

学生需要理解平行线之间的角对应关系，例如错角、同旁内角、同旁外角等。

此外，学生还需要掌握平行线与横线交错时所形成的各类角的性质。

解决这类问题需要学生有较强的空间想象力和逻辑推理能力。

综上所述，初中数学中的几何题目是许多学生认为较为困难的题目。

其中涉及到三角形内角和、相似三角形、圆的性质以及平行线与角关系等问题。

解决这些难题需要学生对几何图形的性质和相关定理有较深入的理解，并能够运用到具体问题中。

通过不断练习和探索，学生可以逐渐掌握解决这些难题的思路和方法，提升数学能力。

因此，在初中数学学习过程中，学生应克服困难，勇敢面对这些最难的几何题目，不断提高自己的数学水平。

初中几何难题(初二超难几何)

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．AP C DB AFG C EBOD D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）E1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）。

初中数学几何题(超难)与答案分析

几何经典难题1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初三）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．5、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初三）A P C D BA FG CE B O D D 2 C 2 B 2 A 2D 1C 1B 1C B DA A 1 A N FE CD MB· ADHE M CBOPCGFBQA DE 6、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初三）7、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初三）8、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）9、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．· GA O DB E CQ P NM ·O QP B DEC NM · A求证：CE ＝CF ．（初二）10、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）11、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）12、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB＝DC ，BC ＝AD ．（初三）13、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．A F D E CB E DA CB F DF E P C B AO D BF AEC P求：∠APB 的度数．（初二）14、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）15、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）16、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）17、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．18、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．AP C B PA D CB CB D AFPDECBA19、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．20、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．解答ACBPDEDCB A1.如下图做GH ⊥AB,连接EO 。