2016-2017学年湖北省荆州中学高一(上)数学期末试卷 及解析(文科)
荆州中学2016-2017学年度高一上学期期末考试数学卷及答案

荆州中学2016〜20仃学年度上学期符合题目要求的)数),已知工厂组装第 4件产品所用的时间为 30分钟,工人组装第 m 件产品所用的时间为 15分钟,则m =() A. 49B. 25C. 16D. 96.已知函数f (x )是定义在闭区间[-a,a ](a 0)上的奇函数,F (x^ f (x ) 1,则F (x )的最大值 与最小值的和为( ) A.4B. 2C. 1D. 07.已知 x 0是函数 f (x )二 e x ,2x-4 的零点,若 x< (-1,X 0),X 2・ (x 0,2),则()、选择题(本大题共12小题,每小题5分,共 60分•在每小题给出的四个选项中,只有一项是1.若点(a,9)在函数y =3x 的图象上,则a tan 二6 的值为()A. 0,3B.3C. 1D. ,32.若 sin 用 > 0 且 tan : ::的终边在() A. 第一象限 B.第二象限C.第一象限或第三象限D.第三象 限或第四象限3.若2弧度的圆心角所对的弦长为4sin1 cm ,则这个圆心角所夹的扇形的面积是()2 A. 2cm B. 4 cm 22 C.2 二 cm 2D. 4- cm4.已知a, b 均为单位向量,它们的夹角为 Ji二,那么a+3b 等于()B. C.4D. .135.据统计,一名工人组装第X 件某产品所用的时间(单位:分钟)f (x )二c丁,xvm,'X(m, c 为常c,x— mA. f(X1) :: 0, f(X2)::0B. f(X1):: 0, f(X2)n8.已知函数g (x )二sin (・,x • )(x ・=R,u ,0)的最小正周期为 二,为了得到函数f (x )二cos^x的4图象,只要将y = g (x )的图象(9.设a =(七,m ), b = (4,3),若a 与b 的夹角是钝角,则实数 m 的范围是()的最大值为()y =丄的图象与函数 y =3sin 二x (- 1乞X 空1)的图象所有交点的横坐标与纵坐标的和等于 xx 2 + x +1 x 》0 f (x)=,-,若 f (sin 工" sin : sin r -1) = —1,[2X +1,X £0,f(cos-:>,cos : cosr 1)=3,贝U cos(-:> “) cos(: - r)的值为()A.向左平移一个单位长度8C. 向左平移一个单位长度4B.向右平移二个单位长度8TTD.向右平移—个单位长度4A. m 4B.m :C. m -4 且 m = 94D.m ::4 且 m—9 410.用min{ a设 f (x)二 min{2X ,x 2,10-XK x_ 0),则 f (x)A. 7B. 6C. 5D. 411.函数A. 4B. 2C. 1D. 012.已知函数A. 1B. 2C. -1D. — 2、填空题(本大题共4小题,每小题5分,共20 分)213- (25).5(¥)3■ (0-1) °-¥(二)0飞2©5 二 _________________________ -9 64 91 a a14 .已知sin a = —,2 兀v3兀,那么sin —+ cos—= ・3 2 2y = f (x)R f(x * 4) = f (4 -x)x・[0, 4],f(x) = x f[2016+ si<n(—兀2)si n(口- )2cos(_______16.给出下列结论:(1)函数f(x)二ta nx 有无数个零点;(2)集合 A={x y =2x 1},集合f (x) = 2cos x ,若存在实数 x 1,x 2,使得对任意的实数N - x 2的最小值为2兀。
2017-2018学年湖北省荆州中学高一上学期期末考试 数学(文)

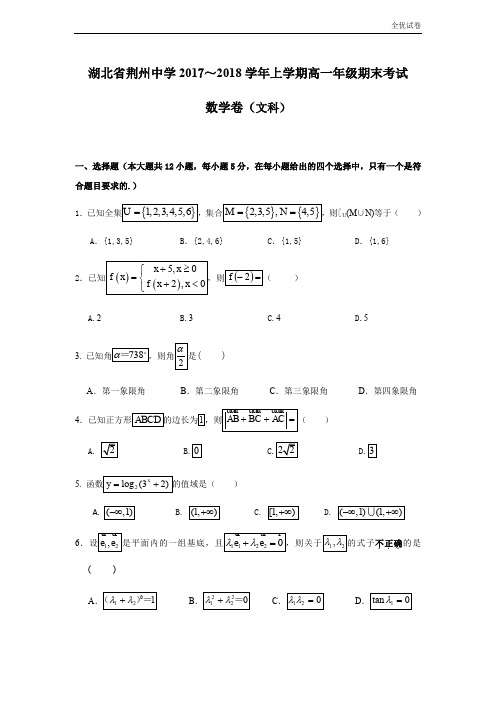
2017-2018学年湖北省荆州中学高一上学期期末考试 数学(文)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的.)1.已知全集{}1,2,3,4,5,6U =,集合{}{}2,3,5,4,5M N ==,则∁U (M ∪N )等于( )A .{1,3,5}B .{2,4,6}C .{1,5}D .{1,6}2.已知()()5,02,0x x f x f x x +≥⎧=⎨+<⎩,则()=-2f ( )A.2B.3C.4D.53. 已知角738α=,则角2α是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角4.已知正方形ABCD 的边长为1,则AB BC AC ++=u u u r u u u r u u u r( )0 C.3 5. 函数2log (32)x y =+的值域是( ) A. (,1)-∞B. (1,)+∞C. [1,)+∞D. (,1)(1,)-∞+∞6.设12,e e u r u r 是平面内的一组基底,且11220e e λλ+=u r u r r,则关于12,λλ的式子不.正确..的是( ) A .121λλ+0()=B .22120λλ+= C .120λλ=D .1tan 0λ=7.若3tan 4α= ,则222cos 4sin cos cos 4sin ααααα+=+ ( ) A .6425 B .4825C . 1613D .4138. 函数()sin()(0,)2f x x πωϕωϕ=+><的部分图象如右图所示,则()f x 的解析式为( )A .()sin()12πf x x =+B .()sin()6πf x x =+C .()sin(2)12πf x x =+D .()sin(2)6πf x x =+ 9. 若两单位向量12,e e u r u r 的夹角为60,则12122,32a e e b e e =+=-r u r u r r u r u r 的夹角为( )A .30B .60C .120D .15010. 已知函数()tan()23f x x ππ=+,则对该函数性质的描述中不正确...的是 ( ) A .()f x 的定义域为12,3x x k k Z ⎧⎫≠+∈⎨⎬⎩⎭B .()f x 的最小正周期为2C .()f x 的单调增区间为51(,)33k k -++()k Z ∈ D .()f x 没有对称轴 11.已知()()11,1(8)2,1a x x f x a x x ⎧-+>=⎨-+≤⎩是定义在R 上的增函数,则实数a 的取值范围为 ( )A .[4,8)B .(4,8)C .[5,8)D .(5,8)12.已知a r 是与单位向量b r 夹角为60的任意向量,则函数()(0)f a b λλλ-> =的最小值为 ( ) A .0 B .12CD . 34二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.) 13.已知函数()20181f x x =++,则()f x 的定义域为_________.147521log (42)ln eπ⨯-=_________. 15.已知向量(3,4),(0,3),(5,3)OA OB OC m m =-=-=---u u r u u r u u u r,若点,,A B C 不.能.构成三角形,则实数m 的取值为____________.16.已知函数21(0)()ln (0)x x f x x x ⎧+≤⎪=⎨>⎪⎩,若函数(())y f f x a =-恰.有5个零点,则实数a 的取值范围为_ _______.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分10分)(1)已知钝角..α满足1sin()3πα-=,求cos(2)απ-的值; (2)已知15x x -+=,求22x x -+.18.(本小题满分12分)已知函数2()ln2xf x x+=-,()cos g x x = (1)已知(0),()2f g παβ==,求tan()αβ+;(2)解不等式()0f x ≥;(3)设()()()h x f x g x =,试判断()h x 的奇偶性,并用定义证明你的判断.19.(本小题满分12分)已知函数()2sin()1f x x ωϕ=++(0,2πωϕ><)的最小正周期为π,且(0)1f =+. (1)求ω和ϕ的值;(2)函数()f x 的图象纵坐标不变的情况下向右平移6π个单位,得到函数()g x 的图象, ①求函数()g x 的单调增区间; ②求函数()g x 在[0,]2π的最大值.20.(本小题满分12分)已知(1,cos ),(sin ,cos )a x b x x =-=-r r ,函数()12f x a b =+⋅r r.(1)求()f x 的解析式,并比较π()4f ,π()6f 的大小; (2)求()f x 的最大值和最小值.21.(本小题满分12分)已知(2,4),(3,1),(3,4)A B C ----,设,,AB a BC b CA c ===u u u r r u u u r r u u r r(1)求33a b c +-r r r ;(2)求满足a mb nc =+r r r的实数m ,n ;(3)若线段AB 的中点为M ,线段BC 的三等分点为N (点.N 靠近点...B ),求MN uuu r 与AB uu ur 夹角的正.切.值.22. (本小题满分12分)已知函数()23kxf x x k=+()0k >. (1)若()f x m >的解集为{|3,2}x x x <->-或,求,m k 的值; (2)若存在03,x > 使不等式()01f x >成立,求k 的取值范围.湖北省荆州中学2017~2018学年上学期高一年级期末考试数学卷(文科)参考答案一、1~12 DDACB ACDBC CD二、13.[2,5) 14、23 15.5416.{}(0,ln 2]2 三、17.解:(1)由已知得1sin 3α=,…… 2分又因为α为钝角,所以cos(2)cos 3απα-===-.…… 5分 (2)由已知得1222()225x x x x --+=++= …… 8分 所以 2223x x-+=.……… 10分18.解:(1)0,0αβ== …… 2分 tan()0αβ+= …… 4分 (2)由212x x +≥-得,02xx ≤-,即02x ≤< …… 8分 (3)()h x 是奇函数 …… 10分2()22()lncos()ln cos ln cos ()2()22x x xh x x x x h x x x x+--+-=⋅-=⋅=-⋅=---+-… 12分19.解:(1)()f x 的最小正周期为π,所以π2πω=,即ω=2……… 3分又因为(0)1f =,则sin 2ϕ=,所以=3πϕ. ……… 6分(2)由(1)可知()2sin(2)+13f x x π=+,则()2sin 21g x x =+,① 由2[2,2]()22x k k k Z ππππ∈-+∈得,函数()g x 增区间为[,]()44k k k Z ππππ-+∈.……… 9分② 因为02x π≤≤,所以02x π≤≤.当22x π=,即4x π=时,函数()f x 取得最大值,最大值为()34f π= ……12分20. 解:(1) 2()12sin 2cos f x x x =-- ……… 2分所以2πππ()12sin 2cos 444f =--= 2πππ3()12sin 2cos 6662f =--=- …………………4分 因为32>-,所以 ππ()()46f f >…………………6分(2)因为2()12sin 2cos f x x x =--22sin 2sin 1x x =--2132(sin )22x =-- ………………… 8分令 sin ,[1,1]t x t =∈-, 所以2132()22y t =--,当12t =,即26x k ππ=+或52()6x k k Z ππ=+∈时,函数取得最小值32-;……10分 当1t =-,即2()2x k k Z ππ=-∈时,函数取得最大值3 ……………12分21. 解:由已知得(5,5)a =- ,(6,3)b =-- ,(1,8)c =(1) 333(5,5)(6,3)3(1,8)(6,42)a b c +-=⨯-+---⨯=-.……… 4分 (2) ∵(6,38)mb nc m n m n +=-+-+,∴65385m n m n -+=⎧⎨-+=-⎩,解得1m n ==-.………… 8分(3) 由题意得13(,)22M (1,2)N -,则1722MN = (,-) …… 10分∴17(5,5)(,)4cos ,5AB MN -⋅-<>== ……… 11分 ∴3tan ,4AB MN <>= ……… 12分22.解:(1)220()303kxk f x m m mx kx km x k>∴>⇔>⇔-+<+ , 不等式230mx kx km -+<的解集为{|3,2}x x x <->-或,3,2--是方程230mx kx km -+=的根,且0m <,252365k k mm k =⎧⎧=-⎪⎪⇒⎨⎨=-⎪⎪=⎩⎩……… 6分 (2)()()222()1103033kx f x k x kx k x k x x k>⇔>>⇔-+<⇔->+ . 存在03,x >使得()01f x >成立,即存在03,x >使得成立2003x k x >-,令()()2,3,3x g x x x =∈+∞-,则()min k g x >, 令3x t -=,则()0,t ∈+∞,2(3)96612t y t t t +==++≥=,当且仅当9t t=,即3t =,亦6x =即时等号成立.()min 12g x ∴=, ∴()12,k ∈+∞ … 12分 .。
2016-2017年湖北省荆州中学高一上学期数学期末试卷(文科)带答案

2016-2017学年湖北省荆州中学高一(上)期末数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5.00分)若点(a,9)在函数y=3x的图象上,则tan的值为()A.0 B.C.1 D.2.(5.00分)若sinα>0且tanα<0,则的终边在()A.第一象限B.第二象限C.第一象限或第三象限D.第三象限或第四象限3.(5.00分)若2弧度的圆心角所对弧长为4cm,则圆心角所夹的扇形面积为()A.2πcm2B.4πcm2C.2cm2D.4cm24.(5.00分)已知均为单位向量,它们的夹角为,那么等于()A.B. C.4 D.5.(5.00分)已知x0是函数f(x)=e x+2x﹣4的一个零点,若x1∈(﹣1,x0),x2∈(x0,2),则()A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0 C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>06.(5.00分)已知函数f(x)=sin(ωx+)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度7.(5.00分)设,若与的夹角是钝角,则实数m的范围是()A.m>4 B.m<4 C.m<4且D.m<4且8.(5.00分)已知幂函数f(x)的图象过点,则f(x)是()A.偶函数B.奇函数C.定义域上的增函数D.定义域上的减函数9.(5.00分)设全集U=R,集合,则(∁U A)∩B=()A.∅B.[﹣1,0)C. D.[0,2]10.(5.00分)f(x)是偶函数,且在(﹣∞,0)上是增函数,则下列关系成立的是()A.f(﹣2)<f(1)<f(3)B.f(1)<f(﹣2)<f(3)C.f(3)<f(﹣2)<f(1)D.f(﹣2)<f(3)<f(1)11.(5.00分)已知函数f (x)是定义在闭区间[﹣a,a](a>0)上的奇函数,F(x)=f (x)+1,则F(x)最大值与最小值之和为()A.1 B.2 C.3 D.012.(5.00分)据统计,一名工人组装第x件某产品所用的时间(单位:分钟)f(x)=(m,c为常数),已知工人组装第4件产品所用的时间为30分钟,工人组装第m件产品所用的时间为15分钟,则m=()A.49 B.25 C.16 D.9二、填空题(本大题共4小题,每小题5分,共20分)13.(5.00分)()0.5+()+(0.1)﹣2﹣(π)0+lg2+lg5=.14.(5.00分)若对于任意正数x,y,都有f(xy)=f(x)+f(y),且f(8)=﹣3,则时,正数a=.15.(5.00分)已知P是函数y=x2图象上的一点,A(1,﹣1),则的最大值为.16.(5.00分)y=f(x)为R上的偶函数,且满足f(x+4)=f(4﹣x),当x∈[0,4]时,f(x)=x且sinα=,则f[2016+sin(α﹣2π)•sin(π+α)﹣2cos2(﹣α)]=.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)17.(12.00分)已知,求a的取值集合.18.(12.00分)已知f(x)=Asin(ωx+φ)(A>0,ω>0,﹣π<φ<π)的图象如图所示.(1)根据图象写出f(x)的解析式;(2)A为锐角三角形的一个内角,求f(A)的最大值,及当f(A)取最大值时A的值.19.(12.00分)已知,是平面内两个不共线的非零向量,=2+,=﹣+λ,=﹣2+,且A,E,C三点共线.(1)求实数λ的值;若=(2,1),=(2,﹣2),求的坐标;(2)已知点D(3,5),在(1)的条件下,若ABCD四点构成平行四边形,求点A的坐标.20.(12.00分)有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.(1)若这个梯形上底为CD=2a,求它的腰长x;(2)求出这个梯形的周长y关于腰长x的函数解析式,并指出它的定义域;(3)求这个梯形周长的最大值,并求出当它最大时,梯形的面积S.21.(12.00分)已知函数是奇函数.(1)求a的值;(2)判断函数f(x)的单调性,(不需证明)(3)若对任意的t∈R,不等式f(kt2+2)+f(t2﹣tk)>0恒成立,求实数k的取值范围.22.(10.00分)在平面直角坐标系中,已知角α的终边经过点P(﹣3,4)(1)求sinα和cosα的值;(2)化简并求值:.2016-2017学年湖北省荆州中学高一(上)期末数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5.00分)若点(a,9)在函数y=3x的图象上,则tan的值为()A.0 B.C.1 D.【解答】解:将(a,9)代入到y=3x中,得3a=9,解得a=2.∴=.故选:D.2.(5.00分)若sinα>0且tanα<0,则的终边在()A.第一象限B.第二象限C.第一象限或第三象限D.第三象限或第四象限【解答】解;∵sinα>0且tanα<0,∴α位于第二象限.∴+2kπ<α<2kπ+π,k∈Z,则+kπ<<kπ+k∈Z当k为奇数时它是第三象限,当k为偶数时它是第一象限的角∴角的终边在第一象限或第三象限,故选:C.3.(5.00分)若2弧度的圆心角所对弧长为4cm,则圆心角所夹的扇形面积为()A.2πcm2B.4πcm2C.2cm2D.4cm2【解答】解:∵2弧度的圆心角所对弧长为4cm,∴扇形的面积S===4cm2,故选:D.4.(5.00分)已知均为单位向量,它们的夹角为,那么等于()A.B. C.4 D.【解答】解:均为单位向量,它们的夹角为,所以=+6•+9=12+6×1×1×cos+9×12=13,那么=.故选:D.5.(5.00分)已知x0是函数f(x)=e x+2x﹣4的一个零点,若x1∈(﹣1,x0),x2∈(x0,2),则()A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0 C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0【解答】解:∵函数f(x)=e x+2x﹣4在R上单调递增,且f(x0)=0,∴由x1∈(﹣1,x0),x2∈(x0,2),可得f(x1)<0,f(x2)>0.故选:B.6.(5.00分)已知函数f(x)=sin(ωx+)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【解答】解:由题知ω=2,所以,故选:A.7.(5.00分)设,若与的夹角是钝角,则实数m的范围是()A.m>4 B.m<4 C.m<4且D.m<4且【解答】解:,当与的夹角是钝角时,•<0…①且与不平行…②;由①得,﹣3×4+3m<0,解得m<4;由②得,﹣3×3﹣4m≠0,解得m≠﹣;综上,实数m的范围是m<4且m≠﹣.故选:D.8.(5.00分)已知幂函数f(x)的图象过点,则f(x)是()A.偶函数B.奇函数C.定义域上的增函数D.定义域上的减函数【解答】解:设f(x)=xα,∵幂函数y=f(x)图象过点(2,),∴=2α,解得α=﹣,∴f(x)=,是定义域上的减函数,故选:D.9.(5.00分)设全集U=R,集合,则(∁U A)∩B=()A.∅B.[﹣1,0)C. D.[0,2]【解答】解:∵集合={x|x≥0},∴∁U A={x|x<0}=(﹣∞,0),由得,,∴,则集合B={y|﹣1≤y≤2}=[﹣1,2],∴(∁U A)∩B=(﹣∞,0)∩[﹣1,2]=[﹣1,0),故选:B.10.(5.00分)f(x)是偶函数,且在(﹣∞,0)上是增函数,则下列关系成立的是()A.f(﹣2)<f(1)<f(3)B.f(1)<f(﹣2)<f(3)C.f(3)<f(﹣2)<f(1)D.f(﹣2)<f(3)<f(1)【解答】解:∵f(x)是偶函数,且在(﹣∞,0)上是增函数,∴f(3)=f(﹣3)<f(﹣2)<f(1)=f(﹣1),故选:C.11.(5.00分)已知函数f (x)是定义在闭区间[﹣a,a](a>0)上的奇函数,F(x)=f (x)+1,则F(x)最大值与最小值之和为()A.1 B.2 C.3 D.0【解答】解:∵函数f (x)是定义在闭区间[﹣a,a](a>0)上的奇函数,则函数的最大值和最小值,分别为f(﹣A),f(A),又∵F(x)=f (x)+1,∴F(x)最大值与最小值分别为f(﹣A)+1,f(A)+1,∴F(x)最大值与最小值之和为2故选:B.12.(5.00分)据统计,一名工人组装第x件某产品所用的时间(单位:分钟)f(x)=(m,c为常数),已知工人组装第4件产品所用的时间为30分钟,工人组装第m件产品所用的时间为15分钟,则m=()A.49 B.25 C.16 D.9【解答】解:由题意可得:f(m)==15,所以c=15,而f(4)==30,可得出c=60,故可得A=16,从而c=15=60,即有m=16.故选:C.二、填空题(本大题共4小题,每小题5分,共20分)13.(5.00分)()0.5+()+(0.1)﹣2﹣(π)0+lg2+lg5=101.【解答】解:()0.5+()+(0.1)﹣2﹣(π)0+lg2+lg5=++[(10)﹣1]﹣2﹣+lg(2×5)=++100﹣+1=101故答案为:10114.(5.00分)若对于任意正数x,y,都有f(xy)=f(x)+f(y),且f(8)=﹣3,则时,正数a=.【解答】解:f(8)=f(2×4)=f(2)+f(4)=f(2)+f(2)+f(2)=3f(2)=﹣3,∴f(2)=﹣1,∴f(2)=2f()=﹣1,∴f()=﹣,∴f()=f(×2)=f()+f(2)=﹣,∴f()=.∴a=,故答案为:.15.(5.00分)已知P是函数y=x2图象上的一点,A(1,﹣1),则的最大值为.【解答】解:设P(x,x2),则:;∴;∴的最大值为.故答案为:.16.(5.00分)y=f(x)为R上的偶函数,且满足f(x+4)=f(4﹣x),当x∈[0,4]时,f(x)=x且s inα=,则f[2016+sin(α﹣2π)•sin(π+α)﹣2cos2(﹣α)]=.【解答】解:∵y=f(x)为R上的偶函数,∴f(﹣x)=f(x),又f(x+4)=f(4﹣x),∴f(x+8)=f[(4﹣(4+x)]=f(﹣x)=f(x),∴y=f(x)的周期是8,又f[2016+sin(α﹣2π)•sin(π+α)﹣cos2(﹣α)]=f[2016+sin2α﹣cos2α]=f (2015+2sin2α)=f(2016﹣)=f(﹣)=f()=,故答案为:.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)17.(12.00分)已知,求a的取值集合.【解答】解:a>1时,,∴⇔⇔=,∴,则a>;当0<a<1时,,∴⇔,∴0<,综上得:a∈(0,)∪(,+∞).18.(12.00分)已知f(x)=Asin(ωx+φ)(A>0,ω>0,﹣π<φ<π)的图象如图所示.(1)根据图象写出f(x)的解析式;(2)A为锐角三角形的一个内角,求f(A)的最大值,及当f(A)取最大值时A的值.【解答】(本题满分为12分)解:(1)由函数图象可得:A=2,,∴可得:ω=2,∵时,2sin[2×(﹣)+φ]=0,由五点作图法可得:,∴,∴.…(6分)(2)∵,∴,∴可得:f(A)=2sin(2A+),当且仅当时f(A)最大,f(A)max=2.…(12分)19.(12.00分)已知,是平面内两个不共线的非零向量,=2+,=﹣+λ,=﹣2+,且A,E,C三点共线.(1)求实数λ的值;若=(2,1),=(2,﹣2),求的坐标;(2)已知点D(3,5),在(1)的条件下,若ABCD四点构成平行四边形,求点A的坐标.【解答】解:(1)∵=,∵A,E,C三点共线,∴存在实数k,使得.即,得.∵,是平面内两个不共线的非零向量,∴,解得,.∴.(2)∵A、B、C、D四点构成平行四边形,∴.设A(x,y),则,又,∴,解得,∴点A(10,7).20.(12.00分)有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.(1)若这个梯形上底为CD=2a,求它的腰长x;(2)求出这个梯形的周长y关于腰长x的函数解析式,并指出它的定义域;(3)求这个梯形周长的最大值,并求出当它最大时,梯形的面积S.【解答】解:(1)∵22﹣a2=x2﹣(2﹣a)2∴x2=8﹣4a,∴它的腰长…(4分)(2)由(1)知:,∴,∵,∴定义域为…(8分)(3)由(2)知,x=1时,y最大此时梯形的上底,高,∴.21.(12.00分)已知函数是奇函数.(1)求a的值;(2)判断函数f(x)的单调性,(不需证明)(3)若对任意的t∈R,不等式f(kt2+2)+f(t2﹣tk)>0恒成立,求实数k的取值范围.【解答】解:(1)由题意:是定义域为R的奇函数,∴f(0)=0即,∴a=1.当a=1时,,,故a=1满足题意;(2)单调递增函数;(3)由(2)得f(kt2+2)+f(t2﹣tk)>0等价于f(kt2+2)>﹣f(t2﹣tk),即kt2+2>﹣t2+tk,∴(k+1)t2﹣tk+2>0对任意t∈R恒成立,①k=﹣1时,t+2>0不恒成立,②k≠﹣1时,即解得:k∈(﹣1,).∴k的取值范围是:(﹣1,).22.(10.00分)在平面直角坐标系中,已知角α的终边经过点P(﹣3,4)(1)求sinα和cosα的值;(2)化简并求值:.【解答】解:(1)∵角α的终边经过点P (﹣3,4),∴x=﹣3,y=4,r=5,∴sinα==,cosα==﹣. (2)==﹣tanα=﹣=.赠送—高中数学知识点【2.1.1】指数与指数幂的运算 (1)根式的概念①如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n n a n 是偶数时,正数a 的正的n n a 表示,负的n 次方根用符号n a -0的n 次方根是0;负数a 没有n 次方根.n a n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:()n n a a =;当n 为奇数时,nn a a =;当n 为偶数时,(0)|| (0) nna a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:(0,,,m nmna a a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 11()()(0,,,mm m nn n aa m n N a a-+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈【2.1.2】指数函数及其性质 函数名称指数函数定义函数(0x y a a =>且1)a ≠叫做指数函数图象1a >01a <<定义域 R值域 (0,)+∞过定点 图象过定点(0,1),即当0x =时,1y =.奇偶性 非奇非偶单调性在R 上是增函数在R 上是减函数函数值的 变化情况1(0)1(0)1(0)x x x a x a x a x >>==<< 1(0)1(0)1(0)x x x a x a x a x <>==>< a 变化对 图象的影响 在第一象限内,a 越大图象越高;在第二象限内,a 越大图象越低.xa y =xy(0,1)O1y =xa y =xy (0,1)O 1y =〖2.2〗对数函数 【2.2.1】对数与对数运算(1)对数的定义①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a a MM N N-= ③数乘:log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质(5)对数函数函数 名称 对数函数定义函数log (0a y x a =>且1)a ≠叫做对数函数图象1a > 01a <<定义域 (0,)+∞值域Rx yO(1,0)1x =log a y x=xyO (1,0)1x =log a y x=过定点 图象过定点(1,0),即当1x =时,0y =.奇偶性 非奇非偶单调性在(0,)+∞上是增函数在(0,)+∞上是减函数函数值的 变化情况log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<a 变化对图象的影响 在第一象限内,a 越大图象越靠低;在第四象限内,a 越大图象越靠高.。
(全优试卷)版湖北省荆州中学高一上学期期末考试数学(文)Word版含答案
湖北省荆州中学2017~2018学年上学期高一年级期末考试数学卷(文科)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的.)1.则∁U(M∪N)等于()A.{1,3,5} B.{2,4,6} C.{1,5} D.{1,6}2)A.2B.3C.4D.53. ( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角4)5. )A. B.6不.正确..的是()A B C D7A B C.Df x的解析式为8. 则()()A BC9. )A B C D10. 不正确...的是( )A B 2C D11R上的增函数,则实数a的取值范围为( )A B C D12.已知是与单位向量夹角为的任意向量,则函数(3)a b b a⋅⋅( )AB 1C D .二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.)13_________.14.15.能.构成三____________.16..有5个零点,的取值范围为_ _______.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分10分)(1)已知(2)18.(本小题满分12(1(2(319.(本小题满分12的最小正周期(1(220.(本小题满分12(1(221.(本小题满分12(1(2m,n;(3),正切..值.22. (本小题满分12(1(2.湖北省荆州中学2017~2018学年上学期高一年级期末考试数学卷(文科)参考答案一、1~12 DDACB ACDBC CD二、13、23 1516三、17.解:(1 2分5分(2 …… 8分所以 10分18.解:(1…… 2分…… 4分(2…… 8分(3 …… 10分…12分19.解:(1……… 3分……… 6分(2)由(1①9分②……12分20.解:(1)……… 2分所以…………………4分因为所以6分(2………………… 8分令10分……………12分21. 解(1)4分(2)………… 8分(3)…… 10分……… 11分……… 12分22.解:(1不等式2mx kx-………6分(2.… 12分。
湖北省部分重点中学高一上学期期末考试试题(9科10份,PDF版)上学期高一文科数学答案

湖北省部分重点中学2015-2016学年度上学期高一期末考试 文科数学参考答案一、选择题(每小题5分,共60分)二、填空题(每小题5分,共20分)①③⑤三、解答题(共70分)17.(本小题满分10分)解:(1)由3(23)(1)02x x x -->⇒>或,3(,1)(,)2A ∴=-∞+∞ 当时,由243013x x x -+-≥⇒≤≤,,(2)当时,若或,解得或,故的取值范围是.18. (本小题满分12分)解:(1)由,. 22t a n 632tan 1941tan 2x x x ∴===---. (2)原式= x x x xx sin )sin 22cos 22(2sin cos 22-- xx x x x x x sin )sin (cos )sin )(cos sin (cos -+-= 14111tan 33x =+=-+=-19.(本小题满分12分)解:(1)(2)不等式转化为: 22sin 24sin 2x x>sin 2cos 2)4x x x π⇒+>⇒+> 即由得,572(0,)44624x x ππππ∴<+<⇒∈. 故不等式的解集为20. (本小题满分12分)解: ( 1 ) 由已知,有1cos 21cos21113()cos22cos222222x x f x x x x π⎛⎫-- ⎪⎛⎫-⎝⎭=-=- ⎪⎝⎭11sin 2cos 2sin 24426x x x π⎛⎫=-=- ⎪⎝⎭. 设3222262k x k πππππ+≤-≤+,解得536k x k ππππ+≤≤+ 故的单调减区间为:5[,]()36k k k Z ππππ++∈ (2) 5[,]2[,]34663x x p p p p p ?\-?结合正弦函数图像可得: 1sin(2)6x p -?? 11s i n (2)2264x p \-?? 故函数函数在区间上的值域为21. (本小题满分12分)解 在Rt △OBC 中,OB =2cos α,BC =2sin α. 在Rt △OAD 中,DA OA==1, ∴AB =OB -OA =2cos α-2sin α. ∴OA =DA =BC =2sin α, 设矩形ABCD 的面积为S ,则S =AB ·BC=(2cos 2sin )2sin ααα-=4sin αcos α-4sin 2α=2sin 2α- (1-cos 2α)=2sin 2α+2cos 2α-2=-由0<α<,得,所以当即时,S 最大=因此,当时,矩形ABCD 的面积最大,最大面积为.22. (本小题满分12分)解析:(1)()()211g x a x b a =-++-,因为a>0,所以在区间 (0,1]上是减函数,[1,3]上是增函数,故()()1135g g =⎧⎪⎨=⎪⎩,解得.(2)由已知可得,所以可化为,化为21112222x x k ⎛⎫+-⋅≥ ⎪⎝⎭,令,则, 因,故,记,因为,故,所以k 的取值范围是.。
数学---湖北省荆州市2016-2017学年高一(上)期末试卷(文科)(解析版)

湖北省荆州市2016-2017学年高一(上)期末数学试卷(文科)一、选择题(共12小题,每小题5分,满分60分)1.(5分)设集合A={x|2x≤4},集合B={x|y=lg(x﹣1)},则A∩B等于()A.(1,2)B.[1,2] C.[1,2)D.(1,2]2.(5分)设x>0,0<b x<a x<1,则正实数a,b的大小关系为()A.1>a>b B.1>b>a C.1<a<b D.1<b<a3.(5分)函数y=log3(x2﹣2x+4)的值域为()A.[1,+∞) B.[0,+∞) C.[3,+∞) D.R4.(5分)sin210°的值为()A.B.﹣C.D.﹣5.(5分)函数的定义域是()A.B.C.D.6.(5分)已知向量=(λ,1),=(λ+1,2),若(+)⊥(﹣),则λ=()A.1 B.0 C.﹣1 D.﹣27.(5分)已知函数f(x)的定义域为(﹣1,0),则函数f(2x+1)的定义域为()A.(﹣1,1)B.C.(﹣1,0)D.8.(5分)函数f(x)=log2x+1与g(x)=2﹣x﹣1在同一平面直角坐标系下的图象大致是()A.B.C.D.9.(5分)设P为等边三角形ABC所在平面内的一点,满足=+2,若AB=1,则•=()A.4 B.3 C.2 D.110.(5分)若函数f(x)=log a(a x﹣t)(a>0且a≠1)在区间[,]上的值域为[m,n],则实数t的取值范围是()A.(0,1)B.(,)C.(0,)D.(,1)11.(5分)函数f(x)=3x﹣﹣a的一个零点在区间(1,2)内,则实数a的取值范围()A.(﹣2,7)B.(﹣1,6)C.(﹣1,7)D.(﹣2,6)12.(5分)函数f(x)的定义域为D,若对于任意x1,x2∈D,当x1<x2时都有f(x1)≤f(x2),则称函数f(x)在D上为非减函数,设f(x)在[0,1]为非减函数,且满足以下三个条件;①f(0)=0;②f()=f(x);③f(1﹣x)=1﹣f(x),则f()+f()等于()A. B. C. D.二、填空题(共4小题,每小题5分,满分20分)13.(5分)已知幂函数f(x)的图象过点(2,16),则f()=.14.(5分)计算=.15.(5分)已知点P在线段AB上,且,设,则实数λ=.16.(5分)下列说法中,所有正确说法的序号是.①终边落在y轴上的角的集合是;②函数图象的一个对称中心是;③函数y=tan x在第一象限是增函数;④为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin2x的图象向右平移个单位长度.三、解答题(共6小题,满分70分)17.(10分)已知集合A={x|a﹣1<x<a+1},B={x|0<x<3}.(1)若a=0,求A∩B;(2)若A⊆B,求实数a的取值范围.18.(12分)平面内的向量=(3,2),=(﹣1,2),=(4,1).(1)若(+k)⊥(2﹣),求实数k的值;(2)若向量满足∥,且||=,求向量的坐标.19.(12分)函数f(x)=A sin(ωx+φ),x∈R(0,ω>0,0<φ<)的图象与x轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为M(,﹣2).(1)求函数f(x)的解析式及单调增区间;(2)求当x∈[,]时,f(x)的值域.20.(12分)扬州瘦西湖隧道长3600米,设汽车通过隧道的速度为x米/秒(0<x<17).根据安全和车流的需要,当0<x≤6时,相邻两车之间的安全距离d为(x+b)米;当6<x<17时,相邻两车之间的安全距离d为米(其中a,b是常数).当x=6时,d=10,当x=16时,d=50.(1)求a,b的值;(2)一列由13辆汽车组成的车队匀速通过该隧道(第一辆汽车车身长为6米,其余汽车车身长为5米,每辆汽车速度均相同).记从第一辆汽车车头进入隧道,至第13辆汽车车尾离开隧道所用的时间为y秒.①将y表示为x的函数;②要使车队通过隧道的时间y不超过280秒,求汽车速度x的范围.21.(12分)如图,在矩形ABCD中,点E是BC边上中点,点F在边CD上.(1)若点F是CD上靠近C的三等分点,设=λ+,求λ+μ的值.(2)若AB=,BC=2,当•=1时,求DF的长.22.(12分)如图,过函数f(x)=log c x(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=log m x(m>c>1)的图象交于点C,且AC与x轴平行.(1)当a=2,b=4,c=3时,求实数m的值;(2)当b=a2时,求﹣的最小值;(3)已知h(x)=a x,φ(x)=b x,若x1,x2为区间(a,b)任意两个变量,且x1<x2,求证:h(f(x2))<φ(f(x1))参考答案一、选择题(共12小题,每小题5分,满分60分)1.D【解析】A={x|2x≤4}={x|x≤2},由x﹣1>0得x>1∴B={x|y=lg(x﹣1)}={x|x>1}∴A∩B={x|1<x≤2}2.A【解析】根据题意,假设有指数函数y=a x与y=b x,若x>0,有0<b x<a x<1,则有a>1且b>1,若0<b x<a x<1,则有=()x<1,又由x>0,则<1,即a>b,则有1>a>b;3.A【解析】函数y=log3(x2﹣2x+4),令u=x2﹣2x+4,那么函数y=log3(x2﹣2x+4)转化为y=log3u是增函数,由u=x2﹣2x+4=(x﹣1)2+3,可得u≥3.∴当u=3时,函数y=log3u取得最小值为1.∴函数y=log3(x2﹣2x+4)的值域为[1,+∞)4.B【解析】sin210°=sin(180°+30°)=﹣sin30°=﹣.5.B【解析】由题意得:2kπ≤2x﹣≤2kπ+π,解得:kπ+≤x≤kπ+π,k∈Z,6.D【解析】∵向量=(λ,1),=(λ+1,2),若(+)⊥(﹣),则(+)•(﹣)=﹣=λ2+1﹣[(λ+1)2+4]=0,求得λ=﹣2,7.B【解析】∵原函数的定义域为(﹣1,0),∴﹣1<2x+1<0,解得﹣1<x<﹣.∴则函数f(2x+1)的定义域为.8.D【解析】∵f(x)=1+log2x的图象是由y=log2x的图象上移1而得,∴其图象必过点(1,1).故排除A、B,又∵g(x)=2﹣x﹣1=2﹣(x+1)的图象是由y=2﹣x的图象左移1而得,故其图象也必过(﹣1,1)点,及(0,)点,故排除C,9.B【解析】∵P为等边三角形ABC所在平面内的一点,=+2,若AB=1,则•=(﹣)•(﹣)=(﹣2)•(﹣﹣)=2•+2 =2•1•1•cos60°+2=3,10.C【解析】∵y=a x﹣t与y=log a x的单调性相同,∴f(x)=log a(a x﹣t)(a>0且a≠1)在定义域上是增函数,∵f(x)区间[,]上的值域为[m,n],∴,∴方程log a(a﹣t)=x有两解,即方程a x=a﹣t有两解,设a=m(m>0),则t=m﹣m2,作出t=m﹣m2(m>0)的函数图象如图所示:∵方程a x=a﹣t有两解,∴关于m的方程t=m﹣m2有两解,∴0<t<.11.C【解析】由题意可得f(1)f(2)=(3﹣4﹣a)(9﹣2﹣a)<0,即(a+1)(a﹣7)<0,解得:﹣1<a<7,故实数a的取值范围是(﹣1,7),12.D【解析】∵函数f(x)在[0,1]上为非减函数,①f(0)=0;③f(1﹣x)+f(x)=1,∴f(1)=1,令x=,所以有f()=.又∵②f()=f(x),∴f(x)=2f(),∴令=1,可得1=2f(),∴f()=.令x=,可得f()=f()=,令x=,可得f()=f()=.∵当x1<x2时都有f(x1)≤f(x2),<<,∴f()≤f()≤f(),∴f()=,∴f()+f()=+=,二、填空题(共4小题,每小题5分,满分20分)13.9【解析】设幂函数f(x)=xα,其图象过点(2,16),∴2α=16,解得α=4,∴f(x)=x4,∴f()==9.故答案为:9.14.【解析】=lg5+lg2+lne+1=1++1=,故答案为;15.【解析】如图所示,点P在线段AB上,且,∴==;又,∴λ=.故答案为:.16.②④【解析】①当角θ的终边落在y轴的非负半轴上时,角θ=2kπ+,k∈Z,当角θ的终边落在y轴的非正半轴上时,角θ=2kπ+,k∈Z,故终边落在y轴上的角的集合是{θ|θ=2kπ+,或θ=2kπ+,k∈Z}={θ|θ=2kπ+,或θ=2kπ+π+,k∈Z}={θ|θ=nπ+,n∈Z },不正确;②令x﹣=kπ+,k∈Z,可得对称中心为(kπ+,0),k∈Z,令k=0,得到一个对称中心的坐标(,0),故正确;③∵390°,45°是第一象限角,390°>45°,但tan390°=<1=tan45°,∴函数y=tan x在第一象限是增函数错误,命题①为假命题;④由于函数y=sin(2x﹣)=sin[2(x﹣)],故只需把函数y=3sin2x的图象向右平移个长度单位即可得到函数y=sin(2x﹣)的图象,故正确;故答案为:②④.三、解答题(共6小题,满分70分)17.解(1)若a=0,集合A={x|a﹣1<x<a+1}={x|﹣1<x<1},B={x|0<x<3}.则A∩B={x|﹣1<x<1}∩{x|0<x<3}={x|0<x<1};(2)若A⊆B,则,即1≤a≤2,∴实数a的取值范围是1≤a≤2.18.解(1)+k=(3+4k,2+k),2﹣=(﹣5,2),∵(+k)⊥(2﹣),∴(+k)•(2﹣)=(3+4k)×(﹣5)+(2+k)×2=0,解得k=﹣.(2)设=(x,y),∵∥,且||=,∴,解得,或,∴向量的坐标为,或.19.解(1)∵依题意,由最低点为,得A=2,又∵周期T=π,∴ω=2.∵由点在图象上,∴得,∴,∴.∵,∴,∴.由,得.∴函数f(x)的单调区间是.(2)∵,,∴.当,即时,f(x)取得最大值2;当,时,f(x)取得最小值﹣1,故f(x)的值域为[﹣1,2].20.解(1)当x=6时,d=x+b=6+b=10,则b=4,当x=16时,,则a=1;所以a=1,b=4.…(4分)(2)①当0<x≤6时,,当6<x<17时,所以.…(10分)②当0<x≤6时,,不符合题意,当6<x<17时,解得15≤x<123,所以15≤x<17∴汽车速度x的范围为[15,17).…(16分)21.解(1)=﹣=+﹣(+)=+﹣(+)=+﹣(+)=﹣=λ+,∴λ=﹣,μ=,∴λ+μ=.(2)以AB,AD为x,y轴建立直角坐标系如图:AB=,BC=2则A(0,0),B(,0),E(,1),设F(x,2),∴=(,1),=(x﹣,2),∵•=1,∴(x﹣)+2=1,∴x=,∴|DF|=.22.解(1)由题意得A(2,log32),B(4,log34),.又AC与x轴平行,∴log m4=log32,解得m=9.(2)由题意得A(a,log c a),B(b,log c b),.∵AC与x轴平行,∴log m b=log c a.∵b=a2,∴m=c2,∴.∴时,﹣取得最小值﹣1.(3)h(f(x2))=a,φ(x1)=b,∵a<x1<x2<b,且c>1,∴log c a<log c x1<log c x2<log c b.又∵a>1,b>1,∴.又∵log c b•log c a=log c a•log c b,∴.∴,∴.即h[f(x2)]<φ(f(x1)).。
荆州中学高一数学(文)上学期期末试卷(有答案)【最新】

荆州中学2016~2017学年度上学期期 末 试 卷年级:高一 科目:数学(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 若点(,9)a 在函数3x y =的图象上,则tan 6aπ的值为( )A. 0B.C. 1D.2. 若sin 0α> 且tan 0α<,则2α的终边在( ) A. 第一象限B. 第二象限C. 第一象限或第三象限D. 第三象限或第四象限3. 若2弧度的圆心角所对的弦长为4sin1cm ,则这个圆心角所夹的扇形的面积是( ) A.22cmB. 24cmC.22cm πD. 24cm π4. 已知,a b 均为单位向量,它们的夹角为3π,那么3a b +等于( )B.C.4D. 5. 已知0x 是函数()24x f x e x =+-的零点,若1020(1,),(,2)x x x x ∈-∈,则( ) A. 12()0,()0f x f x << B. 12()0,()0f x f x <> C. 12()0,()0f x f x ><D. 12()0,()0f x f x >>6. 已知函数()sin()(,0)4g x x x R πωω=+∈>的最小正周期为π,为了得到函数()cos f x x ω=的图象,只要将()y g x =的图象( ) A. 向左平移8π个单位长度 B. 向右平移8π个单位长度 C. 向左平移4π个单位长度D. 向右平移4π个单位长度 7. 设(3,),(4,3)a m b =-=,若a 与b 的夹角是钝角,则实数m 的范围是( ) A. 4m >B. 4m <C. 4m <且94m ≠D. 4m <且94m ≠-8. 已知幂函数()f x的图象过点2,则()f x 是( ) A. 偶函数B. 奇函数C. 定义域上的增函数D. 定义域上的减函数9. 设全集U R =,集合219{{log (),[1,]}22A x yB y y x x ====-∈,则()U A B =u ð( )A. φB. [1,0)-C. 9[1,]2D. [0,2]10. ()f x 是偶函数,且在(,0)-∞上是增函数,则下列关系成立的是( )A. (2)(1)(3)f f f -<<B. (1)(2)(3)f f f <-<C. (3)(2)(1)f f f <-<D. (2)(3)(1)f f f -<<11. 已知函数()f x 是定义在闭区间[,](0)a a a ->上的奇函数,()()1F x f x =+,则()F x 的最大值与最小值的和为( ) A.4B. 2C. 1D. 012. 据统计,一名工人组装第x 件某产品所用的时间(单位:分钟),()(,x m f x m c x m <=≥为常数),已知工厂组装第4件产品所用的时间为30分钟,工人组装第m 件产品所用的时间为15分钟,则m =( ) A.49 B. 25 C. 16 D. 9二、填空题(本大题共4小题,每小题5分,共20分)13.20.5203252731()()(0.1)()lg 2lg59649π--++-++= ______________.14. 若对于任意正数,x y ,都有()()()f xy f x f y =+,且(8)3f =-,则1()2f a =时,正数a = .15. 已知P 是函数2y x =图象上的一点,(1,1)A -,则OP OA ⋅的最大值为 . 16.()y f x =为R 上的偶函数,且满足(4)(4)f x f x +=-,当[0,4]x ∈时,()f x x =,则2[2016sin(2)sin()cos ()]f αππαα+-⋅+--= _____________.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.) 17.(本题12分)已知3log 14a<,求a 的取值集合.18. (本题12分)已知()sin()(0,0,)f x A x A ωϕωπϕπ=+>>-<<的图象如图所示.(1)根据图象写出()f x 的解析式;(2)A 为锐角三角形的一个内角,求()f A 的最大值,及当()f A 取最大值时A 的值.19.(本题12分)已知12,e e 是平面内两个不共线的非零向量,122,AB e e =+1212,2,BE e e EC e e λ=-+=-+且,,A E C 三点共线.(1)求实数λ的值;若12(2,1),(2,2)e e ==-,求BC 的坐标;(2)已知点(3,5)D ,在(1)的条件下,若四边形ABCD 为平行四边形,求点A 的坐标.20. (本题12分)有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD 的形状,它的下底AB 是是半圆的直径,上底CD 的端点在半圆上.(1)若这个梯形上底为2CD a =,求它的腰长x ;(2)求出这个梯形的周长y 关于腰长x 的函数解析式,并指出它的定义域; (3)求这个梯形周长的最大值,并求出当它最大时,梯形的面积S.xyO21.(本题12分)已知函数2()()21x f x a a R =-∈+ 是奇函数. (1)求a 的值;(2)判断函数()f x 的单调性,(不需证明)(3)若对任意的t R ∈,不等式22(2)()0f kt f t tk ++->恒成立,求实数k 的取值范围.22.(本题10分)在平面直角坐标系中,已知角α的终边经过点(3,4)P -[] (1)求sin α和cos α的值;(2)化简并求值:11sin(2)cos()cos()cos()229cos()sin(3)sin()sin()2πππαπαααππαπαπαα-++-----+.荆州中学2016~2017学年度上学期期 末 试 卷年级:高一 科目:数学(文科) 命题人:朱代文 审题人: 徐法章参考答案一、选择题:13. 101 14.215.1416. 1三、解答题: 17. 解:1a >时,3331log 0,log 1,log 1log 444aa a a a<∴-<>-= 314,43a a ∴<< 413a ∴<<……………………5分 当01a <<时,3log 04a > 3l o g 1l o g4a a a ∴>= 34a ∴< 314a ∴<<……………………10分 综合得:34(,1)(1,)43a ∈……………………12分18. 解:(1)2A =373(),,41264T T ππππ=--== 2w ∴= 6x π=-时, 2()0,6πϕ-+= 3πϕ∴=()2sin(2)3f x x π∴=+……………………6分(2)(0,)2A π∈42(,)333A πππ∴+∈ ∴当且仅当2,3212A A πππ+==时()f A 最大,max ()2f A =……………………12分19. 解:(1)1212(2)()AE AB BE e e e e =+=++-+12(1)e e λ=++A E C 、、三点共线 ∴存在实数k 使得AE k EC = 即1212(1)(2)e e k e e λ++=-+ 得12(1)(1)e k e λλ+=--由题意得12013,122k k k λλ+=⎧∴=-=-⎨=-⎩……………4分此时1213(7,2)2BC BE EC e e =+=--=--……………6分(2)四边形ABCD 为平行四边形AD BC ∴= 设(,)A x y 则(3,5)AD x y =--又(7,2)BD =--3752x y -=-⎧⎨-=-⎩ 得107x y =⎧⎨=⎩(10,7)A ∴……………12分20. 解:(1)22222(2)a x a -=--284,x a ∴=- x ∴=4分(2)由(1)知:242,2x a -=224124622x y x x x -∴=++=-++0a x >∴< 定义域为……………8分(3)由(2)知,1x =时,y 最大此时梯形的上底72,2a =高h =17(4)22416S ∴=+⋅=21. 解:(1) 由题意:2()21x f x a =-+是定义域为R 的奇函数 (0)0f ∴= 即02021a -=+ 1a ∴= 当1a =时,221()12121x x x f x -=-=++ 211221()()212121x x x x x x f x f x -------===-=-+++故1a =进满足题意………………5分(2)单调递增函数……………7分(3)由(2)得22(2)()0f kt f t tk ++->等价于22(2)()f kt f t tk +>-即222kt t tk +>-+ ∴2(1)20k t tk +-+>对任意t R ∈恒成立①1k =-时,20t +>不恒成立②1k ≠-时,100t +>⎧⎨∆<⎩解得:(4k ∈-+综合得:k 的取值范围是(4-+. …………12分 22. 解(1)3,4,5x y r =-==43sin ,cos 55y x r r αα∴====-………………3分 (2)原式=(sin )(cos )(sin )(sin )(cos )sin sin cos αααααααα-----sin 4tan cos 3ααα-=-==-………………10分。
湖北省荆州中学2016-2017学年高一上学期第一次质检数学试卷 Word版含解析

2016-2017学年湖北省荆州中学高一(上)第一次质检数学试卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的选项中,只有一项是符合题目要求的1.已知全集U={1,2,3,4,5,6},集合M={2,3,5},N={4,5},则∁U(M∪N)等于()A.{1,3,5}B.{2,4,6}C.{1,5}D.{1,6}2.有五个命题如下:(1)集合N*中最小元素是1;(2)若a∈N*,b∈N*,则(a﹣b)∈N*;(3)空集是任何集合的真子集;(4)区间[2,4]是函数f(x)=x2﹣2x+3的一个单调增区间;(5)若集合A={x|1<x<3},集合B={t|1<t<3},则A≠B;其中正确的命题的个数是()A.1 B.2 C.3 D.43.下列各组函数中,表示同一函数的是()A.f(x)=x0,g(x)=1B.f(x)=x,g(x)=C.f(x)=×,g(x)=0,(x∈{﹣1,1})D.f(x)=|x|,g(x)=()24.如果全集U=R,A={x|2<x≤4},B={3,4},则A∩(∁U B)=()A.(2,3)∪(3,4)B.(2,4)C.(2,3)∪(3,4] D.(2,4]5.已知f(x)=,则f(﹣2)=()A.2 B.3 C.4 D.56.已知集合M满足{1,2,3}⊆M⊆{1,2,3,4,5},则集合M的个数为()A.4 B.5 C.6 D.77.设全集为R,函数f(x)=的定义域为集合M,则∁R M为()A.[﹣1,1] B.(﹣1,1)C.(﹣∞,﹣1]∪[1,+∞)D.(﹣∞,﹣1)∪(1,+∞)8.函数f(x)=的单调递减区间是()A.(﹣∞,]B.[,+∞)C.(﹣1,]D.[,4]9.若函数y=ax与y=﹣在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是()A.增函数B.减函数C.先增后减 D.先减后增10.已知函数,则方程f(x)=1的解是()A .或2B .或3C .或4D .或411.已知f (x )=是R 上的单调递增函数,则实数a 的取值范围为( )A .(1,+∞)B .[4,8)C .(4,8)D .(1,8) 12.已知函数f (x )=﹣x 2+2x +1的定义域为(﹣2,3),则函数y=f (|x |)的单调递增区间是( ) A .(﹣∞,﹣1)和(0,1) B .(﹣2,﹣1)和(0,1) C .(﹣3,﹣1)和(0,1) D .(﹣1,0)和(1,3)二、填空题(每题5分,满分20分,) 13.不等式﹣2x (x ﹣3)(3x +1)>0的解集为 . 14.已知全集U={x ∈Z |﹣2<x <3},A={﹣1,1},函数f (x )=﹣x 2,x ∈(∁U A ),则函数f (x )的值域为 .15.已知函数y=f ()的定义域为(0,2],则函数y=f (x +1)的定义域为 .16.已知集合A={x |mx 2+2x ﹣2≤0},B={x |mx 2+2x ﹣1≥0},且A ∩B 有且仅有一个元素,则实数m 的取值的集合为 .三、解答题(本大题共7小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.解下列关于x 的不等式:(1)≤2;(2)x 2﹣(a +1)x +a <0.18.已知集合A={x ∈R |ax 2﹣2x +1=0}(1)若集合A 中只有一个元素,用列举法写出集合A ;(2)若集合A 中至多只有一个元素,求出实数a 的取值范围. 19.已知集合S=(﹣2,8),P={x |a +1<x <2a +5}.集合∅是空集 (1)若P=∅,求实数a 的取值范围; (2)若S ∩P=∅,求实数a 的取值范围. 20.已知f (x )是定义域为(﹣1,1),且满足f (x +y )=f (x )+f (y ),且f (x )在(﹣1,1)上是减函数.(1)若f (﹣)=﹣,求f (); (2)解不等式f (1﹣x )+f (1﹣x 2)<0.21.已知函数f (x )=,其中 a ∈R .(1)若函数f (x )的定义域为R ,求实数a 的范围; (2)若函数f (x )的值域为[0,+∞),求实数a 的范围. 22.(理科)(1)证明:(a +b )3=a 3+3a 2b +3ab 2+b 3(2)已知f (x )=,记f 1(x )=f (x ),对任意n ∈N *,满足f n (x )=f [f n ﹣1(x )],①求f2()的值;②求f10(x)的解析式.23.(文科)已知函数f(x)=,(1)当a=3,x∈[﹣5,﹣3]时,求f(x)的取值范围;(2)若函数f(x)在区间(﹣2,+∞)是增函数,求实数a的取值范围.2016-2017学年湖北省荆州中学高一(上)第一次质检数学试卷参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的选项中,只有一项是符合题目要求的1.已知全集U={1,2,3,4,5,6},集合M={2,3,5},N={4,5},则∁U(M∪N)等于()A.{1,3,5}B.{2,4,6}C.{1,5}D.{1,6}【考点】交、并、补集的混合运算.【分析】先求出M∪N,再求出C U(M∪N)即可【解答】解;∵M={2,3,5},N={4,5}∴M∪N={2,3,4,5}∵U={1,2,3,4,5,6}∴C U(M∪N)={1,6}故选;D2.有五个命题如下:(1)集合N*中最小元素是1;(2)若a∈N*,b∈N*,则(a﹣b)∈N*;(3)空集是任何集合的真子集;(4)区间[2,4]是函数f(x)=x2﹣2x+3的一个单调增区间;(5)若集合A={x|1<x<3},集合B={t|1<t<3},则A≠B;其中正确的命题的个数是()A.1 B.2 C.3 D.4【考点】命题的真假判断与应用;集合的含义.【分析】运用集合的定义、性质及真子集的定义与性质,二次函数的单调性逐一判断.【解答】解:对于(1),正整数集中最小元素是1,故(1)是正确的;对于(2),若a∈N*,b∈N*,则a﹣b 可能为负整数,故(2)错;对于(3),空集不能是本身的真子集,故(3)错;对于(4),f(x)=x2﹣2x+3在[1,+∞)是增函数,所以区间[2,4]是函数f(x 的一个单调增区间,故(4)正确;对于(5)集合中的代表元素可以不是同一字母,故集合A=B,故(5)错;故答案选B.3.下列各组函数中,表示同一函数的是()A.f(x)=x0,g(x)=1B.f(x)=x,g(x)=C.f(x)=×,g(x)=0,(x∈{﹣1,1})D.f(x)=|x|,g(x)=()2【考点】判断两个函数是否为同一函数.【分析】根据两个函数的定义域相同,对应关系也相同,即可判断它们是同一函数.【解答】解:对于A,f(x)=x0=1(x≠0),与g(x)=1(x∈R)的定义域不同,不是同一函数;对于B,f(x)=x(x∈R),与g(x)==|x|(x∈R)的对应关系不同,不是同一函数;对于C,f(x)=×=0,x∈{﹣1,1},与g(x)=0,x∈{﹣1,1}的定义域和值域相同,解析式相同,是同一函数;对于D,f(x)=|x|(x∈R),与g(x)==x(x≥0)的定义域不同,不是同一函数.故选:C.4.如果全集U=R,A={x|2<x≤4},B={3,4},则A∩(∁U B)=()A.(2,3)∪(3,4)B.(2,4)C.(2,3)∪(3,4] D.(2,4]【考点】交、并、补集的混合运算.【分析】A∩(C∪B)即求在A中但不在B中的元素组成的集合.【解答】解:由题意A∩(∁U B)={x|2<x≤4且x≠3,x≠4}=(2,3)∪(3,4)故选A5.已知f(x)=,则f(﹣2)=()A.2 B.3 C.4 D.5【考点】函数的值.【分析】由已知得f(﹣2)=f(0)=f(2)=f(4)=f(6)=f(8),由此能求出结果.【解答】解:∵f(x)=,∴f(﹣2)=f(0)=f(2)=f(4)=f(6)=f(8)=8﹣5=3.故选:B.6.已知集合M满足{1,2,3}⊆M⊆{1,2,3,4,5},则集合M的个数为()A.4 B.5 C.6 D.7【考点】子集与真子集.【分析】根据子集的定义可知,M至少含有三个元素,根据子集的定义知M最多含有五个元素,采用列举法进行求解.【解答】解:∵{1,2,3}⊆M,∴M中至少含有3个元素,且必有1,2,3,∵M⊆{1,2,3,4,5},∴M中至多含有5个元素,∴M={1,2,3},{1,2,3,4},{1,2,3,5},或{1,2,3,4,5}共有4个故选A7.设全集为R,函数f(x)=的定义域为集合M,则∁R M为()A.[﹣1,1] B.(﹣1,1)C.(﹣∞,﹣1]∪[1,+∞)D.(﹣∞,﹣1)∪(1,+∞)【考点】补集及其运算.【分析】根据题意,先求出f(x)的定义域M,再求∁R M.【解答】解:∵f(x)=,∴x2﹣1>0,解得x>1或x<﹣1,∴f(x)的定义域M=(﹣∞,﹣1)∪(1,+∞).∴∁R M=[﹣1,1],故选:A8.函数f(x)=的单调递减区间是()A.(﹣∞,]B.[,+∞)C.(﹣1,]D.[,4]【考点】复合函数的单调性.【分析】令t=4+3x﹣x2≥0,求得函数的定义域,且f(x)=g(t)=,本题即求函数t在定义域内的减区间,利用二次函数的性质可得结论.【解答】解:令t=4+3x﹣x2≥0,求得﹣1≤x≤4,可得函数的定义域为[﹣1,4],f(x)=g(t)=,故本题即求函数t在定义域内的减区间,利用二次函数的性质可得t在定义域内的减区间为[,4],故选:D.9.若函数y=ax与y=﹣在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上是()A.增函数B.减函数C.先增后减 D.先减后增【考点】函数单调性的判断与证明.【分析】根据y=ax与y=﹣在(0,+∞)上都是减函数,得到a<0,b<0,对二次函数配方,即可判断y=ax2+bx在(0,+∞)上的单调性.【解答】解:∵y=ax与y=﹣在(0,+∞)上都是减函数,∴a<0,b<0,∴y=ax2+bx的对称轴方程x=﹣<0,∴y=ax2+bx在(0,+∞)上为减函数.故答案B10.已知函数,则方程f(x)=1的解是()A.或2 B.或3 C.或4 D.或4【考点】函数的零点.【分析】由方程f(x)=1可得①,或②,分别求出①②的解集,取并集即得所求.【解答】解:由方程f(x)=1可得①,或②,解①可得x=,解②可得x=4,故方程f(x)=1的解是x=或x=4,故选C.11.已知f(x)=是R上的单调递增函数,则实数a的取值范围为()A.(1,+∞)B.[4,8)C.(4,8)D.(1,8)【考点】函数单调性的性质.【分析】由条件利用函数的单调性的性质可得,由此求得实数a的取值范围.【解答】解:∵f(x)=是R上的单调递增函数,∴,解得4≤a<8,故选:B.12.已知函数f(x)=﹣x2+2x+1的定义域为(﹣2,3),则函数y=f(|x|)的单调递增区间是()A.(﹣∞,﹣1)和(0,1)B.(﹣2,﹣1)和(0,1)C.(﹣3,﹣1)和(0,1)D.(﹣1,0)和(1,3)【考点】二次函数的性质.【分析】先求定义域,再将函数转化为分段函数,然后在定义域内求二次函数的单调区间即可.【解答】解:∵f(x)的定义域是(﹣2,3),又|x|<3⇒﹣3<x<3,∴y=f(|x|)的定义域是(﹣3,3)f(|x|)=﹣x2+2|x|+1=∴函数y=f(|x|)的单调递增区间是(﹣3,﹣1)和(0,1).故选C二、填空题(每题5分,满分20分,)13.不等式﹣2x(x﹣3)(3x+1)>0的解集为(﹣∞,﹣)∪(0,3).【考点】一元二次不等式的解法.【分析】把原不等式化为2x(x﹣3)(3x+1)<0,求出不等式对应方程的实数根,即可写出不等式的解集.【解答】解:不等式﹣2x(x﹣3)(3x+1)>0可化为2x(x﹣3)(3x+1)<0,且不等式对应方程的实数根为0,3和﹣;根据符号法则得出不等式的解集为(﹣∞,﹣)∪(0,3).故答案为:(﹣∞,﹣)∪(0,3).14.已知全集U={x∈Z|﹣2<x<3},A={﹣1,1},函数f(x)=﹣x2,x∈(∁U A),则函数f (x)的值域为{﹣4,0} .【考点】风险决策的必要性和重要性;函数的值域;二次函数的性质.【分析】求解出∁U A,即可求解函数f(x)=﹣x2的值域.【解答】解:全集U={x∈Z|﹣2<x<3},A={﹣1,1},∴∁U A={0,2}f(x)=﹣x2,x∈(∁U A),即x∈{0,2},当x=0时,函数f(0)=0,当x=2时,函数f(2)=﹣4.∴函数f(x)的值域为{﹣4,0}.故答案为:{﹣4,0}.15.已知函数y=f()的定义域为(0,2],则函数y=f(x+1)的定义域为(﹣1,﹣] .【考点】函数的定义域及其求法.【分析】由函数y=f()的定义域为(0,2],可求的值域,即函数f(x)的定义域,再由x+1∈(﹣1,﹣],即可求得y=f(x+1)的定义域.【解答】解:函数y=f()的定义域为(0,2],则=1﹣∈(0,],即函数f(x)的定义域为(0,],令x+1∈(0,],解得x∈(﹣1,﹣].则函数y=f(x+1)的定义域为(﹣1,﹣].故答案为:(﹣1,﹣].16.已知集合A={x|mx2+2x﹣2≤0},B={x|mx2+2x﹣1≥0},且A∩B有且仅有一个元素,则实数m的取值的集合为{﹣2} .【考点】交集及其运算.【分析】由A∩B有且仅有一个元素,得到1≤mx2+2x≤2,有唯一的解,需要分类讨论,问题得以解决.【解答】解:∵A∩B有且仅有一个元素,∴1≤mx2+2x≤2,有唯一的解,当m=0时,此时A∩B={x|≤x≤},不满足题意,当m≠0时,设f(x)=mx2+2x,则对称轴为x=﹣,f(﹣)=﹣,若m>0,则f(x)min=f(﹣)=﹣=2,解得m=﹣1(舍去),若m<0,则f(x)max=f(﹣)=﹣=1,解得m=﹣2,故实数m的取值的集合为{﹣2}三、解答题(本大题共7小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.解下列关于x的不等式:(1)≤2;(2)x2﹣(a+1)x+a<0.【考点】其他不等式的解法.【分析】(1)利用分式不等式的解法,移项通分化简解之;(2)首先分解因式,讨论两个根的大小,得到不同情况下的解集.【解答】解:(1)变形为,即,所以(x+3)x≥0,且x≠0,所以x>0或者x≤﹣3;不等式的解集为{x|x>0或x≤﹣3};(2)不等式变形为(x﹣a)(x﹣1)<0,当a=1时不等式的解集为∅;当a>1时,不等式的解集为(1,a);当A<1时,不等式的解集为(a,1).18.已知集合A={x∈R|ax2﹣2x+1=0}(1)若集合A中只有一个元素,用列举法写出集合A;(2)若集合A中至多只有一个元素,求出实数a的取值范围.【考点】集合的表示法.【分析】(1)用描述法表示的集合元素个数问题,用到一元方程解的个数,用判别式与零的关系,当方程有一个解时,判别式等于零.(2)A中至多只有一个元素包含只有一个根或无根,只有一个根包含两种情况:一次方程或二次方程只有一个根,二次方程根的个数通过判别式为0;无根时,判别式小于0,解得.【解答】解:(1)当a=0时,A={};当a≠0时,若集合A只有一个元素,由一元二次方程判别式△=4﹣4a=0得a=1.此时A={1}综上,当a=0时,A={}.当a=1时,A={1};(2)∵A中至多只有一个元素,∴A中只有一个元素,或A=∅.若A中只有一个元素,则当a=0时,A={x|﹣2x+1=0}={},符合条件;当a≠0时,方程ax2﹣2x+1=0为一元二次方程,要使A中只有一个元素,则方程ax2﹣2x+1=0只有一个实数解,所以△=4﹣4a=0⇒a=1.所以,a的值为0或1.若A=∅,则方程ax2﹣2x+1=0无实数解,所以△=4﹣4a<0⇒a>1.所以,a≥1或a=0.19.已知集合S=(﹣2,8),P={x|a+1<x<2a+5}.集合∅是空集(1)若P=∅,求实数a的取值范围;(2)若S∩P=∅,求实数a的取值范围.【考点】交集及其运算.【分析】(1)根据P为空集列出关于a的不等式,求出不等式的解集即可确定出a的范围;(2)由S,P,以及两集合交集为空集,确定出a的范围即可.【解答】解:(1)∵P={x|a+1<x<2a+5}=∅,∴a+1≥2a+5,解得:a≤﹣4;(2)∵S=(﹣2,8),P={x|a+1<x<2a+5},且S∩P=∅,∴a+1≥2a+5或,解得:a≤﹣4或﹣4<a≤﹣或a≥7,即a≤﹣或a≥7,则a的范围是(﹣∞,﹣]∪[7,+∞).20.已知f(x)是定义域为(﹣1,1),且满足f(x+y)=f(x)+f(y),且f(x)在(﹣1,1)上是减函数.(1)若f(﹣)=﹣,求f();(2)解不等式f(1﹣x)+f(1﹣x2)<0.【考点】抽象函数及其应用.【分析】(1)求出f(﹣)的值,根据0=f()+f(﹣),求出f()的值即可;(2)根据函数的单调性单调关于x的不等式,解出即可.【解答】解:(1)∵f(x+y)=f(x)+f(y)且f(﹣)=,∴f(﹣﹣)=f(﹣)+f(﹣)=﹣,∴f(﹣)=﹣,∵f(﹣)=f()+f(﹣),∴f(0)=f()+f(﹣),而f(0+0)=f(0)+f(0),∴f(0)=0,∴0=f()+f(﹣),∴f()=﹣f(﹣)=;(2)∵f(1﹣x)+f(1﹣x2)<0,且f(x+y)=f(x)+f(y),∴f(1﹣x+1﹣x2)<f(0),即f(﹣x2﹣x+2)<f(0),又f(x)是定义在R上的减函数,∴﹣x2﹣x+2>0,解得:﹣2<x<1,故不等式的解集是(﹣2,1).21.已知函数f(x)=,其中a∈R.(1)若函数f(x)的定义域为R,求实数a的范围;(2)若函数f(x)的值域为[0,+∞),求实数a的范围.【考点】函数的值域;函数的定义域及其求法.【分析】(1)由函数f(x)的定义域为R,可得ax2﹣x+3≥0对x∈R恒成立,得到,求解不等式组得答案;(2)由函数f(x)=的值域为[0,+∞),得a=0或,求解不等式组后再取并集得答案.【解答】解:(1)∵函数f(x)=的定义域为R,∴ax2﹣x+3≥0对x∈R恒成立,则,解得,∴实数a的范围为[);(2)∵函数f(x)=的值域为[0,+∞),∴a=0或,解得0.∴实数a的范围为[0,].22.(理科)(1)证明:(a+b)3=a3+3a2b+3ab2+b3(x)],(2)已知f(x)=,记f1(x)=f(x),对任意n∈N*,满足f n(x)=f[f n﹣1①求f2()的值;②求f10(x)的解析式.【考点】函数与方程的综合运用.【分析】(1)由(a+b)3=(a+b)2(a+b)=(a2+2ab+b2)(a+b),展开化简即可证明.(2)①f(x)=,可得=,可得f2()=f==.②由==,利用递推关系可得:f10(x)=,即可得出.【解答】(1)证明:∵(a+b)3=(a+b)2(a+b)=(a2+2ab+b2)(a+b)=a3+3a2b+3ab2+b3,∴(a+b)3=a3+3a2b+3ab2+b3,即可证明.(2)①f(x)=,∴=,∴f2()=f===.②∵===,∴===…=,∴f10(x)=,∴f10(x)=.23.(文科)已知函数f(x)=,(1)当a=3,x∈[﹣5,﹣3]时,求f(x)的取值范围;(2)若函数f(x)在区间(﹣2,+∞)是增函数,求实数a的取值范围.【考点】函数单调性的判断与证明;函数的值域.【分析】(1)当a=3时,化简f(x),利用函数f(x)在区间[﹣5,﹣3]上的单调性即可求出f(x)的取值范围;(2)利用分离常数法化简函数f(x),根据f(x)的单调性即可求出a的取值范围.【解答】解:(1)当a=3时,f(x)==3﹣,所以x∈[﹣5,﹣3]时,函数f(x)=3﹣单调递增;且f(﹣5)=3﹣=,f(﹣3)=3﹣=8,所以x∈[﹣5,﹣3]时,f(x)的取值范围是[,8];(2)因为函数f(x)===a+,当函数f(x)在区间(﹣2,+∞)是增函数时,1﹣2a<0,解得a>,所以实数a的取值范围是a>.2016年12月27日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年湖北省荆州中学高一(上)期末数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5.00分)若点(a,9)在函数y=3x的图象上,则tan的值为()A.0 B.C.1 D.2.(5.00分)若sinα>0且tanα<0,则的终边在()A.第一象限B.第二象限C.第一象限或第三象限D.第三象限或第四象限3.(5.00分)若2弧度的圆心角所对弧长为4cm,则圆心角所夹的扇形面积为()A.2πcm2B.4πcm2C.2cm2D.4cm24.(5.00分)已知均为单位向量,它们的夹角为,那么等于()A.B. C.4 D.5.(5.00分)已知x0是函数f(x)=e x+2x﹣4的一个零点,若x1∈(﹣1,x0),x2∈(x0,2),则()A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0 C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>06.(5.00分)已知函数f(x)=sin(ωx+)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度7.(5.00分)设,若与的夹角是钝角,则实数m的范围是()A.m>4 B.m<4 C.m<4且D.m<4且8.(5.00分)已知幂函数f(x)的图象过点,则f(x)是()A.偶函数B.奇函数C.定义域上的增函数D.定义域上的减函数9.(5.00分)设全集U=R,集合,则(∁U A)∩B=()A.∅B.[﹣1,0)C. D.[0,2]10.(5.00分)f(x)是偶函数,且在(﹣∞,0)上是增函数,则下列关系成立的是()A.f(﹣2)<f(1)<f(3)B.f(1)<f(﹣2)<f(3)C.f(3)<f(﹣2)<f(1)D.f(﹣2)<f(3)<f(1)11.(5.00分)已知函数f (x)是定义在闭区间[﹣a,a](a>0)上的奇函数,F(x)=f (x)+1,则F(x)最大值与最小值之和为()A.1 B.2 C.3 D.012.(5.00分)据统计,一名工人组装第x件某产品所用的时间(单位:分钟)f(x)=(m,c为常数),已知工人组装第4件产品所用的时间为30分钟,工人组装第m件产品所用的时间为15分钟,则m=()A.49 B.25 C.16 D.9二、填空题(本大题共4小题,每小题5分,共20分)13.(5.00分)()0.5+()+(0.1)﹣2﹣(π)0+lg2+lg5=.14.(5.00分)若对于任意正数x,y,都有f(xy)=f(x)+f(y),且f(8)=﹣3,则时,正数a=.15.(5.00分)已知P是函数y=x2图象上的一点,A(1,﹣1),则的最大值为.16.(5.00分)y=f(x)为R上的偶函数,且满足f(x+4)=f(4﹣x),当x∈[0,4]时,f(x)=x且sinα=,则f[2016+sin(α﹣2π)•sin(π+α)﹣2cos2(﹣α)]=.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)17.(12.00分)已知,求a的取值集合.18.(12.00分)已知f(x)=Asin(ωx+φ)(A>0,ω>0,﹣π<φ<π)的图象如图所示.(1)根据图象写出f(x)的解析式;(2)A为锐角三角形的一个内角,求f(A)的最大值,及当f(A)取最大值时A的值.19.(12.00分)已知,是平面内两个不共线的非零向量,=2+,=﹣+λ,=﹣2+,且A,E,C三点共线.(1)求实数λ的值;若=(2,1),=(2,﹣2),求的坐标;(2)已知点D(3,5),在(1)的条件下,若ABCD四点构成平行四边形,求点A的坐标.20.(12.00分)有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.(1)若这个梯形上底为CD=2a,求它的腰长x;(2)求出这个梯形的周长y关于腰长x的函数解析式,并指出它的定义域;(3)求这个梯形周长的最大值,并求出当它最大时,梯形的面积S.21.(12.00分)已知函数是奇函数.(1)求a的值;(2)判断函数f(x)的单调性,(不需证明)(3)若对任意的t∈R,不等式f(kt2+2)+f(t2﹣tk)>0恒成立,求实数k的取值范围.22.(10.00分)在平面直角坐标系中,已知角α的终边经过点P(﹣3,4)(1)求sinα和cosα的值;(2)化简并求值:.2016-2017学年湖北省荆州中学高一(上)期末数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5.00分)若点(a,9)在函数y=3x的图象上,则tan的值为()A.0 B.C.1 D.【解答】解:将(a,9)代入到y=3x中,得3a=9,解得a=2.∴=.故选:D.2.(5.00分)若sinα>0且tanα<0,则的终边在()A.第一象限B.第二象限C.第一象限或第三象限D.第三象限或第四象限【解答】解;∵sinα>0且tanα<0,∴α位于第二象限.∴+2kπ<α<2kπ+π,k∈Z,则+kπ<<kπ+k∈Z当k为奇数时它是第三象限,当k为偶数时它是第一象限的角∴角的终边在第一象限或第三象限,故选:C.3.(5.00分)若2弧度的圆心角所对弧长为4cm,则圆心角所夹的扇形面积为()A.2πcm2B.4πcm2C.2cm2D.4cm2【解答】解:∵2弧度的圆心角所对弧长为4cm,∴扇形的面积S===4cm2,故选:D.4.(5.00分)已知均为单位向量,它们的夹角为,那么等于()A.B. C.4 D.【解答】解:均为单位向量,它们的夹角为,所以=+6•+9=12+6×1×1×cos+9×12=13,那么=.故选:D.5.(5.00分)已知x0是函数f(x)=e x+2x﹣4的一个零点,若x1∈(﹣1,x0),x2∈(x0,2),则()A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0 C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0【解答】解:∵函数f(x)=e x+2x﹣4在R上单调递增,且f(x0)=0,∴由x1∈(﹣1,x0),x2∈(x0,2),可得f(x1)<0,f(x2)>0.故选:B.6.(5.00分)已知函数f(x)=sin(ωx+)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【解答】解:由题知ω=2,所以,故选:A.7.(5.00分)设,若与的夹角是钝角,则实数m的范围是()A.m>4 B.m<4 C.m<4且D.m<4且【解答】解:,当与的夹角是钝角时,•<0…①且与不平行…②;由①得,﹣3×4+3m<0,解得m<4;由②得,﹣3×3﹣4m≠0,解得m≠﹣;综上,实数m的范围是m<4且m≠﹣.故选:D.8.(5.00分)已知幂函数f(x)的图象过点,则f(x)是()A.偶函数B.奇函数C.定义域上的增函数D.定义域上的减函数【解答】解:设f(x)=xα,∵幂函数y=f(x)图象过点(2,),∴=2α,解得α=﹣,∴f(x)=,是定义域上的减函数,故选:D.9.(5.00分)设全集U=R,集合,则(∁U A)∩B=()A.∅B.[﹣1,0)C. D.[0,2]【解答】解:∵集合={x|x≥0},∴∁U A={x|x<0}=(﹣∞,0),由得,,∴,则集合B={y|﹣1≤y≤2}=[﹣1,2],∴(∁U A)∩B=(﹣∞,0)∩[﹣1,2]=[﹣1,0),故选:B.10.(5.00分)f(x)是偶函数,且在(﹣∞,0)上是增函数,则下列关系成立的是()A.f(﹣2)<f(1)<f(3)B.f(1)<f(﹣2)<f(3)C.f(3)<f(﹣2)<f(1)D.f(﹣2)<f(3)<f(1)【解答】解:∵f(x)是偶函数,且在(﹣∞,0)上是增函数,∴f(3)=f(﹣3)<f(﹣2)<f(1)=f(﹣1),故选:C.11.(5.00分)已知函数f (x)是定义在闭区间[﹣a,a](a>0)上的奇函数,F(x)=f (x)+1,则F(x)最大值与最小值之和为()A.1 B.2 C.3 D.0【解答】解:∵函数f (x)是定义在闭区间[﹣a,a](a>0)上的奇函数,则函数的最大值和最小值,分别为f(﹣A),f(A),又∵F(x)=f (x)+1,∴F(x)最大值与最小值分别为f(﹣A)+1,f(A)+1,∴F(x)最大值与最小值之和为2故选:B.12.(5.00分)据统计,一名工人组装第x件某产品所用的时间(单位:分钟)f(x)=(m,c为常数),已知工人组装第4件产品所用的时间为30分钟,工人组装第m件产品所用的时间为15分钟,则m=()A.49 B.25 C.16 D.9【解答】解:由题意可得:f(m)==15,所以c=15,而f(4)==30,可得出c=60,故可得A=16,从而c=15=60,即有m=16.故选:C.二、填空题(本大题共4小题,每小题5分,共20分)13.(5.00分)()0.5+()+(0.1)﹣2﹣(π)0+lg2+lg5=101.【解答】解:()0.5+()+(0.1)﹣2﹣(π)0+lg2+lg5=++[(10)﹣1]﹣2﹣+lg(2×5)=++100﹣+1=101故答案为:10114.(5.00分)若对于任意正数x,y,都有f(xy)=f(x)+f(y),且f(8)=﹣3,则时,正数a=.【解答】解:f(8)=f(2×4)=f(2)+f(4)=f(2)+f(2)+f(2)=3f(2)=﹣3,∴f(2)=﹣1,∴f(2)=2f()=﹣1,∴f()=﹣,∴f()=f(×2)=f()+f(2)=﹣,∴f()=.∴a=,故答案为:.15.(5.00分)已知P是函数y=x2图象上的一点,A(1,﹣1),则的最大值为.【解答】解:设P(x,x2),则:;∴;∴的最大值为.故答案为:.16.(5.00分)y=f(x)为R上的偶函数,且满足f(x+4)=f(4﹣x),当x∈[0,4]时,f(x)=x且sinα=,则f[2016+sin(α﹣2π)•sin(π+α)﹣2cos2(﹣α)]=.【解答】解:∵y=f(x)为R上的偶函数,∴f(﹣x)=f(x),又f(x+4)=f(4﹣x),∴f(x+8)=f[(4﹣(4+x)]=f(﹣x)=f(x),∴y=f(x)的周期是8,又f[2016+sin(α﹣2π)•sin(π+α)﹣cos2(﹣α)]=f[2016+sin2α﹣cos2α]=f (2015+2sin2α)=f(2016﹣)=f(﹣)=f()=,故答案为:.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)17.(12.00分)已知,求a的取值集合.【解答】解:a>1时,,∴⇔⇔=,∴,则a>;当0<a<1时,,∴⇔,∴0<,综上得:a∈(0,)∪(,+∞).18.(12.00分)已知f(x)=Asin(ωx+φ)(A>0,ω>0,﹣π<φ<π)的图象如图所示.(1)根据图象写出f(x)的解析式;(2)A为锐角三角形的一个内角,求f(A)的最大值,及当f(A)取最大值时A的值.【解答】(本题满分为12分)解:(1)由函数图象可得:A=2,,∴可得:ω=2,∵时,2sin[2×(﹣)+φ]=0,由五点作图法可得:,∴,∴.…(6分)(2)∵,∴,∴可得:f(A)=2sin(2A+),当且仅当时f(A)最大,f(A)max=2.…(12分)19.(12.00分)已知,是平面内两个不共线的非零向量,=2+,=﹣+λ,=﹣2+,且A,E,C三点共线.(1)求实数λ的值;若=(2,1),=(2,﹣2),求的坐标;(2)已知点D(3,5),在(1)的条件下,若ABCD四点构成平行四边形,求点A的坐标.【解答】解:(1)∵=,∵A,E,C三点共线,∴存在实数k,使得.即,得.∵,是平面内两个不共线的非零向量,∴,解得,.∴.(2)∵A、B、C、D四点构成平行四边形,∴.设A(x,y),则,又,∴,解得,∴点A(10,7).20.(12.00分)有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.(1)若这个梯形上底为CD=2a,求它的腰长x;(2)求出这个梯形的周长y关于腰长x的函数解析式,并指出它的定义域;(3)求这个梯形周长的最大值,并求出当它最大时,梯形的面积S.【解答】解:(1)∵22﹣a2=x2﹣(2﹣a)2∴x2=8﹣4a,∴它的腰长…(4分)(2)由(1)知:,∴,∵,∴定义域为…(8分)(3)由(2)知,x=1时,y最大此时梯形的上底,高,∴.21.(12.00分)已知函数是奇函数.(1)求a的值;(2)判断函数f(x)的单调性,(不需证明)(3)若对任意的t∈R,不等式f(kt2+2)+f(t2﹣tk)>0恒成立,求实数k的取值范围.【解答】解:(1)由题意:是定义域为R的奇函数,∴f(0)=0即,∴a=1.当a=1时,,,故a=1满足题意;(2)单调递增函数;(3)由(2)得f(kt2+2)+f(t2﹣tk)>0等价于f(kt2+2)>﹣f(t2﹣tk),即kt2+2>﹣t2+tk,∴(k+1)t2﹣tk+2>0对任意t∈R恒成立,①k=﹣1时,t+2>0不恒成立,②k≠﹣1时,即解得:k∈(﹣1,).∴k的取值范围是:(﹣1,).22.(10.00分)在平面直角坐标系中,已知角α的终边经过点P(﹣3,4)(1)求sinα和cosα的值;(2)化简并求值:.【解答】解:(1)∵角α的终边经过点P(﹣3,4),∴x=﹣3,y=4,r=5,∴sinα==,cosα==﹣.(2)==﹣tanα=﹣=.。
