人教版数学八年级上册12.3《角的平分线的性质(1)》提升训练1

合集下载

人教版八年级数学(上册)12.3角的平分线的性质(第1课时) 课时习题(附参考答案)

12.3角的平分线的性质
（第1课时）
1. 用尺规作下列角的平分线：
2. 画出三角形三个内角的平分线
你发现了什么特点吗？ .
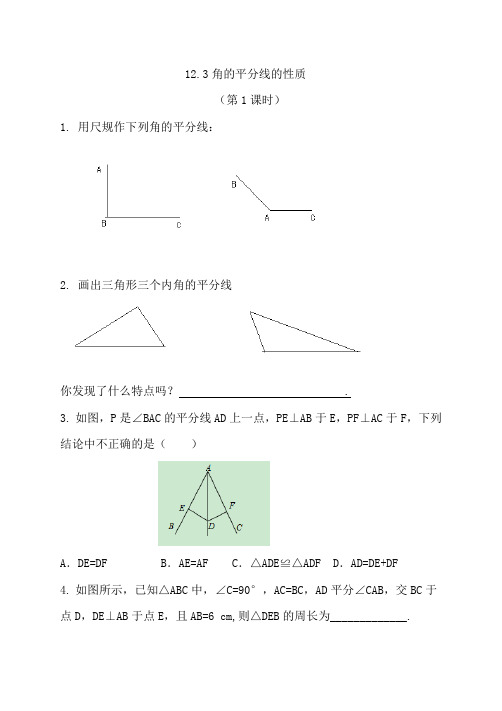
3.如图，P是∠BAC的平分线AD上一点，PE⊥AB于E，PF⊥AC于F，下列结论中不正确的是（）
A．DE=DF B．AE=AF C．△ADE≌△ADF D．AD=DE+DF
4.如图所示，已知△ABC中，∠C=90°，AC=BC，AD平分∠CAB，交BC于点D，DE⊥AB于点E，且AB=6 cm,则△DEB的周长为_____________.
5.如图，已知AB∥CD，O为∠A、∠C的角平分线的交点，OE⊥AC于E，且OE=2，则两平行线间AB、CD的距离等于。

6.如图，已知BD是∠ABC的内角平分线，CD是∠ACB的外角平分线，由D 出发，作点D到BC、AC和AB的垂线DE、DF和DG，垂足分别为E、F、G，则DE、DF、DG的关系是。

7.如图，∠AOP=∠BOP，AD⊥OB于D，BC⊥OA于C，AD与BC交于点P。

求证：AP=BP。

参考答案
1.略
2.三角形的三条角平分线相交于一点.
3.D
4. 6
5. 4
6.DE=DF=DG.
7.证明：∵∠AOP=∠BOP，AD⊥OB于D，BC⊥OA于C，∴PC=PD 在△PAC与△PBD中，
∵∠APC=∠BPD，∠ACP=∠BDP，PC=PD
∴△PAC≌△PBD，即AP=BP.。

新人教版八年级数学上册12.3角的平分线的性质(第1课时)课时同步习题(含答案)

12.3 角的平分线的性质一、选择题1. 用尺规作已知角的平分线的理论依据是（）A ．SASB ．AASC ．SSSD ．ASA2. 如图，∠1＝∠2，PD ⊥OA ，PE ⊥OB ，垂足分别为D ，E ，下列结论错误的是（）A 、PD ＝PEB 、OD ＝OEC 、∠DPO＝∠EPOD 、PD ＝OD 3. 如图，Rt △ABC 中，∠C =90°，∠ABC 的平分线BD 交AC 于D ，若CD =3cm ，则点D 到AB 的距离DE 是（）A ．5cmB ．4cmC ．3cmD ．2cm4. 如图，△ABC 中，∠C ＝90°，AC ＝BC ，AD 平分∠CAB 交BC 于D ，DE ⊥AB 于E ，且AB ＝6㎝，则△DEB 的周长为（）A. 4㎝B. 6㎝C. 10㎝D. 不能确定 21D A PO EB第2题图第3题图第4题图 5.如图，OP 平分AOB ∠，PA OA ⊥，PB OB ⊥，垂足分别为A ，B ．下列结论中不一定成立的是（） A.PA PB = B.PO 平分APB ∠ C.OA OB = D.AB 垂直平分OP6.如图，AD 是△ABC 中∠BAC 的平分线，DE ⊥A B 于点E ，DF ⊥AC 交AC 于点F ．S △ABC =7，DE=2，AB=4，则AC 长是（）第5题图第6题图第7题图7.如图，AD 是△ABC 的角平分线，DF ⊥AB ，垂足为F ，DE=DG ，△ADG 和△AED 的面积分别为50和39，则△EDF 的面积为（）DCA EBF E O D C ABA 、11B 、5.5C 、7D 、3.5 8.已知：如图，△ABC 中，∠C ＝90o ，点O 为△ABC 的三条角平分线的交点，OD ⊥BC ，OE ⊥AC ，OF ⊥AB ，点D 、E 、F 分别是垂足，且AB ＝10cm ，BC ＝8cm ，CA ＝6cm ，则点O 到三边AB 、AC 和BC 的距离分别等于（）（A ）2cm 、2cm 、2cm ．（B ）3cm 、3cm 、3cm ．（C ）4cm 、4cm 、4cm ．（D ）2cm 、3cm 、5cm ．二、填空题 9．如图，P 是∠AOB 的角平分线上的一点，PC ⊥OA 于点C ，PD ⊥OB 于点D ，写出图中一对相等的线段（只需写出一对即可） .10．如图，在△ABC 中，∠A ＝90°，BD 平分∠ABC ，AD ＝2 cm ，则点D 到BC 的距离为________cm ．11 .如图，OP 平分∠MON ，PA ⊥ON 于点A ，点Q 是射线OM 上一个动点，若PA=3，则PQ 的最小值为．第9题图第10题图第11题图12.如图，在Rt △ABC 中，∠A=90°，∠ABC 的平分线BD 交AC 于点D ，AD=3，BC=10，则△BDC 的面积是．第12题图第13题图第15题图13.如图，在Rt △ABC 中，∠C=90°，若BC=10，AD 平分∠BAC 交BC 于点D ，且BD ：CD=3：2，则点D 到线段AB 的距离为．14.已知△ABC 中，AD 是角平分线，AB=5，AC=3，且S △ADC =6，则S △ABD = ．15.如图，AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别为点E ，F ，连接EF ，则EF 与AD 的关系是．16.通过学习我们已经知道三角形的三条内角平分线是交于一点的．如图，P 是△ABC 的内角平分线的交点，已知P 点到AB 边的距离为1，△ABC 的周长为10，则△ABC 的面积为．17.如图，AD ∥BC ，∠ABC 的角平分线BP 与∠BAD 的角平分线AP 相交于点P ，作PE ⊥AB 于点E ．若PE=2，则两平行线AD 与BC 间的距离为．第16题图第17题图第18题图18. 如图，△ABC 的三边AB 、BC 、CA 长分别为40、50、60．其三条角平分线交于点O ，则S △ABO ：S △BCO ：S △CAO = ．三、解答题19．已知：AD 是△ABC 的角平分线，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，BD ＝CD ，求证：∠B ＝∠C. 20. 如图，画∠AOB=90°，并画∠AOB 的平分线OCP 上，使三角尺的两条直角边与∠AOB 的两边分别相交于点E 、F21.如图，AB ∥CD ，以点A 为圆心，小于AC 长为半径作圆弧，分别交AB ，AC 于E ，F 两点，再分别以E ，F 为圆心，大于EF 长为半径作圆弧，两条圆弧交于点P ，作射线AP ，交CD 于点M ．（1）若∠ACD=114°，求∠MAB 的度数；（2）若CN ⊥AM ，垂足为N ，求证：△ACN ≌△MCN ．22. 如图，已知△ABC 中，AB=AC ，BE 平分∠ABC 交AC 于E ，若∠A=90°，那么BC 、B A 、AE 三者之间有何关系？并加以证明．23. 如图，△ABC中，D为BC的中点，DE⊥BC交∠BAC的平分线AE于点E，EF⊥AB于F，EG⊥A G交AC的延长线于G．求证：BF=CG．12.3 角的平分线的性质第1课时角的平分线的性质一、选择题1.C2.D3.C4.B5.D6.B7.B8.A二、填空题9.PC=PD（答案不唯一）10. 2 11. 3 12. 15 13. 4 14. 1015. AD垂直平分EF 16. 5 17. 4 18. 4：5：6三、解答题19．证明：∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，∴DE＝DF，在Rt△DEB与Rt△DFC中，BD＝CD，DE＝DF，∴Rt△DEB≌Rt△DFC（HL），∴∠B＝∠C．理由是：过点∴∠ACD+∠CAB=18的平分线，∴∠MAB=∠CAB=33°22 . 解：BC、BA、AE三者之间的关系：BC=BA+AE，理由如下：过E作ED⊥BC交BC于点D，∵BE平分∠ABC，BA⊥CA，∴AE=DE，∠EDC=∠A=∠BDE=90°，∵在Rt△BAE和Rt△BDE中，∴Rt△BAE≌Rt△BDE（HL），∴BA=BD，∵AB=AC，∠A=90°∴∠C=45°，∴∠CED=45°=∠C，∴DE=CD，∵AE=DE，∴AE=CD=DE，∴BC=BD+DC=BA+AE．∵EF⊥AB EG⊥A G，。

专训12.3.1角平分线的性质+判定-八年级上册考点专训(解析版)(人教版)

专训12.3.1角平分线的性质+判定1．如图，在Rt △ABC 中，∠C ＝90°，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP 交边BC 于点D ，若CD ＝4，AB ＝15，则△ABD 的面积是_______．【答案】30【分析】作DE AB ⊥于E ，如图，利用基本作图得到AP 平分∠BAC ，根据角平分线的性质得4DC DE ==，然后根据三角形面积公式．【详解】解：作DE AB ⊥于E ，如图，由作法得AP 平分∠BAC ，∴4DC DE ==，∴△ABD 的面积=1154302⨯⨯=．故答案为：30．【点睛】本题考查了基本作图：熟练掌握5种基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．2．如图，OC 是AOB ∠的角平分线，点P 是OC 上一点，PM OB ⊥于点M ，点N 是射线OA 上的一个动点，若6PM =，则PN 的最小值为______．【答案】6【分析】根据垂线段最短可得PN ⊥OA 时，PN 最短，再根据角平分线上的点到角的两边的距离相等可得PM =PN ，从而得解．【详解】当PN ⊥OA 时，PN 的值最小，∵OC 平分∠AOB ，PM ⊥OB ，∴PM =PN ，∵PM =6，∴PN 的最小值为6．故答案为：6．【点睛】本题考查了角平分线上的点到角的两边的距离相等的性质，垂线段最短的性质，熟记性质是解题的关键．3．如图，在ABC 中，AD 为BAC ∠的平分线，DE AB ⊥于点E ，DF AC ⊥于点F ．若ABC 的面积是228cm ，20cm AB =，8cm AC =，则DE =____cm ．【答案】2【分析】先根据角平分线的性质得出DE =DF ，再根据三角形的面积公式即可得出结论．【详解】解：在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，∴DE =DF ，∴S △ABC =S △ABD +S △ACD =12AB •DE +12AC •DF ，∵△ABC 面积是28cm 2，AB =20cm ，AC =8cm ，∴12×20DE +12×8DF =10DE +4DF =14DE =28，解得DE =2cm ．故答案为：2．【点睛】本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．4．如图，在ABC 中，90C ∠=︒，AD 平分BAC ∠，过点D 作DE AB ⊥于E ，若3BE =，BDE 的周长为11，则BC =______．【答案】8【分析】利用角平分线的性质推出DE DC =，再根据三角形的周长计算得出答案．【详解】解：∵AD 平分BAC ∠，过点D 作DE AB ⊥于E ，90C ∠=︒，∴DE DC=∴BDE 的周长311BE BD DE BE BD CD BE BC BC =++=++=+=+=，∴8BC =．故答案为：8【点睛】此题考查角平分线的性质：角平分线上的点到角两边的距离相等，熟记定理是解题的关键．5．如图所示，AD 是△ABC 的平分钱，DF ⊥AB 于点F ，DE ＝DG ，若S △DEF ＝2，S △ADG ＝9：则△ADE 的面积为________．【答案】5【分析】过点D 作DH ⊥AC 于H ，根据角平分线的性质得到DH ＝DF ，进而证明Rt △DEF ≌Rt △DGH ，根据全等三角形的性质得到△DEF 的面积＝△DGH 的面积=2，同理：△ADF 的面积＝△ADH 的面积=7，进而即可求解．【详解】解：过点D 作DH ⊥AC 于H，∵AD 是△ABC 的角平分线，DF ⊥AB ，DH ⊥AC ，∴DH ＝DF ，在Rt △DEF 和Rt △DGH 中，∵DF DH DE DG ⎧⎨⎩＝＝，∴Rt △DEF ≌Rt △DGH （HL ），∴△DEF 的面积＝△DGH 的面积=2，同理可证，Rt △ADF ≌Rt △ADH ，∴△ADF 的面积＝△ADH 的面积=9-2=7，∴△ADE 的面积=7-2=5．故答案是：5．【点睛】本题考查的是全等三角形的判定与性质、角平分线的性质，作辅助线构造出全等三角形并利用角平分线的性质是解题的关键．6．如图，在ABC 中，90,C AD ∠=︒是ABC 的角平分线，DE AB ⊥，垂足为E ，若2,CD DE ==_______．【答案】2【分析】根据角平分线的性质定理即可完成．【详解】∵AD 平分∠CAB ，且∠C =90°，DE AB⊥∴DE =CD =2故答案为：2．【点睛】本题考查了角平分线的性质定理，关键是清楚定理的条件：一是角平分线，二是经过角平分线的点的直线，且这两条直线垂直角的两边，即要有两个垂直，具体在有些题目中，往往缺少一个或两个垂直，这时要作一个垂直或两个垂直．7．如图在ABC 中，=90ACB ∠︒，BE 平分ABC ∠，DE AB ⊥于D ，如果+=3AE DE ，那么=AC ________．【答案】3【分析】根据角平分线上的点到角的两边距离相等可得CE =DE ，然后求出AC =AE +DE ．【详解】解：∵∠ACB =90°，BE 平分∠ABC ，DE ⊥AB ，∴CE =DE ，∴AC =AE +CE =AE +DE =3．故答案为：3．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，是基础题，熟记性质是解题的关键．8．如图，在ABC 中，90C ∠=，AD 是BAC ∠的平分线，若2CD =，6AB =，则ABD 的面积是________．【答案】6【分析】设点D 到AB 的距离为h ，根据角平分线的性质即可求解【详解】设点D 到AB 的距离为h ，AD 是BAC ∠的平分线，90C = ∠，2CD =DC AC ∴⊥，2CD h == 6AB =∴1162622ABC S AB h =⨯=⨯⨯=△故答案为：6【点睛】本题考查了角平分线的性质，熟悉角平分线的性质是解题的关键．9．如图，OP 平分∠AOB ，PC ⊥OA ，点D 是OB 上的动点，若PC ＝1cm ，则PD 的长的最小值为___．【答案】1cm【分析】根据垂线段最短可知，当PD OB ⊥时最短，再根据角平分线上的点到角的两边的距离相等可得PD PC =，从而得解．【详解】解：垂线段最短，∴当PD OB ⊥时PD 最短，OP 是AOB ∠的平分线，PC OA ⊥，PD PC ∴=，1PC = ，1PD ∴=，即PD 长度最小为1．故答案为：1cm ．【点睛】本题考查了角平分线上的点到角的两边的距离相等的性质，垂线段最短的性质，解题的关键是：确定出PD 最小时的位置是解题的关键．10．如图，//AB CD ，108CDM ∠=︒，GF 交MEB ∠的角平分线EF 于点F ，120BGF ∠=︒．则F ∠=______．【答案】84︒【分析】根据//AB CD ，求出AED ∠，由对顶角相等及角平分线性质求出FEG ∠，最后根据三角形的外角性质求出F ∠即可．【详解】解：//,108AB CD CDM ∠=︒ ，72AED ∴∠=︒，72MEG ∴∠=︒，EF 是MEB ∠的角平分线，1362FEG MEG ∴∠=∠=︒，120BGF ∠=︒ 为三角形的外角，BGF FEG F ∴∠=∠+∠，1203684F ∴∠=︒-︒=︒，故答案是：84︒．【点睛】本题考查了平行线的性质、对顶角、角平分线的性质、三角形的外角，解题的关键是掌握相关的性质，灵活运用．11．如图，AD 是ABC 的角平分线．若90,B BD ∠=︒=，则点D 到AC 的距离是_________．【分析】根据角平分线的性质，角平分线上的点到角的两边的距离相等，即可求得．【详解】如图，过D 作DE AC ⊥，则D 到AC 的距离为DEAD平分CAB ∠，90,B BD ∠=︒=，∴DE BD ==∴点D 到AC【点睛】本题考查了角平分线的性质，点到直线的距离等知识，理解点到直线的距离的定义，熟知角平分线的性质是解题关键．12．如图，在ABC 中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ，DE AB ⊥，垂足为E ，若4BC =，1.6DE =，则BD 的长为______．【答案】2.4【分析】先根据角平分线的性质可得 1.6CD DE ==，再根据线段的和差即可得．【详解】解：AD 平分BAC ∠，90C ∠=︒，DE AB ⊥， 1.6DE =，1.6CD DE ∴==，4BC = ，4 1.6 2.4BD BC CD ∴=-=-=，故答案为：2.4．【点睛】本题考查了角平分线的性质，熟练掌握角平分线的性质是解题关键．13．如图，在 ABC 中，BD 平分∠ABC 交AC 于点D ，EF ∥BC 交BD 于点G ，若∠BEG ＝130°，则∠DGF ＝_____°．【答案】25【分析】根据角平分线的定义得到∠EBG ＝∠CBG ，根据平行线的性质得到∠EGB ＝∠CBG ，等量代换得到∠EBG ＝∠EGB ，再根据三角形的内角和定理和对顶角的性质于是得到结论．【详解】解：∵EF ∥BC ，∴∠EGB ＝∠CBG ，∵BD 平分∠ABC ，∴∠EBG ＝∠CBG ，∴∠EBG ＝∠EGB ，∵∠BEG ＝130°，∴∠EGB ＝1801302︒︒-＝25°，∴∠DGF ＝∠EGB ＝25°．故答案为：25．【点睛】本题考查了角平分线的定义，平行线的性质，三角形的内角和定理，熟练掌握这些性质是解题的关键．14．如图，在ABC 中，90C ∠=︒，以点A 为圆心，任意长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 长为半径画弧，两弧交于点O ，作射线AO ，交BC 于点E ．已知14CB =，8BE =，则点E 到AB 的距离为________．【答案】6【分析】如图，过点E 作ET ⊥AB 于T ．证明ET =EC ，可得结论．【详解】解：如图，过点E 作ET ⊥AB 于T ．∵BC =14，BE =8，∴EC =BC -BE =6，由作图可知，AE 平分⊥CAB ，∵EC ⊥AC ，ET ⊥AB ，∴ET =EC =6，故答案为：6．【点睛】本题考查作图——复杂作图，角平分线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．15．判断正误：三角形三条角平分线交于一点，且这一点到三顶点的距离相等__．【答案】⨯【分析】根据三角形角平分线的性质分析，即可得到答案．【详解】由角平分线性质可知：三角形的三条角平分线交于一点，这点到三角形的三边的距离相等；故答案为：⨯．【点睛】本题考查了三角形角平分线的知识；解题的关键是熟练掌握三角形角平分线的性质，从而完成求解．16．如图，在AOB 和COD △中，OA OB =，OC OD =，OA OC <，36AOB COD ∠=∠=︒，连接AC 、BD 交于点M ，连接OM ．下列结论：①36AMB ∠=︒，②AC BD =，③OM 平分AOD ∠，④MO 平分AMD ∠．其中正确的结论是______（填序号）．【答案】①②④【分析】由SAS 证明△AOC ≌△BOD 得出，得出∠OAC ＝∠OBD ，由扇形内角和：∠AMB=180-∠OBD-∠MGB ＝180°-∠OAC -∠OGA =∠AOC =36°，得出∠AMB ＝∠AOB ＝36°，①正确；由△AOC ≌△BOD 得出AC ＝BD ，②正确；作OG ⊥AM 于G ，OH ⊥DM 于H ，如图所示：则∠OGA ＝∠OHB ＝90°，利用全等三角形对应边上的高相等，得出OG ＝OH ，由角平分线的判定方法得出MO 平分∠AMD ，④正确；假设MO 平分∠AOD ，则∠DOM ＝∠AOM ，由全等三角形的判定定理可得△AMO ≌△DMO ，得AO ＝OD ，而OC ＝OD ，所以OA ＝OC ，而OA ＜OC ，故③错误；即可得出结论．【详解】解：设AC 与OB 交于G∵∠AOB ＝∠COD ＝36°，∴∠AOB +∠BOC ＝∠COD +∠BOC ，即∠AOC ＝∠BOD ，在△AOC 和△BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△BOD （SAS ），∴∠OAC ＝∠OBD ，∵∠OGA ＝∠MGB ，∴∠AMB=180-∠OBD-∠MGB ＝180°-∠OAC -∠OGA =∠AOC =36°，∴∠AMB ＝∠AOB ＝36°，故①正确；∵△AOC ≌△BOD （SAS ），∴AC=BD ，故②，作OG ⊥AM 于G ，OH ⊥DM 于H，如图所示，则∠OGA ＝∠OHB ＝90°，∵△AOC ≌△BOD ，∴S △OAC =S △OBD ，即AC·OG =BD·OH ，∵AC ＝BD ，∴OG ＝OH ，∴MO 平分∠AMD ，故④正确；假设MO 平分∠AOD ，则∠DOM ＝∠AOM ，在△AMO 与△DMO 中，AOM DOM OM OM AMO DMO ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AMO ≌△DMO （ASA ），∴AO ＝OD ，∵OC ＝OD ，∴OA ＝OC ，而OA ＜OC ，∴假设不正确，OM 不能平分AOD∠故③错误；正确的序号有①②④．故答案为①②④．【点睛】本题考查了全等三角形的判定与性质、三角形的内角和性质、角平分线的判定与性质，反证法等知识；掌握全等三角形的判定与性质、三角形的内角和性质、角平分线的判定与性质，反证法等知识，证明三角形全等是解题的关键．17．如图，已知ABC ∆中，90,C AC BC ∠=︒=，点D 在BC 上，DE AB ⊥，点E 为垂足，且DC DE =，联结AD ，则ADB ∠的大小为___________．【答案】112.5°【分析】首先根据角平分线的判定方法判定AD 是∠BAC 的平分线，然后利用外角性质求∠ADB 的度数即可.【详解】解：∵∠C ＝90°，DE ⊥AB∴∠C=∠AED=90°，在Rt∆ACD 和Rt∆AED 中DE DC AD AD =⎧⎨=⎩，∴Rt∆ACD ≌Rt∆AED ，∴∠CAD=∠EAD ，∴AD 平分∠BAC ，∴∠CAD ＝12∠BAC ，∵∠C ＝90°，AC ＝BC ，∴∠B ＝∠CAB ＝45°，∴∠CAD ＝22.5°，∴∠ADB=∠CAD ＋∠C ＝112.5°.故答案为：112.5°．【点睛】本题考查了角平分线的判定方法以及三角形外角的性质，角平分线的判定方法是：到角的两边距离相等的点在这个角的平分线上．18．如图，△ABC 中，∠ACB =90°，点D 在边AC 上，DE ⊥AB 于点E ，DC =DE ，∠A =32°，则∠BDC 的度数为________．【答案】61°【分析】首先利用直角三角形的性质求得∠ABC的度数，然后利用角平分线的判定方法得到BD为∠ABC的平分线，再求出∠ABD的度数，根据三角形外角的性质进而求得结论．【详解】解：∵∠A=32°，∠ACB=90°，∴∠CBA=58°，∵DE⊥AB，DC⊥BC，DC=DE，∴BD为∠ABC的平分线，∴∠CBD=∠EBD，∴∠CBD=12∠CBA=12×58°=29°,∴∠BDC=∠A+∠ABD=32°+29°=61°．故答案为：61°．【点睛】本题考查了角平分线的判定与性质，解题的关键是根据已知条件得到BD为∠ABC的平分线，难度不大．19．数学课上，同学们兴致勃勃地尝试着利用不同画图工具画一个角的平分线．小明用直尺画角平分线的方法如下：（1）用直尺的一边贴在∠AOB的OA边上，沿着直尺的另一条边画直线m；（2）再用直尺的一边贴在∠AOB的OB边上，沿着直尺的另一条边画直线n，直线m与直线n交于点D；（3）作射线OD．射线OD是∠AOB的平分线．请回答：小明的画图依据是____________________．【答案】角的内部到角的两边距离相等的点在这个角的平分线上【分析】根据角平分线的判定定理即可得出答案．【详解】∵作图时使用同一把尺子，尺子的宽度是一致的，∴点D 到OA 和OB 的距离是一样的，∴射线OD 是∠AOB 的平分线（角的内部到角的两边距离相等的点在这个角的平分线上）．故答案为：角的内部到角的两边距离相等的点在这个角的平分线上．【点睛】本题考查了角平分线的判定定理，熟练掌握角平分线判定定理是解题关键．20．如图，ABC 中，ABC ∠、EAC ∠的角平分线BP 、AP 交于点P ，延长BA 、BC ，则下列结论中正确的有_______．（将所有正确序号填在横线上）①CP 平分ACF ∠；②2180ABC APC ︒∠+∠=，③2ACB APB =∠∠；④若PM BE ⊥，PN BC ⊥，则AM CN AC +=．【答案】①②③④【分析】①作PD ⊥AC 于D ．由角平分线的性质得出PM=PN ，PM=PD ，得出PM=PN=PD ，即可得出①正确；②首先证出∠ABC+∠MPN=180°，证明Rt △PAM ≌Rt △PAD （HL ），得出∠APM=∠APD ，同理：Rt △PCD ≌Rt △PCN（HL ），得出∠CPD=∠CPN ，即可得出②正确；③由角平分线和三角形的外角性质得出∠CAE=∠ABC+∠ACB ，∠PAM=12∠ABC+∠APB ，得出∠ACB=2∠APB ，③正确；④由全等三角形的性质得出AD=AM ，CD=CN ，即可得出④正确；即可得出答案．【详解】解：①作PD ⊥AC 于D ．∵PB 平分∠ABC ，PA 平分∠EAC ，PM ⊥BE ，PN ⊥BF ，∴PM=PN ，PM=PD ，∴PM=PN=PD ，∴点P 在∠ACF 的角平分线上，故①正确；②∵PM ⊥AB ，PN ⊥BC ，∴∠ABC+90°+∠MPN+90°=360°，∴∠ABC+∠MPN=180°，在Rt △PAM 和Rt △PAD 中，PA PA PM PD=⎧⎨=⎩，∴Rt △PAM ≌Rt △PAD （HL ），∴∠APM=∠APD ，同理：Rt △PCD ≌Rt △PCN （HL ），∴∠CPD=∠CPN ，∴∠MPN=2∠APC ，∴∠ABC+2∠APC=180°，②正确；③∵PA 平分∠CAE ，BP 平分∠ABC ，∴∠CAE=2∠PAM ，∵∠CAE=∠ABC+∠ACB ，∠PAM=12∠ABC+∠APB ，∴∠ACB=2∠APB ，③正确；④∵Rt △PAM ≌Rt △PAD （已证），∴AD=AM ，∵Rt △PCD ≌Rt △PCN （已证），∴CD=CN ，∴AM+CN=AD+CD=AC ，④正确；故答案为：①②③④．【点睛】本题考查了角平分线的性质定理和判定定理，全等三角形的判定与性质，三角形的一个外角等于与它不相邻的两个内角的和，有一定综合性，但难度不大，只要仔细分析便不难求解．21．如图，在△ABC 中，∠A ＝90°，DE ⊥BC ，垂足为E ．若AD ＝DE 且∠C ＝50°，则∠ABD ＝_____°．【答案】20︒【分析】利用三角形的内角和定理先求解ABC ∠，再利用角平分线的性质定理的逆定理证明：BD 平分,ABC ∠从而可得答案．【详解】解：9050A C ∠=︒∠=︒ ，，180905040ABC ∴∠=︒-︒-︒=︒，90,,A DE BC DA DE ∠=︒⊥= ，BD ∴平分,ABC ∠1202ABD ABC ∠=∠=︒，故答案为：20.︒【点睛】本题考查的是三角形的内角和定理，角平分线的定义及性质定理的逆定理，掌握角平分线的性质定理的逆定理是解题的关键．22．如图，BD⊥AE于点B，DC⊥AF于点C，且DB=DC，∠BAC=60°，∠ADG=120°，则∠DGF=_____________【答案】150°【分析】先根据到角的两边距离相等的点在角的平分线上得到AD是∠BAC的平分线，求出∠CAD的度数，再根据三角形的一个外角等于与它不相邻的两个内角的和即可求解．【详解】解：∵BD⊥AE于B，DC⊥AF于C，且DB=DC，∴AD是∠BAC的平分线，∵∠BAC=60°，∴∠CAD=12∠BAC=30°，∴∠DGF=∠CAD+∠ADG=30°+120°=150°．故答案为：150°．【点睛】本题考查了角平分线的判定与三角形的一个外角等于与它不相邻的两个内角的和的性质，仔细分析图形是解题的关键．23．如图，O是△ABC内一点，且O到三边AB，BC，CA的距离OF＝OD＝OE，若∠BAC＝80°，则∠BOC 的度数为_________．【答案】130°根据到角的两边距离相等的点在角的平分线上判断出点O 是三角形三条角平分线的交点，再根据三角形的内角和定理求出∠ABC+∠ACB ，然后求出∠OBC+∠OCB ，再利用三角形的内角和定理列式计算即可得解．【详解】解：∵O 到三边AB 、BC 、CA 的距离OF=OD=OE ，∴点O 是三角形三条角平分线的交点，∵∠BAC=80°，∴∠ABC+∠ACB=180°-80°=100°，∴∠OBC+∠OCB=12（∠ABC+∠ACB ）=12×100°=50°，在△OBC 中，∠BOC=180°-（∠OBC+∠OCB ）=180°-50°=130°．故答案为：130°．【点睛】本题考查了到角的两边距离相等的点在角的平分线上的性质，三角形的内角和定理，要注意整体思想的利用．24．如图，ABC 中，A 60∠=︒，AB>AC ，两内角的平分线CD 、BE 交于点O ，OF 平分BOC ∠交BC 于F ，（1）BOC 120∠=︒；（2）连AO ，则AO 平分BAC ∠；（3）A 、O 、F 三点在同一直线上；（4）OD=OE ；（5）BD+CE=BC ．其中正确的结论是__________．（填序号）【答案】①②④⑤．【分析】根据三角形内角和定理求出∠ABC+∠ACB 度数，求出∠EBC+∠DCB 度数，根据三角形内角和定理求出∠BOC 即可判断①，过O 作OM ⊥AB 于M ，OQ ⊥AC 于Q ，ON ⊥BC 于N ，根据角平分线性质求出OQ=OM=ON ，根据角平分线性质求出AO 平分∠BAC 即可判断②；假设,,A O F 三点共线，利用三角形的外角的性质逆推可得：ABC ACB ∠=∠，与已知条件AB>AC ，得ACB ∠＞ABC ∠，互相矛盾，可判断③，证MOD QOE ≌，即可推出OD=OE ，从而判断④，通过全等求出BM=BN ，CN=CQ ，代入即可求出BD+CE=BC ，从而判断⑤．解：∵∠A=60°，∴18060120ABC ACB ∠+∠=︒-︒=︒，∴()1602ABC ACB ∠+∠=︒，∵BE 平分∠ABC ，CD 平分∠ACB ，∴1122EBC ABC DCB ACB ∠=∠∠=∠，，∴()1602EBC DCB ABC ACB ∠+∠=∠+∠=︒，∴()180120BOC EBC DCB ∠=︒-∠+∠=︒，∴①正确；过O 作OM ⊥AB 于M ，OQ ⊥AC 于Q ，ON ⊥BC 于N ，∵O 是∠ABC 和∠ACB 的角平分线交点，∴OM=ON ，ON=OQ ，∴OQ=OM ，∴O 在∠A 平分线上，∴②正确；如图，若,,A O F 三点共线，BOF BAO ABO COF OAC OCA ∴∠=∠+∠∠=∠+∠，，BOF COF BAO CAO ∠=∠∠=∠ ，，ABO ACO ∴∠=∠，ABC ACB ∴∠=∠，∵AB ＞AC ，∴∠ABC ＜∠ACB ，所以：A 、O 、F 不在同一直线上，∴③错误；∵120BOC ∠=︒，∴120DOE ∠=︒，OM ⊥AB ，OQ ⊥AC ，ON ⊥BC ，∴∠AMO=∠AQO=90°，∵∠A=60°，∴∠MOQ=120°，∴∠DOM=∠EOQ ，在OMD 和OQE 中，MOD EOQ OMD OQE OM ON ∠=∠⎧⎪∠=∠⎨⎪=⎩∴OMD OQE ≌（AAS ），∴OE=OD ，∴④正确；在Rt BNO 与Rt BMO 中，BO BO ON OM=⎧⎨=⎩∴()Rt BNO Rt BMO HL ≌，BN BM BD DM∴==+同理，Rt CNO Rt CQO ≌，CN CQ CE EQ ∴==-，∴BN CN BD DM CE EQ +=++-，∵DM=EQ，∴BC=BD+CE ，∴⑤正确；故答案为：①②④⑤．【点睛】本题考查了角平分线性质，三角形的内角和定理，三角形的外角的性质，全等三角形的性质和判定的应用，掌握以上知识是解题的关键．25．如图，已知OQ 平分∠AOB ，且PM ⊥OA ，PN ⊥OB ，根据角平分线的性质，则有___________；反之如果PM=PN ，且___________，那么OP 平分∠AOB．【答案】PM=PN PM ⊥OA ，PN ⊥OB【分析】依据角平分线的定理和逆定理可知．【详解】解： OQ 平分∠AOB ，且PM ⊥OA ，PN ⊥OB ，PNO PMONOP MOP OP OP∠=∠⎧⎪∴∠=∠⎨⎪=⎩()PMO PNO AAS ∴≅ PM PN∴=反之PM=PN ，且PM ⊥OA ，PN ⊥OB ，PM PNOP OP=⎧∴⎨=⎩()Rt PMO Rt PNO HL ∴≅ POM PON∴∠=∠∴OP 平分∠AOB故答案为：PM=PN ；PM ⊥OA ，PN ⊥OB【点睛】本题考查角平分线性质及其逆定理、全等三角形的判定与性质，是重要考点，难度较易，掌握相关知识是解题关键．26．如图，已知点D 是△ABC 的两外角平分线的交点，下列说法：（1）AD =CD ；（2）D 到AB 、BC 的距离相等；（3）D 到△ABC 的三边的距离相等；（4）点D 在∠B 的平分线上；其中正确的说法的序号是________________.【答案】（2）,（3）,（4）【解析】试题解析：如图，过点D 作DE BA ⊥交BA 的延长线于E ，作DF BC ⊥交BC 的延长线于F ，作DG AC ⊥于G ，∵点D 是ABC 的两外角平分线的交点，DE DG DF DG ∴==，，故()2正确；DE DF DG ∴==，故()3正确；∴点D 在B Ð的平分线上，故()4正确；只有AB BC =时，AE CF =，AD CD =，故()1错误.综上所述，说法正确的是()2()3()4.故答案为()2()3()4.点睛:角平分线上的点到角两边的距离相等.27．如图，90,C D E ∠=∠=︒为CD 中点，AE 平分,DAB ∠若32,DEA ∠= 则ABE ∠的度是__________．【答案】32︒【分析】根据已知条件以及直角三角形两锐角互余、角平分线的定义、四边形的内角和是360︒可求出64ABC ∠=︒，再根据角平分线的判定和性质即可求得答案．【详解】解:过点E 作EF AB ⊥于点F ，如图：∵90D ∠=︒,32DEA ∠=︒∴90903258DAE DEA ∠=︒-∠=︒-︒=︒∵AE 平分DAB∠∴2258116DAB DAE ∠=∠=⨯︒=︒∵90C D ∠=∠=︒∴在四边形ABCD 中，360909011664ABC ∠=︒-︒-︒-︒=︒∵EF AB ⊥，90D ∠=︒，AE 平分DAB∠∴EF ED=∵E 为CD 中点∴ED EC=∴EF EC =∵EF AB ⊥，90C ∠=︒∴BE 平分ABC∠∴11643222ABE ABC ∠=∠=⨯︒=︒故答案是：32︒【点睛】本题重点考查了角平分线的定义、判定和性质，涉及到的知识点有直角三角形的两锐角互余和四边形的内角和，其中证得EF EC =是解题的关键．28．如图，在OAB ∆和OCD ∆中，OA OB =，OC OD =，OA OC >，40AOB COD ∠=∠= ，连接AC ，BD 交于点M ，连接OM ，下列结论：①AC BD =；②40CMD ∠= ；③OM 平分AOD ∠；④MO 平分BMC ∠，其中正确的序号是__________．【答案】①②④【分析】由SAS 证明△AOC ≌△BOD 得出∠OCA=∠ODB ，AC=BD ，①正确；由全等三角形的性质得出∠OAC=∠OBD ，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD ，得出∠AMB=∠AOB=40°，②正确；作OG ⊥MC 于G ，OH ⊥MB 于H ，如图所示：则∠OGC=∠OHD=90°，由AAS 证明△OCG ≌△ODH （AAS ），得出OG=OH ，由角平分线的判定方法得出MO 平分∠BMC ，④正确；先假设OM 平分∠AOD ，推出OA=OC 与条件中OA OC >相矛盾，推出③错误．【详解】解：∵∠AOB=∠COD=40︒，∴∠AOB+∠AOD=∠COD+∠AOD ，即∠AOC=∠BOD ，在△AOC 和△BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≅△BOD ，∴∠OCA=∠ODB ，AC=BD ，①正确；∵△AOC ≅△BOD∴∠OAC=∠OBD ，由三角形的外角性质得：∠AMB+∠OAC=∠AOB+∠OBD ，∴∠AMB=∠AOB=40︒，∴∠CMD=∠AMB=40︒，②正确；作OG ⊥MC 于G ，OH ⊥MB 于H ，如图2所示：则∠OGC=∠OHD=90︒，在△OCG 和△ODH 中，OCA ODB OGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△OCG ≅△ODH ，∴OG=OH ，∵OG ⊥MC ，OH ⊥MB∴MO 平分∠BMC ，④正确；∵∠AOB=∠COD ，假设OM 平分∠AOD ，∵OM 平分∠AOD，∴∠AOM=∠DOM ，∵△AOC ≌△BOD ，∴∠COM=∠BOM ，∵MO 平分∠BMC ，∴∠CMO=∠BMO ，在△COM 和△BOM 中，∴△COM ≌△BOM(ASA)，∴OB=OC ，∵OA=OB ，∴OA=OC ，与OA>OC 矛盾，故假设不成立，OM 不平分∠AOD∴③错误；故答案为：①②④【点睛】本题主要考查了全等三角形的判定与性质，掌握全等三角形的判定与性质是解题的关键．29．如图，52A ∠=︒，O 是ABC ∠、ACB ∠的角平分线交点，P 是ABC ∠、ACB ∠外角平分线交点，则BOC ∠=______︒，BPC ∠=_____︒，联结AP ，则PAB ∠=______︒，点O ____（选填“在”、“不在”或“不一定在”）直线AP 上．【答案】1166426在【分析】∠ABC+∠ACB=180°-∠A ，∠OBC+∠OCB=12（∠ABC+∠ACB ）,∠BOC=180°-（∠OBC+∠OCB ），据此可求∠BOC 的度数；∠BCP=12∠BCE=12（∠A+∠ABC），∠PBC=12∠CBF=12（∠A+∠ACB），由三角形内角和定理得：∠BPC=180°-∠BCP-∠PBC，据此可求∠BPC的度数；作PG⊥AB于G，PH⊥AC于H，PK⊥BC于K，利用角平分线的性质定理可证明PG=PH，于是可证得AP 平分∠BAC，据此可求∠PAB的度数；同理可证OA平分∠BAC，故点O在直线AP上．【详解】解：∵O点是∠ABC和∠ACB的角平分线的交点，∴∠OBC+∠OCB=12（∠ABC+∠ACB）=12（180°-∠A）=90°-12∠A，∴∠BOC=180°-（∠OBC+∠OCB）=180°-90°+12∠A=90°+12∠A=90°+26°=116°；如图，∵BP、CP为△ABC两外角的平分线，∴∠BCP=12∠BCE=12（∠A+∠ABC），∠PBC=12∠CBF=12（∠A+∠ACB），由三角形内角和定理得：∠BPC=180°-∠BCP-∠PBC=180°-12[∠A+（∠A+∠ABC+∠ACB）]=180°-12（∠A+180°）=90°-12∠A=90°-26°=64°．如图，作PG⊥AB于G，PH⊥AC于H，PK⊥BC于K，连接AP，∵BP、CP为△ABC两外角的平分线，PG⊥AB，PH⊥AC，PK⊥BC，∴PG=PK，PK=PH，∴PG=PH，∴AP平分∠BAC，∴PAB∠=26°同理可证OA平分∠BAC，点O在直线AP上．故答案是：(1)116；(2)64；(3)26；(4)在.【点睛】此题主要考查了角平分线的性质定理和判定定理及三角形内角和定理，熟知定理并正确作出辅助线是解题关键．30．小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”小明的做法，其理论依据是__【答案】在角的内部，到角两边距离相等的点在角的平分线上【分析】根据角平分线的性质即可证明.【详解】因为直尺的宽度一样，故点P 到AO 与BO 的距离相等，故可知PO 为角平行线.【点睛】此题主要考查角平行线的性质，解题的关键是熟知角平分线的性质.31．如图,在平面直角坐标系xOy 中,点A 、B 分别在x 轴的正半轴、y 轴的正半轴上移动,点M 在第二象限，且MA 平分∠BAO ，做射线MB ，若∠1=∠2，则∠M 的度数是_______。

人教版八年级数学上册练习 12.3《角的平分线的性质》

12.3 角的平分线的性质1．如图11-100所示，在Rt △ABC中，∠C＝90°，AD是角平分线，DE⊥AB于点E，下列结论错误的是（）A．BD＋DE＝BC B．DE平分∠ADBC．DA平分∠EDC D．DE＋AC>AD2．如图11－101所示，在△ABC中，AD平分∠BAC，DE⊥AB于E，DF⊥AC 于F，则下列结论中错误的是（）A．DE＝DF B．AD上任意一点到E，F两点的距离相等C．AE＝AF D．BD＝DC3．如图11-102所示，BE⊥AC于E，CF⊥AB于F，AE＝AF，BE与CF交于点D，则：①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上．以上结论正确的是（）A.①B．②C．①②D．①②③4．如图11-103所示，△ABC中，P，Q分别是BC，AC上的点，作PR⊥AB，P S⊥AC，垂足分别是R，S，若A Q＝P Q，P R＝P S，下面三个结沦：①A S＝A R：②Q P∥AR；③△B R P≌△C S P．其中正确的是（）A.①③B．②③C．①②D．①②③5．在△ABC中，∠C＝90°，AD平分∠BA C，BC＝10 cm，BD＝7 cm，则点D 到AB的距离是．6．如图11-104所示，在直线l上找一点，使这点到∠AOB的两边OA，OB的距离相等，则这个点是．7．如图11-105所示，已知O为∠BAC的平分线与∠ACD的平分线的交点，OE⊥AC于E，若OE＝2，则点O到AB的距离与点O到CD的距离的和是．8．如图11-106所示，已知△ABC的角平分线BM，CN相交于点P，求证点P 到AB，BC，CA的距离相等．9．如图1l-107所示，BD是∠ABC的平分线，BA＝BC，点P在BD上，且PM⊥AD，PN⊥CD．求证PM＝PN．10．如图11-108所示，BF⊥AC于点F，CE⊥AB于点E，BF与CE交于D，且BD＝CD．（1）求证D在∠BAC的平分线上；（2）若将条件：BD＝CD和结论：D在∠BAC的平分线上互换，结论成立吗?试说明理由．11．如图11-109所示，点B，C在∠A的两边上，且AC＝AB，P为∠A内一点，PC＝PB，PE⊥AB、PF⊥AC，垂足分别为E，F．求证PE＝PF．12．如图11-110所示，已知点B，C分别在∠MAN的两边上，BD⊥AM，CE⊥AN，垂足分别为D，E，BD，CE相交于点F，且BF＝CF．求证点F在∠A的平分线上．（提示：在同一个三角形中，等边对等角，等角对等边）13．如图11-111所示，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB，交BC于D，能否在AB上确定一点E，使△BDE的周长等于AB的长?请说明理由．参考答案1．B[提示：由AD 是∠BAC 的平分线，DE ⊥AB ，∠C ＝90°，可知DC ＝DE ，所以BD ＋DE ＝BD ＋CD ＝BC ，选项A 成立；DE ＋AC ＝DC ＋AC >AD ，选项D 成立；由AD 平分∠BAC ，∠DEA ＝90°，∠C ＝90°，可知∠EDA ＝∠CDA ，所以选项C 成立．]2．D [提示：利用角平分线的性质及全等三角形的有关知识可解本题．]3．D [提示：由ASA 可知Rt △ABE ≌Rt △ACF ，从而AC ＝AB ，又AE ＝AF ，故CE ＝BF ，从而可由AAS 得Rt △DFB ≌Rt △DEC ，有DE ＝DF ，又DE ，DF 分别垂直于AC ，AB ，故点D 在∠BAC 的平分线上．故①②③均正确．]4．C[提示：连接AP ，由P R ＝P S 及已知条件易证Rt △A R P ≌Rt △A S P （HL ），故A R ＝A S ，∠R AP ＝∠S AP ，又Q A ＝Q P ，故∠Q AP ＝∠Q PA ＝∠RAP .从而P Q ∥A R ，但无法证明△B R P ≌△C S P ．]5．3 cm[提示：由AD 平分∠BAC 知D 到AB ，AC 的距离相等，又BC ＝10 cm ，BD ＝7 cm ，故CD ＝3 ，又∠ACD ＝90°，则点D 到AC 的距离即是CD 的长，为3 cm ，故D 到AB 的距离也是3 cm ．]6．∠AOB 的平分线与直线l 的交点7．4[提示：过O 分别作AB ，CD 的垂线．则点O 到AB ，CD 的距离均等于OE ，故它们的和为4．]8．证明：过P 点分别作PE ⊥AB 于E ，PF ⊥ BC 于 F ，PG ⊥CA 于G ．∵BM 平分∠ABC ，∴PE ＝PF ．同理PF ＝PC ．∴PE ＝PF ＝PG ，即点P 到AB ，BC ，CA 的距离相等．9．证明：∵BD 是∠ABC 的平分线，∴∠ABD ＝∠CBD ．在△ABD 和△CBD 中，ABD CBD BD BD ⎧⎪∠=∠⎨⎪=⎩A B =A B (已知)（已证）∴△ABD ≌△CBD （SAS ）．∴∠ADB ＝∠CDB （全等三角形的对应角相等），即DB 是∠ADC 的平分线．又∵PM ⊥AD ，PN ⊥ DC ，∴PM ＝PN ．10．（1）证明：∵BF ⊥AC ，CE ⊥AB ，∴∠BED ＝∠CFD ＝90°．在Rt △BED（公共边）和Rt △CFD 中()BED CFD EDB FDC BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩已知（对顶角相等）∴Rt △BED ≌Rt △CFD（AAS ）．∴DE ＝DF （全等三角形的对应边相等）．∴D 在∠ BAC 的平分线上（到角的两边距离相等的点在角的平分线上）．（2）解：成立．理由如下：∵点D 在∠BAC 的平分线上，且BF ⊥AC ，CE ⊥AB ，∴DE ＝DF ，∠BED ＝∠CFD ＝90°．在Rt △BED 和Rt △CFD 中，BED CFD DE DF EDB FDC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴Rt △BED ≌Rt △CFD （A S A ）． ∴BD ＝DC （全等三角形的对应边相等）．11．证明：连接AP ，在Rt △ABP 和△ACP 中，AB AC AP AP PB PC =⎧⎪=⎨⎪=⎩，，（公共边），∴△ABP ≌△ACP （SSS ）∴∠BAP ＝∠CAP ．又∵PE ⊥AB ，PF ⊥AC ，∴PE ＝PF ．12．证明：如图11-112所示，连接BC ，作射线AF ．∵BD ⊥AM ，CE ⊥AN ，∴∠ADB ＝∠AEC ＝∠BDC ＝∠CEB ＝90°．∵BF ＝CF ，∵∠DBC ＝∠ECB ．又∵BC ＝CB ，∴△BCD ≌△CBE ．∴BD ＝CE ，∴EF ＝DF ，∴点F 在∠CAB 的平分线上．13．解：能．过D 作DE ⊥AB ，交AB 于E 点，则E 点即可满足要求．理由：∵AD 平分∠CAB ，CD ⊥AC ，DE ⊥AB ，∴CD ＝DE ．在Rt △ACD 和Rt △AED 中，,,CD DE AD AD =⎧⎨=⎩∴Rt △ACD ≌Rt △AED （HL ）∴AC ＝AE ．∵AC ＝BC ，．BC ＝AE ．∴△BDE 的周长＝BD ＋DE ＋EB ＝BD ＋DC ＋EB ＝BC ＋EB ＝AE ＋EB ＝AB ．（已证）。

12.3.1 角的平分线的性质初中数学人教版八年级上册课时习题(含答案)

12.3角的平分线的性质一、选择题（本大题共10小题，在每小题列出的选项中，选出符合题目的一项）1.如图，点P到AE，AD，BC的距离相等，则下列说法：①点P在∠BAC的平分线上；②点P在∠CBE的平分线上；③点P在∠BCD的平分线上；④点P是∠BAC，∠CBE，∠BCD的平分线的交点．其中正确的是( )A. ①②③④B. ①②③C. ④D. ②③2.如图，已知点P到AE，AD，BC的距离相等，下列说法：①点P在∠BAC的平分线上；②点P在∠CBE的平分线上；③点P在∠BCD的平分线上；④点P在∠BAC，∠CBE，∠BCD的平分线的交点上．其中正确的是( )A. ④B. ②③C. ①②③D.①②③④3.到三角形的三边距离相等的点是( )A. 三角形三条高的交点B. 三角形三条内角平分线的交点C. 三角形三条中线的交点D. 无法确定4.如图所示，∠B=∠C=90∘，M是BC的中点，DM平分∠ADC，且∠ADC =110∘，则∠MAB= ( )A. 30∘B. 35∘C. 45∘D. 60∘5.三角形内部到三边距离相等的点是( )A. 三边中线的交点B. 三边垂直平分线的交点C. 三内角平分线的交点D. 三边上高的交点6.如图，AB//CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直.若AD=8，则点P到BC的距离是( )A. 8B. 6C. 4D. 27.在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是．( )A. 点CB. 点DC. 点ED. 点F8.在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是( )A. 点MB. 点NC. 点PD. 点Q9.如图，在△ABC中，∠B=90°，AB=6，BC=8，AD为∠BAC的角平分线，则三角形ADC的面积为( )A. 3B. 10C. 12D. 1510.如图，△ABC的外角平分线BD，CE相交于点P.若点P到AC的距离为3，则点P到AB的距离为( )A. 1B. 2C. 3D. 4二、填空题（本大题共4小）11.如图，点O在△ABC内，且到三边的距离相等.若∠A=60∘，则∠BOC=°．12.如图，点P到∠AOB两边的距离相等，若∠POB=30°，则∠AOB=________．13.如图，在△ABC中，∠C=90∘，AD平分∠BAC与BC边交于点D，BD=2CD，若点D到AB的距离等于5cm，则BC的长为cm．14.如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC、AB于点M、N，再分别以M、N为圆心，MN的长为半径画弧，两弧交于点P，作射线AP交BC于点D，大于12若CD=3，AB=10，则△ABD的面积是________．三、解答题（本大题共3小题，解答应写出文字说明，证明过程或演算步骤）15.如图，∠1=∠2，∠3=∠4.求证：AP平分∠BAC．16.已知：如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.求证：AM平分∠DAB．17.如图，点B，C分别在∠A的两边上，点D是∠A内一点，DE⊥AB，DF⊥AC，垂足分别为E，F，且AB=AC，DE=DF.求证：BD=CD．参考答案1.【答案】A2.【答案】D3.【答案】B4.【答案】B5.【答案】C6.【答案】C7.【答案】C8.【答案】A9.【答案】D10.【答案】C11.【答案】12012.【答案】60°13.【答案】1514.【答案】1515.【答案】证明：过P作PQ⊥AB于Q，PN⊥BC于N，PM⊥AC于M，∵∠1=∠2.∠3=∠4，∴PQ=PN，PN=PM，∴PQ=PM，∵PQ⊥AB，PM⊥AC，∴AP平分∠BAC．16.【答案】证明：过点M作ME⊥AD，垂足为E，∵∠B=∠C=90°，∴MC⊥CD，MB⊥AB，∵DM平分∠ADC，∴∠CDM=∠EDM，又∵MC⊥CD，ME⊥AD，∴ME=MC，又∵MC=MB，∴ME=MB，又∵MB⊥AB，ME⊥AD，∴AM平分∠DAB．17.【答案】证明：连接AD，∵DE⊥AB，DF⊥AC，DE=DF，∴∠BAD=∠CAD，在△ABD和△ACD中AB=AC∠BAD=∠CAD，AD=AD∴△ABD≌△ACD，(SAS)，∴BD=CD．。

人教版_部编版八年级数学上册第十二章第三节角的平分线的性质习题(含答案) (1)

人教版_部编版八年级数学上册第十二章第三节角的平分线的性质考试复习题（含答案)一、单选题1．△ABC是一个任意三角形，用直尺和圆规作出∠A，∠B的平分线，如果两条平分线交于点O，那么下列选项中不正确的是（）A．点O一定在△ABC的内部B．点O到△ABC的三边距离一定相等C．∠C的平分线一定经过点O D．点O到△ABC三顶点的距离一定相等【答案】D【解析】由三角形的三条角平分线在三角形内相交于一点可知：A、C正确；而由角平分线的性质可证得点O到△ABC的三边距离相等，所以B正确；而三角形三条角平分线的交点到三个顶点的距离不一定相等，所以D错误.故选D.2．如图，△ABC的两条外角平分线AP、CP相交于点P，PH⊥AC于H；如果∠ABC=60º，则下列结论：①∠ABP=30º；②∠APC=60º；③PB=2PH；④∠APH=∠BPC；其中正确的结论个数是（）A．1 B．2 C．3 D．4【答案】B【解析】【分析】作PM ⊥BC 于M ，PN ⊥BA 于N ．根据角平分线的性质定理可证得PN=PM ，再根据角平分线的判定定理可得PB 平分∠ABC ，即可判定①；证明⊥PAN ⊥⊥PAH ，⊥PCM ⊥⊥PCH ，根据全等三角形的性质可得⊥APN=⊥APH ，⊥CPM=⊥CPH ，由此即可判定②；在Rt ⊥PBN 中，∠PBN=30°，根据30°角直角三角形的性质即可判定③；由⊥BPN=⊥CPA=60°即可判定④.【详解】如图，作PM ⊥BC 于M ，PN ⊥BA 于N ．⊥⊥PAH=⊥PAN ，PN ⊥AD ，PH ⊥AC ，⊥PN=PH ，同理PM=PH ，⊥PN=PM ，⊥PB 平分∠ABC ，⊥⊥ABP=12⊥ABC=30°，故①正确， ∵在Rt ⊥PAH 和Rt ⊥PAN 中，PA PA PN PH =⎧⎨=⎩， ⊥⊥PAN ⊥⊥PAH ，同理可证，△PCM ⊥⊥PCH ，⊥⊥APN=⊥APH ，⊥CPM=⊥CPH ，⊥⊥MPN=180°-⊥ABC=120°，⊥⊥APC=12⊥MPN=60°，故②正确，在Rt⊥PBN中，∵∠PBN=30°，⊥PB=2PN=2PH，故③正确，⊥⊥BPN=⊥CPA=60°，⊥⊥CPB=⊥APN=⊥APH，故④正确．综上，正确的结论为①②③④.故选D.【点睛】本题考查了角平分线的性质定理及判定定理、全等三角形的判定与性质及30°角直角三角形的性质，熟练运用相关知识是解决问题的关键.3．如图，AD是△ABC中△BAC的角平分线，DE△AB于点E，S△ABC=9，DE=2，AB=5，则AC长是（）A．3 B．4 C．5 D．6【答案】B【解析】如图，作DF⊥AC交AC于点F，∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE=DF,∴S△ABC=S△ADC+S△ADB=12AC·DF+12AB·DE=12DE（AC+AB）=9，∴12×2×（AC+5）=9，∴AC=4.故选B.点睛：（1）遇到角平分线较常用的一类辅助线的作法是过角平分线上一点向角的两边作垂线.（2）三角形的面积除了用公式法还可以用割补法将三角形的面积用别的形式表示出来，此题将三角形面积表示为两个三角形的面积之和，然后列方程求解.4．若△ABC内一点O到三角形三条边的距离相等，则O为△ABC（）的交点．A．角平分线B．高线C．中线D．边的中垂线【答案】A【解析】试题分析：由角平分线性质的逆定理：到角的两边的距离相等的点在角的平分线上，则这个点是三角形三条角平分线的交点，即可确定答案.解：∵到角的两边的距离相等的点在角的平分线上，∴这个点是三角形三条角平分线的交点.故选A.5．如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，若BD=5cm，DE=3cm，则AC的长为（）A．8 cm B．10 cm C．6cm D．16 cm【答案】A【解析】解：⊥AD平分⊥BAC，⊥C=90°，DE⊥AB，⊥CD=DE，⊥BD=5，DE=3，⊥CD=3，⊥AC=BC=CD+DB=3+5=8．故选A．6．如图，在△ABC中，△1＝△2，G为AD的中点，BG的延长线交AC 于点E，F为AB上的一点，CF与AD垂直，交AD于点H，则下面判断正确的有（）△AD是△ABE的角平分线；△BE是△ABD的边AD上的中线；△CH是△ACD的边AD上的高；△AH是△ACF的角平分线和高A．1个B．2个C．3个D．4个【答案】B【解析】解：①根据三角形的角平分线的概念，知AG是△ABE的角平分线，故此说法错误；②根据三角形的中线的概念，知BG是△ABD的边AD上的中线，故此说法错误；③根据三角形的高的概念，知CH为△ACD的边AD上的高，故此说法正确；④根据三角形的角平分线和高的概念，知AH是△ACF的角平分线和高线，故此说法正确．故选B．点睛：本题考查了三角形的角平分线、三角形的中线、三角形的高的概念，注意：三角形的角平分线、中线、高都是线段，且都是顶点和三角形的某条边相交的交点之间的线段．透彻理解定义是解题的关键．7．如图，BD、CD分别是△ABC的两个外角∠CBE、∠BCF•的平分线，若∠=︒，则∠D的度数是（）A70A．40°B．50°C．65°D．55°【答案】D【解析】∵∠A=70°，∴∠ABC+∠ACB=110°，∴∠EBC+∠FCB=360°－110°=250°，∵BD、CD分别平分∠CBE、∠BCF，∴∠DBC=∠DBE，∠DCB=∠DCF，∴∠DBC+∠DCB=125°，∴∠D=55°.故选D.点睛:充分利用三角形的内角和，平角的性质，以及角平分线的性质.8．如图，△1＝△2，PD△OA，PE△OB，垂足分别为D，E，下列结论错误的是（）A．PD＝PE B．OD＝OE C．△DPO＝△EPO D．PD＝OP【答案】D【解析】试题分析：根据角平分线的性质可得：PD=PE，根据题意HL判定定理可得：Rt△POE△Rt△POD，则OD=OE，△DPO=△EPO.考点：角平分线的性质9．若∠α与∠β互为余角，则∠α的补角与∠β的补角之和为( )A．90°B．180°C．270°D．360°【答案】C【解析】∵∠α与∠β互为余角，∴∠α+∠β=90°，∵∠α的补角为180°-∠α，∠β的补角为180°-∠β，∴(180°-∠α)+(180°-∠β)=360°-(∠α+∠β)=360°-90°=270°．故选C．【点睛】这是一道有关余角和补角的题目，需明确余角和补角的含义；由于互补的两角之和为180°，于是可以表示出∠α和∠β的补角，进而得到它们的之和；再根据互余的两角之和为90°得到∠α+∠β=90°，即可求出∠α与∠β的补角之和.10．在ABC △内部取一点P ，使得点P 到ABC △的的三边距离相等，则点P 是ABC △的（）．A ．三条高的交点B ．三条角平分线的交点C ．三条中线的交点D ．三边的垂直平凡线的交点【答案】B【解析】如图：PD PF PE ==．故选B ．。

人教版八年级数学上册第12单元第3节第1课时角平分线的性质同步练习题(含答案)

12.3 角的平分线的性质一、选择题1．下列说法：①角的内部任意一点到角的两边的距离相等；•②到角的两边距离相等的点在这个角的平分线上；③角的平分线上任意一点到角的两边的距离相等；④△ABC 中∠BAC 的平分线上任意一点到三角形的三边的距离相等，其中正确的（）A ．1个B ．2个C ．3个D ．4个2. 已知AD 是△ABC 的角平分线，DE ⊥AB 于E,且DE=3cm,则点D 到AC 的距离是( ) A.2cm; B.3cm; C.4cm; D.6cm3．如图1，已知CE 、CF 分别是△ABC 的内角和外角平分线，•则图中与∠BCE 互余的角有（）A ．4个B ．3个C ．2个D ．1个4．如图2，已知点P 到AE 、AD 、BC 的距离相等，则下列说法：①点P 在∠BAC 的平分线上；②点P 在∠CBE 的平分线上；③点P 在∠BCD 的平分线上；④点P 是∠BAC 、∠CBE 、∠BCD 的平分线的交点，其中正确的是（）A ．①②③④B ．①②③C ．④D ．②③D CBA EFPDCBAEPDCBA E（1） (2) (3) 二、填空题5．用直尺和圆规平分已知角的依据是______________．6．角的平分线上的点到_______________相等；到___________________________相等的点在这个角的平分线上．7．如图3，AB ∥CD ，AP 、CP 分别平分∠BAC 和∠ACD ，PE ⊥AC 于E ，且PE=•2cm ，则AB 与CD 之间的距离是___________．三、解题题8．请你画一个角，并用直尺和圆规把这个角两等分．9．如图，四边形ABCD 中AB=AD ，CB=CD ，点P 是对角线AC 上一点，PE ⊥BC 于E ，PF ⊥CD 于F ，求证PE=PF ．PDC BAEF10．如图，四边形ABCD 中AB=AD ，AB ⊥BC ，AD ⊥CD ，P 是对角线AC 上一点，•求证：PB=PC ．PDCBA参考答案:1．B 2．B 3．C 4．A 5．SSS6．角的两边的距离；角的两边的距离 7.4cm 8．略 9．证明AC 平分∠BCD10．先证Rt△ABC≌Rt△ADC，再证△APB≌△APD。

人教版八年级数学上册《12.3角的平分线的性质》同步练习题(附答案)

人教版八年级数学上册《12.3角的平分线的性质》同步练习题（附答案）姓名班级学号成绩一、选择题：（本题共8小题，每小题5分，共40分．）1．已知△ABC内一点P，如果点P到AB、AC两边的距离相等，则点P（）A．在BC边的垂直平分线上B．在BC边的高上C．在BC边所对角的平分线上D．在BC边的中线上2．如图，已知AB∥CD，EF平分∠CEG，∠1=80°，则∠2的度数为（）A．20°B．40°C．50°D．60°3．如图，在△ABC中，∠C＝90°，使点P到AB、BC的距离相等，则符合要求的作图痕迹（）A． B． C． D．4．如图，ABC中，AD平分∠BAC，AB＝4，AC＝2，若ACD的面积等于3，则ABD的面积为（）A．B．4 C．6 D．125．如图，在中，∠A=90°，AB=2，BC=5，是的平分线，设和的面积分别是和，则的值为（）A．B．C．D．6．如图，AB//CD，BP和CP分别平分∠ABC和∠BCD，AD过点P，且与AB垂直.若AD=8，BC=10，则BCP 的面积为（）A．16 B．20 C．40 D．807．如图，中，是边的高线，平分，DE=1cm，BC=4cm，则的面积是（）A．B．C．D．8．如图，中，∠ACB=90°，的角平分线、相交于点，过点作交的延长线于点，交于点，则下列结论：①；②BF=BA；③；④连接，平分．其中正确的是（）A．1个B．2个C．3个D．4个二、填空题：（本题共5小题，每小题3分，共15分．）9．已知点在第四象限角平分线上，则该点的坐标是．10．已知，AD是△ABC的角平分线，过点D作，垂足为点E，作，交边AB所在直线于点F，若，则AB的长为cm。

11．如图所示，BD是∠ABC的平分线，DE⊥AB于点E，AB=36cm，BC=24cm，S△ABC=144cm，则DE的长是．12．如图，在△ABC中，∠ABC，∠ACB的平分线交于点O，OD⊥BC于D，如果AB=25cm，BC=20cm，AC=15cm，且S△ABC=150cm2，那么OD= cm．13．如图，在中，点O是和的平分线的交点，点D是BC延长线上的点，和的平分线交于点E，∠A=a，则的度数为．（用含的式子表示）三、解答题：（本题共5题，共45分）14．如果，在△ABC中，AD是高，AE是∠BAC的平分线，∠BAC=54°，∠C=70°．求∠EAD的度数．15．如图，D、E、F分别是△ABC的三条边上的点，CE＝BF，△DCE和△DBF的面积相等．求证：AD平分∠BAC．16．如图，在中，∠ABC=90°，CD平分交AB于点D，于点E，交CD于点F．求证： DE=BF ．17．如图，DE⊥AB于E，DF⊥AC于F，若BD = CD，BE = CF．求证：（1）AD平分∠BAC；（2）AC=AB+2BE.18．已知：如图，在△ABC中，AB＝AC，在△ADE中，AD＝AE，且∠BAC＝∠DAE，连接BD，CE交于点F，连接AF．（1）求证：△ABD≌△ACE；（2）求证：FA平分∠BFE．参考答案：1．C 2．C 3．C 4．C 5．B 6．B 7．B 8．D 9．（11，-11）10．4或811．4.8cm12．513．14．解：∵AD是高∴∠ADC=90°∵∠C=70°∴∠DAC=20°∵AE是∠BAC的平分线，∠BAC=54°∴∠EAC= ∠BAC=27°∴∠EAD=∠EAC﹣∠DAC=27°﹣20°=7°.15．证明：过D作DN⊥AC，DM⊥AB△DBF的面积为： BF·DM△DCE的面积为： DN·CE∵△DCE和△DBF的面积相等∴ BF·DM＝ DN·CE∵CE＝BF∴DM＝DN又∵DM⊥AB，DN⊥AC∴AD平分∠BAC（到角两边距离相等的点在角的平分线上）．16．证明：如图∵CD平分∠ACB17．（1）证明：∵DE⊥AB于E，DF⊥AC于F∴∠E=∠DFC=90°在Rt△BDE与Rt△CDE中∴Rt△BDE≌Rt△CDF(HL)∴DE=DF∴AD平分∠BAC；（2）证明：由(1)可知AD平分∠BAC∴∠EAD=∠CAD∵DE⊥AB于E，DF⊥AC于F∴∠E=∠DFA=90°又∵AD=AD∴△AED≌△AFD(AAS)∴AE=AF∵CF=BE∴AC=AF+CF=AE+BE=AB+BE+BE=AB+2BE．18．（1）证明：∵∠BAC＝∠DAE∴∠BAC+∠CAD＝∠DAE+∠CAD即∠BAD＝∠CAE在△BAD和△CAE中∴△BAD≌△CAE（SAS）；（2）证明：如图，作AM⊥BD于M，作AN⊥CE于N．由△BAD≌△CAE∴BD＝CE，S△BAD＝S△CAE ∵∴AM＝AN∴点A在∠BFE平分线上∴FA平分∠BFE。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

12.3角的平分线的性质
课时1角的平分线的性质
1.[2018江苏南京二十九中课时作业]如图，AD是△ABC中∠BAC的平分线，DE丄AB于点E，S△ABC=7，DE=2，AB=4，则AC的长是（）
A.3
B.4
C.5
D.6
2.[2016浙江湖州中考]如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直.若AD=8，则点P到BC的距离是（）
A.8
B.6
C.4
D.2
3.[2018江西吉安一中课时作业]如图，在四边形ABCD中，∠A=90°，AD=4，连接BD，BD丄CD，∠ADB=∠C.若P是BC边上一动点，则DP的最小值为______.
4.[2018陕西汉中四中课时作业]如图，在△ABC中，D为BC的中点，DE丄BC 交∠BAC的平分线AE于点E，EF丄AB交AB的延长线于点F，EG丄AC于点G.求证：BF=CG.
5.[2018河南新乡一中课时作业]如图，已知∠AOB=90°，OM平分∠AOB，直角三角板的顶点P在射线OM上移动，∠CPD=90°，两直角边分别与OA，OB 交于点C，D.问：PC与PD相等吗？请说明理由.
6.[2018河北保定十三中课时作业]如图，在△ABC 中，∠BAD=∠DAC ，DF 丄AB 于点P ，DM 丄AC 于点M ，AB=16cm ，AF=10cm ，AC=14cm ，动点E 以2cm/s 的速度从A 点向F 点运动，同时动点G 以1cm/s 的速度从C 点向A 点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为ts.
（1）S △ABD ：S △ACD .
（2）求证：在运动过程中，无论t 取何值，都有S △AED =2S △DGC .
（3）当t 取何值时，△DFE 与△DMG 全等？
（4）若BD=8cm ，求CD 的长.。