期末复习(一) 三角形.ppt
期末复习(一) 直角三角形

期末复习(一) 直角三角形各个击破命题点1 直角三角形的性质与判定【例1】 在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D.(1)如图1,若∠C =30°,求证:BD =14BC ;(2)如图2,若∠C =45°,写出点D 到△ABC 的三个顶点A ,B ,C 的距离的关系;(3)在(2)的基础上,如果点M ,N 分别在线段AB ,AC 上移动,在移动过程中保持AN =BM ,请判断△DMN 的形状,请证明你的结论.【思路点拨】 (1)先由同角的余角相等可以得到∠BAD =∠C =30°,再根据直角三角形中30°角所对的直角边等于斜边的一半,可以在Rt △ABD 和Rt △ABC 中分别找出BD 与AB ,AB 与BC 的关系,从而得出BD 与BC 的数量关系;(2)根据∠C =45°,∠BAC =90°,可得△ABC 是等腰直角三角形.又AD ⊥BC ,由等腰三角形三线合一的性质可知,D 为直角三角形斜边的中点.再由直角三角形斜边中线的性质,即可求出AD ,BD ,DC 之间的关系;(3)先由题目所给的条件证明△BDM ≌△ADN ,从而得到MD =DN 及∠BDM =∠ADN ,进而可得∠MDN =∠ADB =90°.【解答】(1)证明:∵∠BAC =90°,AD ⊥BC ,∴∠B +∠C =90°,∠B +∠BAD =90°.∴∠BAD =∠C =30°.∴在Rt △ABD 中,BD =12AB , 在Rt △ABC 中,AB =12BC. ∴BD =14BC. (2)∵∠C =45°,∠BAC =90°,∴△ABC 是等腰直角三角形.∵AD ⊥BC ,∴D 为BC 的中点.∴AD =BD =CD.(3)△DMN 是等腰直角三角形.证明:∵BM =AN ,∠B =∠DAN =45°,BD =AD ,∴△BDM ≌△ADN(SAS).∴MD =ND ,∠BDM =∠ADN.∴∠MDN =∠ADB =90°.∴△MDN 是等腰直角三角形.【方法归纳】 (1)由直角三角形斜边中线的性质可得到两条线段之间的数量关系;(2)由角来判断一个三角形是直角三角形,只要说明这个三角形中有一个直角或有两个角互余即可.1.如图,△ABC 中,CD ⊥AB 于D ,且E 是AC 的中点.若AD =6,DE =5,则CD 的长等于(D)A .5B .6C .7D .82.一个三角形的三个角的度数之比是3∶3∶6,则这个三角形是等腰直角三角形.3.在△ABC 中,AB =AC ,∠A =120°,AB 的垂直平分线交BC 于点D ,交AB 于点E.如果DE =1,求BC 的长.解:连接AD.∵DE 垂直平分AB ,∴AD =BD ,∠DEB =90°.∵AB =AC ,∠BAC =120°,∴∠B =∠C =30°.在Rt △BDE 中,∠B =30°,∴DE =12BD.∴BD =2. ∵AD =BD ,∴∠BAD =∠B.∴∠DAC =∠BAC -∠BAD =120°-30°=90°.又∵∠C =30°,∴AD =12CD.∴CD =2AD =2BD =4. ∴BC =CD +BD =4+2=6.命题点2 勾股定理及其逆定理【例2】 如图,四边形ABCD ,AB =AD =2,BC =3,CD =1,∠A =90°,求∠ADC 的度数.【思路点拨】 首先在Rt △BAD 中,利用勾股定理求出BD 的长,而由题意可知,△ABD 为等腰直角三角形,则∠ADB =45°,再根据勾股定理逆定理,证明△BCD 是直角三角形,即可求出答案.【解答】 连接BD.在Rt △BAD 中,∵AB =AD =2,∴∠ADB =45°,BD =AD 2+AB 2=2 2.在△BCD 中,DB 2+CD 2=(22)2+12=9=CB 2,∴△BCD 是直角三角形.∴∠BDC =90°.∴∠ADC =∠ADB +∠BDC =45°+90°=135°.【方法归纳】 当不能直接求一个角的度数时,可通过作辅助线,求几个角的和或差.4.已知三组数据:①2,3,4;②3,4,5;③1,3,2.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有(D)A .②B .①②C .①③D .②③5.如果三角形有一条边上的中线长恰好等于这条边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣。
八年级数学上册 第1章 全等三角形章末复习课件

则( )
D
A.△ABD≌△AFE B.△AFE≌△ADC
C.△AFE≌△DFC D.△ABC≌△ADE
第十四页,共三十二页。
3. 如图,点B在AE上,且∠CAB=∠DAB,若要使△ABC≌△ABD,可补充的条件(tiáojiàn)
是 AC=AD .(写出一个即可)
4.如图,把一长一短两根细木棍的一端用螺钉铰合在一起,使长木棍的另一端与射线BC的端点B重
第三页,共三十二页。
讲练结合
1、下列(xiàliè)四个图形中,全等的图形是( C )
A.①和② B.①和③ C.②和③ D.③和④
2、下面(xià mian)是5个全等的正六边形 A、B、C、D、E ,请你仔细观察 A、B、C、D 四个
图案,其中与 E 图案完全相同的是(
).
C
第四页,共三十二页。
角,EF=2.1 cm ,EH=1.1 cm ,HN=3.3 cm .
(1)写出其他(qítā)对应边及对应角; (2)求线段NM及线段HG的长度.
解: (1)∵△EFG≌△NMH,∴最长边FG和MH是对应(duìyìng)边, 其他对应边是EF和NM、EG和NH;对应角是∠E和∠N、 ∠EGF和∠NHM. (2)由(1)知NM=EF=2.1 cm ,GE=HN=3.3 cm ,
5.尺规作图
作一个角等于(děngyú)已知角
知道△ABC 的六个元素中的某三个元素,根据确定三角形的条件,以下四种情 况可作出△ABC: ① 已知三边;
② 已知两边(liǎngbiān)及其夹角; ③ 已知两角及其夹边;
④ 已知两角和其中一角的对边.
2021/12/13
第二十九页,共三十二页。
布置作业
全等三角形的基本模型复习正式经典ppt课件
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
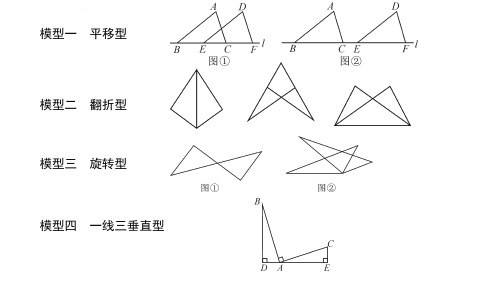
模型三 旋转型 模型解读:将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全 重合,则称这两个三角形为旋转型三角形.识别旋转型三角形时,如图①, 涉及对顶角相等;如图②,涉及等角加(减)公共角的条件.
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
解:∵AB⊥CD,∴∠EBC=∠DBA=90°.在 Rt△CEB 与 Rt△ADB 中 CBEE= =ABDD,,∴Rt△CEB≌Rt△ADB(HL),∴∠C=∠A,又∵∠C+∠CEB= 90°,∠CEB=∠AEF,∴∠A+∠AEF=90°,∴CF⊥AD
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
解:∵AD⊥AB,BE⊥AB,CD⊥CE,∴∠DAC=∠CBE=∠DCE=90 °,又∵∠DCB=∠D+∠DAC=∠DCE+∠ECB,∴∠D=∠ECB.在△ACD
“雪亮工程"是以区(县)、乡(镇) 、村( 社区) 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
完整版-全等三角形总复习PPT教学课件

AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上,△ABD,△BCE都是等边 三角形,AE交BD于F,DC交BE于G,求证:BF=BG。
AB
=
DB
∠ABE = ∠ DBC
BE=BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3: 已知一边一角(边与角相邻):
找夹这个角的另一边
AD=CB (SAS)
找夹这条边的另一角
∠ACD=∠CAB(ASA)
找边的对角
∠D=∠(B AAS)
15
如图,已知∠B= ∠E,要识别△ABC≌ △AED,需 要添加的一个条件是--------------
A
D
C
E
思路4:
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中,AE < AB+BE=AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA, CD过点E,则AB与AC+BD相等吗?请说明理由。
C A
∵ QD⊥OA,QE⊥OB,QD=QE(已知). ∴点Q在∠AOB的平分线上.(到角的两边的距
离相等的点在角的平分线上)
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证:点P到三边AB、BC、CA的距离相等
人教版数学八上第十一章三角形复习课件共34张PPT

2
。
(3,3,1;2,2,3)
1、如图,求△ABC各内角的度数。 A
解:3x + 2x + x = 180
35xx
6x=180
X=30
23xx
B
xx C
∴三角形各内角的度数分别为:30°,60°,90°
2、已知三角形三个内角的度数比为1:3:5, 求解这:三设个三内个角内的角度分数别。为x,3x,5x
B A
小莉的设计方案:先在池塘旁取一个能
直接到达A和B处的点C,连结AC并延长至
D点,使AC=DC,连结BC并延长至E点,
使BC=EC,连结CD,用米尺测出DE的长,
这个长度就等于A,B两点的距离。请你说
明理由。
解: AC=DC
∠ACB=∠DCE
A
B
BC=EC
C
△ACB≌△DCE(SAS)
E
D
AB=DE
则x + 3x + 5x = 180 x=20
∴三角形三个内角分别为:20°,60°,100°
题型考查
1.符合条件∠A+∠B=62°的三角形是( C )
A、锐角三角形 C、钝角三角形
B、直角三角形 D、不能确定
2.在下列长度的四根木棒中,能与4㎝,9㎝ 两根木棒围成三角形的是( C )
A、4㎝ B、5㎝ C、9㎝ D、14㎝ 3.如图,在△ABC中,∠A=70° A
点,∠1=∠2,AE=DE,
试求AB=DC。
AD
12
BEC
简解:∵E是BC的中点, ∴BE=EC。又∴ ∠1=∠2,AE=DE, △ABE≌△DCE(SAS),∴AB=DC 。
3.如图,已知BE⊥AD, CF⊥AD,且BE=CF,请你 判断AD是△ABC的中线还是
第三章《三角形》期末复习课件

D
三、三角形的三种重要线段 3、三角形的高: 从三角形的一个顶点向它的对边
所在的直线作垂线,顶点和垂足之间的线段叫做
Байду номын сангаас
三角形的高线,简称三角形的高。
A 如左图,若有AD⊥BC, B 则线段AD是△ABC的一条高 D C
四、三角形的性质
1、三角形内角和定理:三角形三个内角 的和等于180˚ 2、三角形三边关系:三角形任意两边 之和大于第三边,任意两边之差小于第 三边。 3、三角形具有稳定性
b
顶点: 三个顶点A、B、C
C
内角: 三个内角:∠A,∠B,∠C
二、三角形的分类 锐角三角形 按角分: 直角三角形 钝角三角形 三角形 等腰三角形 按边分: 一般等腰三 角形 等边三角形 不等边三角形
三、三角形的三种重要线段
在三角形中,连接一个顶点 1、三角形的中线:
与它对边中点的线段,叫做这个三角形的中线。
A C B D
三、说理题
1、如图AB=AC,∠B=∠C,点D、E 在BC边上,且BD= CE,那么图中有哪些 三角形全等?请说明理由。
A
B
D
E
C
2、如图,AB=DC,AC=DB, 你能说明图中∠1=∠2的理由吗?
A D
1
2
B
C
利用全等三角形测距离
A、B间有多远呢?
小明在上周末游览风景
区时,看到了一个美丽的
● ●
B
C E
●
长了。
理由如下: 在△ACB与△DCE中, AC=C D(已知)
D
∠BCA=∠ECD(对顶角相等) BC=CE(已知) ∴△ACB≌△DCE(SAS ) ∴AB=DE( 全等三角形的对应边相等 )
三角形期末复习

三角形的角平分线
A
●
︶
几何语言:
1 2
B
●
D
C
∵AD是 △ ABC的角平分线
1 ∴∠ BAD = ∠ CAD = 2∠BAC 用处:求相等的角,求角度
练一练
1、能将△ABC的面积分成相等的两部分的 是( B )
A、高 B、中线 C、角平分线 D、对角线
2、画△ABC中BC边上的高,下列各图中 正确的是( D ) D
2cm<x<12cm 范围是_____________;这个三角形周长c的取 14cm<c <24cm 值范围是_____________;
练一练
3、已知△ABC是等腰三角形,如果它的周长 为20cm,一条边长为4cm,求等腰三角形其它 两边的长为(8cm,8cm )。
4、已知△ABC是等腰三角形,如果它的一边 长为3cm,一边长为6cm,则这个等腰三角形的 周长为(15cm )。
多边形外角和为360°
1. 三角形的三边关系:
(1) 三角形两边的和大于第三边 (2) 三角形两边的差小于第三边
2. 判断三条已知线段a、b、c能否 组成三角形.
当a最长,且有b+c>a时,就可构成三角形.
3. 确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
练一练
1、下列条件中能组成三角形的是( C ) A、 5cm, 13cm, 7cm B、 3cm, 5cm, 9cm C、 14cm, 9cm, 6cm D、 5cm, 6cm, 11cm 2、三角形的两边为7cm和5cm,则第三边x的
重难点: 三角形的三边关系定理,内外角的 性质,多边形的内角和公式的应用
本章知识结构
三角形的相关证明期末复习

角与角的关系
内角和定理
三角形的内角和等于180度。
外角定理
三角形的一个外角等于与它不相邻的两个内角的和。
边与边的关系
三角形的两边之和大于第三边
在三角形中,任意两边之和大于第三边。
三角形的两边之差小于第三边
在三角形中,任意两边之差小于第三边。
等腰三角形的性质与
02
证明
形的全等的证明
04
SSS全等条件
定义
如果两个三角形的三边分别相等, 则这两个三角形全等。
证明方法
利用边边边定理,通过比较三边 长度来确定三角形是否全等。
适用场景
当已知三角形的三边长度时,可 以使用此条件进行全等证明。
SAS全等条件
定义
如果两个三角形有一边和两角分别相 等,则这两个三角形全等。
对应边成比例
如果两个三角形相似,则它们的对应边长之间存 在一定的比例关系。
面积比恒定
相似三角形的面积之比等于其对应边长比的平方。
三角形相似的判定
角角判定
如果两个三角形的两组对应角分别相等,则这两个三角形 相似。
边边判定
如果两个三角形的三组对应边成比例,则这两个三角形相 似。
角边判定
如果一个三角形的两个角与另一个三角形的两个角分别相 等,并且这两个三角形中相对的一组对应边成比例,则这 两个三角形相似。
如果一个三角形中,两条边的 平方和等于第三边的平方,则 这个三角形是直角三角形。
如果一个三角形中,两条边的 比值为1:2或2:1,则这个三角 形是直角三角形。
勾股定理及其逆定理
勾股定理
直角三角形中,斜边的平方等于两直角边的平方和,即$c^2 = a^2 + b^2$。
