三角函数的图象 2
三角函数公式及其图像

初等函数1、基本初等函数及图形基本初等函数为以下五类函数:(1) 幂函数μxy=,μ是常数;1.当u为正整数时,函数的定义域为区间),(+∞-∞∈x,他们的图形都经过原点,并当u>1时在原点处与X轴相切。
且u为奇数时,图形关于原点对称;u为偶数时图形关于Y轴对称;2.当u为负整数时。
函数的定义域为除去x=0的所有实数。
3.当u为正有理数m/n时,n为偶数时函数的定义域为(0, +∞),n为奇数时函数的定义域为(-∞+∞)。
函数的图形均经过原点和(1 ,1).如果m>n图形于x轴相切,如果m<n,图形于y轴相切,且m为偶数时,还跟y轴对称;m,n均为奇数时,跟原点对称.4.当u为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数.(2) 指数函数 xa y = (a 是常数且01a a >≠,),),(+∞-∞∈x ;1. 当a>1时函数为单调增,当a<1时函数为单调减.2. 不论x 为何值,y 总是正的,图形在x 轴上方.3. 当x=0时,y=1,所以他的图形通过(0,1)点.(3) 对数函数x y a log =(a是常数且01a a >≠,),(0,)x ∈+∞;(4) 三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,1. 他的图形为于y 轴的右方.并通过点(1,0)2. 当a>1时在区间(0,1),y 的值为负.图形位于x 的下方,在区间(1, +∞),y 值为正,图形位于x 轴上方.在定义域是单调增函数.a<1在实用中很少用到/正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;(5) 反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数 x y cot arc =,),(+∞-∞∈x ,),0(π∈y .希腊字母读音1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Δ δ delta delt 德尔塔5 Ε ε epsilon ep`silon 伊普西龙6 Ζ ζ zeta zat 截塔7 Η η eta eit 艾塔8 Θ θ thet θit 西塔9 Ι ι iot aiot 约塔10 Κ κ kappa kap 卡帕11 Λ λ lambda lambd 兰布达12 Μ μ mu mju 缪13 Ν ν nu nju 纽14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 Π π pi pai 派17 Ρ ρ rho rou 柔18 Σ σ sigma`sigma 西格马19 Τ τ tau tau 套20 Υ υ upsilon jup`silon 宇普西龙21 Φ φ phi fai 佛爱22 Χ χ chi phai 西23 Ψ ψ psi psai 普西24 Ω ω omega o`miga 欧米伽。
三角函数公式及图像

锐角三角函数公式sin α=∠α的对边 / 斜边cos α=∠α的邻边 / 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°) /2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·s inγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·s inγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2si nαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2诱导公式sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*( n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0三角、反三角函数图像六个三角函数值在每个象限的符号:sinα·cscα cosα·secα tanα·cotα三角函数的图像和性质:1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx函数 y=sinx y=cosx y=tanx y=cotx定义域RR{x |x ∈R 且x≠kπ+2π,k ∈Z } {x |x ∈R 且x≠kπ,k ∈Z }值域[-1,1]x=2kπ+2π 时y max =1 x=2kπ-2π时y min =-1[-1,1] x=2kπ时y max =1 x=2kπ+π时y min =-1R无最大值 无最小值R 无最大值 无最小值 周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z).反三角函数:arcsinx arccosx名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数。
2_常见三角函数的图象

公众号“草木叶影数学谈”整理
第4页共4页
6、y | sin x |,偶函数,T 7、y | sin 2x |,偶函数,T
2
公众号“草木叶影数学谈”整理
第2页共4页
8、y | cos x |,偶函数,T 9、y | cos 2x |,偶函数,T
2 10、y sin | x |,偶函数,在R上不是周期函数 11、y sin | 2x |,偶函数,在R上不是周期函数
公众号“草木叶影数学谈”整理
第3页共4页
12、y cos | x | cos x, y cos | x |的图象与y cos x的图象一样 13、y cos | 2x | cos 2x, y cos | 2x |的图象与y cos 2x的图象一样 14、y | tanx |,偶函数,T
常见三角函数的图象
【公众号“草木叶影数学谈”整理】
1、y sin x, x R,奇函数,T 2 2、y cos x, x R,偶函数,T 2
3、y tan x, x R, x k , k Z,奇函数,T 2
公众号“草木叶影数学谈”整理
第1页共4页
4、y sin 2x,奇函数,T 5、y cos 2x,偶函数,T
常见三角函数图像及其性质
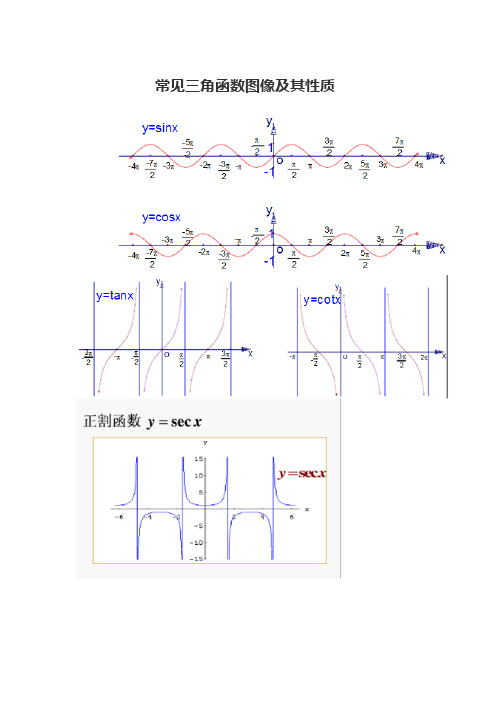
常见三角函数图像及其性质三角函数介绍正弦函数主词条:正弦函数格式:sin(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比斜边长度的比值求出,函数值为上述比的比值,也是csc(θ)的倒数函数图像:波形曲线值域:[]1,1-余弦函数主词条:余弦函数格式:cos(θ)作用:在直角三角形中,将大小为(单位为弧度)的角邻边长度比斜边长度的比值求出,函数值为上述比的比值,也是sec(θ)的倒数函数图像:波形曲线值域:[]1,1-正切函数主词条:正切函数格式:tan(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比邻边长度的比值求出,函数值为上述比的比值,也是cot(θ)的倒数。
函数图像:上图平面直角坐标系反映值域:()∞-∞,+余切函数主词条:余切函数格式:cot(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角邻边长度比对边长度的比值求出,函数值为上述比的比值,也是tan(θ)的倒数值域:()∞-∞,+正割函数主词条:正割函数格式:sec(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角邻边长度的比值求出,函数值为上述比的比值,也是cos(θ)的倒数函数图像:上图平面直角坐标系反映值域:(][)∞-1-,1∞,+余割函数主词条:余割函数格式:csc(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角对边长度的比值求出,函数值为上述比的比值,也是sin(θ)的倒数值域:(][)∞-1-∞,+,1。
高三数学三角函数的图象2

4.图象的对称性 ① y sin x与y cos x 的图象既是中心对称图形又 是轴对称图形。 ② y tan x的图象是中心对称图形,有无穷多条 垂直于x轴的渐近线。
1.三角函数线的应用 cos x 0 例1:解三角不等式组 1
y
1 2
sin x 0 2
白荌苒失神的笑了笑“没事”,虽然那孩子的爱一直有些偏执,但是终归是一个勇敢的孩子。
三、小结: 1.用五点法作图 2.图象变换 3.三角函数图象的应用
四、作业
; / 福利群 想要放开他的手,也许是因为他的那些话语,我便真的慢慢好了起来,可是,当我完全康复的时候,他又开始寻找了不同的大姐姐,我很生气, 每次都会去搅他的局,他还是那样无关痛痒的样子,后来也算倒霉、碰上了一个性格火爆的大姐姐,在我搅局的时候泼了我一杯红酒还甩了我 一耳光,我当时就被打愣住了,知北当时说了一个‘滚’字,哪位大姐姐便得意的看向我‘听到了没有,让你滚呐,不要再在这里碍眼了’, 我当时真的是有一种生无可恋的心情。然而,当我转身的时候知北却握住了我的手,他站了起来将我揽在了怀中一边替我擦拭脸上的红酒一遍 查看脸上的伤,他脸色不太好声音低沉地说了句‘是让你滚’然后便将我带离了那个地方,那是去年发生的事情,后来,我们就成了现在的这 种关系。”游悠还是笑得一脸的无害“他终于愿意跟我在一起了,他说等我大学一毕业就跟我结婚,我这一辈子好像都是为了不断地走向他而 努力着,不过,我觉得这样很好,因为我一直的梦想就是要跟他在一起呀!”游悠忽然又冲她眨了眨眼睛“姐姐,也许你不相信,但是,只有 我自己知道我从很小很小的时候就开始梦想着成为他的新娘!” 游悠抬起头来冲着白荌苒笑了笑“姐姐啊,今天真是太感谢你了,从来都没有人真正的听我说这么长时间的话了。”
三角函数图像-三角函数图像。

在信号处理中,三角函数图像可以用来进行频谱 分析和滤波。
测量技术
在测量技术中,三角函数图像可以用来进行角度、 距离等测量。
在数学分析中的应用
微积分
在微积分中,三角函数图像可以用来理解函数的极限、连续性、 可导性等概念。
复数分析
在复数分析中,三角函数图像可以用来理解复数的概念和性质。
线性代数
04
正切函数图像
正切函数的定义
总结词
正切函数是三角函数的一种,定义为直 角三角形中锐角的对边长度除以邻边长 度。
VS
详细描述
在直角坐标系中,以原点为顶点,x轴为 对边,y轴为邻边的单位圆上,正切函数 定义为直角三角形中锐角的对边长度除以 邻边长度。
正切函数的性质
总结词
正切函数具有周期性、奇偶性、单调性等性 质。
三角函数图像
目录
• 三角函数图像概述 • 正弦函数图像 • 余弦函数图像 • 正切三角函数图像概述
三角函数图像的定义
三角函数图像
三角函数图像是指将三角函数的值域映射到平面坐标 系上形成的图形。
常见的三角函数
常见的三角函数包括正弦函数、余弦函数、正切函数 等。
通过使用数学软件或绘图工具,可以绘制出余弦函数的图 像。
要点二
详细描述
绘制余弦函数的图像需要确定函数的定义域和值域,然后 选择适当的坐标系和单位。接下来,可以使用数学软件或 绘图工具,如MATLAB、Python的matplotlib库等,来绘 制余弦函数的图像。在绘制过程中,可以选择不同的参数 和颜色来展示函数的形状和变化趋势。最终得到的图像是 一个周期性的波形,具有对称性和有界性等特点。
01
02
03
手工绘制
三角函数公式及图像[2]
![三角函数公式及图像[2]](https://img.taocdn.com/s3/m/040fe91bfad6195f302ba604.png)
锐角三角函数公式sin α=∠α的对边 / 斜边cos α=∠α的邻边 / 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-sin²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°) /2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·s inγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·s inγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2诱导公式sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*( n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0三角、反三角函数图像六个三角函数值在每个象限的符号:sinα·cscα cosα·secα tanα·cotα三角函数的图像和性质:.反三角函数:arcsinx arccosx。
三角函数的图象和性质

三角函数的图象和性质知识网络三角函数的图象和性质结构简图画龙点晴 概念三角函数的图象:(1) 函数x y sin =的图象叫做正弦曲线, 如图1; (2) 函数x y cos =的图象叫做余弦曲线, 如图2; (3) 函数x y tan =的图象叫做正切曲线, 如图3; (4) 函数x y cot =的图象叫做余切曲线, 如图4;周期函数: 对于函数f (x ),如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有:f (x +T)=f (x )那么函数f (x )就叫做周期函数,非零常数T 叫做这个函数的周期。
说明:1︒周期函数x ∈定义域M ,则必有x+T ∈M, 且若T>0则定义域无上界;T<0则定义域无下界;2︒“每一个值”只要有一个反例,则f (x )就不为周期函数(如f (x 0+t)≠f (x 0)); 3︒T 往往是多值的(如y=sinx 2π,4π,…,-2π,-4π,…都是周期)周期T 中最小的正数叫做f (x )的最小正周期(有些周期函数没有最小正周期). 三角函数的性质: 三角函数的性质如下表:[活用实例][例1] 求下列函数的最值: (1)y=sin(3x+4π)-1 ; (2) y=sin 2x-4sinx+5 ; (3) y=x x cos 3cos 3+- ; (4))3cos(2π-=x y (6π≤x ≤32π).[题解] (1) 当3x+4π=2k π+2π即 x=1232ππ+k (k ∈Z)时y max =0; 当3x+4π=2k π-2π即x=432ππ-k (k ∈Z)时y min =-2. (2) y=(sinx-2)2+1 ∴当x=2k π-2π k ∈Z 时y max =10; 当x=2k π-2πk ∈Z 时y min = 2. (3)y=-1+xcos 31+ 当x=2k π+π k ∈Z 时 y max =2; 当x=2k π k ∈Z 时 y min = 21.(4)∵x ∈[6π,32π] ∴x-3π∈[-6π,3π], ∴当x-3π=0 即x=3π时 y max =2; 当x-3π=3π 即x=32π时 y min =1. [例2] 求下列函数的定义域:(1)y=x x 2cos 21cos 3-- ; (2)y=lg(2sinx+1)+1cos 2-x ; (3)y=)cos(sin x . [题解] (1)∵3cosx-1-2cos 2x ≥0 ∴21≤cosx ≤1 ∴定义域为:[2k π-3π, 2k π+3π] (k ∈Z). (2))(32326726221cos 21sin Z k k x k k x k x x ∈⎪⎩⎪⎨⎧+≤≤-+<<-⇒⎪⎩⎪⎨⎧≥->ππππππππ )(3262Z k k x k ∈+≤<-⇒ππππ ∴定义域为:)](32,62(Z k k k ∈+-ππππ.(3) ∵cos(sinx)≥0 ∴ 2k π-2π≤x ≤2k π+2π(k ∈Z) ∵-1≤sinx ≤1 , ∴x ∈R , 1cos ≤y ≤1.[例3] 已知函数f(x)=2asin 2x-23asinxcosx+b 的定义域为[0,2π],值域为[-5,4],求常数a,b 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的图象与性质
考纲要求:B
1.“五点法”作图原理
在确定正弦函数y =sin x 在[0,2π]上的图象形状时,起关键作用的五个点是________、__________、__________、__________、__________.余弦函数呢?
2.三角函数的图象和性质
都有f (x +T )=f (x ),那么函数f (x )就叫做周期函数,非零常数T 叫做这个函数的周期,把所有周期中存在的最小正数,叫做最小正周期(函数的周期一般指最小正周期).函数y =A sin(ωx +φ)或y =A cos(ωx +φ)(ω>0且为常数)的周期T =2π
ω,函数y =A tan(ωx +φ)(ω>0)
的周期T =π
ω.
基础自测
1.函数y =tan ⎝⎛⎭⎫
π4-x 的定义域为_________________________. 2.函数f (x )=3sin ⎝⎛⎭⎫x 2-π4,x ∈R 的最小正周期为________.
3.设点P 是函数f (x )=sin ωx (ω≠0)的图象C 的一个对称中心,若点P 到图象C 的对称轴的距离的最小值是π
4
,则f (x )的最小正周期是________.
4.y =2-3cos ⎝⎛⎭⎫x +π
4的最大值为________,此时x =______________. 5.下列区间是函数y =2|cos x |的单调递减区间的是
( )
A. (0,π)
B.⎝⎛⎭⎫-π2,0
C.⎝⎛⎭⎫3π2,2π
D.⎝
⎛⎭⎫-π,-π
2 题型一 与三角函数有关的函数定义域问题 例1 求下列函数的定义域: (1)21
cos )lg(sin -
+=x x y 求函数y =x 2
1log 2++tan x 的定义域.
题型二 三角函数的单调性与周期性 例2 写出下列函数的单调区间及周期: (1))3
2sin(π
+
=x y ; (2)y =sin ⎝
⎛⎭⎫-2x +π
3; (3)y =|tan x |.
变式训练:(1)求函数y =sin ⎝⎛⎭⎫π3+4x +cos ⎝
⎛⎭⎫4x -π
6的周期、单调区间及最大、最小值; (2) 求函数)6
6
)(3
2sin(2π
π
π
<
<-
+=x x y 的值域
题型三 三角函数的对称性与奇偶性
例3 (1)已知f (x )=sin x +3cos x (x ∈R ),函数y =f (x +φ) ⎝⎛⎭⎫|φ|≤π
2的图象关于直线x =0对称,则φ的值为________.
(2)如果函数y =3cos(2x +φ)的图象关于点⎝⎛⎭⎫
4π3,0中心对称,那么|φ|的最小值为___________
函数y =A sin(ωx +φ)的图象(A 级)
1.用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点. 如下表所示.
2.函数y = 方法一
画出y =sin x 的图象
_______________________
得到y =sin (x +φ)的图象
____________
得到y =sin (ωx +φ)的图象____________________得到y =A sin (ωx +φ)的图象 方法二
画出y =sin x 的图象______________________得到y =sin ωx 的图象__________________ 得到y =sin (ωx +φ)的图象___________________________得到y =A sin (ωx +φ)的图象 以上两种方法的区别:方法一先平移再伸缩;方法二先伸缩再平移.特别注意方法二中的平移量.
3.当函数y =A sin(ωx +φ) (A >0,ω>0,x ∈[0,+∞))表示一个振动时,A 叫做________,T =2πω叫做________,f =1
T 叫做________,ωx +φ叫做________,φ叫做________. 基础自测
1. y =2sin ⎝
⎛⎭⎫2x -π
4的振幅为________,频率和初相分别为________、________. 2.要得到函数y =3sin ⎝⎛⎭⎫2x +π
4的图象,只需将函数y =3sin 2x 的图象向________平移________个单位.
3(2011·大纲全国)设函数f (x )=cos ωx (ω>0),将y =f (x )的图象向右平移π
3
个单位长度后,所得
的图象与原图象重合,则ω的最小值等于_____________
4.把函数y =sin ⎝⎛⎭⎫5x -π2的图象向右平移π
4个单位,再把所得函数图象上各点的横坐标缩短为原来的1
2,所得的函数解析式为________________
题型一 作y =A sin(ωx +φ)的图象 例1 已知函数y =2sin ⎝⎛⎭⎫2x +π3, (1)求它的振幅、周期、初相;
(2)用“五点法”作出它在一个周期内的图象;
(3)说明y =2sin ⎝⎛⎭⎫2x +π
3的图象可由y =sin x 的图象经过怎样的变换而得到.
题型二 求函数y =A sin(ωx +φ)的解析式
例2 已知曲线y =A sin(ωx +φ) (A >0,ω>0)上的一个最高点的坐标为⎝⎛⎭⎫π
2,2,由此点到相邻最低点间的曲线与x 轴交于点⎝⎛⎭⎫32π,0,若φ∈⎝⎛⎭⎫-π2,π
2.
(1)(2011·江苏)已知f (x )=A sin(ωx +φ) (A ,ω,φ为常数,A >0,ω>0)的部分图象如图所
示,则f (0)的值是______.
(2)(2011·辽宁)已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π
2),
y =f (x )的部分图象如图所示,则f (π
24)等于
( )
A. 2+ 3
B.3
C.
3
3
D.2- 3
巩固练习
1.【2012高考安徽文7】要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象 (A ) 向左平移1个单位 (B ) 向右平移1个单位 (C ) 向左平移
12个单位 (D ) 向右平移1
2
个单位 2.【2012高考新课标文9】已知ω>0,πϕ<<0,
直线4
π
=x 和4
5π
=
x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=___________
3.【2012高考山东文8】函数2sin (09)63x y x ππ⎛⎫
=-≤≤
⎪⎝⎭的最大值与最小值之和为_________ 4.【2012高考全国文3】若函数()sin
([0,2])3
x f x ϕ
ϕπ+=∈是偶函数,则=ϕ________ 5【2012高考浙江文6】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是( )
6.【2102高考福建文8】函数f(x)=sin(x-4
π
)的图像的一条对称轴是( ) A.x=4π B.x=2π C.x=-4π D.x=-2
π
7.【2012高考天津文科7】将函数f(x)=sin x ω(其中ω>0)的图像向右平移4
π
个单位长度,
所得图像经过点(
34
π,0),则ω的最小值是___________
8.【2012高考湖南文18】(本小题满分12分) 已知函数()sin()(,0,02
f x A x x R π
ωϕωω=+∈><<的部分图像如图5所示.
(Ⅰ)求函数f (x )的解析式;
(Ⅱ)求函数()()()12
12
g x f x f x π
π
=-
-+
的单调递增区间.。
