三角函数图像与性质题型专题
三角函数图像与性质-知识点总结及题型归纳讲义
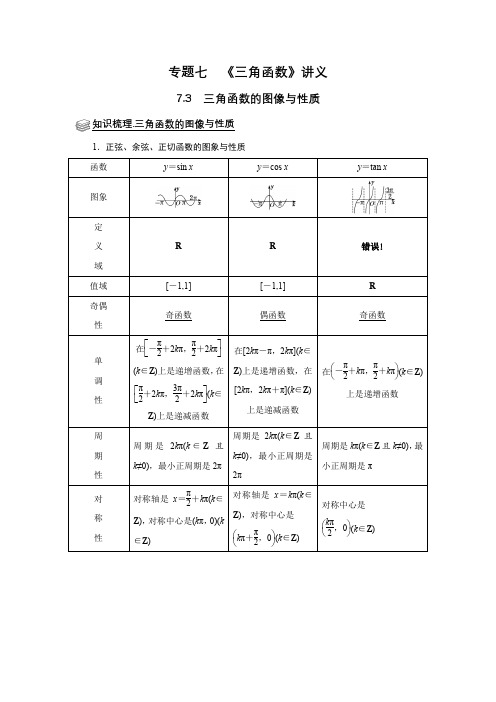
专题七《三角函数》讲义7.3 三角函数的图像与性质知识梳理.三角函数的图像与性质1．正弦、余弦、正切函数的图象与性质函数y＝sin x y＝cos x y＝tan x 图象定义域R R错误!值域[－1,1][－1,1]R奇偶性奇函数偶函数奇函数单调性在⎣⎡⎦⎤－π2＋2kπ，π2＋2kπ(k∈Z)上是递增函数，在⎣⎡⎦⎤π2＋2kπ，3π2＋2kπ(k∈Z)上是递减函数在[2kπ－π，2kπ](k∈Z)上是递增函数，在[2kπ，2kπ＋π](k∈Z)上是递减函数在⎝⎛⎭⎫－π2＋kπ，π2＋kπ(k∈Z)上是递增函数周期性周期是2kπ(k∈Z且k≠0)，最小正周期是2π周期是2kπ(k∈Z且k≠0)，最小正周期是2π周期是kπ(k∈Z且k≠0)，最小正周期是π对称性对称轴是x＝π2＋kπ(k∈Z)，对称中心是(kπ，0)(k∈Z)对称轴是x＝kπ(k∈Z)，对称中心是⎝⎛⎭⎫kπ＋π2，0(k∈Z)对称中心是⎝⎛⎭⎫kπ2，0(k∈Z)题型一. 三角函数图像的伸缩变换1．要得到函数y ＝3sin （2x +π3）的图象，只需要将函数y ＝3cos2x 的图象（ ） A ．向右平行移动π12个单位 B ．向左平行移动π12个单位C ．向右平行移动π6个单位D ．向左平行移动π6个单位2．（2017•新课标Ⅰ）已知曲线C 1：y ＝cos x ，C 2：y ＝sin （2x +2π3），则下面结论正确的是（ ）A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 23．（2021春•闵行区校级期中）函数y ＝cos （2x +φ）的图象向右平移π2个单位长度后与函数y ＝sin （2x +2π3）的图象重合，则|φ|的最小值为 ．4．（2016春•南通期末）将函数f(x)=sin(ωx +φ)，(ω＞0，−π2＜φ＜π2)图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移π4个单位长度得到y ＝sin x 的图象，则f(π6)= ．5．（2015•湖南）将函数f （x ）＝sin2x 的图象向右平移φ（0＜φ＜π2）个单位后得到函数g （x ）的图象．若对满足|f （x 1）﹣g （x 2）|＝2的x 1、x 2，有|x 1﹣x 2|min =π3，则φ＝（ ） A ．5π12B ．π3C ．π4D ．π6题型二. 已知图像求解析式1．图是函数y ＝A sin （ωx +φ）（x ∈R ）在区间[−π6，5π6]上的图象，为了得到这个函数的图象，只要将y ＝sin x （x ∈R ）的图象上所有的点（ ）A ．向左平移π3个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变B ．向左平移π3个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变C ．向左平移π6个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变D ．向左平移π6个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变2．已知函数y =sin(ωx +φ)(ω＞0，|φ|＜π2)的部分图象如图所示，则（ ）A ．ω=π2，φ=−π4 B ．ω=π2，φ=π4C ．ω=π，φ=−π4D ．ω=π，φ=π43．已知函数f （x ）＝A cos （ωx +φ）的图象如图所示，f （π2）=−23，则f （0）＝（ ）A ．−23B ．−12C ．23D ．124．已知函数f （x ）＝A tan （ωx +φ）（ω＞0，|φ|＜π2）的部分图象如图所示，下列关于函数g （x ）＝A cos （ωx +φ）（x ∈R ）的表述正确的是（ ）A ．函数g （x ）的图象关于点（π4，0）对称B ．函数g （x ）在[−π8，3π8]递减 C ．函数g （x ）的图象关于直线x =π8对称D ．函数h （x ）＝cos2x 的图象上所有点向左平移π4个单位得到函数g （x ）的图象题型三. 三角函数的性质 考点1.单调性1．函数y ＝sin （﹣2x +π3）的单调递减区间是（ ） A ．[k π−π12，k π+5π12]，k ∈Z B ．[2k π−π12，2k π+5π12]，k ∈ZC ．[k π−π6，k π+5π6]，k ∈ZD ．[2k π−π6，2k π+5π6]，k ∈Z2．已知函数f(x)=Asin(x +φ)(A ＞0，−π2＜φ＜0)在x =5π6时取得最大值，则f （x ）在[﹣π，0]上的单调增区间是（ ） A ．[−π，−5π6] B ．[−5π6，−π6] C ．[−π3，0]D ．[−π6，0]3．已知函数f （x ）＝sin （2x +π3）在区间[0，a ]（其中a ＞0）上单调递增，则实数a 的取值范围是（ ） A ．{a |0＜a ≤π12} B ．{a |0＜a ≤π2} C ．{a |a ＝k π+π12，k ∈N *} D ．{a |2k π＜a ≤2k π+π12，k ∈N *} 4．已知ω＞0，函数f （x ）＝sin （ωx +π4）在区间（π2，π）上单调递减，则实数ω的取值范围是（ ） A ．[12，54] B ．[12，34]C ．(0，12]D ．（0，2]考点2.周期性、奇偶性、对称性1．已知函数f （x ）＝cos 2x +sin 2（x +π6），则（ ）A ．f （x ）的最小正周期为π，最小值为12B ．f （x ）的最小正周期为π，最小值为−12C ．f （x ）的最小正周期为2π，最小值为12D ．f （x ）的最小正周期为2π，最小值为−122．已知f （x ）＝sin2x +|sin2x |（x ∈R ），则下列判断正确的是（ ） A ．f （x ）是周期为2π的奇函数 B ．f （x ）是值域为[0，2]周期为π的函数 C ．f （x ）是周期为2π的偶函数 D ．f （x ）是值域为[0，1]周期为π的函数3．将函数y ＝sin2x −√3cos2x 的图象沿x 轴向右平移a 个单位（a ＞0）所得图象关于y 轴对称，则a 的最小值是（ ） A ．712π B ．π4C ．π12D ．π64．已知函数f （x ）＝a sin x ﹣b cos x （ab ≠0，x ∈R ）在x =π4处取得最大值，则函数y ＝f （π4−x ）是（ ）A ．偶函数且它的图象关于点（π，0）对称B ．偶函数且它的图象关于点(3π2，0)对称 C ．奇函数且它的图象关于点(3π2，0)对称 D ．奇函数且它的图象关于点 （π，0）对称考点3.三角函数性质综合1．（2019•天津）已知函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，|φ|＜π）是奇函数，将y ＝f （x ）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为g （x ）．若g （x ）的最小正周期为2π，且g （π4）=√2，则f （3π8）＝（ ）A ．﹣2B ．−√2C ．√2D ．22．（2015•天津）已知函数f （x ）＝sin ωx +cos ωx （ω＞0），x ∈R ，若函数f （x ）在区间（﹣ω，ω）内单调递增，且函数y ＝f （x ）的图象关于直线x ＝ω对称，则ω的值为 ．3．（2014•大纲版）若函数f （x ）＝cos2x +a sin x 在区间（π6，π2）是减函数，则a 的取值范围是 ．4．（2016•新课标Ⅰ）若函数f （x ）＝x −13sin2x +a sin x 在（﹣∞，+∞）单调递增，则a 的取值范围是（ ） A ．[﹣1，1]B ．[﹣1，13]C ．[−13，13]D ．[﹣1，−13]5．（2013•安庆二模）已知函数f （x ）＝sin （ωx +π6），其中ω＞0，若f （π6）＝f （π3），且f （x ）在区间（π6，π3）上有最小值、无最大值，则ω等于（ ）A ．403B ．283C ．163D ．436．（2014•北京）设函数f （x ）＝A sin （ωx +φ）（A ，ω，φ是常数，A ＞0，ω＞0）若f （x ）在区间[π6，π2]上具有单调性，且f （π2）＝f（2π3）＝﹣f （π6），则f （x ）的最小正周期为 ．题型四. 三角函数最值1．函数f （x ）=15sin （x +π3）+cos （x −π6）的最大值为（ ） A ．65B ．1C ．35D ．152．函数f （x ）＝cos （ωx +π3）（ω＞0）在[0，π]内的值域为[﹣1，12]，则ω的取值范围为（ ） A ．[32，53]B ．[23，43]C ．[23，+∞)D ．[23，32]3．已知函数f （x ）＝cos2x +sin x ，则下列说法中正确的是（ ） A ．f （x ）的一条对称轴为x =π4 B ．f （x ）在（π6，π2）上是单调递减函数C ．f （x ）的对称中心为（π2，0）D ．f （x ）的最大值为14．若0＜x ≤π3，则函数y ＝sin x +cos x +sin x cos x 的值域为 ．5．已知函数f(x)=2sinωx ⋅cos 2(ωx 2−π4)−sin 2ωx(ω＞0)在区间[−2π5，5π6]上是增函数，且在区间[0，π]上恰好取得一次最大值1，则ω的取值范围是（ ） A ．(0，35]B ．[12，35]C ．[12，34]D ．[12，52)6．已知函数f （x ）＝cos x •sin （x +π3）−√3cos 2x +√34，x ∈R （1）求f （x ）的最小正周期；（2）求f （x ）在闭区间[0，π2]上的最大值和最小值及相应的x 值；（3）若不等式|f （x ）﹣m |＜2在x ∈[0，π2]上恒成立，求实数m 的取值范围．题型五.三角函数零点1．已知函数f （x ）＝sin ωx −√3cos ωx （ω＞0），若方程f （x ）＝﹣1在（0，π）上有且只有四个实数根，则实数ω的取值范围为 ．2．已知函数f （x ）=√3sin ωx cos ωx +cos 2ωx −12，（ω＞0，x ∈R ），若函数f （x ）在区间（π2，π）内没有零点，则ω的取值范围（ ） A ．（0，512] B ．（0，512]∪[56，1112]C ．（0，58]D ．（0，56]∪[1112，1）3．函数f(x)=2sin(2ωx +π6)(ω＞0)图象上有两点A （s ，t ），B （s +2π，t ）（﹣2＜t ＜2），若对任意s ∈R ，线段AB 与函数图象都有五个不同交点，若f （x ）在[x 1，x 2]和[x 3，x 4]上单调递增，在[x 2，x 3]上单调递减，且x 4−x 3=x 2−x 1=23(x 3−x 2)，则x 1的所有可能值是课后作业. 三角函数的图像与性质1．函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，﹣π＜φ＜0）的部分图象如图所示，为了得到g （x ）＝A sin ωx 的图象，只需将函数y ＝f （x ）的图象（ ）A ．向左平移π3个单位长度B ．向左平移π12个单位长度 C ．向右平移π3个单位长度D ．向右平移π12个单位长度2．关于函数y ＝2sin （3x +π4）+1，下列叙述正确的是（ ） A ．其图象关于直线x =−π4对称 B ．其图象关于点（π12，1）对称 C ．其值域是[﹣1，3]D ．其图象可由y ＝2sin （x +π4）+1图象上所有点的横坐标变为原来的13得到 3．已知函数f （x ）＝（12a −√3）sin x +（√32a +1）cos x ，将f （x ）的图象向右平移π3个单位长度得到函数g （x ）的图象，若对任意x ∈R ，都有g （x ）≤g （π4），则a 的值为 ． 4．已知函数f （x ）＝sin （ωx +φ）（ω＞1，0≤φ≤π）是R 上的偶函数，其图象关于点M （3π4，0）对称，且在区间[0，π2]上是单调函数，则ω和φ的值分别为（ ）A ．23，π4B ．2，π3C ．2，π2D ．103，π25．已知函数f （x ）＝sin （ωx +φ），其中ω＞0，|φ|≤π2，−π4为f （x ）的零点：且f （x ）≤|f （π4）|恒成立，f （x ）在区间（−π12，π24）上有最小值无最大值，则ω的最大值是（ ）A ．11B ．13C ．15D ．176．已知函数f （x ）＝2sin （ωx −π6）sin （ωx +π3）（ω＞0），若函数g （x ）＝f （x ）+√32在[0，π2]上有且只有三个零点，则ω的取值范围为（ ）A ．[2，113） B ．（2，113） C ．[73，103） D ．（73，103）。
三角函数的图像与性质专项训练(解析版)
三角函数的图像与性质专项训练一、单选题1．（23-24高一上·浙江宁波·期末）为了得到πsin 53y x ⎛⎫=+ ⎪⎝⎭的图象，只要将函数sin 5y x =的图象（）A ．向左平移π15个单位长度B ．向右平移π15个单位长度C ．向右平移π3个单位长度D ．向左平移π3个单位长度2．（23-24高一上·浙江丽水·期末）已知函数()()2sin f x x ωϕ=+的图象向左平移π6个单位长度后得到函数π2sin 23y x ⎛⎫=+ ⎪⎝⎭的图象，则ϕ的一个可能值是（）A ．0B ．π12C ．π6D ．π33．（23-24高一下·浙江杭州·期末）为了得到函数()sin2f x x =的图象，可以把()cos2g x x =的图象（）A ．向左平移π2个单位长度B ．向右平移π2个单位长度C ．向左平移π4个单位长度D ．向右平移π4个单位长度4．（23-24高一上·浙江宁波·期末）已知函数()()sin 0,π2f x x ϕωϕω⎛⎫=+>< ⎪⎝⎭.若π8f x ⎛⎫- ⎪⎝⎭为奇函数，π8f x ⎛⎫+ ⎪⎝⎭为偶函数，且()f x 在π0,6⎛⎫⎪⎝⎭上没有最小值，则ω的最大值是（）A ．2B ．6C ．10D ．145．（23-24高一上·浙江湖州·期末）我们知道，每一个音都是由纯音合成的，纯音的数学模型是sin y A x ω=．已知某音是由3个不同的纯音合成，其函数为()11sin sin 2sin 323f x x x x =++，则（）A ．π3f ⎛⎫=⎪⎝⎭B ．()f x 的最大值为116C ．()f x 的最小正周期为2π3D ．()f x 在π0,6⎛⎫⎪上是增函数6．（23-24高一上·浙江杭州·期末）已知函数()*2sin 6f x x ωω⎛⎫=+∈ ⎪⎝⎭N 有一条对称轴为23x =，当ω取最小值时，关于x 的方程()f x a =在区间,63ππ⎡⎤-⎢⎥⎣⎦上恰有两个不相等的实根，则实数a 的取值范围是（）A ．(2,1)--B ．[1,1)-6⎣7．（23-24高一下·浙江丽水·期末）已知函数1()2sin(32f x x x π=ω-ω>∈，R)，若()f x 的图象的任意一条对称轴与x 轴交点的横坐标均不属于区间(3π,4π)，则ω的取值范围是（）A ．1287(,[]2396B ．1171729(,][,]2241824C ．52811[,][,]93912D ．11171723[,][]182418248．（23-24高一下·浙江杭州·期末）已知函数()()sin ,0f x x ωω=>，将()f x 图象上所有点向左平移π6个单位长度得到函数()y g x =的图象，若函数()g x 在区间π0,6⎡⎤⎢⎥⎣⎦上单调递增，则ω的取值范围为（）A ．(]0,4B ．(]0,2C ．30,2⎛⎤⎥⎝⎦D ．(]0,1【答案】C【详解】因为函数()()sin ,0f x x ωω=>，二、多选题9．（23-24高一上·浙江台州·期末）已知函数()ππsin cos sin cos 44f x x x x x ⎛⎫⎛⎫=+++ ⎪ ⎝⎭⎝⎭，则（）A ．函数()f x 的最小正周期为2πB ．点π,08⎛⎫- ⎪⎝⎭是函数()f x 图象的一个对称中心C ．函数()f x 在区间π5π,88⎡⎤⎢⎥上单调递减D ．函数()f x 的最大值为110．（23-24高一上·浙江湖州·期末）筒车是我国古代发明的一种水利灌溉工具，因其经济又环保，至今还在农业生产中得到使用，现有一个筒车按逆时针方向匀速转动．每分钟转动5圈，如图，将该筒车抽象为圆O ，筒车上的盛水桶抽象为圆O 上的点P ，已知圆O 的半径为4m ，圆心O 距离水面2m ，且当圆O 上点P 从水中浮现时（图中点0P ）开始计算时间，点P 的高度()h t 随时间t （单位秒）变化时满足函数模型()()sin h t A t b ωϕ=++，则下列说法正确的是（）A ．函数()h t 的初相为π6B ．1秒时，函数()h t 的相位为0故选：BC ．11．（23-24高一上·浙江丽水·期末）已知函数π()tan(2)6f x x =-，则（）A ．()f x 的最小正周期是π2B ．()f x 的定义域是π{|π,Z}3x x k k ≠+∈C ．()f x 的图象关于点π(,0)12对称D ．()f x 在ππ(,)32上单调递增三、填空题12．（23-24高一上·浙江金华·期末）函数()π2π200cos 30063f n n ⎛⎫=++ ⎪⎝⎭（{}1,2,3,,12n ∈⋅⋅⋅为月份），近似表示某地每年各个月份从事旅游服务工作的人数，游客流量越大所需服务工作的人数越多，则可以推断，当n =时，游客流量最大．13．（23-24高一上·浙江湖州·期末）已知()3sin 4f x x ϕ⎛⎫=+ ⎪⎝⎭，其中0,2ϕ⎛⎫∈ ⎪⎝⎭，且ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，若函数()f x 在区间2π,3θ⎛⎫⎪上有且只有三个零点，则θ的范围为．14．（23-24高一上·浙江温州·期末）已知函数()π2sin (0)6f x x ωω⎛⎫=+> ⎪⎝⎭，对x ∀∈R 都有()π3f x f ⎛⎫⎪⎝⎭≤，且在,163⎛⎫ ⎪⎝⎭上单调，则ω的取值集合为四、解答题15．（23-24高一下·浙江丽水·期末）已知函数22()sin2f x x x x =.(1)求函数()f x 的最小正周期及单调递减区间；(2)将函数()f x 的图象上每个点的纵坐标缩短到原来的12，横坐标也缩短到原来的12，得到函数()g x 的图象，若函数()y g x m =-在区间π0,4⎡⎤⎢⎥内有两个零点，求实数m 的取值范围.16．（23-24高一下·浙江衢州·期末）已知函数()cos2f x x x =+.(1)求函数()f x 的最小正周期和对称中心；(2)求函数()f x 在π0,2⎡⎤⎢⎥上的值域.17．（23-24高一上·浙江杭州·期末）已知函数22()sin 2sin cos 3cos ,R f x x x x x x =++∈．求：(1)函数()f x 的最小值及取得最小值的自变量x 的集合；(2)函数()f x 的单调增区间．18．（23-24高一下·浙江杭州·期末）已知实数0a <，设函数22()cos sin2f x x a x a =+-，且()64f =-．(1)求实数a ，并写出()f x 的单调递减区间；(2)若0x 为函数()f x 的一个零点，求0cos2x ．19．（23-24高一上·浙江嘉兴·期末）已知函数()24cos 2f x x x a x =--．(1)若1a =-，求函数()f x 在[]0,2上的值域；(2)若关于x 的方程()4f x a =-恰有三个不等实根123,,x x x ，且123x x x <<，求()()131278f x f x x --的最大值，并求出此时实数a 的值．，。
高考数学专题复习：三角函数的图像与性质
高考数学专题复习：三角函数的图像与性质一、单选题1．函数()41sin 2x xf x x -=⋅的部分图像可能是（ ） A ． B ．C ．D ．2．已知函数()y f x =的图象如图所示，则此函数的解析式可能是（ ）A ．()sin 733x xxf x -=- B ．()sin 733x xxf x -=- C ．()cos 733x xxf x -=- D ．()cos 733x xxf x -=- 3．函数()sin 6f x A x πω⎛⎫=+ ⎪⎝⎭()0ω>的部分图象如图，()f x 的最小正零点是512π，则()f x =（ ）A ．72sin 12x π⎛⎫+⎪⎝⎭B ．2sin 26x π⎛⎫+ ⎪⎝⎭C ．2sin 26x π⎛⎫-+ ⎪⎝⎭D ．sin(2)6x π+4．函数()43f x cos x ππ⎛⎫=- ⎪⎝⎭图象的一条对称轴可能是直线x =（ ）A ．53-B ．13- C ．3π D ．43π5．现有四个命题： ①()0,1x ∃∈，tan 2x x +=； ②ππ,42x ⎛⎫∀∈ ⎪⎝⎭，1tan 4tan 1x x +≥-； ③函数()cos tan f x x x x =+的图象存在对称中心；④函数函数()πtan 23f x x ⎛⎫=- ⎪⎝⎭的最小为π．其中真命题的个数是（ ） A ．1B ．2C ．3D ．46．将函数()sin(2)f x x ϕ=-的图象向右平移6π个单位长度后，得到的图象关于y 轴对称，则ϕ的值可以为（ ） A ．2π-B ．6πC ．3π D ．2π 7．将函数()πsin 26f x x ⎛⎫=+ ⎪⎝⎭的图象向左平移π6个单位，得到函数()g x 的图象，则下列说法不正确的是（ ） A ．函数()g x 的周期为π B ．π162g ⎛⎫= ⎪⎝⎭C ．函数()g x 是奇函数D ．直线πx =是函数()g x 的一条对称轴8．已知函数()sin (0)f x x ωω=>在3,44ππ⎡⎤-⎢⎥⎣⎦上单调递增，则ω的取值范围是（ ）A ．[)2,+∞B ．(]0,2C ．2,3⎡⎫+∞⎪⎢⎣⎭D ．20,3⎛⎤⎥⎝⎦9．已知函数()1sin ,0,21cos ,0,2x x f x x x ⎧+<⎪⎪=⎨⎪+≥⎪⎩若()f x 在区间3,2a π⎡⎤-⎢⎥⎣⎦上至少有5个零点，()f x 在区间[],a π-上至多有5个零点，则正数a 的取值范围是（ ） A ．138,63ππ⎡⎤⎢⎥⎣⎦ B ．1310,63ππ⎡⎫⎪⎢⎣⎭C ．1910,63ππ⎡⎫⎪⎢⎣⎭D ．819,36ππ⎡⎤⎢⎥⎣⎦10．函数()()sin 0,2f x A x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图像如图所示，那么=2f π⎛⎫⎪⎝⎭（ ）AB ．12CD11．函数()()sin f x A x =+ωϕ(其中0A >，0>ω，0ϕπ<<)的图像的一部分如图所示，则此函数的解析式是（ ）A ．()3sin 42f x x ππ⎛⎫=+ ⎪⎝⎭B ．3()3sin 44f x x ππ⎛⎫=+ ⎪⎝⎭C ．()3sin 84f x x ππ⎛⎫=+ ⎪⎝⎭D ．3()3sin 84f x x ππ⎛⎫=+ ⎪⎝⎭12．下列函数为偶函数的是（ ） A ．2cos y x x = B ．sin y x =- C ．tan2y x = D ．cos sin y x x =+二、填空题13．设函数()sin f x x =，[],x a b ∈，其值域为1,12⎡⎤-⎢⎥⎣⎦，设b a -最大值为M ，最小值为N ，则M N -=________14．函数sin 35y x π⎛⎫=- ⎪⎝⎭的最小正周期为________．15．已知()()cos f x x ωϕ=+（0>ω，π02ϕ<<）的图像过点10,2⎛⎫ ⎪⎝⎭，要使该函数解析式为()πcos 23f x x ⎛⎫=+ ⎪⎝⎭，还应该给出的一个条件是________．16．若函数()()sin 0y x ωϕω=+>的部分图象如图，则ω=________．三、解答题17．已知函数()sin 6f x x πωϕ⎛⎫=+- ⎪⎝⎭（0ϕπ<<，0>ω）图象的一条对称轴方程为12x π=，且()f x 相邻的两个零点间的距离为2π.（1）求()f x 的解析式； （2）求方程()34f x =在区间[]0,2π内的所有实数根之和.18．已知函数()4sin()10,||2f x x πωϕωϕ⎛⎫=++>< ⎪⎝⎭的最小正周期为π，且(0)3f =.（1）求ω和ϕ的值.（2）将函数()f x 的图象向右平移3π个单位长度(纵坐标不变)，得到函数()g x 的图象， ①求函数()g x 的单调递增区间；②求函数()g x 在0,3π⎡⎤⎢⎥⎣⎦上的最大值.19．已知()()()()()()2sin cos sin 2cos 6211cos cos cos 22x x x x f x x x x πππππππ⎛⎫---⋅--⋅- ⎪⎝⎭=⎛⎫-⋅-++ ⎪⎝⎭．（1）化简函数()f x 的解析式； （2）设函数()324g x f x π⎛⎫=+⎪⎝⎭，求函数()g x 的单调增区间．20．已知函数()()sin 0,π2f x x ϕωϕω⎛⎫=+>< ⎪⎝⎭的部分图象如图所示.（1）求函数()f x 的解析式；（2）求函数()f x 在区间,44ππ⎛⎤- ⎥⎝⎦上的值域.21．已知函数()15sin 22cos 242f x x x π⎛⎫=--+ ⎪⎝⎭，（1）求()f x 的最小正周期和单调区间；（2）若()2f x t =在744ππ⎡⎤⎢⎥⎣⎦，上有4个解，求t 的取值范围.22．已知点()()11,A x f x ，()()22,B x f x 是函数()()2sin f x x ωϕ=+0,02πωϕ⎛⎫>-<< ⎪⎝⎭图象上的任意两点，且角ϕ的终边经过点(1,P ，当12()()4f x f x -=时，12x x -的最小值为3π. （1）求函数()f x 的单调减区间;（2）求函数()f x 在4,99x ππ⎛⎫∈ ⎪⎝⎭内的值域; （3）若方程()23()0f x f x m ⎡⎤-+=⎣⎦在4,99x ππ⎛⎫∈ ⎪⎝⎭内有两个不相等的实数解，求实数m 的取值范围.参考答案1．A 【分析】确定函数的奇偶性，排除两个选项，再根据特殊的函数值排除一个后可得． 【详解】4141()sin()sin ()22x x x x f x x x f x -----=⋅-=⋅=，为偶函数，排除BD ，又(0)0f =，排除C ． 故选：A ． 2．D 【分析】由图象知()f x 是奇函数且当0x +→时()f x →+∞，结合各选项的解析式，利用奇偶性定义排除偶函数选项及0lim ()x f x +→=-∞的选项即可. 【详解】由图象知：()f x 是奇函数，而()()sin(7)sin 7()3333()x x x x f x x xf x -----===---，即为偶函数，排除A ；同理B 中()f x 也是偶函数，排除；当0x +→时，由图知()f x →+∞，而cos 71x →且33x x ->，此时cos 73(3)x xxf x -=→-∞-，故排除C. 故选：D 3．B 【分析】由图可得2A =，令()0f x =有(61)6k x πω-=，根据()f x 的最小正零点是512π求ω，即可写出()f x 的解析式.【详解】由图知：2A =，令()2sin()06f x x πω=+=，∴sin()06x πω+=，则(61)66k k x πππωωω-=-=，∵()f x 的最小正零点是512π，且0>ω， ∴当1k =时，55612x ππω==，得2ω=. ∴()2sin(2)6f x x π=+.故选：B 4．A 【分析】先计算出函数的对称轴，再适当地取k 的值进而得到答案. 【详解】 令(3)Z x k k πππ-=∈，解得()1Z 3k x k =+∈. 当2k =-时，53x =-.故选：A. 5．B 【分析】根据单调性判断①，结合基本不等式判断②，根据函数的奇偶性判断③，由正切型函数的周期判断④． 【详解】因为()tan f x x x =+在()0,1上单调递增，且()00f =，()π11tan11tan 24f =+>+=， 所以()0,1x ∃∈，tan 2x x +=．①正确当ππ,42x ⎛⎫∈ ⎪⎝⎭时，tan 1x >，()1,x ∀∈+∞，1111311x x x x +=-++≥--，当且仅当2x =时等号成立，②错；因为()()cos tan f x x x x f x -=--=-，所以()cos tan f x x x x =+为奇函数， 图象关于原点对称．③正确；函数()πtan 23f x x ⎛⎫=- ⎪⎝⎭的最小正周期π2T =．④错误．故①③为真命题． 故选：B ． 6．B写出平移后解析式，再由对称性得出ϕ值． 【详解】平移后解析式为()sin 2()sin(2)63g x x x ππϕϕ⎡⎤=--=--⎢⎥⎣⎦，它的图象关于y 轴对称，则,32k k Z ππϕπ+=+∈，,6k k Z πϕπ=+∈，只有B 满足．故选：B ． 7．C【分析】由三角函数图象变换写出()g x 的解析式，然后余弦函数性质判断各选项． 【详解】由题意()sin 2()sin(2)cos 2662g x x x x πππ⎡⎤=++=+=⎢⎥⎣⎦，最小正周期是22T ππ==，A 正确； 1cos 632g ππ⎛⎫== ⎪⎝⎭，B 正确；()cos(2)cos 2()g x x x g x -=-==，()g x 是偶函数，C 错误；()cos 21g ππ==为最大值，x π=是()g x 的一条对称轴，D 正确．故选：C ． 8．D【分析】根据正弦型函数的单调性，结合题意进行求解即可. 【详解】 当22()22k x k k Z πππωπ-≤≤+∈时，因为0>ω，所以有11(2)(2)()22k x k k Z ππππωω-⋅≤≤+⋅∈，因此函数()sin (0)f x x ωω=>的递增区间为：2222[,]()k k k Z ππππωω-+∈，因为函数()sin (0)f x x ωω=>在3,44ππ⎡⎤-⎢⎥⎣⎦上单调递增，所以令0k =，且有32424ππωππω⎧⎪≤⎪⎪⎨⎪-⎪-≥⎪⎩，因为0>ω，所以解得：203ω<≤，9．B 【分析】作出1sin 2x =-与1cos 2x =-的图象，结合图象即可求解【详解】因为方程1sin 2x =-在[),0π-上的解为56π-，6π-，所以当()f x 在区间[],a π-上至多有5个零点时，100.3a π<<因为方程1cos 2x =-在30,2π⎡⎤⎢⎥⎣⎦上的解为23π，43π，所以当()f x 在区间3,2a π⎡⎤-⎢⎥⎣⎦上至少有5个零点时，136a π-≤-，即136a π≥ 综上，正数a 的取值范围是1310,63ππ⎡⎫⎪⎢⎣⎭故选：B 10．B 【分析】本题可根据最大值为1求出1A =，然后根据周期的14为4π求出2ω=，再然后根据过点,13π⎛⎫⎪⎝⎭求出6πϕ=-，最后代入2x π=，即可得出结果.【详解】因为最大值为1，所以1A =，()()sin f x x ωϕ=+，因为周期的14为4π，所以最小正周期为π，2ω=，()()sin 2f x x ϕ=+，因为过点,13π⎛⎫⎪⎝⎭，2πϕ<，所以21sin 3πϕ⎛⎫=+⎪⎝⎭，解得6πϕ=-，()sin 26f x x π⎛⎫=- ⎪⎝⎭， 则51sin sin6226f ππππ⎛⎫⎛⎫=-== ⎪ ⎪⎝⎭⎝⎭，11．C 【分析】根据图象可以求出最大值，结合函数的零点，根据正弦型函数的最小正周期公式，结合特殊值法进行求解即可. 【详解】由函数图象可知函数的最大值为3，所以3A =， 由函数图象可知函数的最小正周期为4(62)16⨯-=， 因为0>ω，所以24(62)168ππωω⨯-==⇒=，所以()3sin 8f x x πϕ⎛⎫=+ ⎪⎝⎭， 由图象可知：(2)3f =，即3sin 32()2()4424k k Z k k Z ππππϕϕπϕπ⎛⎫+=⇒+=+∈⇒=+∈ ⎪⎝⎭，因为0ϕπ<<， 所以令0k =，所以4πϕ=，因此()3sin 84f x x ππ⎛⎫=+ ⎪⎝⎭， 故选：C 12．A 【分析】根据奇偶性的定义判断各选项函数的奇偶性即可. 【详解】A ：22()()cos()cos ()y f x x x x x f x =-=--==且x ∈R ，偶函数；B ：()sin()sin ()y f x x x f x =-=--==-且x ∈R ，奇函数；C ：()tan2()tan 2()y f x x x f x =-=-=-=-且24k x ππ≠+ ()k ∈Z ，奇函数； D ：()cos()sin()cos sin y f x x x x x =-=-+-=-且x ∈R ，非奇非偶函数. 故选：A 13．23π【分析】令117sin ,2+26x x k ππ=-∴=或2122,6x k k k Z ππ=-∈，.令33sin 1,2,2x x k k Z ππ=∴=+∈.求出,M N 即得解.令117sin ,2+26x x k ππ=-∴=或2122,6x k k k Z ππ=-∈，.令33sin 1,2,2x x k k Z ππ=∴=+∈.当172+6a k ππ=或2122,,6a k k k Z ππ=-∈，且332,2b k k Z ππ=+∈所以3122()3b a k k ππ-=--或3222()3b a k k ππ-=-+.当320k k -=时，23b a N π-==；当2126a k ππ=-，且172,6b k k Z ππ=+∈时， 所以1242()3b a k k ππ-=-+.当120k k -=时，43b a M π-==.所以23M N π-=.故答案为：23π 14．23π 【分析】根据正弦函数的周期求解． 【详解】函数sin 35y x π⎛⎫=- ⎪⎝⎭的最小正周期为23T π=．故答案为：23π． 15．2ω=或周期πT = 【分析】由余弦型三角函数的周期可判断所需条件. 【详解】解：由图像过点10,2⎛⎫ ⎪⎝⎭可知3πϕ=，若求出解析式还需要一个和ω相关的量，故可直接给出条件2ω=或周期T π=. 故答案为：2ω=或周期T π=. 16．4根据正弦函数图象的对称性求得函数的周期，进而可求得ω. 【详解】由正弦函数图象的对称性得函数的周期00242T x x ππ⎡⎤⎛⎫=+-= ⎪⎢⎥⎝⎭⎣⎦，所以22ππω=，解得4ω=.故答案为：4.17．（1）()sin 23f x x π⎛⎫=+ ⎪⎝⎭；（2）133π. 【分析】（1）依题意可得T π=，即可求出ω，再根据函数的对称轴求出ϕ，即可求出函数解析式； （2）作出()y f x =与34y =的大致图象，根据函数的对称性计算可得； 【详解】 （1）()f x 相邻的两个零点间的距离2π， ∴()f x 的最小正周期222T πππω==⨯=，∴2ω=.又函数()f x 图象的一条对称轴方程为2x π=，∴21262k πππϕπ⨯+-=+()k Z ∈，即2k πϕπ=+()k Z ∈，而0ϕπ<<，∴2ϕπ=. 故()sin 23f x x π⎛⎫=+ ⎪⎝⎭.（2）因为()f x 的最小正周期为π，所以()f x 在[]0,2π内恰有2个周期. 令2,32πππ+=+∈x k k Z ，解得,122k x k Z ππ=+∈，即函数的对称轴为,122k x k Z ππ=+∈，因为34<，作出()y f x =与34y =的大致图象如图.由图可知两个图象在[]0,2π内有4个交点，横坐标依次为1x ，2x ，3x ，4x ， 且1x 与2x 关于712x π=对称，3x 与4x 关于1912x π=对称， 所以1276x x π+=，34196x x π+=， 故所有实数根之和为133π18．（1）2ω=，6π=ϕ；（2）①,(k )2k k πππ⎡⎤+∈⎢⎥⎣⎦Z ；②最大值为3.【分析】（1）根据正弦型函数的最小正周期公式，结合特殊角的三角函数值进行求解即可； （2）根据正弦型函数图象的变换性质，得到()g x 的解析式. ①根据余弦型函数的单调性进行求解即可； ②根据余弦型函数的最值性质进行求解即可. 【详解】解：（1）()f x 的最小正周期为π，0>ω 所以2ππ=ω， 即2ω=. 又因为(0)3f =， 所以1sin 2ϕ=，因为|2πϕ<，所以6π=ϕ. （2）由（1）可知()4sin 216f x x π⎛⎫=++ ⎪⎝⎭，函数()f x 的图象向右平移3π个单位长度(纵坐标不变)， 所以2()()4sin(2)14cos 21336g x f x x x πππ=-=-++=-+. ①由2[2,2]()x k k k Z πππ∈+∈，得函数()g x 的单调递增区间为,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦.②因为03x π≤≤，所以2023x π≤≤. 当223x π=， 即3x π=时，函数()g x 取得最大值，最大值为33g π⎛⎫= ⎪⎝⎭.19．（1）()2cos f x x =-；（2）3,88k k ππππ⎡⎤-++⎢⎥⎣⎦()k Z ∈． 【分析】（1）利用三角上的诱导公式，准确运算，即可求解；（2）由（1）得到()2sin 24g x x π⎛⎫=+ ⎪⎝⎭，结合三角函数的性质，即可求解.【详解】（1）结合诱导公式得()()()()()()2sin cos sin 2cos 6211cos cos cos 22x x x x f x x x x πππππππ⎛⎫---⋅--⋅- ⎪⎝⎭=⎛⎫-⋅-++ ⎪⎝⎭ ()()()()22cos sin cos cos sin cos x x x x x xπ⋅-⋅-=-⋅-2sin cos 12cos 2cos cos sin cos x x x x x x x -=⋅⋅⋅=---， 所以函数()2cos f x x =-．（2）根据（1）可得()322cos 22sin 24244g x f x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫=+=-++=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，令222242k x k πππππ-+≤+≤+，k Z ∈，得388k x k ππππ-+≤≤+，k Z ∈， 所以函数()g x 的单调增区间为3,88k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈． 20．（1）()sin 23f x x π⎛⎫=+ ⎪⎝⎭；（2）1,12⎛⎤- ⎥⎝⎦.【分析】（1）由最大值求得A ，由周期求得ω，代入一个点的坐标求得ϕ，得解析式； （2）求出x ωϕ+的范围，然后由正弦函数的性质得出值域． 【详解】解：(1)根据函数()()sin (0,)2f x x πωϕωϕ=+><的部分图象，可得32134123πππω⋅=-，求得2ω=，∴最小正周期22T ππ==， 再根据五点法作图可得23πϕπ+=，;3πϕ∴=∴函数()f x 的解析式为()sin(2)3f x x π=+．(2)?,44x ππ⎛⎤∈- ⎥⎝⎦，52,366x πππ⎛⎤∴+∈- ⎥⎝⎦1sin 2,132x π⎛⎫⎛⎤∴+∈- ⎪ ⎥⎝⎭⎝⎦，函数()f x 在区间,44ππ⎛⎤- ⎥⎝⎦上的值域1,12⎛⎤- ⎥⎝⎦21．（1）2T π=，单调增区间是52244k k ππππ⎡⎤++⎢⎥⎣⎦，，单调减区间是592244k k ππππ⎡⎤++⎢⎥⎣⎦，，k Z ∈；（2）(22t ⎤⎡∈-⋃⎦⎣.【分析】（1）利用二倍角公式结合二次函数化简函数，利用周期的概念求得周期，利用复合函数单调性求得函数单调性；（2）根据x 的范围求得2t 的范围，从而求得结果. 【详解】解：（1）()215cos 22cos cos 2cos 2224244f x x x x x ππππ⎛⎫⎛⎫⎛⎫⎛⎫=---+=---+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2cos 114x π⎛⎫⎛⎫=--+ ⎪ ⎪⎝⎭⎝⎭，∵()()22cos 211cos 12144x x f x f x ππππ⎛⎫⎛⎫⎛⎫⎛⎫=---+=--+= ⎪ ⎪ ⎪ ⎪⎝⎭⎭⎝⎭+⎝⎝⎭，所以()f x 的最小正周期是2T π=，设cos 4m x π⎛⎫- ⎝=⎪⎭，[]1,1m ∈-，则函数()211y m =-+在[]1,1-上单调递减，对于函数cos cos 44y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭，当224k x k ππππ≤-≤+，k Z ∈，即 x ∈52244k k ππππ⎡⎤++⎢⎥⎣⎦，时，cos 4y x π⎛⎫=- ⎪⎝⎭单调递减， 当2224k x k πππππ+≤-≤+，k Z ∈，即 x ∈592244k k ππππ⎡⎤++⎢⎥⎣⎦，时，cos 4y x π⎛⎫=- ⎪⎝⎭单调递增，故函数()f x 单调增区间是52244k k ππππ⎡⎤++⎢⎥⎣⎦，，单调减区间是592244k k ππππ⎡⎤++⎢⎥⎣⎦，，k Z ∈.()2由上述单调性知若()2f x t =在744ππ⎡⎤⎢⎥⎣⎦，上有4个解，且74f π⎛⎫ ⎪⎝⎭27cos 1144ππ⎛⎫⎛⎫=--+=⎪ ⎪⎝⎭⎝⎭2，且34f π⎛⎫ ⎪⎝⎭23cos 1144ππ⎛⎫⎛⎫=--+= ⎪ ⎪⎝⎭⎝⎭2，()54f x f π⎛⎫≤ ⎪⎝⎭25cos 11544ππ⎛⎫⎛⎫=--+= ⎪⎪⎝⎭⎝⎭所以225t ≤<，所以(22t ⎤⎡∈-⋃⎦⎣.22．（1）()52112,183183k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦；（2）(]0,2；（3）112⎧⎫⎨⎬⎩⎭或(]10,0- 【分析】（1）利用三角函数的定义求出ϕ的值，由题意知223T ππω==可得ω的值，进而可得()f x 的解析式，利用整体代入法以及正弦函数的单调性即可求解； （2）由x 的范围求出33x π-的范围，利用正弦函数的性质即可求解； （3）设()(]0,2f x t =∈，将问题转化为y m =-与(]23,0,2y t t t =-∈的图象只有一个交点，数形结合可得112m -=-或010m ≤-<，即可求解. 【详解】（1）因为角ϕ的终边经过点(1,P ，所以tan ϕ= 因为02πϕ-<<，所以3πϕ=-，因为当12()()4f x f x -=时，12x x -的最小值为3π， 所以223T ππω==，可得：3ω=，所以()2sin 33f x x π⎛⎫=- ⎪⎝⎭，令()3232232k x k k Z πππππ+≤-≤+∈解得：()52112183183k k x k Z ππππ+≤≤+∈， 所以函数()f x 的单调减区间为()52112,183183k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦（2）当4,99x ππ⎛⎫∈ ⎪⎝⎭时，033x ππ<-<， 所以0sin 313x π⎛⎫<-≤ ⎪⎝⎭，所以()02sin 323f x x π⎛⎫<=-≤ ⎪⎝⎭，所以函数()f x 在4,99x ππ⎛⎫∈ ⎪⎝⎭内的值域为(]0,2，（3）设()(]0,2f x t =∈，因为方程()23()0f x f x m ⎡⎤-+=⎣⎦在4,99x ππ⎛⎫∈ ⎪⎝⎭内有两个不相等的实数解， 则230t t m -+=在(]0,2t ∈内有一根或两个相等的实根，因为23m t t -=-，所以y m =-与(]23,0,2y t t t =-∈的图象只有一个交点，作出y m =-与(]23,0,2y t t t =-∈的图象，由图知：当16t =时211136612y ⎛⎫=⨯-=- ⎪⎝⎭；当0t =时，0y = ；当2t =时，232210y =⨯-=， 所以112m -=-或010m ≤-≤直线y m =-与(]23,0,2y t t t =-∈的图象只有一个交点， 当10m -=时，2t =，此时方程()2sin 323f x x π⎛⎫=-= ⎪⎝⎭只有一解，不符合题意，所以112m -=-或010m ≤-<，即方程()23()0f x f x m ⎡⎤-+=⎣⎦在4,99x ππ⎛⎫∈ ⎪⎝⎭内有两个不相等的实数解， 所以：112m =或100m -<≤所以实数m 的取值范围为：112⎧⎫⎨⎬⎩⎭或(]10,0-。
第11讲 三角函数的图象与性质6大题型(解析版)
第11讲三角函数的图象与性质6大题型【题型目录】题型一：三角函数的周期性题型二：三角函数对称性题型三：三角函数的奇偶性题型四：三角函数的单调性题型五：三角函数的值域题型六：三角函数的图像【典例例题】题型一：三角函数的周期性【例1】（2022·全国·兴国中学高三阶段练习（文））下列函数中，最小正周期为π的奇函数是（）．A ．tan y x =B ．sin 2y x =C ．sin cos y x x =D ．sin y x=【例2】（2022江西景德镇一中高一期中（文））下列函数中①sin y x =；②sin y x =；③tan y x =；④12cos y x =+，其中是偶函数，且最小正周期为π的函数的个数为（）A ．1B ．2C ．3D ．4【答案】B【解析】①的图象如下，根据图象可知，图象关于y 轴对称，sin y x =是偶函数，但不是周期函数，∴排除①；②的图象如下，根据图象可知，图象关于y 轴对称，sin y x =是偶函数，最小正周期是π，∴②正确；③的图象如下，根据图象可知，图象关于y 轴对称，tan y x =是偶函数，最小正周期为π，∴③正确；④的图象如下，根据图象可知，图象关于y 轴对称，12cos y x =+是偶函数，最小正周期为2π，∴排除④.故选：B.【例3】（2022·全国·高三专题练习）函数ππ()sin 2cos 233f x x x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭的最小正周期是（）A ．π4B ．π2C ．πD ．2π【例4】设函数()c x b x x f ++=sin 2cos ，则()x f 的最小正周期()A ．与b 有关，且与c 有关B ．与b 有关，但与c 无关C ．与b 无关，且与c 无关D ．与b 无关，但与c 有关【答案】B【解析】因x y 2cos =的最小正周期为ππ==22T ，x y sin =的最小正周期为ππ212==T 所以当0≠b 时，()x f 的最小正周期为π2；当0=b 时，()x f 的最小正周期为π；【例5】（2022·全国·高一课时练习）函数22cos 14y x π⎛⎫=+- ⎪⎝⎭的最小正周期为（）A ．4πB ．2πC ．πD ．2π【例6】（2022·广西桂林·模拟预测（文））函数()2sin6cos6f x x x =+的最小正周期是（）A ．2πB ．3πC ．32πD ．6π【例7】（2022·全国·高一专题练习）()|sin ||cos |f x x x =+的最小正周期是（）A ．2πB ．πC ．2πD ．3π【题型专练】1.（2023全国高三题型专练）在函数①cos |2|y x =，②|cos |y x =，③πcos 26y x ⎛⎫=+ ⎪⎝⎭，④πtan 24y x ⎛⎫=- ⎪⎝⎭中，最小正周期为π的所有函数为（）A ．②④B ．①③④C ．①②③D ．②③④【答案】C【解析】∵cos |2|y x ==cos2x ，∴T =22π=π；|cos |y x =图象是将y =cos x 在x 轴下方的图象对称翻折到x 轴上方得到，所以周期为π，由周期公式知，cos(2)6y x π=+为π，tan(2)4y x π=-为2π，故选：C .2.（2022·河北深州市中学高三阶段练习）下列函数中，最小正周期为π的奇函数是（）A ．sin 4y x π⎛⎫=+ ⎪⎝⎭B ．()()sin cos y x x ππ=+-C ．22cos cos 2y x x π⎛⎫=-+ ⎪D ．sin 2y x=3.（2022·北京昌平·高一期末）下列函数中，最小正周期为π的奇函数是（）A ．sin 4y x π⎛⎫=+ ⎪⎝⎭B ．sin 2y x =C ．sin cos y x x =D ．22cos sin y x x=-4.（2022·陕西渭南·高二期末（理））函数()2sin cos f x x x x =+的最小正周期是________．5．（2022·全国·高一专题练习）已知函数()cos f x x x ωω=-(0)ω>的最小正周期为π，则ω=___．6．（2022·浙江·杭十四中高一期末）函数2cos cos cos 2y x x x π⎛⎫=+- ⎪的最小正周期为__________．题型二：三角函数对称性【例1】（江西省“红色十校”2023届高三上学期第一联考数学（文）试题）已知函数π()sin()0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的两个相邻的零点为12,33-，则()f x 的一条对称轴是（）A ．16x =-B ．56x =-C ．13x =D ．23x =【例2】（2022全国高一课时练习）函数cos 23y x ⎛⎫=+ ⎪⎝⎭的图象（）A ．关于点,03π⎛⎫⎪⎝⎭对称B ．关于点,06π⎛⎫⎪⎝⎭对称C ．关于直线6x π=对称D ．关于直线3x π=对称【答案】D【解析】由题设，由余弦函数的对称中心为,2)0(k ππ+，令232x k πππ+=+，得212k x ππ=+，k Z ∈，易知A 、B 错误；由余弦函数的对称轴为x k π=，令23x k ππ+=，得26k x ππ=-，k Z ∈，当1k =时，3x π=，易知C 错误，D 正确；故选：D 【例3】（2022·江西省万载中学高一阶段练习）把函数4πsin 23y x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0ϕϕ>个单位长度，所得图像关于y 轴对称，则ϕ的最小值是（）A ．5π6B ．2π3C ．5π12D ．π6【例4】（2023福建省福州屏东中学高三开学考试多选题）已知函数()()3sin 222f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图像关于直线3x π=对称，则（）A ．函数12f x π⎛⎫+ ⎪⎝⎭为奇函数B ．函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递增C ．函数()f x 的图像向右平移()0a a >个单位长度得到的函数图像关于6x π=对称，则a 的最小值是3πD ．若方程()f x a =在2,63ππ⎡⎤⎢⎥上有2个不同实根12,x x ，则12x x -的最大值为2π故结合正弦函数的性质可知，若方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根12,x x ，不妨设12x x <，则12x x -取得最大值时满足1266x ππ-=且25266x ππ-=，所以，12x x -的最大值为3π，故错误.故选：AC【例5】(2023江西省高三月考)若函数y cos 6x πω⎛⎫=+ ⎪⎝⎭(ω∈N +)图象的一个对称中心是,06π⎛⎫⎪⎝⎭，则ω的最小值为()A ．1B ．2C ．4D ．8【答案】B 【解析】当6x π=时，0y =，即cos 066πωπ⎛⎫+=⎪⎝⎭，()662k k Z πωπππ∴+=+∈，解得62k ω=+，N ω*∈ ，故当0k =时，ω取最小值2.【例6】【2016高考新课标2理数】若将函数2sin 2y x =的图像向左平移12π个单位长度，则平移后图象的对称轴为（）（A ）()26k x k Z ππ=-∈（B ）()26k x k Z ππ=+∈（C ）()212k x k Z ππ=-∈（D ）()212k x k Z ππ=+∈【答案】B【解析】由题意，将函数2sin 2y x =的图像向左平移12π个单位得2sin 2()2sin(2)126y x x ππ=+=+，则平移后函数的对称轴为2,62x k k Z πππ+=+∈，即,62k x k Z ππ=+∈，故选B.【题型专练】1.(2020·四川省泸县第四中学高三开学考试)已知函数()sin 22f x x π⎛⎫=+ ⎪⎝⎭，则函数()f x 的图象的对称轴方程为()A ．,4x k k Z ππ=-∈B ．+,4x k k Z ππ=∈C ．1,2x k k Z π=∈D ．1+,24x k k Zππ=∈【答案】C【解析】由已知，()cos 2f x x =，令2,π=∈x k k Z ，得1,2x k k Z π=∈.故选：C.2.【2017·天津卷】设函数()2sin()f x x ωϕ=+，x ∈R ，其中0ω>，||ϕ<π．若5(28f π=，(08f 11π=，且()f x 的最小正周期大于2π，则A ．23ω=，12ϕπ=B ．23ω=，12ϕ11π=-C ．13ω=，24ϕ11π=-D ．13ω=，24ϕ7π=【答案】A【解析】由题意得125282118k k ωϕωϕππ⎧+=π+⎪⎪⎨π⎪+=π⎪⎩，其中12,k k ∈Z ，所以2142(2)33k k ω=--，又22T ωπ=>π，所以01ω<<，所以23ω=，11212k ϕ=π+π，由ϕ<π得12ϕπ=，故选A ．3．（2023·全国·高三专题练习）将函数sin 22y x x =的图象沿x 轴向右平移a 个单位（a ＞0）所得图象关于y 轴对称，则a 的最小值是（）A ．712πB ．4πC ．12πD ．6π4.【2018·江苏卷】已知函数()ππsin 2()22y x =+-<<ϕϕ的图象关于直线π3x =对称，则ϕ的值是________．【答案】π6-【解析】由题意可得2sin π13⎛⎫+=± ⎪⎝⎭ϕ，所以2πππππ()326k k k +=+=-+∈Z ，ϕϕ，因为ππ22-<<ϕ，所以π0,.6k ==-ϕ5．（2022·广西南宁·高二开学考试多选题）把函数()sin f x x =的图像向左平移π3个单位长度，再把横坐标变为原来的12倍（纵坐标不变）得到函数()g x 的图像，下列关于函数()g x 的说法正确的是（）A ．最小正周期为πB ．单调递增区间5πππ,π()1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z C ．图像的一个对移中心为π,03⎛⎫- ⎪⎝⎭D ．图像的一条对称轴为直线π12x =题型三：三角函数的奇偶性【例1】（2022·全国·清华附中朝阳学校模拟预测）已知函数()sin 2sin 23f x x x π⎛⎫=++ ⎪⎝⎭向左平移θ个单位后为偶函数，其中0,2π⎡⎤θ∈⎢⎥⎣⎦.则θ的值为（）A ．2πB ．3πC ．4πD ．6π【例2】（2022·广东·执信中学高一期中）对于四个函数sin y x =，cos y x =，sin y x =，tan y x =，下列说法错误的是（）A ．sin y x =不是奇函数，最小正周期是π，没有对称中心B ．cos y x =是偶函数，最小正周期是π，有无数多条对称轴C ．sin y x =不是奇函数，没有周期，只有一条对称轴D ．tan y x =是偶函数，最小正周期是π，没有对称中心由图可知，函数sin y x =不是奇函数，最小正周期是π，没有对称中心，A 对；对于B 选项，如下图所示：由图可知，cos y x =是偶函数，最小正周期是π，有无数多条对称轴，B 对；对于C 选项，如下图所示：由图可知，sin y x =不是奇函数，没有周期，只有一条对称轴，C 对；对于D 选项，如下图所示：由图可知，函数tan y x =是偶函数，不是周期函数，没有对称中心，D 错.故选：D.【例3】（2022·陕西师大附中高一期中）已知函数2π()sin ()24f x x =++，若(lg5)a f =，1(lg 5b f =，则（）A ．0a b +=B ．0a b -=C ．5a b +=D ．5a b -=【例4】（2022·江西省铜鼓中学高二开学考试）将函数()sin 22f x x x =+的图象向左平移()0ϕϕ>个单位长度得到一个偶函数，则ϕ的最小值为（）A ．12πB ．6πC ．3πD ．56π【例5】（2022·四川成都·模拟预测（理））函数2()ln(2)sin(1)211f x x x x x x -=+--+++在[0,2]上的最大值与最小值的和为（）A ．-2B ．2C ．4D ．6【例6】（2022·贵州贵阳·高三开学考试（理））已知函数()2cos(2)02f x x πϕϕ⎛⎫=+<< ⎪⎝⎭的图象向右平移3π个单位长度后，得到函数()g x 的图象，若()g x 的图象关于原点对称，则ϕ=（）A ．3πB ．4πC ．6πD ．12π【例7】（2022·陕西·定边县第四中学高三阶段练习（理））已知函数()sin cos f x a x b x =-在4x π=处取到最大值，则4f x π⎛⎫+ ⎪⎝⎭（）A ．奇函数B ．偶函数C ．关于点(),0π中心对称D ．关于2x π=轴对称【例8】（2023·全国·高三专题练习）写出一个最小正周期为3的偶函数()f x =___________.【题型专练】1．（2022·全国·高一课时练习）下列函数中，既为偶函数又在,02π⎛⎫- ⎪⎝⎭上单调递增的是（）A ．cos y x =B ．cos y x=C ．sin 2y x π⎛⎫=- ⎪D ．tan cos y x x=-2.（2022·陕西·武功县普集高级中学高三阶段练习（文））已知函数()e e sin x xf x x a -=-++，若()1ln 1,ln 3f m f m ⎛⎫== ⎪⎝⎭，则=a （）A ．1B ．2C ．1-D ．2-3.（2022·湖南·周南中学高二期末）函数为()sin 23f x x πϕ⎛⎫=++ ⎪⎝⎭偶函数的一个充分条件是（）A ．6π=ϕB ．3πϕ=C ．2ϕπ=D ．()3k k πϕπ=+∈Z故选：A4．（2022·贵州黔东南·高二期末（理））已知函数()πcos 2(0)3f x x ωω⎛⎫=-> ⎪⎝⎭的最小正周期为π，将其图象向右平移(0)ϕϕ>个单位长度，得到函数()g x 的图象，若函数()g x 为偶函数，则ϕ的最小值为（）A ．6πB ．π4C ．π3D ．π25.（2023·全国·高三专题练习）已知函数2()(2)sin(1)1f x x x x x =--+-在[1,1)-(1,3]⋃上的最大值为M ，最小值为N ，则M N +=（）A ．1B ．2C ．3D ．4可得()h t 的最大值与最小值之和为0，那么()g t 的最大值与最小值之和为2．故选：B ．6.（2022辽宁丹东·高一期末）写出一个最小正周期为1的偶函数()f x =______．【答案】cos2πx【解析】因为函数cos y x ω=的周期为2π||ω，所以函数cos 2πy x =的周期为1.故答案为：cos2πx .（答案不唯一）7.（2022·全国·高三专题练习）已知()2sin()cos f x x x α=++是奇函数，则sin α的值为______．8．（2022·河南·高二开学考试）将函数()()cos 06f x x πωω⎛⎫=+> ⎪⎝⎭的图像向左平移4π个单位长度后得到偶函数()g x 的图像，则ω的最小值是______．【答案】1039.（2022·全国·高一单元测试）写出一个同时具有性质①()02f =；②()()πf x f x +=的函数()f x =______（注：()f x 不是常数函数）．题型四：三角函数的单调性【例1】（湖南省永州市2023届高三上学期第一次高考适应性考试数学试题）将函数2()cos cos 1f x x x x =+-的图象向右平移6π个单位长度，然后将所得函数图象上所有点的横坐标变为原来的12（纵坐标不变），得到函数()y g x =的图象，则()g x 的单调递增区间是（）A ．ππππ,(Z)12262k k k ⎡⎤-++∈⎢⎥⎣⎦B ．ππ5ππ,(Z)242242k k k ⎡⎤-++∈⎢⎥⎣⎦C ．π2π2π,2π(Z)33k k k ⎡⎤-++∈⎢⎥D ．π5π2π,2π(Z)66k k k ⎡⎤-++∈⎢⎥故选：A【例2】（2022·陕西师大附中高一期中）sin1,sin 2,sin 3按从小到大排列的顺序为（）A ．sin3sin2sin1＜＜B ．sin3sin1sin2＜＜C ．sin1sin2sin3＜＜D ．sin2sin1sin3＜＜【例3】（2022·全国·高一单元测试）下列四个函数中，以π为周期且在π0,2⎛⎫ ⎪⎝⎭上单调递增的偶函数有（）A ．cos 2y x =B ．sin 2y x =C ．tan y x =D ．lg sin y x=【例4】（2023·全国·高三专题练习）已知函数()()cos 02f x x πωϕωϕ⎛⎫=+≤ ⎪⎝⎭＞，，4x π=-为f （x ）的零点，4x π=为y ＝f （x ）图象的对称轴，且f （x ）在186ππ⎛⎫⎪⎝⎭，上单调，则ω的最大值为（）A ．3B ．4C ．5D ．6当ππ,π2u k k ⎡⎤=+⎢⎥⎣⎦，k Z ∈时，函数sin y u =递增．即πππ,π42x k k ⎡⎤+∈+⎢⎥⎣⎦，解得：πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦，k Z ∈，所以函数sin()4πy x =+的单调递增区间是πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦，k Z ∈.故答案为：πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦，k Z ∈.【例6】（2023·全国·高三专题练习）函数πsin(2)3y x =-+的单调递减区间是（）A ．π5π[π,π],Z 1212k k k -+∈B ．π5π[2π,2π],Z 1212k k k -+∈C ．π5π[π,πZ66k k k -+∈D ．π5π[2π,2πZ66k k k -+∈【题型专练】1．（2022·辽宁·新民市第一高级中学高一阶段练习）已知函数2sin()y x ωθ=+为偶函数(0)θπ<<，其图像与直线2y =的两个交点的横坐标分别为12x x 、，若21||x x -的最小值为π，则该函数的一个单调递增区间为（）A ．ππ,24⎛⎫-- ⎪B ．ππ,44⎛⎫- ⎪C ．π0,2⎛⎫ ⎪⎝⎭D ．π3π,44⎛⎫⎪⎝⎭2.（2022·四川省成都市新都一中高二开学考试（理））已知函数()sin(),022f x x ππωϕϕω⎛⎫=+-<<> ⎪⎝⎭，若()00166f x f x ππ⎛⎫⎛⎫==≠ ⎪ ⎪⎝⎭⎝⎭，0min6x ππ-=，则函数()f x 的单调递减区间为（）A ．2,()63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z B ．22,2()63Z k k k ππππ⎛⎫++∈ ⎪⎝⎭C ．,()36Z k k k ππππ⎛⎫-++∈ ⎪D ．2,2()36Z k k k ππππ⎛⎫-++∈ ⎪3.（2022六盘山高级中学）函数tan 23y x π⎛⎫=- ⎪⎝⎭的单调增区间为（）A ．5,()212212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B ．5,()212212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭C ．5,()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦D ．5,()1212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭【答案】B【解析】因为函数tan y x =的单调递增区间为,()22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭，所以2()223,k k k x Z πππππ-<-<+∈，解得5,()212212k k x k Z ππππ-<<+∈，所以函数tan 23y x π⎛⎫=- ⎪⎝⎭的单调增区间为5,()212212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭.故选：B 4.（2023·全国·高三专题练习）已知函数()()sin 2f x x ϕ=+，其中()0,2πϕ∈，若()6f x f π⎛⎫≤ ⎪⎝⎭对于一切R x ∈恒成立，则()f x 的单调递增区间是（）A ．,2k k πππ⎡⎤+⎢⎥⎣⎦()k ∈Z B ．,36k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z C ．2,63k k ππππ⎡⎤++⎢⎥()k ∈Z D ．,2k k πππ⎡⎤-⎢⎥()k ∈Z 5.（2022·全国·高二单元测试）已知函数()cos f x x x =，()()g x f x '=，则（）．A ．()g x 的图像关于点π,06⎛⎫⎪⎝⎭对称B ．()g x 图像的一条对称轴是π6x =C ．()g x 在5π5π,66⎛⎫- ⎪上递减D ．()g x 在ππ,33⎛⎫- ⎪的值域为(0,1)6．(2022天津市静海区大邱庄中学高三月考)设函数()cos 26f x x π⎛⎫=- ⎪⎝⎭，给出下列结论：①()f x 的一个周期为π②()y f x =的图象关于直线12x π=对称③()y f x =的图象关于点,06π⎛⎫-⎪⎝⎭对称④()f x 在2,63ππ⎡⎤⎢⎥⎣⎦单调递减其中所有正确结论的编号是()A ．①④B ．②③C ．①②③D ．②③④【答案】C【解析】对于①，2T ππω==，故①正确；对于②，12x π=时，(112f π=，函数取得最大值，故②正确；对于③，6x π=-时，()06f π-=，故③正确；对于④，2,63x ππ⎡⎤∈⎢⎥⎣⎦ ，当712x π=时，7112f π⎛⎫=- ⎪⎝⎭，函数取得最小值，()f x ∴在2,63ππ⎡⎤⎢⎥⎣⎦有增有减，故④不正确.故选：C ．7．（2022·全国·高一课时练习）关于函数1()sin sin f x x x=+，下列说法正确的是（）A ．()f x 的一个周期是πB ．()f x 的最小值为2C ．()f x 在π(0,2上单调递增D ．()f x 的图象关于直线π2x =对称8．（2022·内蒙古包头·高三开学考试（文））若()sin cos f x x x =+在[]0,a 是增函数，则a 的最大值是（）A ．4πB ．2πC ．34πD ．π9．（2022·全国·高一专题练习）若函数()sin 23f x x ⎛⎫=- ⎪⎝⎭与()cos 4g x x ⎛⎫=+ ⎪⎝⎭都在区间()(),0πa b a b <<<上单调递减，则b a -的最大值为（）A ．π3B ．π2C ．6πD ．π10．（2022·全国·高三专题练习）将函数()2sin()(0)3f x x ωω=->的图象向左平移3ωπ个单位得到函数()y g x =的图象，若()y g x =在[,64ππ-上为增函数，则ω最大值为（）A ．32B ．2C ．3D ．11．（2022·全国·高一课时练习多选题）已知直线8x =是函数()sin(2)(0π)f x x ϕϕ=+<<图象的一条对称轴，则（）A ．π8f x ⎛⎫+ ⎪⎝⎭是偶函数B ．3π8x =是()f x 图象的一条对称轴C ．()f x 在ππ,82⎡⎤⎢⎥⎣⎦上单调递减D ．当π2x =时，函数()f x 取得最小值题型五：三角函数的值域【例1】（2022·陕西·安康市教学研究室高三阶段练习（文））下列函数中，最大值是1的函数是（）A ．|sin ||cos |=+y x xB ．2cos 4sin 4y x x =+-C ．cos tan y x x =⋅D ．y =【例2】（2022·全国·高三专题练习）函数1ππ()sin()cos()363f x x x =++-的最大值是（）A ．43B ．23C ．1D ．13【答案】8【解析】【分析】由题意可得()22sin sin 1f x x x =-++,令[]sin 0,1x t ∈＝,可得[]221,0,1y t t t =-++∈,利用二次函数的性质可求f (x )的最大值．【详解】解:()22cos 2sin 2sin sin 12sin sin 1f x x x x x x x =+=-++=-++,令[]sin 0,1x t ∈＝,可得[]2219212,0,148y t t t t ⎛⎫=-++=--+∈ ⎪⎝⎭,当14t =时,y 取得最大值为98,故答案为:98．【例4】（2022·江西·高三开学考试（文））已知函数()()2πsin sin 022f x x x x ωωωω⎛⎫+--> ⎪⎝⎭的最小正周期为π，则()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的值域为（）A ．11,22⎡⎤-⎢⎥⎣⎦B ．22⎡-⎢⎥⎣⎦C ．⎡⎤⎢⎥⎣⎦D ．⎡-⎢⎣⎦【例5】（2022·湖北·襄阳五中模拟预测）已知函数()sin()0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭在区间,33ππ⎛⎫⎪⎝⎭上单调，且对任意实数x 均有4()33f f x f ππ⎛⎫⎛⎫≤≤⎪ ⎪⎝⎭⎝⎭成立，则ϕ=（）A ．12πB ．6πC ．4πD ．3π【例6】（2023·全国·高三专题练习）已知函数()22sin s ()3in f x x x π+=+，则()f x 的最小值为（）A ．12B ．14C ．D ．2【例7】（2022·全国·高三专题练习）函数2()cos 2f x x x =+-0,2x π⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是__________．【答案】14-##-0.25【解析】【详解】22()1sin 2sin 1f x x x x x =--=--=21sin24x ⎛⎫-- ⎪ ⎪⎝⎭，所以当sin x =时，有最大值14-．故答案为14-.【例8】（2022·全国·高三专题练习）已知函数()sin cos 2sin cos 2f x x x x x =+++，则（）A ．()f x 的最大值为3，最小值为1B ．()f x 的最大值为3，最小值为-1C ．()f x的最大值为3，最小值为34D ．()f x的最大值为33【例9】（2022·全国·高一课时练习）已知关于x 的方程2cos sin 20x x a -+=在02π⎛⎤⎥⎝⎦，内有解，那么实数a 的取值范围（）A ．58a -≤B ．102a -≤≤C ．1122a -＜≤D ．12a -＜≤0【题型专练】1．（2022·江西九江·高一期末）函数()193sin cos 2R 24y x x x =+-∈的最小值是（）A ．14B ．12C ．234-D ．414-2．（2022·河南焦作·高一期末）函数2cos22cos y x x =+的最小值为（）A ．3-B ．2-C ．1-D ．0【答案】C【分析】利用二倍角的降幂公式化简函数解析式，利用余弦型函数的有界性可求得结果.【详解】2cos 22cos cos 2cos 212cos 21y x x x x x =+=++=+ ，min 211y ∴=-+=-.故选：C.3.【2018·北京卷】设函数f （x ）=πcos(0)6x ωω->，若π()()4f x f ≤对任意的实数x 都成立，则ω的最小值为__________．【答案】23【解析】因为()π4f x f ⎛⎫≤ ⎪⎝⎭对任意的实数x 都成立，所以π4f ⎛⎫⎪⎝⎭取最大值，所以()()ππ22π 8463k k k k -=∈∴=+∈Z Z ，ωω，因为0>ω，所以当0k =时，ω取最小值为23.4．（2022·广西南宁·高二开学考试）已知函数ππ()sin ,0,36f x x x ⎛⎫⎡⎤=+∈ ⎪⎢，则函数()f x 的最大值为__________．5．（2022·全国·高一课时练习）函数()1sin cos =++f x x x的值域为_____________．6．（2022·全国·高一专题练习）若奇函数()f x 在其定义域R 上是单调减函数，且对任意的R x ∈，不等式2(cos 3sin )(sin )0f x x f x a -+-≤恒成立，则a 取值范围是_________.【答案】(,2]-∞-【分析】根据给定条件，脱去法则“f ”，再利用含sin x 的二次函数求解作答.【详解】因奇函数()f x 在R 上单调递减，则R x ∀∈，2(cos 3sin )(sin )0f x x f x a -+-≤2(cos 3sin )(sin )f x x f a x ⇔-≤-22cos 3sin sin cos 2sin x x a x a x x ⇔-≥-⇔≤-，令222cos 2sin sin 2sin 1(sin 1)2y x x x x x =-=--+=-++，而1sin 1x -≤≤，因此当sin 1x =时，min 2y =-，即有2a ≤-，所以a 取值范围是(,2]-∞-.故答案为：(,2]-∞-【点睛】思路点睛：涉及求含正(余)的二次式的最值问题，可以换元或整体思想转化为二次函数在区间[-1,1]或其子区间上的最值求解.7.【2018·全国Ⅲ】函数()πcos 36f x x ⎛⎫=+ ⎪⎝⎭在[]0π，的零点个数为________．【答案】3【解析】0πx ≤≤ ，ππ19π3666x ∴≤+≤，由题可知πππ3π336262x x +=+=，或π5π362x +=，解得π4π,99x =，或7π9，故有3个零点.8.（2022·上海市第十中学高一期末）已知函数()2cos 2cos 1f x x x x =+-（R x ∈）.求函数()f x 的最小正周期及在区间0,2π⎡⎤⎢⎥上的最大值和最小值.9．（2022·湖南·雅礼中学高一期末）已知函数()2cos sin 4f x x a x a =-++-，[]0,x π∈．(1)求()f x 的最小值()g a ；(2)若()f x 在[]0,π上有零点，求a 的取值范围，并求所有零点之和．题型六：三角函数的图像【例1】（2022·陕西师大附中高三开学考试（理））函数()sin()(0,0,0)f x A x A ωϕωπϕ=+>>-<<的部分图象如图所示，为了得到()sin g x A x ω=的图象，只需将函数()y f x =的图象（）A ．向左平移6π个单位长度B ．向左平移12π个单位长度C ．向右平移6π个单位长度D ．向右平移12π个单位长度【答案】B【分析】根据函数图象得到()f x 、()g x 的解析式，然后利用图象平移的结论进行图象平移即可.【详解】根据图象可得2A =，周期T π=，因为2T πω=，所以2ω=，()()2sin 2f x x ϕ=+，将,23π⎛⎫ ⎪⎝⎭代入()f x 可得()2222sin 2332k k πππϕϕπ⎛⎫=+⇒+=+∈⎪⎝⎭Z ，解得()26k k πϕπ=-+∈Z ，因为0πϕ-<<，所以6πϕ=-，所以()2sin 26f x x π⎛⎫=- ⎪⎝⎭，()2sin 2g x x =，因为()2sin 212f x x π⎛⎫=- ⎪⎝⎭，所以()f x 向左平移12π个单位长度即可得到()g x 的图象.故选：B.【例2】（2022·陕西·延安市第一中学高一期中）函数()()sin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，则()2f π的值为（）A ．62B ．32C ．22D ．1-【答案】A【分析】由函数()f x 的部分图象以及五点法作图，求出()f x 的解析式，再计算2f π⎛⎫⎪⎝⎭的值．【例3】（2022·湖南·宁乡市教育研究中心模拟预测）如图表示电流强度I 与时间t 的关系()()()sin 0,0I A x A ωϕω=+>>在一个周期内的图像，则下列说法正确得是（）A ．50πω=B ．π6ϕ=C ．0=t 时，I =D ．1300100t I ==时，【例4】（2022·江苏·沭阳如东中学高三阶段练习多选题）已知函数()()sin f x A x ωϕ=+（其中0A >，0>ω，2πϕ<）的部分图象如图所示，则（）A ．2ω=B ．()f x 的图象关于直线23x π=对称C ．()2cos 26f x x π⎛⎫=- ⎪⎝⎭D ．()f x 在5[,63ππ--上的值域为[2,1]-【例5】（2022·河北·沧县风化店中学高二开学考试多选题）函数()()cos 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，且满足223f π⎛⎫=- ⎪⎝⎭，现将()f x 图象沿x 轴向左平移4π个单位，得到函数()y g x =的图象.下列说法正确的是（）A ．()g x 在,126ππ⎡⎤-⎢⎥⎣⎦上是增函数B ．()g x 的图象关于56x π=对称C ．()g x 是奇函数D ．()g x 的最小正周期为23π【例6】（2022·福建·高三阶段练习多选题）函数()sin()(0,0,02π)f x A x A ωϕωϕ=+>><<的部分图像如图所示，则（）A ．3π2ωϕ+=B ．(2)2f -=-C ．()f x 在区间()0,2022上存在506个零点D ．将()f x 的图像向右平移3个单位长度后，得到函数π()cos 4g x x ⎛⎫=- ⎪的图像【例7】（2022·江苏南通·高三开学考试多选题）已知函数()()sin 20,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图所示，则下列结论正确的是（）A ．()f x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称B ．()f x 的图象向右平移π12个单位后得到sin2y x =的图象C ．()f x 在区间π,2π⎡⎤--⎢⎥⎣⎦上单调递増D ．π6f x ⎛⎫+ ⎪为偶函数【例8】（2022·全国·高一单元测试多选题）已知函数()()sin f x A x =+ωϕ（0A >，0>ω，2πϕ<）的部分图象如图所示，下列说法错误的是（）A ．()f x 的图象关于直线23x π=-对称B ．()f x 的图象关于点5,012π⎛⎫-⎪⎝⎭对称C ．将函数2sin 26y x π⎛⎫=- ⎪⎝⎭的图象向左平移2π个单位长度得到函数()f x 的图象D ．若方程()f x m =在,02π⎡⎤-⎢⎥上有两个不相等的实数根，则m 的取值范围是(2,-【题型专练】1．（2022·广东·仲元中学高三阶段练习多选题）已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示.将函数()f x 的图象向右平移316π个单位长度，再将图象上所有点的横坐标变为原来的2倍（纵坐标不变），得到函数()y g x =的图象，则（）A ．()2sin 24x f x π⎛⎫=+ ⎪⎝⎭B ．()g x 的图象关于直线8x π=-对称C ．()g x 的图象关于点,08π⎛⎫⎪⎝⎭对称D ．函数()()f x g x +的最小值为4-2．（2022·湖北·襄阳市襄州区第一高级中学高二阶段练习多选题）函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图像如图所示，则下列结论正确的是（）A ．()12sin 33f x x π⎛⎫=- ⎪⎝⎭B ．若把()f x 图像上的所有点的横坐标变为原来的23倍，纵坐标不变，得到函数()g x 的图像，则函数()g x 在[],ππ-上是增函数C ．若把函数()f x 的图像向左平移2π个单位长度，得到函数()h x 的图像，则函数()h x 是奇函数D ．,33x ππ⎡⎤∀∈-⎢⎥，若()332f x a f π⎛⎫+≥ ⎪恒成立，则a 的取值范围为)2,+∞3．（2022·安徽·高三开学考试）已知函数π()2sin()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示，其中ππ,2,,0123A B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭，则下列说法错误的是（）A ．()f x 的最小正周期为πB ．将()f x 的图象向右平移6π个单位长度后关于原点对称C ．()f x 在2ππ,3⎡⎤--⎢⎣⎦上单调递减D ．直线7π12x =为()f x 图象的一条对称轴【答案】C【分析】根据已知图象可确定相关参数，求得函数解析式，判断A;根据正弦函数的图象的平移变换规律可得平移后的解析式，判断B;利用正弦函数的单调性可判断C ；将7π12x =代入函数中解析式求得其值，可判断D.【详解】由题意得，πππ43124T =-=，则2ππ,2T T ω===，而π212f ⎛⎫= ⎪⎝⎭，即ππ2π(Z)62k k ϕ+=+∈，解得π2π(Z)3k k ϕ=+∈，∵||2ϕπ<，∴π3ϕ=，∴π()2sin 23f x x ⎛⎫=+ ⎪⎝⎭，故A 正确；函数()f x 的图象向右平移6π个单位长度后，得到π2sin 26f x x ⎛⎫-= ⎪⎝⎭,该函数图象关于原点对称，放B 正确；∵2ππ,3x ⎡⎤∈--⎢⎥⎣⎦，∴π5π2,π33x ⎡⎤+∈--⎢⎥⎣⎦，则()f x 在2ππ,3⎡⎤--⎢⎥⎣⎦上先增后减，故C 错误；∵7π3π2sin 2122f ⎛⎫==- ⎪⎝⎭，∴直线712x π=为()f x 图象的一条对称轴，故D 正确．故选：C ．4．（2022·天津·南开中学高三阶段练习）已知函数π()sin()(R,0,0,)2f x A x x A ωϕωϕ=+∈>><的部分图象如图所示，则下列说法正确的是（）A ．直线πx =是()f x 图象的一条对称轴B ．()f x 图象的对称中心为π(π,0)12k -+，Z k ∈C ．()f x 在区间ππ,36⎡⎤-⎢⎥⎣⎦上单调递增D ．将()f x 的图象向左平移π12个单位长度后，可得到一个奇函数的图象【答案】C【分析】由已知图象求得函数解析式，将πx =代入解析式，由其结果判断A;求出函数的对称中心可判断B;当ππ,36x ⎡⎤∈-⎢⎥⎣⎦时，πππ2[,]622x +∈-，结合正弦函数的单调性判断C;根据三角函数图象的平移变换可得平移后函数解析式，判断D.【详解】由函数图象可知，2A =,最小正周期为5ππ4()π126T =-=，所以2π2πω==，将点π(,2)6代入函数解析式中，得：π22sin()3ϕ=+，结合π2ϕ<，所以π6ϕ=，故π()2sin(2)6f x x =+，对于A ，当πx =时，π(π)2sin(2π)16f =+=，故直线πx =不是()f x 图象的一条对称轴，A 错误;对于B ，令π()2sin(2)06f x x =+=，则πππ2π,Z,,Z 6122k x k k x k +=∈∴=-+∈，即()f x 图象的对称中心为ππ(,0)122k -+，Z k ∈，故B 错误；对于C ，当ππ,36x ⎡⎤∈-⎢⎥⎣⎦时，πππ2[,]622x +∈-，由于正弦函数sin y x =在ππ[,]22-上递增，故()f x 在区间ππ,36⎡⎤-⎢⎥⎣⎦上单调递增，故C 正确；对于D ，将()f x 的图象向左平移π12个单位长度后，得到πππ()2sin[2()]2sin(2)1263g x x x =++=+的图象，该函数不是奇函数，故D 错误；故选：C5．（2022·江苏省如皋中学高三开学考试多选题）函数()()sin 0,0,0πy A x A ωϕωϕ=+>><<在一个周期内的图象如图所示，则（）．A ．该函数的解析式为2π2sin 33y x ⎛⎫=+ ⎪⎝⎭B ．该函数图象的对称中心为ππ,03k ⎛⎫- ⎪⎝⎭，Zk ∈C ．该函数的单调递增区间是5ππ3π,3π44k k ⎛⎫-+ ⎪⎝⎭，Zk ∈D ．把函数π2sin 3y x ⎛⎫=+ ⎪的图象上所有点的横坐标伸长为原来的32倍，纵坐标不变，可得到该函数图象6．（2021·福建·福州十八中高三开学考试多选题）已知函数()sin()(010f x x ωϕω=+<<，0π)ϕ<<的部分图象。
专题46 三角函数的图象与性质(多选题)(解析版)
专题46 三角函数的图象与性质（多选题）一、题型选讲题型一 、三角函数的基本概念例1、（2020届山东师范大学附中高三月考）在平面直角坐标系xOy 中，角α顶点在原点O ，以x 正半轴为始边，终边经过点()()1,0P m m <，则下列各式的值恒大于0的是（ ） A ．sin tan ααB ．cos sin αα-C ．sin cos ααD ．sin cos αα+【答案】AB【解析】由题意知sin 0α<，cos 0α>，tan 0α<. 选项Asin 0tan αα>； 选项B ，cos sin 0αα->； 选项C ，sin cos 0αα<； 选项D ，sin cos αα+符号不确定. 故选：AB.变式1、（2020·枣庄市第三中学高三月考）下列函数，最小正周期为的偶函数有（ ） A ． B ．C ．D ．【答案】BD【解析】对于A 选项，函数为奇函数，不符合题意. 对于B 选项，函数是最小正周期为的偶函数，符合题意. 对于C 选项，函数的最小正周期为，不符合题意. 对于D 选项，函数，是最小正周期为的偶函数，符合题意. 故选：BD变式2、定义：角θ与ϕ都是任意角，若满足+=2πθϕ，则称θ与ϕ“广义互余”.已知1sin(+)=-4πα，下列角β中，可能与角α“广义互余”的是()A. sin βB. 1cos(+)=4πβC. tan βD. tan β 【答案】ACπtan y x =|sin |y x =2cos y x =sin 22y x π⎛⎫=- ⎪⎝⎭tan y x =sin y x =π2cos y x =2ππsin 2cos 22y x x ⎛⎫=-= ⎪⎝⎭π【解析】：11sin()sin sin 44πααα+=-=-∴=，cos α=，对于A ，sin sin()cos 2πβαα=-=可能成立，角β可能与角α“广义互余”，故A 符合条件;对于B ，假设角β与角α“广义互余”，11cos()cos()sin 244ππβαα+=--=-=-≠，故B 不符合条件;对于C ，tan β=，即sin ββ=，又22sin cos 1ββ+=，故sin β=若广义互余即cos α=，即C 符合条件;对于D ，tan β=即sin ββ=，又22sin cos 1ββ+=，故sin β=，若广义互余即cos α=，故D 不符合条件 故选：.AC题型二、三角函数的性质的简单运用例2、（2020届山东省济宁市高三上期末）将函数()sin 2f x x =的图象向右平移4π个单位后得到函数()g x 的图象,则函数()g x 具有性质( ) A ．在0,4π⎛⎫⎪⎝⎭上单调递增,为偶函数 B ．最大值为1,图象关于直线32x π=-对称 C ．在3,88ππ⎛⎫-⎪⎝⎭上单调递增,为奇函数 D ．周期为π,图象关于点3,04π⎛⎫⎪⎝⎭对称 【答案】ABD【解析】()sin 2sin 2cos 242x x x g x ππ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭0,4x π⎛⎫∈ ⎪⎝⎭则20,2x π⎛⎫∈ ⎪⎝⎭，()cos2g x x =-单调递增，为偶函数，A 正确C 错误；最大值为1，当32x π=-时23x π=-，为对称轴，B 正确； 22T ππ==，取2,,242k x k x k Z ππππ=+∴=+∈，当1k =时满足，图像关于点3,04π⎛⎫ ⎪⎝⎭对称，D 正确； 故选：ABD变式1、（2020届山东省烟台市高三上期末）已知函数()()sin 322f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图象关于直线4x π=对称，则（ ）A ．函数12f x π⎛⎫+⎪⎝⎭为奇函数 B ．函数()f x 在,123ππ⎡⎤⎢⎥⎣⎦上单调递增 C ．若()()122f x f x -=，则12x x -的最小值为3πD ．函数()f x 的图象向右平移4π个单位长度得到函数cos3y x =-的图象 【答案】AC【解析】因为直线4x π=是()()sin 322f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的对称轴,所以()342k k Z ππϕπ⨯+=+∈,则()4k k Z πϕπ=-+∈,当0k =时,4πϕ=-,则()sin 34f x x π⎛⎫=- ⎪⎝⎭,对于选项A,sin 3sin 312124f x x x πππ⎡⎤⎛⎫⎛⎫+=+-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,因为()sin 3sin3x x -=-,所以12f x π⎛⎫+ ⎪⎝⎭为奇函数,故A 正确； 对于选项B,()232242k x k k Z πππππ-+<-<+∈,即()21212343k kx k Z ππππ-+<<+∈,当0k =时,()f x 在,124ππ⎡⎤-⎢⎥⎣⎦当单调递增,故B 错误；对于选项C,若()()122f x f x -=,则12x x -最小为半个周期,即21323ππ⨯=,故C 正确； 对于选项D,函数()f x 的图象向右平移4π个单位长度,即()sin 3sin 3sin 344x x x πππ⎡⎤⎛⎫--=-=- ⎪⎢⎥⎝⎭⎣⎦,故D错误 故选：AC变式2、（2020·山东日照·高三月考）将函数的图像向左平移个单位，得到函数的图像，sin y x =2π()y f x =则（ ）A ．是偶函数B ．的最小正周期为C ．的图像关于直线对称D ．的图像关于点对称【答案】AD【解析】函数的图象向左平移个单位后， 得到函数的图象， 为偶函数，故A 正确； 的周期为，排除B ；因为，所以的图象不关于直线对称，排除C ；，故D 正确 故选：AD.变式3、（2020届山东省枣庄市高三上学期统考）将函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移2π个单位长度得到()g x 图象，则下列判断正确的是（ ） A ．函数()g x 在区间,122ππ⎡⎤⎢⎥⎣⎦上单调递增 B ．函数()g x 图象关于直线712x π=对称 C ．函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减 D ．函数()g x 图象关于点,03π⎛⎫⎪⎝⎭对称 【答案】ABD()y f x =()y f x =π()y f x =2x π=()y f x =,02π⎛⎫- ⎪⎝⎭sin y x =2π()sin cos 2f x x x π⎛⎫=+= ⎪⎝⎭()cos f x x =()cos f x x =2πcos 022f ππ⎛⎫== ⎪⎝⎭()f x 2x π=cos 022f ππ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭【解析】函数()sin 23f x x π⎛⎫=+⎪⎝⎭的图像向右平移2π个单位长度得到()ππsin 223g x x ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦2πsin 23x ⎛⎫=- ⎪⎝⎭.由于7π7π2ππsin sin 112632g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭，故7π12x =是()g x 的对称轴，B 选项正确. 由于π2π2πsin sin 00333g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭，故,03π⎛⎫ ⎪⎝⎭是()g x 的对称中心，D 选项正确. 由π2ππ2232x -≤-≤，解得π7π1212x ≤≤，即()g x 在区间π7π,1212⎡⎤⎢⎥⎣⎦上递增，故A 选项正确、C 选项错误. 故选：ABD.变式4、（2020届山东省潍坊市高三上期末）已知()()22210f x cosx x ωωω=->的最小正周期为π，则下列说法正确的有（ ）A ．2ω=B ．函数()f x 在[0,]6π上为增函数C ．直线3x π=是函数()y f x =图象的一条对称轴D ．5,012π⎛⎫⎪⎝⎭是函数()y f x =图象的一个对称中心 【答案】BD【解析】()cos 222sin 26f x x x x πωωω⎛⎫=+=+⎪⎝⎭， 22ππω=，1ω∴= ()2sin 26f x x π⎛⎫∴=+ ⎪⎝⎭ ，故A 不正确；当0,6x π⎡⎤∈⎢⎥⎣⎦时，2,662x πππ⎡⎤+∈⎢⎥⎣⎦是函数sin y x =的单调递增区间，故B 正确； 当3x π=时，52366πππ⨯+=，51sin 162π=≠±，所以不是函数的对称轴，故C 不正确；、当512x π=时，52126πππ⨯+=，sin 0π=，所以5,012π⎛⎫⎪⎝⎭是函数()y f x =的一个对称中心，故D 正确. 故选：BD题型三、三角函数图像与性质的综合运用例3、（2020·蒙阴县实验中学高三期末）关于函数()22cos cos(2)12f x x x π=-+-的描述正确的是（ ）A ．其图象可由2y x =的图象向左平移8π个单位得到 B ．()f x 在(0,)2π单调递增C ．()f x 在[]0,π有2个零点D ．()f x 在[,0]2π-的最小值为【答案】ACD【解析】由题：()22cos cos(2)1cos 2sin 2)24f x x x x x x ππ=-+-=+=+，由2y x =的图象向左平移8π个单位，得到)))84y x x ππ=+=+，所以选项A 正确；令222,242k x k k Z πππππ-≤+≤+∈，得其增区间为3[,],88k k k Z ππππ-+∈ ()f x 在(0,)8π单调递增，在(,)82ππ单调递减，所以选项B 不正确；解()0,2,4f x x k k Z ππ=+=∈，得：,28k x k Z ππ=-∈，[0,]x π∈， 所以x 取37,88ππ，所以选项C 正确；3[,0],2[,],sin(2)[24444x x x πππππ∈-+∈-+∈-，()[f x ∈， 所以选项D 正确. 故选：ACD变式1、已知函数())3f x x π=+，则下列结论正确的是（ ）A ．函数()f x 的最小正周期为πB ．函数()f x 在[0,π]上有2个零点C ．当x =56π时，函数()f x 取得最大值 D ．为了得到函数()f x的图象，只要把函数())3g x x π=+图象上所有点的横坐标变为原来的12倍(纵坐标不变) 【答案】ABCD 【详解】22T ππ==，则A 正确； 当x ∈[0，π]时，23x π+∈3,37ππ⎡⎤⎢⎥⎣⎦，此时余弦函数cos y x =只有两个零点，则可知B 正确； 因为23x π+∈3,37ππ⎡⎤⎢⎥⎣⎦，所以当223x ππ+=时，即x =56π时，函数()f x 取得最大值，则可知C 正确；函数())3g x x π=+图象上所有点的横坐标变为原来的12倍(纵坐标不变)得出23y x π⎛⎫=+ ⎪⎝⎭的图象，则D 正确；.变式2、已知函数()sin()(0)f x x ωϕω=+>满足()()001f x f x =+=且()f x 在()00,1x x +上有最大值，无最小值，则下列结论正确的是（ ） A ．0112f x ⎛⎫+= ⎪⎝⎭B ．若00x =，则()sin 4f x x ππ⎛⎫=+⎪⎝⎭C ．()f x 的最小正周期为4D ．()f x 在(0,2020)上的零点个数最少为1010个【答案】AC 【详解】对A ，()00,1x x +的区间中点为012x +， 根据正弦曲线的对称性知0112f x ⎛⎫+= ⎪⎝⎭，故A 正确； 对B ，若00x =，则()0sin 211sin 122f f ϕωϕ⎧==⎪⎪⎨⎛⎫⎛⎫⎪=+= ⎪ ⎪⎪⎝⎭⎝⎭⎩，()f x 在()00,1x x +上有最大值，无最小值， ∴24k ϕπ=+π，则()42k k z πωπ=+∈， ωπ∴≠，故B 错误；对C ，()()0000211sin 122sin 2x f x f x x ωϕωϕ⎧+⎛⎫⎛⎫+=+= ⎪ ⎪⎪⎪⎝⎭⎝⎭⎨⎪=+=⎪⎩，又()f x 在()00,1x x +上有最大值，无最小值，002122224x k x k πωϕππωϕπ+⎧+=+⎪⎪∴⎨⎪+=+⎪⎩，(其中k z ∈)，解得：2πω=，2242T πππω∴===，故C 正确；对D ，当4T =时，区间(0,2020)的长度恰好为505个周期， 当()00f =时，即k ϕπ=时，()f x 在开区间(0,2020)上零点个数至多为50521010⨯=个零点，故D 错误.变式3、（2020·山东高三开学考试）将函数的图象向右平移个单位长度后得到函数的图象，且，则下列说法正确的是（ ） A ．为奇函数 B ． C ．当时，在上有4个极值点()()πcos 02f x x ωω⎛⎫=-> ⎪⎝⎭π2()g x ()01g =-()g x π02g ⎛⎫-= ⎪⎝⎭5ω=()g x ()0,πD ．若在上单调递增，则的最大值为5【答案】BCD 【解析】∵ ∴，且， ∴，即为奇数，∴为偶函数，故A 错. 由上得：为奇数，∴，故B 对. 由上得，当时，，,由图像可知在上有4个极值点,故C 对，∵在上单调，所以,解得：，又∵， ∴的最大值为5，故D 对 故选：BCD.二、达标训练()g x π0,5⎡⎤⎢⎥⎣⎦ω()()πcos sin 02f x x x ωωω⎛⎫=-=> ⎪⎝⎭()sin ()2g x x πω⎡⎤=-⎢⎥⎣⎦(0)1g =-()1222k k Z πωπ⎛⎫-=-∈ ⎪⎝⎭14k ω=-()sin ()cos 2g x x x πωω⎡⎤=-=±⎢⎥⎣⎦ω()cos 022g ππω⎛⎫-=±-= ⎪⎝⎭5ω=5()sin(5)cos52g x x x π=-=-25T π=()g x ()0,π()g x π0,5⎡⎤⎢⎥⎣⎦π052T πω-≤=05ω<≤14k ω=-ω1、已知函数()cos 6f x x π⎛⎫=+ ⎪⎝⎭，则（ ） A ．2π为()f x 的一个周期 B ．()y f x =的图象关于直线43x π=对称 C ．()f x 在,2ππ⎛⎫⎪⎝⎭上单调递减 D ．()f x π+的一个零点为3π【答案】AD【详解】根据函数()cos 6f x x π⎛⎫=+⎪⎝⎭知最小正周期为2π，A 正确. 当43x π=时，443cos cos 03362f ππππ⎛⎫⎛⎫=+== ⎪ ⎪⎝⎭⎝⎭，由余弦函数的对称性知，B 错误； 函数()cos 6f x x π⎛⎫=+⎪⎝⎭在5,26ππ⎛⎫⎪⎝⎭上单调递减，在5,6ππ⎛⎫ ⎪⎝⎭上单调递增，故C 错误；7()cos 6f x x ππ⎛⎫+=+⎪⎝⎭， 73cos cos 03632f πππππ⎛⎫⎛⎫∴+=+== ⎪ ⎪⎝⎭⎝⎭，故D 正确.2、已知函数()()πcos 0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的最小正周期为π，其图象的一条对称轴为5π12x =，则（ ） A ．π3ϕ=B ．函数()f x 的图象可由sin 2y x =的图象向左平移π3个单位长度得到C ．函数()f x 在π0,2⎡⎤⎢⎥⎣⎦上的值域为1,2⎡-⎢⎣⎦D ．函数()f x 在区间ππ,2⎡⎤--⎢⎥⎣⎦上单调递减【答案】BC【详解】()()πcos 0,02f x x ωϕωϕ⎛⎫=+><<⎪⎝⎭的最小正周期为π，22Tπω∴==，又2x π=为()f x 的对称轴，52,0122k ππϕπϕ∴⨯+=<<，=6πϕ∴， ()cos(2)6f x x π∴=+；对于A ，=6πϕ，A 错；对于B ，sin 2y x =的图象向左平移π3个承位长度得到2sin(2)3y x π=+，而2sin(2)sin(2)cos(2)()3266y x x x f x ππππ=+=++=+=，所以，B 对；对于C ，7cos 22666x x ππππ≤⇒≤+≤，1cos(2)62x π∴-≤+≤，则函数()f x 在π0,2⎡⎤⎢⎥⎣⎦上的值域为1,2⎡-⎢⎣⎦，C 对；对于D ，11522666x x πππππ-≤≤-⇒-≤+≤-，cos x 在11,6ππ⎡⎤--⎢⎥⎣⎦单调递减，在5,6ππ⎡⎤--⎢⎥⎣⎦单调递增，()f x ∴在ππ,2⎡⎤--⎢⎥⎣⎦上不是单调的，D 错；3、已知函数()()sin (0,0,0)f x A x A ωϕωϕπ=+>><<的最小正周期为4，其图象的一个最高点为1,23A ⎛⎫ ⎪⎝⎭，下列结论正确的是（ ） A ．ωπ= B ．3πϕ=C ．将()f x 图象上各点的横坐标变为原来的12，纵坐标不变，得到()h x 图象；再将()h x 图象向右平移16个单位长度，得到函数2sin 6y x ππ⎛⎫=+ ⎪⎝⎭的图象 D ．() y f x =的图象关于1x =对称 【答案】BC 【详解】由已知24πω=，2πω=，A 错；2A =，2sin()223πϕ1⨯+=，23k πϕπ=+，k Z ∈，又0ϕπ<<，∴3πϕ=．B 正确；∴()2sin 23f x x ππ⎛⎫=+⎪⎝⎭，将()f x 图象上各点的横坐标变为原来的12，纵坐标不变，得()2sin()3h x x ππ=+，再将()h x 图象向右平移16个单位长度，得图象的解析式为2sin ()2sin()636y x x πππππ⎡⎤=-+=+⎢⎥⎣⎦，C 正确；大()f x 中，令1x =，5,2362x k k Z πππππ+=≠+∈，D 错．4、已知函数()3sin sin3f x x x =+，则（ ） A ．()f x 是奇函数 B ．()f x 是周期函数且最小正周期为2π C ．()f x 的值域是[4,4]- D ．当(0,)x π∈时()0f x >【答案】ABD【详解】A.()3sin()sin(3)3sin sin3()f x x x x x f x -=-+-=--=-，故()f x 是奇函数，故A 正确；B.因为sin y x =的最小正周期是2π，sin3y x =的最小正周期为23π，二者的“最小公倍数”是2π，故2π是()f x 的最小正周期，故B 正确；C.分析()f x 的最大值，因为3sin 3x ≤，sin31x ≤，所以()4f x ≤，等号成立的条件是sin 1x =和sin31x =同时成立，而当sin 1x =即2()2x k k ππ=+∈Z 时，336()2x k k ππ=+∈Z ，sin31x =-故C 错误； D.展开整理可得()2()3sin sin cos2cos sin 2sin 4cos 2f x x x x x x x x =++=+，易知当(0,)x π∈时，()0f x >，故D 正确.5、已知函数()sin() f x x ωϕ=+（其中0,0 ωϕπ><<）图象的两条相邻的对称轴之间的距离为2π，16f π⎛⎫= ⎪⎝⎭，下列结论正确的是（ ） A ．()sin 26f x x π⎛⎫=+⎪⎝⎭B ．将函数()y f x =的图象向右平移6π个单位后得到函数sin2y x =的图象 C ．当0,2x π⎛⎫∈ ⎪⎝⎭时，()f x 有且只有一个零点D ．()f x 在06π⎡⎤⎢⎥⎣⎦，上单调递增 【答案】ACD【详解】由题意，函数图象的两条相邻的对称轴之间的距离为2π，16f π⎛⎫= ⎪⎝⎭，可得T π=， 因为0 ω>，则2T w ππ==，解得2w =，即sin(2)16πϕ⨯+=， 解得2,32k k Z ππϕπ+=+∈，因为0ϕπ<<，所以6π=ϕ，即函数()f x 的解析式()sin 26f x x π⎛⎫=+ ⎪⎝⎭，所以A 正确； 对于B 中，函数()f x 的图象向右平移6π个单位，得到()sin[2()]66g x x ππ=-+ πsin(2)6x =-的图象，所以B 不正确；对于C 中，由0,2x π⎛⎫∈ ⎪⎝⎭，所以72(,)666x πππ+∈，当512x π=时，函数5()012f π=， 所以C 正确；对于D 中，当06x π⎡⎤∈⎢⎥⎣⎦，时，2[,]662x πππ+∈，根据正弦函数的性质，可得函数()f x 在该区间上单调递增，所以D 正确.6、函数()()sin f x A x =+ωϕ0,0,2A πωϕ⎛⎫>><⎪⎝⎭的部分图像如图所示，下列结论中正确的是（ ）A ．直线23x π=-是函数()f x 图像的一条对称轴B ．函数()f x 的图像关于点,062k ππ⎛⎫-+ ⎪⎝⎭k Z ∈对称 C ．函数()f x 的单调递增区间为5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦k Z ∈D ．将函数()f x 的图像向右平移12π个单位得到函数()sin(2)4g x x π=+的图像【答案】BC【详解】由图知：()min 1f x =-，所以1A =， 因为741234T πππ=-=，T π=，即2ππω=，2ω=。
三角函数的图像与性质练习题
三角函数的图像与性质练习题一、选择题1. 在三角函数sin(x)的定义域内，函数值的范围是：A. (-∞, ∞)B. [-1, 1]C. [0, 1]D. [0, 2π]2. 函数y = cos(x)的一个周期是：A. πB. 2πC. π/2D. 4π3. 函数y = tan(x)的导数是：A. sec^2(x)B. cos^2(x)C. sin^2(x)D. csc^2(x)4. 在函数y = sin(x)的图像中，当x = π/2时，函数值等于：B. 1C. -1D. 不存在5. 函数y = cos(x)的对称轴是：A. y轴B. x轴C. 原点D. 平行于x轴且距离x轴1个单位的直线6. 函数y = tan(x)在定义域内的奇点是：A. x = 0B. x = π/2C. x = πD. x = 2π7. 函数y = sin^2(x) + cos^2(x)等于：A. 1B. 0C. 28. 函数y = sin(x) + cos(x)的一个周期是：A. 2πB. 4πC. π/2D. π/4二、填空题1. 函数y = sin(x)在区间[0, π]内的最小值是____，最大值是____。
2. 函数y = cos(2x)的周期是____。
3. 函数y = cos(x)在区间[-π/2, π/2]内的最小值是____，最大值是____。
4. 函数y = tan(x)的定义域是____。
5. 函数y = sin(2x)的一个周期是____。
6. 函数y = cos(x)的对称中心是____。
7. 函数y = tan(x)在区间[0, π]内的最小值是____，最大值是____。
8. 函数y = sin^2(x)的对称轴是____。
三、解答题1. 画出函数y = sin(x)在区间[0, 2π]上的图像。
2. 画出函数y = cos(2x)的图像，并求出它在区间[0, 2π]上的最小值和最大值。
3. 画出函数y = tan(x)在区间[-π/2, π/2]上的图像，并指出它的所有零点。
专题5.4 三角函数图像与性质(原卷版)
专题5.4三角函数图像与性质1.正弦函数R x x y ∈=,sin 的性质.(1).定义域:R .(2).值域:sin [1,1]x ∈-.(3).周期性:周期函数，周期是)0(,2≠∈k Z k k 且π,最小正周期为π2.(4).奇偶性:奇函数，其图象关于原点对称.(5).单调性:增区间：2,2()22k k k Z ππππ-++∈（）减区间：32,2()22k k k Z ππππ++∈（）(6).对称性:对称轴：)(,2Z k k x ∈+=ππ，对称中心：)(),0,(Z k k ∈π2.余弦函数R x x y ∈=,cos 的性质.(1).定义域:R .(2).值域:]1,1[cos -∈x (3).周期性:周期函数，周期是)0(,2≠∈k Z k k 且π，最小正周期为π2.(4).奇偶性:偶函数，其图象关于y 轴对称.(5).单调性:减区间：)(),2,2(Z k k k ∈+πππ增区间：)(),22,2(Z k k k ∈++ππππ(6).对称性:对称轴：)(,Z k k x ∈=π，对称中心：)(),0,2(Z k k ∈+ππ3.正切函数x y tan =的图象与性质.(1).定义域:},2|{Z k k x R x x ∈+≠∈ππ且.(2).值域:R(3).周期性:周期函数，周期是)0(,≠∈k Z k k 且π，最小正周期为π.(4).奇偶性:奇函数，其图象关于原点对称.(5).单调性:增函数，)2,2(ππππ+-k k 为增区间.(6).对称性:对称中心：)(),0,2(Z k k ∈π4.正弦型函数R x A x A y ∈>+=,0),sin(ϕω的性质.(1).定义域:R .(2).值域:],[A A -(3).周期性:周期函数，周期是||2ωπ=T .(4).奇偶性:当Z k k ∈=,πϕ时为奇函数；当Z k k ∈±=,2ππϕ时为偶函数.(5).单调性:当0>ω时：令Z k k x k ∈+≤+≤+-,2222ππϕωππ，求解增区间.令Z k k x k ∈+≤+≤+,22322ππϕωππ，求解减区间.当0<ω时：注意单调区间的转化.(6).对称性:对称轴：令)(,2Z k k x ∈+=+ππϕω，求解对称轴方程，对称轴处取最值.对称中心：令)(,Z k k x ∈=+πϕω，求解对称中心坐标.5.余弦型函数R x A x A y ∈>+=,0),cos(ϕω的性质.(1).定义域:R .(2).值域:],[A A -(3).周期性:周期函数，周期是||2ωπ=T .(4).奇偶性:当Z k k ∈=,πϕ时为偶函数；当Z k k ∈±=,2ππϕ时为奇函数.(5).单调性:当0>ω时：令Z k k x k ∈+≤+≤,22ππϕωπ，求解减区间.令Z k k x k ∈+≤+≤+,222ππϕωππ，求解增区间.当0<ω时：注意单调区间的转化.(6).对称性:对称轴：令)(,Z k k x ∈=+πϕω，求解对称轴方程，对称轴处取最值.对称中心：令)(,2Z k k x ∈+=+ππϕω，求解对称中心坐标.一、单选题1．已知函数()tan 2f x x =，则（）A ．()f x 的最小正周期为π，对称中心为1,0,2k k Zπ⎛⎫∈ ⎪⎝⎭B ．()f x 的最小正周期为π，对称中心为1,0,4k k Zπ⎛⎫∈ ⎪⎝⎭C ．()f x 的最小正周期为2π，对称中心为1,0,2k k Z π⎛⎫∈ ⎪⎝⎭D ．()f x 的最小正周期为2π，对称中心为1,0,4k k Z π⎛⎫∈ ⎪⎝⎭2．用“五点法”作函数cos 46y x π⎛⎫=- ⎪⎝⎭在一个周期内的图像时，第四个关键点的坐标是A ．5,012π⎛⎫⎪⎝⎭B ．5,112π⎛⎫- ⎪⎝⎭C ．5,112π⎛⎫ ⎪⎝⎭D ．5,012π⎛⎫-⎪⎝⎭3．若函数()sin 3f x x πω⎛⎫=+ ⎪⎝⎭(0)>ω在区间()2ππ，内没有最值，则ω的取值范围是（）A ．][117012612⎛⎤⋃ ⎥⎝⎦，，B ．][1120633⎛⎤⋃ ⎥⎝⎦，，C ．7012⎛⎤⎥⎝⎦，D ．1233⎡⎤⎢⎥⎣⎦，4．已知函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭在区间,2ππ⎡⎤⎢⎥⎣⎦内单调递减，则实数ω的取值范围是（）A ．2,13⎡⎤⎢⎥⎣⎦B ．24,33⎡⎤⎢⎥⎣⎦C ．[)1,2D ．3,22⎡⎫⎪⎢⎣⎭5．已知()()()sin 0,0f x x ωϕωϕπ=+><≤是R 上的奇函数，若()f x 的图象关于直线4x π=对称，且()f x 在区间,2211ππ⎡⎤-⎢⎥⎣⎦内是单调函数，则6f π⎛⎫= ⎪⎝⎭（）A ．B ．12-C ．12D ．26．函数ππ5πtan ,,6612y x x ⎛⎫⎛⎫=-∈- ⎪ ⎪⎝⎭⎝⎭的值域为（）A ．()B ．3⎛⎫- ⎪ ⎪⎝⎭C ．(,(1,)-∞+∞D ．3⎛⎫ ⎪ ⎪⎝⎭7．已知1tan tan αα≥且22,ππα⎛∈-⎫⎪⎝⎭，则α的取值范围为（）A ．,04π⎡⎫-⎪⎢⎣⎭B ．,0,442πππ⎡⎫⎡⎫-⎪⎪⎢⎢⎣⎭⎣⎭C ．0,4π⎛⎤ ⎥⎝⎦D ．,0,244πππ⎛⎤⎛⎤--⋃ ⎥⎥⎝⎦⎝⎦8．已知函数()()sin f x x α=+在,43x ππ⎛⎫∈- ⎪⎝⎭上单调递增，则α的值可以是（）A ．3π-B ．4π-C ．4πD ．3π9．函数()23sin 23f x x π⎛⎫=- ⎪⎝⎭的一个单调递减区间是（）A ．7131212ππ⎡⎤⎢⎥⎣⎦，B ．71212ππ⎡⎤⎢⎥⎣⎦，C ．22ππ⎡⎤-⎢⎥⎣⎦，D ．566ππ⎡⎤-⎢⎥⎣⎦，10．已知函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭在[]0,2π上有且只有4个零点，则ω取值范围是（）A ．1519,44⎡⎫⎪⎢⎣⎭B ．1519,88⎡⎫⎪⎢⎣⎭C ．1721,44⎡⎫⎪⎢⎣⎭D ．1721,88⎡⎫⎪⎢⎣⎭11．函数1tan 24y x π⎛⎫=+ ⎪⎝⎭的定义域是（）A ．4,2xx k k Z ππ⎧⎫≠-+∈⎨⎬⎩⎭∣B ．2,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣C ．32,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣D ．,2xx k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭∣12．函数sin(2)4y x π=-的单调减区间是（）A ．3[,],(Z)88k k k ππππ-+∈B ．3[2,2],(Z)88k k k ππππ-+∈C ．37[22],(Z)88k k k ππππ++∈D ．37[,Z)88k k k ππππ++∈13．已知函数()sin()f x x ϕ=+为偶函数，则ϕ的取值可以为（）A ．π2-B ．πC ．π3D ．014．记函数()sin 4f x x b πω⎛⎫=++ ⎪⎝⎭（0>ω）的最小正周期为T ．若23T ππ<<，且()y f x =的图象关于点3,22π⎛⎫ ⎪⎝⎭中心对称，则10f π⎛⎫= ⎪⎝⎭（）A ．1B ．32C ．52D ．315．已知函数()sin 0,0,2y A x m A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭的最大值为4，最小值为0，且该函数图象的相邻两个对称轴之间的最短距离为2π，直线6x π=是该函数图象的一条对称轴，则该函数的解析式是（）A ．4sin 26y x π⎛⎫=+ ⎪⎝⎭B ．2sin 226y x π⎛⎫=++ ⎪⎝⎭C ．2sin 23y x π⎛⎫=-++ ⎪⎝⎭D ．2sin 23y x π⎛⎫=++ ⎪⎝⎭二、多选题16．已知函数()tan 23f x x π⎛⎫=+ ⎪⎝⎭，则下列说法正确的是（）A ．()f x 在定义域内是增函数B ．6y f x π⎛⎫=- ⎪⎝⎭是奇函数C ．()f x 的最小正周期是πD ．()f x 图像的对称中心是,0,46k k Z ππ⎛⎫-∈⎪⎝⎭17．已知()f x 为R 上的奇函数，且当0x >时，()lg f x x =，记()()sin cos g x x f x x =+⋅，下列结论正确的是（）A ．()g x 为奇函数B ．若()g x 的一个零点为0x ，且00x <，则()00lg tan 0x x --=C ．()g x 在区间,2ππ⎛⎫- ⎪⎝⎭的零点个数为3个D ．若()g x 大于1的零点从小到大依次为12,,x x ⋅⋅⋅，则1273x x π<+<18．已知函数()()tan 0,2f x x πωϕωϕ⎛⎫=+≠< ⎪⎝⎭，点,03π⎛⎫ ⎪⎝⎭和5,06π⎛⎫⎪⎝⎭是其相邻的两个对称中心，且在区间2,33ππ⎛⎫⎪⎝⎭内单调递减，则ϕ=（）A ．3πB ．6πC ．3π-D ．6π-19．设函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭，若()f x 在[]0,π上有且仅有3条对称轴，则（）A ．()f x 在[]0,π上有且仅有2个最大值点B ．()f x 在[]0,π上有且仅有2个零点C ．ω的取值范围是710,33⎡⎫⎪⎢⎣⎭D ．()f x 在0,10π⎛⎫⎪⎝⎭上单调递增20．已知函数()sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭，则下列命题正确的是（）A ．若()f x 在[0,)π上有10个零点，则3943,44ω⎛⎤∈ ⎥⎝⎦B ．若()f x 在[0,)π上有11条对称轴，则3943,44ω⎛⎤∈ ⎥⎝⎦C ．若()f x ＝22在[0,)π上有12个解，则21,122ω⎛⎤∈ ⎥⎝⎦D ．若()f x 在,32ππ⎛⎫⎪⎝⎭上单调递减，则35,42ω⎡⎤∈⎢⎥⎣⎦21．函数()214f x x π⎛⎫=++ ⎪⎝⎭，对于任意的[)0,1a ∈，方程()()10f x a x m -=≤≤仅有一个实数根，则m 的取值可以为（）A ．8πB ．58πC ．38πD ．34π22．已知函数()tan 3f x x π⎛⎫=+ ⎪⎝⎭，则下列关于()f x 的判断正确的是（）A ．在区间,6ππ⎛⎫⎪⎝⎭上单调递增B ．最小正周期是πC ．图象关于直线6x π=成轴对称D ．图象关于点,06π⎛⎫⎪⎝⎭成中心对称三、解答题23．已知()sin ,()cos f x x g x x==(1)函数()y f x ω=（0>ω）在区间[)0,p 上恰有三条对称轴，求ω的取值范围．(2)函数2()2()()6,h x g x af x a =-++为常数，①当9a =-时，求函数h (x )的零点；②当[,]62x ππ∈-，恒有()0h x >，求实数a 的取值范围．24．已知函数()cos (0)3f x x πωω⎛⎫=+> ⎪⎝⎭，图象上任意两条相邻对称轴间的距离为2π．(1)求函数的单调区间和对称中心．(2)若关于x 的方程22sin cos 40x m x --=在02x π⎛⎫∈ ⎪⎝⎭，上有实数解，求实数m 的取值范围．25．已知函数2π()sin(2)3f x x =+.(1)请用五点法做出()f x 一个周期内的图像；(2)若函数()()g x f x m =-在区间π[0,2上有两个零点，请写出m 的取值范围，无需说明理由.26．已知函数()()3sin 2f x x πϕϕ=+∈-，（，2π）函数关于4x π=对称.(1)求()f x ϕ的值及的解析式；(2)用五点法在下列直角坐标系中画出()f x 在744ππ⎡⎤-⎢⎥⎣⎦，上的图象；(3)写出()f x 的单调增区间及最小值，并写出取最小值时自变量x 的取值集合．27．已知函数()1sin 62f x x π⎛⎫=+- ⎪⎝⎭.(1)求函数()f x 的单调递增区间；(2)求函数()f x 在区间[]0,2π上的所有零点之和.。
三角函数概念图像与性质复习题型总结(最全)
三角函数概念和性质复习1.终边相同的角: 与角α终边相同角的集合为（1）试写出与角16800终边相同的最小正角和最大负角.（2）已知与角的终边相同, 则为第象限角.（3）第二象限角的集合为________________________________________（4）如果角为第三象限角, 则为第________________象限角2.弧度制（1）, , 度≈（2）弧长公式: = , 扇形面积公式: =（1）扇形的圆心角为1200, 半径为6cm, 扇形的弧长是cm.（2）若弧度的圆心角所对的弧长为cm, 则这个圆心角所在的扇形面积为．3.任意角的三角函数定义角终边上任意一点P的坐标, 它与原点的距离是.规定: = ；= ；.（1）①已知角的终边经过点, 则= .②已知角的终边过点, 且, 则= .③已知角的终边在直线上, 则= ；= .（1）已知0tan cos <⋅θθ,则角θ是第 象限角.（2）设角 是三角形的一个内角, 在 中, 有可能取负值. （3）函数cos sin tan sin cos tan x x xy x x x=++的值域为 . 5.同角三角函数关系: ①平方关系: ；②商关系: .（1）①已知 , 且 是第二象限角, 则 = ； = . ②若 , 则 = ； = . ③已知 , 则 的值为__________.（2）化简：①若 是第二象限角, 则 = ；= ； ③若(,0)2πα∈-,= （3）已知 . ①求 的值；②求sin αcos α－sin2α的值.（4）①已知 , 求 及 的值.6.诱导公式（2）已知 , 且 , 则sin( )= ． （3）整体角思维应用（角的内在关系）①已知, 则 = . ②已知 且 , 则 = . ③已知1sin(),64x π+=则25sin()sin ()63x x ππ-+-= .7.三角函数的周期设 为常数, 且 , 则 的周期T= ； 的周期T= ； 的周期T= . （1）①函数cos(2)3y x π=-的最小正周期是 ； ②函数tan(3)6y x ππ=+的最小正周期是 。
三角函数图像与性质知识点总结和经典题型（已打）
三角函数图像与性质知识点总结和经典题型1．正弦函数、余弦函数、正切函数的图像1-1y=sinx-3p 2-5p 2-7p 27p 25p23p 2p 2-p 2-4p -3p-2p 4p3p2p p-poy x1-1y=cosx-3p2-5p 2-7p27p 25p 23p 2p 2-p 2-4p -3p -2p 4p3p2pp -po yxy=tanx3p 2pp 2-3p 2-p-p 2oyx2．三角函数的单调区间：x y sin =的递增区间是úûùêëé+-2222p p pp k k ，)(Z k Î，递减区间是úûùêëé++23222p p pp k k ，)(Z k Î；x y cos =的递增区间是[]p p p k k 22，-)(Z k Î，递减区间是[]p p p +k k 22，)(Z k Î，x y tan =的递增区间是÷øöçèæ+-22p p pp k k ，)(Z k Î，3．函数B x A y ++=)sin(j w ），（其中00>>w A最大值是B A +，最小值是A B -，周期是wp 2=T ，频率是pw 2=f ，相位是j w +x ，初相是j ；其图象的对称轴是直线)(2Z kk x Î+=+p p j w ，凡是该图象与直线B y =的交点都是该图象的对称中心。
4．由y ＝sinx 的图象变换出y ＝sin(ωx ＋j )的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。
利用图象的变换作图象时，提倡先平移后伸缩，但先伸缩后平移也经常出现无论哪种变形，请切记每一个变换总是对字母x 而言，即图象变换要看“变量”起多大变化，而不是“角变化”多少。
专题4-2 三角函数图像与性质归类-(原卷版)
专题4-2 三角函数图像与性质归类目录一、热点题型归纳【题型一】平移1：正弦←→余弦 (1)【题型二】平移2：识图平移 (3)【题型三】平移3：恒等变形平移 (4)【题型四】平移4：中心对称，轴对称，单调性等性质 (5)【题型五】平移5：最小平移 (6)【题型六】平移6：求w 最值 (7)【题型七】正余弦函数对称轴 (8)【题型八】正余弦对称中心 (9)【题型九】三角函数周期 (9)【题型十】单调性与最值 (11)【题型十一】正余弦“和”与“积”性质、最值 (11)【题型十二】三角函数零点 (12)【题型十三】图像与性质：x1与x2型 (13)【题型十四】三角函数最值 (14)【题型十五】万能代换与换元 (15)【题型十六】图像和性质综合 (15)二、真题再现 (16)三、模拟检测 (178)【题型一】平移1：正弦←→余弦【典例分析】（2022·安徽省太和中学高三阶段练习）已知函数()()πcos 0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭，若()f x 的图象向右平移π12个单位后，得到函数()2πsin 23g x x ⎛⎫=+ ⎪⎝⎭的图象，则（ ）A ．6π=ϕB ．π4ϕ= C ．π3ϕ= D ．2π5ϕ=1（2023·全国·高三专题练习）已知直线8x π=是函数()2sin(2)||2πϕϕ⎛⎫=+< ⎪⎝⎭f x x 的图像的一条对称轴，为了得到函数()y f x =的图像，可把函数2cos 26y x π⎛⎫=- ⎪⎝⎭的图像（ ）A ．向左平移24π个单位长度B ．向右平移24π个单位长度C ．向左平移12π个单位长度 D ．向右平移12π个单位长度2.（2022·全国·高三专题练习）为得到函数cos 23y x π⎛⎫=- ⎪⎝⎭的图象，只需将函数sin 24y x π⎛⎫=-- ⎪⎝⎭图象上所有的点（ ）A ．向左平移712π个单位长度B ．向右平移712π个单位长度 C ．向左平移724π个单位长度D ．向右平移724π个单位长度3.（2023·全国·高三专题练习）为了得到函数πsin 24y x ⎛⎫=+ ⎪⎝⎭的图象，可以将函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图象（ ）A ．向左平移5π24个单位 B ．向右平移7π24个单位 C ．向右平移5π24个单位D ．向左平移7π24个单位【题型二】平移2：识图平移【典例分析】（2022·陕西·渭南市华州区咸林中学高三开学考试（理））如图，函数()()π2sin 0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的图像过()π,0,2π,22⎛⎫⎪⎝⎭两点，为得到函数()()2cos g x x ωϕ=-的图像，应将()f x 的图像（ ）A ．向右平移7π6个单位长度 B ．向左平移7π6个单位长度 C ．向右平移5π2个单位长度D ．向左平移5π2个单位长度()++(0)0Asin x b A ，的步骤和方法：确定函数的最大值M 和最小值2M mA ，2M mb； ：确定函数的周期T ，则可2T得＝； ：常用的方法有代入法和五点法． 把图象上的一个已知点代入(此时A b ，，已知)或代入图象与直线y b ＝的交点求解注意交点是在上升区间上还是在下降区间上)．五点法”中的某一个点为突破口．【变式演练】1.（2022·河南·高三阶段练习（理））函数()()2sin f x x ωϕ=+（0>ω且0πϕ<<）在一个周期内的图象如图所示，将函数()y f x =图象上的点的横坐标伸长为原来的2倍，再向右平移π4个单位长度，得到函数()y g x =的图象，则π3g ⎛⎫= ⎪⎝⎭（ ）AB ．1C ．－1D ．2.（2022·全国·长垣市第一中学高三开学考试（理））将函数sin y x =的图象上所有点的横坐标变为原来的(0)m m >倍，纵坐标不变，再将所得函数图象向左平移(0)ϕϕπ<<个单位长度，最后将所得函数图象上所有点的纵坐标变为原来的(0)n n >倍，横坐标不变，得到如图所示的函数()f x 的部分图象，则,,m n ϕ的值分别为（ ）A ．22,2,3m n πϕ===B ．12,2,23m n πϕ===C ．2,2,3m n πϕ===D ．1,2,23m n πϕ===3.（2022·四川省内江市第六中学模拟预测（文））已知函数()()cos 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭，将函数()f x 的图象向左平移34π个单位长度，得到函数()g x 的部分图象如图所示，则3f π⎛⎫= ⎪⎝⎭（ ）A ．12 B ．12-C D ．【题型三】平移3：恒等变形平移【典例分析】（2022·湖北·高三开学考试）要得到2()sin 43g x x π⎛⎫=+⎪⎝⎭的图象，只需要将22()cos 2sin 2f x x x =-的图象（ ） A ．向左平移24π个单位长度 B ．向右平移24π个单位长度 C ．向左平移12π个单位长度D ．向右平移12π个单位长度【变式演练】1.（2023·全国·高三专题练习）已知函数()2sin cos f x x x =+的图象向左平移()0ϕϕ>个单位长度后得到函数()sin 2cos g x x x =+的图象，则()g ϕ=（ ）A ．65B ．115C ．15 D ．852.（2022·全国·高三专题练习）为了得到函数2cos2y x =的图象，只需把函数2cos 2y x x =+的图象（ ） A ．向左平移3π个单位长度 B ．向右平移3π个单位长度C ．向左平移6π个单位长度 D ．向右平移6π个单位长度3.（【百强校】2015届浙江省宁波市镇海中学高三5月模拟考试理科数学）设()cos 22f x x x =，把()y f x =的图像向左平移(0)ϕϕ>个单位后，恰好得到函数()cos 22g x x x =-的图象，则ϕ的值可以为（ ） A ．6π B ．3πC ．23πD ．56π【题型四】平移4：中心对称，轴对称，单调性等性质【典例分析】（2022·安徽·高三开学考试）将函数()sin(2)(0)f x x ϕϕπ=+<<的图象向右平移6π个单位长度得到()g x 的图象，若()g x 的图象关于直线3x π=对称，则6g π⎛⎫= ⎪⎝⎭（ ）A ．B ．12-C ．0D ．12)+)00((Asin x A ，两个点关于中心对称，则函数值互为相反数。
三角函数的图像与性质题型归纳总结
三角函数的图像与性质题型归纳总结The Standardization Office was revised on the afternoon of December 13, 2020三角函数的图像与性质题型归纳总结题型归纳及思路提示题型1 已知函数解析式确定函数性质【思路提示】一般所给函数为y ＝A sin(ω x ＋φ)或y ＝A cos(ω x ＋φ)，A>0,ω>0,要根据y ＝sin x ，y ＝cos x 的整体性质求解。
一、函数的奇偶性例1 f (x )＝sin ()x ϕ+（0≤ϕ<π）是R 上的偶函数，则ϕ等于（ ） A.0 B ．4π C ．2πD ．π 【评注】由sin y x =是奇函数，cos y x =是偶函数可拓展得到关于三角函数奇偶性的重要结论：sin()();y A x k k Z ϕϕπ=+=∈(1)若是奇函数，则sin()+();2y A x k k Z πϕϕπ=+=∈(2)若是偶函数，则 cos()();2y A x k k Z πϕϕπ=+=+∈(3)若是奇函数，则cos()();y A x k k Z ϕϕπ=+=∈(4)若是偶函数，则tan()().2k y A x k Z πϕϕ=+=∈(5)若是奇函数，则.()sin ||a R f x x a a ∈=-变式1已知，函数为奇函数，则等于（ ）A.0 B ．1 C ．1- D ．1±2.0()cos()()R f x x x R ϕϕϕ∈==+∈变式设，则“”是“为偶函数”的（ ）A 充分不必要条件B ．必要不充分条C ．充要条件D ．无关条件3.()sin()0()f x x f x ωϕω=+>变式设，其中，则是偶函数的充要条件是（ ）A.(0)1f = B ．(0)0f = C ．'(0)1f = D ．'(0)0f =2.()sin(2)()()2f x x x R f x π=-∈例设，则是( )A.π最小正周期为的奇函数 B ．π最小正周期为的偶函数C ．2π最小正周期为的奇函数D ．2π最小正周期为的偶函数2()sin 1()()f x x x R f x =-∈变式1.若，则是( )A.π最小正周期为的奇函数 B ．π最小正周期为的偶函数 C ．π最小正周期为2的奇函数 D ．π最小正周期为2的偶函数2.(0,)2ππ变式下列函数中，既在递增，又是以为周期的偶函数的是( )A.cos 2y x = B ．|sin 2|y x = C ．|cos 2|y x = D ．|sin |y x =二、函数的周期性3.sin(2)cos(2)66y x x ππ=++例函数的最小正周期为( )A.2π B ．4πC ．2πD ．π【评注】关于三角函数周期的几个重要结论：sin()b,cos()b,tan()b22,,.||||||y A x y A x y A x ωϕωϕωϕπππωωω=++=++=++(1)函数的周期分别为|sin()|,|cos()|,|tan()|.||y A x y A x y A x πωϕωϕωϕω=+=+=+(2)函数的周期均为2|sin()b |(b 0),|cos()b |(b 0).||y A x y A x πωϕωϕω=++≠=++≠(3)函数的周期均为1.sin(2)cos(2)63y x x ππ=+++变式函数的最小正周期和最大值分别为( )A.,1π B．π．2,1π D．2π()sin (sin cos ),()f x x x x f x =-变式2.若则的最小正周期是________.()sin 3|sin 3|()f x x x f x =+变式3.若则是( )A.3π最小正周期为的周期函数 B ．23π最小正周期为的周期函数C ．π最小正周期为2的周期函数D ．非周期函数三、函数的单调性.sin(2)([0,])6y x x ππ=-∈例4函数的递增区间是( )A.[0,]3π B ．7[,]1212ππ C ．5[,]36ππD ．5[,]6ππ【评注】求三角函数的单调区间：sin()(0,0)y A x A ωϕω=+>>若函数则22()22322()22(3)sin()0,0sin()sin()(4)cos()tan()k x k k Z k x k k Z y A x A y A x y A x y A x y A x πππωϕππππωϕπωϕωωϕωϕωϕωϕ-≤+≤+∈+≤+≤+∈=+><=---=--=+=+(1)函数的递增区间由决定；(2)函数的递减区间由决定；若函数中，可将函数变为则的增区间为原函数的减区间，减区间为原函数的增区间；对于函数和单调性的讨论同上。
三角函数的图像与性质题型归纳总结
三角函数的图像与性质题型归纳总结题型归纳及思路提示题型1 已知函数解析式确定函数性质【思路提示】一般所给函数为y ＝A sin(ω x ＋φ)或y ＝A cos(ω x ＋φ)，A>0,ω>0,要根据 y ＝sin x ，y ＝cos x 的整体性质求解。
一、函数的奇偶性例1 f (x )＝sin ()x ϕ+（0≤ϕ<π）是R 上的偶函数，则ϕ等于（ ）A.0 B ．4π C ．2πD ．π 【评注】由sin y x =是奇函数，cos y x =是偶函数可拓展得到关于三角函数奇偶性的重要结论：sin()();y A x k k Z ϕϕπ=+=∈(1)若是奇函数，则sin()+();2y A x k k Z πϕϕπ=+=∈(2)若是偶函数，则cos()();2y A x k k Z πϕϕπ=+=+∈(3)若是奇函数，则 cos()();y A x k k Z ϕϕπ=+=∈(4)若是偶函数，则tan()().2k y A x k Z πϕϕ=+=∈(5)若是奇函数，则.()sin ||a R f x x a a ∈=-变式1已知，函数为奇函数，则等于（ ）A.0 B ．1 C ．1- D ．1±2.0()cos()()R f x x x R ϕϕϕ∈==+∈变式设，则“”是“为偶函数”的（ ）A 充分不必要条件B ．必要不充分条C ．充要条件D ．无关条件3.()sin()0()f x x f x ωϕω=+>变式设，其中，则是偶函数的充要条件是（ ）A.(0)1f = B ．(0)0f = C ．'(0)1f = D ．'(0)0f =2.()sin(2)()()2f x x x R f x π=-∈例设，则是( )A.π最小正周期为的奇函数 B ．π最小正周期为的偶函数 C ．2π最小正周期为的奇函数 D ．2π最小正周期为的偶函数2()sin 1()()f x x x R f x =-∈变式1.若，则是( )A.π最小正周期为的奇函数 B ．π最小正周期为的偶函数 C ．π最小正周期为2的奇函数 D ．π最小正周期为2的偶函数2.(0,)2ππ变式下列函数中，既在递增，又是以为周期的偶函数的是( )A.cos 2y x = B ．|sin 2|y x = C ．|cos 2|y x = D ．|sin |y x =二、函数的周期性3.sin(2)cos(2)66y x x ππ=++例函数的最小正周期为( )A.2π B ．4πC ．2πD ．π【评注】关于三角函数周期的几个重要结论：sin()b,cos()b,tan()b22,,.||||||y A x y A x y A x ωϕωϕωϕπππωωω=++=++=++(1)函数的周期分别为|sin()|,|cos()|,|tan()|.||y A x y A x y A x πωϕωϕωϕω=+=+=+(2)函数的周期均为2|sin()b |(b 0),|cos()b |(b 0).||y A x y A x πωϕωϕω=++≠=++≠(3)函数的周期均为1.sin(2)cos(2)63y x x ππ=+++变式函数的最小正周期和最大值分别为( )A.,1π B ．,2π C ．2,1π D ．2,2π()sin (sin cos ),()f x x x x f x =-变式2.若则的最小正周期是________.()sin 3|sin 3|()f x x x f x =+变式3.若则是( )A.3π最小正周期为的周期函数 B ．23π最小正周期为的周期函数 C ．π最小正周期为2的周期函数 D ．非周期函数三、函数的单调性.sin(2)([0,])6y x x ππ=-∈例4函数的递增区间是( )A.[0,]3π B ．7[,]1212ππ C ．5[,]36ππD ．5[,]6ππ【评注】求三角函数的单调区间：sin()(0,0)y A x A ωϕω=+>>若函数则22()22322()22(3)sin()0,0sin()sin()(4)cos()tan()k x k k Z k x k k Z y A x A y A x y A x y A x y A x πππωϕππππωϕπωϕωωϕωϕωϕωϕ-≤+≤+∈+≤+≤+∈=+><=---=--=+=+(1)函数的递增区间由决定；(2)函数的递减区间由决定；若函数中，可将函数变为则的增区间为原函数的减区间，减区间为原函数的增区间；对于函数和单调性的讨论同上。
三角函数图像和性质(含答案)--题型全面
应有 ，
，解得
．
14.【答案】C 解：
ȁ ܿጡ sin ጡ
ጡ ȁ ܿጡ ܿൌ ጡ ȁ ܿጡ 1，
ܿൌ ጡȁ ܿጡ ȁ ܿጡ ܿൌ ጡ 1
ጡ
的最小正周期为
，A 错误；
由
8
ܿൌ 1 1，B 错误；
由
8
sin 1 1，C 正确；
ጡ 的图象向左平移 个单位长度后得到
误． 故选 C．
cos ጡ
1，不为偶函数，故 D 错
（﹣ω，ω）内单调递增，且函数 y=f（x）的图象关于直线 x=ω对称，则ω
的值为 ．
第 页，共 9页
答案和解析
1.【答案】A 解： 函数
的最小正周期为 ，
cos 丨 2x 丨 ȁ ܿጡ，它
丨
cosx
丨的最小正周期为1
1
，
cos ጡ
的最小正周期为
，
tan ጡ 的最小正周期为 ，
2.【答案】C 解：由题意可得 ጡ1
三角函数的图像和性质
一、选择题（本大题共 14 小题，共 70.0 分）
1. 在函数
cos ጡ ，
ȁ ܿጡ ，
cos ጡ ，
tan ጡ 中，最小正周期为 的所有函数为
A.
B.
C.
D.
. 设函数 ጡ sin ጡ
，若对任意 ጡ 都有 ጡ1
ጡ
ጡ
成立，那么 ጡ1 ጡ 的最小值为
A. 1
B. 2
C. 4
D. 8
在[ ]的零点个数为
第 页，共 9页
17. 设函数 ጡ cos ጡ
，若 ጡ
对任意的实数 x 都
成立，则 的最小值为______．
18. 函数 ጡ sin ጡ
专题4 三角函数的图象与性质-重难点题型精讲(举一反三)(新高考地区专用)(解析版)
专题4.7 三角函数的图象与性质-重难点题型精讲1．正弦函数与余弦函数的图象(1)正弦函数的图象①根据三角函数的定义，利用单位圆，我们可以得到函数y=,x∈[0,2π]的图象，如图所示.②五点法观察图，在函数y=,x∈[0,2π]的图象上，以下五个点：,1),( π,0),(-1),(2π,0)在确定图象形状时起关键作用.描出这五个点，函数y=,x∈[0,2π]的图象形状就基本确定了.因此，在精确度要求不高时，常先找出这五个关键点，再用光滑的曲线将它们连接起来，得到正弦函数的简图.这种作图的方法叫做“五点(画图)法”.(2)余弦函数的图象①图象变换法作余弦函数的图象由诱导公式六，我们知道，而函数x∈R的图象可以通过正弦函数y=,x∈R的图象向左平移个单位长度而得到.所以将正弦函数的图象向左平移个单位长度，就得到余弦函数的图象，如图所示.②五点法作余弦函数的图象类似于正弦函数图象的作法，从余弦函数y=,x∈R的图象可以看出，要作出函数y=在[0,2]上的图象，起关键作用的五个点是：(0,1),(,0),(,-1),(,0),(2,1).先描出这五个点，然后把这五个点用一条光滑的曲线连接起来就得到了函数y=在[0,2]上的简图，再通过左右平移(每次移动2个单位长度)即可得到余弦函数y=,x∈R的图象.(3)正弦曲线、余弦曲线正弦函数的图象和余弦函数的图象分别叫做正弦曲线和余弦曲线.它们是具有相同形状的“波浪起伏”的连续光滑曲线.2．正弦函数与余弦函数的性质(1)周期函数①定义：一般地，设函数f(x)的定义域为D，如果存在一个非零常数T，使得对每一个x∈D都有x+T∈D，且f(x+T)=f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.②最小正周期：如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.(2)正弦函数与余弦函数的性质正弦函数与余弦函数的图象与性质如下表：3．正弦型函数的性质的性质4．正切函数的性质与图象(1)正切函数的图象及性质(2)三点两线法作正切曲线的简图类比于正、余弦函数图象的五点法，我们可以采用三点两线法作正切函数的简图.“三点”是指点(-,-1),(0,0),(,1);“两线”是指直线x=-和x=.在三点、两线确定的情况下,可以大致画出正切函数在区间(-上的简图.5．余切函数的图象及性质正切函数的图象及性质：的图象先向右平移个单位长度，再以x轴为对称轴上下翻折，可得的图象.余切函数的图象与性质如下表：【题型1 三角函数的定义域和值域（最值）】【方法点拨】求与三角函数有关的函数的值域(最值)的常用方法有：(1)借助三角函数的有界性、单调性求解；(2)转化为关于的二次函数求解.注意求三角函数的最值对应的自变量x的值时，要考虑三角函数的周期性.【例1】（2022·甘肃·高二开学考试）函数f(x)=tan(x+π4)的定义域为（）A．{x|x≠kπ+π4,k∈Z}B．{x|x≠2kπ+π4,k∈Z}C．{x|x≠kπ−π4,k∈Z}D．{x|x≠kπ,k∈Z}【解题思路】根据正切函数的定义域可得结果.【解答过程】因为x+π4≠kπ+π2,k∈Z，所以x≠kπ+π4,k∈Z.故f(x)的定义域为{x|x≠kπ+π4,k∈Z}.故选：A.【变式1-1】（2022·四川省高三阶段练习（理））若x∈[π4,2π3]，则函数f(x)=3sin x cos x+√3sin2x的值域为（ ） A ．[0,3√32]B ．[0,√32] C ．[0,√3]D ．[0,3+√3]【解题思路】利用二倍角公式和辅助角公式化简原式为f (x )=√3sin(2x -π6)+√32，结合正弦函数的图像和性质，求解即可. 【解答过程】由题意，f (x )=3sin x cos x +√3sin 2x =32sin2x +√32(1-cos2x )=√3×(√32sin2x -12cos2x )+√32=√3×(cos π6sin2x -sin π6cos2x )+√32=√3sin(2x -π6)+√32,当x ∈[π4,2π3]时，有2x -π6∈[π3,7π6]，当2x -π6=π2，即x =π3时，f (x )max =f (π3)=√3+√32=3√32； 当2x -π6=7π6，即x =2π3时，f (x )min =f (2π3)=0.即函数f (x )的值域为[0,3√32].故选：A.【变式1-2】（2022·福建省高二阶段练习）函数f (x )=sinx +cos (x +π6)的值域为（ ） A ．[−2,2]B ．[−√3,√3]C ．[−1,1]D ．[−√32,√32] 【解题思路】利用两角和的余弦公式和辅助角公式进行化简，即可得到答案 【解答过程】解：函数f (x )=sinx +cos (x +π6)=sinx +√32cosx −12sinx =√32cosx +12sinx =cos (x −π6)，∵x ∈R ，∴cos (x −π6)∈[−1,1]，∴函数的值域为[−1,1]， 故选：C ．【变式1-3】（2022·全国·高一单元测试）若x ∈[−π3,2π3]，则函数y =cos 2(x +π6)+sin (x +2π3)的最大值与最小值之和为（ ）A ．12B ．1C ．74D ．√2【解题思路】利用诱导公式可化简函数为y =(cos (x +π6)+12)2−14，根据余弦型函数值域的求法可求得cos(x+π6)∈[−√32,1]，结合二次函数最值的求法可求得y的最大值和最小值，加和即可求得结果.【解答过程】y=cos2(x+π6)+sin(x+2π3)=cos2(x+π6)+sin(π2+x+π6)=cos2(x+π6)+cos(x+π6)=(cos(x+π6)+12)2−14，当x∈[−π3,2π3]时，x+π6∈[−π6,5π6]，∴cos(x+π6)∈[−√32,1]，∴当cos(x+π6)=1时，y max=94−14=2；当cos(x+π6)=−12时，y min=−14；∴y max+y min=2−14=74.故选：C.【方法点拨】证明一个函数是否为周期函数或求函数周期的大小常用以下方法：(1)定义法：即对定义域内的每一个x值，看是否存在非零常数T使f(x+T)=f(x)成立，若成立，则函数是周期函数且T是它的一个周期.(2)公式法：利用三角函数的周期公式来求解.(3)图象法：画出函数的图象，通过图象直观判断即可.【例2】（2023·广东·高三学业考试）函数f(x)=sin(x2−π4)的最小正周期是（）A．π2B．πC．2πD．4π【解题思路】利用正弦函数的周期求解．【解答过程】f(x)的最小正周期为T=2π12=4π．故选：D．【变式2-1】（2023·广东·高三学业考试）函数f(x)=cos(12x+π6)的最小正周期为（）A．π2B．πC．2πD．4π【解题思路】利用余弦型函数的周期公式进行求解.【解答过程】∵f(x)=cos(12x+π6)，∴f(x)最小正周期T=2π12=4π．故A，B，C错误.故选：D.【变式2-2】（2022·甘肃临夏·高二期末（理））函数f(x)=cos(ωx+π6)(ω>0)的最小正周期为π，则f(π2)=（）A．−√32B．−12C．12D．√32【解题思路】由周期求出ω，从而可求出f(x)，进而可求出f(π2).【解答过程】因为函数f(x)的最小正周期为π，ω>0，所以ω=2ππ=2，得f(x)=cos(2x+π6)，所以f(π2)=cos(2×π2+π6)=−cosπ6=−√32．故选：A.【变式2-3】（2022·广东佛山·高三阶段练习）在下列函数中，最小正周期为π且在(0,π2)为减函数的是（）A．f(x)=sin|2x|B．f(x)=cos(2x+π6)C．f(x)=|cosx|D．f(x)=tan(2x−π4)【解题思路】根据三角函数的图像性质，逐个选项进行判断即可得出答案.【解答过程】对于A，f(x)=sin|2x|的图像关于y轴对称，在(0,π2)为增函数，不符题意，故A错；对于B，f(x)=cos(2x+π6)的最小正周期为π，x∈(0,π2),2x+π6∈(π6,7π6)，不是减函数，不符题意，故B错；对于C，f(x)=|cosx|的最小正周期为π，在(0,π2)为减函数，符合题意，故C对；对于D，f(x)=tan(2x−π4)的最小正周期为π2，不符题意，故D错；故选：C.【题型3 三角函数的奇偶性】【方法点拨】掌握正弦、余弦、正切函数的奇偶性相关知识，结合具体题目，灵活求解.【例3】（2022·广东·高三学业考试）若函数f(x)=sin(x+φ)是偶函数，则φ可取一个值为（）A．−πB．−π2C．π4D．2π【解题思路】根据偶函数的定义得φ=kπ+π2,k∈Z,结合选项可确定答案.【解答过程】∵函数f(x)=sin(x+φ)是偶函数，∴f(−x)=f(x)，即sin(−x+φ)=sin(x+φ).∴−x+φ=x+φ+2kπ或−x+φ+x+φ=π+2kπ,k∈Z.当−x+φ=x+φ+2kπ时，可得x=−kπ，不满足函数定义.当−x+φ+x+φ=π+2kπ时，φ=kπ+π2,k∈Z,若φ=kπ+π2=−π，解得k=−32∉Z，故A错误;若φ=kπ+π2=−π2，解得k =−1∈Z ，故B 正确; 若φ=kπ+π2=π4，解得k =−14∉Z ，故C 错误;若φ=kπ+π2=2π，解得k =32∉Z ，故D 错误;故选:B.【变式3-1】（2022·全国·高一）下列函数中，在其定义域上是偶函数的是（ ） A ．y =sinxB ．y =|sinx |C ．y =tanxD ．y =cos (x −π2)【解题思路】根据奇偶性定义，结合三角函数的奇偶性可直接得到结果.【解答过程】对于A ，∵y =sinx 定义域为R ，sin (−x )=−sinx ，∴y =sinx 为奇函数，A 错误；对于B ，∵y =|sinx |定义域为R ，|sin (−x )|=|−sinx |=|sinx |，∴y =|sinx |为偶函数，B 正确；对于C ，∵y =tanx 定义域为(kπ−π2,kπ+π2)(k ∈Z )，即定义域关于原点对称，tan (−x )=−tanx ，∴y =tanx 为奇函数，C 错误；对于D ，∵y =cos (x −π2)=sinx 定义域为R ，sin (−x )=−sinx ，∴y =cos (x −π2)为奇函数，D 错误. 故选：B.【变式3-2】（2022·北京高三阶段练习）函数f (x )=cos x +cos2x 是（ ） A ．奇函数，且最大值为2 B ．偶函数，且最小值为-98 C ．奇函数，且最小值为-98D ．偶函数，且最大值为98【解题思路】利用函数奇偶性的定义可判断出函数f (x )的奇偶性，利用二次函数的基本性质可求得函数f (x )的最值.【解答过程】函数f (x )的定义域为R ，f (-x )=cos (-x )+cos (-2x )=cos x +cos2x =f (x )， 故函数f (x )为偶函数，因为-1≤cos x ≤1，则f (x )=2cos 2x +cos x -1=2(cos x +14)2-98， 所以，f (x )min =-98，f (x )max =2+1-1=2.故选：B.【变式3-3】（2022·广西·模拟预测（理））若将函数f (x )=sin2x −√3cos2x 的图象向右平移m (m >0)个单位后，所得图象对应的函数为奇函数，则m 的最小值是（ ） A ．π6B ．π3C ．2π3D ．5π6【解题思路】首先对f (x )化简得到f (x )=2sin (2x −π3)，再写出平移后的解析式y =2sin (2x −2m −π3)，因为其为奇函数，则−2m −π3=k π,k ∈Z ，解出m 即可得到最小值.【解答过程】f (x )=sin2x −√3cos2x =2(12sin2x −√32cos2x)=2sin (2x −π3)，向右平移m(m >0)个单位后得到函数y =2sin [2(x −m )−π3]=2sin (2x −2m −π3)，由于是奇函数，因此，得−2m −π3=k π,k ∈Z ，m =−π6−k π2,k ∈Z.又∵m >0，则当k =−1时，m 的最小值是π3，故选：B.【方法点拨】掌握正弦、余弦、正切函数的对称性相关知识，结合具体题目，灵活求解.【例4】（2022·安徽·高三开学考试）函数f (x )=tan (2x −π3)的图象的一个对称中心为（ ） A ．(π12,0)B ．(7π12,0)C ．(−5π12,0)D ．(−π12,0)【解题思路】根据正切型函数的对称中心为(k π2,0) k ∈Z ，求解即可. 【解答过程】由2x −π3=k π2,k ∈Z ，可得x =k π4+π6,k ∈Z ，当k =0时，x =π6，当k =1时，x =π4+π6=5π12，当k =2时，x =8π12=23π， 当k =−1时，x =−π4+π6=−π12， 当k =−2时，x =−4π12=−13π， 当k =−3时，x =−7π12，所以(−π12,0)为f (x )图象的一个对称中心， 故选：D.【变式4-1】（2022·河南·高三阶段练习（理））已知函数f (x )=2cos (ωx −π6)(ω>0)在[0,2π]内恰有三条对称轴，则ω的取值范围是（ ） A ．[43,116)B ．(43,116]C ．[1312,1912)D ．(1312,1912]【解题思路】根据余弦函数的性质可得2π≤2ωπ−π6<3π，进而即得. 【解答过程】因为0≤x ≤2π， 所以−π6≤ωx −π6≤2ωπ−π6， 所以2π≤2ωπ−π6<3π， 解得1312≤ω<1912．故选：C.【变式4-2】已知函数f(x)=sin (12x −π6)，则结论正确的是（ ）A ．f (x )的图象关于点(5π3,0)中心对称B ．f (x )的图象关于直线x =−π3对称C ．f (x )在区间(−π,π)内有2个零点D ．f (x )在区间[−π2,0]上单调递增【解题思路】A 、B 应用代入法判断对称轴和对称中心；C 、D 根据给定区间求12x −π6的范围，结合正弦型函数的性质求零点和单调性. 【解答过程】A ：f(5π3)=sin (12×5π3−π6)=sin2π3≠0，故(5π3,0)不是对称中心，错误；B ：f(−π3)=sin[12×(−π3)−π6]=−sin π3≠±1，故x =−π3不是对称轴，错误；C ：在x ∈(−π,π)，则12x −π6∈(−2π3,π3)，故f(x)=0，可得12x −π6=0，所以x =π3为f (x )在(−π,π)内的唯一零点，错误；D ：在x ∈[−π2,0]，则12x −π6∈[−5π12,−π6]，故f(x)=sin (12x −π6)递增，正确. 故选：D.【变式4-3】（2022·贵州·高三阶段练习（文））已知函数f (x )=2cos (ωx +φ)（ω>0，0<φ<π）的相邻两条对称轴之间的距离为2π，且为奇函数，将f (x )的图象向右平移π3个单位得到函数g (x )的图象，则函数g (x )的图象（ ） A ．关于点(−5π3,0)对称B ．关于点(π2,0)对称 C ．关于直线x =−π3对称D ．关于直线x =π2对称【解题思路】两个相邻对称轴的为半个周期，奇函数可以确定f (x )为正弦函数，由此条件得出f (x )的解析式，再根据平移得出g (x )的解析式，根据解析式写出对称中心和对称轴的通式即可得出答案.【解答过程】由相邻两条对称轴之间的距离为2π可知T2=2π，即T =4π，ω=2πT ，ω=12, 因为f (x )为奇函数，根据0<φ<π可知φ=π2，f (x )=2sin 12x , g (x )=2sin (12(x −π3))=2sin (12x −π6),对称中心：12x −π6=k π(k ∈Z )，x =2k π+π3(k ∈Z )，故A 正确，B 错误;对称轴：12x −π6=π2+k π(k ∈Z )，x =2k π+4π3(k ∈Z )，故C 、D 错误;故选：A.【方法点拨】三角函数的单调性问题主要有：三角函数的单调区间的求解、比较函数值的大小、根据三角函数的单调性求参数；结合具体条件，根据三角函数的图象与性质进行求解即可.【例5】（2022·江西·高三阶段练习（理））函数y =sin (π6−2x)(x ∈[0,π])为增函数的区间是（ ） A ．[0,π3]B ．[π12,7π12]C ．[π3,5π6]D ．[5π6,π]【解题思路】根据三角函数单调性的求法求得正确答案. 【解答过程】y =sin (π6−2x)=−sin (2x −π6)，2k π+π2≤2x −π6≤2k π+3π2，k π+π3≤x ≤k π+5π6，k ∈Z ， 令k =0可的y =sin (π6−2x)(x ∈[0,π])的递增区间为[π3,5π6]. 故选：C.【变式5-1】（2022·河南信阳·一模（理））已知函数f (x )=2√3cos (x -π2)cos x -2sin 2x ，若f (x )在区间[m ,π4]上单调递减，则实数m 的取值范围（ ）A ．[π6,π4]B ．[π3,π2]C ．[π6,π4)D ．[π6,π3)【解题思路】利用三角恒等变换，化简三角函数，利用正弦型函数的单调性，建立不等式组，可得答案.【解答过程】f (x )=2√3cos (x -π2)cos x -2sin 2x =2√3sin x cos x -2·1-cos2x 2=√3sin2x -1+cos2x=2(√32sin2x +12cos2x)-1 =2sin (2x +π6)-1，由x ∈[m ,π4]，则2x +π6∈[2m +π6,2π3]，由题意，[2m +π6,2π3]⊆[π2,3π2]，则π2≤2m +π6<2π3，解得π6≤m <π4. 故选：C.【变式5-2】（2022·江苏·高三阶段练习）已知a =log 168，b =πln0.8，c =sin2.5，则a ，b ，c 的大小关系是（ ） A ．c <a <b B ．c <b <a C ．a <b <cD ．a <c <b【解题思路】由对数的运算法则求出a ，又πln0.8，sin2.5分别可看做y =πx ，y =sinx 的函数值，考虑构造指数函数和正弦函数，利用函数的单调性对其值进行估计，又因为ln0.8估值困难，故考虑利用与函数y =lnx 近似的有理函数y =1−1x 对其大小进行估值，最后求得答案.【解答过程】由题意，a =log 168=log 2423=34=0.75， 设f (x )=lnx +1x −1，则f ′(x )=1x −1x 2=x−1x 2，当0<x <1时，f ′(x )<0，函数f (x )在(0,1)上单调递减，当x >1时，f ′(x )>0，函数f (x )在(1,+∞)上单调递增，所以f (0.8)>f (1)，即ln0.8+54−1>0，所以ln0.8>−14，因为函数y =πx 在(−∞,+∞)上单调递增，所以πln0.8>π−14，又(π−14)−4=π，(34)−4=25681≈3.16，所以(34)−4>(π−14)−4，因为y =x−4在(0,+∞)单调递减，所以34<π−14，所以πln0.8>34，故b >a ， 因为3π4<2.5<5π6，函数y =sinx 在(π2,π)上单调递减，所以sin 5π6<sin2.5<sin3π4，所以12<sin2.5<√22，所以sin2.5<34，即c <a ，所以c <a <b ， 故选：A.【变式5-3】（2022·内蒙古·高三阶段练习（文））若函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，则ω的最大值为（ ）A ．37 B ．34C ．14D ．1【解题思路】由题知ωx +π4∈(π4,7π4ω+π4)，再根据函数y =√2cosx 在(0,π)上单调递减可得7π4ω+π4≤π，进而解不等式求解即可.【解答过程】解：因为函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，所以7π4≤12T =πω，解得0<ω≤47，因为x ∈(0,7π4)，所以ωx +π4∈(π4,7π4ω+π4)，因为函数y =√2cosx 在(0,π)上单调递减， 所以，函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，则有7π4ω+π4≤π，解得ω≤37，所以ω的取值范围是ω∈(0,37]，即ω的最大值为37. 故选：A.【方法点拨】解决正(余)弦型函数性质的综合应用问题的思路： (1)熟练掌握函数或的图象，利用基本函数法得到相应的函数性质，然后利用性质解题.(2)直接作出函数图象，利用图象形象直观地分析并解决问题. 【例6】已知函数f (x )=4sinxcos (x +π6)+1.(1)求f (x )的最小正周期及单调区间； (2)求f (x )在区间[−π6,π4]上的最大值与最小值.【解题思路】（1）先利用三角恒等变换化简得到f (x )=2sin (2x +π6)，从而利用T =2π|ω|求出最小正周期，再利用整体法求解函数的单调区间；（2）根据x ∈[−π6,π4]求出2x +π6∈[−π6,2π3]，从而结合函数图象求出最大值为2，最小值为−1.【解答过程】（1）因为f (x )=4sinx (cosxcos π6−sinxsin π6)+1=2√3sinxcosx −2sin 2x +1 =√3sin2x +cos2x =2sin (2x +π6) 所以f (x )的最小正周期T =2π2=π；令−π2+2k π≤2x +π6≤π2+2k π，k ∈Z ，解得：[−π3+k π,π6+k π]，k ∈Z ， 令π2+2k π≤2x +π6≤3π2+2k π，k ∈Z ，解得：[π6+k π,2π3+k π]，k ∈Z ，单调增区间为[−π3+k π,π6+k π]，k ∈Z ，单调减区间为[π6+k π,2π3+k π]，k ∈Z ；（2）已知x ∈[−π6,π4]，所以2x +π6∈[−π6,2π3]，当2x +π6=π2，即x =π6时，f (x )取得最大值，最大值为2， 当2x +π6=−π6，即x =−π6时，f (x )取得最小值，最小值为-1， 所以f (x )在区间[−π6,π4]上的最大值为2，最小值为−1.【变式6-1】（2022·陕西·高三阶段练习（文））已知函数f (x )=4sin (ωx +φ)（ω>0，|φ|<π2）图象的一条对称轴为直线x =−π12，这条对称轴与相邻对称中心之间的距离为π8．(1)求f (x )；(2)求f (x )在[−π24,π4]上的值域．【解题思路】（1）先求出周期，由此求出ω的值，利用对称轴方程求出φ，即可得到函数的解析式；（2）根据自变量的范围求得4x −π6∈[−π3,5π6]，根据正弦函数的取值求得函数的值域【解答过程】（1）因为函数f(x)图象的对称轴与相邻对称中心之间的距离为π8， 所以T =π2，故ω=2πT=4，又f(x)的图象的一条对称轴方程为x =−π12， 则4×(−π12)+φ=π2+k π，k ∈Z ，即φ=5π6+k π，k ∈Z ，又|φ|<π2，所以φ=−π6， 故f(x)=4sin (4x −π6)；（2）因为x ∈[−π24,π4]，所以4x −π6∈[−π3,5π6]，所以sin (4x −π6)∈[−√32,1]，所以4sin (4x −π6)∈[−2√3,4]， 故f (x )在[−π24,π4]上的值域为[−2√3,4].【变式6-2】（2021·天津·高一期末）已知函数f (x )=2√3cos 2(π2+x)-2sin(π+x )cos x -√3 (1)求f (x )的最小正周期及单调递减区间； (2)求f (x )在区间[π4,π2]上的最值；(3)若f (x 0-π6)=1013,x 0∈[3π4,π]，求sin2x 0的值．【解题思路】（1）根据三角恒等变换可得f (x )=2sin (2x -π3)，然后根据三角函数的性质即得；（2）根据正弦函数的性质即得；（3）由题可得sin (2x 0-2π3)=513，然后根据同角关系式及和差角公式即得. 【解答过程】（1）因为f (x )=2sin x cos x +2√3sin 2x -√3 =sin2x -√3cos2x =2sin (2x -π3)． 所以f (x )的最小正周期T =2π2=π，∵π2+2k π≤2x -π3≤3π2+2k π,k ∈Z ，∴5π12+k π≤x ≤11π12+k π，所以f (x )的单调递减区间为[5π12+k π,11π12+k π](k ∈Z)；（2）由（1）知f (x )的单调递减区间为[5π12+k π,11π12+k π](k ∈Z)，∵x ∈[π4,π2]，∴f (x )在[π4,5π12]上单调递增，在[5π12,π2]上单调递减，又f (5π12)=2sin π2=2,f (π4)=2sin π6=1,f (π2)=2sin2π3=√3，故f (x )min =1,f (x )max =2； 另解：∵x ∈[π4,π2]， ∴t =2x -π3∈[π6,2π3]，∵y =sin t 在t ∈[π6,π2]单调递增，在[π2,2π3]上单调递减， ∴当t =π2时，(sin t )max =1,f (x )max =2×1=2， ∴当t =π6时，(sin t )min =12,f (x )min =2×12=1； （3）∵f (x 0-π6)=1013，∴sin (2x 0-2π3)=513， 由x 0∈[3π4,π]，得2x 0-2π3∈[5π6,4π3]，∴cos (2x 0-2π3)=-1213， ∴sin2x 0=sin [(2x 0-2π3)+2π3]=sin (2x 0-2π3)cos2π3+cos (2x 0-2π3)sin 2π3=513×(-12)+(-1213)×√32=-5+12√326． 【变式6-3】（2022·黑龙江·高三阶段练习）已知函数f (x )=[(1+√2)sin x -cos x]⋅[(1-√2)sin x -cos x]. (1)求f (x )的最小正周期T 和单调递减区间；(2)四边形ABCD 内接于⊙O ，BD =2，锐角A 满足f (3A4)=-1，求四边形ABCD 面积S 的取值范围.【解题思路】（1）利用三角函数恒等变换公式对函数化简变形得f (x )=√2cos (2x +π4)，从而可求出最小正周期，再由2kπ≤2x +π4≤2kπ+π(k ∈Z )求出其单调区间，（2）由f (3A4)=-1，求得A =π3，再由圆的性质可得C =2π3，设AB =a ，AD =b ，BC =c ，CD =d ，分别在△ABD 和△CBD 中利用余弦定理结合基本不等式可得0<ab ≤4，0<cd ≤43，从而可求出四边形ABCD 面积S 的取值范围.【解答过程】（1）[(1+√2)sin x -cos x]⋅[(1-√2)sin x -cos x]=[(sin x -cos x )+√2sin x]⋅[(sin x -cos x )-√2sin x]=(sin x -cos x )2-2sin 2x =sin 2x -2sin x cos x +cos 2x -2sin 2x=1-2sin 2x -sin2x =cos2x -sin2x=√2cos (2x +π4)， ∴f (x )=√2cos (2x +π4) ∴T =π.由2kπ≤2x +π4≤2kπ+π(k ∈Z )，得kπ-π8≤x ≤kπ+3π8(k ∈Z )，所以f (x )单调递减区间为[kπ-π8,kπ+3π8](k ∈Z ). （2）由于f (3A4)=-1，根据（1）得√2cos (2×3A 4+π4)=-1，∵0<A <π2，∴A =π3，C =2π3.分别设AB =a ，AD =b ，BC =c ，CD =d .因BD =2，分别在△ABD 和△CBD 中由余弦定理得a 2+b 2-2ab cos π3=4，c 2+d 2-2cd cos2π3=4，∴a 2+b 2=4+ab ，c 2+d 2=4-cd .∵a 2+b 2≥2ab ，c 2+d 2≥2cd ，等号在a =b =2，c =d =2√33时成立，∴4+ab ≥2ab ，4-cd ≥2cd ，解得0<ab ≤4，0<cd ≤43. ∴0<ab +cd ≤163.等号在a =b =2，c =d =2√33时成立，∵S =12ab sin A +12cd sin C =√34(ab +cd )， 所以S 的取值范围是(0,4√33].。
三角函数的图象与性质6大题型
三角函数的图象与性质6大题型三角函数的图象与性质是高考的热点，函数sin()y A x ωϕ=+的图象变换以及三角函数的周期性、对称性、单调性之间逻辑关系则是重心。
随着新高考改革的推进，更加注重对以周期性为核心的三大性质之间的逻辑关系的考查，要求考生能用几何直观和代数运算来研究三角函数。
高考中的相关试题多以选择题、填空题的形式考查，难度中等或偏下。
一、三角函数性质问题相关方法1、周期的计算公式:函数)0()cos(),sin(>+=+=ωϕωϕωx A y x A y 的周期为ωπ2=T ，函数)0()tan(>+=ωϕωx A y 的周期为ωπ=T 求解.2、奇偶性的判断方法:三角函数中奇函数一般可化为x A y ωsin =或x A y ωtan =的形式，而偶函数一般可化为b x A y +=ωcos 的形式.3、解决对称性问题的关键：熟练掌握三角函数的对称轴、对称中心.方法：整体处理法、代入验证法对于函数)0()cos(),sin(>+=+=ωϕωϕωx A y x A y ，其对称轴一定经过图象的最高点或最低点，对称中心的横坐标一定是函数的零点，因此在判断直线0x x =或点)0,(0x 是否是函数的对称轴或对称中心时，可通过检验)(0x f 的值进行判断.4、确定函数)0,0()sin(>>+=ωϕωA x A y 单调区间的方法采用“换元”法整体代换，将‘ϕω+x ’看作一个整体，可令“ϕω+=x z ”，即通过求z A y sin =的单调区间而求出函数的单调区间.若0<ω，则可利用诱导公式先将x 的系数转变为正数，再求单调区间.二、三角函数图形变换问题解决三角函数图像变换问题的两种方法分别为先平移后伸缩和先伸缩后平移.破解此类题的关键如下：1、定函数：一定要看准是将哪个函数的图像变换得到另一个函数的图像.2、变同名：函数的名称要一样.3、选方法：即选择变换方法.要注意：对于函数)0(sin >=ωωx y 的图像，向左平移ϕ个单位长度得到的是函数)(sin ϕω+=x y 的图象，而不是函数)sin(ϕω+=x y 的图像.【题型1【例1】（2023·湖南湘潭·统考二模）函数2cos2()sin xf x x+=的部分图象大致为（）A ．B ．C ．D ．【变式1-1】（2023秋·云南·高三云南师大附中校考阶段练习）函数()21sin 2f x x x x =-的图象大致为（）A ．B ．C ．D ．【变式1-2】（2022秋·河南·高三校联考阶段练习）函数()cos e =xf x 的部分图象大致为（）A ．B ．C ．D ．【变式1-3】（2022秋·云南·高三校联考阶段练习）函数()cos ln xf x x xππ+=⋅-在(),ππ-上的图象大致为（）A ．B ．C ．D ．【变式1-4】（2022秋·四川遂宁·高三遂宁中学校考阶段练习）函数()(tan sin 2)22x x y x x -=--的部分图象大致为（）A ．B ．C ．D ．【题型2根据图象求三角函数解析式】【例2】（2023秋·湖南怀化·高三统考期末）已知函数()2cos()(0)f x x ωϕω=+>的部分图象如图所示，则()0f =（）A ．1B ．1-CD ．【变式2-1】（2022秋·贵州铜仁·高三校考阶段练习）已知A ，B ，C ，D ，E 是函数sin()y x ωϕ=+0,02πωϕ⎛⎫><< ⎪⎝⎭一个周期内的图像上的五个点，如图，A ,06π⎛⎫- ⎪⎝⎭，B 为y 轴上的点，C 为图像上的最低点，E 为该函数图像的一个对称中心，B 与D 关于点E 对称，CD 在x 轴上的投影为12π，则ωφ，的值为（）A ．2ω=，3πϕ=B ．2ω=，6πϕ=C ．12ω=，3πϕ=D ．12ω=，6πϕ=【变式2-2】（2023秋·山西太原·高三山西大附中校考阶段练习）函数()sin()(0,0)f x x ωϕωϕπ=+><<的部分图象如图，BC x ∥轴，当π0,4x ⎡⎤∈⎢⎥⎣⎦时，若不等式()sin 2f x m x ≥-恒成立，则m 的取值范围是（）A．⎛-∞ ⎝⎦B ．1,2⎛⎤-∞ ⎥⎝⎦C ．(-∞D ．(],1-∞【变式2-3】（2023秋·北京朝阳·高三统考期末）已知函数π()sin()0,||2ωϕωϕ⎛⎫=+>< ⎪⎝⎭f x x ，若()()1g x f x ⋅=，且函数()g x 的部分图象如图所示，则ϕ等于（）A ．π3-B ．π6-C ．π6D ．π3【变式2-4】（2023·全国·模拟预测）（多选）已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，若将()f x 的图象向右平移()0m m >个单位长度后得到函数()()sin 2g x A x ωϕ=-的图象，则m 的值可以是（）A ．π4B ．π3C ．4π3D ．9π4【题型3三角函数图象变换问题】【例3】（2023秋·江西赣州·高三统考期末）函数()()sin f x x ωϕ=+（其中0ω>，π2ϕ<）的图象如图所示，为了得到cos y x ω=的图象，只需把()y f x =的图象上所有点（）A ．向左平移π6个单位长度B ．向右平移π12个单位长度C ．向左平移π12个单位长度D ．向右平移π6个单位长度【变式3-1】（2022·四川·高三统考对口高考）为了得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象，只需把函数sin 24y x π⎛⎫=- ⎪⎝⎭的图象上所有的点（）A ．向左平移4π个单位B ．向右平移4π个单位C ．向左平移2π个单位D ．向右平移2π个单位【变式3-2】（2022·陕西汉中·统考一模）为得到函数cos 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将sin2y x =的图象（）A ．向左平移512π个单位长度B ．向右平移512π个单位长度C ．向左平移23π个单位长度D ．向右平移23π个单位长度【变式3-3】（2023秋·江苏南通·高三统考期末）已知函数π()3sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭的图象向左平移()0ϕϕ>个单位长度后与其导函数()y f x '=的图象重合，则()f ϕ的值为（）A ．0B ．32C ．62D ．32【变式3-4】（2022·全国·模拟预测）已知函数()3sin cos f x x x =-的图象向左平移ϕ（0ϕ>）个单位长度后得到()f x 的导函数()f x '的图象，则()f ϕ=（）A ．3-B ．3C ．1D ．1-【变式3-5】（2023·河南信阳·河南省信阳市第二高级中学校联考一模）将函数()sin 2c 2πos π63f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭图象上的所有点的横坐标缩短为原来的12（纵坐标不变），然后再将其图象向左平移()0θθ>单位得到图象()g x ，若函数()g x 图象关于y 轴对称，则θ的最小值为（）A ．π3B ．π6C ．π12D ．π24【题型4三角函数的四种性质】【例4】（2023秋·河南南阳·高三统考期末）已知函数()()()sin cos f x x x ϕϕ=+++是偶函数,则3sin 2cos 2sin 3cos ϕϕϕϕ-=+______．【变式4-1】（2023秋·河北邢台·高三邢台市第二中学校考期末）函数9cos 24y x π⎛⎫=- ⎪⎝⎭的单调递减区间为______.【变式4-2】（2022秋·辽宁沈阳·高三沈阳市第一二〇中学校考期中）已知函数()tan tan f x x x =+，则下列结论中正确的是（）A ．()f x 的最小正周期为π2B ．点π,02⎛⎫- ⎪⎝⎭是()f x 图象的一个对称中心C ．()f x 的值域为[)0,∞+D ．不等式()2f x >的解集为()ππ2,2πZ 42k k k π⎛⎫++∈ ⎪⎝⎭【变式4-3】（2023·四川内江·统考一模）已知函数()()1sin cos sin (0)2f x x x x ωωωω=-+>，若函数()f x 在π,π2⎛⎫⎪⎝⎭上单调递减，则ω不能取（）A ．23B ．13C ．58D ．14【变式4-4】（2023秋·江苏南通·高三统考期末）（多选）设函数()()sin f x x ωϕ=+，x ∈R ，其中0ω>，3πϕ<.若1409f π⎛⎫-= ⎪⎝⎭，419f π⎛⎫=⎪⎝⎭，且()f x 的最小正周期大于52π，则（）A ．14ω=B ．6πϕ=C ．()f x 在()2,3ππ上单调递增D ．()f x 在()0,3π上存在唯一的极值点【变式4-5】（2023·安徽淮南·统考一模）（多选）已知函数()()πsin ,12,2f x x ωϕωϕ⎛⎫=+<<< ⎪⎝⎭图像过点10,2⎛⎫- ⎪⎝⎭，且存在12,x x ，当122πx x -=时，()()120f x f x ==，则（）A ．()f x 的周期为4π3B ．()f x 图像的一条对称轴方程为5π9x =-C ．()f x 在区间4π10π,99⎡⎤⎢⎣⎦上单调递减D ．()f x 在区间()0,5π上有且仅有4个极大值点【变式4-6】（2023秋·湖北·高三统考期末）（多选）已知函数()2sin sin 2f x x x =，则下列说法正确的是（）A ．π是()f x 的一个周期B ．()f x 的图象关于点π,02⎛⎫⎪⎝⎭中心对称C ．()f x 在区间[]0,2π上的零点个数为4D ．()f x 的最大值为8【变式4-7】（2023春·浙江·高三校联考开学考试）（多选）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则（）A ．()0f =B ．()f x 的最小正周期为π2C ．()f x 在π0,6⎛⎫⎪⎝⎭上单调递减D ．()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增【题型5三角函数的最值问题】【例5】（2022秋·北京·高三北京市八一中学校考阶段练习）定义运算,,,.a a b a b b a b ≤⎧=⎨>⎩※例如，121=※，则函数()sin cos f x x x =※的值域为（）A ．1,2⎡⎤-⎢⎥⎣⎦B ．22⎡⎤⎢⎥⎣⎦C ．2,12⎡⎤⎢⎥⎣⎦D ．22⎡-⎢⎣⎦【变式5-1】（2023秋·湖南株洲·已知定义域为R 的函数(),()f x g x 满足()()πf x f x +=-，且()()cos π,g x x f x =++()()sin πf x x g x =-+，则当π0,4x ⎡⎤∈⎢⎥⎣⎦时，函数()()y f x g x =的最小值为（）A ．0B ．2CD ．38【变式5-2】（2022秋·安徽·高三石室中学校联考阶段练习）如图是函数()cos()(0)f x x ωϕω=+>的部分图象，则()f x 在,9045⎡⎤-⎢⎥⎣⎦π22π上的值域为（）A ．[]1,1-B ．1322⎡⎢⎣⎦C ．11,2⎡⎤-⎢⎥⎣⎦D ．32⎡-⎢⎣⎦【变式5-3】（2023·河北衡水·河北衡水中学校考模拟预测）函数()25cos 4sin 53cos f x x x x -+的最大值为（）.A ．22B ．23C ．5D ．3【变式5-4】（2023秋·北京丰台·高三统考期末）已知函数π()sin (0)6f x x ωω⎛⎫=+>⎪⎝⎭，若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，且()f x 在区间ππ,62⎛⎫⎪⎝⎭上有最小值无最大值，则ω=___________．【变式5-4】（2020秋·吉林白城·高三校考阶段练习）已知向量1(cos ,)2a x = ，(3,cos 2),Rb x x x =∈，设函数()f x a b =⋅ ．（1）求()f x 的最小正周期；（2）求()f x 在π[0,]2上的最大值和最小值．【题型6三角函数的零点问题】【例6】（2022·四川宜宾·统考模拟预测）若函数()π2sin 213f x x ⎛⎫=+- ⎪⎝⎭，则()f x 在区间[]0,2π上零点的个数是_______．【变式6-1】（2023·全国·高三对口高考）已知0ω>，函数()πsin 16f x x ω⎛⎫=+- ⎪⎝⎭在区间[]0,π上有且仅有两个零点，则ω的取值范围是________．【变式6-2】（2022秋·河南濮阳·高三统考阶段练习）已知函数5π()cos (0)6f x x ωω⎛⎫=-> ⎪⎝⎭在π0,4⎛⎫⎪⎝⎭上有且仅有1个零点，则实数ω的取值范围为______.【变式6-3】（2023秋·福建宁德·高三校考阶段练习）若函数()1cos42f x x x m =-+-在π04⎡⎤⎢⎥⎣⎦，上存在两个零点，则实数m 的取值范围为（）A ．3522⎛⎤ ⎥⎝⎦，B ．3522⎡⎫⎪⎢⎣⎭，C．1522⎛⎤+ ⎥⎝⎦，D．1522⎡⎫+⎪⎢⎪⎣⎭，【变式6-4】（2023秋·山西·高三校联考阶段练习）已知函数()()221sin 2π,,3213,,x a x a f x x a x a x a ⎧⎡⎤⎛⎫-+<⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪-+++≥⎩.若()f x 在()0,∞+上恰好有5个零点，则a 的取值范围是（）A ．411,36⎡⎫⎪⎢⎣⎭B ．411717,,3636⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦C ．1167,3⎡⎫⎪⎢⎣⎭D ．43117,,3263⎛⎤⎛⎤⋃ ⎝⎦⎝⎦【变式6-5】（2022秋·广西桂林·高三校考阶段练习）已知定义在R 上的函数()y f x =是偶函数，当0x ≥时，()2sin ,01213,122x x x f x x π⎧≤≤⎪⎪=⎨⎛⎫⎪+> ⎪⎪⎝⎭⎩，若关于x 的方程()()()20,R f x af x b a b ++=∈⎡⎤⎣⎦，有且仅有6个不同实数根，则实数a 的取值范围是（）A ．34,2⎛⎫-- ⎪⎝⎭B ．74,2⎛⎫-- ⎪⎝⎭C ．7734,222⎛⎫⎛⎫--⋃-- ⎪⎝⎭⎝⎭D ．324,1,27⎛⎫⎛⎫--⋃-- ⎪ ⎪⎝⎭⎝⎭【变式6-6】（2023秋·山东烟台·高三统考期末）已知定义在R 上的函数()f x 满足：2f x π⎛⎫- ⎪⎝⎭为偶函数，且()()8sin ,021,02x x f x f x x ππ⎧--≤≤⎪⎪=⎨⎪->⎪⎩；函数()lg 2g x x π=+，则当[]4,3x ππ∈-时，函数()()y f x g x =-的所有零点之和为（）A ．7π-B ．6π-C ．72π-D ．3π-（建议用时：60分钟）1．（2022秋·河北唐山·高三开滦第二中学校考阶段练习）将函数()π3cos (0)6f x x ωω⎛⎫=+> ⎪⎝⎭的图象向右平移π6ω个单位长度，得到函数()g x 的图象，若函数()y g x =在π3π,24⎡⎤⎢⎥⎣⎦上单调递增，则ω的最大值为（）A ．2B ．83C ．103D ．42．（2022秋·广西钦州·高三校考阶段练习）已知函数()()sin f x x ϕ=-且2cos πcos 3ϕϕ⎛⎫-= ⎪⎝⎭，则函数()f x 的图象的一条对称轴是（）A ．5π6x =B ．7π12x =C ．π3x =D ．π6x =3．（2023·四川绵阳·统考模拟预测）函数()πcos()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图像如图所示，且()302f =．则下列选项正确的是（）A ．π3ϕ=-B ．π122f ⎛⎫=-⎪⎝⎭C ．()f x 在区间2π,π3⎡⎤⎢⎥⎣⎦上为减函数D ．()102f f ⎛⎫> ⎪⎝⎭4．（2023·全国·高三专题练习）已知函数π()2sin (0)6f x x ωω⎛⎫=-> ⎪⎝⎭在[]0,π上单调递增，且2π()3f x f ⎛⎫≥-⎪⎝⎭恒成立，则ω的值为（）A ．2B ．32C ．1D ．125．（2022·四川成都·成都市第二十中学校校考一模）已知函数()πsin 23f x x ⎛⎫=- ⎪⎝⎭，则下列结论不正确的是（）A ．π为函数()f x 的一个周期B ．2π,03⎛⎫⎪⎝⎭是函数()f x 图象的一个对称中心C ．函数()f x 在区间[],a a -上单调递增，则实数a 的最大值为5π12D ．将函数()f x 的图象向右平移π12个单位长度后，得到一个偶函数的图象6．（2022·河北衡水·衡水市第二中学校考一模）已知()()()π2tan 0,,02f x x f ωϕωϕ⎛⎫=+><= ⎪⎝，周期π3ππ,,446T ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭是()f x 的对称中心，则π3f ⎛⎫⎪⎝⎭的值为（）A ．BC D ．3-7．（2023秋·山东东营·高三东营市第一中学校考期末）（多选）关于函数2()cos 4cos 1f x x x =++，下列说法正确的是（）A ．函数()f x 在π3π,42⎡⎤⎢⎥⎣⎦上的最大值为6B ．函数()f x 在π3π,42⎡⎤⎢⎥⎣⎦上的最小值为-2C ．函数()f x 在π,02⎛⎫- ⎪⎝⎭上单调递增D ．函数()f x 在π0,2⎛⎫⎪⎝⎭上单调递减8．（2022秋·河北唐山·高三开滦第二中学校考阶段练习）（多选）设()sin 22cos f x x x =+，x ∈R ，则（）.A ．()f x 在区间[]0,2π上有2个零点B ．()f x 的单调递增区间为π7ππ,π26k k ⎛⎫++⎪⎝⎭，k ∈Z C ．()f x 的图象关于直线ππ3x k =+对称D ．()f x 的值域为0,2⎡⎢⎣⎦9．（2023·湖南长沙·统考一模）已知函数()()()2sin 0f x x ωϕω=+>,若函数()f x 的图象关于点π,06⎛⎫⎪⎝⎭中心对称,且关于直线π3x =轴对称,则ω的最小值为______．10．（2022秋·四川遂宁·高三校考阶段练习）已知函数()()7ππsin 12f x x x ⎛⎫=---+ ⎪⎝⎭则函数()f x 的对称中心_________11．（2021·上海浦东新·华师大二附中校考模拟预测）已知函数23()sin sin cos (,,0)2f x a x x x a b a b a =-+<，（1）若当π0,2x ⎡⎤∈⎢⎥⎣⎦时，函数()f x 的值域为[]5,1-，求实数,a b 的值；（2）在（1）条件下，求函数()f x 图像的对称中心和单调区间.12．（2023秋·江苏扬州·高三校联考期末）已知函数()()(0,0f x x ωϕωϕ=+><<sin π的最小正周期为π，且直线π2x =-是其图像的一条对称轴.（1）求函数()f x 的解析式；（2）将函数()y f x =的图像向右平移π4个单位，再将所得的图像上每一点的纵坐标不变，横坐标伸长为原来的2倍后所得到的图像对应的函数记作()y g x =，已知常数R λ∈，*n ∈N ，且函数()()212sin F x x g x λ=-+在()0,πn 内恰有2021个零点，求常数λ与n 的值.参考答案【题型1三角函数的图象辨析】【例1】（2023·湖南湘潭·统考二模）函数2cos2()sin xf x x+=的部分图象大致为（）A ．B ．C ．D ．【答案】A【解析】()f x 的定义域为{}π,Z x x k k ≠∈，关于原点对称，因为2cos(2)2cos2()()sin()sin x xf x f x x x+-+-==---，所以()f x 为奇函数，故排除C,D ,又π102f ⎛⎫=> ⎪⎝⎭，所以排除B,故选：A【变式1-1】（2023秋·云南·高三云南师大附中校考阶段练习）函数()21sin 2f x x x x =-的图象大致为（）A ．B ．C ．D ．【答案】A【解析】()f x 的定义域为R ，2211()()()sin()sin ()22f x x x x x x x f x -=----=-=，所以()f x 为偶函数，图象关于y 轴对称，排除C ，D 选项；()21ππ02f =>，排除B 选项.所以A 选项正确.故选：A【变式1-2】（2022秋·河南·高三校联考阶段练习）函数()cos e =xf x 的部分图象大致为（）A ．B ．C ．D ．【答案】C【解析】由题意得函数定义域为R ，且()()()cos cos ee --===x xf x f x ，∴()f x 为偶函数，故排除选项B ，∵()()cos e2πe xf x f k =≤=，Z k ∈，()0e f =为最大值，∴排除选项D ，∵()()()cos 2πcos 2πee x xf x f x ++===，∴()f x 是2π为周期的周期函数，∴排除选项A.故选：C【变式1-3】（2022秋·云南·高三校联考阶段练习）函数()cos ln xf x x xππ+=⋅-在(),ππ-上的图象大致为（）A ．B ．C ．D ．【答案】B【解析】因为()()cos lnxf x x f x xππ--=⋅=-+，所以f （x ）是奇函数，排除A ，D ，当0,2x π⎛⎫∈ ⎪⎝⎭时，cos 0x >，ln0xxπ+>π-，所以()0f x >，排除C ，故选：B ．【变式1-4】（2022秋·四川遂宁·高三遂宁中学校考阶段练习）函数()(tan sin 2)22x x y x x -=--的部分图象大致为（）A ．B ．C ．D ．【答案】A【解析】由题得函数的定义域为π{|π,}2x x k k Z ≠+∈，定义域关于原点对称.设()()(tan sin 2)22x xf x x x -=--，所以()()(tan sin 2)22x x f x x x --=-+-()(tan sin 2)22()x xx x f x -=--=，所以函数()f x 是偶函数，其图象关于y 轴对称，排除选项D.又(π)=0f ，所以排除选项B.当π2x →时，tan ,sin 20,x x →+∞→()220x x-->，所以此时()0f x >.故选：A【题型2根据图象求三角函数解析式】【例2】（2023秋·湖南怀化·高三统考期末）已知函数()2cos()(0)f x x ωϕω=+>的部分图象如图所示，则()0f =（）A ．1B ．1-CD ．【答案】C【解析】观察函数图象得，函数()f x 的周期413()3123T πππ=-=，则22Tπω==，而13212f π⎛⎫= ⎪⎝⎭，即13cos 16πϕ⎛⎫+= ⎪⎝⎭，则有132,Z 6k k πϕπ+=∈，因此132Z 6k k πϕπ=-∈，即有13()2cos(22)2cos(2)66f x x k x πππ=+-=-，所以()02cos()6f π=-故选：C【变式2-1】（2022秋·贵州铜仁高三校考阶段练习）已知A ，B ，C ，D ，E 是函数sin()y x ωϕ=+0,02πωϕ⎛⎫><< ⎪⎝⎭一个周期内的图像上的五个点，如图，A ,06π⎛⎫- ⎪⎝⎭，B 为y 轴上的点，C 为图像上的最低点，E 为该函数图像的一个对称中心，B 与D 关于点E 对称，CD在x 轴上的投影为12π，则ωφ，的值为（）A ．2ω=，3πϕ=B ．2ω=，6πϕ=C ．12ω=，3πϕ=D ．12ω=，6πϕ=【答案】A【解析】因B 与D 关于点E 对称，CD 在x 轴上的投影为12π，则B 与图像最高点（最靠近B 点）连线所对应向量在x 轴上的投影为12π，又A ,06π⎛⎫- ⎪⎝⎭，则A 与图像最高点(最靠近B 点)连线对应向量在x 轴上的投影为πππ6124+=，故函数最小正周期为24πππ=4ω⨯=，又0ω>，则2ω=.又因函数图像过点,06π⎛⎫- ⎪⎝⎭，则2ππ,Z 3φk k -+=∈，得2ππ,Z 3φk k =+∈，又02πϕ<<，则0k =，得π3ϕ=.综上，有2ω=，π3ϕ=.故选：A【变式2-2】（2023秋·山西太原·高三山西大附中校考阶段练习）函数()sin()(0,0)f x x ωϕωϕπ=+><<的部分图象如图，BC x ∥轴，当π0,4x ⎡⎤∈⎢⎥⎣⎦时，若不等式()sin 2f x m x ≥-恒成立，则的取值范围是（）A ．⎛-∞ ⎝⎦B ．1,2⎛⎤-∞ ⎥⎝⎦C ．(-∞D ．(],1-∞【答案】A【解析】因为//BC x 轴，所以()f x 图象的一条对称轴方程为1π2π7π()22312x =+=，所以7πππ41234T =-=，则πT =，所以2π2T ω==，又π2π2π3k ϕ⨯+=+，Z k ∈，且0πϕ<<，所以π3ϕ=，故π()sin(23f x x =+，因为当π[0,]4x ∈时，不等式()sin 2f x m x ≥-恒成立，所以π3π()sin 2sin(2)sin 2sin 2cos 2sin(2)3226m f x x x x x x x ≤+=++=++，令()π26g x x ⎛⎫=+ ⎪⎝⎭，因为π0,4x ⎡⎤∈⎢⎥⎣⎦，则ππ2π2,663x ⎡⎤+∈⎢⎥⎣⎦，所以π1sin 2,162x ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦所以π())6g x x +的最小值为2，所以2m ≤，即m ⎛∈-∞ ⎝⎦．故选：A ．【变式2-3】（2023秋·北京朝阳·高三统考期末）已知函数π()sin()0,||2ωϕωϕ⎛⎫=+>< ⎪⎝⎭f x x ，若()()1g x f x ⋅=，且函数()g x 的部分图象如图所示，则ϕ等于（）A ．π3-B ．π6-C ．π6D ．π3【答案】B【解析】由图可知，函数()g x 过点π,13⎛⎫⎪⎝⎭和点5π,16⎛⎫- ⎪⎝⎭，即π135π16g g⎧⎛⎫= ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩，又因为()()1g x f x ⋅=，所以π135π16f f ⎧⎛⎫= ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩，结合正弦型函数的性质可知，5ππ263T =-，解得πT =，所以2ππω=，解得2ω=±，因为0ω>，所以2ω=所以()sin(2)f x x ϕ=+，所以πsin(2)13ϕ⨯+=，即2ππ2π32k ϕ+=+，Z k ∈解得π2π6k ϕ=-+，Zk ∈因为π||2ϕ<，所以π6ϕ=-，故选：B.【变式2-4】（2023·全国·模拟预测）（多选）已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，若将()f x 的图象向右平移()0m m >个单位长度后得到函数()()sin 2g x A x ωϕ=-的图象，则m 的值可以是（）A ．π4B ．π3C ．4π3D ．9π4【答案】AD【解析】由图象可知：2A =，最小正周期5ππ4π126T ⎛⎫=⨯-=⎪⎝⎭，2π2T ω∴==，ππ2sin 263f ϕ⎛⎫⎛⎫∴=+= ⎪ ⎪⎝⎭⎝⎭，()ππ2π32k k ϕ∴+=+∈Z ，解得：()π2π6k k ϕ=+∈Z ，又π2ϕ<，π6ϕ∴=，()π2sin 26f x x ⎛⎫∴=+ ⎪⎝⎭，()π2sin 23g x x ⎛⎫=- ⎪⎝⎭，()()π2sin 226f x m x m g x ⎛⎫-=-+= ⎪⎝⎭ ，()ππ22π63m k k ∴-+=-+∈Z ，解得：()ππ4m k k =-∈Z ，当0k =时，π4m =；当2k =-时，9π4m =.故选：AD.【题型3三角函数图象变换问题】【例3】（2023秋·江西赣州·高三统考期末）函数()()sin f x x ωϕ=+（其中0ω>，π2ϕ<）的图象如图所示，为了得到cos y x ω=的图象，只需把()y f x =的图象上所有点（）A ．向左平移π6个单位长度B ．向右平移π12个单位长度C ．向左平移π12个单位长度D ．向右平移π6个单位长度【答案】C【解析】由图象可知，712344Tπππ-==，所以T π=，又因为2T πω=，所以2ω=，所以()()sin 2f x x ϕ=+，又因为771,sin 211212f ππϕ⎛⎫⎛⎫=-∴⨯+=-⎪ ⎪⎝⎭⎝⎭，又||2ϕπ<，所以,3πϕ=所以()sin 2cos 2cos 2cos 2332612f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=+=+-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭又因为()cos 2g x x =，所以只需把()y f x =的图象上所有点向左平移π12个单位长度可得()cos 2g x x=的图象.故选：C.【变式3-1】（2022·四川·高三统考对口高考）为了得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象，只需把函数sin 24y x π⎛⎫=- ⎪⎝⎭的图象上所有的点（）A ．向左平移4π个单位B ．向右平移4π个单位C ．向左平移2π个单位D ．向右平移2π个单位【答案】A【解析】依题意，sin(2)sin(2)sin[2()]42444y x x x πππππ=+=+-=+-，所以把函数sin 24y x π⎛⎫=- ⎪⎝⎭图象上所有的点向左平移4π个单位可以得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象，A 正确.故选：A 【变式3-2】（2022·陕西汉中·统考一模）为得到函数cos 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将sin2y x =的图象（）A ．向左平移512π个单位长度B ．向右平移512π个单位长度C ．向左平移23π个单位长度D ．向右平移23π个单位长度【答案】A【解析】555cos 2cos 2sin 2sin 2362612y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+=+-=+=+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦故可由sin2y x =的图象向左平移512π个单位长度得到.故选：A.【变式3-3】（2023秋·江苏南通·高三统考期末）已知函数π()sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭的图象向左平移()0ϕϕ>个单位长度后与其导函数()y f x '=的图象重合，则()f ϕ的值为（）A ．0B ．2C ．2D ．32【答案】D【解析】因为π()sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭，所以()ππcos sin (0)63f x x x ωωω⎛⎫⎛⎫=-=+> ⎪ ⎪⎝⎭⎝⎭'，而函数()f x 的图象向左平移()0ϕϕ>个单位长度后得到()()ππsin (0)66f x x x ϕωϕωωϕω⎡⎤⎛⎫++-+-> ⎪⎢⎥⎣⎦⎝⎭，由题意得()()f x f x ϕ+='，所以ππ2π,Z 63k k ωϕ=⎨-=+∈⎪⎩,解得1π2π,Z 2k k ωϕ=⎧⎪⎨=+∈⎪⎩且0ϕ>，所以πππ3()2π2632f k ϕ⎛⎫=+-= ⎪⎝⎭，故选：D 【变式3-4】（2022·全国·模拟预测）已知函数()3sin cos f x x x =-的图象向左平移ϕ（0ϕ>）个单位长度后得到()f x 的导函数()f x '的图象，则()f ϕ=（）A ．3-B ．3C ．1D ．1-【答案】B【解析】因为()3sin cos f x x x =-，所以()3cos sin f x x x =+'，而()()()3sin cos 3sin cos 3cos sin cos cos sin sin f x x x x x x x ϕϕϕϕϕϕϕ+=+-+=+-+()()3cos sin sin 3sin cos cos x x ϕϕϕϕ=++-⋅，由题意得()()f x f x ϕ+='，所以3cos sin 13sin cos 3ϕϕϕϕ+=⎧⎨-=⎩,解得sin 1cos 0ϕϕ=⎧⎨=⎩，所以()3sin cos 3f ϕϕ=-=，故选：B.另解：因为()3sin cos f x x x =-，所以()3cos sin f x x x =+'，由题意知()()f x f x ϕ+='对一切实数x 恒成立，所以令0x =，得()()03cos 0sin 03f f ϕ'==+=，故选：B.【变式3-5】（2023·河南信阳·河南省信阳市第二高级中学校联考一模）将函数()sin 2c 2πos π63f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭图象上的所有点的横坐标缩短为原来的12（纵坐标不变），然后再将其图象向左平移()0θθ>单位得到图象()g x ，若函数()g x 图象关于y 轴对称，则θ的最小值为（）A ．π3B ．π6C ．π12D ．π24【答案】C 【解析】()πsin 2cos 2sin 2co i ππs 22s n26366πππ62f x x x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++-=+++-=+ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,由()π2sin 26f x x ⎛⎫=+ ⎪⎝⎭，横坐标缩短为原来的12（纵坐标不变）得到π2sin 46⎛⎫=+ ⎪⎝⎭y x ，将其图象向左平移()0θθ>单位得到图象()46π2sin 4g x x θ⎛⎫=++ ⎪⎝⎭，而()g x 图象关于y 轴对称，∴4π,Z 6π2πk k θ+=+∈，∵0θ>，∴当0k =时，θ取最小值π12.故选：C.【题型4三角函数的四种性质】【例4】（2023秋·河南南阳·高三统考期末）已知函数()()()sin cos f x x x ϕϕ=+++是偶函数,则3sin 2cos 2sin 3cos ϕϕϕϕ-=+______．【答案】15【解析】由题知数()()()sin cos f x x x ϕ=+++是R 上偶函数，所以()()ππ22f f =-,即()()()()ππππsin cos sin cos 2222ϕϕϕϕ+++=-++-+，即cos sin cos sin ϕϕϕϕ-=-+，即cos sin ϕϕ=，tan 1ϕ=,所以3sin 23sin 2cos 321cos 2sin 2sin 3cos 2353cos ϕϕϕϕϕϕϕϕ---===+++.故答案为:15【变式4-1】（2023秋·河北邢台·高三邢台市第二中学校考期末）函数9cos 24y x π⎛⎫=- ⎪⎝⎭的单调递减区间为______.【答案】()π5ππ,πZ 88k k k ⎡⎤++∈⎢⎥⎣⎦【解析】由9πcos 24y x ⎛⎫=-⎪⎝⎭＝cos π24x ⎛⎫- ⎪⎝⎭＝cos π24x ⎛⎫- ⎪⎝⎭，得2kπ≤2x －4π≤2k π＋π(k ∈Z )，解得kπ＋π8≤x ≤kπ＋58π(k ∈Z )，所以函数的单调递减区间为π5ππ,π88k k ⎡⎤++⎢⎥⎣⎦(k ∈Z ).故答案为：()π5ππ,πZ 88k k k ⎡⎤++∈⎢⎥⎣⎦.【变式4-2】（2022秋·辽宁沈阳·高三沈阳市第一二〇中学校考期中）已知函数()tan tan f x x x =+，则下列结论中正确的是（）A ．()f x 的最小正周期为π2B ．点π,02⎛⎫- ⎪⎝⎭是()f x 图象的一个对称中心C ．()f x 的值域为[)0,∞+D ．不等式()2f x >的解集为()ππ2,2πZ 42k k k π⎛⎫++∈ ⎪⎝⎭【答案】C【解析】()π2tan ,[π,π),Z 2tan tan π0,(π,π),Z 2x x k k k f x x x x k k k ⎧∈+∈⎪⎪=+=⎨⎪∈-+∈⎪⎩，作出()f x的图象，如图，观察图象，()f x 的最小正周期为π，A 错误；()f x 的图象没有对称中心，B 错误；()f x 的值域为[)0,∞+，C 正确；不等式()2f x >，即π[π,π)(Z)2x k k k ∈+∈时，2tan 2x >，得tan 1x >，解得ππππ,Z 42k x k k +<<+∈，所以()2f x >的解集为ππ(π,π)()42Z k k k +∈+，故D 错误.故选：C【变式4-3】（2023·四川内江·统考一模）已知函数()()1sin cos sin (0)2f x x x x ωωωω=-+>，若函数()f x 在π,π2⎛⎫⎪⎝⎭上单调递减，则ω不能取（）A ．23B ．13C ．58D ．14【答案】A【解析】因为()()1sin cos sin 2f x x x x ωωω=-+21sin cos sin 2x x x ωωω=⋅-+11cos 21sin 2222x x ωω-=-+1(sin 2cos 2)2x x ωω=+(sin 2cos 2)222x x ωω=⋅⋅π)4x ω=+由ππ3π2π22π242k x k ω+≤+≤+，Z k ∈，得ππ5ππ88k k x ωωωω+≤≤+，Z k ∈，所以函数()f x 的单调递减区间为ππ5ππ,88k k ωωωω⎡⎤++⎢⎥⎣⎦()k ∈Z .又函数()f x 在π,π2⎛⎫ ⎪⎝⎭上单调递减，所以π,π2⎛⎫ ⎪⎝⎭⊆ππ5ππ,88k k ωωωω⎡⎤++⎢⎥⎣⎦()k ∈Z ，所以πππ825πππ8k k ωωωω⎧+≤⎪⎪⎨⎪+≥⎪⎩，Z k ∈，因为0ω>，所以15248k k ω+≤≤+，Z k ∈，当23ω=时，得1252438k k +≤≤+，得152424k ≤≤，不成立；所以23ω=不可取；当13ω=时，得1152438k k +≤≤+，得712412k -≤≤,因为Z k ∈，所以0k =时，13ω=可取到；当58ω=时，得1552488k k +≤≤+，得3016k ≤≤，因为Z k ∈，所以0k =时，58ω=可取到；当14ω=时，得1152448k k +≤≤+，得308k -≤≤，因为Z k ∈，所以0k =时，14ω=可取到.综上所述：ω不能取23.故选：A【变式4-4】（2023秋·江苏南通·高三统考期末）（多选）设函数()()sin f x x ωϕ=+，x ∈R ，其中0ω>，3πϕ<.若1409f π⎛⎫-= ⎪⎝⎭，419f π⎛⎫= ⎪⎝⎭，且()f x 的最小正周期大于52π，则（）A ．14ω=B ．6πϕ=C ．()f x 在()2,3ππ上单调递增D ．()f x 在()0,3π上存在唯一的极值点【答案】BC【解析】函数()()sin f x x ωϕ=+的最小正周期为T ，由1409f π⎛⎫-= ⎪⎝⎭及419f π⎛⎫= ⎪⎝⎭得：414(21)()2,N 499T k k πππ*⋅-=--=∈，则8,N 21T k k π*=∈-，而52T π>，即有5822,N 1k k ππ*>∈-，解得21,N 10k k *<∈，即1k =或2k =，当1k =时，18,4T πω==，由419f π⎛⎫= ⎪⎝⎭得1114,Z 492k k ππϕπ⨯+=+∈，有117,Z 18k k πϕπ=+∈，而3πϕ<，显然不存在整数1k ，使得3πϕ<，当2k =时，83,34T πω==，由419f π⎛⎫= ⎪⎝⎭得2234,Z 492k k ππϕπ⨯+=+∈，有22,Z 6k k πϕπ=+∈，而3πϕ<，于是得20,6k πϕ==，符合题意，所以83,,346T ππωϕ===，A 不正确，B 正确；3()sin()46f x x π=+，当23x ππ<<时，532934612x πππ<+<，而函数sin y x =在529(,)312ππ上单调递增，所以函数()f x 在()2,3ππ上单调递增，C 正确；当03x π<<时，32964612x πππ<+<，而函数sin y x =在29(,)612ππ上两个极值点，一个极大值点，一个极小值点，所以函数()f x 在()0,3π上有两个极值点，一个极大值点，一个极小值点，D 不正确.故选：BC【变式4-5】（2023·安徽淮南·统考一模）（多选）已知函数()()πsin ,12,2f x x ωϕωϕ⎛⎫=+<<< ⎪⎝⎭图像过点10,2⎛⎫- ⎪⎝⎭，且存在12,x x ，当122πx x -=时，()()120f x f x ==，则（）A ．()f x 的周期为4π3B ．()f x 图像的一条对称轴方程为5π9x =-C ．()f x 在区间4π10π,99⎡⎤⎢⎣⎦上单调递减D ．()f x 在区间()0,5π上有且仅有4个极大值点【答案】ACD【解析】因为()f x 图像过点10,2⎛⎫- ⎪⎝⎭且π2ϕ<，所以1sin 2ϕ=-，解得π6ϕ=-，因为存在12,x x ，当122πx x -=时，()()120f x f x ==，所以π2π2T k k ω⋅==，即2k ω=，*N k ∈，又因为12ω<<，所以32ω=，所以()3πsin 26f x x ⎛⎫=-⎪⎝⎭，选项A ：()f x 的周期2π4π332T ==，正确；选项B ：()f x 图像的对称轴为3πππ262x k -=+，解得4π2π93kx =+，Z k ∈，令5π4π2π993k-=+，k 无整数解，B 错误；选项C ：当4π10π,99x ⎡⎤∈⎢⎥⎣⎦时，3ππ3π,2622x ⎡⎤-∈⎢⎣⎦，所以由正弦函数的图像和性质可得()f x 在区间4π10π,99⎡⎤⎢⎥⎣⎦上单调递减，C正确；选项D ：当()0,5πx ∈时，3ππ22π,2663x ⎛⎫-∈- ⎪⎝⎭，所以由正弦函数的图像和性质可得()f x 在区间()0,5π有4个极大值点，3个极小值点，D 正确；故选：ACD【变式4-6】（2023秋·湖北·高三统考期末）（多选）已知函数()2sin sin 2f x x x =，则下列说法正确的是（）A ．π是()f x 的一个周期B ．()f x 的图象关于点π,02⎛⎫ ⎪⎝⎭中心对称C ．()f x 在区间[]0,2π上的零点个数为4D ．()f x 的最大值为8【答案】ABD 【解析】对于A ，因为()2(π)sin (π)sin 2(π)f x x x +=++()22sin sin 2sin sin 2()x x x x f x =-==，所以π是()f x 的一个周期，故A 正确；对于B ，()2π(2)(π)sin (π)sin 2(π)2f x f x x x ⨯-=-=--22sin sin(2)sin sin 2()x x x x f x =-=-=-，所以()f x 的图象关于点π,02⎛⎫⎪⎝⎭中心对称，故B 正确；对于C ，由()2sinsin 2f x x x =0=，得πx k =或2πx k =，Z k ∈，得πx k =或π2k x =，Z k ∈，由0π2πk ≤≤及Z k ∈得0k =或1k =或2k =，所以0x =或2πx =或πx =，由π02π2k ≤≤及Z k ∈得0k =或1k =或2k =或3k =或4k =，所以0x =或π2x =或πx =或3π2x =或2πx =，所以()f x 在区间[]0,2π的零点为0x =，π2x =，πx =，3π2x =，2πx =,共5个,故C 错误；对于D ，()2sinsin 2f x x x =2sin 2sin cos x x x =⋅32sin cos x x =，所以()262()4sin cos f x x x =624sin (1sin )x x =-，设2sin [0,1]t x =∈，34(1)y t t =-3444(01)t t t =-≤≤，则23212164(34)y t t t t '=-=-，令0'>y ，得304t <<，令0'<y ，得314t <≤，所以3444(01)y t t t =-≤≤在3[0,)4上为增函数，在3(,1]4上为减函数，所以当3t 4=时，y 取得最大值为333274(1)4464⎛⎫⨯-= ⎪⎝⎭，0=t 或1t =时，y 取得最小值为0，所以()2()f x y =27[0,64∈，所以()[f x ∈，所以()f x D 正确；故选：ABD 【变式4-7】（2023春·浙江·高三校联考开学考试）（多选）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则（）A ．()0f =B ．()f x 的最小正周期为π2C ．()f x 在π0,6⎛⎫ ⎪⎝⎭上单调递减D ．()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增【答案】BD【解析】()ππ0tan tan 66f ⎛⎫=-=-= ⎪⎝⎭A 错误；函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭的最小正周期为π2T =，故B 正确；π0,6x ⎛⎫∈ ⎪⎝⎭时，2,πππ666x ⎛⎫-∈- ⎪⎝⎭，故()f x 在π0,6⎛⎫⎪⎝⎭上单调递增，故C 错误；π,06x ⎛⎫∈- ⎪⎝⎭时，2,π626ππx ⎛⎫-∈-- ⎪⎝⎭，故()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增，故D 正确．故选：BD ．【题型5三角函数的最值问题】【例5】（2022秋·北京·高三北京市八一中学校考阶段练习）定义运算,,,.a a b a b b a b ≤⎧=⎨>⎩※例如，121=※，则函数()sin cos f x x x =※的值域为（）A．1,2⎡⎤-⎢⎥⎣⎦B．22⎡⎤⎢⎥⎣⎦C．,12⎡⎤⎢⎥⎣⎦D．2⎡-⎢⎣⎦【答案】D【解析】根据题设中的新定义，得()sin ,sin cos cos ,sin cos x x x f x x x x≤⎧=⎨>⎩，由sin cos x x ≤可得sin cos 0x x -≤π04x ⎛⎫-≤ ⎪⎝⎭，所以π2ππ2π4k x k -≤-≤，Z k ∈，即3ππ2π2π+44k x k -≤≤，Z k ∈，由sin cos x x >可得sin cos 0x x ->π04x ⎛⎫-> ⎪⎝⎭，所以π2π2π+π4k x k <-<，Z k ∈，即π5π2π+2π+44k x k <<，Z k ∈，所以()3ππsin ,2π2π,Z 44π5πcos ,2π2π,Z44x k x k k f x x k x k k ⎧-≤≤+∈⎪⎪=⎨⎪+<<+∈⎪⎩，当3ππ2π2π+44x k x k ∈-≤≤，Z k ∈，()()()2πsin 2πsin f x x x f x +=+==，当π5π2π+2π+44x k x k ∈<<，Z k ∈时，()()()2πcos 2πcos f x x x f x +=+==，所以函数()f x 为周期函数，周期为2π，作出函数()f x 在一个周期内的图象（实线部分），观察图象，可知函数()f x 的值域为22⎡-⎢⎣⎦，故选:D.【变式5-1】（2023秋·湖南株洲·高三校联考期末）已知定义域为R 的函数(),()f xg x满足()()πf x f x +=-，且()()cos π,g x x f x =++()()sin πf x x g x =-+，则当π0,4x ⎡⎤∈⎢⎥⎣⎦时，函数()()y f x g x =的最小值为（）A ．0B ．2CD 【答案】A【解析】()cos ()=-g x x f x ，()()()()πcos ππcos +=+-+=-+g x x f x x f x ，所以()sin cos ()f x x x f x =+-，得sin cos ()2x x f x +=，cos sin ()2x xg x -=，所以22cos sin 1()()cos 244x x y f x g x x -===，π0,4x ⎡⎤∈⎢⎥⎣⎦，所以0cos 21x ≤≤，10()()4≤≤f x g x ，得()()y f x g x =的最小值为0.故选：A.【变式5-2】（2022秋·安徽·高三石室中学校联考阶段练习）如图是函数()cos()(0)f x x ωϕω=+>的部分图象，则()f x 在,9045⎡⎤-⎢⎥⎣⎦π22π上的值域为（）A ．[]1,1-B ．122⎡⎢⎣⎦C ．11,2⎡⎤-⎢⎥⎣⎦D ．⎡-⎢⎣⎦【答案】D【解析】由图象知函数的周期13ππ2π230103T ⎛⎫=⨯-=⎪⎝⎭，即2π2π=3ω，即3ω=，由五点对应法得ππ32π+()102k k ϕ⨯+=∈Z ，得π2π+5k ϕ=，则π()cos 35f x x ⎛⎫=+ ⎪⎝⎭，因为π22π,9045x ⎡⎤∈-⎢⎥⎣⎦，所以ππ5π3,563x ⎡⎤+∈⎢⎣⎦，所以πcos 31,52x ⎡⎛⎫+∈-⎢ ⎪⎝⎭⎣⎦.故选：D【变式5-3】（2023·河北衡水·河北衡水中学校考模拟预测）函数()3cos f x x 的最大值为（）.A ．B ．C ．D ．3【答案】D 【解析】2225cos 4sin 59cos 4cos 4sin 5x x x x x -+=--+()()22229cos 4sin 4sin 13cos 2sin 1x x x x x =+-+=+-，所以()3cos f x x ==故()f x 的最大值转化为点()3cos ,2sin P x x 到()0,1A 与()0,2sin B x 的距离之差的最大值，因为1sin 1x -≤≤，22sin 2x -≤-≤，112sin 3x -≤-≤，所以12sin 3PA PB AB x -≤=-≤，当且仅当sin 1x =-时，等号成立，则3PA PB -≤，经检验，此时cos 0x =，()303f x =⨯=，所以()3f x ≤，即()f x 的最大值为3.故选：D.【变式5-4】（2023秋·北京丰台·高三统考期末）已知函数π()sin (0)6f x x ωω⎛⎫=+>⎪⎝⎭，若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，且()f x 在区间ππ,62⎛⎫ ⎪⎝⎭上有最小值无最大值，则ω=___________．【答案】4【解析】由于若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，且()f x 在区间ππ,62⎛⎫ ⎪⎝⎭上有最小值无最大值，πππ6223+=，则πππsin 1336f ω⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭，所以πππ2π,62,Z 362k k k ωω+=-=-∈，又ππππ,62366T ωω=≥-=≤，由于0ω>，所以ω的值为4.故答案为：4。
(完整word版)三角函数图像与性质试题及配套答案
xO y1 2 3三角函数测试题一、选择题1、函数)32sin(2π+=x y 的图象（ ）A ．关于原点对称B ．关于点(－6π,0)对称C ．关于y 轴对称D ．关于直线x=6π对称 2、函数sin(),2y x x R π=+∈是 （ )A ．[,]22ππ-上是增函数 B ．[0,]π上是减函数C ．[,0]π-上是减函数D ．[,]ππ-上是减函数 3、如图，曲线对应的函数是 ( ） A ．y=｜sin x | B ．y=sin ｜x ｜C ．y=－sin ｜x |D ．y=－|sin x |4.下列函数中，最小正周期为π，且图象关于直线3x π=对称的( ）. A 。
)62sin(+=x y B.sin()26x y π=+ C.sin(2)6y x π=- D.sin(2)3y x π=-5.函数)sin(ϕω+=x y 的部分图象如右图,则ω，ϕ可以取的一组值是（ )。
A 。
,24ωϕππ== B.,36ωϕππ==C.5,44ωϕππ==D.,44ωϕππ==6。
要得到3sin(2)4y x π=+的图象，只需将x y 2sin 3=的图象（ ）.A.向左平移4π个单位B.向右平移4π个单位C 。
向左平移8π个单位 D.向右平移8π个单位7。
设tan()2απ+=，则sin()cos()sin()cos()αααα-π+π-=π+-π+（ ）.A.3 B 。
13C 。
1D 。
1- 8。
A 为三角形ABC 的一个内角，若12sin cos 25A A +=，则这个三角形的形状为（ ）.A. 锐角三角形B. 钝角三角形C. 等腰直角三角形D. 等腰三角形9.定义在R 上的函数)(x f 既是偶函数又是周期函数,若)(x f 的最小正周期是π，且当[0,]2x π∈时，x x f sin )(=,则5()3f π的值为（ ）.A.21-B.23 C.23-D 。
2110.函数2cos 1y x =+的定义域是( )。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A、 y sin(3x 2) 2
B、 y sin(3x 6) 2
C、 y sin(3x 2) 2
D、 y sin(3x 6) 2
4..将函数
的图象上所有点的横坐标伸长到原来的 倍（纵坐标不变），
再将所得的图象向左平移 个单位，得到的图象对应的解析式是
（）
3
3
A．3π
B． 4 3
C． 3 2
D． 7 6
6·如果函数 y=sin2x+acos2x 的图象关于直线 x=－ 对称，那么 a 等于（ ）
8
A. 2
B.－ 2
C.1
D.－1
平移问题
1．把曲线 ycosx+2y－1=0 先沿 x 轴向右平移 个单位，再沿 y 轴向下平移 1 个单位，得
3
A．
B．
C.
D.
5.若函数 y=f(x)的图象上每点的纵坐标保持不变，横坐标伸长到原来的 2 倍，然后再将整个
1
图象沿 x 轴向左平移 个单位，沿 y 轴向下平移 1 个单位，得到函数 y= sinx 的图象，则
2
2
y=f(x)是（ ）
1
A.y= sin(2x+ )+x－ )+1
2
到的曲线方程是（ ） A．（1－y）sinx+2y－3=0 C．（y+1）sinx+2y+1=0
B．（y－1）sinx+2y－3=0 D．－(y+1)sinx+2y+1=0
2．将函数 y sin x 的图像上所有的点向右平行移动 个单位长度，再把所得各点的横坐 10
标伸长到原来的 2 倍（纵坐标不变），所得图像的函数解析式是
B． y sin( x 5 )(x R) 2 12
C． y sin( x )(x R) 2 12
D． y sin( x 5 )(x R) 2 24
7..将函数 y sin 2x 的图象向左平移 个单位, 再向上平移 1 个单位,所得图象的函数解 4
（2）f (x)在（0， ）上是增函数，求 ω 最大值。
3
9..已知函数
f(x)=2sin
x(
>0)在区间[
,
]上的最小值是－2，则
的最小值等于（
34
）
2
3
A.
B.
C.2
D.3
3
2
9·.函数 y Asin(x ) （ A,, 为常数， A 0, 0 ）在闭区间[ , 0]上的图象
三角函数图像与性质题型专题
值域
1．函数 y＝cos2x－3cosx＋2 的最小值为（ ）
A.2
B.0
1
C.－
D.6
4
2．函数 y sin2 x sin x 1 的值域为
A． 1,1
B．
5 4
,
1
C．
5 4
,1
D．
1,
5 4
,
3．函数 y 2 cos x 的最大值为________ 2 cos x sin －1
3
4．若 f (x) 2sinx(0 1) 在区间[0, ]上的最大值是 2 ，则 =________. 3
5．使 y sin x （ω＞0）在区间[0，1]至少出现 2 次最大值，则 ω 的最小值为（ ）
A． 5 2
B． 5 4
C．π
D． 3 2
6．函数 y sin(2x )(0 ) 是 R 上的偶函数，则 的值是（ ）
4．函数 f( ) = cos －2的最大值和最小值分别是
4 (A) 最大值 3和最小值 0
4 (C) 最大值 －3和最小值 0
3 (B) 最大值不存在和最小值 4
3 (D) 最大值不存在和最小值－4
参数问题求（和 ）
()
1．已知函数 f (x) sin x ( 0, 0 ) 是 R 上的偶函数，其图象关于点
如图所示，则 =
.
11·已知函数 f (x) sin( x )( 0) 的图象如图所示，则 ＝
14·.若函数
y
cos(x
)
(
0)
的图象相邻两条对称轴间距离为
，则
等于
3
2
．
1
A．
2
B．12
C．2
D．4
关对称轴对称中心的题
1·函数 y＝2sin（x＋ ）图象的一条对称轴方程是( )
M
( 3 4
, 0)
对称，且在区间
0,
2
上是单调函数，求
和
的值
,
2.设 ω＞0，若函数 f(x)=2sinωx 在［－ 3 4 ，］上单调递增，则 ω 的取值范围是 _________.
3． 若函数 f (x) 2sin(2kx ) 的最小正周期T 满足1 T 2 ,则自然数 k 的值为______.
A y sin(2x ) 10
C） y sin(1 x ) 2 10
B y sin(2x ) 5
D y sin(1 x ) 2 20
3.把函数 y f (x) 的图象沿着直线 x y 0 的方向向右下方平移 2 2 个单位，得到函数
y sin 3x 的图象，则 （ ）
3
A．x＝－
2
Ｂ．x＝0
Ｃ．x＝
6
Ｄ．x＝－
6
2
3·. 函数 y sin(2x 5 ) 的一条对称轴方程（ A ） 2
A． x 2
B． x 4
C． x 8
D． x 5 4
2·. f (x) sin 2 x cos 2 x 的图象中相邻的两条对称轴间距离为 （ ）
2
2
1
C.y= sin(2x－ )+1
2
4
1 1
D.y= sin( x+ )+1
2 24
6..将函数 y sin(x )(x R) 的图象上所有的点向左平行移动 个单位长度，再把图象
6
4
上各点的横坐标扩大到原来的 2 倍（纵坐标不变），则所得到的图象的解析式为
A． y sin(2x 5 )(x R) 12
1
A. 0 B.
C.
D.
4
2
7．将函数 y sin 4x 的图象向左平移 个单位，得到 y sin(4x ) 的图象，则 等
12
A． 12
B． 3
C．
3
D．
12
8. f (x) 2 3 sin(3x ) （ω＞0） 3
（1）若 f (x +θ)是周期为 2π 的偶函数，求 ω 及 θ 值; .