应用统计学总复习(计算题)
应用统计学期末复习试卷8套含答案大学期末复习资料

E.样本指标是样本变量的函数
9.销售额与流通费用率,在一定条件下,存在相关关系,这种相关关系属于()。
A.正相关B.单相关
C.负相关D.复相关
E.完全相关
10.职工平均工资上调8%,职工人数减少了10%,则()。
A.平均工资指数为108%B.职工人数指数为90%
6.任何两个总体比较其平均数的代表性时,都可以采用标准差指标。
7.所谓序时平均数就是将同一总体的不同时期的平均数按时间顺序排列起来。
8.全面调查包括普查和统计报表。
9.某地区某年人均工资7500元,这是个相对指标。
10.若逐期增长量每年相等,则其各年的环比发展速度是年年下降的。
四.计算题(20%,每小题10分)
E.平均增长速度
7.某企业产品总成本报告期为183150元,比基期增长10%,单位成本综合指数为104%,则(ABC)。
A.总成本指数为110%
B.产量增长了%
C.基期总成本为166 500元
D.单位成本上升使总成本增加了7 044元
E.产量增产使总成本增加了9 606元
8.简单随机抽取调查单位时其方法有(ABE)。
2.某地区粮食生产资料如表5-21所示。
表5-21某地区粮食生产资料
耕地每公顷生产量分组(千克)
耕地面积(万公顷)
5 250以下
5 250~6 000
6 000~6 375
6 375~6 750
6 750~7 050
7 050~7 500
3.将某地区40个工业企业按产值多少分组而编制的变量数列中,变量值是(D)。
A.产值B.工厂数
C.各组的产值数D.各组的工厂数
统计学计算题复习(学生版)

统计学计算题复习(学生版)统计学复习提纲一、期末考卷题型1. 单项选择题;2. 多项选择题;3. 简答题4. 计算题二、知识点复习1. 统计学分类、指标、变量、参数、统计量等概念,以及各种统计图形;2.统计数据的相关内容,以及测量数据分布的测度的描述;平均数、中位数和众数的计算公式。
3. 调查的各种方式; 4. 组距数列的相关概念。
5. 置信区间的相关概念,以及单个总体均值、比例、方差的区间估计;6. 估计单个总体均值、比例时的样本容量的计算公式;7. 单个总体均值、比例、方差的假设检验;8. 相关系数和回归系数的相关知识;9. 一元、二元回归模型的EXCEL操作结果的解释以及模型的建立和检验;10. 时间序列的各种分类;平均速度等指标、移动平均法的概念等;平均发展水平的计算和季节指数的计算; 11.统计指数的相关概念,制作综合指数要点和原则,综合指数、平均指数的计算。
1统计学计算题复习一.平均数、中位数和众数的计算和三者之间的关系1.算术平均数。
也叫均值,是全部数据的算术平均,是集中趋势的最主要测度值。
主要适用于定距数据和定比数据,但不适用于定类数据和定序数据。
2.众数。
众数是一组数据中出现次数最多的变量值,用Mo表示。
主要用于测度定类数据的集中趋势。
组距式数列确定众数,是先根据出现次数确定众数所在组,然后利用下列公式计算众数的近似值:M?L?0f?f?1?i (f?f?1)?(f?f?1) 3.中位数。
中位数是一组数据按从小到大排序后,处于中间位置上的变量值,用Me表示。
主要用于测度定序数据的集中趋势。
分组数据计算中位数时,先根据公式N确定中位数所在的组,然后用下列公式计算2N?Sm?1中位数的近似值: M?L?2?i efm4.众数、中位数和算术平均数的关系 x?Me?Mo,数据是对称分布; x<Me<Mo,数据是左偏分布; x>Me>Mo,数据是右偏分布。
例题1:某地区有下列资料:人均月收入400以下400~500 500~600 600~700 700~800 800~900 900以上合计要求计算算术平均数、众数、中位数。
《应用统计学》复习题库

第一章思考题及练习题(一)填空题1.统计工作与统计资料的关系是和的关系。
2.统计工作与统计学的关系是和的关系。
3.统计活动具有...和的职能。
4.统计指标反映的是的数量特征,数量标志反映的是的数量特征。
5.在人口总体中,个体是“”,“文化程度”是标志。
6.统计研究过程的各个阶段,运用着各种专门的方法,如大量观察法..综合指标法.和统计推断法等。
7.统计标志是总体中各个体所共同具有的属性或特征的名称。
它分为和两种。
8.要了解一个企业的产品质量情况,总体是.个体是。
9.性别是标志,标志表现则具体为或两种结果。
10.一件商品的价格在标志分类上属于。
11.一项完整的统计指标应该由....和等构成。
12.统计指标按所反映的数量特点不同,可以分为和。
13.反映社会经济现象相对水平或工作质量的指标称为指标。
14.统计活动过程通常被划分为.和三个阶段。
15.经过余年的发展,形成了今天的统计学。
16.古典统计学时期有两大学派,它们分别是和。
17.《关于死之表的自然和政治观察》一书的作者是,他第一次编制了“生命表”。
18.提出了著名的误差理论和“平均人”思想。
19.统计研究的数量性是指通过数来反映事物的量的.量的.量的和量的。
20.统计学包括和两部分内容。
21.总体中所包含的个体数量的多少称为;样本中所包含的个体数量的多少称为。
22.总体中的一个组或类,可被称为一个研究域或。
23.从总体中随机抽取的一部分个体所组成的集合称为。
24.统计理论与方法,事实上就是关于的理论和方法。
25.总体的三大特征是.和。
26.总体的差异性要求体现在至少具有一个用以说明个体特征的。
27.企业性质标志适用的测定尺度是,产品质量等级标志适用的测定尺度是,企业利润标志适用的测定尺度是,企业产量标志适用的测定尺度是。
28.可变的数量标志的抽象化称为。
它按其所受影响因素不同,可分为和两种,按其数值的变化是否连续出现,可分为和两种。
29.个体是的承担者。
统计学试题库计算题部分
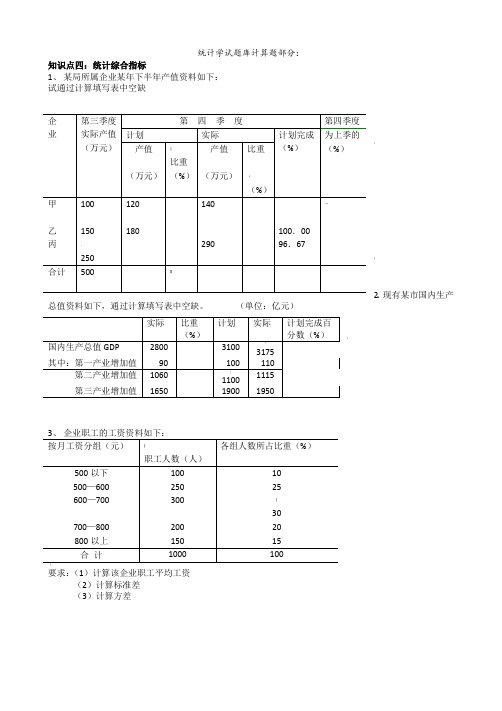
统计学试题库计算题部分:知识点四:统计综合指标1、 某局所属企业某年下半年产值资料如下: 试通过计算填写表中空缺:;2、现有某市国内生产总值资料如下,通过计算填写表中空缺。
(单位:亿元):要求:(1)计算该企业职工平均工资(2)计算标准差 (3)计算方差(2)比较哪个企业职工平均年龄更具代表性'、(7、甲、乙两企业工人有关资料如下:~要求:(1)比较哪个企业职工工资偏高(2)比较哪个企业职工平均工资更具代表性?10、甲、乙两钢铁生产企业某月上旬的钢材供货量资料如下:试比较甲、乙两企业该月上旬钢材供货的均衡性【11、某校甲、乙两班学生的统计学原理考试成绩分组情况如下:…要求:(1)计算各班学生的平均成绩(2)通过计算说明哪个班学生平均成绩的代表性强\求平均利润率。
问哪一个公司招员考试的成绩比较整齐(用标准差)!知识点五:时间数列及动态分析:试计算该市“九五”时期国民生产总值的年均递增率|(2)预测2004年存款余额将达到多少4、1997—2002年某企业职工人数和非生产人数资料如下:人员占全部职工人数的平均比重|要求:根据上述资料计算该企业这种产品第一季度单位产品成本(2)计算上半年平均计划完成程度,(2)计算四年平均工业增加值占国内生产总值的比重^^(2)用最小平方法配合直线趋势方程)年的销售额。
|知识点六:统计指数'(2)编制产量总指数、计算由于产量变动而增减的产值(3)编制出厂价格总指数,计算由于价格变动而增减的产值(2)计算销售量总指数(3)对总销售额的变动进行因素分析—(2)三种商品价格及销售量的综合变动指数(3)由于价格提高和销售量的增加各使销售额增加多少[(2)物价总指数(3)由于物价变动所引起的总产值的增加或减少额5、&(2)销售量总指数以及由于销售量变动对销售额的影响(8、[.8、某商店出售三种商品,资料如下:试计算价格总指数Array@~'11、某工业企业生产甲、乙两种产品,基期和报告期的产量、单位产品成本和出厂价格资料如下: 试计算:(1)以单位成本为同度量因素的产量总指数;(2)单位成本总指数;(3)对总成本进行两因素分析。
统计学期末复习资料_计算题

五、计算题(要求写出公式、列出计算步骤) 1. 某产品资料如下:要求按以下三种方法计算产品的平均收购价格:(1) 不加权的平均数;(2)加权算术平均数;(3)调和平均数 解:不加权05.139.005.12.1=++=x (元/斤)加权02.140003000200040009.0300005.120002.1=++⨯+⨯+⨯==∑∑fxf x (元/斤)加权调和02.19.0360005.131502.1240036000315024001=++++==∑∑m xm x (元/斤)2. 某公司所属三个企业生产同种产品,2004年实际产量、计划完成情况及产品优质品率资料如下:要求计算:(1)该公司产量计划完成百分比; (2)该公司的实际优质品率。
解:1)以实际产值为m,完成计划百分比为x,该公司产量计划完成百分比:%95.9320.5325008.02501.11502.1100250150100==++++==∑∑x m m x2)以实际优质品率为x,以实际产量为f,该公司的实际优质品率:%8.9650048425015010098.025096.015095.0100==++⨯+⨯+⨯==∑∑fxfx3. 某企业有50名工人,其月产值(万元)如下:要求:(1)根据上述资料将50名工人按产值分7组编制组距为10万元的等组距数列;(2)按上述分组编制向上累计的累计频数和累计频率数列;(3)并以第三组为例说明累计频数和累计频率的含义。
解:(1)根据上述资料将50名工人按产值分7组编制组距为10万元的等组距数列;(2)按上述分组编制向上累计的累计频数和累计频率数列;(3)并以第三组为例说明累计频数和累计频率的含义。
第三组数据说明在50名工人中,月产值在105以下的有30人,占总数的60%4. 南宁化工厂2008年现有生产工人600人。
现用不重复抽样抽出40人调查其年产值(万元)如下:(1)将40个工人按产值分组,编制组距为10万元的等组距数列,并列出向上累计频数和累计频率。
统计学复习题解答

《应用统计学》期末复习解答一、单选题1.统计总体的同质性是指( A )A.总体各单位具有某一共同的品质标志或数量标志B.总体各单位具有某一共同的品质标志属性或数量标志值C.总体各单位具有若干互不相同的品质标志或数量标志D.总体各单位具有若干互不相同的品质标志属性或数量标志值2.按某一标志分组的结果,表现出( A )A.组内同质性和组间差异性B.组内差异性和组间差异性C.组内同质性和组间同质性D.组内差异性和组间同质性3.设某地区有800家独立核算的工业企业,要研究这些企业的产品生产情况,总体是( D )A.全部工业企业B.800家工业企业C.每一件产品D.800家工业企业的全部工业产品4.统计调查的基本任务是取得原始统计资料,所谓原始统计资料是(C)A.统计部门掌握的资料B.对历史统计资料进行整理后取得的资料C.直接向调查单位进行登记取得的资料D.统计年鉴或统计公报上发布的资料5.已知两个同类企业的职工平均工资的标准差分别为10元和6元,而平均工资分别为3000元、3500元,则两个企业的工资离散程度为( A )A.甲大于乙B.乙大于甲C.两者相等D.无法判断6.一个连续性生产的工厂,为检验产品的质量,在一天中每隔1小时取5分钟的产品做检验,这种抽样方法属于( C )A.简单随机抽样B.整群抽样C.系统抽样D.分层抽样7.进行统计分组的关键是(B)A.划分各组组限B.正确选择分组标志C.确定各组组距D.计算各组组中值8.对一批进口商品的质量进行假设检验,在显著性水平为0.01时,原假设被拒绝;如果使用0.05的显著性水平,则原假设( A)A.一定会被拒绝B.可能会被拒绝C.一定会被接受D.必须重新假设检验 9.下列分组中按品质标志分组的是(B )A.人口按年龄分组B.产品按质量优劣分组C.企业按固定资产原值分组D.乡镇按工业产值分组 10.当一组数据属于右偏分布时,则(B ) A.平均数、中位数与众数是合而为一的 B.众数在左边,平均数在右边C.众数的数值较小,平均数的数值较大D.众数在右边,平均数在左边11.下列关于相关系数的陈述中哪一个是错误的( A ) A.数值越大说明两个变量之间的关系就越强B.仅仅是两个变量之间线性关系的一个度量,不能用于描述非线性关系C.只是两个变量之间线性关系的一个度量,不一定意味两个变量之间存在因果关系D.绝对值不会大于112.如果报告期商品价格计划降低5%,销售额计划增加10%,则销售量应增加( D ) A.15% B.5% C.5.25% D.15.79% 13.某橡胶厂生产汽车轮胎,根据历史资料统计结果,平均里程为25000公里,标准差为1900公里。
应用统计学网上复习题库

应⽤统计学⽹上复习题库《应⽤统计学》课程⽹上考试题库第⼀章数据与统计学⼀、单项选择题1、统计学具有()特点A.数量性和总体性B.数量性和差异性C.总体性和差异性D.数量性和答案:A2、“统计”作为社会经济⽣活中经常使⽤的名词,以下哪项不是其含义()A.统计⼯作B.统计资料C.统计数据D.统计科学答案:C3、专业、性别属于以下哪项统计数据的计量尺度()。
A.定类尺度B.定序尺度C.定距尺度D.定⽐尺度答案:A4、在对⼯业企业的⽣产设备进⾏普查时,调查对象是()。
A . 所有⼯业企业 B. 每⼀个⼯业企业C . ⼯业企业的所有⽣产设备D. ⼯业企业的每台⽣产设备答案:C5、统计有三种涵义,其中()是基础、是源。
A. 统计学B. 统计资料C. 统计⼯作D. 统计⽅法答案:C6、要了解 100 个学⽣的学习情况,则总体单位()。
A. 100 个学⽣D. 每⼀个学⽣的学习情况答案:C⼆、多项选择题1、下列哪项可以归于⽆限总体内。
()A.中国⽬前居民B.电脑内所有零件C.某快递公司所有订单D.报警电话E.美国现在的农业科研所数答案:CD2、要了解 100 个⼯业企业的⽣产情况,则统计指标有()。
A. 100 个⼯业企业的⼯业总产值B. 每⼀个⼯⼈的⽉⼯资C. 全部⼯业企业D. ⼀个⼯业企业的⼯资总额E.全部⼯业企业的劳动⽣产率答案:AE3、下⾯哪些属于变量()。
A、可变品质标志B、质量指标C、数量指标D、可变的数量标志E、某⼀指标数值答案:BCD三、判断题1、总体性是统计研究的前提。
()答案:错2、总体单位是构成统计总体的个别事物。
()答案:对3、推断统计学是研究在⼀定的概率下,如何⽤样本资料去推断总体数量特征的⽅法。
()答案:对4、全国⼈⼝数量是统计总体。
()答案:错答案:错6、⼈的年龄是离散变量。
()答案:错第⼆章统计数据的描述⼀、单项选择题1、要了解居民消费⽀出状况,应该采⽤()A.普查B.重点调查C.统计报表制度D.抽样调查答案:D2、以下哪种集中趋势的描述指标适⽤于任意分布类型。
统计学期末复习计算题汇总

3—5
5—7 7—9 合计
30
40 30 100
4
6 8 -
120
0 120 240
3—5
5—7 7—9 合计
40
40 20 100
4
6 8 -
1.024
0.064 1.152 2.24
σ
甲
=
(x - x) f f
2
2
=
240 = 1.55 100
f σ乙 = (x - x) Σf = 2.24 = 1.5
年份 2008 2009 2010 2011
工业总产值(万元)
增长量(万元) 发展速度(%)
(
─ ─
)
(
5000 (
) (
( ) 106
) (
) ( (
)
) )
增长速度(%)
增长1%的绝对值(万元)
─
─
(
800
) (
(
)
) (
4
)
2.某企业历年工业总产值资料如下表,试填上表中所缺 的各种动态分析指标,并计算该企业工业总产值平均每 年的发展速度。 年 份 2008 2009 2010 ( 2011
9.某企业两个生产班组,各有100名工人,它们生产某 种产品的日产量资料如下表,计算有关指标,比较哪 个班组平均日产量的代表性强。
甲班组 日产量 工人数 (件) f 3—5 5—7 7—9 合计 30 40 30 100 组中值 xf x 4 6 8 — 120 240 240 600 日产量 (件) 3—5 5—7 7—9 合计 乙班组 x 生产工人 f
比重% Σf
x
f Σf
4 6 8 —
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
105-120 17 42.5 26 65.0 31 77.5
120-135 7 17.5 33 82.5 14 35.0
135-150 6 15.0 39 97.5 7 17.5
150-165 1 2.5 40 100.0 1
2.5
合计
50 100 —
—
—
—
第五章计算题的重点
◆均值、方差、标准差、变异系数的计算; ◆掌握几何平均数的计算; ◆掌握调和平均数的计算;
求这10名成年人的平均身高。
[例]某企业青年班组100名工人每月奖金分组数 据及有关计算如下表,要求计算平均奖金。
月奖金分组 (元)
组中值
x
工人人数(人)f
500—600
550
10
600—700
650
10
700—800
750
30
800—900
850
40
900—10几何均值的计算
企业数(个)
3 6 17 7 6 1 40
比重 (%) 7.5 15.0 42.5 17.5 15.0 2.5 100.0
累积频数分布表
向上累积
向下累积
分组 企业数 比重
企业数 比重 企业数 比重
75-90 3 7.5 3 7.5 40 100.0
90-105 6 15.0 9 22.5 37 92.5
0.953
0.951
Std. Error of the Estimate
559.33047
【例】请预测当可支配收入xf =7500(元)时, 消费性支出的点预测值。
地区 甲 乙
平均产量(千克)
1000 1200
标准差(千克)
45 49
第七章计算题的重点
◆拟合优度检验。 ◆一元线性回归模型的建立、回归系数经济 含义的解释、回归系数显著性检验,点预测。
一元线性回归方程的系数表
Model
Unstandardized coefficients
B
Std.error
(constant) 450.334 388.906
把40个企业1999年的产品销售收入数据 按从小到大的顺序进行整理,结果如下:
76 87 88 92 95 100 103 103 104 105 105 107 108 108 110 112 113 114 115 115 116 117 117 118 119 119 120 123 124 125 126 127 129 135 136 137 138 142 146 164
t 第三步:对于显著 平性水0.05,临界值 (n 2) 2.306 2
t 第四步:作出t决策24.148 2.306 2
拒绝原假设,表明 配可 收支 入和消费性支 存出 在间 显著的线性相 系关
回归方程显著性r2检验
Model
R
1
0.976
R Square Adjusted R Square
Unstandardized coefficients
beta
t 1.158
Sig. 0.256
X可支配收入 0.692
0.029
0.976
24.148 0.000
yˆ 450.334 0.692x
【例】对回归系数的显著性进行检验
第一步:提出H假0:设 0,H1: 0 第二步:计算检验 量t统计ˆ/ˆSxx 24.148
xh
1
n 1
1
x1 x2 x3
111 1 11
3 3 0.40.51 1.9
1.58(元/公斤)
2.5 2 1
4、方差计算
n
2
x x 2
i 1
i
S n 1
k
S x x f 2
i 1
i
k
2 i
f 1
i
i 1
[例]从某车间抽取100名工人的月工资如下,计
算其方差。(已知 x =780元)
n
x x x x G n ... n
1
2
n
i
i 1
G x x x x f f 1 f 2 ... f n f n
f i
1
2
n
i
i 1
[例]某厂有4个流水作业车间,某月它们的产品 合格率分别为:98%、97%、95%和90%,问4个车 间产品的平均合格率是多少?
G 4 98%97%95%90% 94.95%
第三章计算题的重点
◆对数值型数据进行组距式分组; ◆编制频数分布表和累积频数分布表;
[例]某行业管理局所属40个企业1999年的产 品销售收入数据如下(单位:万元):
116 95 135 88 123 164 129 103 117 105 136 107 108 138 110 112 113 114 115 137 146 117 104 118 119 92 120 87 124 125 126 127 103 119 105 115 108 142 76 100
3、调和均值的计算
xh
111L1
11 nL1
n n1
x1 x2
xn x1 x2
xn x i1 i
n
k
xh
m1 m2 m1 m2
L L
mk mk
mi
i1
k mi
x1 x2
xk
x i1 i
【例】菜场上有一种蔬菜,价格分别为:早市 2.5元/公斤;午市2元/公斤;晚市1元/公斤。 若早、中、晚各花1元钱买蔬菜,求一天中买 到蔬菜的平均价格?
1、均值的计算
n
x ...
i
x x x x 1
2
n
i 1
n
n
k
x
x1
f
1
x2
f
....
2
xk
f f .... f
1
2
k
f
k
xi f
i1 k f
i
i
i 1
[例]已知10名成年人的身高资料如下(单位: 厘米):
166 169 172 177 180 170 172 174 168 173
[解]确定组数,根据经验公式 组 数 1lgn1lg406.32 lg2 lg2
确定组距 组距 全部数 组 全 据 数 部 最数 大据 1 值 6 6 7 最 4 61小 .7 4
因此,根据组距15,组数6把数据分组整理 成次数分布表。
频数分布表
销售收入 (万元) 75—90 90—105 105—120 120—135 135—150 150—165 合计
月工资分组 (元)
500—600 600—700 700—800 800—900 900—1000
Σ
工人人数
f
10 10 30 40 10 100
组中值
x
550 650 750 850 950
—
5、变异系数的计算
变异系数
标准差 均值
s x
[例]甲乙两地粮食的平均产量及标准差如下。 试计算比较:甲乙两地中,哪一地的平均产量 的代表性最好?
