安徽省蚌埠铁中2020届高三数学上学期期中试题文
安徽省蚌埠市第一中学2020届高三数学上学期期中试题文

蚌埠一中 2020 学年度第一学期期中考试高三数学(文科)考试时间: 120 分钟试卷分值 150 分命题人:审查人:一、选择题:本大题共12 个小题,每题 5 分,共 60分。
在每题给出的四个选项中,只有一个选项切合题目要求.1. 已知全集 U R, A { x | x 0}, B { x | x 1} ,则会合 C U ( A U B) ()A . { x | x 0}B . { x | x 1}C . { x | 0 x 1}D . { x |0 x 1}2. 若复数 z知足z i 1 i ( i是虚数单位 ) ,则 z的共轭复数是()A . 1 iB.1 iC .1 iD . 1 i3.如图是导函数 yf / (x) 的图象,那么函数 yf ( x) 在下边哪个区间是减函数()A. (x 2 , x 4 )B.(x 1, x 3 )C.( x 5 , x 6 )D.( x 4 , x 6 )4.已知 m , n 表示两条不一样直线, 表示平面,以下说法正确的选项是( ).若 m / / , n / / , 则m / / n B .若m ,n,则m nAC .若 m, mn ,则 n / / D .若 m / / , mn ,则 n5. 函数 f ( x) ln( x 2 x) 的定义域为()A. (0,1)B. [0,1]C. (,0) (1, ) D. ( ,0] [1, )6.为了获得函数 y sin 3x cos3x 的图像,能够将函数 y 2 sin 3x 的图像()A.向右平移个单位B.向左平移4 个单位4C.向右平移个单位 D.向左平移 个单位12127.已知数列﹛ a n ﹜为等差数列,且 a 1 a 7 a 13 4 ,则 tan(a 2 a 12 ) 的值为()A. 3 B . 3 C . 3 D.3 38.若a、b、c是常数,则“a> 0 且b2- 4ac< 0”是“对随意x∈R,有 ax2+bx+c>0”的()A.充足不用要条件B.必需不充足条件C.充要条件 D .必需条件9.平面直角坐标系中, O为坐标原点,已知两点 A( 3,1)、 B(- 1,3),若点 C 知足OC =α OA+β OB,此中α、β∈R,且α+β=1,则点C的轨迹方程为()A. 3x+2y - 11=0 B.( x-1)2+( y- 2)2=5 C. x+2y -5=0 D. 2x- y=010.已知f (x) (3 a) x a, x 1, ) 上是增函数,那么实数a的取值范围是(log a x, x是 ( )1A. (1, ) B.(3,3) C. [3,3) D. (1,3) 2 211.已知抛物线的极点在原点,焦点在y 轴上,其上的点P(m, 3) 到焦点的距离为5,则抛物线方程为()A.x2 8 y B.x2 4 y C. x 2 4y D.x2 8y12.假如存在实数x 1x 的取值范围是()x,使cos 成立,那么实数2 2xA. {-1 , 1} B .{ x | x 0或x 1} C .{ x | x 0或 x 1} D. { x | x 1或 x 1} 二、填空题:每题 5 分,共 20 分,将答案填在答题纸上.:R, 2 0,则命题p:13.若命题p x0 x0 .14.若某程序框图如所示,则该程序运作后输出的y 等于.15.在△ ABC中,AB 2 3, AC 2 ,且∠B6,则△ ABC的面积为 _____________ .16.在平面直角坐标系xOy中,已知x12 ln x1 y1 0,x2y2 2 0,则(x1 x2 )2 (y1 y2 )2的最小值为.三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17~ 21 题为必考题.第22、 23 题为选考题,考生依据要求作答.(一)必考题:60 分17. (本小题满分12 分)已知公差不为0 的等差数列{ a }中,a 2 a 1,a41,a 1成等比数列 .n 1,且 2 8(1) 求数列a n 通项公式;(2) 设数列 { b3,求合适方程45知足bnb1b2 b2b3 ...bnbn 1的正整数 n 的值.n } a n 3218.(本小题满分 12 分)某市组织高三全体学生参加计算机操作竞赛,等级分为 1 至 10 分,随机调阅了A、B 两所学校各 60 名学生的成绩,获得样本数据以下:( 1)计算两校样本数据的均值和方差,并依据所得数据进行比较.(2) 取的从A 校样本数据成绩分别为7 分、8 分和6人中任选 2 人参加更高一级的竞赛,求这9 分的学生中按分层抽样方法抽取 6 人,若从抽2 人成绩之和大于或等于15 的概率 .19.(本小题满分 12 分)如图 (1) ,在边长为 4 的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF = O,沿 EF将△ CEF翻折到△ PEF,连结 PA,PB,PD,获得如图(2)所示的五棱锥 P- ABFED,且 PB=10.(1)求证: BD⊥ PA;(2)求四棱锥 P-B FED的体积.20.(本小题满分 12 分)点 A、 B 分别是椭圆x2 y 2 1长轴的左、右端点,点 F 是椭圆的右焦点,点P 在椭圆上,36 20且位于 x 轴上方, PA PF 。
安徽蚌埠地区2020学年度高三数学第一学期期中测验试卷(文科)

安徽蚌埠地域2020学年度高三数学第一学期期中测试试卷(文科)(试卷满分150 分,考试时间为120 分钟)一、选择题(每题 5 分,共40 分)1.已知会合M {0, x} , N {1,2}, 若M N {1}, 则M N ()A .{0, x,1,2} B.{1,2,0,1} C.{0,1,2} D.没法确立2.方程2cos x 1的解集为()5A .{ x | x 2k ,k Z} B.{ x | x 2k ,k Z}3 3kC.{ x | x 2k ,k Z} D.{ x | x k ( 1),k Z}3 33 x在3.函数y x [ 1,2 ]的最小值为()A .2 B.0 C.-4 D.-24.若等比数列的公比为2,但前 4 项和为1,则这个等比数列的前8 项和等于()A .21 B.19 C.17 D.155.以下四个函数中,同时拥有性质:①最小正周期为 2 ;②图象对于直线x对称的一3 个函数是()A .y sin( x ) B.y sin( x )6 6C.y sin( x ) D.y sin( 2x )3 32 x6.等差数列{ a n }中,a3、a8是方程x 3 5 0 的两个根,则S10 是()A .15 B.25 C.30 D.507.函数 f (x) 的定义域为R,f (2 x) f (2 x) ,1x又 2 , f ( x) ( ,则有1 x 时)2()1A .f (1) ( 4) B.f f2 f ( 4) f (1) f121C.f (1 ) f f (4) D.2 f (1) f (4) f128.命题p:函数y log a (ax 2a)( a0且a 1)的图象必过定点(-1,1);命题q:假如函数y f (x)的图象对于(3,0)对称,那么函数y f (x 3) 的图象对于原点对称,则有()A .“p 且q”为真B.“p 或q”为假C.p 真q 假D.p 假q 真二、填空题(每题 5 分共30 分)29.函数y 3 cos x 的最小正周期为.1 3 210.曲线在y x x 5在x 1处的切线的倾斜角为.32 n11.已知数列{a n} 的前n 项和S n n 9 ,则其通项a n ;若它的第k 项知足5 a k 8 ,则k= .2 x 12.函数y f (x)在定义域(,0)内存在反函数,若 f (x1) x2 ,1则f (3) = ,则 f (3) .13.数列1,2,2,3,3,3,4,4,4,4,5⋯⋯的第100 项是.14.给出以下命题:①函数y a x (a0且a 1) 与函数y log a x (a 0 a 1)a 且的定义域同样;②函数y x y 33与函数x 值域同样;3与函数x 值域同样;ax 1 1③使函数( 2, )y 上为增函数的 a 的范围是,在区间x 2 2,此中错误命题的序号为.三、解答题(本大题共 6 小题,共80 分)15.(本小题13 分)已知:a,b,c 分别是△ABC 三个内角A、B、C 的对.3(1)若△ABC 面积为,c 2, A 60 , 求a、b 的值;2(2)若a cos A bcos B, 试判断△ABC 的形状,证明你的结论.2 x 16.(本小题13 分)已知: f (x) 是定义在R 上的奇函数,当x 0时,f (x) x 1,(1)求函数 f (x) 在R 上的分析式;(2)解不等式 f (x) 1.2 x x a a R 17.(本小题13 分)已知:函数 f (x) 2 cos3 sin 2 ( ).(1)若x R,求: f ( x) 的单一递加区间;(2)若x [0, ] 时, f (x) 的最大值为4,求:a 的值,并指出这时x 的值.23 ax2 bx a2 x18.(本小题满分13 分)已知: f ( x) x 3 在1时有极值0.(1)求:常数a、b 的值;(2)求: f (x) 的单一区间.n 2n 1 , 19.(本小题13 分)已知:数列{a n }知足a 3a 3 a 3 a n a N1 .2 33 (1)求数列{a n }的通项;n(2)设b ,求数列{b n }的前n 项和S n.n an2ax 120.(本小题14 分)已知:函数 f ( x) (a, b,c R) 是奇函数,又f (1) 2, f (2) 3 .bx c(1)求:a、b、c 的值;(2)当x (0, )时,议论函数f (x) 的单一性,并写出证明过程.参照答案一、选择题(每题 5 分,共40 分)1.C 2.C 3.D 4.C 5.B 6.A 7.D 8.B 二、填空题(每题 5 分共30 分)9.10.3411.2n 10 8 12.8 -213.14 14.②③三、解答题3 115.解:(1)由已知得bc sin A b sin 60 ,2 22 b2 c2 b Ab 1, 由余弦定理 a 2 cos 3,a 3 .⋯⋯⋯⋯⋯⋯⋯⋯ 5 分(2)由正弦定理得:2R s in A a,2 R s in B b,2R s in A cos A 2R s in B cos B,即sin 2A cos 2B, 由已知A、B 为三角形内角,∴A+B=90 °或A=B ,∴△ABC 为直角三角形或等腰三角形.⋯⋯⋯⋯⋯⋯⋯⋯12 分2x x 1 ( x 0)16.(1)f (x) 0 (x 0) ;2x x 1 (x 0)(2)( , 1)Y[ 0,2)17.分析:(1)f (x) 3 sin 2x cos 2x 1 a 2 sin( 2x ) 1 a.6解不等式.2k 2x 2k2 6 2得( ),k x k k Z3 6f ( x) 的单一区间为[k , k ]( k Z).3 6(2)],x [0,26 2x676.∴当, ( ) 3 .2x 即x 时 f x max a6 2 63 a 4, a 1,此时x.62 ax b18.解:(1)f (x) 3x 6 , 由题知:f ( 1) 0 3 6a b 0 12 f ( 1)01 3a b a 0 2联立<1>、<2>有:ab1 a 2或⋯⋯⋯⋯⋯⋯⋯⋯ 4 分3 b 9当a=1,b=3 时, f ( x) 3x2 6x 9 3(x 1)2 0这说明此时 f (x) 为增函数,无极值,舍去⋯⋯⋯⋯⋯⋯ 6 分2 x x x当2, 9 , ( ) 3 12 9 3( 3)( 1)a b 时 f x x故方程 f (x) 0有根x 3或x 1x (-,-3)-3 (3,-1)-1 (-1,+ )f (x) + 0 0 |f (x) ↑极大值↓极大值↑由表可见,当x 1时,f (x) 有极小值0,故ab29切合题意⋯⋯⋯⋯⋯⋯9 分(Ⅱ)由上表可知: f (x) 的减函数区间为(-3,-1)f (x) 的增函数区间为(-,-3)或(-,+ )⋯⋯⋯⋯⋯⋯12 分n 2 n 119.(Ⅰ)a 3a 3 a 3 a n ,1 2 33n 12 n 2a1 3a 3 a 3 a n 1 (n2 332),n 3n n 1 11 na n (3 3 32),an 1n3(n 2)1考证n=1 时也知足上式:( *)a n Nnn3(Ⅱ)nb n n 32 3 nS n 1 3 2 3 3 3 n 32 2 33 3 34 3n3S n 1 3 n12 3 n n 2 S n 3 3 3 3 n 3 1 ,n 13 32 S n n1 3n31,Sn n2n311 n34134.20.(1) f (x) 为奇函数,2 2ax 1 ax 1f ( x) f (x) ,即,bx c bx c比较分母的系数,得c=0,又f(1)=2,f(2)=3.a 12,3b得.解得a 2,b4a 1 23.2b3a 2,b ,c 0为所求.22 22x 1 4x 2 4 2x 4 2 22(2).f (x) ,由4x 2(x 0)得 x33x 3x 3 2 x 2f Q(4x x ) x2 2 2 1 1 4x 2 4x 22 1(x ) f ( x )2 1 33x 3x x x2 1 1 2 x212安徽蚌埠地域2020学年度高三数学第一学期期中测试试卷(文科) 21 / 2121 / 212 1 当0 x 1 x 2 时,(x 2 x 1) 0, x 1 x 2 0, x 1x 2 022 2 f ( x 2 f x 1 f x 在 上是减函数 .) ( ), ( )0, 2 当 2 21 x x 时, x 2x 0, x 1x 2 0, x 1 x 2 0. 1 21 2 2 f ( x 2 f x 1 f x 在上是增函数 . ) ( ), ( ) ,2。
安徽省蚌埠铁中2020届高三上学期期中考试数学试卷(文)

安徽省蚌埠铁中2020届高三上学期期中考试数学试卷(文)一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只 有一项是符合题目要求的)1.设集合{}(5)4A x x x =-,{}|B x x a =≤,若A B B ⋃=,则a 的值可以是( ) A. 1B. 2C. 3D. 42.已知i 为虚数单位,若复数11tiz i-=+在复平面内对应的点在第四象限,则t 的取值范围为 ( ) A. [1,1]- B. (1,1)- C. (,1)-∞- D. (1,)+∞3.已知1sin 123πα⎛⎫-= ⎪⎝⎭,则17cos 12πα⎛⎫+ ⎪⎝⎭的值等于( )A.13B.C. 13- D. 4.若1,01a c b ><<<,则下列不等式不正确的是( ) A. 20192019log log a b > B. log log c b a a > C. ()()cbc b a c b a ->- D. ()()cba c a a c a ->-5.在等比数列{}n a 中,“412a ,a 是方程2x 3x 10++=的两根”是“8a 1=±”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件6.已知()f x 是定义在[2,1]b b -+上的偶函数,且在[2,0]b -上为增函数,则(1)(2)f x f x -≤的解集为( )A. 2[1,]3-B. 1[1,]3-C. [1,1]-D. 1[,1]37.《九章算术》教会了人们用等差数列的知识来解决问题,《张丘建算经》卷上第22题 为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一 天织6尺布,现一月(按30天计)共织540尺布”,则从第2天起每天比前一天多织( )尺布. A.12B.2429 C. 1631 D. 16298.某几何体的三视图如图所示,则该几何体的体积为( )A. 5B.163C. 7D.1739.执行如图所示的程序框图,如果输出6T =,那么判断框内应填入的条件是( )A. 32k <B. 33k <C. 64k <D. 65k <10.函数()sin (0)f x x ωω=>的图象向右平移12π个单位得到函数()y g x =的图象,并且函数()g x 在区间[,]63ππ上单调递增,在区间[,]32ππ上单调递减,则实数ω的值为 ( ) A.74B.32C. 2D.5411.经过双曲线2222:1(0,0)x y M a b a b-=>>的左焦点作倾斜角为60︒的直线l ,若l 交双曲线M 的左支于,A B ,则双曲线M 离心率的取值范围是( ) A ()2,+∞B. ()1,2C. (D.)+∞.12.已知x ,y 满足约束条件20,{53120,3,x y x y y --≤--≥≤当目标函数z ax by =+(0a >,0b >)在该约束条件下取得最小值1时,则123a b+的最小值为( )A. 4+B.C. 3+D. 3二.填空题(共4小题,每小题5分,合计20分)13. 若函数()ln 2f x x ax =-的图象存在与直线20x y +=垂直的切线,则实数a 的取值范 围是____.14.ABC ∆的内角,,A B C 的对边分别为,,a b c)cos cos ,60a C c A b B -==︒, 则A 的大小为__________.15.在平行四边形ABCD 中,已知1AB =,2AD =,60BAD ∠=︒,若CE ⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ ,DF ⃗⃗⃗⃗⃗ = 2FB ⃗⃗⃗⃗ ,则AE⃗⃗⃗⃗⃗ ∙AF ⃗⃗⃗⃗⃗ =____________. 16.已知球O 是正三棱锥(底面为正三角形,顶点在底面射影为底面中心)A-BCD 的外接球,BC=3,AB =E 在线段BD 上,且BD=3BE ,过点E 作圆O 的截面,则所 得截面圆面积的取值范围是__.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 第17题~第21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.)(一)必考题:共60分 17.(本小题满分10分)已知数列{}n a 是等差数列,前n 项和为n S ,且533S a =,468a a +=. (1)求n a .(2)设2nn n b a =⋅,求数列{}n b 的前n 项和n T .的18. (本小题满分12分)如图所示,正四棱椎P ABCD -中,底面ABCD 的边长为2,侧棱长为E 为PD 的中点.(1)求证:PB 平面AEC ; (2)若F 为PA 上的一点,且3PFFA=,求三棱椎A BDF -的体积.19.(本小题满分12分)随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用等,其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元新个税政策的税率表部分内容如下:(1)现有李某月收入19600元,膝下有一名子女,需要赡养老人,(除此之外,无其它专项附加扣除)请问李某月应缴纳的个税金额为多少?(2)现收集了某城市50名年龄在40岁到50岁之间的公司白领的相关资料,通过整理资料可知,有一个孩子的有40人,没有孩子的有10人,有一个孩子的人中有30人需要赡养老人,没有孩子的人中有5人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的50人中,任何两人均不在一个家庭).若他们的月收入均为20000元,试求在新个税政策下这50名公司白领的月平均缴纳个税金额为多少?20.(本小题满分12分)在平面直角坐标系中,()2,0A -,()2,0B ,设直线AC 、BC斜率分别为1k 、2k 且1212k k ⋅=- ,(1)求点C 的轨迹E 的方程;(2)过()F 作直线MN 交轨迹E 于M 、N 两点,若MAB △的面积是NAB △ 面积的2倍,求直线MN 的方程.21.(本小题满分12分)已知函数()()()ln f x x x ax a R =-∈.(1)若1a =,求函数()f x 的图像在点()()1,1f 处的切线方程; (2)若函数()f x 有两个极值点1x ,2x ,且12x x <,求证:()212f x >-.的(二)选考题:(共10分。
安徽省蚌埠市铁路中学届高三数学上学期期中试卷文(含解析)【含答案】

2014-2015学年安徽省蚌埠市铁路中学高三(上)期中数学试卷(文科)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合A={x||x|≤2,x∈R},,则A∩B=()A.(0,2) B. [0,2] C. {1,2} D. {0,1,2}2.三个数0.76,60.7,log0.76的大小关系为()A. 0.76<log0.76<60.7 B. 0.76<60.7<log0.76C. log0.76<60.7<0.76 D. log0.76<0.76<60.73.已知tanα=2,那么的值为()A.﹣2 B. 2 C.﹣ D.4.已知=(3,4),=(5,12),则与夹角的余弦为()A. B. C. D.5.已知P:(2x﹣3)2<1,Q:x(x﹣3)<0,则P是Q的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件6.己知函数,那么f(1)+f(2)+f(3)+…+f(2009)+=()A. 2005 B. 2006 C. 2007 D. 20087.函数的最小值为()A. B. C. D. 18.已知f(x)是奇函数,且方程f(x)=0有且仅有3个实根x1、x2、x3,则x1+x2+x3的值为()A. 0 B.﹣1 C. 1 D.无法确定9.设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,不可能正确的是()A. B.C. D.10.函数f(x)=log a(1﹣ax)在(1,3)上递增,则a的取值范围是()A.(0,1) B. C. D.二、填空题(本大题共5小题,每小题5分,共25分)11.复数的值是.12.全称命题“∀x∈R,x2+x+3>0”的否定是.13.若||=1,||=2,与的夹角为60°,若(3+5)⊥(m﹣),则m的值为.14.若函数y=﹣x3+bx有三个单调区间,则b的取值范围是.15.给出下列五个命题:①函数的一条对称轴是;②函数y=tanx的图象关于点(,0)对称;③正弦函数在第一象限为增函数;④若,则x1﹣x2=kπ,其中k∈Z.以上四个命题中正确的有(填写正确命题前面的序号)三、解答题:(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.)16.集合,集合B={x|y=ln(x2﹣x﹣6)}(1)求集合A∩B;(2)若不等式ax2+2x+b>0的解集为A∪B,求a,b的值.17.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos=,=3.(1)求△ABC的面积;(2)若c=1,求a的值.18.已知函数(Ⅰ)求函数f(x)的最小正周期及在区间上的最大值和最小值;(Ⅱ)若,求cos2x0的值.19.已知函数y=f(x)是定义在(0,+∞)上的增函数,对于任意的x>0,y>0,都有f (xy)=f(x)+f(y),且满足f(2)=1.(1)求f(1)、f(4)的值;(2)求满足f(x)+f(x﹣3)>2的x的取值范围.20.已知函数f(x)=2x3﹣3ax2+(a2+2)x﹣a(a∈R).(I)若当x=1时,函数f(x)取得极值,求a的值;(II)若函数f(x)仅有一个零点,求a的取值范围.21.已知函数f(x)=e x﹣ln(x+1)(I)求函数f(x)的单调区间;(II)证明:.2014-2015学年安徽省蚌埠市铁路中学高三(上)期中数学试卷(文科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合A={x||x|≤2,x∈R},,则A∩B=()A.(0,2) B. [0,2] C. {1,2} D. {0,1,2}考点:交集及其运算.专题:计算题.分析:分别求出两集合中其他不等式的解集,确定出两集合,然后求出两集合的交集即可.解答:解:由集合A中的不等式|x|≤2,解得:﹣2≤x≤2,所以集合A=[﹣2,2],由集合B中的不等式≤2,解得:0≤x≤4,又x∈Z,所以集合B={0,1,2,3,4},则A∩B={0,1,2}.故选D点评:解得本题的关键是确定出两集合,方法是求出两集合中其他不等式的解集.学生容易出错的地方是忽略负数没有平方根这个条件,没有找全集合B中的元素.2.三个数0.76,60.7,log0.76的大小关系为()A. 0.76<log0.76<60.7 B. 0.76<60.7<log0.76C. log0.76<60.7<0.76 D. log0.76<0.76<60.7考点:指数函数单调性的应用.专题:计算题;转化思想.分析:由对数函数的图象和性质,可得到log0.76<0,再指数函数的图象和性质,可得0.76<1,60.7>1从而得到结论.解答:解:由对数函数y=log0.7x的图象和性质可知:log0.76<0由指数函数y=0.7x,y=6x的图象和性质可知0.76<1,60.7>1∴log0.76<0.76<60.7故选D点评:本题主要考查指数函数,对数函数的图象和性质,在比较大小中往往转化为函数的单调性或图象分面来解决.3.已知tanα=2,那么的值为()A.﹣2 B. 2 C.﹣ D.考点:弦切互化;同角三角函数基本关系的运用.专题:计算题.分析:的分子、分母同除cosα,代入tanα,即可求出它的值.解答:解:=因为tanα=2,所以上式=故选D.点评:本题考查弦切互化,同角三角函数基本关系的运用,考查计算能力,是基础题.4.已知=(3,4),=(5,12),则与夹角的余弦为()A. B. C. D.考点:数量积表示两个向量的夹角.专题:计算题.分析:利用向量的模的坐标公式求出向量的坐标,利用向量的数量积公式求出两个向量的数量积;利用向量的数量积求出向量的夹角余弦.解答:解:=5,=13,=3×5+4×12=63,设夹角为θ,所以cosθ=故选A.点评:本题考查向量的模的坐标公式、向量的坐标形式的数量积公式、利用向量的数量积求向量的夹角余弦.5.已知P:(2x﹣3)2<1,Q:x(x﹣3)<0,则P是Q的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据不等式的解法以及充分条件和必要条件的定义进行判断即可.解答:解:由(2x﹣3)2<1,即﹣1<2x﹣3<1,即1<x<2,即P:1<x<2由x(x﹣3)<0,得0<x<3,即Q:0<x<3,则P是Q的充分不必要条件,故选:A点评:本题主要考查充分条件和必要条件的判断,根据不等式的关系是解决本题的关键.6.己知函数,那么f(1)+f(2)+f(3)+…+f(2009)+=()A. 2005 B. 2006 C. 2007 D. 2008考点:函数的值.专题:计算题.分析:题目中给出了函数解析式,当然可以逐项求解,再相加.审题后,应当注意到所给的自变量的取值有特点:倒数关系,由此应先考虑f(x)+f()的结果的特殊性,以期减少重复的运算.解答:解:∵,∴f(x)+f()===1∴f(1)+f(2)+f(3)+…+f(2009)+=f(1)+[f(2)+f()]+f(3)+f()]+…+[f(2009)+f()]=+1+1+…+1=2008故选:D.点评:本题考查函数值求解,函数性质.意识到先考虑f(x)+f()的结果的特殊性,是本题的关键,精彩之处.也是良好数学素养的体现.7.函数的最小值为()A. B. C. D. 1考点:函数的最值及其几何意义;函数单调性的性质.专题:综合题.分析:由题意,可先令2x﹣1≥0,解出函数的定义域,由于两个函数y=x与y=在定义域[,+∞)上都是增函数,两个增函数的和仍然是一个增函数,由此判断出函数的单调性,再由单调性确定出函数的最值,即可选出正确选项解答:解:由题设知必有2x﹣1≥0,解得x≥,即函数的定义域是[,+∞)由于y=x与y=在定义域[,+∞)上都是增函数所以函数在定义域[,+∞)上都是增函数所以当x=时函数取到最小值为故选C点评:本题考查求函数的最值及函数单调性的判断,利用函数的单调性求函数最值是常规方法,判断单调性是解此类题的关键8.已知f(x)是奇函数,且方程f(x)=0有且仅有3个实根x1、x2、x3,则x1+x2+x3的值为()A. 0 B.﹣1 C. 1 D.无法确定考点:奇偶函数图象的对称性.专题:常规题型.分析:首先根据f(x)是奇函数,分析一个根为零,另外两个根互为相反数.然后即可求出x1+x2+x3的值.解答:解:∵f(x)是奇函数,∴f(x)一定过原点∵方程f(x)=0有且仅有3个实根x1、x2、x3∴其中一个根为0,不妨设x2=0∵f(x)是奇函数∴方程的两个根关于原点对称,即x1+x3=0∴x1+x2+x3=0故答案为:A点评:本题考查奇偶函数图象的性质问题,通过分析奇偶函数的性质求出3个根的关系.本题属于基础题.9.设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,不可能正确的是()A. B. C.D.考点:利用导数研究函数的单调性;导数的几何意义.专题:压轴题.分析:本题可以考虑排除法,容易看出选项D不正确,因为D的图象,在整个定义域内,不具有单调性,但y=f(x)和y=f′(x)在整个定义域内具有完全相同的走势,不具有这样的函数.解答:解析:检验易知A、B、C均适合,不存在选项D的图象所对应的函数,在整个定义域内,不具有单调性,但y=f(x)和y=f′(x)在整个定义域内具有完全相同的走势,不具有这样的函数,故选D.点评:考查函数的单调性问题.10.函数f(x)=log a(1﹣ax)在(1,3)上递增,则a的取值范围是()A.(0,1) B. C. D.考点:对数函数的单调区间.专题:计算题.分析:先将函数f(x)=log a(1﹣ax)转化为y=log a t,t=1﹣ax,两个基本函数,再利用复合函数求解.解答:解:令y=log a t,t=1﹣ax,∵a>0∴t=1﹣ax在(1,3)上单调递减∵f(x)=log a(1﹣ax)(a>0a≠1)在区间(1,3)内单调递增∴函y=log a t是减函数,且t(x)>0在(1,3)上成立∴∴0<a≤.故选D.点评:本题主要考查复合函数,关键是分解为两个基本函数,利用同增异减的结论研究其单调性,再求参数的范围.本题容易忽视t=1﹣ax≥0的情况导致出错.二、填空题(本大题共5小题,每小题5分,共25分)11.复数的值是 2 .考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:利用复数的运算法则即可得出.解答:解:原式==2,故答案为:2.点评:本题考查了复数的运算法则,属于基础题.12.全称命题“∀x∈R,x2+x+3>0”的否定是∃x∈R,有x2+x+3≤0 .考点:命题的否定.专题:阅读型.分析:利用含量词的命题的否定形式写出命题的否定.解答:解:“∀x∈R,x2+x+3>0”的否定是∃x∈R,有x2+x+3≤0故答案为∃x∈R,有x2+x+3≤0.点评:本题考查含量词的命题的否定形式.13.若||=1,||=2,与的夹角为60°,若(3+5)⊥(m﹣),则m的值为.考点:数量积表示两个向量的夹角.专题:平面向量及应用.分析:由条件可求得,根据两向量垂直,则两向量的数量积为0,从而会得到关于m的方程,解方程即可求出m.解答:解:∵∴=0;∴m=.故答案为:.点评:本题考查向量数量积的计算公式,量向量垂直的充要条件是两向量的数量积为0.14.若函数y=﹣x3+bx有三个单调区间,则b的取值范围是b>0 .考点:利用导数研究函数的单调性.专题:计算题;数形结合;转化思想.分析:根据函数y=﹣x3+bx有三个单调区间,可知y′有正有负,而导函数是二次函数,故导函数的图象与x轴有两个交点,△>0,即可求得b的取值范围.解答:解:∵数y=﹣x3+bx有三个单调区间,∴y′=﹣4x2+b的图象与x轴有两个交点,∴△=﹣4(﹣4)b=16b>0∴b>0,故答案为:b>0.点评:考查利用导数研究函数的单调性,把函数有三个单调区间,转化为导函数的图象与x轴的交点个数问题,体现了转化的思想,属中档题.15.给出下列五个命题:①函数的一条对称轴是;②函数y=tanx的图象关于点(,0)对称;③正弦函数在第一象限为增函数;④若,则x1﹣x2=kπ,其中k∈Z.以上四个命题中正确的有①②(填写正确命题前面的序号)考点:正弦函数的对称性;三角函数的化简求值;正切函数的奇偶性与对称性.专题:三角函数的图像与性质.分析:把x=代入函数得 y=1,为最大值,故①正确.由正切函数的图象特征可得(,0)是函数y=tanx的图象的对称中心,故②正确.通过举反例可得③是不正确的.若,则有 2x1﹣=2kπ+2x2﹣,或 2x1﹣=2kπ+π﹣(2x2﹣),k∈z,即 x1﹣x2=kπ,或x1+x2=kπ+,故④不正确.解答:解:把x=代入函数得 y=1,为最大值,故①正确.结合函数y=tanx的图象可得点(,0)是函数y=tanx的图象的一个对称中心,故②正确.③正弦函数在第一象限为增函数,不正确,如390°>60°,都是第一象限角,但sin390°<sin60°.若,则有 2x1﹣=2kπ+2x2﹣,或 2x1﹣=2kπ+π﹣(2x2﹣),k∈z,∴x1﹣x2=kπ,或x1+x2=kπ+,k∈z,故④不正确.故答案为①②.点评:本题考查正弦函数的单调性、奇偶性、周期性、对称性,掌握正弦函数的图象和性质,是解题的关键,属于中档题.三、解答题:(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.)16.集合,集合B={x|y=ln(x2﹣x﹣6)}(1)求集合A∩B;(2)若不等式ax2+2x+b>0的解集为A∪B,求a,b的值.考点:并集及其运算;交集及其运算.专题:计算题.分析:(1)根据负数没有平方根、分母不为0,求出集合A中函数的定义域,确定出A,根据负数与0没有对数,求出集合B中函数的定义域,确定出B,找出两集合的公共部分,即可确定出两集合的交集;(2)找出既属于A又属于B的部分,确定出两集合的并集,由不等式ax2+2x+b>0的解集为两集合的并集,得到方程ax2+2x+b=0的两根分别为﹣2和0,利用根与系数的关系即可求出a与b的值.解答:解:(1)由集合A中的函数得:2x﹣1>0,即2x>20,解得:x>0,∴A=(0,+∞),由集合B中的函数得:x2﹣x﹣6>0,即(x﹣3)(x+2)>0,解得:x<﹣2或x>3,∴B=(﹣∞,﹣2)∪(3,+∞),则A∩B=(3,+∞);(2)∵不等式ax2+2x+b>0的解集为A∪B,A∪B═(﹣∞,﹣2)∪(0,+∞),∴方程ax2+2x+b=0的两根分别为﹣2和0,∴﹣2+0=﹣,﹣2×0=,解得:a=1,b=0.点评:此题考查了交、并、补集的混合运算,熟练掌握交、并、补集的定义是解本题的关键.17.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos=,=3.(1)求△ABC的面积;(2)若c=1,求a的值.考点:余弦定理;同角三角函数间的基本关系;二倍角的余弦.专题:计算题.分析:(1)利用二倍角的余弦函数公式化简cosA,把cos的值代入求出cosA的值,由A为三角形的内角,利用同角三角函数间的基本关系求出sinA的值,又bc=5,根据三角形的面积公式即可求出三角形ABC的面积;(2)由bc=5,且c=1,求出b的值,再由cosA的值,利用余弦定理即可求出a的值.解答:解:(1)∵,∴,又A∈(0,π),∴,由AB•AC=3得:bccosA=3,即bc=5,所以△ABC的面积为=2;(6分)(2)由bc=5,而c=1,所以b=5,又cosA=,根据余弦定理a2=b2+c2﹣2bc•cosA,得:=2.(12分)点评:此题考查了二倍角的余弦函数公式,同角三角函数间的基本关系,三角形的面积公式以及余弦定理,熟练掌握公式及定理是解本题的关键.18.已知函数(Ⅰ)求函数f(x)的最小正周期及在区间上的最大值和最小值;(Ⅱ)若,求cos2x0的值.考点:二倍角的余弦;两角和与差的正弦函数;三角函数的周期性及其求法.专题:三角函数的求值.分析:(1)利用两角和差的正弦化简函数f(x)的解析式为,由此求得函数的最小正周期,再根据∈,求得函数的最大值和最小值.(Ⅱ)由(1)可知,再根据 2x0+的范围利用同角三角函数的基本关系求得的值,再根据,利用两角差的余弦公式求得结果.解答:解:(1)由题知:==,所以函数f(x)的最小正周期为π.…(5分)因为 x∈,∴∈.…(7分)故当2x+=时,函数f(x)取得最小值为﹣;当2x+=时,函数f(x)取得最大值为1,故函数在区间上的最大值为1,最小值为..…(9分)(Ⅱ)由(1)可知,又因为,所以,由,得 2x0+∈[,],从而.…(12分)所以==.…(15分)点评:本题主要考查两角和差的正弦和余弦公式、二倍角公式、同角三角函数的基本关系的应用,正弦函数的定义域和值域,属于中档题.19.已知函数y=f(x)是定义在(0,+∞)上的增函数,对于任意的x>0,y>0,都有f (xy)=f(x)+f(y),且满足f(2)=1.(1)求f(1)、f(4)的值;(2)求满足f(x)+f(x﹣3)>2的x的取值范围.考点:抽象函数及其应用;奇偶性与单调性的综合.专题:函数的性质及应用.分析:(1)根据已知条件,只需取x=1,y=1,便可求出f(1);取x=2,y=2,便可求出f (4).(2)根据已知条件可以得到:f[x(x﹣3)]>f(4),根据已知的条件解这个不等式即可.解答:解:(1)取x=y=1,则:f(1)=f(1)+f(1),∴f(1)=0;取x=y=2,则:f(4)=f(2)+f(2)=2,即f(4)=2.(2)由题意得,f[x(x﹣3)]>f(4);∴x应满足:;解得,x>4.∴满足f(x)+f(x﹣3)>2的x的取值范围是(4,+∞).点评:考查对条件f(xy)=f(x)+f(y)的运用,利用函数的单调性解不等式,注意限制x>0,x﹣3>0.20.已知函数f(x)=2x3﹣3ax2+(a2+2)x﹣a(a∈R).(I)若当x=1时,函数f(x)取得极值,求a的值;(II)若函数f(x)仅有一个零点,求a的取值范围.考点:函数在某点取得极值的条件;函数零点的判定定理.专题:计算题.分析:(I)先求导数fˊ(x)然后在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,fˊ(x)>0的区间为单调增区间,fˊ(x)<0的区间为单调减区间,从而得出函数的极值情况.(II)由函数零点的存在定理,我们可以将函数的解析式进行因式分解,最后综合条件,即可得到f(x)=0有且仅有一个实数解,则实数a的取值可得.解答:解:f′(x)=6x2﹣6ax+(a2+2),(I)f′(1)=6﹣6a+(a2+2),令f′(x)=0,解得a=2或a=4,当a=2时,f′(x)=6x2﹣12x+6=6(x﹣1)2,显然f(x)在x=1处不取得极值;当a=4时,f′(x)=6x2﹣24x+18=6(x﹣1)(x﹣3),显然f(x)在x=1处取得极大值.故a的值为4.(II)f(x)=2x3﹣3ax2+(a2+2)x﹣a=(2x3﹣2ax2+2x)﹣(ax2﹣a2x+a)=(x2﹣ax+1)(2x﹣a)得f(x)的一个零点是,又函数f(x)仅有一个零点,∴△=(﹣a)2﹣4×1×1<0,解得﹣2<a<2,故a的取值范围(﹣2,2).点评:本题考查了函数在某点取得极值的条件、利用导数研究函数的极值,函数零点的判定定理,属于基础题.21.已知函数f(x)=e x﹣ln(x+1)(I)求函数f(x)的单调区间;(II)证明:.考点:利用导数研究函数的单调性;函数恒成立问题.专题:证明题.分析:(I)先求导数fˊ(x)然后在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,fˊ(x)>0的区间为单调增区间,fˊ(x)<0的区间为单调减区间.(II)由(I)知当x=0时,f(x)取得最小值,即f(x)≥1,即e x﹣ln(x+1)≥1,即e x≥ln(x+1)+1,取x=,则,再分别令n=1,2,3,…,n得到n个不等式,相加即得.解答:解:x>﹣1,f′(x)=e x﹣.(I)由于f′(x)=e x﹣在(﹣1,+∞)上是增函数,且f′(0)=0,∴当x∈(0,+∞)时,f′(x)>0,当x∈(﹣1,0)时,f′(x)<0,故函数f(x)的单调增区间(0,+∞),函数f(x)的单调减区间(﹣1,0).(II)由(I)知当x=0时,f(x)取得最小值,即f(x)≥1,∴e x﹣ln(x+1)≥1,即e x≥ln(x+1)+1,取x=,则,于是e≥ln2﹣ln1+1,≥ln3﹣ln2+1,≥ln4﹣ln3+1,…≥ln(n+1)﹣lnn+1.相加得,,得证.点评:本题考查函数的单调区间及极值的求法和不等式的证明,具体涉及到导数的性质、函数增减区间的判断、极值的计算和不等式性质的应用.解题时要认真审题,仔细解答.。
安徽省蚌埠铁中2020届高三上学期期中考试数学文Word版含答案

蚌埠铁中2019-2020学年度第一学期期中检测试卷高三数学(文)考试时间:120分钟试卷分值:150分一、选择题(本题共12小题,每小题5分,共60分•在每小题给出的四个选项中,只有一项是符合题目要求的)1. 设集合A ={x x(5 —x))4}, B={x|xWa},若AuB =B ,则a 的值可以是()A. 1B. 2C. 3D. 41 -ti2. 已知i为虚数单位,若复数z 在复平面内对应的点在第四象限,则t的取值范1+i围为()A.[-1,1]B.(-1,1)C.(-::,-1)D.(1,.(H ) 1(丄17兀3.已知sin :----- 丨=—贝y cos. « + ---- 的值等( )I12 3'I 12A.1B.2、2c 12.2— C. D.33334.若a 1,0 :::c ::: b ::: 1,则下列不等式不正确的是()A. log 2019 a■ log 2019 bB. log c a log b aC. (c_b )a c>(c_b )a bD. (a_c)a c>(a_c)a b5.在等比数列中,“ a4,a12是方程x23x ^0的两根”是“ a^ -1 ”的()A.充分不必要条件B. 必要不充分条件C.充要条件D. 既不充分也不必要条件6.已知f (x)是定义在[-2b,1 b]上的偶函数,且在[-2b,0]上为增函数,则f (x T)空f (2x)的解集为()C. 24 241 A.—2B.24 29C.16 31D.16 298.某几何体的三视图如图所示, 则该几何体的体积为(C. 7D.17 310.函数f (x )二sin ,・x (「・0)的图象向右平移 个单位得到函数y =g (x )的图象,并且函数g (x )在区间[―,—]上单调递增,在区间 6 3Tt JI[-,—]上单调递减,则实数-■的值3 2为( ) A.D. §21A.[七]B. [-1,3]337•《九章算术》教会了人们用等差数列的知识来解决问题,为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),天多织( )尺布.C. [-1,1]D.[3,1]《张丘建算经》卷上第 22题第一天织6尺布,现一月(按 30天计)共织540尺布” ,则从第 2天起每天比前一 A. 5 兀2 211. 经过双曲线M :笃-爲=1(a 0, b 0)的左焦点作倾斜角为60的直线丨,若la b交双曲线M的左支于A, B,则双曲线M离心率的取值范围是()A (2, +珀) B. (1,2) C. (1,73)D. (应,址)x _y _2 _ 0,12. 已知x,y满足约束条件{5x-3y -12 _0,当目标函数^ax by(a . 0 , b . 0)y空3,1 2在该约束条件下取得最小值1时,则的最小值为()3a bA. 4 2 2B. 4.2C. 3 2x2D. 3 2二•填空题(共4小题,每小题5分,合计20分)13. 若函数f(x) =1 nx-2ax的图象存在与直线2x • y =0垂直的切线,则实数a的取值范围是____ •14. ;ABC的内角A, B,C的对边分别为a,b,c,已知3 acosC= b,B =60,贝y A的大小为15. 在平行四边形ABCD中,已知AB=1, AD =2 , BAD =60,若,,则= _____________ •16. 已知球O是正三棱锥(底面为正三角形,顶点在底面射影为底面中心)A-BCD的外接球,BC=3 AB=2^3,点E在线段BD上,且BD=3BE过点E作圆O的截面,则所得截面圆面积的取值范围是__.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤第17题〜第21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.)(一)必考题:共60分17. (本小题满分10分)已知数列laj是等差数列,前n项和为S n,且55=393, a4 8 .(1)求a n .(2)设b n =2n 9n,求数列:b n / 的前n项和T n.18. (本小题满分12分)如图所示,正四棱椎P —ABCD中,底面ABCD的边长为2,侧棱长为2、、2,E为PD的中点.(1)求证:PBU平面AEC ;求三棱椎A-BDF的体积.随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)二收入-个税起征点- 专项附加扣除;(3 )专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用等,其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元级数一级二级三级四级・・・(1 )现有李某月收入」八元,膝下有一名子女,需要赡养老人,(除此之外,无其它专项附加扣除)请问李某月应缴纳的个税金额为多少?(2)现收集了某城市 0.名年龄在40岁到"岁之间的公司白领的相关资料,通过整理资料可知,有一个孩子的有40人,没有孩子的有10人,有一个孩子的人中有30人需要赡养老人,没有孩子的人中有5人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的"人中,任何两人均不在一个家庭).若他们的月收入均为]元,试求在新个税政策下这"i.名公司白领的月平均缴纳个税金额为多少?20. (本小题满分12 分)在平面直角坐标系中, A -2,0 , B 2,0,设直线AC、BC 斜率分别为k1、1k2 且k i k2:2(1)求点C的轨迹E的方程;(2)过F -\2,0作直线MN交轨迹E于M、N两点,若△ MAB的面积是面积的2倍,求直线MN的方程.21. (本小题满分12分)已知函数f x =x Inx-ax a R .(1 )若a =1,求函数f x的图像在点1,f 1处的切线方程;, 12(2)若函数f x有两个极值点N , X2,且X1 :::X2,求证:f x2△ NAB(二)选考题:(共10分。
安徽省蚌埠铁中高三数学上学期期中考试试卷 文 新人教A版

一、选择题:(每小题5分,共50分)1.设全集{}12345U =,,,,,集合{}{}1335A B ==,,,,则()B A C U ⋃等于( ) A.{}4,1 B.{}5,1 C.{}5,2 D.{}4,22.若cos sin 0αα⋅<,且cos 0α<,则角α是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角 3.下列不等式中正确的是( )A .若x y >,则22x y >B .若225x >,则5x >C .若0a b >>,则1/a <1/bD .若a b >,c d >,则ac bd >4.已知向量a =(1,2),b =(1,-3),则向量a 与b 的夹角等于( )A .45°B .60°C .120°D .135 5.已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos 2θ=( )A .45-B .35-C .35 D .456.“30A =︒”是“1sin 2A =”的 ( )A .充分不必要条件B .必要不充分条件C .既不充分也不必要条件D .充要条件 7.设集合A={3123|≤-≤-x x },集合B 为函数)1lg(-=x y 的定义域,则A ⋂B=( ) (A )(1,2 ] (B )[1,2] (C ) [ 1,2) (D )(1,2) 8.将函数y=sin2x 的图象向右平移4π个单位,再向上平移1个单位,所得函数图象对应 解析式为( ) A .sin(2)14y x π=-+B .22cos y x =C .22sin y x = D .cos 2y x =- 9.已知函数()f x 定义在R 上为偶函数,且(0,)x ∈+∞时, )(x f '>0,(3)0f =,解关于x 的不等式()0f x x>的解集为( ) A.(,3)(0,3)-∞-⋃ B.(,3)(3,)-∞-+∞ C.(0,3)(3,0)⋃- D.(3,0)(3,)-⋃+∞10. 对函数,sin )(x x x f ⋅=现有下列命题:①函数)(x f 是偶函数; ②函数)(x f 的最小正周期是;2π ③点)0,(π是函数)(x f 的图像的一个对称中心; ④函数)(x f 在区间]2,0[π上单调递增,在区间]0,2[π-上单调递减.其中是真命题的是( ).A ①③ .B ①④ .C ②③ .D ②④蚌埠铁中2012-2013年度高三第一学期期中考试数学(文)试卷答题卷一、 选择题:(每小题5分,共50分)二、填空题:(每小题5分,共25分)11.命题“∃x ∈R ,x 2-2x +4>0”的否定是 12.已知向量a =(3,1),b =(x ,-3),且a ⊥b ,则实数x =_______ 13..复数=-ii215_________________ 14.设数列{n a }的前n 项和2n S n = ,则=8a15.已知,53sin =α且),,2(ππα∈那么αα2cos 2sin 的值等于.________三、解答题:(本大题共6小题,共75分)16.(本小题12分)已知集合{26},{15}A x x B x x =≤≤=<<︱︱ 求,()R A B C A B ⋃⋂两位座位号 17.(本小题12分)已知不等式)0(0622≠<+-k k x x k ,如果不等式的解集是}23|{->-<x x x 或,求k 的值;18.(本小题12分)已知函数1()f x x x=+, (Ⅰ) 证明()f x 在[1,)+∞上是增函数; (Ⅱ) 求()f x 在[1,4]上的最大值及最小值.19.(本小题满分12分)等差数列{}n a 的前n 项和记为n S ,已知3010=a ,5020=a 。
安徽蚌埠铁路中学高三数学文科试卷

蚌埠铁中2019-2020学年度第一学期期中检测试卷高 三 数 学(文)考试时间:120分钟 试卷分值:150 分一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}(5)4A x x x =-,{}|B x x a =≤,若A B B ⋃=,则a 的值可以是( ) A. 1B. 2C. 3D. 42.已知i 为虚数单位,若复数11tiz i-=+在复平面内对应的点在第四象限,则t 的取值范围为( ) A. [1,1]- B. (1,1)- C. (,1)-∞- D. (1,)+∞3.已知1sin 123πα⎛⎫-= ⎪⎝⎭,则17cos 12πα⎛⎫+ ⎪⎝⎭的值等于( )A. 13C. 13- D. 4.若1,01a c b ><<<,则下列不等式不正确的是( ) A. 20192019log log a b > B. log log c b a a > C. ()()cbc b a c b a ->- D. ()()cba c a a c a ->-5.在等比数列{}n a 中,“412a ,a 是方程2x 3x 10++=的两根”是“8a 1=±”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件6.已知()f x 是定义在[2,1]b b -+上的偶函数,且在[2,0]b -上为增函数,则(1)(2)f x f x -≤的解集为( )A. 2[1,]3-B. 1[1,]3-C. [1,1]-D. 1[,1]37.《九章算术》教会了人们用等差数列的知识来解决问题,《张丘建算经》卷上第22题为:“今有女善织,日益功疾(注:从第2天开始,每天比前一天多织相同量的布),第一天织6尺布,现一月(按30天计)共织540尺布”,则从第2天起每天比前一天多织( )尺布. A.12B.2429 C. 1631 D. 16298.某几何体的三视图如图所示,则该几何体的体积为( )A. 5B.163C. 7D.1739.执行如图所示的程序框图,如果输出6T =,那么判断框内应填入的条件是( )A. 32k <B. 33k <C. 64k <D. 65k <10.函数()sin (0)f x x ωω=>的图象向右平移12π个单位得到函数()y g x =的图象,并且函数()g x 在区间[,]63ππ上单调递增,在区间[,]32ππ上单调递减,则实数ω的值为( ) A.74B.32C. 2D.5411.经过双曲线2222:1(0,0)x y M a b a b-=>>的左焦点作倾斜角为60︒的直线l ,若l交双曲线M 的左支于,A B ,则双曲线M 离心率的取值范围是( ) A ()2,+∞B. ()1,2C. (D.)+∞12.已知x ,y 满足约束条件20,{53120,3,x y x y y --≤--≥≤当目标函数z ax by =+(0a >,0b >)在该约束条件下取得最小值1时,则123a b+的最小值为( )A. 4+B.C. 3+D. 3二.填空题(共4小题,每小题5分,合计20分)13. 若函数()ln 2f x x ax =-的图象存在与直线20x y +=垂直的切线,则实数a 的取值范围是____.14.ABC ∆的内角,,A B C 的对边分别为,,a b c,已知)cos cos ,60a C c A b B -==︒,则A 的大小为__________.15.在平行四边形ABCD 中,已知1AB =,2AD =,60BAD ∠=︒,若 ,,则 =____________. 16.已知球O 是正三棱锥(底面为正三角形,顶点在底面射影为底面中心)A-BCD 的外接球,BC=3,AB =E 在线段BD 上,且BD=3BE ,过点E 作圆O 的截面,则所得截面圆面积的取值范围是__.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 第17题~第21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.) (一)必考题:共60分 17.(本小题满分10分)已知数列{}n a 是等差数列,前n 项和为n S ,且533S a =,468a a +=. (1)求n a .(2)设2nn n b a =⋅,求数列{}n b 的前n 项和n T .18. (本小题满分12分)如图所示,正四棱椎P ABCD -中,底面ABCD 的边长为2,侧棱长为E 为PD 的中点.(1)求证:PB 平面AEC ; (2)若F 为PA 上的一点,且3PFFA=,求三棱椎A BDF -的体积.19.(本小题满分12分)随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用等,其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元 新个税政策的税率表部分内容如下:(1)现有李某月收入19600元,膝下有一名子女,需要赡养老人,(除此之外,无其它专项附加扣除)请问李某月应缴纳的个税金额为多少?(2)现收集了某城市50名年龄在40岁到50岁之间的公司白领的相关资料,通过整理资料可知,有一个孩子的有40人,没有孩子的有10人,有一个孩子的人中有30人需要赡养老人,没有孩子的人中有5人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的50人中,任何两人均不在一个家庭).若他们的月收入均为20000元,试求在新个税政策下这50名公司白领的月平均缴纳个税金额为多少?20.(本小题满分12分)在平面直角坐标系中,()2,0A -,()2,0B ,设直线AC 、BC斜率分别为1k 、2k 且1212k k ⋅=- ,(1)求点C 的轨迹E 的方程;(2)过()F 作直线MN 交轨迹E 于M 、N 两点,若MAB △的面积是NAB △面积的2倍,求直线MN 的方程.21.(本小题满分12分)已知函数()()()ln f x x x ax a R =-∈.(1)若1a =,求函数()f x 的图像在点()()1,1f 处的切线方程;(2)若函数()f x 有两个极值点1x ,2x ,且12x x <,求证:()212f x >-. 的(二)选考题:(共10分。
安徽省蚌埠铁中2020届高三数学上学期期中考试文【会员独享】
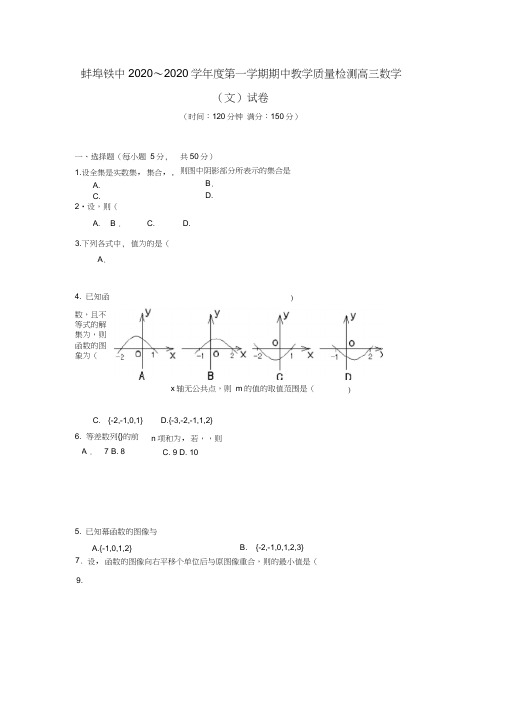
9.蚌埠铁中2020〜2020学年度第一学期期中教学质量检测高三数学(文)试卷(时间:120分钟 满分:150分)一、选择题(每小题 5分, 1.设全集是实数集,集合,, A.C.共50分)则图中阴影部分所表示的集合是B . D.2•设,则(A .4. 已知函数,且不等式的解集为,则函数的图象为(5. 已知幕函数的图像与B. {-2,-1,0,1,2,3}设,函数的图像向右平移个单位后与原图像重合,则的最小值是( A. B .C.D.3.下列各式中, 值为的是(C. {-2,-1,0,1} 6. 等差数列{}的前D.{-3,-2,-1,1,2} n 项和为,若,,则A . 7 B. 8C. 9D. 10A.{-1,0,1,2}7. ))x 轴无公共点,则 m 的值的取值范围是(9.C 充要条件 .既不充分也不必要条件已知则=( A .B10.设、分别是定义在R 上的奇函数和偶函数,当时,.且.则不等式的解集是A. (- 3,0) U (3,+ s )(—3,0) U (0, 3)8. A. B .已知且」厂'”是“”的A充分不必要条件 B .必要不充分条件C . ( —g ,- 3) U (3,+ g) (—g , —3) U (0, 3)蚌埠铁中2020〜2020学年度第一学期期中教学质量检测高三数学(文)答题卷、选择题(每小题5分,共50分)二•填空题(每小题5分,共25分)11. 已知,则12. 函数的单调递增区间是13. 已知等差数列的前项的和为,那么的最大值为14•设实数满足贝y的取值范围是_____ . _____15•设实数使得不等式对任意实数恒成立,则满足条件的所组成的集合是三.解答题(共6题,共75分,写出必要的文字说明)16.(本题满分12分)已知x>0, y>0, 且x+y=1,求的最小值。
17.(本题满分12 分)已知.(1)求sin x-cos x 的值;(2)求的值.18.(本题满分12 分)已知函数,常数.(1)讨论函数的奇偶性,并说明理由;(2)若函数在上为增函数,求的取值范围.19. (本题满分12分)已知函数f(x)=cos+2sin • sin.( 1)求函数f(x) 的最小正周期和图象的对称轴方程;( 2)求函数f(x) 在区间上的值域.20. (本题满分13 分)已知数列{a n}是首项为,公比为的等比数列,设(nN*),数列{}满足(1 ) 求数列{} 的通项公式;(2) 求数列{} 的前n 项和21 .(本题满分14分)已知定义在R上的函数,其中a为常数.(1)若x=1 是函数的一个极值点,求a 的值;(2)若函数在区间(一1, 0)上是增函数,求a的取值范围;(3)若函数,在x=0处取得最大值,求正数a的取值范围.蚌埠铁中2020〜2020学年度第一学期期中教学质量检测1-10CABBB BCABD11.12. (开闭区间都可)13. 2514.15.k € R成立。
