例;求图示刚架C点的竖向位移。各杆截面为矩形。ppt课件
合集下载
建筑结构力学--8位移计算1-PPT精品文档29页

1
0 1.5
N
材料 钢 筋 砼
杆件 N P N
l
A
N N Pl EA
AD 4.74P 1.58 0.263l Ac
1 .97 Pl Ec Ac
DC DE
4.42P 1.58 0.95P 0
0.263l Ac 0.088l0.75Ac
1 .84 Pl Ec Ac
0
NN Pl EA
3 .81 Pl Ec Ac
产生位移的原因
位移发生的位置
2、虚功原理
பைடு நூலகம்
虚力原理:在给定的位移状态与虚设的力状态之间应用虚
3、虚功原理
功原理,这种虚功原理的形式称为虚力原理。
虚位移原理:在给定的力状态与虚设的位移状态之间应用
虚功原理,这种虚功原理的形式称为虚位移原理。
30.11.2019
课件
5
三、虚力原理
c1 A a
A
R1
a
——虚设力系求刚体体系位移
d dsds
R
dds dds
刚体虚功原理求位移。
应用刚体虚功原理求位移d-即前例的结论。
d M N Q M d N d Q d
30.11.2019
课件
11
二、结构位移计算的一般公式
i
d(M N Q )ds i
1 2l
cA
A
1 2l
B
C
2
l
D
3 2l
所得正号表明位移方 向与假设的单位力方向 一致。
30.11.2019
课件
7
例1、悬臂梁在截面B处由于某种原因
例2、悬臂梁在截面B处由于某种原因
含无限刚性杆结构的位移法PPT课件
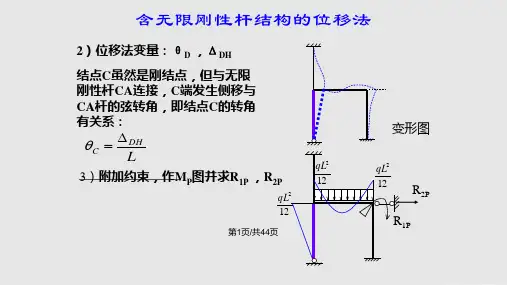
15/42 8/42
4/42
第31页/共44页
3.5/42
例7. 含弹簧支座结构的位移法
求作弯矩图,
KN
EI 16
q
A EI1
KN
B
2EI
EI
C EI 4m
4m
D
6m
E
解:1)位移法变量:θB ,第3θ2C页/共44页
例7. 含弹簧支座结构的位移法
2)附加约束,作MP图,并求R1P ,R2P
2)附加约束,作MP图,并求R1P ,R2P
7.5 kNm R1P
R2P
2kN
R1P VBC
R1P= -2+7.5/4= -0.125 R2P=0
第28页/共44页
例6. 含弹簧支座结构的位移法
3)...作M1图与M2图,求rij
3i/L
B
r11
C
8i/L
4i/L r21
B点侧移1,B、C结点各转角1/4
例4. 含无限刚性杆结构的位移法
3)...作M1图与M2图,求rij
Δ=1 C
A
θ=1/2
R11 先作出ΔBV=1时的变形图,观察各杆 的杆端侧移、转角情况。 AB杆:侧移Δ= -1 ,B端转角θ=1/2 ; BC杆:侧移Δ= 1,弦转角θ=1/2 ; CD杆:无侧移,C端转角θ第=118页/2/,共44页 DE杆:无侧移,无杆端转角。
第26页/共44页
例6.
求作弯矩图。 KM
4EI L
10 KN 2 kN
B A EI
EI1
EI C
EI
解:1)由于BC杆无限 刚性,C点无侧移,B 加水平支杆后,BC杆 无弦转角。位移法变量: 4m ΔBH ,θD D
结构力学(第三章)-图乘法

( M x tan ) 1 x tan M P dx EI tan
xM P dx
图乘法求位移公式为:
图乘法的 适用条件是 什么?
EI tan 1 xc yc EI EI
ip
yc
EI
例. 试求图示梁B端转角.
A
P
B B
MP
A
M 1 B 1
B
c
y c
ql 2 / 2
ql 2 / 8
例 4. 图示梁 EI 为常数,求C点竖向位移 。 q ql 2 / 8 ql 2 / 2
MP
A
l/2 C
1
q q
l/2
B
l/2
Mi
c
y c
C ql / 2 ql 2 / 8
ql 2 / 8 ql 2 / 4 ql 2 / 8
ql / 2
§3.4 图乘法及其应用
(Graphic Multiplication Method and its Applications)
刚架与梁的位移计算公式为:
iP MM P ds EI
在杆件数量多的情况下,不方便. 下面介绍 计算位移的图乘法.
一、图乘法
MM P ds EI 1 图乘法是Vereshagin于 M M P ds (对于等 截面杆) EI 1925年提出的,他当时 1 为莫斯科铁路运输学院 MM P dx (对于直杆) EI 的学生。
1 1
B
Mi
l
ql / 4
2
l
ql 2 / 4
1/ l
0 解:作荷载弯矩图和单位荷载弯矩图
q
MP
静定结构位移PPT课件
x
dx
M(x)
α
x
x0
M
y0
l M ( x) M ( x)dx
tg x M( x)dx l M图静矩 Sy tgα A x0
A y0
以上简化Mohr积分的方法
——图乘法
1. 二图同侧为+,反之为- ;
2. 其中一图必须是直线;
y0 须取自直线图
第26页/共52页
二.图形面积和形心
• 一次斜直线
F1
M T
N Q
变形体系的两状态:
外力与内力 (平衡)
彼此独立
位移与变形(连续协调) 互不无关
(荷载/支座移动/变温…)
变形体的虚功原理:
ds
∆
d
d
d
外虚功 =
(荷载/反力在 位移上作功)
内虚功 (内力在 变形上作功)
单位荷载求变形体系位移
ds d
Nd Qd Md Td
第10页/共52页
Rk Ck
MM EI
ds
ห้องสมุดไป่ตู้
NN EA
l
TT GIt
d
s
应用莫尔定理求位移时, 需计算下列形式积分:
M(x)M(x)dx
l
M(x)、M(x) 中,只要有一是线性(一次函数) ——以上积分即可简化:
一.方法
下设 M(x)图形是直线,
(直杆M(x)图必定是直线)
第25页/共52页
y y
O
M(x)
(M图形面积) M CA
1/l
l B
AB
AB
W
1 l
C
1 l
B
B
(力偶矩=1)
C B
第6章 静定结构位移计算

二、 单位荷载法 1、定义:在所求点所在位移方向加上单位 力,将实际状态的真实位移视作虚拟平衡状态的 虚位移。应用虚功原理,通过加单位荷载求实际 位移的方法。 2、计算结构位移的一般公式
F K+ FRiCi= M d + FNdu + FQdv
式中, F =1 则
六.线弹性体系的特征 1)结构的变形与其作用力成正比
若单位力P1=1作用下产生
的位移δ ,则力P作用下在 K处产生的位移为Pδ
2)结构的变形或位移服从叠加原理
P1
P2
Pi
K Δ
Pn
δ K i 表示Pi=1时 在K处产生的位移。
Δ= P1 K 1 P2 K 2 Pn Kn
P
i i 1
n
Ki
6.2 变形体系的虚功原理 一、变形体的虚功原理 功:力对物体作用的累计效果的度量。 功=力×力作用点沿力方向上的位移 实功 :力在自身引起的位移上所作的功 静力荷载:荷载由零逐渐以微小的增量缓慢地增加 到最终值。结构在静力加载过程中,荷载及内力始 终保持平衡。
虚功: 力在其他因素引起的位移上作的功 其特点是位移与作功的力无关,在作功的过程 中,力的大小保持不变 梁弯曲后,再在点2处加静力荷载FP2,梁产生新 的弯曲。位移△12为力FP2引起的FP1的作用点沿FP1 方向的位移。力FP1在位移△12 上作了功,为虚功, 大小为 W12=FP1△12,此时力不随位移而变化,是 常力。
单位广义力有截然相反的两种设向,计算出的 广义位移则有正负之分: 正值表示广义位移的方向与广义力所设的指向相同 负值表示广义位移的方向与广义力所设的指向相反
力的虚设方法
Fp=1 C Fp=1 B C
结构力学——静定结构位移计算 ppt课件

-FP ΔP +FB ΔB=0
ΔP
FP
FAx
ΔB
FAy
ppt课件
FB
第二节
变形体虚功原理
2 虚功原理 (1)刚体系的虚功原理
刚体系处于平衡的必要和充分条件是:对于任何可能的 虚位移,作用于刚体系的所有外力所做虚功之和为零。
(2)变形体的虚功原理
任何一个处于平衡状态的变形体,当发生任意一个虚位 移时,变形体所受外力在虚位移上所作的总虚功 We恒 等于变形体各微段外力在微段变形上作的虚功之和 Wi。
ppt课件
回顾
(1)质点系的虚功原理
具有理想约束的质点系,在某一位 置处于平衡的必要和充分条件是: 对于任何可能的虚位移,作用于质 点系的主动力所做虚功之和为零。也 即
FP1
FN 1
→. → Σfi δri=0
ppt课件
FP 2
m m
2
1
FN 2
(2)刚体系的虚功原理
去掉约束而代以相应的反力,该反力便可看成外力。 则有:刚体系处于平衡的必要和充分条件是: 对于任何可能的虚位移, 作用于刚体系的所有外力所做 虚功之和为零。
ppt课件
第一节
位移计算概述
建筑起拱
如屋架在竖向荷 载作用下,下弦 各结点产生虚线 所示位移。
将各下弦杆做得 比实际长度短些, 拼装后下弦向上 起拱。 在屋盖自重作用下,下弦各杆位于原设计的水平位置。
ppt课件
第一节
位移计算概述
3、产生位移的主要原因 各种因素对静定结构的影响
内力
荷载
温度改变或 材料胀缩 支座移动或 制造误差
dWz=dWe+dWi Wz= We+ Wi
1 2 作功双方其一是虚设的; 作功双方均是实际存在的,但彼此无关。 ppt课件
ΔP
FP
FAx
ΔB
FAy
ppt课件
FB
第二节
变形体虚功原理
2 虚功原理 (1)刚体系的虚功原理
刚体系处于平衡的必要和充分条件是:对于任何可能的 虚位移,作用于刚体系的所有外力所做虚功之和为零。
(2)变形体的虚功原理
任何一个处于平衡状态的变形体,当发生任意一个虚位 移时,变形体所受外力在虚位移上所作的总虚功 We恒 等于变形体各微段外力在微段变形上作的虚功之和 Wi。
ppt课件
回顾
(1)质点系的虚功原理
具有理想约束的质点系,在某一位 置处于平衡的必要和充分条件是: 对于任何可能的虚位移,作用于质 点系的主动力所做虚功之和为零。也 即
FP1
FN 1
→. → Σfi δri=0
ppt课件
FP 2
m m
2
1
FN 2
(2)刚体系的虚功原理
去掉约束而代以相应的反力,该反力便可看成外力。 则有:刚体系处于平衡的必要和充分条件是: 对于任何可能的虚位移, 作用于刚体系的所有外力所做 虚功之和为零。
ppt课件
第一节
位移计算概述
建筑起拱
如屋架在竖向荷 载作用下,下弦 各结点产生虚线 所示位移。
将各下弦杆做得 比实际长度短些, 拼装后下弦向上 起拱。 在屋盖自重作用下,下弦各杆位于原设计的水平位置。
ppt课件
第一节
位移计算概述
3、产生位移的主要原因 各种因素对静定结构的影响
内力
荷载
温度改变或 材料胀缩 支座移动或 制造误差
dWz=dWe+dWi Wz= We+ Wi
1 2 作功双方其一是虚设的; 作功双方均是实际存在的,但彼此无关。 ppt课件
结构力学(第五版)第六章 结构位移计算
相对位移 △CD= △C+ △D
3. 计算位移的目的
(1)校核结构的刚度。 (2)结构施工的需要。 (3)为分析超静定结构打 基础。
△ 起拱高度
除荷载外,还有一些因素如温度变化、支座移动、 材料收缩、制造误差等,也会使结构产生位移。 结构力学中计算位移的一般方法是以虚功原理为 基础的。本章先介绍变形体系的虚功原理,然后讨论 静定结构的位移计算。 返4回
B
变力 W= 1 M· ϕ 2
(d )
返6回
P
(2)实功与虚功 实功: 力本身引起的位移上所作的功。 例如: W=
A 力在其它 虚功: 因素引起的位移上所作 的功。力与位移是彼此无关的量,分别属于同一体系 的两种彼此无关的状态。
△2
2
A
P1
△1
1
B P2 B
例如:
W12=P1·△2
返7回
2. 变形体的虚功原理:
A RA
P
M
q B dS
q
RB N+dN Q+dQ
Q N 力状态 A
ds B dS
dWi=Ndu+QγdS+Mdϕ Wi=
(6—2)
整个结构内力的变形虚功为
虚功方程为
W=
(6—3)
dS du
dϕ
γ γ
dS
位移状态
dS
9
返dx γ回
§6—3 位移计算的一般公式
k 1. 位移计算的一般公式 t1 K △K t2 c3 K ds 设平面杆系结构由 ds k R 3 K′ 于荷载、温度变化及支 k P1 座移动等因素引起位移 du、dϕ、γdS N MQ 、、 如图示。 R 1 c2 求任一指定截面K K c1 2 沿任一指定方向 k—k 实际状态-位移状态 R 虚拟状态-力状态 上的位移△K 。
结构力学I-第五章 虚功原理与结构位移计算(温度位移、虚功、互等)
温度改变时的位移计算
结构位移计算的一般公式
普遍性
Δ = ∑ ∫ ( Mκ + FNε + FQγ0 ) ds- ∑FRK·cK
⑵ 变形因素:荷载、温度改变或支座移动引起的位移;
温度改变的位移计算公式
应用背景
Page 10
14:26
LOGO
温度改变时的位移计算
温度改变的位移计算公式
基本假设
FQ FN
dFN
pdx
0
dFQ qdx 0
dM FQdx 0
• 集M M 0 0
M
FQ FN
M
Page 22
q
FQ+ dFQ
p
FN+ dFN
O
x
M+ dM dx
y
dx
M0 O
Fx
Fy y
FQ+ ΔFQ FN+ ΔFN x
M+ ΔM
14:26
D 1
α=1×10-5,求D点的竖向位移ΔDV。
2m 2m
解:⑴ 在D点作用一向上的单位力F=1,
4m
作弯矩图 M 和轴力图 F N;
⑵ 由于各杆 α,t0,Δt,h 相同,
故可先计算
+1
1
M ds
1 2
4
4
4
4
24(m2
)
M
FN
F Nds 1 2 1 4 2(m)
Page 15
14:26
LOGO
结构力学I
第五章 虚功原理与 结构位移计算
2021年4月15日
LOGO
3-12(g)
指出弯矩图错误并改正;
作业点评
结构力学第四章位移计算-精品文档45页
Q0l1.2G qxA dx0.G 6qA 2l
M
lqx3 dxql4 02EI 8EI
l qx 0.6q2l A
Q01.2G
dx A
GA
q
B
L
Q 4.8 EI
M
GA2l
E 2(1) 8
G
3
I h2 A 12
M Q 4.8GEA 2Il1.06(h 7 l)2
2F Pd(22)6.8F aphic Multiplication Method
一 图乘法应用条件与计算公式
梁和刚架在荷载作用下的位移计算式
MMPd EI
s
当结构的各杆段符合下列条件时:
(1)杆轴为直线; (2)各段EI=常数; (3)两个弯矩图中至少有一个是直线图形 则可用下述图乘法来代替积分运算,从而简化计算工作
形相乘法的计算位移的方法,简称为图乘法
根据上面的推证过程,可知在使用图乘法时应注意下列各点:
(1)必须符合上述三个条件
(2)纵距 y 0只能取自直线图形
(3)A与 y 0 若在杆件的同侧则乘积取正号,否则取负号
常用的几种图形的面积和形心
2l/3
l/3
a
b
A
形心
l
h
h
形心
A
(l+a)/3
(l+b)/3
第四章 结构位移计算
§4.1 概述
一 结构的位移
在荷载、温度改变、支座移动等外因作用下,结构上各点 各截面发生移动、转动,这些移动和转动统称为结构位移
A △Ay
A △A
A′ A′
△Ax
θA
△A A A′
材料力学PPT课件14-第十四讲-平面刚架空间受力-位移法
位移法应用: •圆轴扭转横截面切应力推导; •直梁弯曲横截面正应力推导。
例题
求图示桁架各杆的轴力,EiAi,li 与 i 均为已知
1. 问题分析 变形 li 可用位移 u 与 v 表示 轴力 FNi 也可用位 移 u 与 v 表示 由平衡条件确定 u 与 v 力法解-n-2个未知量;位移法解-2个基本未知量
转角 θ= 0
仅存在反对称性内力 -剪力 FS
而M=0,FN= 0 横向挠度 f = 0
§4 平面刚架空间受力分析
平面刚架空间受力及其特点 平面静不定刚架空间受力分析
平面刚架空间受力及其特点 平面刚架空间受力
平面刚架-轴线位于同一平面的刚架 空间受力-外载荷均垂直于刚架的轴线平面
变形与受力的特点
1. 问题分析
n-1度静不定, n大时力法 求解不便
确定后, li 与FNi 亦确定 2. 以 为基本未知量求解
三 方
li ai
FNi
n
Ei Ai li
ai
面 M A 0, FNiai Fa 0
i 1
n
i 1
Ei Ai li
ai2
Fa
0
n Fal FNi
Ei Aiai2
i 1
第十四讲
第十四章 静不定问题分析
§1 引言 §2 用力法分析静不定问题 §3 对称与反对称静不定问题分析 上讲回顾 §4 平面刚架空间受力分析
第十八章 杆与杆系分析的计算机方法
§1 位移法概念
对称面上受力与变形特点——特点
对 称 承 载
反 对 称 承 载
仅存在对称性内力- 弯矩M与轴力FN,
而剪力 FS = 0 轴向位移 Δ= 0
2Me GI p
例题
求图示桁架各杆的轴力,EiAi,li 与 i 均为已知
1. 问题分析 变形 li 可用位移 u 与 v 表示 轴力 FNi 也可用位 移 u 与 v 表示 由平衡条件确定 u 与 v 力法解-n-2个未知量;位移法解-2个基本未知量
转角 θ= 0
仅存在反对称性内力 -剪力 FS
而M=0,FN= 0 横向挠度 f = 0
§4 平面刚架空间受力分析
平面刚架空间受力及其特点 平面静不定刚架空间受力分析
平面刚架空间受力及其特点 平面刚架空间受力
平面刚架-轴线位于同一平面的刚架 空间受力-外载荷均垂直于刚架的轴线平面
变形与受力的特点
1. 问题分析
n-1度静不定, n大时力法 求解不便
确定后, li 与FNi 亦确定 2. 以 为基本未知量求解
三 方
li ai
FNi
n
Ei Ai li
ai
面 M A 0, FNiai Fa 0
i 1
n
i 1
Ei Ai li
ai2
Fa
0
n Fal FNi
Ei Aiai2
i 1
第十四讲
第十四章 静不定问题分析
§1 引言 §2 用力法分析静不定问题 §3 对称与反对称静不定问题分析 上讲回顾 §4 平面刚架空间受力分析
第十八章 杆与杆系分析的计算机方法
§1 位移法概念
对称面上受力与变形特点——特点
对 称 承 载
反 对 称 承 载
仅存在对称性内力- 弯矩M与轴力FN,
而剪力 FS = 0 轴向位移 Δ= 0
2Me GI p
