2019年春季高考数学模拟试题答案
2019年山东省春季高考数学模拟试题及答案
→ → → → 21．已知| a |=4，| b |=1，<→ a ，→ b >=120°，则| a –2 b |＝__________． 7 22．函数 f (x)＝－sin2x＋sin x＋ 的最小值是____________． 4
10．过直线 x＋y＋2＝0 与 x－y＝0 的交点，且法向量→ n ＝(－2，3) 的直线方程是（ A．– 3x＋2y＋1＝0 C．－2x＋3y＋1＝0 B．3x－2y＋1＝0 D．2x－3y＋1＝0 ）
11．在△ABC 中，边 a, b, c 成等比数列，且 a2－c2＝ac－bc，则A 的大小是（ A．30 B．60 C．150 D．120
8．已知角 ( A．
4 3
3 3 , 2 ),sin , 则 tan 等于（ ） 2 5 3 4 B． C． 4 3
D．
3 4
）
9．从 1，2，…，9 这九个数中，随机抽取 2 个不同的数，则这 2 个数的和为偶数的概率是（ 5 A． 9 4 B． 9 11 C． 21 10 D． 21 ）
2．设 p、q 是两个命题，并且 p q 是真命题，则下列的命题为真命题的是（ A． p q B． p q ） B． {x|x＜－1 或 x＞4} D． {x|x＜－4 或 x＞1} ）
D． p q 12．若函数 f ( x) 是定义在 R 上的奇函数，当 x (0,) 时， f ( x) x 1 ，则使得 f ( x) 0 的 x 的取值范围是 （ A． (1,0) ） C．(−∞, −1) ∪(1, ＋∞) D． (1,0) ∪ (1,) ）
山东省2019年普通高校招生(春季)考试 数学试题-答案
山东省2019年普通高校招生(春季)考试数学试题答案及评分标准卷一(选择题 共60分)一㊁选择题(本大题20个小题,每小题3分,共60分)1.C2.A3.B4.A5.D6.C7.A8.D9.C 10.B 11.B 12.D 13.C 14.D15.A 16.B 17.C 18.D 19.B 20.C 卷二(非选择题 共60分)二㊁填空题(本大题5个小题,每小题4分,共20分)21.36ʎ 22.-4 23.54 24.2ʌ填1.41亦可ɔ 25.y =ʃ62x 三㊁解答题(本大题5个小题,共40分)26.(本小题7分)解:因为f (1)=-1,f (3)=-1,所以二次函数f (x )的对称轴为x =1+32=2,2分 又因为函数f (x )图像的顶点在直线y =2x -1上,则联立方程组x =2,y =2x -1,{解得x =2,y =3,{1分 故函数f (x )图像的顶点坐标为(2,3).1分 可设二次函数的解析式为f (x )=a (x -2)2+3,1分因为f (1)=-1,则a (1-2)2+3=-1,解得a =-4,1分 所以f (x )=-4(x -2)2+3,即f (x )=-4x 2+16x -13.1分 (第27题图)27.(本小题8分)解:(1)由图像可知,函数f (x )的最大值是2,最小值是-2,A >0,所以A =2.1分因为5π12-π6=π4,π4是最小正周期的14,所以函数f (x )的最小正周期T =π4ˑ4=π,故2πω=π,解得ω=2,1分 东博文化传媒可得函数f (x )=2s i n (2x +φ),又因为函数f (x )图像经过点π6,0æèçöø÷,所以2s i n 2ˑπ6+φæèçöø÷=0,即s i n π3+φæèçöø÷=0,1分 因此π3+φ=2k π,k ɪZ ,解得φ=2k π-π3,k ɪZ ,又因为|φ|<π2,所以φ=-π3,1分 所以该函数的解析式为f (x )=2s i n 2x -π3æèçöø÷.1分 (2)因为f (x )ȡ1,所以2s i n 2x -π3æèçöø÷ȡ1,即s i n 2x -π3æèçöø÷ȡ12,1分 所以π6+2k πɤ2x -π3ɤ5π6+2k π,k ɪZ ,1分 即π4+k πɤx ɤ7π12+k π,k ɪZ ,故当f (x )ȡ1时,实数x 的取值范围是x π4+k πɤx ɤ7π12+k π,k ɪZ {}.1分 注:x 的取值范围写为 π4+k π,7π12+k πéëêêùûúú,k ɪZ ,亦可.(第28题图)28.(本小题8分)(1)证明:因为平面S A C ʅ平面A B C ,平面S A C ɘ平面A B C =A C ,且S A ʅA C ,所以S A ʅ平面A B C ,2分又因为B C ⊂平面A B C ,所以S A ʅB C ,1分又因为A B ʅB C ,S A ɘA B =A ,所以B C ʅ平面S A B .1分 (2)解:由(1)知,S A ʅ平面A B C ,所以点S 到平面A B C 的距离即为线段S A 的长度.1分 并且可知,S B 在平面A B C 内的射影为A B ,1分所以øS B A 即为S B 与平面A B C 所成角,即øS B A =30ʎ,1分 在R t әS A B 中,øS A B =90ʎ,øS B A =30ʎ,S B =2,所以S A =12S B =1,所以点S 到平面A B C 的距离是1.1分东博文化传媒(第29题图)29.(本小题8分)解:(1)因为四边形F 1B 2F 2B 1为正方形,所以|F 1F 2|=|B 1B 2|.因为|F 1F 2|=2c ,|B 1B 2|=2b ,所以c =b ,1分 因为a 2=b 2+c 2,所以a =2b ,1分因此椭圆的方程可化为x 22b 2+y 2b2=1,因为椭圆经过点P 1,22æèçöø÷,所以12b 2+22æèçöø÷2b 2=1,解得b =1,故a =2b =2,1分所以椭圆的标准方程是x 22+y 2=1.1分 (2)由(1)可知c =1,1分 设双曲线的实半轴长为a ',因为e =322,且双曲线与椭圆有公共的焦点,故c a '=322,即1a '=322,解得a '=23.1分 由椭圆和双曲线的定义可知|M F 1|+|M F 2|=2a ,|M F 1|-|M F 2|=2a ',{即|M F 1|+|M F 2|=22,|M F 1|-|M F 2|=223,ìîíïïïï1分 解得|M F 1|=423,|M F 2|=223,ìîíïïïïï所以线段M F 1,M F 2的长度分别是423,223.1分 注:线段M F 1,M F 2的长度分别写为 1.89,0.94,亦可.30.(本小题9分)解:(1)由题意知,自2018年起,每年的人口总数构成等差数列{a n },其中首项a 1=50,公差d =1.5,1分通项公式为a n =a 1+(n -1)d =50+(n -1)ˑ1.5,2分 设第n 项a n =60,即50+(n -1)ˑ1.5=60,解得n =7.7,1分 因为n ɪN +,所以n =8,2018+8-1=2025.答:到2025年年底,该城市人口总数达到60万.1分 (2)由题意知,自2018年起,每年的绿化面积数构成数列{b 1},其中b 1是2018年年底的绿化面积数,b 1=35,b 2是2019年年底的绿化面积数,b 2=35ˑ(1+5%)-0.1=35ˑ1.05-0.1,东博文化传媒b 3是2020年年底的绿化面积数,b 3=(35ˑ1.05-0.1)ˑ1.05-0.1=35ˑ1.052-0.1ˑ1.05-0.1, b k 是(2018+k -1)年年底的绿化面积数,b k =35ˑ1.05k -1-0.1ˑ1.05k -2-0.1ˑ1.05k -3- -0.1ˑ1.05-0.1,1分 =35ˑ1.05k -1-0.1ˑ(1-1.05k -1)1-1.05.1分 设b k =60ˑ0.9,即35ˑ1.05k -1-0.1ˑ(1-1.05k -1)1-1.05=60ˑ0.9,解得k ʈ10.3,1分 因为k ɪN +,所以k =11,2018+11-1=2028.答:到2028年年底,该城市人均绿化面积达到0.9平方米.1分 东博文化传媒。
201x年山东省春季高考数学试题及答案
山东省2019年普通高校招生（春季）考试数学试题1．本试卷分卷一（选择题）和卷二（非选择题）两部分，满分120分，考试时间120分钟。
考生清在答题卡上答题，考试结束后，请将本试卷和答题卡一并交回。
2．本次考试允许使用函数型计算器，凡使用计算器的题目，除题目有具体要求外，最后结果精确到0.01。
卷一（选择题共60分）一、选择题（本大题20个小题，每小题3分，共60分。
在每小题列出的四个选项中，只有一项符合题目要求，请将符合题目要求的选项字母代号选出．并填涂在答题卡上）1. 已知集合M={0,1}，N={1,2}，则M ∪N 等于（ ）A. {1}B. {0,2}C. {0,1,2}D. 2. 若实数a ，b 满足ab>0，a+b>0，则下列选项正确的是（ ）A. a>0，b>0B. a>0，b<0C. a<0，b>0D. a<0，b<0 3. 已知指数函数y=a x ，对数函数y=log b x 的图像如图所示，则下列关系式正确的是（ ） A. 0<a<b<1 B. 0<a<1<b C. 0<b<1<a D. a<0<1<b4. 已知函数f(x)=x 3+x ，若f(a)=2，则f(-a)的值是（ ）A. -2B. 2C. -10D. 10 5. 若等差数列{a n }的前7项和为70，则a 1+a 7等于（ ）A. 5B. 10C. 15D. 206. 如图所示，已知菱形ABCD 的边长是2，且∠DAB =60°，则AB AC ⋅ 的值是（ ） A. 4 B. 423+ C. 6 D. 423-7. 对于任意角α，β，“α=β”是“sinα=sin β”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 8. 如图所示，直线l ⊥OP ，则直线l 的方程是（ ）yx y Oy=a xy=log b 第3题 图 ABD第6题 图A. 3x －2y=0B. 3x+2y －12=0C. 2x －3y+5=0D. 2x+3y －13=09. 在（1+x ）n 的二项展开式中，若所有项的系数之和为64，则第3项是（ ） A. 15x 3 B. 20x 3 C. 15x 2 D. 20x 210. 在Rt ABC 中，∠ABC =90°，AB=3，BC=4，M 是线段AC 上的动点. 设点M 到BC 的距离为x ， MBC 的面积为y ，则y 关于x 的函数是（ ） A. y=4x ，x∈(0,4] B. y=2x ，x∈(0,3] C. y=4x ，x∈(0,)+∞ D. y=2x ，x∈(0,)+∞ 11. 现把甲、乙等6位同学排成一排，若甲同学不能排在前两位，且乙同学必须排在甲同学前面（相邻或不相邻均可），则不同排法的种树是（ ）A. 360B. 336C. 312D. 240 12. 设集合M={-2，0，2，4}，则下列命题为真命题的是（ ） A. ,a M ∀∈ a 是正数 B. ,b M ∀∈ b 是自然数 C. ,c M ∃∈ c 是奇数 D. ,d M ∃∈ d 是有理数 13. 已知sinα=12，则cos2α的值是（ ） A.89 B. 89- C. 79 D. 79- 14. 已知y=f(x)在R 上是减函数，若f(|a |+1)<f(2)，则实数a 的取值范围是（ ）A. （－∞，1）B. （－∞，1）∪（1，+∞）C. （－1，1）D.（－∞，－1）∪（1，+∞） 15. 已知O 为坐标原点，点M 在x 轴的正半轴上，若直线MA 与圆x 2+y 2=2相切于点A ，且|AO|=|AM|，则点M 的横坐标是（ ） A. 2 B.2 C. 22 D. 416. 如图所示，点E 、F 、G 、H 分别是正方体四条棱的中点，则直线EF 与GH 的位置关系是（ ） A. 平行 B. 相交 C. 异面 D. 重合17. 如图所示，若x ，y 满足线性约束条件 2 01x y x y -+⎧⎪⎨⎪⎩≥≤≥ ， 则线性目标函数z=2x-y 取得最小值时的最优解是（ ） A. （0，1） B. （0，2） C. （-1，1） D . （-1，2）18. 箱子中放有6张黑色卡片和4张白色卡片，从中任取一张，恰好取得黑色卡片的概率是（ ）EFGH第16题 图A. 16B. 13C. 25D. 3519. 已知抛物线的顶点在坐标原点，对称轴为坐标轴，若该抛物线经过点M（-2，4），则其标准方程是（）A. y2=-8xB. y2=－8x 或x2=yC. x2=yD. y2=8x 或x2=－y20. 已知ABC的内角A，B，C的对边分别是a，b，c，若a=6，sinA=2cosBsinC，向量m =(3)a b,向量n=(－cosA，sinB)，且m∥n，则ABC的面积是（）333 D. 3卷二（非选择题共60分）二、填空题（本大题5个小题，每小题4分，共20分。
2019年山东春季高考数学真题(含答案)
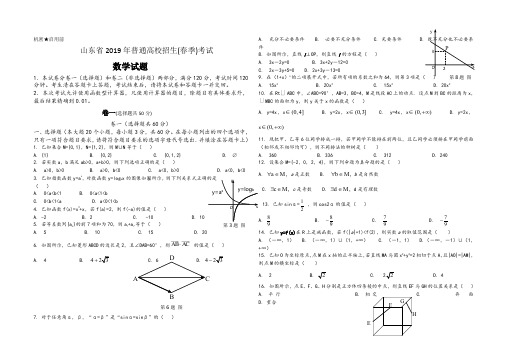
机密★启用前山东省2019年普通高校招生(春季)考试数学试题1．本试卷分卷一（选择题）和卷二（非选择题）两部分，满分120分，考试时间120分钟。
考生清在答题卡上答题，考试结束后，请将本试卷和答题卡一并交回。
2．本次考试允许使用函数型计算器，凡使用计算器的题目，除题目有具体要求外，最后结果精确到0.01。
卷一(选择题共50分)卷一（选择题共60分）一、选择题（本大题20个小题，每小题3分，共60分。
在每小题列出的四个选项中，只有一项符合题目要求，请将符合题目要求的选项字母代号选出．并填涂在答题卡上）1. 已知集合M={0,1}，N={1,2}，则M ∪N 等于（ ）A. {1}B. {0,2}C. {0,1,2}D. ∅ 2. 若实数a ，b 满足ab>0，a+b>0，则下列选项正确的是（ ）A. a>0，b>0B. a>0，b<0C. a<0，b>0D. a<0，b<0 3. 已知指数函数y=a x，对数函数y=log b x 的图像如图所示，（ ）A. 0<a<b<1B. 0<a<1<bC. 0<b<1<aD. a<0<1<b4. 已知函数f(x)=x 3+x ，若f(a)=2，则f(-a)的值是（ ）5. 若等差数列{a n }的前7项和为70，则a1+a 7等于（ ）A. 5B. 10C. 15D. 20 6. 如图所示，已知菱形ABCD 的边长是2，且∠DAB =60°，则AB AC ⋅ 的值是（ ）A. 4B. 4+-7. 对于任意角α，β，“α=β”是“sinα=sin β”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件件 8. 如图所示，直线l ⊥OP ，则直线l 的方程是（ ） A. 3x －2y=0 B. 3x+2y －12=0C. 2x －3y+5=0D. 2x+3y －13=09. 在（1+x ）n的二项展开式中，若所有项的系数之和为64，则第3A. 15x 3 B. 20x 3 C. 15x 2 D. 20x 210. 在RtABC 中，∠ABC =90°，AB=3，BC=4，M 是线段AC 上的动点. 设点M 到BC 的距离为x ，MBC 的面积为y ，则y 关于x 的函数是（ ）A. y=4x ，x∈(0,4]B. y=2x ，x∈(0,3]C. y=4x ，x∈(0,)+∞D. y=2x ，x∈(0,)+∞11. 现把甲、乙等6位同学排成一排，若甲同学不能排在前两位，且乙同学必须排在甲同学前面（相邻或不相邻均可），则不同排法的种树是（ ）A. 360B. 336C. 312D. 240 12. 设集合M={-2，0，2，4}，则下列命题为真命题的是（ ） A. ,a M ∀∈ a 是正数 B. ,b M ∀∈ b 是自然数 C. ,c M ∃∈ c 是奇数 D. ,d M ∃∈ d 是有理数13. 已知sinα=12，则cos2α的值是（ ） 89 B. 89- C.79 D. 79- 14. 已知y=f(x)在R 上是减函数，若f(|a |+1)<f(2)，则实数a 的取值范围是（ ）A. （－∞，1）B. （－∞，1）∪（1，+∞）C. （－1，1）D.（－∞，－1）∪（1，+∞）15. 已知O 为坐标原点，点M 在x 轴的正半轴上，若直线MA 与圆x 2+y 2=2相切于点A ，且|AO|=|AM|，则点M 的横坐标是（ ）D. 416. 如图所示，点E 、F 、G 、H 分别是正方体四条棱的中点，则直线EF 与GH 的位置关系是（ ） A. 平行 B. 相交 C. 异面 D. 重合y第3题 图B第6题 图EFGH17. 如图所示，若x ，y 满足线性约束条件 2 0 0 1x y x y -+⎧⎪⎨⎪⎩≥≤≥ ， 则线性目标函数z=2x-y 取得最小值时的最优解是（ ） A. （0，1） B. （0，2） C. （-1，1） D . （-1，2）18. 箱子中放有6张黑色卡片和4张白色卡片，从中任取一张，恰好取得黑色卡片的概率是（ ）A. 16B. 13C. 25D. 3519. 已知抛物线的顶点在坐标原点，对称轴为坐标轴，若该抛物线经过点M （-2，4），则其标准方程是（ ） A. y 2=-8x B. y 2=－8x 或x 2=y C. x 2=y D. y 2=8x 或x 2=－y 20. 已知ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，若a =6，sinA=2cosBsinC ，向量m=()a ,向量n =(－cosA ，sinB)，且m ∥n ，则ABC 的面积是（ ）卷二（非选择题 共60分）二、填空题（本大题5个小题，每小题4分，共20分。
19年春考数学试题及答案
19年春考数学试题及答案一、选择题（每题4分，共40分）1. 若函数f(x)=x^2-4x+3，则f(1)的值为：A. 0B. 1C. 2D. 32. 已知等差数列{an}的首项a1=2，公差d=3，则a5的值为：A. 14B. 17C. 20D. 233. 若复数z=1+i，则|z|的值为：A. 1C. 2D. √34. 已知函数f(x)=x^3-3x^2+2，求f'(x)的值为：A. 3x^2-6xB. x^2-3xC. 3x-6D. x^3-3x^25. 若直线l的方程为y=2x+1，且与x轴交于点A，求A的坐标为：A. (0,1)B. (1,0)C. (-1/2,0)D. (1/2,0)6. 已知向量a=(3,-2)，b=(2,1)，则a·b的值为：A. 4C. -2D. -47. 若函数f(x)=x^2-6x+8，求f(x)的最小值：A. -4B. 2C. 8D. 108. 已知双曲线C的方程为x^2/9-y^2/16=1，求其渐近线方程为：A. y=±4/3xB. y=±2/3xC. y=±4/3xD. y=±2/3x9. 已知圆C的方程为(x-1)^2+(y+2)^2=9，求圆心C的坐标为：A. (1,-2)B. (-1,2)C. (1,2)D. (-1,-2)10. 若函数f(x)=sin(x)+cos(x)，则f(π/4)的值为：A. √2B. 1C. 2D. 0二、填空题（每题4分，共20分）11. 已知等比数列{bn}的首项b1=1，公比q=2，则b3的值为______。
12. 若函数f(x)=x^2-4x+3，则f(-1)的值为______。
13. 已知向量a=(1,2)，b=(-3,2)，则|a+b|的值为______。
14. 若直线l的方程为x-2y+3=0，则l与y轴交于点B，求B的坐标为______。
15. 已知圆C的方程为x^2+y^2-6x+8y-24=0，求圆C的半径r为______。
2019山东省春季高考模拟试题数学附答案
1．已知全集 U={1，2}，集合 M={1}，则∁UM 等于（ A．∅ B．{1} C．{2} D．{1，2} 【考点】1F：补集及其运算． 【分析】根据补集的定义求出 M 补集即可．
）
【解答】解：全集 U={1，2}，集合 M={1}，则∁UM={2}． 故选：C．
3．下列函数中，在区间（﹣∞，0）上为增函数的是（
1
）
A．y=x B．y=1 C．
D．y=|x|
【考点】3E：函数单调性的判断与证明． 【分析】根据基本初等函数的单调性，判断选项中的函数是否满足条件即可． 【解答】解：对于 A，函数 y=x，在区间（﹣∞，0）上是增函数，满足题意； 对于 B，函数 y=1，在区间（﹣∞，0）上不是单调函数，不满足题意； 对于 C，函数 y= ，在区间（﹣∞，0）上是减函数，不满足题意； 对于 C，函数 y=|x|，在区间（﹣∞，0）上是减函数，不满足题意． 故选：A．
， 得：
直线的斜率 k=﹣3， 故直线方程是：y+2=﹣3（x﹣1） ， 整理得：3x+y﹣1=0， 故选：A．
11． 文艺演出中要求语言类节目不能相邻， 现有 4 个歌舞类节目和 2 个语言类节 目， 若从中任意选出 4 个排成节目单， 则能排出不同节目单的数量最多是 （ A．72 B．120 C．144 D．288 【考点】D8：排列、组合的实际应用． 【分析】根据题意，分 3 种情况讨论：①、取出的 4 个节目都是歌舞类节目，②、 取出的 4 个节目有 3 个歌舞类节目，1 个语言类节目，③、取出的 4 个节目有 2 个歌舞类节目，2 个语言类节目，分别求出每种情况下可以排出节目单的数目， 由分类计数原理计算可得答案． 【解答】解：根据题意，分 3 种情况讨论： ①、 取出的 4 个节目都是歌舞类节目， 有 1 种取法， 将 4 个节目全排列， 有 A44=24 种可能，即可以排出 24 个不同节目单， ②、取出的 4 个节目有 3 个歌舞类节目，1 个语言类节目， 有 C21C43=8 种取法，将 4 个节目全排列，有 A44=24 种可能， 则以排出 8×24=192 个不同节目单， ③、取出的 4 个节目有 2 个歌舞类节目，2 个语言类节目，
2019年山东省春季高考数学模拟试题及答案
第 1页
9．要得到函数 y=sin2x 的图像，需要将函数 y=sin( A.向左平移 B.向右平移 C.向左平移
的图像作怎样的平移才能得到（ D.向右平移
）
10．如图所示，设 A，B 两点在河的两岸，一测量者在 A 所在的同侧河岸边选定一点 C， 测出 AC 的距离为 50 m，∠ACB＝45°，∠CAB＝105°后，就可以计算出 A，B 两点的距离为( )
19. 设 a (1, 2) ， b (1,1) ， c a kb ．若 b c ，则实数 k 的值等于（
A． 20.
）
5 3
B． 5 3C来自 3 2D．3 2
)
的展开式中各项系数之和为 64，则展开式的常数项为(
（数学试题共 7页）
第 3页
A．－540
(
D. 2 ）
7. 已知等差数列{an}中，若 a4=15，则它的前 7 项和为（
D．105 ） D． （4,0）
8．已知 AB ( 5, 3), C (1, 3), CD 2 AB,则点 D 的坐标是（ A． （11，-3） B． （9，-3） C． （9,3）
（数学试题共 7页）
C．{－1,0,1} )．
2
2. 命题“对任意 x∈R，都有 x2≥0”的否定为( A．对任意 x∈R，都有 x ＜0 C．存在 x0∈R，使得 x0 ≥0
2 2
B．存在 x0∈R，使得 x0 ＜0 D．不存在 x∈R，使得 x ＜0 ） D．a=3,b=6
2
3. 已知 x a b 的解集是 {x 3 x 9} ，则实数 a,b 的值是（ A．a= -3, b=6 4. 已知 f (2 x ) log2 A．-1 B．a= -3, b= -6 C．a=6,b=3 ) D． 2
(完整版)2019年山东省春季高考数学试题及答案.doc
山东省 2019 年普通高校招生（春季）考试数学试题1．本试卷分卷一（选择题）和卷二（非选择题）两部分，满分120 分，考试时间120 分钟。
考生清在答题卡上答题，考试结束后，请将本试卷和答题卡一并交回。
2．本次考试允许使用函数型计算器，凡使用计算器的题目，除题目有具体要求外，最后结果精确到 0.01。
卷一（选择题共60 分）一、选择题（本大题 20 个小题，每小题 3 分，共 60 分。
在每小题列出的四个选项中，只有一项符合题目要求，请将符合题目要求的选项字母代号选出．并填涂在答题卡上）1. 已知集合 M={0,1} ，N={1,2}，则 M∪ N 等于（）A. {1}B. {0,2}C. {0,1,2}D.2. 若实数 a， b 满足 ab>0 ， a+b>0 ，则下列选项正确的是（）A. a>0 ， b>0B. a>0 ， b<0yC. a<0 ， b>0D. a<0 ， b<03. 已知指数函数y=a x，对数函数 y=log b x的图像如图所示，则下列关系式正确的是（y）y=log b y=a xA. 0<a<b<1B. 0<a<1<bO x C. 0<b<1<a D. a<0<1<b4. 已知函数 f(x)=x 3 +x ，若 f(a)=2 ，则 f(-a) 的值是（）第 3 题图A. -2B. 2C. -10D. 105. 若等差数列 {a n }的前 7 项和为 70 ，则 a 1+a 7等于（）A. 5B. 10C. 15D. 20uuur uuur6. 如图所示，已知菱形ABCD 的边长是 2 ，且∠ DAB =60 °，则AB AC 的值是（）A. 4B. 4 2 3C. 6D. 4 2 3DA CB第 6 题图7. 对于任意角α，β，“ α = β ”是“ sinα =sin β”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件8. l⊥ OP ，则直线 l 的方程是（y如图所示，直线）A. 3x － 2y=0B. 3x+2y － 12=0 3PC. 2x － 3y+5=0D. 2x+3y － 13=0 O2 x9. 在（ 1+x ）n的二项展开式中，若所有项的系数之和为64 ，则第 3 项是（第 8 题图）A. 15x 3B. 20x 3C. 15x 2D. 20x 210. 在 RtV ABC 中，∠ ABC =90 °，AB=3 ， BC=4 ， M 是线段 AC 上的动点 . 设点 M 到 BC 的距离为 x ，V MBC的面积为y，则y关于x的函数是（）A. y=4x ， x ∈(0, 4]B. y=2x ， x ∈(0,3]C. y=4x ， x ∈(0, )D. y=2x ， x ∈(0,)11.现把甲、乙等 6 位同学排成一排，若甲同学不能排在前两位，且乙同学必须排在甲同学前面（相邻或不相邻均可），则不同排法的种树是（）A. 360B. 336C. 312D. 24012. 设集合 M={-2 ， 0 ， 2 ， 4} ，则下列命题为真命题的是（）A. a M , a 是正数B. b M , b是自然数C. c M , c 是奇数D. d M , d 是有理数13. 已知 sin1α的值是（）α=，则 cos22A. 8B. 8C. 7D. 79 9 9 914. 已知 y=f(x) 在 R 上是减函数，若f(| a|+1)<f(2) ，则实数 a 的取值范围是（）A. （－∞，1 ）B. （－∞， 1 ）∪（ 1 ，+∞）C. （－ 1 ， 1 ）D.（－∞，－ 1 ）∪（ 1， +∞）15.已知 O 为坐标原点，点 M 在 x 轴的正半轴上，若直线 MA 与圆 x2 +y 2=2 相切于点 A ，且 |AO|=|AM| ，则点 M 的横坐标是（）A. 2B.2C.22D. 416. 如图所示，点 E 、F 、 G 、 H 分别是正方体四条棱的中点，则直线 EF 与 GH 的位置关系是（）A. 平行B. 相交C.异面D. 重合FGHE第 16 题 图x y 2 ≥017. 如图所示，若 x ，y 满足线性约束条件x ≤0，y ≥1则线性目标函数 z=2x-y 取得最小值时的最优解是 （ ）A. （ 0 ， 1 ）B. （ 0 ， 2 ）C. （ -1 ，1 ） D . （ -1 ， 2 ）18. 箱子中放有 6 张黑色卡片和 4 张白色卡片，从中任取一张，恰好取得黑色卡片的概率是（）A.1 B.1 C.2D.3635519. 已知抛物线的顶点在坐标原点， 对称轴为坐标轴， 若该抛物线经过点 M （ -2 ，4 ），则其标准方程是 （ ） A. y 2=-8x B. y 2= － 8x 或 x 2=yC. x 2=yD. y 2=8x 或 x 2 = － y20. 已知V ABC 的内角 A ，B ，C 的对边分别是 a ，b ，c ，若 a=6 ，sinA=2cosBsinC ，向量 m = ( a, 3b),向量 n =( － cosA ， sinB) ，且 m ∥ n ，则 V ABC 的面积是（）A. 18 3B. 93C. 3 3D.3卷二（非选择题共 60 分）二、填空题（本大题 5 个小题，每小题 4 分，共 20 分。
山东省2019年春季高考数学试题附答案
山东省2019年春季高考数学试题1. 已知集合M={0,1}，N={1,2}，则M ∪N 等于（ ）A. {1}B. {0,2}C. {0,1,2}D.2. 若实数a ，b 满足ab>0，a+b>0，则下列选项正确的是（ ）A. a>0，b>0B. a>0，b<0C. a<0，b>0D. a<0，b<03. 已知指数函数y=a x ，对数函数y=log b x 的图像如图所示，则下列关系式正确的是（）A. 0<a<b<1B. 0<a<1<bC. 0<b<1<aD. a<0<1<b4. 已知函数f(x)=x 3+x ，若f(a)=2，则f(-a)的值是（ ）A. -2B. 2C. -10D. 105. 若等差数列{a n }的前7项和为70，则a 1+a 7等于（ ）A. 5B. 10C. 15D. 20 y第3题 图6. 如图所示，已知菱形ABCD的边长是2，且∠DAB=60°，则AB AC⋅的值是（）A. 4B.4+ C. 6D. 4-7. 对于任意角α，β，“α=β”是“sinα=sinβ”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件必要条件8. 如图所示，直线l⊥OP，则直线l的方程是（）A. 3x－2y=0B. 3x+2y－12=0C. 2x－3y+5=0D. 2x+3y－13=09. 在（1+x）n的二项展开式中，若所有项的系数之和为64，则第3项是（）A. 15x3B. 20x3C. 15x2D. 20x210. 在Rt ABC中，∠ABC=90°，AB=3，BC=4，M是线段AC上的动点. 设点M到BC 的距离为x，第6题图MBC 的面积为y ，则y 关于x 的函数是（ ）A. y=4x ，x ∈(0,4]B. y=2x ，x ∈(0,3]C. y=4x ，x ∈(0,)+∞D. y=2x ，x ∈(0,)+∞11. 现把甲、乙等6位同学排成一排，若甲同学不能排在前两位，且乙同学必须排在甲同学前面（相邻或不相邻均可），则不同排法的种树是（ ）A. 360B. 336C. 312D. 24012. 设集合M={-2，0，2，4}，则下列命题为真命题的是（ ）A. ,a M ∀∈ a 是正数B. ,b M ∀∈ b 是自然数C. ,c M ∃∈ c 是奇数D. ,d M ∃∈ d 是有理数13. 已知sin α=12，则cos2α的值是（ ） A. 89 B. 89- C. 79 D. 79- 14. 已知y=f(x)在R 上是减函数，若f(|a |+1)<f(2)，则实数a 的取值范围是（ ）A. （－∞，1）B. （－∞，1）∪（1，+∞）C. （－1，1）D.（－∞，－1）∪（1，+∞）15. 已知O 为坐标原点，点M 在x 轴的正半轴上，若直线MA 与圆x 2+y 2=2相切于点A ，且|AO|=|AM|，则点M 的横坐标是（ ）A. 2B. C.D. 416. 如图所示，点E 、F 、G 、H 分别是正方体四条棱的中点，则直线EF 与GH 的位置关系是（ ）A. 平行B. 相交C. 异面D. 重合17. 如图所示，若x ，y 满足线性约束条件 2 0 01x y x y -+⎧⎪⎨⎪⎩≥≤≥ ， 则线性目标函数z=2x-y 取得最小值时的最优解是（ ）A. （0，1）B. （0，2）C. （-1，1） D . （-1，2）18. 箱子中放有6张黑色卡片和4张白色卡片，从中任取一张，恰好取得黑色卡片的概率E FG H 第16题 图是（）A. 16B. 13C. 25D. 3519. 已知抛物线的顶点在坐标原点，对称轴为坐标轴，若该抛物线经过点M（-2，4），则其标准方程是（）A. y2=-8xB. y2=－8x 或x2=yC. x2=yD. y2=8x 或x2=－y20. 已知ABC的内角A，B，C的对边分别是a，b，c，若a=6，sinA=2cosBsinC，向量m =()a,向量n=(－cosA，sinB)，且m∥n，则ABC的面积是（）D.21. 弧度制与角度制的换算：5rad= .22. 若向量a =(2，m)，b =(m，8)，且<a，b> =180°，则实数m的值是 .23. 某公司A，B，C三种不同型号产品的库存数量之比为2:3:1，为检验产品的质量，现采用分层抽样的方法从库存产品中抽取一个样本，若在抽取的产品中，恰有A型号产品18件，则该样本容量是__ __.24．已知圆锥的高与底面圆半径相等，若底面圆的面积为1，则该圆锥的侧面积是．25. 已知O为坐标原点，双曲线22221(0,0)x ya ba b-=>>的右支与焦点为F的抛物线x2=2py(p>0)交于A，B两点，若|AF|+|BF|=8|OF|，则该双曲线的渐近线方程是 .26.（本小题7分）已知二次函数f(x)图像的顶点在直线y=2x-l上，且f(1)=－l，f(3)= －l，求该函数的解析式．27.（本小题8分）已知函数f(x) =Asin(ωx+ψ)，其中A>O，|ψ|<2π,此函数的部分图像如图所示，求：(1)函数f(x)的解析式；(2)当f(x)≥1时，求实数x的取值范围．28.（本小题8分）已知三棱锥S-ABC ，平面SAC ⊥ABC ，且SA ⊥AC ，AB ⊥BC ．（1）求证：BC ⊥平面SAB;（2）若SB=2，SB 与平面ABC 所成角是30°的角，求点S 到平面ABC 的距离．29．（本小题8分）如图所示，已知椭圆22221(0)x y a b a b+=>> 的两个焦点分别是F 1，F 2，短轴的两个端点分别是B 1、B 2，四边形F 1B 1F 2B 2为正方形，且椭圆经过点P (1,2. (l)求椭圆的标准方程；(2)与椭圆有公共焦点的双曲线，其离心率e =，且与椭圆在第一象限交于点M ， 求线段MF 1、MF 2的长度．30．（本小题9分）某城市2018年底人口总数为50万，绿化面积为35万平方米. 假定今后每年人口总数比上—年增加1.5万，每年新增绿化面积是上一年年底绿化面积的5%，并第27题 图且每年均损失0.1万平方米的绿化面积（不考虑其他因素）.(l)到哪—年年底，该城市人口总数达到60万（精确到1年）?(2)假如在人口总数达到60万并保持平稳、不增不减的情况下，到哪—年年底，该城市人均绿化面积达到0.9平方米（精确到1年）?。
2019春考数学答案
机密★启用前山东省2019年普通高校招生(春季)考试数学试题答案及评分标准 卷一(选择题共60分)题号 1 2 3 4 5 6 7 8 9 10 答案 C A B A D C A D C B 题号 11 12 13 14 15 16 17 18 19 20 答案 B D C D A B C D B C卷二(非选择题共60分)二、填空题(本大题5个小题，每小题4分，共20分) 21.36° 22.-4 23.5424.2[填1.41 亦可]25. y= ±26X 三、解答题(本大题5个小题，共40分) 26.(本小题7分)解:因为f(1)=-1, f(3)=-1， 所以二次函数f(x)的对称轴为x=231+=2，(2分) 又因为函数f(x)图像的顶点在直线y=2x -1上,则联立方程组⎩⎨⎧-==1x 2y 2x ，解得⎩⎨⎧==32y x ，（1分）故函数f(x)图像的顶点坐标为(2, 3)1分可设二次函数的解析式为f(x)=a(x -2)2+3，（1分） 因为f(1)=-1, 则a(1-2)2+3=-1,解得a=-4，（1分） 所以f(x)= -4(x -2)2+3，即f(x)=-4x2+16x -13 （1分 27. (本小题8分)解: (1)由图像可知，函数f(x)的最大值是2， 最小值是-2 ，A>0. 所以A=2 ，（1分）因为125π-6π=4π，4π最小正周期的41， 所以函数f(x) 的最小正周期T=4πX4=π，故ωπ2=π，解得ω=2，（1分）可得函数f(x)=2 sin(2x+φ)，又因为函数f(x)图像经过点(6π，0)， 所以2sin(2x 6π+φ）=0 ,即sin( 3π+φ)=0，（1分）因此3π+φ=2K π ，k ∈Z ，解得φ=2k π-3π，k ∈Z ，又因为|φ|<2π，所以φ=-3π（1分）所以该函数的解析式为f(x)=2 sin(2x -3π)（1分）(2)因为f(x)≥l ，所以2sin(2x -3π)≥l ,即sin(2x -3π)≥21,（1分） 所以6π+2k π≤2x -3π≤65π+2k π，k ∈Z ，（1分）即4π+k π≤x ≤127π+k π，k ∈Z ， 故当f(x)≥1时，实数x 的取值范围是{x| 4π+k π≤x ≤127π+k π，k ∈Z}.（1分）注: x 的取值范围写为“[ 4π+k π，127π+k π]，k ∈Z",亦可。
2019年山东省春季高考数学试题及答案版
山东省2019年普通高校招生（春季）考试数学试题1. 本试卷分卷一（选择趣）和卷二（非选释题）两部分，满分120分，考试时间120分鉀。
考生清在答翹卡上答翹，考试结東后，请將本试卷和答體卡一并交回。
2. 本次考试允许使用函数塑廿算器，凡使用廿算器的题目，除题目有具体要求外，最后结果 精晞到0.01 o卷一（选择题共60分）一、选择題（本大題20个小題,每小題3分,共60分。
在毎小题列出的四个选顶中，只有 一顶符合題目要求，请将符合题目要求的选项字母代号选出.并填涂在答題卡上）1.已知集 & M={0.1l, N={1,2}, 1MU N 等于（） A.⑴ B. {0,2} C. {0,1,2} D.02•若实数a, b 满足ab>0, a+b>0,则下列选项正晞的是（）A. a>0, b>0B. a>0, b<0C. a<0, b>0D. a<0, b<03. 已知指数函数片X,对裁函8 y=log 6x 的图像如图妬示，則下列关系氏正彌的是（A. 0<a<b<1B. 0<a<1<bC. 0<b<1<aD.a<0<1<b 4. 已知因数f （x ）=x 3+x,若f （a ）=2, H f （・a ）的值是（） A. -2 B.2 C. -10 D. 10 5. 若等差数列{a4的前7项和为70, R a l+a 7等于（）A. 5B. 10C ・ 15D.206. 如图所示，已知菱形ABCD 的血长是2,目乙DAB=60。
，團而•疋的值是（） D. 4-2石C.充要条件D 戕不充分也不必要条件3x - 2y=0B. 3x+2y-12=0 2x - 3y+5=0 D.2x+3y - 13=0y=a xy=logb第3题图A . A. 4B. 4 + 2 吳C.6A.充分不必要条件B.必要不再少6鋭片冈 &如图所示，I S/1OP,则頁找加齐擬'（）ZABC=9O°, AB=3, BC=4, M 是SB AC 上的动点.设点M 到BC 的距离为x,15.已知0为坐标原点，自M 在x 轴的正半轴上，若童裁MA 与g ^+/=2相切于点A, fl|AO|=|AM|f 则点 M 的横坐标是（）D.416•如图所示，点E 、F 、G 、H 分别是正方体四条校的中点，iSSEF^G H 的位置关系是（） C. （-1,1）D . （ -1, 2 ）18. 箱子中故有6张黑色卡片相4张白色卡片，从中任用 尿得黒色卡片的枫率是（）19. 已知牠物找的顶点在坐标原点，对祢轴为坐标轴，若孩抛物线经过点M （・2, 4）,崛其标准方样是（）A. y 2=-8xB. /=-8x 或 x 2二yC. x 2=yD. y 2=8x 或 x 2=-y20. Bffl A ABC 的内角A, B, C 的对边分别是乩b, c,若去6, sinA=2cosBsinC,向量m = (a ®)10.在 RtA ABC 中, AMBC 的面枳为y,则y 关于x 的函数是A.y=4x, XG (0,4]B.y=2x, xe (0,3] C ・ y=4x, xe (0,+oc) D.y=2x, XG (0,+OC )11•现把甲、乙等6位间学诽成一 fib 若甲同学不能丼在前两位, 不相邻均可），则不间排法Wttffl 是（）冃乙同学必须择在甲间学前面（《!邻或 A. 360 B.336 C. 312 12.设集合MM-2, 0, 2, 4},则下列命題为真命JS 的是（） D.240 A. PciwMd 是正数 B. PbwM 、b 是自然数 C.是奇数13.已知沁专，Mcos2amO （）14. Bfly=f （x ）在R 上是績函数,若f （l 刼）＜f ⑵, 则实数£的取值范围是（） A. (-8,1) B. ( - co, 1 ) U ( 1, +oo )C. ( - 1 , 1 )D. ( - 8, - 1 ) U ( 1 , +OO )一张，恰好A.平行B.相交C.异面D.垂合 (第 17JKM)63 5 5向量n=(-cosA, sinB), fl m/Zn F M A ABC 的面枳是()A. 18巧B.9JJ G.3羽 D.也卷二(非选择题共60分)二、填空題(本大題5个小題，毎小題4分，共20分。
2019年山东春季高考数学真题及答案
23. 某公司 A，B，C 三种不同型号产品的库存数量之比为 2:3:1，为检验产品的质量，现采
用分层抽样的方法从库存产品中抽取一个样本，若在抽取的产品中，恰有 A 型号产品 18 件，
则该样本容量是__ __.
24．已知圆锥的高与底面圆半径相等，若底面圆的面积为 1，则该圆锥的侧面积是
．
25.
已知 O 为坐标原点，双曲线 x2 a2
A. -2
B. 2
C. -10
D. 10
5. 若等差数列{an}的前 7 项和为 70，则 a1+a7 等于（ ）
A. 5
B. 10
C. 15
D. 20
6. 如图所示，已知菱形 ABCD 的边长是 2，且∠DAB=60°，则 AB AC 的值是（ ）
A. 4
B. 4 2 3
C. 6
D. 4 2 3
A. 15x3
B. 20x3
C. 15x2
D. 20x2
10. 在 Rt ABC 中，∠ABC=90°，AB=3，BC=4，M 是线段 AC 上的动点. 设点 M 到 BC
的距离为 x，
MBC 的面积为 y，则 y 关于 x 的函数是（ ）
A. y=4x，x∈ (0, 4]
B. y=2x，x∈ (0,3] C. y=4x，x∈ (0, )
（1，+∞） 15. 已知 O 为坐标原点，点 M 在 x 轴的正半轴上，若直线 MA 与圆 x2+y2=2 相切于点 A，
且|AO|=|AM|，则点 M 的横坐标是（ ）
A. 2
B. 2
C. 2 2
D. 4
16. 如图所示，点 E、F、G、H 分别是正方体四条棱的中点，则直线 EF 与 GH 的位置关系
2019上海春季高考数学模拟试题及解析
2019上海春季高考数学模拟试题1．设集合A={1，2，3}，集合B={3，4}，则A∪B={1，2，3，4} ．【考点】并集及其运算．【分析】根据集合的并集的定义求出A、B的并集即可．【解答】解：集合A={1，2，3}，集合B={3，4}，则A∪B={1，2，3，4}，故答案为：{1，2，3，4}．【点评】本题考查了集合的并集的定义以及运算，是一道基础题．2．不等式|x﹣1|＜3的解集为（﹣2，4）．【考点】绝对值不等式的解法．【分析】根据绝对值的性质去掉绝对值，求出不等式的解集即可．【解答】解：∵|x﹣1|＜3，∴﹣3＜x﹣1＜3，∴﹣2＜x＜4，故不等式的解集是（﹣2，4），故答案为：（﹣2，4）．【点评】本题考查了解绝对值不等式问题，是一道基础题．3．若复数z满足2﹣1=3+6i（i是虚数单位），则z=2﹣3i．【考点】复数代数形式的乘除运算．【分析】直接利用复数代数形式的乘除运算化简得答案．【解答】解：∵2﹣1=3+6i，∴，则，∴z=2﹣3i．故答案为：2﹣3i．【点评】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．4．若，则=．【考点】运用诱导公式化简求值．【分析】由已知利用诱导公式即可化简求值．【解答】解：∵，∴=﹣cosα=﹣．故答案为：﹣．【点评】本题主要考查了诱导公式在三角函数化简求值中的应用，属于基础题．5．若关于x、y的方程组无解，则实数a=6．【考点】根的存在性及根的个数判断．【分析】把方程组无解转化为两条直线无交点，然后结合两直线平行与系数的关系列式求得a值．【解答】解：若关于x、y的方程组无解，说明两直线x+2y﹣4=0与3x+ay﹣6=0无交点．则，解得：a=6．故答案为：6．【点评】本题考查根的存在性与根的个数判断，考查数学转化思想方法，是中档题．6．若等差数列{a n}的前5项的和为25，则a1+a5=10．【考点】等差数列的前n项和．【分析】由等差数列前n项和公式得=25，由此能求出a1+a5．【解答】解：∵等差数列{a n}的前5项的和为25，∴=25，∴a1+a5=25×=10．。
2019年普通高等学校春季招生考试数学试题及答案
2019年普通高等学校春季招生考试(北京、内蒙古、安徽卷)数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷至2页.第Ⅱ卷3至8页.共150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的(1) 集合M ={1，2，3，4，5}的子集个数是 ( )(A) 32(B) 31(C) 16(D) 15(2) 函数f (x ) = a x (a > 0且a ≠ 1)对于任意的实数x ，y 都有 ( )(A) f (xy ) = f (x ) f (y ) (B) f (xy ) = f (x ) + f (y ) (C) f (x + y ) = f (x ) f (y ) (D) f (x + y ) = f (x ) + f (y )(3) =++∞→1222limn n n n n C C( )(A) 0 (B) 2 (C)21(D)41 (4) 函数)1(1≤--=x x y 的反函数是 ( )(A) y = x 2－1 (－1≤x ≤0) (B) y = x 2－1 (0≤x ≤1) (C) y = 1－x 2 (x ≤0)(D) y = 1－x 2 (0≤x ≤1)(5) 极坐标系中，圆θθρsin 3cos 4+=的圆心的坐标是 ( )(A) ），（53arcsin 25(B) ），（54arcsin5 (C) ），（53arcsin 5 (D) ），（54arcsin 25(6) 设动点P 在直线x = 1上，O 为坐标原点. 以OP 为直角边、点O 为直角顶点作等腰Rt △OPQ ，则动点Q 的轨迹是( )(A) 圆(B) 两条平行直线(C) 抛物线(D) 双曲线(7) 已知f (x 6) = log 2x ，那么f (8)等于( )(A)34 (B) 8 (C) 18 (D)21 (8) 若A 、B 是锐角△ABC 的两个内角，则点P (cos B －sin A ，sin B －cos A )在 ( ) (A) 第一象限(B) 第二象限(C) 第三象限(D) 第四象限(9) 如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角(圆锥轴截面中两条母线的夹角)是( )(A) 30°(B) 45°(C) 60°(D) 90°(10) 若实数a ，b 满足a + b = 2，则3a + 3b 的最小值是 ( )(A) 18(B) 6(C) 32(D) 432(11) 右图是正方体的平面展开图.在这个正方体．．．中， ① BM 与ED 平行 ② CN 与BE 是异面直线 ③ CN 与BM 成60º角 ④ DM 与BN 垂直以上四个命题中，正确命题的序号是 ( ) (A) ①②③(B) ②④(C) ③④(D) ②③④(12) 根据市场调查结果，预测某种家用商品从年初开始的n 个月内累积的需求量S n (万件)近似地满足)521(902--=n n nS n (n =1，2，……，12)． 按此预测，在本年度内，需求量超过1.5万件的月份是 ( )(A) 5月、6月 (B) 6月、7月(C) 7月、8月(D) 8月、9月第Ⅱ卷二.填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.(13) 已知球内接正方体的表面积为S ，那么球体积等于___________(14) 椭圆x 2 + 4y 2 = 4长轴上一个顶点为A ，以A 为直角顶点作一个内接于椭圆的等腰直角三角形，该三角形的面积是______________(15) 已知1sin sin sin 222=++γβα(α、β、γ均为锐角)，那么cos αcos βcos γ的最大值等于______________(16) 已知m 、n 是直线，α、β、γ是平面，给出下列命题： ① 若α⊥β，α∩β= m ，n ⊥m ，则n ⊥α或n ⊥β； ② 若α∥β，α∩γ= m ，β∩γ= n ，则m ∥n ；③ 若m 不垂直于α，则m 不可能垂直于α内的无数条直线； ④ 若α∩β= m ，n ∥m ；且α⊄n ，β⊄n ，则n ∥α且n ∥β.其中正确的命题的序号是______________ (注：把你认为正确的命题的序号都填上)三.解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.(17) (本小题满分12分) 设函数)0()(>>++=b a bx ax x f ，求f ( x )的单调区间，并证明f ( x )在其单调区间上的单 调性.(18) (本小题满分12分) 已知z 7=1(z ∈C 且z ≠1).(Ⅰ)证明 1 + z + z 2 + z 3 + z 4 + z 5 + z 6 = 0；(Ⅱ)设z 的辐角为α，求cos α+cos2α+cos4α的值. (19) (本小题满分12分)已知VC 是△ABC 所在平面的一条斜线，点N 是V 在平面ABC 上的射影，且在△ABC 的高CD 上.AB = a ，VC 与AB 之间的距离为h ，点M ∈VC .(Ⅰ)证明∠MDC 是二面角M －AB －C 的平面角； (Ⅱ)当∠MDC = ∠CVN 时，证明VC ⊥平面AMB ； (Ⅲ)若∠MDC =∠CVN =θ(20πθ<<)，求四面体MABC 的体积. (20)(本小题满分12分)在1与2之间插入n 个正数a 1，a 2，a 3，…，a n ，使这n +2个数成等比数列；又在1与2之间插入n 个正数b 1，b 2，b 3，…，b n ，使这n +2个数成等差数列.记A n = a 1 a 2 a 3…a n ，B n = b 1 + b 2 + b 3 + … + b n .(Ⅰ)求数列{A n}和{B n}的通项；(Ⅱ)当n≥7时，比较A n和B n的大小，并证明你的结论.(21)(本小题满分12分)某摩托车生产企业，上年度生产摩托车的投入成本为1万元/辆，出厂价为1.2万元/辆，年销售量为1000辆.本年度为适应市场需求，计划提高产品档次，适度增加投入成本.若每辆车投入成本增加的比例为x(0 < x < 1)，则出厂价相应的提高比例为0.75x，同时预计年销售量增加的比例为0.6x.已知年利润= (出厂价－投入成本)×年销售量.(Ⅰ)写出本年度预计的年利润y与投入成本增加的比例x的关系式；(Ⅱ)为使本年度的年利润比上年有所增加，问投入成本增加的比例x应在什么范围内？(22)(本小题满分14分)已知抛物线y2=2px(p>0).过动点M(a，0)且斜率为1的直线l与该抛物线交于不同的两点A、B，| AB | ≤2p.(Ⅰ)求a的取值范围；(Ⅱ)若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值.2001年普通高等学校春季招生考试（北京、内蒙古、安徽卷）数学试题（理工农医类）参考解答及评分标准说明：一．本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则.二．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分.三．解答右端所注分数，表示考生正确做到这一步应得的累加分数.四．只给整数分数.选择题和填空题不给中间分.一．选择题：本题考查基本知识和基本运算.每小题5分，满分60分.（1）A （2）C （3）D （4）C （5）A （6）B（7）D （8）B （9）C （10）B （11）C （12）C二．填空题：本题考查基本知识和基本运算，每小题4分，满分16分.(13) π242SS (`14)2516 (15)692 (16) ② ④三．解答题（17）本小题主要考查函数的单调性及不等式的基础知识，考查数学推理判断能力.满分12分. 解：函数bx ax x f ++=)(的定义域为（－∞，－b ）∪（－b ，+∞）. f ( x )在（－∞，－b ）内是减函数，f ( x )在（－b ，+∞）内也是减函数. ……4分 证明f ( x )在（－b ，+∞）内是减函数. 取x 1，x 2∈（－b ，+∞），且x 1 < x 2，那么 bx ax b x a x x f x f ++-++=-221121)()( ))(())((2112b x b x x x b a ++--=， ……6分∵ a －b > 0，x 2－x 1>0，（x 1+b ）(x 2+b ) > 0， ∴ f (x 1)－f (x 2) > 0，即f (x )在（－b ，+∞）内是减函数. ……9分 同理可证f (x )在（－∞，－b ）内是减函数. ……12分 （18）本小题主要考查复数的基本概念和基本运算，考查综合运用复数的知识解决问题的能力，满分12分.解：（Ⅰ）由 z （1 + z + z 2 + z 3 + z 4 + z 5 + z 6）= z + z 2 + z 3 + z 4 + z 5 + z 6+ z 7 =1 + z + z 2 + z 3 + z 4 + z 5 + z 6，得 （z －1）（1 + z + z 2 + z 3 + z 4 + z 5 + z 6）= 0. …… 4分 因为 z ≠1，z －1≠0，所以 1 + z + z 2 + z 3 + z 4 + z 5 + z 6= 0. …… 6分 （Ⅱ）因为z 7= 1.可知 | z | = 1，所以 1=⋅z z ，而z 7= 1，所以z ·z 6 = 1，z z =6，同理52z z =，34z z =， 65342z z z z z z ++=++由（Ⅰ）知 z + z 2 + z 4 + z 3 + z 5 + z 6= －1， 即 14242-=+++++z z z z z z ， 所以42z z z ++的实部为21-， …… 8分 而z 的辐角为α时，复数42z z z ++的实部为ααα4cos 2cos cos ++，所以214cos 2cos cos -=++ααα. …… 12分 （19）本小题主要考查线面关系的基本概念，考查运用直线与直线、直线与平面的基本性质进行计算和证明的能力.满分12分. （Ⅰ）证明：由已知，CD ⊥AB ，VN ⊥平面ABC ，N ∈CD ，⊂AB 平面ABC ， ∴VN ⊥AB .∴AB ⊥平面VNC . ……2分 又 V 、M 、N 、D 都在VNC 所在的平面内， 所以，DM 与VN 必相交，且AB ⊥DM ，AB ⊥CD ， ∴∠MDC为二面角M －AB －C的平面角. ……4分 （Ⅱ）证明：由已知，∠MDC = ∠CVN ，在△VNC 与△DMC 中， ∠NCV = ∠MCD ， 又∵∠VNC = 90º，∴ ∠DMC =∠VNC = 90º， 故有DM ⊥VC ，又AB ⊥VC ， ……6分 ∴ VC ⊥平面AMB . ……8分 （Ⅲ）解：由（Ⅰ）、（Ⅱ），MD ⊥AB ，MD ⊥VC ，且D ∈AB ，M ∈VC ， ∴ MD = h . 又 ∵ ∠MDC =θ. 在Rt △MDC 中，CM = h ·tg θ. ……10分 V 四面体MABC = V 三棱锥C －ABMABM S CM ∆⋅=31ah tg h 2131⋅⋅=θ θtg 612ah =. ……12分 （20）本小题主要考查等差数列、等比数列的基础知识，考查观察、猜想并进行证明的数学思想方法.满分12分.解：（Ⅰ）∵ 1，a 1，a 2，a 3，……，a n ，2成等比数列，∴ a 1a n = a 2 a n －1 = a 3 a n －2 = … = a k a n －k +1 = … = 1×2 = 2 ，∴ n n n n n n n na a a a a a a a a a A 2)21()()()()()(121231212=⨯==--- ， ∴ 22n n A =. ……4分∵ 1，b 1，b 2，b 3，……，b n ，2成等差数列，∴ b 1 + b 2 = 1 + 2 = 3， ∴ n n b b B n n 2321=⋅+=. 所以，数列{A n }的通项22nn A =，数列{B n }的通项n B n 23=. ……6分 （Ⅱ）∵ 22n n A =，n B n 23=， ∴ n n A 22=，2249n B n =， 要比较A n 和B n 的大小，只需比较2n A 与2n B 的大小，也即比较当n ≥ 7时，2n 与249n 的大小.当n = 7时，2n = 128，4949492⨯=n ，得知2492n n >， 经验证n = 8，n = 9时，均有命题2492n n >成立.猜想当n ≥ 7时有2492n n >. 用数学归纳法证明. ……9分 （ⅰ）当n = 7时，已验证2492n n >，命题成立.（ⅱ）假设n = k （k ≥ 7）时，命题成立，即2492k k >， 那么 214922k k ⨯>+， 又当k ≥ 7时，有k 2 > 2k + 1， ∴ )1249221++⨯>+k k k （ 2149）（+⨯=k . 这就是说，当n = k + 1时，命题2492n n >成立. 根据（ⅰ）、（ⅱ），可知命题对于n ≥ 7都成立.故当n ≥ 7时，A n > B n . ……12分。
2019年山东省春季高考数学试题与答案
2019年⼭东省春季⾼考数学试题与答案省2019年普通⾼校招⽣（春季）考试数学试题1．本试卷分卷⼀（选择题）和卷⼆（⾮选择题）两部分，满分120分，考试时间120分钟。
考⽣清在答题卡上答题，考试结束后，请将本试卷和答题卡⼀并交回。
2．本次考试允许使⽤函数型计算器，凡使⽤计算器的题⽬，除题⽬有具体要求外，最后结果精确到0.01。
卷⼀（选择题共60分）⼀、选择题（本⼤题20个⼩题，每⼩题3分，共60分。
在每⼩题列出的四个选项中，只有⼀项符合题⽬要求，请将符合题⽬要求的选项字母代号选出．并填涂在答题卡上）1. 已知集合M={0,1}，N={1,2}，则M ∪N 等于（）A. {1}B. {0,2}C. {0,1,2}D. 2. 若实数a ，b 满⾜ab>0，a+b>0，则下列选项正确的是（）A. a>0，b>0B. a>0，b<0C. a<0，b>0D. a<0，b<0 3. 已知指数函数y=a x ，对数函数y=log b x 的图像如图所⽰，则下列关系式正确的是（） A. 04. 已知函数f(x)=x 3+x ，若f(a)=2，则f(-a)的值是（）A. -2B. 2C. -10D. 10 5. 若等差数列{a n }的前7项和为70，则a 1+a 7等于（）A. 5B. 10C. 15D. 206. 如图所⽰，已知菱形ABCD 的边长是2，且∠DAB=60°，则AB AC ?u u u r u u u r的值是（）A. 4B. 423+C. 6 423-7. 对于任意⾓α，β，“α=β”是“sin α=sin β”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件8. 如图所⽰，直线l ⊥OP ，则直线l 的⽅程是（）A. 3x －2y=0B. 3x+2y －12=0C. 2x －3y+5=0D. 2x+3y －13=09. 在（1+x ）n 的⼆项展开式中，若所有项的系数之和为64，则第3项是（）yx y Oy=a xy=log b 第3题图 ABD第6题图y 3P10. 在Rt V ABC 中，∠ABC=90°，AB=3，BC=4，M 是线段AC 上的动点. 设点M 到BC 的距离为x ，V MBC 的⾯积为y ，则y 关于x 的函数是（）A. y=4x ，x ∈(0,4]B. y=2x ，x ∈(0,3]C. y=4x ，x ∈(0,)+∞D. y=2x ，x ∈(0,)+∞ 11. 现把甲、⼄等6位同学排成⼀排，若甲同学不能排在前两位，且⼄同学必须排在甲同学前⾯（相邻或不相邻均可），则不同排法的种树是（）A. 360B. 336C. 312D. 240 12. 设集合M={-2，0，2，4}，则下列命题为真命题的是（） A. ,a M ?∈ a 是正数 B. ,b M ?∈ b 是⾃然数 C. ,c M ?∈ c 是奇数 D. ,d M ?∈ d 是有理数 13. 已知sin α=12，则cos2α的值是（） A.89 B. 89- C. 79 D. 79- y=f(x)在R f(|a |+1)2 C. 22 D. 416. 如图所⽰，点E 、F 、G 、H 分别是正⽅体四条棱的中点，则直线EF 与GH 的位置关系是（） A. 平⾏ B. 相交 C. 异⾯ D.重合17. 如图所⽰，若x ，y 满⾜线性约束条件2 00 1x y x y -+≥≤≥ ，则线性⽬标函数z=2x-y 取得最⼩值时的最优解是（） A. （0，1） B. （0，2） C. （-1，1） D . （-1，2）18. 箱⼦中放有6⿊⾊卡⽚和4⽩⾊卡⽚，从中任取⼀，恰好取得⿊⾊卡⽚的概率是（） A.16 B. 13 C. 25 D. 35 M （-2（） A. y 2=-8x B. y 2=－8x 或x 2=y C. x 2=y D. y 2=8x 或x 2=－yEF G H 第16题图向量n =(－cosA ，sinB)，且m ∥n ，则V ABC 的⾯积是（）A. 183B. 93C. 33 3卷⼆（⾮选择题共60分）⼆、填空题（本⼤题5个⼩题，每⼩题4分，共20分。
2019年上海市春季高考数学试卷及答案
2019年上海市普通高等学校春季招生考试数 学 试 卷一. 填空题（本大题满分36分）本大题共有12题，要求直接填写结果，每题填对得3分，否则一律得0分1．函数2log (2)y x =+的定义域是 2．方程28x=的解是 3．抛物线28y x =的准线方程是 4．函数2sin y x =的最小正周期是5．已知向量(1 )a k =，，(9 6)b k =-，。
若//a b ，则实数 k = 6．函数4sin 3cos y x x =+的最大值是 7．复数23i +（i 是虚数单位）的模是8．在ABC ∆中，角 A B C 、、所对边长分别为 a b c 、、，若5 8 60a b B ===，，，则b= 9．在如图所示的正方体1111ABCD A B C D -中，异面直线1A B 与1B C 所成角的大小为10．从4名男同学和6名女同学中随机选取3人参加某社团活动，选出的3人中男女同学都有的概率为 （结果用数值表示）。
11．若等差数列的前6项和为23，前9项和为57，则数列的前n 项和n =S 。
12．36的所有正约数之和可按如下方法得到：因为2236=23⨯，所以36的所有正约数之和为22222222(133)(22323)(22323)(122)133)91++++⨯+⨯++⨯+⨯=++++=（参照上述方法，可求得2000的所有正约数之和为二．选择题（本大题满分36分）本大题共有12题，每题都给出四个结论，其中有且只有一个结论是正确的。
考生必须把真确结论的代码写在题后的括号内，选对得3分，否则一律得0分13．展开式为ad-bc 的行列式是（ ）D 1 C 1B 1A 1D C AB（A ）a bd c (B)a cb d (C)a db c (D)b ad c14．设-1()f x为函数()f x =）(A) 1(2)2f-= (B) 1(2)4f -= (C) 1(4)2f-= (D) 1(4)4f -=15．直线2310x y -+=的一个方向向量是（ ）(A) (2 3)-， (B) (2 3)， (C) (3 2)-， (D) (3 2)， 16．函数12()f x x -=的大致图像是（ ）17．如果0a b <<，那么下列不等式成立的是（ ） (A)11a b < (B) 2ab b < (C) 2ab a -<- (D) 11a b-<- 18．若复数12 z z 、满足21z z =，则12 z z 、在复数平面上对应的点12 Z Z 、（ ） (A) 关于x 轴对称 (B)关于y 轴对称(C) 关于原点对称 (D)关于直线y x =对称 19． 10(1)x +的二项展开式中的一项是（ ）（A ）45x （B ）290x （C ） 3120x （D ）4252x20．既是偶函数又在区间(0 )π，上单调递减的函数是（ ） （A ）sin y x = （B ）cos y x = （C ）sin 2y x = （D ）cos 2y x = 21．若两个球的表面积之比为1:4，则这两个球的体积之比为（ ）（A ）1:2 （B ）1:4 （C ）1:8 （D ）1:16 22．设全集U R =，下列集合运算结果为R 的是（ ） （A ）u ZN ð （B ）u N N ð （C ）()u u ∅痧 （D ）{0}u ð23．已知 a b c R ∈、、，“240b ac -<”是“函数2()f x ax bx c =++的图像恒在x 轴上方”的（ ）（A ）充分非必要条件 （B ）必要非充分条件 （C ）充要条件 （D ）既非充分又非必要条件 24．已知 A B 、为平面内两定点，过该平面内动点M 作直线AB 的垂线，垂足为N .若2MN AN NB λ=⋅，其中λ为常数，则动点M 的轨迹不可能是（ ）（A ）圆 （B ） 椭圆 （C ） 抛物线 （D ）双曲线三、解答题（本大题满分78分）本大题共有7题，解答下列各题必须写出必要的步骤 25．（本题满分7分）如图，在正三棱锥111ABC A B C -中，16AA =，异面直线1BC 与1AA 所成角的大小为6π，求该三棱柱的体积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
济南市2018年春季高考第一次模拟考试
数学试题答案及评分标准
第Ⅰ卷（选择题，共60分）
（非选择题，共60分）
二、填空题（本大题5个小题，每题4分，共20分）
21．11， 22．10, 1
23．179.59
24．3x-4y-25=0
25．11
三、解答题（本大题5个小题，共40分）
26．（7分）解：(1)由题意可得
{ 解得k ＝－1，b ＝160，-------------2分 ∴P ＝－x ＋160(60≤x ≤160)．-----------------------------------------------------------3分 (2)∵y ＝P(x －60)＝－(x －110)
2
＋2500，----------------------------------------------5分
当x ＝110元/件时，y 取得最大值，最大值为2500，
∴每件售价为110元时，每天利润最大，最大利润为2500元． ----------------7分 27．（7分) 解： (1)由题意可得
{
解得q=2
∴a n =2⨯21n -=2n --------------------------------------------2分
(2) ｛b n ｝为等差数列，b 1=1,d=2 ∴b n =2n-1
a n +
b n =2n
+2n-1--------------------------------------------4分 ∴s n =21
+1+22
+3+23
+5+ (2)
+2n-1 =(21
+22
+23
(2)
)+(1+3+5+…+2n-1) =2
1n ++n 2
-2--------------------------------------------7分
28．（8分）解：f(x)＝2cosxcos (x- π6 )- 3 sin 2
x ＋sinxcosx
＝2cosx (cosxcos π6 +sinxsin π6 )- 3 sin 2
x ＋sinxcosx
＝ 3 cos 2
x ＋sinxcosx - 3 sin 2
x ＋sinxcosx
＝ 2(sin2xcos π3 +cos2xsin π3 )=2sin(2x+π
3
)-----------------4分
a 1
=2 aq 2
=a 1q+4
75x +b=85
90x +b=70
(1)f(x)的最小正周期T ＝2π
2 =π-----------------------------6分
(2)∵f(x)＝1，即2sin(2x+π
3
)=1
∴2x ＋ π3 ＝2k π＋ π6 或2x ＋π3 ＝2k π＋ 5π
6 ，k ∈Z ，
解得x ＝k π - π12 或x ＝k π＋ π
4 ，k ∈Z ，
又∵x ∈[0，π]，
x ＝ 11π12 或x ＝ π
4 ---------------------------------------8分
29．（9分）证明：
(1)∵PA ⊥平面ABCD ，AB ⊂平面ABCD ，
F 所以PA ⊥AB ，----------------------------------1分 又∵AB ⊥AD ，PA ∩AD=A ，AD ⊂平面PAD ，PA ⊂平面PAD ， ∴AB ⊥平面PAD ，-----------------------------2分 ∵AB ∥CD ，
∴CD ⊥平面PAD ．又CD ⊂平面PCD
∴平面PCD ⊥平面PAD-----------------------------3分 ∵PA=AD, E 为PD 中点
∴AE ⊥ PD, 又平面PCD 平面PAD=PD , AE 平面PAD ∴AE ⊥平面PCD.---------------------------------------4分 （2）取PC 的中点为F ，连接EF ，BF ， ∵E 为PD 的中点， ∴EF 为△PCD 的中位线， ∴EF ∥CD ，EF=
2
1
CD ，---------------------------------1分 又∵AB=
2
1
CD ，AB ∥CD ， ∴EF=AB ，EF ∥AB ，
∴四边形ABEF 为平行四边形，
∴BF ∥AE ， ---------------------------------3分 ∵BF ⊂平面PBC ，
∴AE ∥平面PBC ．---------------------------------------4分 . 30．（9分）
A
B
C
D
E
P
解：（1
）由题意可得12222b c a a b c ⎧=⎪
⎪
=
⎨⎪
⎪=+⎩
解得2,1a b c ==
∴椭圆的方程为22
143x y +
=----------------------------------3分
（2）由题意可得以21F F 为直径的圆方程为12
2
=+y x
∴圆心到直线l 的距离为d=
5
m 2，
由d<1得 |m|<
25
------------------------------4分
∴|CD|=22
d 1-=25
m 4-12=2m 4-555
2 设A(x 1,y 1),B(x 2,y 2)
联立
y=-2
1
x +m
22
143x y +=
整理得
x 2-m x +m 2-3=0
----------------------------------6分
可得：12x x m +=，2123x x m =-
||AB ∴==||||4
AB CD =
1=
解方程得m =，且满足||m <∴直线l 的方程为12y x =-或12y x =-.-------------10分。