天津大学版工程力学习题答案
天津大学2021年春季学期《工程力学》在线作业一附参考答案

天津大学2021年春季学期《工程力学》在线作业一附参考答案
试卷总分:100 得分:100
一、单选题 (共 20 道试题,共 100 分)
1.一下说法错误的是()
A.拱主要承受压力,因此可以使用抗拉弱、抗压强的材料
B.拱需要坚实的基础
C.带拉杆三铰拱不是静定拱
D.三铰拱两个水平支座反力互等
答案:C
2.矩形截面梁受均布荷载作用,梁的高为h,宽为b,其跨度为L,若梁的跨度减小一半,问梁的正应力是跨度为L多少倍()
A.2倍
B.0.5倍
C.0.25倍
D.4倍
答案:C
更多加微boge30619
3.一下关于拱内力图制作错误的是()
A.需要沿拱的跨度方向将拱轴分为若干等分
B.只需要计算各等分点截面上的内力值
C.需要将已得各截面内力值用曲线光滑连接
D.不管是在均布荷载下还是在集中荷载下,拱的三个内力图都是曲线图形
答案:B
4.{图}
A.A
B.B
C.C
D.D
答案:A
5.{图}
A.A
B.B
C.C
D.D
答案:C
6.弯曲梁,当某截面的剪力Q=0时,( )。
工程力学(天津大学)第14章答案

第十四章 组合变形习 题14−1 截面为20a 工字钢的简支梁,受力如图所示,外力F 通过截面的形心,且与y 轴成φ角。
已知:F =10kN ,l =4m ,φ=15°,[σ]=160MPa ,试校核该梁的强度。
解:kN.m 104104141=⨯⨯==Fl M kN.m;58821510kN.m;65991510.sin φsin M M .cos φcos M M y z =⨯===⨯==查附表得:33cm 531cm 237.W ;W y z ==122.9MPa Pa 109122105311058821023710569966363=⨯=⨯⨯+⨯⨯=+=--....W M W M σy y z z max[]σσmax <,强度满足要求。
14−2 矩形截面木檩条,受力如图所示。
已知:l =4m ,q =2kN/m ,E =9GPa ,[σ]=12MPa ,4326'= α,b =110mm ,h =200mm ,2001][=lf。
试验算檩条的强度和刚度。
z解:kN.m 442818122=⨯⨯==ql M kN.m;789143264kN.m;578343264.sin φsin M M .cos φcos M M y z ='⨯==='⨯== m ...W ;m ...W y z 42421003341102206110333722011061--⨯=⨯⨯=⨯=⨯⨯=MPa 329Pa 1032910033410789110333710578364343......W M W M σy y z z max=⨯=⨯⨯+⨯⨯=+=-- []σσmax <,强度满足要求。
m...sin EI φsin ql f m...cos EI φcos ql f y y zz 33943433943410931411022012110938443264102538451003492201101211093844326410253845--⨯=⨯⨯⨯⨯⨯'⨯⨯⨯⨯==⨯=⨯⨯⨯⨯⨯'⨯⨯⨯⨯==mm ..f f f y z 4517104517322=⨯=+=-20012291<=l f ,所以挠度满足要求。
天津大学工程力学习题答案

3-10 求图示多跨梁支座A 、C 处的约束力。
已知M =8kN ·m ,q =4kN/m ,l =2m 。
解:(1)取梁BC 为研究对象。
其受力如图(b)所示。
列平衡方程 (2)取整体为研究对象。
其受力如图(c)所示。
列平衡方程3-11 组合梁 AC 及CD 用铰链C 连接而成,受力情况如图(a)所示。
设F =50kN ,q =25kN/m ,力偶矩M =50kN ·m 。
求各支座的约束力。
F BkN1842494902332,0=⨯⨯===⨯⨯-⨯=∑ql F ll q l F M C C B kN624318303,0=⨯⨯+-=+-==⨯-+=∑ql F F l q F F F C A C A ymkN 32245.10241885.10405.334,022⋅=⨯⨯+⨯⨯-=+⨯-==⨯⨯-⨯+-=∑ql l F M M l l q l F M M MC A C A A解:(1)取梁CD 为研究对象。
其受力如图(c)所示。
列平衡方程(2)取梁AC 为研究对象。
其受力如图(b)所示,其中F ′C =F C =25kN 。
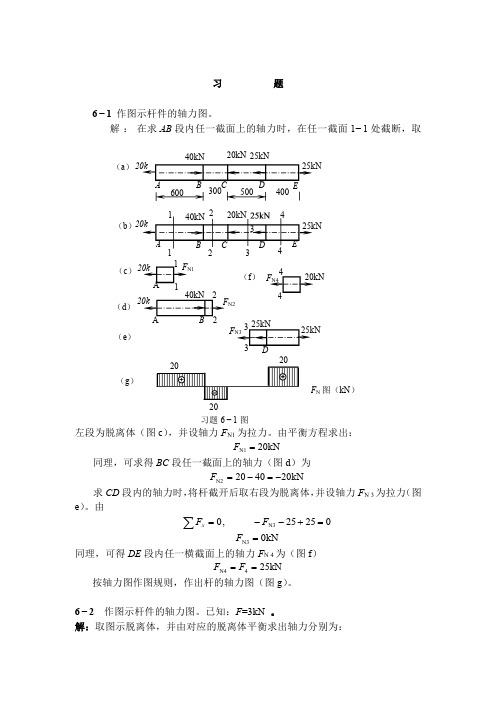
列平衡方程F C(b)(c)´CkN 25450252420124,0=+⨯=+==-⨯⨯-⨯=∑M q F M q F MD D CkN 25450256460324,0=-⨯=-==-⨯⨯+⨯-=∑M q F M q F MC C D)kN(25225225250222021212,0↓-=⨯-⨯-='--==⨯'-⨯⨯-⨯+⨯-=∑CA C A BF q F F F q F F MkN150225425650246043212,0=⨯+⨯+='++==⨯'-⨯⨯-⨯-⨯=∑CB CB AF q F F F q F F M6−1作图示杆件的轴力图。
解:在求AB 段内任一截面上的轴力时,在任一截面1−1处截断,取左段为脱离体(图c ),并设轴力F N1为拉力。
工程力学(天津大学)第4章答案

M z 230.95 0.707 Mo 326.60
4-6 轴AB与铅直线成 角,悬臂CD垂直地固定在轴上,其长为a,并与铅直面zAB成 角,如图所示。如在点D作用铅直向下的力P,求此力对轴AB的矩。 解:力P对轴AB的矩为 z B
M AB P sin sin a Pa sin sin
M o (F ) M 2 x (F ) M 2 y (F ) M 2 z (F ) 230.952 (230.95) 2 326.60N m M cos( M o , i ) x 0, Mo
cos( M o , j ) cos( M o , k ) My Mo 230.95 0.707, 326.60
B
D A
B J y
F x
C
解:取矩形平板为研究对象,其上受一汇交于D点的空间汇交力系作用,连 接DH、DI、DJ,如图b所示。列平衡方程
F F F
y
0,
AH BH FB 0 AD BD AH BH , AD BD, FA FA
FA FB
1 2
x
0,
z
100 100 5
1 5
100
0.3 100 13 100 5 3 1 300 0.1 200 0.3 13 5 51.78 N m 200 M y M y ( F ) F1 0.2 F2 0.1 100 13 2 100 0.2 300 0.1 13 36.64 N m 300 200 M z M z ( F ) F2 0.2 F3 0.3 100 13 100 5 3 2 300 0.2 200 0.3 13 5 103.59 N m
工程力学(天津大学)第11章答案

第十一章 梁弯曲时的变形习 题11−1 用积分法求下列简支梁A 、B 截面的转角和跨中截面C 点的挠度。
解:(a )取坐标系如图所示。
弯矩方程为:xlM M e=挠曲线近似微分方程为:xlM y EI e-=''积分一次和两次分别得:Cxl My EI e +-='22, (a )DCx xlMEIy e++-=36 (b)边界条件为:x =0时,y =0,x =l 时,y =0, 代入(a )、(b)式,得:0,6==D l M Ce梁的转角和挠度方程式分别为:)62(12l M xlMEIy e e+-=',)66(13lx M xlMEIyee+-=所以:EIlM y l EIMθEIl M θe C eB e A 16,3,62=-==(b )取坐标系如图所示。
AC 段弯矩方程为:)20(11l x x lM M e≤≤=BC段弯矩方程为:)2(22l x l Mx lM M ee≤≤-=两段的挠曲线近似微分方程及其积分分别为:(a)(b)习题11−1图xAC 段:11x lM y EI e-=''12112C x l My EI e+-=', (a ) 1113116D x C x lMEIye++-= (b)BC 段:eeMx lM y EI +-=''2222222C Mx l My EI ee++-=', (c )22223226D x C x M x lMEIye e+++-= (d)边界条件为:x 1=0时,y 1=0,x 2=l 时,y 2=0, 变形连续条件为:2121212y y y y l x x '='===,时,代入(a )、(b)式、(c )、(d)式,得:,8D 0,2411,2422121l M D l M C l MC eee==-==,梁的转角和挠度方程式分别为:AC 段:)242(121l M x lMEIy e e+-=',)246(11311lx Mx lMEIy ee+-=BC 段:)24112(12222l M x M x lMEIy e e e-+-=',)8241126(12222322l M lx M x M x lMEIy e eee+-+-=所以:0,24,24===C eB e A y l EIMθEIl M θ11−2 用积分法求下列悬臂梁自由端截面的转角和挠度。
工程力学(天津大学)第12章答案

第十二章 用能量法计算弹性位移习 题12−1 两根杆拉伸刚度均为EA ,长度相同,承受荷载如图所示,分布荷载集度q =F/l ,试求这两根杆的应变能,并作比较。
解:EAl F V 221=,EA l F dx EA l )qx (dx EA l F V l l N622202022===⎰⎰ 213V V =12−2 试求图示受扭圆轴内所积蓄的应变能,杆长为l ,直径为d ,材料的剪变模量为G 。
解:4320420232163222Gdl m dx d πGl )mx (dx GI l T V l lP ===⎰⎰ 12−3 试计算下列梁内所积蓄的应变能,略去剪力的影响。
习题12−2图解:(a )先求支座反力: ql F ,ql F RB RA 8381==以A 为坐标原点,x 1以向右为正,AC 段的弯矩方程为:118x qlM = 以B 为坐标原点,x 2以向左为正,BC 段的弯矩方程为:22222183qx x ql M -= 梁的变形能为:EIl q dx EI )qx qlx (dx EI )qlx (dx EIMdx EI M V l l l l 153601722183282252202222202120222021=-+=+=⎰⎰⎰⎰(b) 以B 为坐标原点,x 以向左为正,AB 段的弯矩方程为:306x lq M =梁的变形能为:EIl q dx EI )l x q (dx EI M V l l 504262520023002===⎰⎰ (c) 以B 为坐标原点,x 以向左为正,AB 段的弯矩方程为:Fx M )x (M +=梁的变形能为:EIl F EI MFl EI l M dx EI )Fx M (dx EI M V l l6222232220202++=+==⎰⎰ (d) 先求支座反力: ,ql F RA 83=以A 为坐标原点,x 1以向右为正,AB 段的弯矩方程为:21112183qx x ql M -= (0≤x 1≤l )以C 为坐标原点,x 2以向左为正,BC 段的弯矩方程为:22221qx M -=(0≤x 2≤l /2) 梁的变形能为:EIl q dx EI )qx (dx EI )qx qlx (dx EIMdx EI M V l ll l12803221221832252220222102211202221=-+-=+=⎰⎰⎰⎰12−4 试求图示结构中的弹性变形能。
423002[工程力学] 天津大学考试 参考资料答案
![423002[工程力学] 天津大学考试 参考资料答案](https://img.taocdn.com/s3/m/42c7255e1a37f111f0855b97.png)
工程力学复习题参考的答案 天津大学1、利用对称性,计算下图所示各结构的内力,并绘弯矩图。
解:取半结构如图(a)所示,为2次超静定结构。
再取半结构的基本体系如图(b)所示,基本方程为1111221P 2112222P 00X X X X δδ∆δδ∆++=⎧⎪⎨++=⎪⎩ 系数和自由项分别为119EIδ=,1221552EIδδ==,223613EIδ=,1P 13603EI ∆=,2P 1900EI∆=解得17.04kN X =-,214.18kN X =-。
原结构弯矩图如图(f)所示。
C BA10kN/m4m3m4mCBA10kN/m2X1X1X=1112X=133710kN/m80807.04202030.4230.4230.4230.4226.326.31(b) 基本体系M图(c)(a) 半结构PM(e)M图(kN·m)(f)2M图(d)图(kN·m)2、用结点法或截面法求图示桁架各杆的轴力。
解:(1)判断零杆(12根)。
(2)节点法进行内力计算,结果如图。
3、分析如图所示体系的几何构造。
解:从A点开始依次去掉二元体,可知为几何不变体系且无多余约束。
4、试求图示刚架在水压力作用下C、D两点的相对水平位移,各杆EI为常数。
解:(1)作荷载作用下弯矩图:在C、D两点加一对反向的单位水平力,并作弯矩图如下:则:5、某条形基础,宽B=2m ,埋深d=1m 。
基底附加压力p=100kPa ,基底至下卧层顶面的距离Z=2m ,下卧层顶面以上土的重度3/20m kN =γ,经修正后,下卧层地基承载力设计值kPa f 110=,扩散角 22=θ,试通过计算,验算下卧层地基承载力是否满足要求?(4.0tan =θ) 解:kPa d cz 60203)2(=⨯=⨯+=γσ kPa Z b b p z 6.554.02222100tan 20=⨯⨯+⨯=⨯+⨯=θσf kPa z cz >=+=+6.115606.55σσ,故不能满足要求。
工程力学(天津大学)第6章答案
考虑微段的静力平衡,有 [A(x) + dA(x)]⋅[σ] = A(x)[σ] +ρA(x)dx dA(x)[σ] =ρA(x)dx 设桥墩顶端截面( x = 0)的面积为A0 ,对上式积分,得x 截面的面积为
F
F
F
5m
15m
5m
5m
(a)
(b)
(c)
习题 6 − 14 图
解:(1)采用等截面石柱
结构如图a 所示,设柱的横截面面积和长度分别为A 、l ,底部截面轴力最
大,为
强度条件为
于是有
所用石料体积为 2、采用三段等长度的阶梯石柱
结构如图b 所示,按从上到下顺序,设各段横截面面积和长度分别为A1 , l 1 , A2 , l 2 和 A3 , l 3 。显然,各阶梯段下端截面轴力最大,分别为
(2)由强度条件确定许用荷载
F A
B 60º
所以许用荷载为[F]=21.6kN。
C
60º
F
6 − 16 图示结构由刚性杆 AB 及两弹性 杆 EC 及 FD 组成,在 B 端受力 F 作用。两弹性
习题 6 − 15 图
杆由相同材料所组成,且长度相等、横截面面 积相同,试求杆 EC 和 FD 的内力。
FN1=FN2。
(2)根据题意,其位移条件为
其中,
分别为螺栓的伸长及套管的缩短,考虑 FN1=FN2,可计算出
将
代入得
(3) 螺栓横截面的应力为拉应力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-10求图示多跨梁支座 A 、C 处的约束力。
已知 M =8 kN - m q = 4kN/m , l =2m(b)习题3 - 10图解:(1)取梁BC 为研究对象。
其受力如图(b )所示。
列平衡方程M B o,F c 21 q 31 色 029ql 9 4 2 F C18kN44(2)取整体为研究对象。
其受力如图(c )所示。
列平衡方程 F y 0, F A F Cq 3l 0F AF C 3ql18 3 426kNM A 0,M A M F C 4l q 3l 3.5l 0M A MF C 4l 10.5ql 28 18 4 2 10.5 4 22 32kN m3- 11组合梁 AC 及CD 用铰链C 连接而成,受力情况如图(a )所示。
设 F =50kN ,q = 25kN/m ,力偶矩 M = 50kN - m 求各支座的约束力。
U UnJl.1 rC F C1 ------ 1—2l _—亠(c) (a )qF AI IF CI~I I■* ------ 21 ------- ----------- 2L -------- l 亠2222FwiuiMab"""B'l" "" " L「BCD F D习题3- 11图解:(1)取梁 CD 为研究对象。
其受力如图 (c)所示。
列平衡方程M C 0, F D F D2q M2 25 5025kNM D 0, F C F C 6q4 25 5025kN(2)取梁AC 为研究对象。
其受力如图 (b)所示,其中 F 'c =F c =25kN 。
列平衡方程M B 0, 2 1 F C 2F AF 2q2F C50 2 25 2 2525kN()M A 0, F B3 F C 40 F B6q 4F C 50 6 25 4 25150kN6- 1作图示杆件的轴力图。
解:在求AB 段内任一截面上的轴力时,在任一截面1- 1处截断,取左段为脱离体(图c ),并设轴力F N 1为拉力。
由平衡方程求出:F N3 0kN同理,可得DE 段内任一横截面上的轴力 F N 4为(图f )F N4按轴力图作图规则,作出杆的轴力图(图6- 8图示钢杆的横截面面积为200mr^钢的弹性模量 E =200GPa 求各段杆的应变、40kN20kN 25kN(a ) 20kN25kN(b )A B C卜一600 - 300 |120kN —500 D 400 E ,40kN 2 20kN- -------------4 ------ 25kN2020(g )II E HII]20 习题6-1图 F N 1 20kN(图 d )为20 40 20kNBC 段任一截面上的轴力 F N2求CD 段内的轴力时,将杆截开后取右段为脱离体,并设轴力同理,可求得 F N 3为拉力(图e ) o 由F x 0,F N3 2525 0F 4 25kNg ) o23(c )(d)(e )3D伸长及全杆的总伸长。
解:(1 )由截面法直接作轴力图(2) 计算各段截面的应力(1)计算各段截面的应变10kN1 W5 张卜JN120kN\ --- r(2)计算各段截面的的伸长计算杆件总伸长9图示一阶梯形截面杆,其弹性模量 E =200GPa 截面面积 A i =300mm A n =250m^6-A rn =200mm ,作用力 F l =30kN , F 2 = 15kN , F 3 = 10kN , F 4 = 25kN 。
试求每段杆的内力、应力、应变、伸长及全杆的总伸长。
解:(1 )由截面法直接作轴力图(2)计算各段截面的应力(3)计算各段截面的应变(4) 计算各段截面的的伸长(5)计算杆件总伸长习题 6-85kN轴力图习题6 -9图轴力图AB段:得AB 段的直径为6 - 11图示一三角架,在节点A受F力作用。
设AB为圆截面钢杆,直径为d,杆长为h;AC为空心圆管,截面积为A,杆长为l 2。
已知:材料的容许应力8 2[c]=160MPa, F=10mm A=50 10- m, 11=, 12=。
试作强度校核。
解:(1)求各杆的轴力,取A节点为脱离体,并由(2)计算各杆截面的应力故满足强度条件,结构是安全的。
8- 12传动轴的转速为n =500r/min,主动轮1输入功率R = 500kW从动轮2、3分别输出功率P2 = 200kW, F3 = 300 kW。
已知材料的许用切应力[]=70MPa材料切变模量G =79GPa轴的单位长度许用扭转角[]=1° /m。
(1)试确定AB端的直径di和BC端的直径d2。
(2)若AB和BC两端选用同一直径,试确定直径d o(3)主动轮和从动轮应如何安排才比较合理解:(1 )圆轴上的外力偶分别为P 1500M 19550」95509550N mn500M 1R9550」95502003820N m n500c c R300M 19550 —95505730N mn500作圆轴的扭矩图。
(2)根据强度条件确定AB段和BC段的直径,maxT1 W P1l 2 l 2h* -------------------------------- H习题6 - 11图F NACF NAB习题8- 121633 316 5730 ------------ 6 ------------ 74.7mm70 106(3) 根据刚度条件确定AB 段:AB 段和BC 段的直径,T 1 Gl P1得AB 段的直径为BC 段:(4) 将主动轮置于中间比较合理,此时T max 最小.BC 段: 得AB 段的直径为’316T 1d1\;T imax3 16 9550688.6mm70 10T 2 卫WP2d 3 d 2 16d 2316T 2[]T id i432T 1432 9550 18079 10991.6mmG32d 24 32 5730 18080.7mm79 109P2 得BC 段的直径为(3)若选同一直径(c)lF-*Fl/41F A L11F F①支反力F A,F C1212②内力方程: 11F l AC段F S x F A(0<X<)12311F l、M x F A.X X(O w x w12311F F l 2l CD段F S x F A F F<x w )1212 3 3L l11F 厂Fl F X FlM x F A.X F. X X F .X312 3 12 3z1 21、3 3DB段F S x F B F(22- w x<l)123Fl F X2l , x M x F B l X<X w l )12123③内力图F S图M图(g)3618F= 9kN q =6kN/m工C D B观---- 6m_解:11F12①支反力F:=28kN,F D=29kN②F S图木材的许用应力[d]=10MPa,试选择圆木的直径d o0.145m 145mm9- 5试列出下列梁的剪力方程和弯矩方程,并画出剪力图和弯矩图。
解:F = 9kN q = 6kN/m||||||||IH11F C F DA B解:作弯矩图则由maxmaxW z得W z max10- 7圆形截面木梁,梁上荷载如图所示,已知I =3m F=3kN, q = 3kN/m,弯曲时32FFI/4uC-l。
