牛头刨床机构运动分析
牛头刨床刨刀往复运动机构的分析与设计

机械工程学院机械原理课程设计说明书设计题目:牛头刨床刨刀往复运动机构的分析与设计专业:机械设计制造及其自动化班级:13级姓名:学号指导教师:侍红岩2016年 1 月 4 日目录1 设计任务 (1)1.1 设计题目 (1)1.2 工作原理及工艺动作过程 (1)1.3 原始数据及设计要求 (1)1.4 设计任务 (2)2 系统传动方案设计 (3)2.1 曲柄滑块机构与摆动导杆机构 (3)2.2 齿轮和摆动导杆机构 (4)2.3 执行机构方案的比较 (5)2.4 执行机构方案的确定 (5)3 机构运动简图及数据分析 (7)3.1 机械结构简图 (7)3.2 牛头刨床数据分析 (8)4 机构运动分解 (10)5 主机构受力分析 (11)5.1 各运动副反力 (11)5.2 曲柄机构平衡力矩 (14)参考文献 (16)1 设计任务1.1 设计题目牛头刨床刨刀往复运动机构的分析与设计。
1.2 工作原理及工艺动作过程牛头刨床是一种用于平面切削加工的机床,整个机构的运转是由原动件1带动杆2的,通过连杆3推动滑块4运动;从而实现刨刀的往复运动。
刨头右行时,刨刀进行切削,称工作行程,此时要求速度较低并且均匀;刨头左行时,刨刀不切削,称空回行程,此时要求速度较高,以提高生产率。
1.3 原始数据及设计要求图1-1已知行程比系数K=1.4原动件曲柄1转速n1=60r/min,刨刀5行程H=400mm,其它参数为,L4=220mm,L5=180mm,L6=350mm,L |3=L3/2,H1=100mm,H2尺寸应满足传动角尽可能大;故刨刀5移动导路位于D点圆弧轨迹弦高一半处;构件重量分别为G2=200N,G5=700N,质心位于S3、S5处;构件3绕质心转动惯量J S3=1.1kg.m2,回程阻力为零,其它忽略不计。
刨刀工作阻力如图1-1所示,回程阻力为零,其它条件忽略不计。
表 11.4 设计任务(1)绘制机构运动简图。
牛头刨床的运动和动力分析

二、牛头刨床的运动、动力分析[H,L1]=solve('H=300','L1=(270*H)/(2*550)',' H','L1')H =300L1 =810/11>> [N1,W1]=solve('N1=23',' W1=(N1*2*PI)/60','N1','W1')N1 =23W1 =23/30*PI一、任务根据牛头刨床的机构简图及必要的数据,进行机构的运动学和动力学分析,并给出刨头的位移、速度、加速度和曲柄平衡力矩的曲线。
二、已知条件1、机构运动简图2、机构尺寸mm a 270=, mm b 520=, mm l 5503=, mm l 1004=3、刨头行程和曲柄转速行程mm H 420=, 转速min /891r n =4、刨头的切削阻力工作行程始终为1000N ,空程为0N 。
三、 表达式推导如图所示以A 点为坐标原点,平行刨头运动方向为x 轴,建立直角坐标系,标出各杆矢量及方位角。
由机构的结构分析有:过D 和D '做刨头所在导轨的垂线DG 和D 'G ',从图形中的角度关系易证明GE= G 'E ',所以有EE '=DD '及EE '=θsin 23l =H al l =132,因而我们可以得到312l aHl =1、推导出刨头()1ϕE E x x =,()1ϕE E v v =,()1ϕE E a a =的数学表达式。
(1) 位置分析由矢量封闭三角形ABC 可得封闭矢量方程为CB AB l l a=+即: 312ii i AB ae l e Se πϕϕ+= (1)应用欧拉公式θθθsin cos i e i +=,将(1)的虚部和实部分离得: 31sin sin ϕϕS l a AB =+ (2)31cos cos ϕϕS l AB = (3) 由上面两式求解可得: 当0cos 1=ϕ即21πϕ=或231πϕ=时,由(3)得 0cos 3=ϕ 及 23πϕ=当0cos 1≠ϕ时:113cos sin tan ϕϕϕAB AB l l a +=(4)此时按照机构结构简图及反正切的定义范围易得: 当0tan 3<ϕ时: 113c o s s i n a r c t a n ϕϕπϕAB AB l l a ++=当0tan 3>ϕ时: 113c o s s i n a r c t a nϕϕϕAB AB l l a +=由矢量封闭图形CFED 可得封闭矢量方程为D E CD FE CF l l l l+=+即: 43432ϕϕπi i iE e l e l be x +=+ (5)应用欧拉公式将(4)的虚部和实部分离得:4433cos cos ϕϕl l x E += (6) 4433sin sin ϕϕl l b += (7)由式(7)可得 4334sin sin l l b ϕϕ-=此时按照机构结构简图及反正弦函数的定义范围易得: 4334sin arcsinl l b ϕπϕ--= (8) 由这两个式子可以消去4ϕ,得到由1ϕ确定的E x 的公式:()()23323324sin cos ϕϕl b l x l E -+-= (9) 显然式(9)作为计算式时难以确定E x 的符号,因此在编程时我选择式(6)作为计算式。
机械原理大作业1
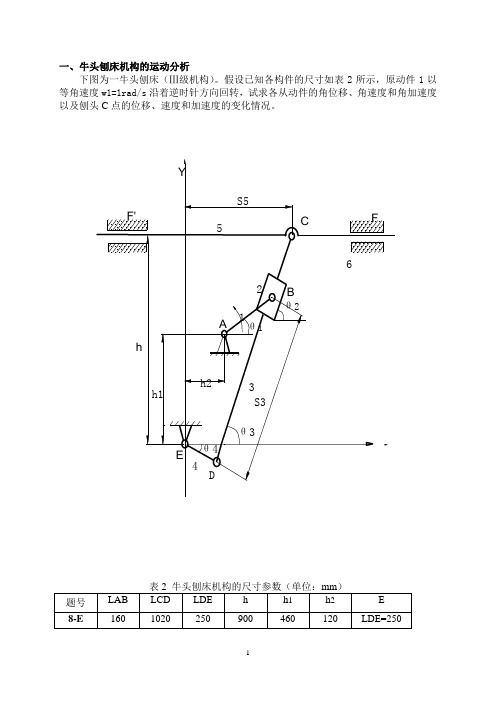
一、牛头刨床机构的运动分析下图为一牛头刨床(Ⅲ级机构)。
假设已知各构件的尺寸如表2所示,原动件1以等角速度w1=1rad/s沿着逆时针方向回转,试求各从动件的角位移、角速度和角加速度以及刨头C点的位移、速度和加速度的变化情况。
二、牛头刨床机构的运动分析方程 1)位置分析建立封闭矢量多边形建立一直角坐标系,并标出各杆矢量及其方位角,其中共有4个未知量3θ(θ2=3θ)、4θ、3S 、5S 。
利用两个封闭图形ABDEFA 和EDCGE ,建立两个封闭矢量方程,由此可得:3125DE AB DE CD l s h h l l l h s →→→→→→→→→⎧+=++⎪⎨⎪+=+⎩(1)把(1)写成投影方程得:433214331143543cos *cos *cos *sin *sin *sin *cos *cos 0*sin *sin DE AB DE AB DE CD DE CD l s h l l s h l l l s l l h θθθθθθθθθθ*+=+⎫⎪+=+⎪⎬+-=⎪⎪+=⎭(2) 由以上各式用型转化法可求得4335s s θθ、、、,滑块2的方位角23θθ=2111*cos *sin b AB b AB x h l y h l θθ=+⎧⎨=+⎩ 44*cos *sin d DE d DE x l y l θθ=⎧⎨=⎩3s =3)*sin *()/*cos *(/c d CD d CD b d c d CD d CD b d s x x l x l x x s y y l y l y y s αα=+=+-⎧⎪⎨=+=+-⎪⎩ 3tan c dc dy y x x θ-=- 5c s x =()ae AE =44()tan *cos d c DE y h y l θθ+-=高斯消去法求解 2)速度分析对(2)求一次导数得:44333331144333331144334433*sin *s '*cos *sin **sin **cos *'*sin *cos **cos **sin **sin *0*cos **cos *0DE AB DE AB DE CD c DE CD l s l l s s l l l v l l θωθθωθωθωθθωθωθωθωθωθω-+-=-⎫⎪++=⎪⎬---=⎪⎪+=⎭(3)矩阵式:3334313334313443cos *sin *sin 0'*sin sin *cos *cos 0*cos 0*sin *sin 100*cos *cos 00DE AB DE AB CD DE CD DE c s l s l s l l l l l l v θθθθθθθθθθωθθ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥ω⎢⎥⎢⎥⎢⎥=ω1⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (4)采用高斯消去法可求解(4)可解得角速度ω2,ω3; 3)加速度分析把(4)对时间求导数得:333433334334434cos *sin *sin 0''sin *cos *cos 00*sin *sin 10*cos *cos 0DE DE CD DE CD DE c s l s s l l l l l a θθθθθθθθαθθ--⎡⎤⎡⎤⎢⎥⎢⎥α⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦33333444433333343443334443344*sin '*sin **cos **cos 0'*cos '*cos **sin **sin 00**cos **cos 00**sin **sin 0DE DE CD DE CD DE c s s l s s s l l l l l v ωθθωθωθωθθωθωθωθωθωωθωθ----⎡⎤⎡⎤⎢⎥⎢⎥--ω⎢⎥⎢⎥=-⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦1111**cos **sin 00AB AB l l ωθωθ-⎡⎤⎢⎥-⎢⎥+ω1⎢⎥⎢⎥⎣⎦(5)采用高斯消去法可求解(5)可解得角加速度α2,α3,α5,α6三、程序流程图四、计算源程序#include<stdio.h>#include<stdlib.h>#include<math.h>/* 定义变量*/const double PI = 3.14159265358979;const int N = 4;const double EPSILON = 0.0001;const int T = 1000;/* 代入已知量*/double Lab=160,Lcd=1020,Lde=250,h=900,h1=460,h2=120,Omega1=1;/* 声明子函数*/void AngleDisplacement(double[12],double);/* 角位移函数*/void AngleVelocity(double[N][N],double[N],double[12],double);/* 角速度函数*/void AngleAcceleration(double[N][N],double[N][N],double[N],double [12]);/* 角加速度函数*/void GaussE(double [N][N],double [N],double [N]);/* 高斯消去法函数*/void ModulusMatrixA(double [12],double [N][N]);/* 矩阵A函数*/void ModulusMatrixB(double [12],double ,double [N]);/* 矩阵B函数*/void MatrixDA(double [12],double [N][N]);/* 矩阵DA函数*/void MatrixDB(double [12],double ,double [N]);/* 矩阵DB函数*//* 主函数*/void main(){int i,j;FILE *fp;double data[36][12];double value[12],a[N][N],da[N][N],b[N],db[N],Phi1;char flag;/* 打开文件*/if((fp = fopen("Data","w")) == NULL){printf("文件打开错误!\n");exit(0);}fprintf(fp,"Lab =%lf \n",Lab);fprintf(fp,"s3\tPhi3\tPhi4\ts5\t");fprintf(fp,"s3'\tOmega3\tOmega4\ts5'\t");fprintf(fp,"s3''\tEpsilon3\tEpsilon4\ts5''");printf("\n\n 牛头刨床机构运动分析程序\n\n\n");printf("\n");printf(" 是否开始计算(Y/N):");scanf("%c",&flag);if(flag =='Y'){/*计算并写入文件*/value[0] = 480;value[1] = 65 * PI / 180;value[2] = 10 * PI / 180;value[3] = 500;for(i = 0;i < 36; i++){Phi1 = i * PI / 18;AngleDisplacement(value,Phi1);ModulusMatrixB(value,Phi1,b);ModulusMatrixA(value,a);AngleVelocity(a,b,value,Phi1);MatrixDA(value,da);MatrixDB(value,Phi1,db);AngleAcceleration(a,da,db,value);for(j = 1;j < 3; j++)value[j] = value[j] * 180 / PI;for(j = 0;j < 12; j++)data[i][j] = value[j];fprintf(fp,"\n");for(j = 0;j < 12; j++)fprintf(fp,"%12.3f\t",data[i][j]);}fclose(fp);/* 输出数据*/printf("\n\n\n计算结果如下:\n");for(i = 0;i < 36; i++){Phi1=i * PI / 18;printf("\n输出Phi1=%d时的求解\n",i*10);printf(" S3 Phi3 Phi5 S5\n");for(j = 0;j < 4; j++)printf("%lf\t",data[i][j]);printf("\n");printf(" S3' Omega3 Omega5S5'\n");for(j = 4;j < 8; j++)printf("%lf\t",data[i][j]);printf("\n");printf(" S3'' Epsilon3 Epsilon5 S5''\n");for(j = 8;j < 12; j++)printf("%lf\t",data[i][j]);printf("\n");}printf("\n程序运行结束,计算结果已写入Date文件中,请打开查看。
牛头刨床的连杆机构运动分析

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是关于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确信从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,因此机构的运动分析是机械设计进程中必不可少的重要环节。
以运算机为手腕的解析方式,由于解算速度快,精准度高,程序有必然的通用性,已成为机构运动分析的要紧方式。
连杆机构作为在机械制造专门是在加工机械制造中要紧用作传动的机构型式,同其他型式机构专门是凸轮机构相较具有很多优势。
连杆机构采纳低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构能够将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,知足给定的运动要求,完成机械的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的操纵。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,现在要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的阻碍。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度和刨刀C点的位移、速度和加速度的转变情形。
牛头刨床的连杆机构运动分析

牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构,按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量,运动参数又是机械动力学分析的依据,所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法,由于解算速度快,精确度高,程序有一定的通用性,已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式,同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接,结构简单,易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件,实现间歇运动,满足给定的运动要求,完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动,实现工件的切削。
工作台的横向运动即是进给运动,实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成,其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时,通过六杆机构驱动刨刀作往复移动。
刨刀右行时,当刨刀处于工作行程时;要求刨刀的速度较低且平稳,以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时,刨刀不工作,称为空行程,此时要求刨刀的速度较高以提高生产率。
由此可见,牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成,其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件,刨刀装在C点上。
假设已知各构件的尺寸如表1所示,原动件1以等角速度ω1=1rad/s沿着逆时针方向回转,要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。
牛头刨床机构运动分析

高等机构学题目: 牛头刨床机构运动分析院系名称:机械与动力学院专业班级:机械工程学生姓名:学号:学生姓名:学号:学生姓名:学号:指导教师:2015年12 月17日目录一问题描述................................................................................................................................ - 1 -二运动分析................................................................................................................................ - 1 -2.1矢量法构建机构独立位置方程 ............................................................................. - 1 -2.2机构速度分析 ............................................................................................................. - 2 -2.3机构加速度分析......................................................................................................... - 2 -2.4机构运动线图绘制.................................................................................................... - 3 -三总结......................................................................................................................................... - 4 -附录一:Matlab程序............................................................................................................... - 4 -牛头刨床机构运动分析一 问题描述如图1-1所示的牛头刨床机构中,800h mm =,1360h mm =,2120h mm =,200AB l mm =,960CD l mm =,160DE l mm =。
牛头刨床平面机构的设计与分析
牛头刨床平面机构的设计与分析引言:牛头刨床平面机构是一种常见的木工加工设备,用于对木材表面进行刨削加工。
在牛头刨床平面机构中,刀具通过机构运动,将工件表面的不平整部分削平,使其具有更加光滑的表面质量。
牛头刨床平面机构的设计与分析对于提高机械加工效率、确保加工质量以及降低设备故障率具有重要意义。
一、牛头刨床平面机构的设计要素1.刀具部分设计:刀具部分是牛头刨床平面机构的关键部分,设计合理与否直接影响到加工质量和效率。
刀具部分包括刨刀和刨刀架。
刨刀的选择要考虑到刨削材料的硬度和机床的工作状态。
刨刀架则需要具备刀具安装方便、切削力平稳传递等特点。
2.主动件设计:主动件主要是传动装置,包括电机、减速器、皮带等。
电机要选择合适的功率和转速,确保机床的正常运转。
减速器可以通过传动比选择来调整机床的切削速度。
皮带的选择要考虑到传动效率和寿命,以及对机床的振动和噪音影响。
3.机构设计:牛头刨床平面机构的机构设计要考虑到机床运动的稳定性和刨削质量。
机构设计的关键是选择合适的导轨和导向方式,确保刨削过程中的工作台和刀具的稳定性。
同时,机构设计还需要考虑到切削力和振动等因素的影响,以减小机床的故障率。
二、牛头刨床平面机构的分析方法1.动力学分析:动力学分析可以通过建立相应的运动学方程和动力学方程,研究机械零件的运动状态和力学特性。
动力学分析可以帮助我们评估机床的运动稳定性和工作状态,以及切削力和振动等因素的影响。
2.有限元分析:有限元分析是一种基于计算机模拟的工程分析方法,可以对机床的结构进行力学和热力学分析。
有限元分析可以评估机床在工作过程中的受力情况和变形程度,为机床结构的优化设计提供参考。
3.模态分析:模态分析是一种研究机械结构动态特性的方法,可以分析机床的固有频率和振型。
模态分析可以帮助我们评估机床的动态性能,以及对切削力和振动等外界扰动的响应能力。
4.可靠性分析:可靠性分析可以通过统计学的方法,评估机床的故障率和寿命。
牛头刨床导杆机构的运动分析、动态静力分析
摘要——牛头刨床运动和动力分析一、机构简介与设计数据1、机构简介牛头刨床是一种用于平面切削加工的机床,如图1-1a。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。
刨床工作时,由导杆机构2 –3 –4 –5 –6 带动刨头6和刨刀7作往复运动。
刨头右行时,刨刀进行切削,称工作行程,此时要求速度较低并且均匀,以减少电动机容量和提高切削质量;刨头左行时,刨刀不切削,称空回行程,此时要求速度较高,以提高生常率。
为此刨床采用有急回作用的导杆机构。
刨刀每切削完一次,利用空回行程的时间,凸轮8通过四杆机构1 – 9 – 10 – 11 与棘轮带动螺旋机构(图中未画),使工作台连同工件做一次进给运动,以便刨刀继续切削。
刨头在工作行程中,受到很大的切削阻力(在切削的前后各有一段约0.05H的空刀距离,图1-1b),而空回行程中则没有切削阻力。
因此刨头在整个运动循环中,受力变化是很大的,这就影响了主轴的匀速运转,故需安装飞轮来减小主轴的速度波动,以提高切削质量和减少电动机容量a b图目录摘要 (III)1设计任务 (1)2 导杆机构的运动分析 (2)导杆机构的动态静力分析 (4)3.1运动副反作用力分析 (4)3.2力矩分析 (6)4方案比较 (7)5总结 (10)6参考文献 (10)《机械原理课程设计》说明书1设计任务机械原理课程设计的任务是对机器的主题机构进行运动分析。
动态静力分析,确定曲柄平衡力矩,并对不同法案进行比较,以确定最优方案。
要求根据设计任务,绘制必要的图纸和编写说明书等。
2 导杆机构的运动分析2.1 速度分析取曲柄位置1’对其进行速度分析,因为2和3在以转动副相连,所以V A2=V A3,其大小等于ω2l02A,指向于ω2相同。
取构件3和4的重合点A进行速度分析。
列速度矢量方程,得υA4 = υA3 + υA4A3大小 ? √ ?方向⊥O4A ⊥O2A ∥O4B选比例尺μv=0.004(m/s)/mm,做出速度矢量图(见图a)νA4=0.088m/sνA3=0.816m/s取5构件作为研究对象,列速度矢量方程,得υC5 = υB5 + υC5B5大小 ? √ ?方向∥XX ⊥O4B ⊥BC取速度极点p,选比例尺μv=0.004(m/s)/mm,做出速度矢量图(见图a)νC5=0.16m/sνC5B5=0.044m/s2.2 加速度分析取曲柄位置“1”进行加速度分析。
(完整版)牛头刨床运动分析实例
例: 如图所示为一牛头刨床的机构运动简图。
设已知各构件尺寸为:1125mm l =,3600mm l =,4150mm l =,原动件1的方位角1=0~360θ︒︒和等角速度1=1rad/s w 。
试用矩阵法求该机构中各从动件的方位角、角速度和角加速度以及E 点的位移、速度和家速度的运动线图。
解:先建立一直角坐标系,并标出各杆矢量及方位角。
其中共有四个未知量3θ、4θ、3s 及E s 。
为求解需建立两个封闭矢量方程,为此需利用两个封闭图形ABCA 及CDEGC ,由此可得,613346,'E l l s l l l s +=+=+(1-1)写成投影方程为: 331133611334433446cos cos sin sin cos cos 0sin sin 'E s l s l l l l s l l l θθθθθθθθ==++-=+= (1-2)解上面方程组,即可求得3θ、4θ、3s 及E s 四个位置参数,其中23θθ=。
将上列各式对时间取一次、二次导数,并写成矩阵形式,即可得以下速度和加速度方程式。
速度方程式:3331133331131334443344cos sin 00sin sin cos 00cos 0sin sin 1000cos cos 0E s l s s l w w l l w l l v θθθθθθθθθθ⎡⎤--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (1-3)机构从动件的位置参数矩阵:33333333443344cos sin 00sin cos 000sin sin 10cos cos 0s s l l l l θθθθθθθθ-⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎣⎦机构从动件的的速度列阵:334E s w w v ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦机构原动件的位置参数矩阵:1111sin cos 00l l θθ-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦1w :机构原动件的角速度加速度方程式:333333333344433443333333333333333344433344cos sin 00sin cos 000sin sin 10cos cos 0sin sin cos 00cos cos sin 000cos cos 00sin sin E s s s l l l l w s s w w s s w l w l w l w l w θθθθαθθαθθαθθθθθθθθθθ⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦----=-----11131113144cos sin 000E l w s l w w w w v θθ⎡⎤⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦(1-4)机构从动件的位置参数矩阵求导:33333333333333333444333444sin sin cos 00cos cos sin 000cos cos 00sin sin 0w s s w w s s w l w l w l w l w θθθθθθθθθθ⎡⎤---⎢⎥⎢⎥-⎢⎥⎢⎥--⎢⎥--⎢⎥⎣⎦机构从动件的的加速度列阵:334E s ααα⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦机构原动件的位置参数矩阵求导:111111cossinl wl wθθ-⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦主程序(matlab):%牛头刨床运动分析主程序s;%x(1)——代表3θ;%x(2)——代表构件3的转角3θ;%x(3)——代表构件4的转角4s;%x(4)——代表E点的线位移El;%x(5)——代表1l;%x(6)——代表3l;%x(7)——代表4l;%x(8)——代表6l;%x(9)——代表'6w。
牛头刨床主传动机构运动方案分析
三、机构选型、方案分析及方案的确定方案一的运动分析及评价(1)运动是否具有确定的运动该机构中构件n=5。
在各个构件构成的的运动副中Pl=6,Ph=1.凸轮和转子、2杆组成运动副中有一个局部自由度,即F'=1。
机构中不存在虚约束。
.由以上条件可知:机构的自由度 F=3n-(2Pl+Ph-p')-F'=1机构的原动件是凸轮机构,原动件的个数等于机构的自由度,所以机构具有确定的运动。
(2)机构传动功能的实现在原动件凸轮1带动杆2会在一定的角度范围内摇动。
通过连杆3推动滑块4运动,从而实现滑块(刨刀)的往复运动。
(3)主传动机构的工作性能凸轮1的角速度恒定,推动2杆摇摆,在凸轮1随着角速度转动时,连杆3也随着杆2的摇动不断的改变角度,使滑块4的速度变化减缓,即滑块4的速度变化在切削时不是很快,速度趋于匀速;在凸轮的回程时,只有惯性力和摩擦力,两者的作用都比较小,因此,机构在传动时可以实现刨头的工作行程速度较低,而返程的速度较高的急回运动。
传动过程中会出现最小传动角的位置,设计过程中应注意增大基圆半径,以增大最小传动角。
机构中存在高副的传动,降低了传动的稳定性。
(4)机构的传力性能要实现机构的往返运动,必须在凸轮1和转子间增加一个力,使其在回转时能够顺利的返回,方法可以是几何封闭或者是力封闭。
几何封闭为在凸轮和转子设计成齿轮形状,如共扼齿轮,这样就可以实现其自由的返回。
机构在连杆的作用下可以有效的将凸轮1的作用力作用于滑块4。
但是在切削过程中连杆3和杆2也受到滑块4的作用反力。
杆2回受到弯力,因此对于杆2的弯曲强度有较高的要求。
同时,转子与凸轮1的运动副为高副,受到的压强较大。
所以该机构不适于承受较大的载荷,只使用于切削一些硬度不高的高的小型工件。
该机构在设计上不存在影响机构运转的死角,机构在运转过程中不会因为机构本身的问题而突然停下。
(5)机构的动力性能分析。
由于凸轮的不平衡,在运转过程中,会引起整个机构的震动,会影响整个机构的寿命。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等机构学题目: 牛头刨床机构运动分析院系名称:机械与动力学院专业班级:机械工程学生姓名:学号:学生姓名:学号:学生姓名:学号:指导教师:2015年12 月17日目录一问题描述................................................................................................................................ - 1 -二运动分析................................................................................................................................ - 1 -2.1矢量法构建机构独立位置方程 ............................................................................. - 1 -2.2机构速度分析 ............................................................................................................. - 2 -2.3机构加速度分析......................................................................................................... - 2 -2.4机构运动线图绘制.................................................................................................... - 3 -三总结......................................................................................................................................... - 4 -附录一:Matlab程序............................................................................................................... - 4 -牛头刨床机构运动分析一 问题描述如图1-1所示的牛头刨床机构中,800h mm =,1360h mm =,2120h mm =,200AB l mm =,960CD l mm =,160DE l mm =。
设曲柄以等角速度15/rad s ω=逆时针方向回转,试对其进行运动分析,求出该机构中各从动件的方位角、角速度和角加速度以及各机构的运动线图。
图1-1 牛头刨床机构二 运动分析2.1矢量法构建机构独立位置方程如图2-1所示,以E 为坐标原点建立直角坐标系,并标出各杆矢量及其方位角。
其中共有四个未知量334,,,c S S θθ。
图2-1 坐标系建立以两个封闭图形ABDEA 和EDCFE 为基准构建两个封闭矢量位置方程,即:134AE l S l +=+34c h S l l +=+将上述矢量方程分别沿X 轴和Y 轴进行投影,得牛头刨床机构的独立位置方程如下:3344211cos cos cos s l h l θθθ+=+ 3344111sin sin sin s l h l θθθ+=+3344cos cos c l l s θθ+= 3344sin sin l l h θθ+=利用Matlab 进行编程求解,可求得各机构的位置,程序见附录一。
2.2机构速度分析将机构的位置方程对时间求一次导数,并写成矩阵的形式,得机构的速度方程如下:33344311333443111334443344cos sin sin 0sin sin cos cos 0cos 0sin sin 100cos cos 00c s l s l s l l l l l l s θθθθθθθωθωθθωθθ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 利用Matlab 进行编程求解,可求得各机构的角速度或速度,程序见附录一。
2.3机构加速度分析将机构的速度方程对时间求一次导数,并写成矩阵的形式,得机构的加速度方程如下:33344333333344433344333333344433444333443344cos sin sin 0sin sin cos cos 0sin cos cos 0cos cos sin sin 00sin sin 10cos 0cos cos 0c s l s s s l s l s s l l l l l l l s θθθθθωθωθθθθαθθωθωθθθαωθωθθ------⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥=-⎢⎥⎢⎥----⎢⎥⎢⎥⎣⎦⎣⎦33443334441111111cos 00sin sin 0cos sin 00c s l l s l l ωθωωθωθωθωθω⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦-⎡⎤⎢⎥-⎢⎥+⎢⎥⎢⎥⎣⎦利用Matlab 进行编程求解,可求得各机构的角加速度或加速度,程序见附录一。
2.4机构运动线图绘制通过Matlab进行计算求解,得到各构件的位置、速度和加速度,如表2-1所示。
根据所求得的各构件的位置、速度及加速度,进行机构运动线图的绘制,如图2-2所示。
程序见附录一。
表2-1 各构件的位置、速度和加速度位移线图时间/s 角位移 / ︒位移/m角速度线图时间/s角速度 / r a d ⋅s -1速度/m ⋅s -1角加速度线图时间/s角加速度 / r a d ⋅s -2加速度/m ⋅s -2牛头刨床运动仿真mmm m图2-2 机构的运动线图三 总结通过对牛头刨床机构的运动分析,让我们学会了如何使用矩阵法建立平面机构的运动方程。
对机构进行运动分析的关键是独立位置方程的建立和求解,由于独立位置方程是一个非线性方程组,计算难度较大。
本文借用了Matlab 软件进行编程求解独立位置方程,同时对牛头刨床机构进行了运动仿真,并绘制了牛头刨床机构的运动线图,完成了从理论分析到编程求解的运动分析过程。
附录一:Matlab 程序(1)子函数PosionFun.mfunction f=Position_Fun(x,theta1,h,h1,h2,l1,l3,l4) f=[ x(1)*cos(x(2))+l4*cos(x(3))-h2-l1*cos(theta1); x(1)*sin(x(2))+l4*sin(x(3))-h1-l1*sin(theta1); l3*cos(x(2))+l4*cos(x(3))-x(4);l3*sin(x(2))+l4*sin(x(3))-h];end(2)子函数Six_Bar.mfunction [theta,omega,alpha]=Six_Bar(theta0,theta1,omega1,alpha1,h,h1,h2,l1,l3,l4) theta=fsolve(@(x)Position_Fun(x,theta1,h,h1,h2,l1,l3,l4),theta0);S3=theta(1);theta3=theta(2);theta4=theta(3);Sc=theta(4);%计算连杆3、连杆4、滑块2和C点的速度A=[ cos(theta3) -S3*sin(theta3) -l4*sin(theta4) 0;sin(theta3) S3*cos(theta3) l4*cos(theta4) 0;0 -l3*sin(theta3) -l4*sin(theta4) 1;0 l3*cos(theta3) l4*cos(theta4) 0];B=[-l1*sin(theta1);l1*cos(theta1);0;0];omega=A\(omega1*B);v3=omega(1);omega3=omega(2);omega4=omega(3);vc=omega(4);%计算连杆3、连杆4的角加速度,滑块2及C点的加速度A=[ cos(theta3) -S3*sin(theta3) -l4*sin(theta4) 0;sin(theta3) S3*cos(theta3) l4*cos(theta4) 0;0 -l3*sin(theta3) -l4*sin(theta4) 1;0 l3*cos(theta3) l4*cos(theta4) 0];At=[-sin(theta3) -v3*sin(theta3)-S3*omega3*cos(theta3) -l4*omega4*cos(theta4) 0;cos(theta3) v3*cos(theta3)-S3*omega3*sin(theta3) -l4*omega4*sin(theta4) 0;0 -l3*omega3*cos(theta3) -l4*omega4*cos(theta4) 0;0 -l3*omega3*sin(theta3) -l4*omega4*sin(theta4) 0];B=[-l1*sin(theta1);l1*cos(theta1);0;0];Bt=[-l1*omega1*cos(theta1);-l1*omega1*sin(theta1);0;0];alpha=A\(-At*omega+alpha1*B+omega1*Bt);a3=alpha(1);alpha3=alpha(2);alpha4=alpha(3);ac=alpha(4);end(3)主程序SixBar_main.m %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 牛头刨床机构运动分析%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%输入已知数据clear;l1=0.2;l3=0.96;l4=0.16;h=0.8;h1=0.36;h2=0.12;omega1=5;alpha1=0;hd=pi/180;du=180/pi;theta0=[0.3;60*hd;270*hd;0.45];%%%调用子函数Six_Bar 计算牛头刨床机构位移,角速度,角加速度for n1=1:459theta1(n1)=-2*pi+5.8119+(n1-1)*hd;[theta,omega,alpha]=Six_Bar(theta0,theta1(n1),omega1,alpha1,h,h1,h2,l1,l3,l4);S3(n1)=theta(1); %滑块2相对于CD杆的位移theta3(n1)=theta(2); %杆3转过的角度theta4(n1)=theta(3); %杆4转过的角度Sc(n1)=theta(4); %杆5的位移v3(n1)=omega(1); %滑块2相对于CD杆的速度omega3(n1)=omega(2); %杆3转过的角速度omega4(n1)=omega(3); %杆4转过的角速度vc(n1)=omega(4); %杆5的速度a3(n1)=alpha(1); %滑块2相对于CD杆的加速度alpha3(n1)=alpha(2); %杆3转过的角加速度alpha4(n1)=alpha(3); %杆4转过的角加速度ac(n1)=alpha(4); %杆5的加速度theta0=theta;endthetaOmegaAlpha=[theta3'*du,theta4'*du,Sc',omega3',omega4',vc',alpha3',alpha4', ac'];xlswrite('Positon_Speed_Acceleration.xls',thetaOmegaAlpha,'sheet1','b1:j459');%%% 位移,角速度,角加速度和四杆机构图形输出figure(1);n1=1:459;t=(n1-1)*2*pi/360;% 绘角位移和位移线图subplot(2,2,1);plot(t,theta3*du,'r-.','LineWidth',1.5);hold on;grid on;axis auto;[haxes,hline1,hline2]=plotyy(t,theta4*du,t,Sc);set(hline1,'LineWidth',1.5);set(hline2,'LineWidth',1.5);grid on;hold on;title('位移线图');xlabel('时间/s');axes(haxes(1));ylabel('角位移/ \circ');axes(haxes(2));ylabel('位移/m');hold on;grid on;text(2.75,-0.4,'\theta_3');text(3,0.65,'\theta_4');text(5,-0.25,'S_c');% 绘角速度及速度线图subplot(2,2,2);plot(t,omega3,'r-.','LineWidth',1.5);grid on;hold on;axis auto;[haxes,hline1,hline2]=plotyy(t,omega4,t,vc); set(hline1,'LineWidth',1.5);set(hline2,'LineWidth',1.5);grid on;hold on;title('角速度线图');xlabel('时间/s');axes(haxes(1));ylabel('角速度/ rad\cdots^{-1}');axes(haxes(2));ylabel('速度/m\cdots^{-1}');grid on;hold on;text(1.25,0.55,'\omega_3');text(4.65,2.25,'\omega_4');text(5,-2.85,'v_c');% 绘角加速度和加速度线图subplot(2,2,3);plot(t,alpha3,'r-.','LineWidth',1.5);grid on;hold on;[haxes,hline1,hline2]=plotyy(t,alpha4,t,ac);set(hline1,'LineWidth',1.5);set(hline2,'LineWidth',1.5);grid on;hold on;title('角加速度线图');xlabel('时间/s');axes(haxes(1));ylabel('角加速度/ rad\cdots^{-2}');axes(haxes(2));ylabel('加速度/m\cdots^{-2}');grid on;hold on;text(3,6.5,'\alpha_3');text(4.25,17.5,'\alpha_4');text(1.25,-4.5,'a_c');%绘制牛头刨床机构subplot(2,2,4);n1=20;x(1)=0;y(1)=0;x(2)=l4*1000*cos(theta4(n1));y(2)=l4*1000*sin(theta4(n1));x(3)=l4*1000*cos(theta4(n1))+(S3(n1)*1000-50)*cos(theta3(n1)); y(3)=l4*1000*sin(theta4(n1))+(S3(n1)*1000-50)*sin(theta3(n1)); x(4)=h2*1000;y(4)=h1*1000;x(5)=x(4)+l1*1000*cos(theta1(n1));y(5)=y(4)+l1*1000*sin(theta1(n1));x(6)=x(3)+100*cos(theta3(n1));y(6)=y(3)+100*sin(theta3(n1));x(7)=l4*1000*cos(theta4(n1))+l3*1000*cos(theta3(n1));y(7)=l4*1000*sin(theta4(n1))+l3*1000*sin(theta3(n1));x(8)=x(7)-900;y(8)=h*1000;x(9)=x(7)+600;y(9)=h*1000;x(10)=l4*1000*cos(theta4(n1))+(S3(n1)*1000-50)*cos(theta3(n1)); y(10)=l4*1000*sin(theta4(n1))+(S3(n1)*1000-50)*sin(theta3(n1)); x(11)=x(10)+25*cos(pi/2-theta3(n1));y(11)=y(10)-25*sin(pi/2-theta3(n1));x(12)=x(11)+100*cos(theta3(n1));y(12)=y(11)+100*sin(theta3(n1));x(13)=x(12)-50*cos(pi/2-theta3(n1));y(13)=y(12)+50*sin(pi/2-theta3(n1));x(14)=x(10)-25*cos(pi/2-theta3(n1));y(14)=y(10)+25*sin(pi/2-theta3(n1));x(15)=x(10);y(15)=y(10);x(16)=0;y(16)=0;x(17)=x(4);y(17)=y(4);k=1:3;plot(x(k),y(k));hold on;k=4:5;plot(x(k),y(k));hold on;k=6:9;plot(x(k),y(k));hold on;k=10:15;plot(x(k),y(k));hold on;k=16:17;plot(x(k),y(k),'-.');hold on;grid on;axis([-350 800 -250 950]);title('牛头刨床运动仿真');grid on;xlabel('mm');ylabel('mm');plot(x(1),y(1),'o');plot(x(2),y(2),'o');plot(x(4),y(4),'o');plot(x(5),y(5),'o');plot(x(7),y(7),'o');%%%牛头刨床机构运动仿真figure(2)m=moviein(20);j=0;for n1=1:5:360j=j+1;clf;x(1)=0;y(1)=0;x(2)=l4*1000*cos(theta4(n1));y(2)=l4*1000*sin(theta4(n1));x(3)=l4*1000*cos(theta4(n1))+(S3(n1)*1000-50)*cos(theta3(n1));y(3)=l4*1000*sin(theta4(n1))+(S3(n1)*1000-50)*sin(theta3(n1));x(4)=h2*1000;y(4)=h1*1000;x(5)=x(4)+l1*1000*cos(theta1(n1));y(5)=y(4)+l1*1000*sin(theta1(n1));x(6)=x(3)+100*cos(theta3(n1));y(6)=y(3)+100*sin(theta3(n1));x(7)=l4*1000*cos(theta4(n1))+l3*1000*cos(theta3(n1));y(7)=l4*1000*sin(theta4(n1))+l3*1000*sin(theta3(n1));x(8)=x(7)-900;y(8)=h*1000;x(9)=x(7)+600;y(9)=h*1000;x(10)=l4*1000*cos(theta4(n1))+(S3(n1)*1000-50)*cos(theta3(n1)); y(10)=l4*1000*sin(theta4(n1))+(S3(n1)*1000-50)*sin(theta3(n1)); x(11)=x(10)+25*cos(pi/2-theta3(n1));y(11)=y(10)-25*sin(pi/2-theta3(n1));x(12)=x(11)+100*cos(theta3(n1));y(12)=y(11)+100*sin(theta3(n1));x(13)=x(12)-50*cos(pi/2-theta3(n1));y(13)=y(12)+50*sin(pi/2-theta3(n1));x(14)=x(10)-25*cos(pi/2-theta3(n1));y(14)=y(10)+25*sin(pi/2-theta3(n1));x(15)=x(10);y(15)=y(10);x(16)=0;y(16)=0;x(17)=x(4);y(17)=y(4);k=1:3;plot(x(k),y(k));hold on;k=4:5;plot(x(k),y(k));hold on;k=6:9;plot(x(k),y(k));hold on;k=10:15;plot(x(k),y(k));hold on;k=16:17;plot(x(k),y(k),'-.');hold on;grid on;axis([-350 800 -250 950]);title('牛头刨床运动仿真');grid on;xlabel('mm');ylabel('mm');plot(x(1),y(1),'o');plot(x(2),y(2),'o');plot(x(4),y(4),'o');plot(x(5),y(5),'o');plot(x(7),y(7),'o');axis equal;m(j)=getframe;endfor i=1:3movie(m)end。
