倾覆力矩计算实例
倾覆力矩与抗倾覆力矩的计算

倾覆力矩与抗倾覆力矩的计算一、引言在物理学中,力矩是描述物体受力时发生旋转的物理量。
对于倾覆力矩与抗倾覆力矩的计算,我们需要了解相关概念和公式,并透彻理解其在实际问题中的应用。
本文将对倾覆力矩和抗倾覆力矩进行详细的介绍和计算方法的说明。
二、倾覆力矩的计算倾覆力矩是指物体受到外力作用时,由于受力点与物体重心之间的距离产生的力矩。
当倾覆力矩超过物体的抗倾覆力矩时,物体将发生倾覆。
1. 定义倾覆力矩可以通过以下公式进行计算:倾覆力矩 = 外力F × 垂直于力的距离d2. 计算方法我们需要确定物体受力的位置和大小。
然后,找到物体的重心位置。
接下来,计算重心和受力点之间的距离d。
最后,将外力F与距离d相乘,即可得到倾覆力矩的大小。
举个例子来说明,假设有一个长方体,长为L,宽为W,高为H,质量为M。
该长方体受到外力F作用在长方体最上方的表面上。
我们需要计算该长方体发生倾覆的倾覆力矩。
我们需要找到该长方体的重心位置。
对于长方体来说,重心位于长方体的中心位置,即重心距离底部的距离为H/2。
然后,我们需要计算受力点与重心之间的距离d。
由于受力作用在长方体最上方的表面上,因此受力点与重心之间的距离为H/2。
将外力F与距离d相乘,即可得到倾覆力矩的大小。
三、抗倾覆力矩的计算抗倾覆力矩是指物体自身的重力产生的力矩,用于抵抗外力作用时的倾覆力矩。
当抗倾覆力矩大于或等于倾覆力矩时,物体将保持稳定不倾倒。
1. 定义抗倾覆力矩可以通过以下公式进行计算:抗倾覆力矩 = 物体自身重力矩2. 计算方法抗倾覆力矩的计算需要先计算物体的自身重力矩。
自身重力矩的大小等于物体的质量乘以重力加速度乘以重心距离。
举个例子来说明,假设有一个长方体,长为L,宽为W,高为H,质量为M。
我们需要计算该长方体的抗倾覆力矩。
我们需要找到该长方体的重心位置。
对于长方体来说,重心位于长方体的中心位置,即重心距离底部的距离为H/2。
然后,计算物体的自身重力矩。
船舶倾覆力矩计算公式(一)

船舶倾覆力矩计算公式(一)船舶倾覆力矩计算公式1. 引言船舶倾覆力矩是指船舶在倾覆过程中,由于重力和浮力之间的不平衡造成的倾覆矩。
在船舶设计和安全评估中,计算船舶倾覆力矩是非常重要的一项工作。
本文将介绍常用的船舶倾覆力矩计算公式,并以具体示例进行说明。
2. 公式一:Archimedes原理Archimedes原理是倾覆力矩计算的基础,它描述了浸没在液体中的物体所受的浮力。
根据Archimedes原理,浮力等于被液体排开的体积乘以液体的密度。
公式:浮力(F_b)= 排开液体的体积(V_b)× 液体密度(ρ)3. 公式二:引起倾覆的力矩计算在倾覆过程中,除了浮力外,还存在其他引起倾覆的力矩,如重力、风力、浪力等。
这些力矩的合力将决定船舶是否倾覆。
公式:倾覆力矩(M)= 正向力矩 - 反向力矩其中,正向力矩是指船舶倾覆方向引起的力矩,反向力矩是指船舶抵抗倾覆力矩的力矩。
4. 公式三:船舶稳定性计算公式船舶的稳性计算是倾覆力矩计算的关键。
在计算船舶的稳性时,需要考虑船舶的重心、浮心、倾覆角度等因素。
公式:倾覆力矩(M)= 转动力(T)× 转动半径(r)其中,转动力是指船舶所受的倾覆产生的力,转动半径是指船舶的重心与浮心之间的水平距离。
5. 示例解释例如,对于一个长为50米,宽为10米的矩形船舶,其重心位于船舶中央,浮心位于水表面以下2米处。
假设船舶所受到的倾覆产生的力为8000牛顿,转动半径为5米。
根据公式三,可以计算得到该船舶的倾覆力矩:M = 8000 N ×5m = 40000 N·m倾覆力矩的计算结果表明,该船舶在倾覆过程中所受的力矩为40000 N·m。
结论本文介绍了船舶倾覆力矩的计算公式,并以示例进行了详细解释。
船舶倾覆力矩的准确计算对于船舶设计和安全评估至关重要。
在实际应用中,需要综合考虑多种因素,如重力、浮力、风力、浪力等,以确保船舶的稳定性和安全运行。
五种常见挡土墙得设计计算实例
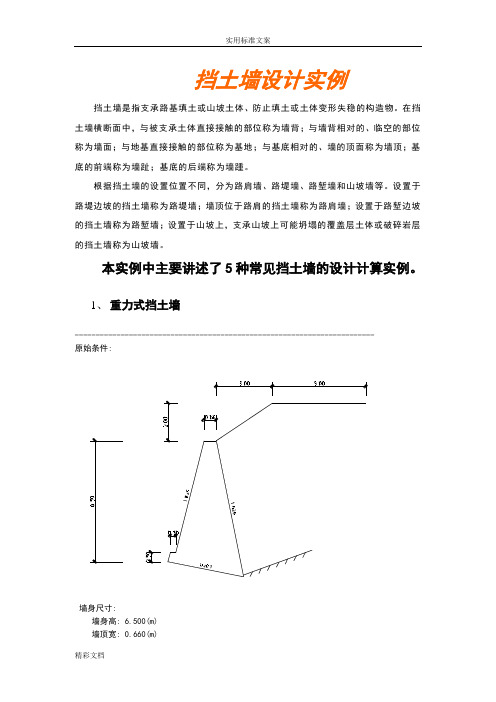
挡土墙设计实例挡土墙是指支承路基填土或山坡土体、防止填土或土体变形失稳的构造物。
在挡土墙横断面中,与被支承土体直接接触的部位称为墙背;与墙背相对的、临空的部位称为墙面;与地基直接接触的部位称为基地;与基底相对的、墙的顶面称为墙顶;基底的前端称为墙趾;基底的后端称为墙踵。
根据挡土墙的设置位置不同,分为路肩墙、路堤墙、路堑墙和山坡墙等。
设置于路堤边坡的挡土墙称为路堤墙;墙顶位于路肩的挡土墙称为路肩墙;设置于路堑边坡的挡土墙称为路堑墙;设置于山坡上,支承山坡上可能坍塌的覆盖层土体或破碎岩层的挡土墙称为山坡墙。
本实例中主要讲述了5种常见挡土墙的设计计算实例。
1、重力式挡土墙------------------------------------------------------------------------原始条件:墙身尺寸:墙身高: 6.500(m)墙顶宽: 0.660(m)面坡倾斜坡度: 1:0.250背坡倾斜坡度: 1:0.200采用1个扩展墙址台阶:墙趾台阶b1: 0.300(m)墙趾台阶h1: 0.500(m)墙趾台阶与墙面坡坡度相同墙底倾斜坡率: 0.200:1物理参数:圬工砌体容重: 23.000(kN/m3)圬工之间摩擦系数: 0.400地基土摩擦系数: 0.500砌体种类: 片石砌体砂浆标号: 5石料强度(MPa): 30挡土墙类型: 一般挡土墙墙后填土内摩擦角: 35.000(度)墙后填土粘聚力: 0.000(kPa)墙后填土容重: 19.000(kN/m3)墙背与墙后填土摩擦角: 17.500(度)地基土容重: 18.000(kN/m3)修正后地基土容许承载力: 500.000(kPa)地基土容许承载力提高系数:墙趾值提高系数: 1.200墙踵值提高系数: 1.300平均值提高系数: 1.000墙底摩擦系数: 0.500地基土类型: 土质地基地基土内摩擦角: 30.000(度)土压力计算方法: 库仑坡线土柱:坡面线段数: 2折线序号水平投影长(m) 竖向投影长(m) 换算土柱数1 3.000 2.000 02 5.000 0.000 0坡面起始距离: 0.000(m)地面横坡角度: 20.000(度)墙顶标高: 0.000(m)挡墙分段长度: 10.000(m)===================================================================== 组合1(仅取一种组合计算)=============================================组合系数: 1.0001. 挡土墙结构重力分项系数 = 1.000 √2. 墙顶上的有效永久荷载分项系数 = 1.000 √3. 墙顶与第二破裂面间有效荷载分项系数 = 1.000 √4. 填土侧压力分项系数 = 1.000 √5. 车辆荷载引起的土侧压力分项系数 = 1.000 √=============================================[土压力计算] 计算高度为 7.309(m)处的库仑主动土压力无荷载时的破裂角 = 28.320(度)按实际墙背计算得到:第1破裂角: 28.320(度)Ea=244.312 Ex=214.072 Ey=117.736(kN) 作用点高度 Zy=2.627(m) 因为俯斜墙背,需判断第二破裂面是否存在,计算后发现第二破裂面不存在墙身截面积 = 15.518(m2) 重量 = 356.925 kN(一) 滑动稳定性验算基底摩擦系数 = 0.500采用倾斜基底增强抗滑动稳定性,计算过程如下:基底倾斜角度 = 11.310 (度)Wn = 349.993(kN) En = 157.432(kN) Wt = 69.999(kN) Et = 186.825(kN) 滑移力= 116.827(kN) 抗滑力= 253.713(kN)滑移验算满足: Kc = 2.172 > 1.300滑动稳定方程验算:滑动稳定方程满足: 方程值 = 164.582(kN) > 0.0地基土摩擦系数 = 0.500地基土层水平向: 滑移力= 214.072(kN) 抗滑力= 252.070(kN)地基土层水平向: 滑移验算不满足: Kc2 = 1.177 <= 1.300(二) 倾覆稳定性验算相对于墙趾点,墙身重力的力臂 Zw = 2.186 (m)相对于墙趾点,Ey的力臂 Zx = 3.521 (m)相对于墙趾点,Ex的力臂 Zy = 1.818 (m)验算挡土墙绕墙趾的倾覆稳定性倾覆力矩= 389.149(kN-m) 抗倾覆力矩= 1194.778(kN-m)倾覆验算满足: K0 = 3.070 > 1.500倾覆稳定方程验算:倾覆稳定方程满足: 方程值 = 649.592(kN-m) > 0.0(三) 地基应力及偏心距验算基础为天然地基,验算墙底偏心距及压应力取倾斜基底的倾斜宽度验算地基承载力和偏心距作用于基础底的总竖向力 = 507.426(kN) 作用于墙趾下点的总弯矩=805.628(kN-m) 基础底面宽度 B = 4.127 (m) 偏心距 e = 0.476(m)基础底面合力作用点距离基础趾点的距离 Zn = 1.588(m)基底压应力: 趾部=208.008 踵部=37.896(kPa)最大应力与最小应力之比 = 208.008 / 37.896 = 5.489作用于基底的合力偏心距验算满足: e=0.476 <= 0.167*4.127 = 0.688(m)墙趾处地基承载力验算满足: 压应力=208.008 <= 600.000(kPa)墙踵处地基承载力验算满足: 压应力=37.896 <= 650.000(kPa)地基平均承载力验算满足: 压应力=122.952 <= 500.000(kPa)(四) 基础强度验算基础为天然地基,不作强度验算(五) 墙底截面强度验算验算截面以上,墙身截面积 = 13.946(m2) 重量 = 320.764 kN相对于验算截面外边缘,墙身重力的力臂 Zw = 2.134 (m)相对于验算截面外边缘,Ey的力臂 Zx = 3.521 (m)相对于验算截面外边缘,Ex的力臂 Zy = 1.818 (m)[容许应力法]:法向应力检算:作用于验算截面的总竖向力 = 438.499(kN) 作用于墙趾下点的总弯矩=710.021(kN-m) 相对于验算截面外边缘,合力作用力臂 Zn = 1.619(m)截面宽度 B = 3.885 (m) 偏心距 e1 = 0.323(m)截面上偏心距验算满足: e1= 0.323 <= 0.250*3.885 = 0.971(m)截面上压应力: 面坡=169.225 背坡=56.514(kPa)压应力验算满足: 计算值= 169.225 <= 800.000(kPa)切向应力检算:剪应力验算满足: 计算值= 9.954 <= 80.000(kPa)[极限状态法]:重要性系数0 = 1.000验算截面上的轴向力组合设计值Nd = 438.499(kN)轴心力偏心影响系数醟 = 0.923挡墙构件的计算截面每沿米面积A = 3.885(m2)材料抗压极限强度Ra = 1600.000(kPa)圬工构件或材料的抗力分项系数鉬 = 2.310偏心受压构件在弯曲平面内的纵向弯曲系数豮 = 0.997计算强度时:强度验算满足: 计算值= 438.499 <= 2484.452(kN)计算稳定时:稳定验算满足: 计算值= 438.499 <= 2478.074(kN)(六) 台顶截面强度验算[土压力计算] 计算高度为 6.000(m)处的库仑主动土压力无荷载时的破裂角 = 29.150(度)按实际墙背计算得到:第1破裂角: 29.150(度)Ea=172.939 Ex=151.533 Ey=83.340(kN) 作用点高度 Zy=2.150(m) 因为俯斜墙背,需判断第二破裂面是否存在,计算后发现第二破裂面不存在墙身截面积 = 12.060(m2) 重量 = 277.380 kN[强度验算]验算截面以上,墙身截面积 = 12.060(m2) 重量 = 277.380 kN相对于验算截面外边缘,墙身重力的力臂 Zw = 1.738 (m)相对于验算截面外边缘,Ey的力臂 Zx = 2.930 (m)相对于验算截面外边缘,Ex的力臂 Zy = 2.150 (m)[容许应力法]:法向应力检算:作用于验算截面的总竖向力 = 360.720(kN) 作用于墙趾下点的总弯矩=400.617(kN-m) 相对于验算截面外边缘,合力作用力臂 Zn = 1.111(m)截面宽度 B = 3.360 (m) 偏心距 e1 = 0.569(m)截面上偏心距验算满足: e1= 0.569 <= 0.250*3.360 = 0.840(m)截面上压应力: 面坡=216.516 背坡=-1.802(kPa)压应力验算满足: 计算值= 216.516 <= 800.000(kPa)拉应力验算满足: 计算值= 1.802 <= 80.000(kPa)切向应力检算:剪应力验算满足: 计算值= 2.156 <= 80.000(kPa)[极限状态法]:重要性系数0 = 1.000验算截面上的轴向力组合设计值Nd = 360.720(kN)轴心力偏心影响系数醟 = 0.744挡墙构件的计算截面每沿米面积A = 3.360(m2)材料抗压极限强度Ra = 1600.000(kPa)圬工构件或材料的抗力分项系数鉬 = 2.310偏心受压构件在弯曲平面内的纵向弯曲系数豮 = 0.994计算强度时:强度验算满足: 计算值= 360.720 <= 1730.509(kN)计算稳定时:稳定验算满足: 计算值= 360.720 <= 1720.261(kN)2、衡重式挡土墙------------------------------------------------------------------------ 原始条件:墙身尺寸:墙身总高: 9.600(m)上墙高: 3.400(m)墙顶宽: 0.660(m)台宽: 1.500(m)面坡倾斜坡度: 1:0.150上墙背坡倾斜坡度: 1:0.200下墙背坡倾斜坡度: 1:-0.200采用1个扩展墙址台阶:墙趾台阶b1: 0.300(m)墙趾台阶h1: 0.500(m)墙趾台阶与墙面坡坡度相同墙底倾斜坡率: 0.200:1下墙土压力计算方法: 力多边形法物理参数:圬工砌体容重: 23.000(kN/m3)圬工之间摩擦系数: 0.400地基土摩擦系数: 0.500砌体种类: 片石砌体砂浆标号: 5石料强度(MPa): 30挡土墙类型: 一般挡土墙墙后填土内摩擦角: 35.000(度)墙后填土粘聚力: 0.000(kPa)墙后填土容重: 19.000(kN/m3)墙背与墙后填土摩擦角: 17.500(度)地基土容重: 18.000(kN/m3)修正后地基土容许承载力: 500.000(kPa)地基土容许承载力提高系数:墙趾值提高系数: 1.200墙踵值提高系数: 1.300平均值提高系数: 1.000墙底摩擦系数: 0.500地基土类型: 土质地基地基土内摩擦角: 30.000(度)坡线土柱:坡面线段数: 2折线序号水平投影长(m) 竖向投影长(m) 换算土柱数1 3.000 2.000 02 5.000 0.000 0地面横坡角度: 20.000(度)墙顶标高: 0.000(m)挡墙分段长度: 10.000(m)===================================================================== 组合1(仅取一种组合计算)=============================================组合系数: 1.0001. 挡土墙结构重力分项系数 = 1.000 √2. 填土重力分项系数 = 1.000 √3. 填土侧压力分项系数 = 1.000 √4. 车辆荷载引起的土侧压力分项系数 = 1.000 √=============================================[土压力计算] 计算高度为 10.242(m)处的库仑主动土压力计算上墙土压力无荷载时的破裂角 = 31.060(度)按假想墙背计算得到:第1破裂角: 32.720(度)Ea=148.041 Ex=56.254 Ey=136.937(kN) 作用点高度 Zy=1.260(m) 因为俯斜墙背,需判断第二破裂面是否存在,计算后发现第二破裂面存在:第2破裂角=17.542(度) 第1破裂角=31.060(度)Ea=102.147 Ex=62.124 Ey=81.085(kN) 作用点高度 Zy=1.465(m) 计算下墙土压力无荷载时的破裂角 = 34.222(度)按力多边形法计算得到:破裂角: 34.222(度)Ea=201.028 Ex=199.855 Ey=21.676(kN) 作用点高度 Zy=2.979(m) 墙身截面积 = 25.299(m2) 重量 = 581.869 kN衡重台上填料重 = 90.539(kN) 重心坐标(1.649,-1.646)(相对于墙面坡上角点) (一) 滑动稳定性验算基底摩擦系数 = 0.500采用倾斜基底增强抗滑动稳定性,计算过程如下:基底倾斜角度 = 11.310 (度)Wn = 659.350(kN) En = 152.144(kN) Wt = 131.870(kN) Et = 236.739(kN) 滑移力= 104.869(kN) 抗滑力= 405.747(kN)滑移验算满足: Kc = 3.869 > 1.300滑动稳定方程验算:滑动稳定方程满足: 方程值 = 353.905(kN) > 0.0地基土摩擦系数 = 0.500地基土层水平向: 滑移力= 261.979(kN) 抗滑力= 396.867(kN)地基土层水平向: 滑移验算满足: Kc2 = 1.515 > 1.300(二) 倾覆稳定性验算相对于墙趾,墙身重力的力臂 Zw = 2.308 (m)相对于墙趾,上墙Ey的力臂 Zx = 4.117 (m)相对于墙趾,上墙Ex的力臂 Zy = 7.665 (m)相对于墙趾,下墙Ey的力臂 Zx3 = 3.807 (m)相对于墙趾,下墙Ex的力臂 Zy3 = 2.337 (m)验算挡土墙绕墙趾的倾覆稳定性倾覆力矩= 943.130(kN-m) 抗倾覆力矩= 2066.104(kN-m)倾覆验算满足: K0 = 2.191 > 1.500倾覆稳定方程验算:倾覆稳定方程满足: 方程值 = 793.025(kN-m) > 0.0(三) 地基应力及偏心距验算基础为天然地基,验算墙底偏心距及压应力取倾斜基底的倾斜宽度验算地基承载力和偏心距作用于基础底的总竖向力 = 811.494(kN) 作用于墙趾下点的总弯矩=1122.975(kN-m) 基础底面宽度 B = 3.275 (m) 偏心距 e = 0.254(m)基础底面合力作用点距离基础趾点的距离 Zn = 1.384(m)基底压应力: 趾部=362.948 踵部=132.600(kPa)最大应力与最小应力之比 = 362.948 / 132.600 = 2.737作用于基底的合力偏心距验算满足: e=0.254 <= 0.167*3.275 = 0.546(m)墙趾处地基承载力验算满足: 压应力=362.948 <= 600.000(kPa)墙踵处地基承载力验算满足: 压应力=132.600 <= 650.000(kPa)地基平均承载力验算满足: 压应力=247.774 <= 500.000(kPa)(四) 基础强度验算基础为天然地基,不作强度验算(五) 上墙截面强度验算上墙重力 Ws = 98.141 (kN)上墙墙背处的 Ex = 62.124 (kN)上墙墙背处的 Ey = 12.425 (kN)相对于上墙墙趾,上墙重力的力臂 Zw = 0.889 (m)相对于上墙墙趾,上墙Ex的力臂 Zy = 1.465 (m)相对于上墙墙趾,上墙Ey的力臂 Zx = 1.557 (m)[容许应力法]:法向应力检算:相对于上墙墙趾,合力作用力臂 Zn = 0.141(m)截面宽度 B = 1.850 (m) 偏心距 e1 = 0.784(m)截面上偏心距验算不满足: e1= 0.784 > 0.250*1.850 = 0.463(m) 截面上压应力: 面坡=211.665 背坡=-92.134(kPa)压应力验算满足: 计算值= 211.665 <= 800.000(kPa)拉应力验算不满足: 计算值= 92.134 > 80.000(kPa) 切向应力检算:剪应力验算满足: 计算值= 9.674 <= 80.000(kPa)斜截面剪应力检算斜剪应力验算满足: 计算值= 41.598 <= 80.000(kPa)[极限状态法]:重要性系数0 = 1.000验算截面上的轴向力组合设计值Nd = 110.566(kN)轴心力偏心影响系数醟 = 0.233挡墙构件的计算截面每沿米面积A = 1.850(m2)材料抗压极限强度Ra = 1600.000(kPa)圬工构件或材料的抗力分项系数鉬 = 2.310偏心受压构件在弯曲平面内的纵向弯曲系数豮 = 0.981计算强度时:强度验算满足: 计算值= 110.566 <= 298.521(kN)计算稳定时:稳定验算满足: 计算值= 110.566 <= 292.889(kN)(六) 墙底截面强度验算验算截面以上,墙身截面积 = 24.226(m2) 重量 = 557.198 kN相对于验算截面外边缘,墙身重力的力臂 Zw = 2.313 (m)[容许应力法]:法向应力检算:作用于截面总竖向力 = 750.498(kN) 作用于墙趾下点的总弯矩=1106.215(kN-m) 相对于验算截面外边缘,合力作用力臂 Zn = 1.474(m)截面宽度 B = 3.340 (m) 偏心距 e1 = 0.196(m)截面上偏心距验算满足: e1= 0.196 <= 0.250*3.340 = 0.835(m)截面上压应力: 面坡=303.826 背坡=145.574(kPa)压应力验算满足: 计算值= 303.826 <= 800.000(kPa)切向应力检算:剪应力验算满足: 计算值= -11.443 <= 80.000(kPa)[极限状态法]:重要性系数0 = 1.000验算截面上的轴向力组合设计值Nd = 750.498(kN)轴心力偏心影响系数醟 = 0.960挡墙构件的计算截面每沿米面积A = 3.340(m2)材料抗压极限强度Ra = 1600.000(kPa)圬工构件或材料的抗力分项系数鉬 = 2.310偏心受压构件在弯曲平面内的纵向弯曲系数豮 = 0.968计算强度时:强度验算满足: 计算值= 750.498 <= 2221.592(kN)计算稳定时:稳定验算满足: 计算值= 750.498 <= 2149.911(kN)(七) 台顶截面强度验算[土压力计算] 计算高度为 9.100(m)处的库仑主动土压力计算上墙土压力无荷载时的破裂角 = 31.060(度)按假想墙背计算得到:第1破裂角: 32.720(度)Ea=148.041 Ex=56.254 Ey=136.937(kN) 作用点高度 Zy=1.260(m) 因为俯斜墙背,需判断第二破裂面是否存在,计算后发现第二破裂面存在:第2破裂角=17.542(度) 第1破裂角=31.060(度)Ea=102.147 Ex=62.124 Ey=81.085(kN) 作用点高度 Zy=1.465(m) 计算下墙土压力无荷载时的破裂角 = 34.075(度)按力多边形法计算得到:破裂角: 34.075(度)Ea=156.451 Ex=155.539 Ey=16.870(kN) 作用点高度 Zy=2.522(m)[强度验算]验算截面以上,墙身截面积 = 22.550(m2) 重量 = 518.644 kN相对于验算截面外边缘,墙身重力的力臂 Zw = 2.358 (m)[容许应力法]:法向应力检算:作用于截面总竖向力 = 707.137(kN) 作用于墙趾下点的总弯矩=830.127(kN-m) 相对于验算截面外边缘,合力作用力臂 Zn = 1.174(m)截面宽度 B = 3.065 (m) 偏心距 e1 = 0.359(m)截面上偏心距验算满足: e1= 0.359 <= 0.250*3.065 = 0.766(m)截面上压应力: 面坡=392.661 背坡=68.767(kPa)压应力验算满足: 计算值= 392.661 <= 800.000(kPa)切向应力检算:剪应力验算满足: 计算值= -21.270 <= 80.000(kPa)[极限状态法]:重要性系数0 = 1.000验算截面上的轴向力组合设计值Nd = 707.137(kN)轴心力偏心影响系数醟 = 0.859挡墙构件的计算截面每沿米面积A = 3.065(m2)材料抗压极限强度Ra = 1600.000(kPa)圬工构件或材料的抗力分项系数鉬 = 2.310偏心受压构件在弯曲平面内的纵向弯曲系数豮 = 0.959计算强度时:强度验算满足: 计算值= 707.137 <= 1823.443(kN)计算稳定时:稳定验算满足: 计算值= 707.137 <= 1749.052(kN)=====================================================================3、加筋土挡土墙------------------------------------------------------------------------ 原始条件:墙身尺寸:墙身总高: 8.200(m)筋带竖向间距是否不等: 否单个筋带厚: 1(mm)筋带水平方向间距: 0.420(m)筋带竖直方向间距: 0.400(m)筋带长度竖向分段数: 2分段序号高度(m) 筋带长(m)1 6.000 6.0002 2.200 4.000筋带序号筋带宽(m)1 0.2002 0.2003 0.2004 0.2005 0.2006 0.2007 0.2008 0.2009 0.20010 0.20011 0.20012 0.20013 0.20014 0.20015 0.20016 0.20017 0.20018 0.20019 0.20020 0.200物理参数:加筋土容重: 20.000(kN/m3)加筋土内摩擦角: 35.000(度)筋带容许拉应力: 50.000(MPa)土与筋带之间的摩擦系数: 0.400加筋土浮容重: 10.000(kN/m3)地基土浮重度: 10.000(kN/m3)筋带抗拔力计算调节系数: 1.400筋带材料抗拉计算调节系数: 1.000筋带材料强度标准值: 240.000(MPa)筋带材料抗拉性能的分项系数: 1.250挡土墙类型: 一般挡土墙墙后填土内摩擦角: 35.000(度)墙后填土粘聚力: 0.000(kPa)墙后填土容重: 19.000(kN/m3)地基土容重: 18.000(kN/m3)修正后地基土容许承载力: 500.000(kPa)地基土容许承载力提高系数:墙趾值提高系数: 1.200墙踵值提高系数: 1.300平均值提高系数: 1.000墙底摩擦系数: 0.500地基土类型: 土质地基地基土内摩擦角: 30.000(度)坡线土柱:坡面线段数: 2折线序号水平投影长(m) 竖向投影长(m) 换算土柱数1 3.000 2.000 02 5.000 0.000 0地面横坡角度: 20.000(度)墙顶标高: 0.000(m)挡墙分段长度: 10.000(m)计算参数:稳定计算目标: 给定圆心,半径计算安全系数圆心X坐标: -2.000(m)圆心Y坐标: 10.000(m)半径: 15.000(m)筋带对稳定的作用: 筋带力沿圆弧切线内部稳定分析采用方法: 应力分析法条分法的土条宽度: 0.500(m)墙后填土粘聚力: 10.000(kPa)墙体填土粘聚力: 10.000(kPa)地基土粘聚力: 10.000(kPa)土条切向分力与滑动方向反向时: 当作下滑力对待===================================================================== 第 1 种情况: 组合1=============================================组合系数: 1.0001. 挡土墙结构重力分项系数 = 1.000 √2. 填土侧压力分项系数 = 1.000 √3. 车辆荷载引起的土侧压力分项系数 = 1.000 √=============================================----------------------------------------------------------内部稳定性验算采用应力分析法(一) 应力分析法筋带号宽度总长度稳定区竖向压应水平应最大拉力抗拉力抗拔力 (m) (m) 长度(m) 力(kPa) 力(kPa) 设计值(kN) (kN) (kN)01 0.200 6.000 3.540 46.000 19.139 3.215 38.400 18.61002 0.200 6.000 3.540 54.000 21.908 3.681 38.400 21.84703 0.200 6.000 3.540 62.000 24.511 4.118 38.400 25.08304 0.200 6.000 3.540 70.000 26.948 4.527 38.400 28.32005 0.200 6.000 3.540 78.000 29.220 4.909 38.400 31.55706 0.200 6.000 3.540 86.000 31.326 5.263 38.400 34.79307 0.200 6.000 3.540 94.000 33.265 5.589 38.400 38.03008 0.200 6.000 3.540 102.000 35.040 5.887 38.400 41.26609 0.200 6.000 3.605 110.000 36.648 6.157 38.400 45.32510 0.200 6.000 3.814 118.000 38.091 6.399 38.400 51.42911 0.200 6.000 4.022 126.000 39.367 6.614 38.400 57.91512 0.200 6.000 4.230 134.000 40.478 6.800 38.400 64.78113 0.200 6.000 4.438 142.000 41.423 6.959 38.400 72.02714 0.200 6.000 4.647 150.000 42.203 7.090 38.400 79.65515 0.200 4.000 2.855 158.000 42.816 7.193 38.400 51.54916 0.200 4.000 3.063 166.000 44.984 7.557 38.400 58.10917 0.200 4.000 3.271 174.000 47.152 7.922 38.400 65.05018 0.200 4.000 3.479 182.000 49.320 8.286 38.400 72.37219 0.200 4.000 3.688 190.000 51.488 8.650 38.400 80.07520 0.200 4.000 3.896 198.000 53.656 9.014 38.400 88.158单个筋带结点抗拔稳定满足: 拉力设计值=3.215 <= 18.610(kN)筋带截面抗拉强度验算满足: 拉力设计值=9.014 <= 38.400(kN)全墙抗拔验算满足: 最小安全系数=11.415 >= 2.000----------------------------------------------------------外部稳定性验算[土压力计算] 计算墙背处的库仑主动土压力按假想墙背计算得到:第1破裂角: 32.600(度)Ea=246.817 Ex=202.181 Ey=141.568(kN) 作用点高度 Zy=3.400(m) 墙身截面积 = 44.800(m2) 重量 = 896.000 kN墙顶上的土重(包括超载) = 171.000(kN) 重心坐标(3.667,0.889)(相对于墙面坡上角点) 墙顶上的土重(不包括超载) = 171.000(kN) 重心坐标(3.667,0.889)(相对于墙面坡上角点) (一) 滑动稳定性验算基底摩擦系数 = 0.500滑移力= 202.181(kN) 抗滑力= 604.284(kN)滑移验算满足: Kc = 2.989 > 1.300滑动稳定方程验算:滑动稳定方程满足: 方程值 = 455.454(kN) > 0.0(二) 倾覆稳定性验算相对于墙趾点,墙身重力的力臂 Zw = 2.804 (m)相对于墙趾点,墙土压力Ey的力臂 Zx = 6.000 (m)相对于墙趾点,墙土压力Ex的力臂 Zy = 3.400 (m)验算挡土墙绕墙趾的倾覆稳定性倾覆力矩= 687.414(kN-m) 抗倾覆力矩= 3988.410(kN-m)倾覆验算满足: K0 = 5.802 > 1.500倾覆稳定方程验算:倾覆稳定方程满足: 方程值 = 2673.196(kN-m) > 0.0(三) 地基应力及偏心距验算基础为天然地基,验算墙底偏心距及压应力作用于基础底的总竖向力 = 1208.568(kN) 作用于墙趾下点的总弯矩=3300.996(kN-m)墙计算宽度 B = 6.000 (m) 偏心距 e = 0.269(m)墙底面合力作用点距离墙趾点的距离 Zn = 2.731(m)基底压应力: 墙趾=255.546 墙踵=147.310(kPa)最大应力与最小应力之比 = 255.546 / 147.310 = 1.735作用于基底的合力偏心距验算满足: e=0.269 <= 0.167*6.000 = 1.000(m) 墙趾处地基承载力验算满足: 压应力=255.546 <= 600.000(kPa)墙踵处地基承载力验算满足: 压应力=147.310 <= 650.000(kPa)地基平均承载力验算满足: 压应力=201.428 <= 500.000(kPa)(四) 整体稳定验算圆心: (-2.000,10.000)半径 = 15.000(m)安全系数 = 1.802总的下滑力 = 1214.149(kN)总的抗滑力 = 2188.340(kN)土体部分下滑力 = 1214.149(kN)土体部分抗滑力 = 2188.340(kN)筋带的抗滑力 = 0.000(kN)整体稳定验算满足: 最小安全系数=1.802 >= 1.2504、桩板式挡土墙原始条件:墙身尺寸:桩总长: 16.000(m)嵌入深度: 6.000(m)截面形状: 方桩桩宽: 1.000(m)桩高: 1.500(m)桩间距: 3.500(m)挡土板的类型数: 2板类型号板厚(m) 板宽(m) 板块数1 0.200 0.500 82 0.200 0.500 8嵌入段土层数: 1柱底支承条件: 铰接计算方法: M法土层序号土层厚(m) 重度(kN/m3) M(MN/m4) 1 50.000 18.000 10.000初始弹性系数A: 0.000(MN/m3)初始弹性系数A1: 0.000(MN/m3)物理参数:桩混凝土强度等级: C40桩纵筋合力点到外皮距离: 35(mm)桩纵筋级别: HRB335桩箍筋级别: HPB235桩箍筋间距: 150(mm)板混凝土强度等级: C30板纵筋合力点到外皮距离: 35(mm)板纵筋级别: HRB335挡土墙类型: 一般挡土墙墙后填土内摩擦角: 35.000(度)墙后填土粘聚力: 0.000(kPa)墙后填土容重: 19.000(kN/m3)墙背与墙后填土摩擦角: 17.500(度)土压力计算方法: 库仑坡线土柱:坡面线段数: 2折线序号水平投影长(m) 竖向投影长(m) 换算土柱数1 3.000 2.000 02 5.000 0.000 0地面横坡角度: 20.000(度)墙顶标高: 0.000(m)挡墙分段长度: 10.000(m)钢筋混凝土配筋计算依据:《混凝土结构设计规范》(GB 50010--2002)===================================================================== 第 1 种情况: 组合1注意:内力计算时,土压力分项(安全)系数 = 1.000[土压力计算] 计算高度为 10.000(m)处的库仑主动土压力无荷载时的破裂角 = 31.530(度)第1破裂角: 31.530(度)Ea=313.264 Ex=298.765 Ey=94.200(kN) 作用点高度 Zy=3.584(m)(一) 桩身内力计算计算方法: m 法背侧——为挡土侧;面侧——为非挡土侧。
ZLP630高处作业吊篮抗倾覆计算

ZLP630高处作业吊篮抗倾覆计算在高处作业中,吊篮的抗倾覆计算十分重要。
高处作业吊篮的抗倾覆计算通常包括吊篮的基本参数、倾覆条件、倾覆力矩以及倾覆稳定性等方面的考虑。
本文将详细说明ZLP630高处作业吊篮的抗倾覆计算。
首先,我们需要明确ZLP630高处作业吊篮的基本参数,包括高度H、宽度W、长度L、自重G、载荷Q等内容。
吊篮的自重和载荷是计算抗倾覆的基础数据,需要准确测量和确定。
倾覆条件是指吊篮在高处作业中容易发生倾覆的工况情况。
倾覆条件通常包括吊篮处于极限工作状态时,吊篮处于开边的工况下以及遇到外力冲击时等。
针对这些倾覆条件,我们需要对吊篮的倾覆力矩进行计算。
倾覆力矩是指使吊篮发生倾覆的力矩大小。
它的计算需要考虑到吊篮的自重、载荷、作用点距离转轴的距离等因素。
对于ZLP630高处作业吊篮来说,倾覆力矩的计算公式可以表示为:M=(G+Q)×L/2其中,M表示倾覆力矩,G表示吊篮的自重,Q表示吊篮的载荷,L表示吊篮的长度。
最后,我们需要考虑吊篮的倾覆稳定性。
倾覆稳定性是指吊篮在面临倾覆力矩时保持平衡的能力。
在计算中,我们需要比较倾覆力矩与吊篮倾覆稳定力矩的大小关系。
如果倾覆力矩大于倾覆稳定力矩,则吊篮将发生倾覆。
为了确保吊篮的倾覆稳定性,我们需要选择合适的倾覆稳定力矩。
倾覆稳定力矩的计算通常采用安全系数的方法。
根据国家标准和相关规范,我们可以查询各种工况下不同安全系数的倾覆稳定力矩数值,然后将倾覆力矩与倾覆稳定力矩进行比较,以确定吊篮的倾覆稳定性。
综上所述,ZLP630高处作业吊篮的抗倾覆计算涉及吊篮的基本参数、倾覆条件、倾覆力矩以及倾覆稳定性等方面的考虑。
通过综合计算和比较,我们能够确保吊篮在高处作业中的稳定性和安全性。
在实际应用中,我们还应该根据工作环境和具体要求进行有针对性的计算和调整,以满足不同的工程需求。
倾覆力矩计算实例

倾覆力矩计算实例
以下是一个倾覆力矩的计算实例:
假设有一个塔吊,其额定载重量为 100 千克,工作幅度为 10 米,风速为 10 级,风速为 100 公里/小时。
根据《建筑结构荷载规范》(GBJ9)的规定,基本风压为 0.40 KN/m2,风荷载高度变化系数为
2.340,风荷载体型系数为 0.065,高度 Z 处的风振系数为 0.70。
首先,通过公式计算得到风荷载的水平作用力为 0.043 KN/m,
塔吊作用宽度为 1.50 米,迎风面积折减系数为 0.20。
接着,根据力矩平衡和力的平衡原理,计算每个轴承上分别承受的径向力和轴向力。
假设塔吊一共有 6 个轴承,分别为 1 号、2 号、3 号、4 号、5 号和 6 号轴承。
在倾覆力矩的作用下,轴承 1 和 5 承受的径向力和轴向力最大,分别为 0.021 KN/m 和 0.018 KN/m。
轴承 2、3、4、6 承受的径向
力和轴向力依次减小,分别为 0.016 KN/m、0.014 KN/m、0.012 KN/m 和 0.011 KN/m。
总的来说,塔吊在倾覆力矩的作用下,轴承承受的径向力和轴向力比较小,不会对塔吊造成损坏。
但是,如果倾覆力矩过大,就可能导致塔吊倒塌,造成安全事故。
因此,在塔吊的设计和使用过程中,需要充分考虑倾覆力矩的影响,以保证塔吊的安全运行。
船舶倾覆力矩计算公式(二)

船舶倾覆力矩计算公式(二)船舶倾覆力矩计算公式在船舶设计和运营中,准确计算船舶倾覆力矩是至关重要的。
下面是一些常用的船舶倾覆力矩计算公式,并对其进行解释和举例说明。
倾覆力矩定义倾覆力矩是指船舶在倾覆过程中,其上浮力产生的力矩。
当倾覆力矩超过船舶抵抗翻覆的能力时,船舶就会倾覆。
公式1:二维倾覆力矩计算公式二维倾覆力矩计算公式适用于对齐艏或对齐艉的倾覆情况。
该公式如下: M = W * h * GM 其中, - M表示倾覆力矩(Nm) - W表示船舶重量(kg) - h表示船舶重心高度与水平面的距离(m) - GM表示船舶的偏心距离(m)举例说明:假设一艘船舶的重量为10000 kg,重心高度为3 m,偏心距离为1 m。
那么倾覆力矩可计算为: M = 10000 * 3 * 1 = 30000 Nm公式2:三维倾覆力矩计算公式三维倾覆力矩计算公式适用于非对齐艏或非对齐艉的倾覆情况。
该公式如下: M = W * (h1 * GM1 + h2 * GM2) 其中, - M表示倾覆力矩(Nm) - W表示船舶重量(kg) - h1表示与艏或艉对齐的重心高度与水平面的距离(m) - h2表示与非对齐部分的重心高度与水平面的距离(m) - GM1表示与艏或艉对齐的偏心距离(m) - GM2表示与非对齐部分的偏心距离(m)举例说明:假设一艘船舶的重量为10000 kg,与艏对齐部分的重心高度为3 m,与非对齐部分的重心高度为2 m,与艏对齐部分的偏心距离为1 m,与非对齐部分的偏心距离为 m。
那么倾覆力矩可计算为:M = 10000 * (3 * 1 + 2 * ) = 30000 Nm公式3:修正倾覆力矩计算公式修正倾覆力矩计算公式用于考虑船舶受风、浪等外部力影响时的倾覆情况。
该公式如下: M = (W + Ww) * (h * GM) 其中, - M表示倾覆力矩(Nm) - W表示船舶重量(kg) - Ww表示风力、浪力产生的附加重量(kg) - h表示船舶重心高度与水平面的距离(m) - GM 表示船舶的偏心距离(m)举例说明:假设一艘船舶的重量为10000 kg,风力和浪力产生的附加重量为500 kg,重心高度为3 m,偏心距离为1 m。
三面环土地下室抗倾覆计算

三面环土地下室抗倾覆计算一、计算模型与基本参数。
1. 地下室几何尺寸。
- 设地下室长度为L,宽度为B,高度为H。
对于三面环土的情况,需要明确未环土一侧(通常为临空面)的相关尺寸关系。
2. 土压力计算参数。
- 确定土的重度γ(kN/m³),内摩擦角φ,粘聚力c。
根据这些参数计算土压力。
- 静止土压力系数K_0 = 1 - sinφ(对于正常固结土)。
3. 地下室结构自重。
- 计算地下室顶板、底板、侧壁等结构构件的自重。
假设地下室顶板厚度为h_1,底板厚度为h_2,侧壁厚度为t。
- 混凝土重度取γ_c(一般为25kN/m³)。
- 顶板自重G_1=γ_c× h_1× L× B- 底板自重G_2=γ_c× h_2× L× B- 侧壁自重(仅考虑三面环土侧)G_3 = γ_c× t× H× (2L + B)- 地下室总自重G = G_1+G_2+G_3二、土压力计算。
1. 静止土压力。
- 对于三面环土的地下室侧壁,临空面一侧无土压力,另外三面土压力计算如下。
- 在深度z处的静止土压力强度p_0=γ× z× K_0。
- 对侧壁积分求土压力合力。
例如,对于高度为H的侧壁,土压力合力E_0=(1)/(2)×γ× H^2× K_0× (2L + B)(考虑三面环土侧壁)。
2. 考虑土的极限平衡状态(如朗肯土压力理论)- 主动土压力系数K_a=tan^2(45^∘-(φ)/(2)),被动土压力系数K_p=tan^2(45^∘+(φ)/(2))。
- 在深度z处的主动土压力强度p_a=γ× z× K_a - 2c√(K_a),被动土压力强度p_p=γ× z× K_p+ 2c√(K_p)。
- 计算主动土压力合力E_a和被动土压力合力E_p(根据实际结构受力情况和土压力分布情况,通过积分计算)。
竖向构件的倾覆力矩及百分比

竖向构件的倾覆力矩及百分比竖向构件的倾覆力矩及百分比一、引言在建筑结构中,竖向构件的倾覆稳定性是一个至关重要的问题。
竖向构件包括柱、墙等,它们承担着建筑物的重要荷载,并且在受到外部作用力的情况下,可能会发生倾覆现象。
倾覆力矩及其百分比是评估这种稳定性的重要参数,本文将对其进行深入探讨。
二、倾覆力矩的概念1. 倾覆力矩的定义倾覆力矩是指竖向构件在受到外部水平荷载作用时,所产生的使其倾覆的力矩。
它是衡量构件倾覆稳定性的重要参数,通常用符号M来表示。
2. 倾覆力矩的计算竖向构件的倾覆力矩可以通过公式M = P × e来计算,其中P代表外部水平荷载的大小,e代表构件中心线至基础边缘的偏心距离。
3. 倾覆力矩的影响因素倾覆力矩的大小受到多种因素的影响,包括外部荷载的大小、构件截面的形状和尺寸、基础的支撑情况等。
在实际工程中,需要对这些因素进行综合考虑,评估构件的倾覆稳定性。
三、倾覆力矩的百分比1. 倾覆力矩的百分比定义倾覆力矩的百分比是指构件的倾覆力矩与构件抗倾覆力矩之比,通常用符号P来表示。
它是评估构件稳定性的重要参数,也是设计中需要非常重视的指标。
2. 倾覆力矩的百分比计算构件的倾覆力矩百分比可以通过公式P = |M| / MR来计算,其中|M|代表构件的实际倾覆力矩大小,MR代表构件的设计抗倾覆力矩。
3. 倾覆力矩的百分比的意义倾覆力矩的百分比反映了构件抵抗倾覆的能力,它是设计中评估构件稳定性的关键参数。
在实际工程中,需要保证构件的倾覆力矩百分比不超过规定的安全范围,以确保构件的倾覆稳定性。
四、个人观点和理解在设计和评估竖向构件的倾覆稳定性时,倾覆力矩及其百分比是非常重要的参数。
通过合理的计算和评估,可以有效地评估构件的稳定性,并采取相应的措施进行加固和防护。
我个人认为,在工程实践中,需要对倾覆力矩及其百分比有着深入的理解,并且严格按照相关规范和标准进行设计和施工,以确保建筑结构的安全性和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倾覆力矩计算实例
倾覆力矩(英语:torque)是指对于一个物体在旋转过程中产生的力矩,表示物体受到的旋转力在其周围空间所做的功。
对于一个非弹性的旋转物体,倾覆力矩的大小等于物体所受到的旋转力矩的总和。
下面是一个计算倾覆力矩的实例:
假设一个质量为50千克的匀质圆盘以每秒10米的速度旋转,半径为5米。
首先,我们需要确定圆盘所受到的旋转力矩。
根据牛顿第二定律,圆盘受到的力矩等于其质量乘以圆盘所受到的加速度。
因此,我们可以计算圆盘受到的力矩为:
M = m * a
其中,m为圆盘的质量,a为圆盘的加速度。
由于圆盘以每秒10米的速度旋转,因此加速度为每秒5米。
接下来,我们需要计算圆盘所受到的所有力矩。
由于圆盘在旋转过程中会受到重力、惯性力和旋转力等力的作用,因此我们需要分别计算这些力对圆盘产生的力矩。
重力对圆盘产生的力矩为零。
因为重力是垂直于物体表面的力,它对物体产生的力矩为零。
惯性力对圆盘产生的力矩为:
I = m * v * v / r = 50 * 10 * 10 / 5 = 1000 Nm
旋转力对圆盘产生的力矩为:
M = m * a = 50 * 5 * 5 / 5 = 100 Nm
因此,圆盘所受到的力矩为1000 Nm。
这个力矩将导致圆盘旋转的速度增加,并最终使其停止。
如果圆盘的质量不变,它将开始以每秒10米的速度旋转,直到达到最大速度并停止。
