定积分的几何意义
定积分的几何意义是什么

定积分的几何意义是什么定积分的几何意义是被积函数与坐标轴围成的面积,x轴之上局部为正,x轴之下局部为负,根据cosx在[0,2π]区间的图像可知,正负面积相等,因此其代数和等于0。
定积分的几何意义是被积函数与坐标轴围成的面积,x轴之上局部为正,x轴之下局部为负,根据cosx 在[0,2π]区间的图像可知,正负面积相等,因此其代数和等于0。
定积分的几何意义
定积分定积分是积分的一种,是函数f(x)在区间[a,b]上积分和的极限。
定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。
即由y=0,x=a,x=b,y=f(X)所围成图形的面积。
这个图形称为曲边梯形,特例是曲边三角形。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。
一个连续函数,一定存在定积分和不定积分;假设只有有限个连续点,那么定积分存在;假设有跳跃连续点,那么原函数一定不存在,即不定积分一定不存在。
定积分几何意义
图形的面积。
y
解 如图所示,阴影部分面积
1
2
S 0 xdx 1 (x 2)dx
1
1
xdx
2
(x 2)dx
60
1
y x 2 yx
y x
1 1 1 11 622
7 6
0
1
2x
(3)用定积分的几何意义求定积分的值的方法 步骤: ①画图形; ②求交点定区间; ③由图像查找“一边恒在一边上”:i全 部就直接作差ii部分就分段。
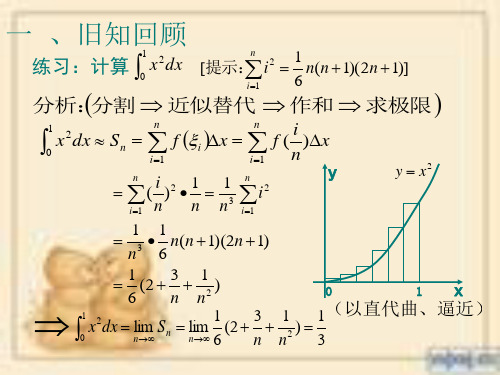
n(n
1)(2n
1)
1 31
1 0
(2 6
x2dx lim n
n n2
Sn
lim
n
)
1 6
(2
3 n
1 n2
)
0
1x
1(以直代曲、逼近)
3
二、探究新知
探究1:你能通过观察图形得到定积分的 几何意义吗?
y
y f (x)
oa
bx
定积分的几何意义:
当
f(x)0
时,积分
b
f
(x)dx
a
一 、旧知回顾
练习:计算 1 x2dx
n
[提示:
i2
1 n(n 1)(2n 1)]
0
i 1
6
分析:分割 近似替代 作和 求极限
1 0
x2dx
Sn
n i 1
f
i
x
n i 1
f ( i )x n
y
n ( i )2 • 1 i1 n n
1 n3
n
i2
i 1
y x2
1 n3
•
1 6
计算定积分
定积分的定义性质和几何意义

b
f ( x)dx
b g( x)dx 。
a
a
15
3.1-3 定积分的定义、性质和几何意义
例1 利用定义计算定积分 1 x2dx. 0
解:∵ x2在[0, 1]上 连续,∴ x2在[0, 1]上 可积。
将[ 0,1]
n等分,分点为 xi
i ,(i 1,2, n
,n)
小区间
[ xi1 , xi ]
曲边梯形的面积 A 是曲边函数 y f ( x) 在区间[a,b]
上的定积分: A b f ( x)dx 。 a
变速直线运动的物体所经过的路程 s 是速度函数
v v(t) 在时间区间[a,b]上的定积分: s
b
v(t )dt
。
a
13
3.1-3 定积分的定义、性质和几何意义
2.定积分定义的剖析
b f ( x)dx 0 。 a
性质 5 若 f R[a,b],则| f | R[a,b],且
b
f ( x)dx
b f ( x) dx 。
a
a
26
3.1-3 定积分的定义、性质和几何意义
例 2 比较下列各对积分值的大小.
(1)
13 xdx 与
1 x3dx ;(2)
1 xdx 与
161n12n1,
当
max
1in
xi
1 n
0 时,即 n
,有
1 x2dx 0
n
lim 0 i1
i2xi
lim 11121 1 . n6 n n 3
17
3.1-3 定积分的定义、性质和几何意义
例 2.用定积分的定义计算 1 e xdx 。 0
解:∵ e x在[0, 1]上 连续,∴ e x在[0, 1]上 可积。
1.5定积分的几何意义

1、求曲边梯形面积 、 分割-----近似代替 近似代替-----求和 求和-----取极限 分割 近似代替 求和 取极限 2、定积分定义 、 3、定积分几何意义 、 4、定积分计算性质 、
1.求由连续曲线 =f(x)对应的曲边梯形面积的方法 求由连续曲线y= 求由连续曲线 对应的
n
O
a
b
x
积分
式
3、定积分的几何意义: 定积分的几何意义:
b ∫a
f ( x) d x
的实质
b (1)当f(x)在区间[a,b]上大于0时,a 在区间[ 大于0 ∫
f ( x) d x 表示
直线x ),y 和曲线y 由 直线x=a,x=b(a≠b),y=0和曲线y=f(x)所围成的曲 边梯形的面积 ,这也是定积分的几何意义. 这也是定积分的几何意义. (2)当f(x)在区间[a,b]上小于0时,b f ( x ) d x 表示 在区间[ 小于0 ∫ a 由直线x ),y 和曲线y 由直线x=a,x=b (a≠b),y=0和曲线y=f(x)所围成的 曲边梯形的面积的相反数.
特别地,当 a=b 时,有 ∫ f (x)dx=0。
a
定积分的几何意义: 定积分的几何意义: 当f(x)≤0时,由y=f (x)、x=a、x=b 与 x 轴所围成的 ≤ 时 = 、 = 、 = 轴的下方, 曲边梯形位于 x 轴的下方,
积分 ∫ f (x)dx 在几何上表示
a b
y y=−f (x)
O
a
c
b
x
1.∫ f ( x)dx =
b a
S
f ( x) ≥ 0
-S f ( x ) < 0 表示以y=f(x)为曲边的曲边梯形面积 S表示以 为曲边的曲边梯形面积 y
定积分知识点和例题

定积分知识点和例题
定积分是积分的一种,是函数在某个区间上的积分和的极限。
定积分的概念起源于求图形面积和其他实际应用的问题。
下面我将列举一些定积分的知识点和例题:
知识点:
1. 定积分的定义:定积分是积分和的极限,即对一个给定区间[a,b]上的函数f(x)和任意分割法,求各小区间上函数值的点乘积和的极限。
如果存在一个常数I,对于任意给定的正数ε,总存在一个δ>0,使得当|ΔSi|<δ时,对区间[a,b]的任意分割法,和Si与I的差的绝对值都小于ε,则称I为f(x)在区间[a,b]上的定积分,记作∫abf(x)dx,其中a、b和I分别为定积分的下限、上限和值。
2. 定积分的几何意义:定积分的值等于由曲线y=f(x)与直线x=a、x=b 以及x轴所围成的曲边梯形的面积。
3. 定积分的性质:定积分的性质包括线性性质、积分中值定理、积分上限函数与被积函数的联系等。
4. 定积分的计算方法:主要包括基本初等函数的积分公式和不定积分的性质及计算方法,如换元法、分部积分法等。
例题:
1. 计算定积分∫10(x^2+1)dx的值。
2. 计算定积分∫π20(sinx+cosx)dx的值。
3. 计算定积分∫10|x-1|dx的值。
4. 计算定积分∫10x^2dx的值。
5. 计算定积分∫21(1/x)dx的值。
1.5.3定积分的几何意义3.14

a
b
f (x)dx =Sf (x)dx
a
c
ba (2)定积分的几何意义: f ( x)dx lim f (i ) a n n i 1
b n
当f(x)0时,由yf (x)、xa、xb 与y=0所围成的曲 边梯形位于 x 轴的下方,
y yf (x)
积分 f (x)dx 在几何上表示
a a
例1、
利用定积分的几何意义 说明等式 成立。
2
2
sin xdx 0
y
解: 在右图中,被积函数 ( x) sin x f
在[
, ]上连续,且在 ,]上 [ 0 2 2 2
2
f(x)=sinx 1
sin x 0, 在[0, ]上sin x 0,并有 2 A1 A2 , 所以
S
y f (x)
x
f ( x) 0,
b
a
f ( x)dx S
曲边梯形的面积的负值
一般地, f(x)在[a, b]上的定积分表示介于y=0、曲线 y=f(x)及直线x=a、x=b之间的各部分面积的代数和.
y
y=f(x)
A1 a
A3
A5
A2
A4
b x
b a
f ( x)d x A1 A2 A3 A4 A5
A1
-1
A2
2
x
2
2
f ( x)dx A2 A1 0
例2、用定积分表示图中四个阴影部分面积
y
f(x)=x2
y
f(x)=x2
定积分的定义及几何意义

定 积 分教学重点:定积分的概念、定积分法求简单的定积分、定积分的几何意义. 教学难点:定积分的概念、定积分的几何意义.教学重点:掌握过程步骤:分割、以不变代变、求和、逼近(取极限). 教学难点:过程的理解.1。
定积分的概念:一般地,设函数()f x 在区间[,]a b 上连续,用分点0121i i n a x x x x x x b -=<<<<<<<=将区间 [,]a b 等分成n 个小区间,每个小区间长度为x ∆(b a x n-∆=),在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=,作和式:11()()n n n i i i i b a S f x f nξξ==-=∆=∑∑ 如果x ∆无限接近于0(亦即n →+∞)时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。
记为:()ba S f x dx =⎰其中()f x 成为被积函数,x 叫做积分变量,[,]a b 为积分区间,b 积分上限,a 积分下限。
说明:(1)定积分()b a f x dx ⎰是一个常数,即n S 无限趋近的常数S (n →+∞时)称为()b af x dx ⎰,而不是n S . (2)用定义求定积分的一般方法是:①分割:n 等分区间[],a b ; ②近似代替:取点[]1,i i i x x ξ-∈; ③求和:1()ni i b a f n ξ=-∑; ④取极限:()1()lim n b i a n i b a f x dx f n ξ→∞=-=∑⎰ (3)积分的几何意义:曲边图形面积:()ba S f x dx =⎰; 积分的物理意义: 变速运动路程21()t t S v t dt =⎰; 变力做功 ()ba W F r dr =⎰ 2.定积分的性质根据定积分的定义,不难得出定积分的如下性质:性质1a b dx b a -=⎰1 性质2⎰⎰=b a b a dx x f k dx x kf )()( (其中k 是不为0的常数) 性质31212[()()]()()b b b a a a f x f x dx f x dx f x dx ±=±⎰⎰⎰ 性质4 ()()()()bc b a a c f x dx f x dx f x dx a c b =+<<⎰⎰⎰其中例题:求曲线2x y =与0,1==y x 所围成的区域的面积 解:(1)分割:将区间[]0,1等分成n 个小区间:11i i t n n n-∆=-= (2)近似代替:2)1(1n i n s i -=∆ (3)求和: 1ni i S S ==∆∑ 从而得到S 的近似值 )12)(11(61n n s --= (4)取极限:1111115lim lim lim 112323n n n n n i i S S v n n n n →∞→∞→∞=-⎡⎤⎛⎫⎛⎫⎛⎫===---+= ⎪ ⎪⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦∑ 例1.利用定积分的定义计算dx x )1(210+⎰的值。
定积分的几何意义

基础部制作
第七章 定积分
在自然科学、工程技术和经济学的许多问题中, 经常需要计算某些“和式的极限”。如:曲边梯 形的面积,变速直线运动的路程等。这就是第七 章我们要学习的内容。
定积分就是从各种计算“和式的极限”问题抽象 出的数学概念,它与不定积分是两个不同的数学 概念。但是,微积分基本定理则把这把这两个概 念联系起来,解决了定积分的计算问题,使定积 分得到了广泛的应用。
牛顿从物理学出发,运用集合方法研究
微积分,其应用上更多地结合了运动学,造 诣高于莱布尼兹。莱布尼兹则从几何问题出 发,运用分析学方法引进微积分概念、得出 运算法则,其数学的严密性与系统性是牛顿 所不及的。莱布尼兹认识到好的数学符号能 节省思维劳动,运用符号的技巧是数学成功 的关键之一。因此,他发明了一套适用的符 号系统,如,引入dx 表示x的微分,∫表示 积分等等。这些符号进一步促进了微积分学 的发展。1713年,莱布尼兹发表了《微积分 的历史和起源》一文,总结了自己创立微积 分学的思路,说明了自己成就的独立性。
例4 设函数f ( x )在区间[ a,a ]上连续,则
(1)当f ( x )为偶函数时,aa f ( x )dx 20a f ( x )dx; ( 2 )当f ( x )为奇函数时,aa f ( x )dx 0.
a
a
a
a
证: (1)
a
0
a
f (x)dx f (x)dx f (x)dx
2、通常也把牛顿--莱布尼兹公式称作微积分基本公式。
例题
例1 求0 sin xdx
解 因为(- cosx) sin x 所以
0
sin xdx
cos x 0
(cos
cos 0 ) 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
在[- , ]上连续,且在[- ,0]上
22
2
y f(x)=sinx
sin x 0,在[0, ]上sin x 0,并有
2
A1 = A2 ,所以
2 -
f
(x)dx
=
A2
-
A1
=
0
2
1
-2
A2
A1
x
-1 2
变式:
1)
2
sin xdx = 0
2) sin xdx = 2
2 sin xdx
3、定积分的几何意义:
b a
f (x)d x
的实质
(1)当f(x)在区间[a,b]上大于0时,ba f (x) d x 表示
由 直线x=a,x=b(a≠b),y=0和曲线y=f(x)所围成的曲
边梯形的面积 ,这也是定积分的几何意义.
(2)当f(x)在区间[a,b]上小于0时,ba f (x) d x 表示
上述曲边梯形面积的负值。
y=-f (x)
b
S = a[- f (x)]dx
b
S = a[- f (x)]dx
=- b f (x)dx ., a
Oa
bx
b
c
b
a f (x)dx ==-aS f (x)dxc f (x
b
c
b
f (x)dx ==-S f (x)dx
a
a
c
f (x)dyx=f。(x)
ba1dx
=1
S = 0-1[(x -1)2 -1]dx - -102[(x -0 1)2 -1 1x]dx 01 2x
S = 2 x2dx 1
S = 1 1- x2 dx -1
例2. 利用定积分的几何意义说明等式
解:在右图中,被积函数f (x) = sin x
2 -
sin
xdx
=
0成立。
0
0
0
例3.利用定积分的几何意义,判断下列定积分值的正、负号。
1) 2 sin xdx 0
2) 2 x 2dx -1
例4.计算 1 xdx的值
0
变式1.计算定积分
5
(2x - 4)dx
变式2. 计 算 积 分 1
y y=f (x)
b
c
b
a f (x)dx =a f (x)dxc f (x)dx
Oa
bx
特别地,当 a=b 时,有b a
f (x)dx=0。
定积分的几何意义:
当f(x)0时,由y=f (x)、x=a、x=b 与 x 轴所围成的
曲边梯形位于 x 轴的下方,
积分 b f (x)dx 在几何上表示 y a
y = f (x)
积分号
b a
f
( x)dx
=
lim
n0
n i =1
b-a n
Oa
f (xi )
bx
被
积分下限
积
函
数
被 积 [a, b]—叫做积分区间
积
分
表 达 式
变 量
3、定积分的几何意义:
当
f(x)0
时,积分
b
f
(x)dx
a
在几何上表示由 y=f (x)、
x=a、x=b与 x轴所围成的曲边梯形的面积。
a
a
即
b a
f
(x)dx
=
lim
n
n i=1
b
n
a
f
(xi )
说明:定积分是一个数值,
它只与被积函数及积分区间有关,
而与积分变量的记法无关,即
b f(x)dx =
b
f (t)dt =
b
f(u)du。
a
a
a
定积分的定义:即
b a
f
(x)dx
=
lim
n
n i=1
b
n
a
f
(xi
)
积分上限
y
由直线x=a,x=b (a≠b),y=0和曲线y=f(x)所围成的
曲边梯形的面积的相反数.
定积分的几何意义:
根据定积分的几何意义,如何用定积分表示图中阴 影部分的面积?
y
y=f (x)
b
S1 = ya= fg((x) dx
Oa
bx
b
b
S = S1 - S2 =
a
f (x)dx -
g ( x)dx
每个小区间宽度⊿x = b - a
n
(2)近似代替:任取xi[xi-1, xi],第i个小曲边梯形的面积用高
为f(xi)而宽为Dx的小矩形面积
y
f(xi)Dx近似之。
y=f(x)
(3)求和:取n个小矩形面积的和
作为曲边梯形面积S的近似值: n S f (xi )Dx
i=1
(4)取极限:所求曲边梯形的面
定积分的几何意义
1、求曲边梯形面积 分割-----近似代替-----求和-----取极限
2、定积分定义
3、定积分几何意义
4、定积分计算性质
1.求由连续曲线y=f(x)对应的曲边梯形面积的方法
(1)分割:在区间[a,b]上等间隔地插入n-1个点,将它等分成
n个小区间:a, x1,x1, x2,L xi-1, xi ,L ,xn-1,b,
b
f
(xf )(dxx)d。x。
aa
aa
cc
Oa
c
bx
S f (x) 0
1.
b a
f
(
x)dx
=
-S
f (x) 0
S表示以y=f(x)为曲边的曲边梯形面积
的ba代f (y数 0xa)y和 d=xSf的表(x) 值示b0 x都可----用 y0--a几区y何=S边f 意(x)梯b义x0 形面积
2.如果f(x)在[a,b]上时正,时负,如下图
a
4.定积分的基本性质
性质1
b
b
kf ( x )dx = k f ( x )dx
a
a
性质2
b
b
b
[ f ( x ) g( x )]dx = f ( x )dx g( x )dx
a
a
a
性质3
b
c
b
f ( x )dx = f ( x )dx f ( x )dx
a
a
c
(a<c<b)
y
y=f(x)
S1
S3
b a
f
(x)dx
=
S1
-
S2
S3
0a
S2
bx
例1.用定积分表示图中四个阴影部分面积
①y
f(x)=x2 ② y
③
f(x)=x2
y
④
f(x)=(x-1)2-1
y
f(x)=1
0 a x -1 0 2 x a 0 b x -1 0 2 x
变S 式(=1:)用0a x定2d积x 分y表yS=示x=下2 列2-(1阴x22影)dx部分面1yS积=x2 。y2
b f (定x 积)dx分y=关c1 于f (积x )分dx区 间c2 具f (有x )可dx加 性b f ( x )dx
a
a
y=f(xc)1
c2
b
c
b
f (x)dx = f (x)dx
f (x)dx。
a
a
c
b
f
b
(xf )(dxx)d=x
c
=
c
b
f (xf )(dxx)dx
积S为
n
S
= lim n
i=1
f (xi )Dx
Oa
{x xi i xi+1
b
x
Dx
2.定积分的定义
分割----近似代替-----求和-----取极限
n
小矩形面积和Sn =
i =1
f (xi )Dx
=
n i =1
f
(xi
)
b
n
a
如果当n∞时,S 无限接近某个常数,这个常数叫做函
数f (x)在区间[a, b]上的定积分,记作 b f (x)dx,即 b f (x)
