无侧移刚架的计算.ppt
用力矩分配法计算连续梁和无侧移刚架
对于具有多个结点角位移但无结点线位移(简称无侧移) 的结构,只需依次反复对各结点使用上节的单刚结点运 算,就可逐次渐近地求出各杆的杆端弯矩。
具体作法是:首先,将所有结点固定,计算各杆固端弯 矩;然后,将各结点轮流地放松,即每次只放松一个结 点(其他结点仍暂时固定),这样把各结点的不平衡力 矩轮流地进行反号分配、传递,直到传递弯矩小到可略 去不计时为止;最后,将以上步骤所得的杆端弯矩(固 端弯矩、分配弯矩和传递弯矩)叠加,即得所求的杆端 弯矩(总弯矩)。一般只需对各结点进行两到三个循环 的运算,就能达到较好的精度。
FP =40kN
A
B
3EI
2m 2m
q=20kN/m 3EI 6m
【例9-3】试用力 C 2EI D 矩分配法作图示连
4m 续梁的弯矩图。
解:运算过程如图所示
A
1
分配系数及传递系数
2
固 端 弯 矩 -20
结点C分配传递 Ⅰ
结点B分配传递 +16.5
Ⅱ 结点C分配传递 结点B分配传递 +0.8
Ⅲ 结点C分配传递 结点B分配传递 +0.05
A
B
C
EI
D
C =1.8cm 4m
9.18
C
D
C 1/4
1 D
M =1
1/4
B
C
1
11AFra bibliotek2BA BC 2 CB CD
2
D
1/2 1/2
4/7 3/7
M F -25
-125 +90
+90 +67.5
0
解:运算过程如图所 示
结构力学 位移法典型方程、计算举例
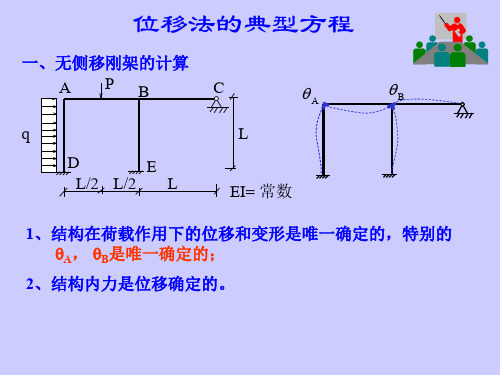
r21 B r22 CH R2
满足此方程,就消去了施加的2个约束
即,
r11 B r12 CH R1P 0 r21 B r22 CH R2 P 0
4)弯矩图的作法----消去最先附加的刚臂 P R1P R2P + MP图 R2
r
j 1
n
ij
Zj
,为消去该处的约束力,令: R iP
r
j 1
n
ij
Z j =0 即可。写成方程组的形式为:
r11 Z1 r12 Z 2 r1n Z n R1P 0 r Z r Z r Z R 0 21 1 22 2 2n n 2P rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
R1P
R2P
+ +
r11 R A
1
r21R 2A
MP图 +
r12 B
r22 B
或
P
qL2/12
PL/8
4i
2i
q
R1P
R2P
+ A•
r11 8i r21 2i
2i
M 1图
MP图
4i
+
B•
4i r22 11i 2i r12 2i 3i 2i
M 2图
M M P M 1 A M 2 B
叠加右侧2个图,意味着结点B转动 及结点C侧移都发生。
叠加后B处的转角和C处的位移
分别为:B CH 则两处的约 束力必为R1,R2
r12 CH
结构力学-7 位移法2
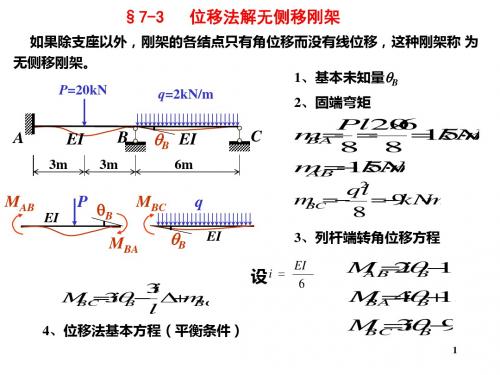
4iB 153iB 90
B
6 7i
16.72
11.57
M AB 2i7 6i1 51.7 6k2N m
M BA 4i7 6i1 51.5 1k7N m M BC 3i7 6i91.5 1k7N m
3.21
M图 kNm
梁 MBC4B2C41.741.1524.8941.746.9kNm
..............................................
柱 MBE443B3B31.153.45kNm
MCF412C2C2(4.89)9.8kNm
MBC
q
mBCq82l 9kNm
MBA
B EI
3、列杆பைடு நூலகம்转角位移方程
MBC3iB3limBC
设i
EI 6
4、位移法基本方程(平衡条件)
MAB2iB15 MBA4iB15
MBC3iB9
1
M超AB静EI定结P构分B 析M必B须C 满足q的三个条件:3、列杆端转角位移方程
2
C
D
1
C
D
A
B
7
线位移数也可以用几何构造分析方法确定。 将结构中所有刚结点和固定支座,代之以铰结点和铰支座,分析新体系的几 何构造性质,若为几何可变体系,则通过增加支座链杆使其变为无多余联系的 几何不变体系,所需增加的链杆数,即为原结构位移法计算时的线位移数。
1
4
0
8
BA EID
MEB
F
MCB
C
MCF
MCD
C
C MC 0
MFC
15
基本未知量为: C
有侧移与无侧移的判别讲解

关于框架钢柱的计算长度可以分为有支撑和无支撑两种情况:如果是纯框架,可以按照刚结构规范的计算方法进行计算,其中又有有侧移和无侧移的区别,关于有侧移可以认为侧移大于1/1000,无侧移为小于1/1000的情况.不过需要注意的是,刚结构规范的计算方法是不完善的,有时计算出来很大,SATWE软件把这种情况简化为计算长度系数为10如果是带支撑的,则需要判断是强支撑还是弱支撑,不过现在好多的软件还不能进行判断,比如PKPM就不能,不过现在的3D3S9.0可以进行判定了,并且和SATWE有数据借口,还算方便.所以计算长度不能简单的相信软件,要分情况而定如果两个方向都打了撑的话,基本上可以视为无侧移计算,楼主必须在SATWE里面有个复选框“是否考虑侧移”打上钩柱的计算长度才正常。
如果只有一个方向有撑,另外一个方向没有的话,要计算两遍,无侧移计算一遍,有侧移计算一遍,然后分别按照PKPM的计算出来的长度系数在按有侧移方向考虑的一侧手动输入。
1,无支撑纯框架按照有侧移框架计算。
2,有支撑框架根据支撑强弱:强支撑按照无侧移框架计算;弱支撑框架介于无侧移、有侧移之间。
3,详细内容见钢规5.3.3条这个问题其实很简单,不管做什么设计首先要对规范运用的很熟练,长细比跟什么有关系呢?柱子的计算长度系数和回转半径,回转半径就不用说了,主要看计算长度系数,楼主说了,你弱轴方向是有支撑的,只要你把支撑截面验算够,并保证支撑与柱的可靠连接,那根据规范,此方向的计算长度应该是支撑之间的这段距离,也就是柱子侧向支撑点之间的距离,如果设置的是单支撑,那就与柱子高度等高,计算长度系数就是1,在计算时需要手动设置钢柱弱轴方向的计算长度系数.那样弱轴方向的长细比就可以满足要求了.另:楼上的说的所谓的按有侧移计算和无侧移都计算一遍的方法,听起来貌似有点道理,其实无根据可循的,不过你按无侧移计算,柱的计算长度系数就1,所以按无侧移就算根本连算都不用算.再:无侧移和有侧移框架的定义确实不是你自己主观臆断的,规范里也有规定的,是要根据计算公式计算确定的,主要是通过计算看你这个结构形式是强支撑框架还是弱支撑框架,也就是看抗侧翼刚度的大小,如果你这个结构的抗侧移刚度足够大,那就是无侧移了,楼主你弱轴加了足够强的支撑,那此方向就是强支撑,那就是无侧移了.还有:楼主这种结构形式是最常见的底层钢框架上层门式刚架的做法,可以用PKPM按照三维建模计算的,不过二层门式刚架部分要将所有参与受力的构件在模型中输入,包括垂直支撑,水平支撑,抗风柱和刚性系杆,计算时要在PKPM中将风荷载体型系数分段设置,下层为1.3,上层应设置为0,此时需要在手动输入特殊风荷载,主要是钢柱的受风面风荷栽(注意角柱),作为集中力加在柱顶和钢梁风吸力和风压力,做为线荷载加在钢梁上,还有抗风柱的风荷载,做为集中力加在柱顶.以上看法,请参见<钢结构规范>还是计算Sb>3(1.2Nbi-Noi),进行判断即可。
建筑工程技术 教材 力矩分配法计算连续梁及无侧移刚架
5〕求最后杆端弯矩。将各杆杆端的固端弯矩与历次的分配弯矩 和传递弯矩代数相加即为最后弯矩。
第七页,共八页。
力矩分配法
第四页,共八页。
力矩分配法
例19-4 试用力矩分配法计算图示刚架,并作弯矩图。
第五页,共八页。
力矩分配法
例19-5 作图示连续梁的弯矩图。
第六页,共八页。
力矩分配法
多结点结构的力矩分配法计算步骤可归纳如下: 1〕求出汇交于各结点每一杆端的分配系数μ,并确定其传递系数C。
2〕计算各杆杆端的固端弯矩。
力矩分配法
• 用附加刚臂分别固定结点B和点C,使之不能转动,那么连续梁被 分隔成三个独立的单跨超静定梁。计算各杆的固端弯矩,计算B、C两 点处的不平衡力矩。
• 先放松不平衡力矩绝对值大的结点B,结点C仍被固定。此时 对ABC局部可利用单结点力矩分配法进行计算。结点B经一次分 配传递后,获得了暂时的平衡。再来考虑结点C,其上仍存在着 不平衡力矩。为了消除这一不平衡力矩,需将结点B重新固定, 而放松结点C,在BCD局部进行力矩的分配和传递。至此,结构 第一轮的计算结束。
第二页,共八页。
力矩分配法
• 最后将每一杆端历次的分配弯矩、传递弯矩和原来的固端 弯矩代数相加,便得到各杆端的最后弯矩。
• 将历次计算结果都记入表中即可。 综上所述,力矩分配法的计算过程,是依次放松各结点,以消去其 上的不平衡力矩,使其逐渐接近于真实的弯矩值,所以它是一种渐 近计算法。
第三页,共八页。
内容总结
• 用附加刚臂分别固定结点B和点C,使之不能转动,那么连续梁被分隔成三个独立的单跨超静定梁。• 用附加刚臂分别固定结点B和点C,使之不能转动,那么连续梁被分隔成三个独立的单跨超静定梁。计算各 杆的固端弯矩,计算B、C两点处的不平衡力矩。• 先放松不平衡力矩绝对值大的结点B,结点C仍被固定。• 如此循环假设干次之后,不平衡力矩越来越小,当其小到可以忽略不计时,便以不再传递力矩作为结束。 5〕求最后杆端弯矩
结构力学第七章力矩分配法

§7-1 引言
➢ 力矩分配法是基于位移法的逐步逼近精确解的 近似方法。
➢ 力矩分配法可以避免解联立方程组,其计算精 度可按要求来控制。在工程中曾经广泛应用。
➢ 从数学上说,是一种异步迭代法。
➢ 单独使用时只能用于无侧移(线位移)的结构。
➢ 力矩分配法的理论基础是位移法,力矩分配法 中对杆端转角、杆端弯矩、固端弯矩的正负号 规定,与位移法相同(顺时针旋转为正号)。
1
远端铰支时: 3i A i B
C=0
1
远端定向时: i A i B
C=-1
与远端支承 情况有关
§7-2 力矩分配法的基本原理
例7-1 结构的A端、B端,C端的支撑及各杆刚度如图
所示,求SBA、SBC、SBD及CBA、CBC、CBD。
(a)
B
C
A EI
EI
EI l
D
l
l
(b) A
B EI
EI
θB C
结点B作用的力偶,按各杆的分配系数分配给各杆的近端;
可见:各杆B 端的弯矩与各杆B 端的转动刚度成正比。 例7-1 结构的A端、B端,C端的支撑及各杆刚度如图所示,求SBA、SBC、SBD及CBA、CBC、CBD。
近端弯矩MBA、MBC为
§7-2 力矩分配法的基本原理
利用结点B的力矩平衡条件∑MB=0,得
A
B
k=EI/l 3 l
A
θ =1
B
Δ =θ l
FyB=k
SAB
A
B
FyB EI/l
解:当A 端转动θ=1时,因AB杆是刚性转动,所以B 产
生向下的竖向位移Δ=l×θ=l ,弹簧反力FyB=kΔ=EI/l2 。则
位移法—位移法的典型方程和计算实例(建筑力学)

i
18.94kN m
i
2
i
3.158
M CD 6i
18.95kN m
i
3 21.05
M BD i
20 35.79kN m
4
i
作M图,如图示
位移法
位移法计算步骤归纳如下
(1)确定基本未知量。在原结构上加入附加约束,得到
衡条件求出杆端剪力。
M
B
FQAB
M
A
0
2.5 4 2 20
kN 0
4
0
FQBA
2.5 4 2 20
kN 10kN
4
位移法
同理,取杆件BC,由平衡条件得
FQCB FQBC 10kN
取杆件BD,由平衡条件得
FQDB FQBD 7.5kN
1.5i1 0.9375i 2 15 0
1
3.16
i
2
21.05
i
位移法
(6)作M图
利用叠加公式 M M1Z1 M 2 Z 2 M 计算杆端弯矩
3.158 3 21.05
M AC 2i
i
25.26kN m
i
2
i
3.158 3 21.05
k211 k22 2 F2 0
位移法
(3)求系数和自由项
k11=4i +6 i=10 i
k12= -1.5 i =k21
k12= -1.5 i
k22 0.75i 0.1875 i 0.9375 i
位移法
F1 0
有侧移和无侧移的判别

关于框架钢柱的计算长度可以分为有支撑和无支撑两种情况:如果是纯框架,可以按照刚结构规范的计算方法进行计算,其中又有有侧移和无侧移的区别,关于有侧移可以认为侧移大于1/1000,无侧移为小于1/1000的情况.不过需要注意的是,刚结构规范的计算方法是不完善的,有时计算出来很大,SATWE软件把这种情况简化为计算长度系数为10如果是带支撑的,则需要判断是强支撑还是弱支撑,不过现在好多的软件还不能进行判断,比如PKPM就不能,不过现在的3D3S9.0可以进行判定了,并且和SATWE有数据借口,还算方便.所以计算长度不能简单的相信软件,要分情况而定如果两个方向都打了撑的话,基本上可以视为无侧移计算,楼主必须在SATWE里面有个复选框“是否考虑侧移”打上钩柱的计算长度才正常。
如果只有一个方向有撑,另外一个方向没有的话,要计算两遍,无侧移计算一遍,有侧移计算一遍,然后分别按照PKPM的计算出来的长度系数在按有侧移方向考虑的一侧手动输入。
1,无支撑纯框架按照有侧移框架计算。
2,有支撑框架根据支撑强弱:强支撑按照无侧移框架计算;弱支撑框架介于无侧移、有侧移之间。
3,详细内容见钢规5.3.3条这个问题其实很简单,不管做什么设计首先要对规范运用的很熟练,长细比跟什么有关系呢?柱子的计算长度系数和回转半径,回转半径就不用说了,主要看计算长度系数,楼主说了,你弱轴方向是有支撑的,只要你把支撑截面验算够,并保证支撑与柱的可靠连接,那根据规范,此方向的计算长度应该是支撑之间的这段距离,也就是柱子侧向支撑点之间的距离,如果设置的是单支撑,那就与柱子高度等高,计算长度系数就是1,在计算时需要手动设置钢柱弱轴方向的计算长度系数.那样弱轴方向的长细比就可以满足要求了.另:楼上的说的所谓的按有侧移计算和无侧移都计算一遍的方法,听起来貌似有点道理,其实无根据可循的,不过你按无侧移计算,柱的计算长度系数就1,所以按无侧移就算根本连算都不用算.再:无侧移和有侧移框架的定义确实不是你自己主观臆断的,规范里也有规定的,是要根据计算公式计算确定的,主要是通过计算看你这个结构形式是强支撑框架还是弱支撑框架,也就是看抗侧翼刚度的大小,如果你这个结构的抗侧移刚度足够大,那就是无侧移了,楼主你弱轴加了足够强的支撑,那此方向就是强支撑,那就是无侧移了.还有:楼主这种结构形式是最常见的底层钢框架上层门式刚架的做法,可以用PKPM按照三维建模计算的,不过二层门式刚架部分要将所有参与受力的构件在模型中输入,包括垂直支撑,水平支撑,抗风柱和刚性系杆,计算时要在PKPM中将风荷载体型系数分段设置,下层为1.3,上层应设置为0,此时需要在手动输入特殊风荷载,主要是钢柱的受风面风荷栽(注意角柱),作为集中力加在柱顶和钢梁风吸力和风压力,做为线荷载加在钢梁上,还有抗风柱的风荷载,做为集中力加在柱顶.以上看法,请参见<钢结构规范>还是计算Sb>3(1.2Nbi-Noi),进行判断即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
技 学 院
MB 0
M BA M BC
0
M AB
2i 6 15 16.72kN m 7i
4iB 15 3iB 9 0
B
6 7i
16.72
11.57
M
BA
4i
6 7i
M CB 4C 2 B 41.7
科 技
柱
学
M BE
4
3 4
B
3 B
M EB
2
3 4
B
1.5B
院 (3)位移法方程
MB 0 MC 0
M BA M CB
M BC MCD
M BE MCF
0 0
A
M CF
4
1 2
C
2C
BA BC
3iAB 4 B
B 2C
mBA 3B 40 41.7 41.15
3
1.15 40
2 4.89
43.5kN m 41.7 46.9k
N
m
科
........................................................................
15
11 .57 k N
m
M
BC
3i
6 7i
9
11.57kN
m
15.85
3.21
M图 kN m
第7章 位移法
例1、试用位移法分析图示刚架。 (1)基本未知量 B、 C
防 灾A 科 技
q=20kN/m
4I0 B 5I0
3I0
E
C 4I0
3I0
防 1、有几个未知结点位移就应建立几个平衡方程;
灾 2、单元分析、建立单元刚度方程是基础;
科
技
3、当结点作用有集中外力矩时,结点平衡方程式中应包括 外力矩。
学
院
P
q
Mq
A
B
C
D
M
MCB
MCD
C
作业:
防 灾 科 技 学 院
第7章 位移法
作业2:
防 灾 科 技 学 院
第7章 位移法
20 6 15kN m 8
mAB 15kN m
mBC
ql2 8
9kN m
MBA
B EI
3、列杆端转角位移方程
M BC
3i B
3i l
mBC
设i EI
6
4、位移法基本方程(平衡条件)
M AB 2iB 15 M BA 4iB 15 M BC 3i B 9
结构力学
主讲:王 丽
第7章 位移法
§7-3 无侧移刚架的计算
防 灾
如果除支座以外,刚架的各结点只有角位移而没有线位移,这种
刚架称 为无侧移刚架。
P=20kN
q=2kN/m
1、基本未知量B
2、固端弯矩
科A 技 学 院 MAB
EI B
3m
3m
B EI
6m
EI P B MBCAB B mBA 3B 40 M CB 4C 2 B 41.7
M BC 4 B 2C 41.7
M CD 3C
第7章 位移法
防梁 灾
M BA 3iAB B mBA 3B 40
M CD 3C
M BC 4 B 2C 41.7
第7章 位移法
防 灾 科
MA(((B 231)))超物平变EI静理衡形定条条P连结M件件续BA构BM::条B必A件M须:BC即即在满MB刚位确C足B 度移定的q方法基三EI程基本个;本未条方知件程量:3、。时列得MMM杆到端BABBAC满转足角243i位i;i移BBB方11程595
M FC
2
1 2
C
C
q=20kN/m
D
4I。B 5I。 C 4I。 3I。 3I。
2m 4m
120BB92CC411..7700
E
F
4m
5m
4m
第7章 位移法
(4) 解方程 B 1.15 C 4.89 (相对值)
(5)杆端弯矩及弯矩图
防 灾
梁
M M
F
(2)杆端弯矩Mi j
D
mBA
ql 2 8
20 42 8
40
2m 4m
mBC
ql2 12
41.7
学 院
4m
5m
4m
计算线性刚度i,设EI0=1,则
梁
iAB
EI AB lAB
E 4I0 4
1
mCB 41.7
iBC
1,
iCD
1,
iBE
3, 4
iCF
1 2
技 学 院
柱
M BE
4
3 4
B
3 B
31.15
3.45kN m
M CF
4
1 2
C
2C
2 (4.89)
9.8kN m
43.5 46.9
24.5 14.7
A
3.45 B
C 9.
8
D
M图 (kN m)
1.7
E
4.89 F
第7章 位移法 小结
