2020年4月全国高等数学(工本)自考试题及答案解析
2020年普通高等学校招生全国统一考试数学带答案解析
F
为双曲线 C :
x2 a2
y2 b2
1(a
0, b
0) 的右焦点，A
为
C
的右顶点，B
为
C
上的点，且
BF
垂直于
x
轴.若 AB 的斜率为 3，则 C 的离心率为
.
16．如图，在三棱锥 P–ABC 的平面展开图中，AC=1， AB AD 3 ，AB⊥AC，AB⊥AD，∠CAE=30°，
则 cos∠FCB=
已知函数 f (x) | 3x 1| 2 | x 1| ． （1）画出 y f (x) 的图像；
精品文档，名师推荐！ 来源网络，造福学生
———————欢迎下载，祝您学习进步，成绩提升———————
（2）求不等式 f (x) f (x 1) 的解集．
选择题答案 一、选择题 1．D 5．D
参考答案
所以E的方程为 x（x2，y2），P（6，t）. 若t≠0，设直线CD的方程为x=my+n，由题意可知–3<n<3.
t
t
由于直线PA的方程为y= 9 （x+3），所以y1= 9 （x1+3）.
t
t
直线PB的方程为y= 3 （x–3），所以y2= 3 （x2–3）.
C． a b2
D． a b2
二、填空题：本题共 4 小题，每小题 5 分，共 20 分。
2x y 2 0,
13．若 x，y 满足约束条件 x y 1 0, 则 z=x+7y 的最大值为
.
y 1 0,
14．设 a,b 为单位向量，且 | a b | 1，则 | a b |
.
15．已知
2．B 6．B
3．C 7．C
自考高等数学试题及答案解析
自考高等数学试题及答案解析一、选择题（每题3分，共30分）1. 下列函数中，哪一个不是周期函数？A. y = sin(x)B. y = cos(x)C. y = e^xD. y = tan(x)答案：C解析：周期函数是指函数在某一固定区间内重复其图形的函数。
y= sin(x)和y = cos(x)都是周期为2π的周期函数，y = tan(x)是周期为π的周期函数，而y = e^x是指数函数，没有周期性。
2. 微积分基本定理指出，如果一个连续函数f(x)在区间[a, b]上有一个原函数F(x)，那么f(x)在该区间上的定积分可以通过F(x)的差值来计算。
设f(x) = 2x，求∫[1, 3] 2x dx。
A. 6B. 12C. 18D. 24答案：B解析：首先找到f(x)的原函数F(x)，F(x) = ∫2x dx = x^2 + C。
根据微积分基本定理，定积分等于原函数的差值，即F(3) - F(1) = (3^2) - (1^2) = 9 - 1 = 8。
3. 以下哪个选项是二阶微分方程y'' - y' - 6y = 0的通解？A. y = e^(3x)B. y = e^x + e^(-2x)C. y = e^(2x) + e^(-3x)D. y = e^(-x) + e^(3x)答案：B解析：这是一个线性常系数微分方程，其特征方程为r^2 - r - 6 = 0。
解这个二次方程得到r1 = 3和r2 = -2。
因此，通解为y = C1 * e^(3x) + C2 * e^(-2x)。
4-10. （略）二、填空题（每题2分，共20分）1. 函数f(x) = x^2在区间[0, 1]上的最大值为______。
答案：1解析：函数f(x) = x^2在区间[0, 1]上是连续的，且在x = 1处取得最大值。
2. 设f(x) = x^3 - 6x^2 + 9x，求f'(x)。
(整理)年4月全国自考高等数学(工本)试题和参考答案.
精品文档全国2011年4月高等教育自学考试高等数学（工本）试题课程代码:00023一、单项选择题（本大题共5小题，每小题3分，共15分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.已知a ={-1，1，-2），b =(1，2，3}，则a ×b =( )A.{-7，-1,3}B.{7，-1，-3}C.{-7,1,3}D.{7,1，-3）2.极限222200)(3sin lim y x y x y x ++→→( ) A.等于0B.等于31C.等于3D.不存在3.设∑是球面x 2+y 2+z 2=4的外侧，则对坐标的曲面积分⎰⎰∑x 2dxdy =( ) A.-2B.0C.2D.4 4.微分方程22y x xy dx dy +=是( ) A.齐次微分方程 B.可分离变量的微分方程C.一阶线性齐次微分方程D.一阶线性非齐次微分方程 5.无穷级数∑∞=023n n n的前三项和S 3=( )A.-2B.419C.827D.865精品文档 二、填空题（本大题共5小题，每小题2分，共10分）请在每小题的空格中填上正确答案。
错填、不填均无分。
6.已知向量a ={2,2，-1），则与a 反方向的单位向量是_________.7.设函数f (x ，y )=yx y x +-，则f （1-x ,1+x ）=_________. 8.设积分区域D ：x 2+y 2≤2，则二重积分⎰⎰Df (x ，y )dxdy 在极坐标中的二次积分为________. 9.微分方程y 〞+y =2e x 的一个特解是y *=_________.10.设f (x )是周期为2π的函数，f (x )在[-π, π]，上的表达式为f (x )=⎩⎨⎧∈-∈),0[,)0,[,0ππx e x x S (x )为f (x )的傅里叶级数的和函数，则S (0)=_________.三、计算题（本大题共12小题，每小题5分，共60分）11.求过点P （-1,2，-3），并且与直线x =3+t ，y =t ，z =1-t 垂直的平面方程.12.设函数z =，求全微分dz |(2,1).13.设函数z=f （cos （xy ），2x-y )，其中f （u ，v ）具有连续偏导数，求x z ∂∂和dyz ∂. 14.已知方程e xy -2z +x 2-y 2+e z =1确定函数z=z (x,y )，求x z ∂∂和y z ∂∂. 15.设函数z=e x （x 2+2xy ），求梯度grad f (x ，y ).16.计算二重积分⎰⎰D y 22x e -dxdy .其中积分区域D 是由直线y=x , x =1及x 轴所围成的区域. 17.计算三重积分⎰⎰⎰Ω(1-x 2-y 2)dxdydz ，其中积分区域Ω是由x 2+y 2=a 2，z =0及z =2所围成的区域.18.计算对弧长的曲线积分⎰C xds ，其中C 是抛物线y=x 2上由点A (0,0)到点B (2,4)的一段弧.精品文档19.验证对坐标的曲线积分⎰C (x+y )dx +(x-y )dy 与路径无关， 并计算I=⎰-++)3,2()1,1()()(dy y x dx y x20.求微分方程x 2y 〞=2ln x 的通解.21.判断无穷级数∑∞=+1)11ln(n n 的敛散性. 22.将函数f (x )=x arctan x 展开为x 的幂级数.四、综合题（本大题共3小题，每小题5分，共15分）23.设函数z =arctan yx ，证明.02222=∂∂+∂∂y z x z 24.求由曲面z =xy ，x 2+y 2=1及z =0所围在第一卦限的立体的体积.25.证明无穷级数∑∞==+1.1)!1(n n n精品文档精品文档精品文档。
2020年全国大学高等数学考试及答案解析
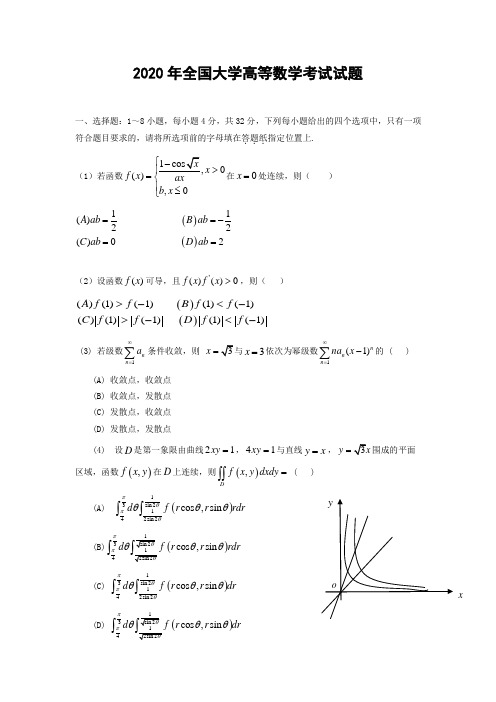
2020年全国大学高等数学考试试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸．．．指定位置上. （1）若函数1,0(),0x f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续，则（ ） ()()11()22()02A abB abC abD ab ==-==（2）设函数()f x 可导，且'()()0f x f x >，则（ ）()()()(1)(1)(1)(1)()(1)(1)(1)(1)A f fB f fC f fD f f >-<->-<-(3) 若级数1∞=∑nn a条件收敛，则=x 3=x 依次为幂级数1(1)∞=-∑n n n na x 的 ( )(A) 收敛点，收敛点 (B) 收敛点，发散点 (C) 发散点，收敛点 (D) 发散点，发散点(4) 设D 是第一象限由曲线21xy =，41xy =与直线y x =，y =围成的平面区域，函数(),f x y 在D 上连续，则(),Df x y dxdy =⎰⎰ ( )(A)()13sin 2142sin 2cos ,sin d f r r rdr πθπθθθθ⎰⎰(B)()34cos ,sin d f r r rdr ππθθθ⎰(C)()13sin 2142sin 2cos ,sin d f r r dr πθπθθθθ⎰⎰(D)()34cos ,sin d f r r dr ππθθθ⎰x（5）设α是n 维单位列向量，E 为n 阶单位矩阵，则（ ）()()()()22T T TT A E B E C E D E αααααααα-++-不可逆不可逆不可逆不可逆（6）设矩阵200210100021,020,020*********A B C ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,则（ ） ()()(),,(),,A A C B C B A C B C C A C B C D A C B C 与相似与相似与相似与不相似与不相似与相似与不相似与不相似(7) 若A,B 为任意两个随机事件，则 ( )(A) ()()()≤P AB P A P B (B) ()()()≥P AB P A P B (C) ()()()2≤P A P B P AB (D) ()()()2≥P A P B P AB(8)设随机变量,X Y 不相关，且2,1,3===EX EY DX ，则()2+-=⎡⎤⎣⎦E X X Y ( )(A) 3- (B) 3 (C) 5- (D) 5二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸．．．指定位置上. (1) 已知函数21()1f x x=+，则(3)(0)f =__________ (2) 微分方程'''230y y y ++=的通解为y =_________(3) 若曲线积分221L xdx aydy x y -+-⎰在区域{}22(,)|1D x y x y =+<内与路径无关，则 a =__________(4)设Ω是由平面1++=x y z 与三个坐标平面平面所围成的空间区域，则(23)__________.x y z dxdydz Ω++=⎰⎰⎰(5)设二维随机变量(,)x y 服从正态分布(1,0;1,1,0)N ，则{0}________.P XY Y -<=三、解答题：15—23小题，共94分.请将解答写在答题纸．．．指定位置上.解答应写出文字说明、证明过程或演算步骤. （1）（本题满分10分）设函数(,)f u v 具有2阶连续偏导数，(,cos )xy f e x =，求0x dy dx=，22x d y dx=（2）（本题满分10分）求21lim ln 1nn k kk nn →∞=⎛⎫+ ⎪⎝⎭∑（3）（本题满分10分）已知函数()y x 由方程333320x y x y +-+-=确定，求()y x 的极值(4)(本题满分 10 分)（I ）设函数()()u x ,v x 可导，利用导数定义证明u x v x u x v x u x v x '''=+[()()]()()()()（II ）设函数()()()12n u x ,u x ,,u x 可导，n f x u x u x u x =12()()()()，写出()f x 的求导公式.(5)(本题满分 10 分)已知曲线L的方程为,z z x ⎧=⎪⎨=⎪⎩起点为()A，终点为()0,B ，计算曲线积分()()2222d d ()d LI y z x z x y y x y z =++-+++⎰.(6) (本题满11分)设向量组1,23,ααα内3R 的一个基，113=2+2k βαα，22=2βα，()313=++1k βαα.（I ）证明向量组1β2β3β为3R 的一个基;（II ）当k 为何值时，存在非0向量ξ在基1,23,ααα与基1β2β3β下的坐标相同，并求所有的ξ.（7）（本题满分11分）设二次型222123123121323(,,)2282f x x x x x ax x x x x x x =-++-+在正交变换X QY =下的标准型221122y y λλ+，求a 的值及一个正交矩阵Q（8）（本题满分11分）设随机变量,X Y 相互独立，且X 的概率分布为1(0)(2)2P X P X ====，Y 的概率密度为201()0,y y f y <<⎧=⎨⎩，其他()I 求()P Y EY ≤()∏求Z X Y =+的概率密度。
历年全国自考高等数学(工本)试题及答案(更新至4月)
全国20XX 年4月高等教育自学考试高等数学（工本）试题课程代码：00023一、单项选择题（本大题共5小题，每小题3分，共15分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题号的括号内。
错选、多选或未选均无分。
1．下列曲面中，母线平行于y 轴的柱面为（ ）A ．z =x 2B ．z = y 2C ．z = x 2 + y 2D ．x + y + z =12．已知函数h (x,y )=x –y+f (x+y ),且h (0,y )=y 2,则f (x+y )为（ ）A ．y (y + 1)B ．y (y - 1)C ．( x + y )( x + y -1)D ．( x + y )( x + y +1)3．下列表达式是某函数u (x,y )的全微分的为（ ）A ．x 2y d x + xy 2d yB ．x d x + xy d yC ．y d x - x d yD ．y d x + x d y4．微分方程y xy d d =x 的阶数是（ ） A ．0B ．1C ．2D ．35．无穷级数∑∞=2!1n n 的和为（ ）A ．e + 1B ．e - 1C ．e - 2D ．e + 2 二、填空题（本大题共5小题，每小题2分，共10分）请在每小题的空格中填上正确答案。
错填、不填均无分。
6．已知向量a ={ -2, c, 6}与向量b ={ 1, 4, -3}垂直，则常数c=______.7.函数z =224y x --ln(x 2+y 2-1)的定义域为______.8．二次积分I =⎰⎰--21011d d y x f ( x, y )y ,交换积分次序后I =______.9．已知y =sin2x +ce x 是微分方程y ''+4y =0的解，则常数c =______.10.幂级数∑∞=+013n n n x 的收敛半径R =______. 三、计算题（本大题共12小题，每小题5分，共60分）11．将直线⎩⎨⎧=-++=++0432023z y x z y x 化为参数式和对称式方程. 12.设方程f ( x + y + z, x, x + y )=0确定函数z = z ( x, y ),其中f 为可微函数，求x z ∂∂和y z ∂∂. 13.求曲面z = 2y + ln yx 在点（1，1，2）处的切平面方程. 14.求函数z = x 2 - y 2在点（2，3）处，沿从点A （2，3）到点B （3，3+3）的方向l 的方向导数.15.计算二重积分()⎰⎰+D y x x yd d sin 32，其中积分区域D 是由y = | x |和y =1所围成.16.计算三重积分I =⎰⎰⎰Ωz y x xy d d d ，其中积分区域Ω是由x 2+y 2=4及平面z =0，z =2所围的在第一卦限内的区域. 17.计算对弧长的曲线积分I =⎰L ds y 2，其中L 为圆周x 2+y 2=9的左半圆. 18.计算对坐标的曲线积分I =⎰-++L y y x x x y d )1(d )1(22，其中L 是平面区域D ：x 2 + y 2 ≤4的正向边界.19.验证y 1 = e x ,y 2 = x 都是微分方程（1 – x ）y ''+y x '-y = 0的解，并写出该微分方程的通解。
自考高数试题及答案
自考高数试题及答案一、选择题（本题共10分，每题1分）1. 函数f(x)=x^3-3x+1的导数是（）A. 3x^2 - 3B. 3x^2 + 3C. x^2 - 3xD. x^2 + 3x答案：A2. 极限lim(x→0) (sin x)/x的值是（）A. 0B. 1C. 2D. ∞答案：B3. 定积分∫(0,1) x^2 dx的值是（）A. 1/3B. 1/2C. 1/4D. 1/6答案：C4. 微分方程y'' - y' - 2y = 0的通解是（）A. y = e^x + e^(-x)B. y = e^(2x) + e^(-2x)C. y = e^x + e^(-x) + xD. y = e^(2x) + e^(-2x) + x答案：A5. 矩阵A = [1, 2; 3, 4]的行列式值是（）A. 2B. -2C. 7D. -7答案：C二、填空题（本题共10分，每题2分）6. 函数f(x) = x^2 - 6x + 8的极值点是______。
答案：37. 函数y = ln(x)的导数是______。
答案：1/x8. 曲线y = x^3 - 3x + 1在点(1, -1)处的切线斜率是______。
答案：39. 函数y = sin(x) + cos(x)的周期是______。
答案：2π10. 矩阵B = [1, 0; 0, 1]的逆矩阵是______。
答案：[1, 0; 0, 1]三、解答题（本题共30分，每题15分）11. 求函数f(x) = x^3 - 3x^2 + 2在区间[-2, 2]上的最大值和最小值。
答案：函数f(x) = x^3 - 3x^2 + 2的导数为f'(x) = 3x^2 - 6x。
令f'(x) = 0，解得x = 0 或 x = 2。
在区间[-2, 2]上，当x = -2时，f(x) = 2；当x = 2时，f(x) = -2；当x = 0时，f(x) = 2。
全国自考公共课高等数学(工本)模拟试卷4(题后含答案及解析)
全国自考公共课高等数学（工本）模拟试卷4(题后含答案及解析) 题型有：1. 单项选择题 2. 填空题 3. 计算题 4. 综合题单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1．已知f(x，y)在点(x0，y0)的偏导数存在．则下列结论正确的是( ) A．f(x，y)在(x0，y0)点连续B．f(x，y)在(x0，y0)点可微C．函数f(x，y0)在x＝x0点连续D．f(x，y)在(x0，y0)点有任意方向的方向导数正确答案：C解析：根据多元函数的连续、可导、可微之间的关系可知A、B是错误的．对于C，因F(x)＝F(x，y0)是关于x的一元函数，从而F’(x0)＝fx(x0，y0)是存在的，因此一元函数F(x)＝f(x，y0)在x＝x0处是连续的．从而C是正确的．对于D，我们知道，如果f(x，y)在点(x0，y0)可微，则在点(x0，y0)处沿任意方向的方向导数都存在．但两个偏导数存在并不意味着可微，所以此结论的正确性是有疑问的．事实上，对于函数f(x，y)＝，可以证明在原点的两个偏导数都为零，但是沿方向{1，1}的方向导数不存在．答案为C．2．极限＝( )A．B．C．D．π正确答案：A解析：.答案为A．3．设D由圆r＝2围成，则＝( )A．B．4πC．D．π正确答案：C解析：本题考查二元积分的计算．积分区域D由圆r＝2围成，令x＝rcosθ，y＝rsinθ则答案为C．4．以y＝sin3x为特解的微分方程为( )A．y”＋y＝0B．y”－y＝0C．y”＋9y＝0D．y”－9y＝0正确答案：C解析：由题可知：特征根r＝±3i 故r2＋q＝0 故所求微分方程为y”＋qy ＝0．答案为C．5．设an＞0，(n＝1，2，3，…)，若收敛，则下列结论正确的是( ) A．发散B．发散C．发散D．收敛正确答案：D解析：本题考查级数的敛散性．填空题请在每小题的空格中填上正确答案。
4月全国自考高等数学(工本)试题及答案解析
1全国2018年4月自学考试高等数学(工本)试题课程代码：00023一、单项选择题（本大题共5小题，每小题3分，共15分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.在空间直角坐标系中,方程1222222=++cz b y a x 表示的图形是( )A.椭圆抛物面B.圆柱面C.单叶双曲面D.椭球面2.设函数z =x 2y ,则=∂∂xz( ) A.212-y yxB.x xyln 2C.x x yln 22 D.()12-y yx3.设Ω是由平面01=-+-z y x 及坐标面所围成的区域,则三重积分=⎰⎰⎰Ωdxdydz ( ) A.81 B.61 C.31 D.21 4.已知微分方程)()(x Q y x P y =+'的两个特解为y 1=2x 和y 2=cos x ,则该微分方程的通解是y =( ) A.2C 1x +C 2cos x B.2Cx +cos x C.cos x +C (2x -cos x ) D.C (2x -cos x )5.设幂级数∑∞--1)3(n n nx a在x =1处收敛,则在x =4处该幂级数( )A.绝对收敛B.条件收敛2C.发散D.敛散性不定二、填空题（本大题共5小题，每小题2分，共10分）请在每小题的空格中填上正确答案。
错填、不填均无分。
6.设函数y x y z cos sin =,则=∂∂xz. 7.已知dy e dx e y x yx +++是某函数()y x u ,的全微分,则()=y x u , .8.设∑是上半球面()01222≥=++z z y x ,则对面积的曲面积分⎰⎰∑=dS .9.微分方程x y 2sin =''的通解为y= .10.无穷级数∑∞=0!2n nn 的和为 .三、计算题（本大题共12小题，每小题5分，共60分） 11.求过点P (3,-1,0)并且与直线321-=-=z y x 垂直的平面方程. 12.设函数()y x x f z -=,3,其中f 是可微函数,求x z ∂∂,yz∂∂. 13.设方程xyx ln=确定函数()y x z z ,=,求全微分dz. 14.求函数()22,xy y x y x f +=在点(1,-1)沿与x 轴正向成30°角的方向l 的方向导数.15.求空间曲线t z t y t x ===,sin ,cos 在点⎪⎪⎭⎫⎝⎛4,22,22π处的切线方程.16.计算二重积分()dxdy e I Dy x⎰⎰+-=22,其中区域D ：.0,422≥≤+y y x17.计算二次积分⎰⎰=22sin ππydx xxdy I . 18.计算对弧长的曲线积分()⎰+-L ds y x 132,其中L 是直线2-=x y 上从点(-1,-3)到点(1,-1)的直线段. 19.计算对坐标的曲线积分⎰+Lydx xdy 其中L 是抛物线2x y =上从点(-2,4)到点(2,4)的一段3弧.20.求微分方程034=+'-''y y y 满足初始条件()8)0(,40='=y y 的特解. 21.判断级数()∑∞=-+-131321n n nn 是否收敛,如果收敛,是条件收敛还是绝对收敛?22.设函数()⎩⎨⎧<≤<≤-=ππx x x x f 0,0,0的傅里叶级数展开式为()∑∞=++10sin cos 2n n n nx b nx a a ,求系数b 7.四、综合题（本大题共3小题，每小题5分，共15分） 23.求函数()y x xy y x y x f 311381021,22-----=的极值.24.设曲线()x y y =在其上点(x ,y )处的切线斜率为x +y ,且过点(-1,e -1),求该曲线方程. 25.将函数()2312+-=x x x f 展开为(x +1)的幂级数.。
2020年大学高等数学考试试题及解析
2020年全国大学高等数学考试试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)设12(sin cos )xy e C x C x =+(12,C C 为任意常数）为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.(2)设222z y x r ++=,则div(gradr))2,2,1(-=_____________.(3)交换二次积分的积分次序:⎰⎰--0112),(y dx y x f dy ＝_____________.(4)从2R 的基⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=11,0121αα到基⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=21,1121ββ的过渡矩阵为 .(5)设二维随机变量(X,Y)的概率密度为，y x x y x f 其他,10,0,6),(≤≤≤⎩⎨⎧=则=≤+}1{Y X P .(6)已知一批零件的长度X (单位：cm)服从正态分布)1,(μN ，从中随机地抽取16个零件，得到长度的平均值为40 (cm)，则μ的置信度为0.95的置信区间是 .(注：标准正态分布函数值.)95.0)645.1(,975.0)96.1(=Φ=Φ二、选择题（本题共6小题，每小题4分，满分24分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内）（1）设函数f(x)在),(+∞-∞内连续，其导函数的图形如图所示，则f(x)有[ ] (A) 一个极小值点和两个极大值点. (B) 两个极小值点和一个极大值点. (C) 两个极小值点和两个极大值点.(D) 三个极小值点和一个极大值点.（2）设}{},{},{n n n c b a 均为非负数列，且0lim =∞→n n a ,1lim =∞→n n b ,∞=∞→n n c lim ,则必有[ ](A) n n b a <对任意n 成立. (B) n n c b <对任意n 成立. (C) 极限n n n c a ∞→lim 不存在. (D) 极限n n n c b ∞→lim 不存在.（3）已知函数f(x,y)在点(0,0)的某个邻域内连续，且1)(),(lim 2220,0=+-→→y x xyy x f y x ，则[ ](A) 点(0,0)不是f(x,y)的极值点. (B) 点(0,0)是f(x,y)的极大值点. (C) 点(0,0)是f(x,y)的极小值点.(D) 根据所给条件无法判断点(0,0)是否为f(x,y)的极值点.(4)设1111400011110000,,1111000011110000A B ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦则A 与B [ ] (A) 合同且相似.(B) 合同但不相似. (C) 不合同但相似.(D) 不合同且不相似.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数, 则X 和Y 的相关系数等于[ ](A)-1.(B) 0.(C)12. (D) 1.三、(本题满分6分)求dx ee xx⎰2arctan .四、（本题满分12分）将函数x x x f 2121arctan )(+-=展开成x 的幂级数，并求级数∑∞=+-012)1(n nn 的和.五、(本题满分8分)设)(x f =210,arctan ,0,1,x x x x x +⎧≠⎨=⎩将)(x f 展开成x 的幂级数,并求级数∑∞=--1241)1(n nn 的和.某建筑工程打地基时，需用汽锤将桩打进土层. 汽锤每次击打，都将克服土层对桩的阻力而作功. 设土层对桩的阻力的大小与桩被打进地下的深度成正比（比例系数为k,k>0）.汽锤第一次击打将桩打进地下a m. 根据设计方案，要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数r(0<r<1). 问(1) 汽锤击打桩3次后，可将桩打进地下多深？ (2) 若击打次数不限，汽锤至多能将桩打进地下多深？ （注：m 表示长度单位米.）七、(本题满分7分)设)(x f 在(1,1)-内具有二阶连续导数且0)(≠''x f ,试证:(1)对于(1,1)-内的任一0x ≠,存在惟一的)1,0()(∈x θ,使)(x f =)0(f +))((x x f x θ'成立;(2)01lim ()2x x θ→=.八 、（本题满分12分）设函数f(x)连续且恒大于零，⎰⎰⎰⎰⎰+++=Ω)(22)(222)()()(t D t d y xf dvz y x f t F σ，⎰⎰⎰-+=tt D dxx f d y x f t G 12)(22)()()(σ，其中}),,{()(2222t z y x z y x t ≤++=Ω，}.),{()(222t y x y x t D ≤+=(1) 讨论F(t)在区间),0(+∞内的单调性.(2) 证明当t>0时，).(2)(t G t F π>九、(本题满分6分)设s ααα,,,21 为线性方程组0Ax =的一个基础解系,11122t t βαα=+,21223,t t βαα=+,121s s t t βαα=+,其中21,t t 为实常数.试问21,t t 满足什么条件时,s βββ,,,21 也为0Ax =的一个基础解系.已知平面上三条不同直线的方程分别为 :1l 032=++c by ax ， :2l 032=++a cy bx ， :3l 032=++b ay cx .试证这三条直线交于一点的充分必要条件为.0=++c b a十一、(本题满分7分)设某班车起点站上客人数X 服从参数为λ(0λ>)的泊松分布,每位乘客在中途下车的概率为p (01p <<),且中途下车与否相互独立.以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率; (2)二维随机变量(,)X Y 的概率分布. 十二 、（本题满分8分） 设总体X 的概率密度为⎩⎨⎧≤>=--,,,0,2)()(2θθθx x e x f x其中0>θ是未知参数. 从总体X 中抽取简单随机样本n X X X ,,,21 ，记).,,,min(ˆ21nX X X =θ (1) 求总体X 的分布函数F(x);(2) 求统计量θˆ的分布函数)(ˆx F θ； (3) 如果用θˆ作为θ的估计量，讨论它是否具有无偏性.2020年全国大学高等数学考试试题与解析一、填空题(1)【分析】 由通解的形式可知特征方程的两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r r r r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】 先求grad r.grad r=,,,,r r r x y z x y z r r r ∂∂∂⎧⎫⎧⎫=⎨⎬⎨⎬∂∂∂⎩⎭⎩⎭. 再求 div grad r=()()()x y zx r y r z r∂∂∂++∂∂∂=222222333311132()()()x y z x y z r r r r r r r r r++-+-+-=-=. 于是div grad r|(1,2,2)-=(1,2,2)22|3r -=.(3)【分析】 这个二次积分不是二重积分的累次积分,因为10y -≤≤时12y -≤.由此看出二次积分0211(,)ydy f x y dx --⎰⎰是二重积分的一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=⎰⎰⎰⎰.由累次积分的内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=0222111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=⎰⎰⎰⎰⎰⎰.（4）从2R 的基⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=11,0121αα到基⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=21,1121ββ的过渡矩阵为⎪⎪⎭⎫ ⎝⎛--2132. 【分析】 n 维向量空间中，从基n ααα,,,21 到基n βββ,,,21 的过渡矩阵P 满足[n βββ,,,21 ]=[n ααα,,,21 ]P ，因此过渡矩阵P 为：P=[121],,,-n ααα [],,,21n βββ .【详解】根据定义，从2R 的基⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=11,0121αα到基⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=21,1121ββ的过渡矩阵为P=[121],-αα[⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=-21111011],121ββ.=.213221111011⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡- （5）设二维随机变量(X,Y)的概率密度为 ，y x x y x f 其他,10,0,6),(≤≤≤⎩⎨⎧=则=≤+}1{Y X P41 . 【分析】 已知二维随机变量(X,Y)的概率密度f(x,y)，求满足一定条件的概率}),({0z Y X g P ≤，一般可转化为二重积分}),({0z Y X g P ≤=⎰⎰≤0),(),(z y x g dxdy y x f 进行计算.【详解】 由题设，有 =≤+}1{Y X P ⎰⎰⎰⎰≤+-=121016),(y x xxxdy dx dxdy y x f=.41)126(2102=-⎰dx x xO211 x【评注】 本题属基本题型，但在计算二重积分时，应注意找出概率密度不为零与满足不等式1≤+y x 的公共部分D ，再在其上积分即可.（6）已知一批零件的长度X (单位：cm)服从正态分布)1,(μN ，从中随机地抽取16个零件，得到长度的平均值为40 (cm)，则μ的置信度为0.95的置信区间是)49.40,51.39( .(注：标准正态分布函数值.)95.0)645.1(,975.0)96.1(=Φ=Φ 【分析】 已知方差12=σ，对正态总体的数学期望μ进行估计，可根据)1,0(~1N nX μ-，由αμα-=<-1}1{2u n X P 确定临界值2αu ，进而确定相应的置信区间. 【详解】 由题设，95.01=-α，可见.05.0=α 于是查标准正态分布表知.96.12=αu 本题n=16, 40=x , 因此，根据 95.0}96.11{=<-nX P μ，有 95.0}96.116140{=<-μP ，即 95.0}49.40,51.39{=P ，故μ的置信度为0.95的置信区间是)49.40,51.39( .二、选择题（本题共6小题，每小题4分，满分24分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内）（1）设函数f(x)在),(+∞-∞内连续，其导函数的图形如图所示，则f(x)有(A) 一个极小值点和两个极大值点. (B) 两个极小值点和一个极大值点. (C) 两个极小值点和两个极大值点.(D)【分析】 答案与极值点个数有关，而可能的极值点应是导数为零或导数不存在的点，共4个，是极大值点还是极小值可进一步由取极值的第一或第二充分条件判定.【详解】 根据导函数的图形可知，一阶导数为零的点有3个，而 x=0 则是导数不存在的点. 三个一阶导数为零的点左右两侧导数符号不一致，必为极值点，且两个极小值点，一个极大值点；在x=0左侧一阶导数为正，右侧一阶导数为负，可见x=0为极大值点，故f(x)共有两个极小值点和两个极大值点，应选(C).【评注】 本题属新题型，类似考题2001年数学一、二中曾出现过，当时考查的是已知f(x)的图象去推导)(x f '的图象，本题是其逆问题.（2）设}{},{},{n n n c b a 均为非负数列，且0lim =∞→n n a ,1lim =∞→n n b ,∞=∞→n n c lim ,则必有(A) n n b a <对任意n 成立. (B) n n c b <对任意n 成立.(C) 极限n n n c a ∞→lim 不存在. (D) 极限n n n c b ∞→lim 不存在. [ D ]【分析】 本题考查极限概念，极限值与数列前面有限项的大小无关，可立即排除(A),(B)； 而极限n n n c a ∞→lim 是∞⋅0型未定式，可能存在也可能不存在，举反例说明即可；极限n n n c b ∞→lim 属∞⋅1型，必为无穷大量，即不存在.【详解】 用举反例法，取n a n 2=，1=n b ，),2,1(21==n n c n ，则可立即排除(A),(B),(C)，因此正确选项为(D).【评注】 对于不便直接证明的问题，经常可考虑用反例，通过排除法找到正确选项.（3）已知函数f(x,y)在点(0,0)的某个邻域内连续，且1)(),(lim2220,0=+-→→y x xyy x f y x ，则 (A) 点(0,0)不是f(x,y)的极值点. (B) 点(0,0)是f(x,y)的极大值点. (C) 点(0,0)是f(x,y)的极小值点.(D) 根据所给条件无法判断点(0,0)是否为f(x,y)的极值点.[ A ]【分析】 由题设，容易推知f(0,0)=0，因此点(0,0)是否为f(x,y)的极值，关键看在点(0,0)的充分小的邻域内f(x,y)是恒大于零、恒小于零还是变号.【详解】 由 1)(),(lim2220,0=+-→→y x xyy x f y x 知，分子的极限必为零，从而有f(0,0)=0, 且222)(),(y x xy y x f +≈- y x ,(充分小时），于是.)()0,0(),(222y x xy f y x f ++≈-可见当y=x 且x 充分小时，04)0,0(),(42>+≈-x x f y x f ；而当y= -x 且x 充分小时，04)0,0(),(42<+-≈-x x f y x f . 故点(0,0)不是f(x,y)的极值点，应选(A).【评注】 本题综合考查了多元函数的极限、连续和多元函数的极值概念，题型比较新，有一定难度. 将极限表示式转化为极限值加无穷小量，是有关极限分析过程中常用的思想. (4)【分析】 由 43||40E A λλλ-=-=,知矩阵A 的特征值是4,0,0,0.又因A 是实对称矩阵,A 必能相似对角化,所以A 与对角矩阵B 相似.作为实对称矩阵,当AB 时,知A 与B 有相同的特征值,从而二次型T x Ax 与T x Bx 有相同的正负惯性指数,因此A 与B 合同.所以本题应当选(A).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ⎡⎤=⎢⎥⎣⎦与1003B ⎡⎤=⎢⎥⎣⎦,它们的特征值不同,故A 与B 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】 解本题的关键是明确X 和Y 的关系:X Y n +=,即Y n X =-,在此基础上利用性质:相关系数XY ρ的绝对值等于1的充要条件是随机变量X 与Y 之间存在线性关系,即Y aX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数的定义式有1XY ρ===-.三、【解】 原式=222211arctan ()[arctan ]22(1)x x x x xxx de e d e e e e e ---=--+⎰⎰=2221(arctan )21x x x xx xde de e e e e ---++⎰⎰=21(arctan arctan )2xx x x e e e e C ---+++. 四 、（本题满分12分）将函数x x x f 2121arctan )(+-=展开成x 的幂级数，并求级数∑∞=+-012)1(n nn 的和.【分析】 幂级数展开有直接法与间接法，一般考查间接法展开，即通过适当的恒等变形、求导或积分等，转化为可利用已知幂级数展开的情形.本题可先求导，再利用函数x-11的幂级数展开 +++++=-n x x x x2111即可，然后取x 为某特殊值，得所求级数的和.【详解】 因为).21,21(,4)1(2412)(202-∈--=+-='∑∞=x x x x f nn n n 又f(0)=4π, 所以 dt t dt t f f x f n n xxn n ]4)1([24)()0()(20⎰⎰∑∞=--='+=π=).21,21(,124)1(24120-∈+--+∞=∑x x n n n n n π因为级数∑∞=+-012)1(n nn 收敛，函数f(x)在21=x 处连续，所以].21,21(,124)1(24)(120-∈+--=+∞=∑x x n x f n n n n π令21=x ，得 ∑∑∞=+∞=+--=⋅+--=012012)1(4]21124)1([24)21(n nn n n n n f ππ,再由0)21(=f ，得.4)21(412)1(0ππ=-=+-∑∞=f n n n 五、【分析与求解】 关键是将arctan x 展成幂级数,然后约去因子x ,再乘上21x +并化简即可.直接将arctan x 展开办不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n nn x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑⎰⎰,[1,1]x ∈-. ②因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑=12200(1)(1)2121n n n nn n x x n n -∞∞==--++-∑∑=21111(1)()2121n n n x n n ∞=+--+-∑221(1)2114n nn x n∞=-=+-∑ , [1,1]x ∈-,0x ≠上式右端当0x =时取值为1,于是221(1)2()1,[1,1]14n nn f x x x n ∞=-=+∈--∑. 上式中令1x =21(1)111[(1)1](21)1422442n n f nππ∞=-⇒=-=⨯-=--∑.六 、（本题满分10分）某建筑工程打地基时，需用汽锤将桩打进土层. 汽锤每次击打，都将克服土层对桩的阻力而作功. 设土层对桩的阻力的大小与桩被打进地下的深度成正比（比例系数为k,k>0）.汽锤第一次击打将桩打进地下a m. 根据设计方案，要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数r(0<r<1). 问(1) 汽锤击打桩3次后，可将桩打进地下多深？ (2) 若击打次数不限，汽锤至多能将桩打进地下多深？ （注：m 表示长度单位米.）【分析】 本题属变力做功问题，可用定积分进行计算，而击打次数不限，相当于求数列的极限.【详解】 (1) 设第n 次击打后，桩被打进地下n x ，第n 次击打时，汽锤所作的功为),3,2,1( =n W n . 由题设，当桩被打进地下的深度为x 时，土层对桩的阻力的大小为kx ，所以22101221a kx k kxdx W x ===⎰，).(2)(22222122221a x k x x k kxdx W x x -=-==⎰由12rW W =可得 2222ra a x =- 即 .)1(222a r x += ].)1([2)(22232223332a r x k x x k kxdx W x x +-=-==⎰ 由1223W r rW W ==可得 22223)1(a r a r x =+-，从而 a r r x 231++=，即汽锤击打3次后，可将桩打进地下am r r 21++.（2） 由归纳法，设a r r r x n n 121-++++= ，则)(222111n n x x n x x k kxdx W n n-==++⎰+=].)1([22121a r r x k n n -++++- 由于1121W r W r rW W nn n n ====-+ ，故得 22121)1(a r a r r x n n n =+++--+ ,从而 .11111a rr a r r x n nn --=+++=++于是 a rx n n -=+∞→11lim 1， 即若击打次数不限，汽锤至多能将桩打进地下a r-11m. 【评注】 本题巧妙地将变力作功与数列极限两个知识点综合起来了，有一定难度.但用定积分求变力做功并不是什么新问题，何况本题的变力十分简单.七、【证明】 (1)由拉格朗日中值定理,(1,1)x ∀∈-,0,(0,1)x θ≠∃∈,使'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一.(2)对'()f x θ使用''(0)f 的定义.由题(1)中的式子先解出'()f x θ,则有'()(0)()f x f f x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f xθ---=.'''2()(0)()(0)(0)f x f f x f xf x x θθθ---⋅=,解出θ,令0x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===.八 、（本题满分12分）设函数f(x)连续且恒大于零，⎰⎰⎰⎰⎰+++=Ω)(22)(222)()()(t D t d y xf dvz y x f t F σ，⎰⎰⎰-+=tt D dxx f d y x f t G 12)(22)()()(σ，其中}),,{()(2222t z y x z y x t ≤++=Ω，}.),{()(222t y x y x t D ≤+=(1) 讨论F(t)在区间),0(+∞内的单调性.(2) 证明当t>0时，).(2)(t G t F π>【分析】 (1) 先分别在球面坐标下计算分子的三重积分和在极坐标下计算分母的重积分，再根据导函数)(t F '的符号确定单调性；(2) 将待证的不等式作适当的恒等变形后，构造辅助函数，再用单调性进行证明即可.【详解】 (1) 因为⎰⎰⎰⎰⎰⎰⎰==ttttrdrr f drr r f rdrr f d drr r f d d t F 020222002200022)()(2)(sin )()(πππθϕϕθ，202022])([)()()(2)(rdr r f drr t r r f t tf t F tt⎰⎰-='，所以在),0(+∞上0)(>'t F ，故F(t) 在),0(+∞内单调增加.（2） 因 ⎰⎰=ttdrr f rdrr f t G 0202)()()(π，要证明t>0时)(2)(t G t F π>，只需证明t>0时，0)(2)(>-t G t F π，即.0])([)()(0202222>-⎰⎰⎰tttrdr r f dr r f dr r r f令 ⎰⎰⎰-=tt trdr r f dr r f dr r r f t g 0202222])([)()()(，则 0)()()()(2022>-='⎰dr r t r f t f t g t，故g(t)在),0(+∞内单调增加.因为g(t)在t=0处连续，所以当t>0时，有g(t)>g(0). 又g(0)=0, 故当t>0时，g(t)>0,因此，当t>0时，).(2)(t G t F π>【评注】 本题将定积分、二重积分和三重积分等多个知识点结合起来了，但难点是证明（2）中的不等式，事实上，这里也可用柯西积分不等式证明：dx x g dx x f dx x g x f bababa⎰⎰⎰⋅≤)()(])()([222，在上式中取f(x)为r r f )(2，g(x)为)(2r f 即可.九、【解】 由于(1,2)i i s β=是12,,s ααα线性组合,又12,,s ααα是0Ax =的解,所以根据齐次线性方程组解的性质知(1,2)i i s β=均为0Ax =的解.从12,,s ααα是0Ax =的基础解系,知()s n r A =-.下面来分析12,,s βββ线性无关的条件.设11220s s k k k βββ++=,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++=.由于12,,s ααα线性无关,因此有112211222132110,0,0,0.s s s t k t k t k t k t k t k t k t k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩(*)因为系数行列式12211211221000000000(1)000s s st t t t t t t t t t +=+-, 所以当112(1)0s s st t ++-≠时,方程组(*)只有零解120s k k k ====.从而12,,s βββ线性无关.十 、（本题满分8分）已知平面上三条不同直线的方程分别为:1l 032=++c by ax ， :2l 032=++a cy bx ， :3l 032=++b ay cx .试证这三条直线交于一点的充分必要条件为.0=++c b a【分析】 三条直线相交于一点，相当于对应线性方程组有唯一解，进而转化为系数矩阵与增广矩阵的秩均为2.【详解】 方法一：必要性设三条直线321,,l l l 交于一点，则线性方程组⎪⎩⎪⎨⎧-=+-=+-=+,32,32,32b ay cx a cy bx c by ax (*) 有唯一解，故系数矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=a c c b b a A 222与增广矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=b a c a c b c b a A 323232的秩均为2，于是.0=A由于 ])[(6323232222bc ac ab c b a c b a ba c a cbcba A ---++++=---==])()())[((3222a c cb b ac b a -+-+-++, 但根据题设 0)()()(222≠-+-+-a c c b b a ，故 .0=++c b a充分性：由0=++c b a ，则从必要性的证明可知，0=A ，故秩.3)(<A 由于])([2)(22222b b a a b ac cb b a ++-=-==0]43)21[(222≠++-b b a ， 故秩(A)=2. 于是，秩(A)=秩)(A =2.因此方程组(*)有唯一解，即三直线321,,l l l 交于一点.方法二：必要性设三直线交于一点),(00y x ，则⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100y x 为Ax=0的非零解，其中 .323232⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=b a c a c b c b a A 于是 0=A .而 ])[(6323232222bc ac ab c b a c b a ba ca c bcb aA ---++++-== =])()())[((3222a c cb b ac b a -+-+-++-, 但根据题设 0)()()(222≠-+-+-a c c b b a ，故 .0=++c b a充分性：考虑线性方程组⎪⎩⎪⎨⎧-=+-=+-=+,32,32,32b ay cx a cy bx c by ax (*)将方程组(*)的三个方程相加，并由a+b+c=0可知，方程组(*)等价于方程组 ⎩⎨⎧-=+-=+.32,32a cy bx c by ax (* *)因为])([2)(22222b b a a b ac cb b a ++-=-==-0])([222≠+++b a b a ,故方程组(* *)有唯一解，所以方程组(*)有唯一解，即三直线321,,l l l 交于一点.【评注】本题将三条直线的位置关系转化为方程组的解的判定，而解的判定问题又可转化为矩阵的秩计算，进而转化为行列式的计算，综合考查了多个知识点.十一、【解】 (1){|}(1),0,0,1,2,m m n mn P Y m X n C p p m n n -===-≤≤=.(2){,}P X n Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--⋅-≤≤=十二 、（本题满分8分）设总体X 的概率密度为⎩⎨⎧≤>=--,,,0,2)()(2θθθx x e x f x其中0>θ是未知参数. 从总体X 中抽取简单随机样本n X X X ,,,21 ，记).,,,min(ˆ21nX X X =θ(1) 求总体X 的分布函数F(x);(2) 求统计量θˆ的分布函数)(ˆx F θ； (3) 如果用θˆ作为θ的估计量，讨论它是否具有无偏性. 【分析】 求分布函数F(x)是基本题型；求统计量θˆ的分布函数)(ˆx F θ，可作为多维相互独立且同分布的随机变量函数求分布函数，直接用定义即可；是否具有无偏性，只需检验θθ=ˆE 是否成立. 【详解】 (1).,,0,1)()()(2θθθ≤>⎩⎨⎧-==⎰∞---x x e dt t f x F xx(2) }),,,{min(}ˆ{)(21ˆx X X X P x P x F n≤=≤= θθ =}),,,{m in(121x X X X P n >- =},,,{121x X x X x X P n >>>- =nx F )](1[1--=.,,0,1)(2θθθ≤>⎩⎨⎧---x x e x n(3) θˆ概率密度为 .,,0,2)()()(2ˆˆθθθθθ≤>⎩⎨⎧==--x x ne dxx dF x f x n因为 ⎰⎰+∞--+∞∞-==θθθθdx nxe dx x xf E x n )(2ˆ2)(ˆ=θθ≠+n21， 所以θˆ作为θ的估计量不具有无偏性. 【评注】本题表面上是一数理统计问题，实际上考查了求分布函数、随机变量的函数求分布和概率密度以及数学期望的计算等多个知识点.将数理统计的概念与随机变量求分布与数字特征结合起来是一种典型的命题形式.。
2020年全国大学高等数学考试试题及答案
．
因为 在 可导，且为极值,所以 ，则
．
(3)(本题满分10分)
【解析】显然 为方程一个实根．
当 时，令
．
令 ，
，
即 ．
又因为 ，
即当 时， ； 当 时， ．
当 时， ；当 时， ．
所以当 时， 单调递减，当 时， 单调递增
又由 ，
，
所以当 时，由零点定理可知 在 ， 内各有一个零点；
当 时，则 在 ， 内均无零点．
(5)若二次曲面的方程 ，经过正交变换化为 ，则 ．
(6)设二维随机变量 服从正态分布 ，则 =．
三、解答题：15～23小题，共94分．请将解答写在答题纸指定的位置上．解答应写出文字说明、证明过程或演算步骤．
(1)(本题满分10分)
求极限 ．
(2)(本题满分9分)
设函数 ，其中函数 具有二阶连续偏导数，函数 可导且在 处取得极值 ，求 ．
综上所述，当 时，原方程有三个根．当 时，原方程有一个根．
（4）（本题满分10分）
设奇函数 上具有2阶导数，且 证明：
（III）存在
（IV）存在 ，使得
【解析】（1）令
则 使得
（2）令 则
又由于 为奇函数，故 为偶函数，可知 ,
则 使
即 ，即
（5）（本题满分10分）
设直线L过 两点，将L绕Z轴旋转一周得到曲面 所围成的立体为 ，
又 ，从而 。
（7）设 是随机变量，且 ,
则（ ）
（A）
（B）
（C）
（D）
【答案】（A）
【解析】由 知，
，
，故 .
由根据 及概率密度的对称性知， ，故选（A）
（8）设随机变量 给定 常数c满足 ,则 （ ）
高等数学自考试题及答案
高等数学自考试题及答案自考是一种灵活的学习方式，许多人通过自考提升自己的学历和知识水平。
高等数学是自考中的一门重要课程，对于理工科和经济管理类专业的学生来说尤为重要。
为了帮助自考生更好地备考高等数学，本文将提供一些典型的高等数学自考试题及答案。
一、选择题1. 在直角坐标系中，点P(x, y)到x轴的距离为7，点P到y轴的距离为5。
则点P的坐标为：A. (7, 5)B. (5, 7)C. (-7, 5)D. (-5, 7)答案：B. (5, 7)解析：根据题意可得点P为(5, 7)。
2. 设函数f(x) = x^2 + 3x - 2，则f(-1)的值为：A. -6B. 2C. 0D. 4答案：D. 4解析：将x代入函数f(x)中，得f(-1) = (-1)^2 + 3*(-1) - 2 = 1 - 3 - 2 = 4。
二、填空题1. 设函数f(x) = 2x^3 - 5x^2 + 3x - 2，求f(1)的值。
答案： -2解析：将x = 1代入函数f(x)中，得f(1) = 2(1)^3 - 5(1)^2 + 3(1) - 2 = 2 - 5 + 3 - 2 = -2。
2. 已知曲线C的方程为y = x^2 + 2x - 3，求曲线C与x轴的交点坐标。
答案：(-3, 0)和(1, 0)解析：将y = 0代入方程中，得x^2 + 2x - 3 = 0，解方程可得x = -3和x = 1，故曲线C与x轴的交点坐标为(-3, 0)和(1, 0)。
三、计算题1. 已知函数f(x) = 2x^2 - 3x + 1，求函数f(x)的导函数f'(x)。
答案：f'(x) = 4x - 3解析：对函数f(x)进行求导，应用导数的基本公式，得到f'(x) = 4x - 3。
2. 设函数f(x) = 3x^2 - x + 2，求函数f(x)在点x = 2处的切线方程。
答案：y = 11x - 18解析：计算函数f(x)在x = 2处的导数f'(2) = 11，并代入点(2, f(2)) = (2, 11)得到切线方程y - 11 = 11(x - 2)，即y = 11x - 18。
2020年自考高等数学(工专)考试题库及答案
2020年自考高等数学（工专）考试题库及答案第一章（函数）之内容方法函数是数学中最重要的基本概念之一。
它是现实世界中量与量之间的依赖关系在数学中的反映，也是高等数学的主要研究对象。
本章主要阐明函数的概念，函数的几个简单性态，反函数，复合函数，初等函数及函数关系的建立等。
重点是函数的概念与初等函数，难点是复合函数。
1－2 函数的概念函数的定义：y=f(x)(x∈D),其中x是自变量，f为对应法则，y为因变量，D是定义域。
∀（对任意）x∈D,∃!(有唯一)y与x对应。
y所对应的取值范围称为函数的值域。
当自变量x取平面的点时，即x=(x1,x2)时，f(x)是二元函数；当x取空间中的点x=(x1,x2,x3)时，f(x)是三元函数。
函数的表示法主要有两种。
其一是解析法，即用代数式表达函数的方法。
例如y=f(x)=e x,符号函数，其中后者是分段函数。
其二是图示法。
如一元函数可表示为平面上的一条曲线，二元函数可表示为空间中的一张曲面等。
给定一个函数y=f(x)，则会求函数的定义域，值域，特殊点的函数值等是最基本的要求。
应综合考虑分母不能为0，偶次根式中的表达式应大于等于0，对数函数的真数应大于0等情形。
1－3 函数的简单性态1．单调性：称函数f(x)在区间I（含于定义域内）单调增，若∀x1,x2∈I,当x1<x2时f(x1)≤f(x2);称函数在区间I（含于定义域内）单调减，若∀x1,x2∈I,当x1<x2时f(x1)≥f(x2).单调增函数和单调减函数统称为单调函数，I称为单调区间。
判断一个函数f(x)在区间I是否为单调函数，可用单调性的定义或者用第四章中函数在I中的导数的符号。
2．奇偶性：设函数f(x)的定义域D关于原点对称。
如果∀x∈D,有f(-x)=f(x),则称f(x)为偶函数；如果∀x∈D,有f(-x) = -f(x),则称f(x)为奇函数。
判断一个函数的奇偶性时一般用定义。
在几何上，偶函数的图像关于y轴对称，而奇函数的图像关于原点对称。
高等数学(工专)自考题-4_真题(含答案与解析)-交互
高等数学(工专)自考题-4(总分100, 做题时间90分钟)第一部分选择题一、单项选择题1.设，则反函数f -1 (x)=______．SSS_SINGLE_SELA x-1B x+1C -x-1D -x+1该题您未回答:х该问题分值: 2答案:A[解析] 令，则，，所以y=f(x)=x+1，x=y-1，因此f -1 (x)=x-1.2.若级数发散，则______A．可能=0，也可能≠0B．必有=0C．一定有=∞D．一定有≠0SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 2答案:A[解析] 级数发散，则其可能为0，也可能不为0．3.当x→0时，下列函数中为x高阶无穷小的是______A．sinx B．x+x 2C．D．1-cosxSSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 2答案:D[解析]4.曲线y= 在点(0，0)处的切线______A．不存在 B．为y=C．为y=0 D．为x=0SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 2答案:D[解析] y= ，则y"= ，在(0，0)处，y"不存在，但其切线存在．即x=0为切线方程.5.当k=______时，方程组只有零解．SSS_SINGLE_SELA k=1B k=-1C k≠1，4D k=4该题您未回答:х该问题分值: 2答案:C[解析] 本题考查线性方程组的求解.由题意得系数矩阵的行列式为当k≠-1，4时，方程组只有零解.第二部分非选择题二、填空题1.=______.SSS_FILL该题您未回答:х该问题分值: 31[解析]2.设在(-∞，+∞)内连续，则a=______．SSS_FILL该题您未回答:х该问题分值: 3-1 [解析] 本题考查函数连续的定义.f(x)在(-∞，+∞)内连续，则f(x)在x=0处连续，则有所以a=-1．3.设f(x)是可导函数，，则=______．SSS_FILL该题您未回答:х该问题分值: 3[解析]4.设参数方程表示函数y=y(x)，则=______.SSS_FILL该题您未回答:х该问题分值: 3cott[解析]5.设f(x)=ln(1+x)，则f"(0)=______．SSS_FILL该题您未回答:х该问题分值: 3-1 [解析] f(x)=ln(1+x) f"(x)=f"(x)= ∴f"(0)=-1.6.函数的水平渐近线是______．SSS_FILL该题您未回答:х该问题分值: 3y=-3[解析] 由于，所以y=-3是水平渐近线.7.不定积分=______．SSS_FILL该题您未回答:х该问题分值: 3[解析] 考查抉元积分法：令，则dx=-t -2 dt∴ =∫t 2 cos2t(-t -2 )dt=-∫cos2tdt= =8.设Ф(x)= ，则Ф"(-2)=______．SSS_FILL该题您未回答:х该问题分值: 3sin(sin2) [解析] Ф(x)是一个积分下限函数，Ф"(x)=-sin(sinx)，所以Ф"(-2)=-sin(sin(-2))=sin(sin2). 9.设矩阵A= ，B= ，则A"-2B=______.SSS_FILL该题您未回答:х该问题分值: 3[解析]10.设矩阵A= ，B=A 2 -3A+2E，则B -1 =______.SSS_FILL该题您未回答:х该问题分值: 3[解析] 本题考查矩阵运算及逆矩阵的求解.∴B11 =0 B12=-2 B21=1 B22=-2 |B|=2∴三、计算题1.求极限．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 62.设，求y"．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6设y=y1 +y2,其中y1= ，y2= ．则y"=y"1+y"23.求由方程x-y+ siny=0所确定的隐函数y=y(x)的一阶导数．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6方程两边对x求导，有4.求函数y=2x 2 -lnx的单调区间和极值．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6定义域(0，+∞)令y"=0，得驻点x=当0＜x＜，y"＜0，故y在(0，)内单调减少；当＜x＜+∞，y"＞0，故y在( ，+∞)内单调增加；在x= ，y取得极小值y = +ln2．5.求不定积分∫lnxdx．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6∫lnxdx=xlnx-∫dx=xlnx-x+C．6.=1的特解．求微分方程y"=1+x+y 2 +xy 2满足初使条件y|x=0SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6=1+x+y 2 +xy 2 =(1+x)(1+y 2 )分离变量得：=(1+x)dx.又x=0，y=1，故arctan1=C.C= .∴特解为arctany= ．7.计算极限.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 68.求线性方程组的全部解．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6对增广矩阵作初等行变换，得因此，同解方程组为：其中x为自由未知量，所以方程组的全部解为3其中k为任意实数．四、综合题1.设某企业某种产品的生产量为x个单位，成本函数C(x)=54+18x+6x 2试求平均成本最小的产量水平．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6平均成本为所以x=3是平均成本g(x)的极小值点，也就是平均成本最小的产量水平，这时g(3)=54．2.求由y=e x，x≤0，y= 所围成的封闭平面图形绕x轴旋转而得旋转体体积．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6y=e x，y≤0与围成的图形为下图所示阴影部分曲线y=e x与的交点横坐标为e x = ，即因此，阴影部分绕x轴旋转的旋转体体积为1。
4月全国高等数学(工专)自考试题及答案解析
1全国2019年4月高等教育自学考试高等数学（工专）试题课程代码：00022一、单项选择题（本大题共30小题，1－20每小题1分，21－30每小题2分，共40分） 在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
（一）（每小题1分，共20分） 1．函数xx)x (f -+=11 的定义域是（ ） A ．（－∞，＋∞） B ．（0，＋∞） C ．（－1，1）D ．[)11,-2．函数3x )x (f =，则=+)y x (f （ ） A ．)y (f )x (f B ．)x (f 2 C ．)x (fD ．)y (f3．函数|x |)x (f -=2是（ ） A ．偶函数B ．非奇非偶函数C ．奇函数D ．周期函数4．=→x x x 1sin lim 20（ ）A ．1B ．∞C ．0D ．不存在 5．曲线y =sin x 在点（π，0）处的法线斜率为（ ） A ．－1B ．1C ．0D ．26．设x )x(f =1，则=')x (f （ ）A ．1B ．21xC ．－21x D ．2x7．设⎪⎩⎪⎨⎧-==ty t x 122，则=dy dx （ ）2A ．tB ．-1C ．－t1D ．－t8．函数x x y -=sin 在［0，2π］上（ ） A ．单调减少 B ．单调增加 C ．无界D ．没有最大值 9．曲线y=x 4（ ） A ．的拐点为（0，0）B ．有两个拐点C ．有一个拐点D ．没有拐点10．曲线x xy ln 2=的垂直渐近线是（ ）A ．x =0B ．x =1C ．y =0D ．y =111．=⎰)dx )x(f (d 1（ ） A ．dx )x (fB ．dx )x (f x 21-C ．dx )x(f x112-D ．dx )x(f 112．=⎰dx x x 2（ ）A ．C x +2992B ．C x +2772C ．2992xD ．2772x13．广义积分⎰+∞22ln )x (x dx（ ） A ．发散 B ．收敛于1C ．收敛于2ln 1D ．的敛散性不能判定14．过点（2，－1，2）且与直线211z y x =-=垂直的平面方程为（ ） A ．072=-+-z y x B ．02=+-z y x C ．032=+-+z y xD ．0922=-+-z y x15．设)y x (e )y ,x (f x +=arctg ，则='),(f y 10（ ） A ．0B ．13216．区域（σ）由抛物线2x y =与直线x y =围成，函数)y ,x (f 在（σ）上连续，二重积分⎰⎰)(d )y ,x (f σσ化为累次积分应为（ ） A ．⎰⎰102xx dydx )y ,x (f B ．⎰⎰102x x dydx )y ,x (fC ．⎰⎰101dydx )y ,x (fD ．⎰⎰xx dydx )y ,x (f 2117．空间区域（V ）由抛物面22y x z +=与平面z =1围成，三重积分⎰⎰⎰++)V (dV )z y x(222可化为累次积分（ ） A ．⎰⎰⎰+πρθρρ20101222d dzd )z (B ．⎰⎰⎰+πρθρρρ20101222d dzd )z ( C ．⎰⎰⎰+πθρρρ20101022d dzd )z (D ．⎰⎰⎰+πρθρρρ20101222d dzd )z (18．微分方程023=+'-''y y y 的通解为（ ） A ．x x e C e C y 221+= B ．x x e C e C y 221+=- C ．x x e C e C y -+=221D ．x x e C e C y --+=22119．级数∑∞=++-111n n nn )(（ ） A ．绝对收敛 B ．发散C ．收敛D ．的部分和S n 无界20．幂级数∑∞=-01n n nnx )(的收敛半径为（ ）A ．R ＝0B ．R ＝1C ．R ＝2D ．R ＝＋∞（二）（每小题2分，共20分）21．=⎥⎦⎤⎢⎣⎡+-++⨯+⨯+⨯+∞→)n )(n (15451161111161611lim n Λ（ ） A ．1 B ．6145422．设⎪⎩⎪⎨⎧>-=<=010001x ,x ,,x ,)x (f ，则x =0为)x (f 的（ ）A ．连续点B ．无穷间断点C ．可去间断点D ．跳跃间断点23．设)x (y +=1ln ，则=)(y )(09（ ） A ．8！B ．－9！C ．－8！D ．9！24．⎰=-dx x 112（ ） A ．|x |1ln 2-B ．C |x |+-1ln 2C ．|x x |11ln 21-+D ．C |x x |++-11ln 2125．=⎰→2x sin lim x tdt x （ ）A ．∞B ．0C ．21D ．126．直线521221+=-+=-z y x 与平面034=-+z y x 的关系是（ ） A ．直线与平面垂直B ．直线在平面上C ．直线与平面无公共点D ．直线与平面相交于一点27．设y x z 2=，则=dz （ ） A ．xdy x dx x y y y ln 22212+•- B ．dy x dx x y y y 21222+•- C ．dy x dx x y y 222+D ．dy x dx x y y 22+28．设区域（σ）为42π≤22y x +≤2π，则⎰⎰++)(d yx y x σσ2222cos ＝（ ）A ．0B ．π2C ．－π2D ．π3529．微分方程xy y dx dy +=62是（ ） A ．一阶线性齐次方程 B ．一阶线性非齐次方程 C ．二阶线性微分方程D ．六阶线性微分方程30．级数∑∞=12sinn nπ（ ）A ．发散B ．的部分和n S 无界C ．是交错级数D ．收敛二、计算题（本大题共7小题，每小题6分，共42分）31．求2301cos lim /x x x -+→． 32．设⎪⎩⎪⎨⎧=≠=0001sin 2x x ,xx )x (f ， ，求)x (f '． 33．求） （022>++⎰a dx xa x a ．34．计算⎰1xarctgxdx ．35．求方程 011=+-+xydy y xdx满足10=)(y 的特解． 36．计算⎰⎰)(d xy σσ3，其中（σ）是由直线x y ,y ==2及y 轴围成的三角区域．37．判别级数∑∞=12n nn n!n 的敛散性．三、应用和证明题（本大题共3小题，每小题6分，共18分） 38．求心形线)a ()cos (a 01>-= θρ所围成的平面图形的面积． 39．求函数y x y xy x )y ,x (f --+-=22的极值． 40．证明：当x >0时，e x >1+x ．。
高等数学一自考题分类模拟题2020年(4)_真题(含答案与解析)-交互
高等数学一自考题分类模拟题2020年(4)(总分100, 做题时间90分钟)一、单项选择题1.计算______．•**•**C.-2**SSS_SIMPLE_SINA B C D分值: 2答案:D先用换元法，令，则x=t2，dx=2tdt．当x=0时，t=0；当x=1时，t=1．于是再用分部积分法，得换元法与分部积分法的结合使用是求积分的常用方法．2.______．A．B．C．D．SSS_SIMPLE_SINA B C D分值: 2答案:A定积分与不定积分计算首先要掌握其基本公式，然后根据换元法和分部积分法来进行计算．3.设[lnf(x)]'=sec2x，则f(x)=______．• A.-k·e tan x•**·etan xC.-k** xSSS_SIMPLE_SINA B C D分值: 2答案:B[lnf(x)]'=sec2x，得lnf(x)是sec2x的一个原函数．因为∫sec2xdx=tan x+C，所以lnf(x)=tan x+C，f(x)=e tan x+C=e C·e tan x=k·e tan x．充分理解原函数的定义，以及清楚掌握原函数与积分之间的关系是本题的宗旨．4.______．A．B．C．πD．-πSSS_SIMPLE_SINA B C D分值: 2答案:A熟练掌握定积分基本公式．5.方程的通解为______．A．B．C．D．SSS_SIMPLE_SINA B C D分值: 2答案:C，则原方程的解为首先判断所求微分方程的类型是很重要的．通常将y视为函数，x视为自变量，按可分离变量、一阶线性方程的解法来求解．6.两条抛物线y2=x，y=x2所围成图形的面积为______．A．B．C．D．1SSS_SIMPLE_SINA B C D分值: 2答案:A作两条抛物线的图形，如下图所示，得两组解即两抛物线交点为(0，0)，(1，1)．法一(公式法)：法二(元素法)：取x为积分变量，区间[0，1]上的任一小区间[x，x+dx]，其面积近似于高为，底为dx的窄曲边梯形面积．这样就得到面积元素于是，所求图形面积为定积分用作图法直观找到答案．二、填空题1.若______．SSS_FILL分值: 2答案:熟练掌握定积分的基本性质．2.______．SSS_FILL分值: 2答案: 0令，因为f(-x)=-f(x)，所以该函数是奇函数，因此熟练掌握函数的奇偶性与定积分之间的关系．3.若则a=______．SSS_FILL分值: 2答案:-1，可得a=-1．熟练掌握牛顿-莱布尼茨公式，并能运用此公式解题．4.若______．SSS_FILL分值: 2答案:8定积分与不定积分的换元法解题是求积分中最重要的方法之一．用换元法求不定积分技巧性比较强，需要有一定的观察能力和感觉．一般来说，带根号的就应想办法(用三角代换)去掉根号．三、计算题(一)1.求不定积分SSS_TEXT_QUSTI分值: 5答案:当n≠-1时，熟记常用的积分．2.SSS_TEXT_QUSTI分值: 5答案:不定积分性质的应用．3.已知∫f(x)dx=2x+x+C，求f(x)．SSS_TEXT_QUSTI分值: 5答案:两边对x求导，(∫f(x)dx)'=(2x+x+C)'，故f(x)=2x ln 2+1．对积分两边求导也是解题的一种技巧．4.SSS_TEXT_QUSTI分值: 5答案:法一：设x=2tan t，则，故在此题中应用倒代换来进行计算更为方便快捷．四、计算题(二)1.已知f(x)的原函数之一为sin 3x，求∫f'(x)dx．SSS_TEXT_QUSTI分值: 5答案:由sin 3x是f(x)的原函数之一，得(sin 3x)'=f(x)，所以f(x)=3cos 3x．∫f'(x)dx=f(x)+C=3cos 3x+C．熟练掌握原函数与积分学之间的关系，并能活用．2.计算SSS_TEXT_QUSTI分值: 5答案:三角函数的积分计算要掌握其基本计算公式，切不可盲目计算．3.且f(2)=15，求f(x)．SSS_TEXT_QUSTI分值: 5答案:由f(x)为原函数，故必连续，即f(0+)=f(0)=C1=f(0-)=C2．由f(2)=22+3×2+C1=15，得C1=5，故由原函数来判断函数的连续性是此题的重点．4.设f(x)在(-∞，+∞)上连续，且是周期为T的函数，证明：SSS_TEXT_QUSTI分值: 5答案:[证明] 因为令x=t+T，则所以所以连续周期函数在一个长度为一个周期的区间上积分是定值．五、综合题1.求由椭圆绕x轴旋转一周而成的旋转体(称旋转椭球体)的体积．SSS_TEXT_QUSTI分值: 5答案:旋转椭球体可看做是由上半个椭圆及x轴围成的图形绕x轴旋转而成的旋转体．如下图所示．取x为积分变量，积分区间为[-a，a]，于是，旋转椭球体的体积利用积分求平面图形的面积或体积是积分学在实际生活中的广泛应用．旋转体的体积公式是需要牢记的．2.实验得出，在给定时刻t，镭的衰变速率(质量减少的即时速度)与镭的现存量M=M(t)成正比．又当t=0时，M=M，求镭的存量与时间t的函数关系．SSS_TEXT_QUSTI分值: 5答案:依题意，有，k＞0，并满足初始条件该方程是可分离变量的，分离变量后得两边积分，得ln M=-kt+ln C，即M=Ce-kt．将初始条件M|t=0=M代入上式，得C=M，故镭的衰变规律可表示为M=Me-kt．分离变量方程的初值问题．3.求微分方程(y2-6x)y'+2y=0满足初始条件y|x=2=1的特解．SSS_TEXT_QUSTI分值: 5答案:这个方程不是未知函数y与y'的线性方程，但是可以将它变形为若将x视为y的函数，则对于x(y)及其导数而言，上述方程是一个线性方程，由通解公式得将当x=2时，y=1代入，得因此，所求特解为熟练掌握线性方程的通解公式，并能活用．4.求解微分方程SSS_TEXT_QUSTI分值: 5答案:原微分方程可以分离变量，分离变量后得两边积分解得ln |y|=x2+C1，即|y|=e x2+C1=e C1·e x2，整理得y=±e C1·e x2，因为±e C1仍是任意常数，把它记为C，便得原方程的通解为y=Ce x2．可分离变量的微分方程的通用解题方法是对方程两边进行积分．5.估计定积分的值．SSS_TEXT_QUSTI分值: 5答案:因为当x∈[0，π]时，0≤sin x≤1，所以由此有于是由估值定理有熟练应用估值定理．6.比较定积分的大小．SSS_TEXT_QUSTI分值: 5答案:令f(x)=e x-x，x∈[-2，0]．因为：f'(x)=e x-1＜0，x∈(-2，0)，所以f(x)在[-2，0]单调递减，故在[-2，0]上，f(x)≥f(0)=1＞0，即f(x)＞0．由性质4，有故判断函数的单调性是此题的基础．7.SSS_TEXT_QUSTI分值: 5答案:设所以f"(x)=g'(x)=ln(1+x2)．熟练掌握积分与微分的关系和计算方法．8.利用定积分求极限：SSS_TEXT_QUSTI分值: 5答案:把此极限式化为某个积分和的极限式，并转化为计算定积分．为此作如下变形：不难看出，其中的和式是函数在区间[0，1]上的一个积分和(这里所取的是等分分割，所以这类问题的解题思想是要把所求的极限转化为某个函数f(x)在某区间[a，b]上的积分和的极限，然后利用牛顿-莱布尼茨公式计算的值．1。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
全国2019年4月高等教育自学考试普通逻辑试题课程代码：00024一、单项选择题（本大题共15小题，每小题1分，共15分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.“p∧q→r”与“p∨q←r”这两个逻辑式子中，它们（）A.变项和逻辑常项相同B.变项不同但逻辑常项相同C.逻辑常项不同但变项相同D.变项和逻辑常项都不同2.对于A、B两概念，如果所有a都是b并且有b不是a，那么，A、B两概念具有（）A.全同关系B.真包含于关系C.交叉关系D.全异关系3.□p与□┐p之间关系是（）A.反对关系B.矛盾关系C.差等关系D.下反对关系4.一个相容选言判断p∨q假，那么，一定为（）A.p真q真B.p真q假C.p假q真D.p假q假5.判断间的反对关系，应是（）关系。
A.对称且传递B.对称且非传递C.非对称且反传递D.非对称且传递6.有学生在上课时间去看电影，老师批评时，学生反问：“看革命题材电影不是好事吗？”学生的说法（）A.违反同一律B.违反矛盾律C.违反排中律D.不违反普通逻辑的基本规律7.直接推理“SEP→PA S”，属于（）推理。
A.换质法B.换位法C.换质位法D.换位质法8.“（p→q）∧（r→s）∧(┐q∨┐s)→(┐p∨┐r)”，这一推理式是（）A.二难推理的简单构成法B.二难推理的简单破坏式C.二难推理的复杂构成式D.二难推理的复杂破坏式9.“因为aRb并且bRc，所以，a R c”,这一推理式是（）A.对称关系推理B.反对称关系推理C.传递关系推理D.反传递关系推理10.反证法是先论证与原论题相矛盾的论断为假，然后根据（）确定原论题真的论证方法。
A.同一律B.矛盾律1C.排中律D.充足理由律11.一国丧失过量的表土，需进口更多的粮食，这就增加了其他国家土壤的压力；一国大气污染，导致邻国受到酸雨的危害；二氧化碳过度排放，造成全球变暖，海平面上升，几乎可以危及所有的国家和地区。
下述（）最能概括上文的主观观点。
A.环境污染已影响到国与国之间的关系，可能引起国际争端B.经济的快速发展必然会导致环境污染的加剧，先污染后治理是一条规律C.在治理污染方面，发达国家应该承担更多的责任和义务D.环境污染问题已经成为区域性、国际性的问题，解决环境污染问题是人类面临的共同任务12.某家饭店中，一桌人在边就餐边谈生意。
其中，1个是哈尔滨人，2个是北方人，1个是广东人，2个人只做电脑生意，3个人只做服装生意。
如果以上介绍涉及餐桌上所有的人，那么下列关于这一桌人数（）的说法是正确的。
A.最少可能是3人，最多可能是8人B.最少可能是5人，最多可能是8人C.最少可能是5人，最多可能是9人D.无法确定13.小李和小张就广告问题争论得面红耳赤，没完没了。
小李说：广告进了百姓门，带来方便送福音。
小张说：广告就会吹，真假难区分。
以下（）对小张的论点提供了最有力的支持。
A.某教师受慢性萎缩性胃炎折磨多年，从电视广告中找到了良药B.电视广告对于不愿意看的观众是一种浪费C.街头的招牌广告被风吹倒，造成人身伤亡，应该引以为戒D.64%的保健品凭着广告走进了市场。
在一次抽样调查中，仅有2%具有所说的效果14.经过对最近十年的统计资料分析，大连市因癌症死亡的人数比例比全国城市的平均值要高两倍。
而在历史上大连市一直是癌症特别是肺癌的低发地区。
看来，大连最近这十年对癌症的防治出现了失误。
以下（）如果为真，最能削弱上述论断。
A.大连的气候和环境适合疗养，外地癌症病人在大连走过了最后一段人生之路B.大连最近几年医疗保健的投入连年上升，医疗设施有了极大的改善C.大连医学院在以中医理论探讨癌症机理方面取得了突破性的进展D.尽管癌症的死亡率上升，但大连的肺结核死亡率几乎降到了零15.如今的音像市场上，正版的激光唱盘和影视盘的销售不如盗版的，盗版的屡禁不绝，销售非常火爆。
有的分析人员认为，这主要是因为价格上盗版盘更有优势，所以在市场上更有活力。
以下（）是这位分析人员在分析中隐含的假定。
A.正版的往往内容呆板，不适应市场的需要B.与价格的差别相比，正版盗版质量差别不大C.盗版的比正版的进货渠道畅通D.正版的不如盗版的销售网络完善二、双项选择题(本大题共10小题，每小题2分，共20分)在每小题列出的五个备选项中有二个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选、少选或未选均无分。
16.当S与P具有关系或关系时，SAP和SEP都假。
（）2A.全同B.S真包含于PC.S真包含PD.交叉E.全异17.在性质判断中，判断和判断的主项周延，谓项不周延。
（）A.全称肯定B.全称否定C.特称肯定D.单称肯定E.单称否定18.“有的大学生是运动员”和“有的大学生不是运动员”，这两个性质判断（）A.不能同真，可以同假B.不能同假，可以同真C.既不能同真，也不能同假D.可以同真，可以同假E.至少有一真，可以同真19.要使一个充分必要条件假言判断p↔q真，那么（）A.p真q真B.p真q假C.p假q真D.p假q假E.p与q不等值20.以MAP为大前提，再增补或为小前提，可有效推出结论SIP。
（）A.SEMB.SAMC.SIMD.MESE.SOM21.判断“┐p∨q”的负判断的等值判断是（）A.p∨┐qB.┐p∨qC.p∧┐qD.┐(q→p)E.┐(p→q)22.若□p真，则必假。
（）A.□┐pB.◇pC.◇┐pD.pE.□p23.不完全归纳推理不是和的推理。
（）A.或然性B.特殊到一般C.前提不蕴涵结论D.必然性E.前提蕴涵结论24.以“p∧q→r”和“┐r”为前提，能有效推出结论或。
（）A.p∧qB.p∨qC.┐p∨┐qD.p→┐qE.┐p→q25.在下列各推理式中，无效推理式为（）A.（p→q）∧┐q→┐pB.（p∨q）∧p→┐qC.（p∨&q）∧p→┐qD.（┐p→┐q）∧┐q→┐pE.（p←q）∧q→p三、填空题（本大题共10小题，每小题1分，共10分）请在每小题的空格中填上正确答案。
错填、不填均无分。
26.普通逻辑是研究思维的___________及其基本规律和简单逻辑方法的科学。
327.如果概念A___________概念B，则概念A为种概念，概念B为属概念。
28.简单判断就是自身中___________的判断。
29.一个充分条件假言判断“p→q”是假的，当且仅当___________。
30.既肯定SAP，又肯定同素材的SEP，这就违反了逻辑上的___________律。
31.一个正确推理必须___________和前提真实。
32.必要条件假言推理有肯定后件式和___________。
33.完全归纳推理是___________性推理。
34.从思维进程来看，类比推理是___________的推理。
35.间接证明有反证法和___________。
四、图表题（本大题共2小题，第36小题4分，第37小题6分，共10分）36.请用欧拉图表示下列概念之间的关系。
A.中国B.黄山C.长城D.旅游胜地37.试用真值表判定下列A、B两个判断是否为矛盾关系。
A：王华要么报考南京大学，要么报考东南大学。
B：王华既不报考南京大学，又不报考东南大学。
设：p表示“王华报考南京大学”，q表示“王华报考东南大学”。
五、分析题（本大题共5小题，每小题5分，共25分）38.（1）“矛盾是旧形式与新内容之间的斗争。
”该句作为定义是否正确？请说明理由。
（2）“微机可分为台式微机、便携式微机、办公用微机和家用微机。
”该句作为划分是否正确？请说明理由。
39.（1）请将“没有一个自学成才者不是经过刻苦努力的”换质位，写出换质位的公式和换质位后的结论。
（2）找出能反驳“所有的被告都是有罪的”的判断，并指出为什么能反驳。
40.写出下列三段论的推理式，指出其格与式，并根据三段论规则说明其是否有效。
“并非所有细菌都有毒；并非所有生物都是细菌；所以，并非所有生物都有毒。
”41.“为了证实吸烟与肺癌的关系，美国弗来明心脏研究中心进行了大量的调查研究。
统计资料显示：每多吸一支烟，肺癌的发病率就上升一倍。
如果一个人每天吸两包烟，那么这个人比不吸烟的人得肺癌的几率高20倍。
可见，吸烟与肺癌的发病有一定的因果关系。
”分析此例运用了何种探求因果联系的方法，说明理由并写出该逻辑方法的公式。
42.“作品愈高，知人愈少”，这是错误的。
因为，倘若作品愈高，知人愈少，那么，推论起来，谁也不懂的东西，就是世界上的绝作了。
分析此例，指出被反驳的论题，用来反驳的论据和反驳所使用的逻辑方法，并分析反驳得是否正确。
六、证明题（本大题共2小题，每小题4分，共8分）443.两个肯定前提必得肯定结论。
44.大前提为I判断，小前提为E判断，不能构成一个有效的三段论。
七、综合题（本大题共2小题，每小题6分，共12分）45.上海某宾馆来了A、B、C三位客人，现已知：①如果A和B都来自北京，那么C就来自昆明；②并非C来自杭州或昆明；③只有B来自北京，C才不是来自杭州。
请问：A是否来自北京？写出推导过程。
（设：A表示“A来自北京”，B表示“B来自北京”，C1表示“C来自昆明”，C2表示“C 来自杭州”）46.某市发生一个抢劫杀人案，经初步侦察，犯罪嫌疑人为A、B、C。
现已知：①如果A无罪或B有罪，那么，C有罪；②只有A有罪，C才有罪。
请问：A是否有罪？写出推导过程。
（设：A表示“A有罪”，A表示“A无罪”，其它类同）5。