自考 高等数学(工本)公式大全
专升本高数公式大全

专升本高数公式大全1.二次函数的图像方程:f(x)=a(x-h)²+k2.平面直角坐标方程:Ax+By+C=03.二次曲线方程:Ax² + By² + Cxy + Dx + Ey + F = 04.圆的标准方程:(x-a)²+(y-b)²=r²5.椭圆的标准方程:(x-a)²/b²+(y-b)²/a²=16.双曲线的标准方程:(x-a)²/b²-(y-b)²/a²=17.抛物线的标准方程:(x-a)²=4p(y-b)8.三角函数的正余弦和差公式:(1) sin(A ± B)= sinAcosB ± cosAsinB(2) cos(A ± B) = cosAcosB ∓ sinAsinB(3) tan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)9.三角函数的倍角公式:(1) sin2A = 2sinAcosA(2) cos2A = cos²A - sin²A(3) tan2A = (2tanA) / (1 - tan²A)10.三角函数的半角公式:(1) sin(A/2) = ±√[(1 - cosA) / 2](2) c os(A/2) = ±√[(1 + cosA) / 2](3) tan(A/2) = ±√[(1 - cosA) / (1 + cosA)]注:±的选取根据A的象限确定。
11.三角方程的化简公式:(1) sin²x + cos²x = 1(2) 1 + tan²x = sec²x(3) 1 + cot²x = csc²x12.导数的基本公式:(1) (cf(x))' = cf'(x)(2)(f(x)±g(x))'=f'(x)±g'(x)(3)(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)(4)(f(x)/g(x))'=[f'(x)g(x)-f(x)g'(x)]/[g(x)]²(5)(f(g(x)))'=f'(g(x))g'(x)(6)(f(x)⋅g(x)⋅h(x))'=f'(x)g(x)h(x)+f(x)g'(x)h(x)+f(x)g(x)h'( x)13.微分的基本公式:(1) dy = f'(x)dx(2) dy = dx/g'(y)(3) dy = p(x)dx + q(x)dx² + r(x)f'(x)14.积分的基本公式:(1) ∫cf(x)dx = c∫f(x)dx(2) ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx(3) ∫f'(x)dx = f(x) + C(4) ∫f'(g(x))g'(x)dx = f(g(x)) + C15.牛顿-莱布尼兹公式:∫[a, b]f(x)dx = F(b) - F(a)注:其中F(x)为f(x)的一个原函数。
自考高等数学全部公式

自考高等数学全部公式为了简化回答,我将提供一些常用的高等数学公式。
由于高等数学的内容非常广泛,无法一一列举所有的公式。
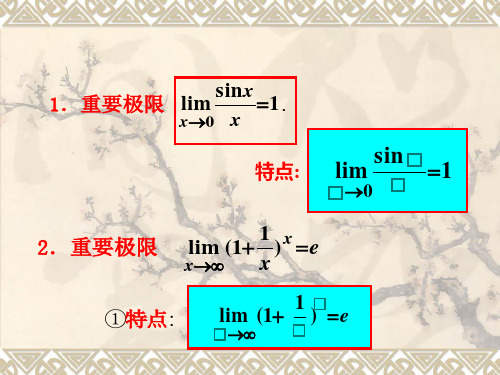
以下是一些常见的高等数学公式分类,并附上一些例子:1.极限公式:- 孙子定理:$\lim_{x \to 0} \frac{\sin x}{x} = 1$- 自然对数的极限:$\lim_{x \to \infty} (1 + \frac{1}{x})^x = e$2.导数公式:-基本导数公式:- $\frac{d}{dx} (a) = 0$ 其中 a 是常数- $\frac{d}{dx} (x^n) = nx^{n-1}$ 其中 n 是常数- $\frac{d}{dx} (e^x) = e^{x}$- $\frac{d}{dx} (\ln x) = \frac{1}{x}$-导数的四则运算规则:- $\frac{d}{dx} (u + v) = \frac{du}{dx} + \frac{dv}{dx}$- $\frac{d}{dx} (uv) = u\frac{dv}{dx}+v\frac{du}{dx}$- $\frac{d}{dx} (\frac{u}{v})= \frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}$- 链式法则:$\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}$3.积分公式:-不定积分公式:- $\int (a) dx = ax + C$ 其中 a 是常数,C 是常数- $\int (x^n) dx = \frac{x^{n+1}}{n+1} + C$ 其中 n 是非零常数,C 是常数- $\int (e^x) dx = e^x + C$ 其中 C 是常数- $\int \frac{1}{x} dx = \ln ,x, + C$ 其中 C 是常数-定积分公式:- $\int_{a}^{b} f(x) dx = F(b) - F(a)$ 其中 F(x) 是 f(x) 的原函数4.级数公式:-等比数列的和:$\sum_{n=0}^{\infty} ar^n = \frac{a}{1-r}$ 其中 a 是首项,r 是公比- 幂级数:$\sum_{n=0}^{\infty} c_n(x-a)^n$ 其中 $c_n$ 是常数系数,a 是中心点5.微分方程公式:- 一阶线性常微分方程:$\frac{dy}{dx} + p(x)y = q(x)$- 二阶齐次线性常微分方程:$\frac{d^2 y}{dx^2} +p(x)\frac{dy}{dx} + q(x)y=0$以上只是高等数学中的一小部分公式,还有很多其他公式如三角函数的和差化积、积化和差等。
专升本高等数学公式定理大全

专升本高等数学公式定理大全一、导数相关公式和定理:1.基本导数公式:-常数函数导数为零:(k)'=0-幂函数导数:(x^n)'=n*x^(n-1)- 指数函数导数:(a^x)' = a^x * ln(a)- 对数函数导数:(log_a(x))' = 1 / (x * ln(a)) 2.常用导数公式:- sin(x)' = cos(x)- cos(x)' = -sin(x)- tan(x)' = sec^2(x)- cot(x)' = -csc^2(x)- sec(x)' = sec(x) * tan(x)- csc(x)' = -csc(x) * cot(x)- arcsin(x)' = 1 / sqrt(1 - x^2)- arccos(x)' = -1 / sqrt(1 - x^2)- arctan(x)' = 1 / (1 + x^2)3.高阶导数公式:-(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)-(f(g(x)))'=f'(g(x))*g'(x)-(f(x)/g(x))'=(f'(x)g(x)-f(x)g'(x))/g^2(x)4.微分中值定理:-罗尔定理:若函数在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),则存在c∈(a,b),使得f'(c)=0。
-拉格朗日定理:若函数在[a,b]上连续,在(a,b)内可导,那么存在c∈(a,b),使得[f(b)-f(a)]/[b-a]=f'(c)。
-柯西中值定理:若函数u(x)和v(x)在[a,b]上连续,在(a,b)内可导,并且v'(x)≠0,那么存在c∈(a,b),使得[u(b)-u(a)]/[v(b)-v(a)]=u'(c)/v'(c)。
专升本数学常用公式

专升本数学常用公式一、代数公式1.二次方程求根公式:对于一元二次方程ax^2 + bx + c = 0:若b^2-4ac > 0,方程有两个不相等的实根;若b^2-4ac = 0,方程有两个相等的实根;若b^2-4ac < 0,方程没有实根;方程的解公式为:x = (-b ± √(b^2-4ac))/(2a)。
2.幂函数的性质:a^m*a^n=a^(m+n)(a^m)^n = a^(mn)a^0=1(a≠0)a^-m=1/(a^m)(a≠0)a^m * b^m = (ab)^m(a/b)^m=a^m/b^m(b≠0)3.对数函数的性质:loga(xy) = logax + logayloga(x/y) = logax - logayloga(x^n) = nlogaxloga1 = 0logaa = 1loga(a^m) = m4.指数函数的性质:a^x*a^y=a^(x+y)(a^x)^y = a^(xy)(a/b)^x=a^x/b^x(ab)^x = a^x * b^xa^x/a^y=a^(x-y)二、几何公式1.三角函数的定义:在直角三角形中,设角A的对边、邻边、斜边分别为a,b,c,定义如下:sinA = a/ccosA = b/ctanA = a/bcotA = b/asecA = c/bcscA = c/a2.三角函数的基本关系:sin^2A + cos^2A = 1tanA = sinA / cosAcotA = 1 / tanAtanA * cotA = 13.勾股定理:直角三角形中,设边长分别为a,b,c,c是斜边,则有:c^2=a^2+b^24.三角形的面积公式:设三角形的底边为b,高为h,则有:三角形面积=(1/2)*b*h5.三角形的海伦公式:设三角形的三边长分别为a,b,c,半周长为s,则有:三角形面积=√(s(s-a)(s-b)(s-c))6.圆的面积和周长:设圆的半径为r,则有:圆的面积=πr^2圆的周长=2πr三、微积分公式1.导数的基本性质:f'(x) = lim(h→0) (f(x+h) - f(x))/hd/dx (c) = 0 (c为常数)d/dx (x^n) = nx^(n-1)d/dx (sinx) = cosxd/dx (cosx) = -sinxd/dx (tanx) = sec^2xd/dx (cotx) = -csc^2xd/dx (e^x) = e^xd/dx (logax) = 1/(xloga)d/dx (lnx) = 1/x2.积分的基本性质:∫ (c)dx = cx + C (c为常数)∫ (x^n)dx = (1/(n+1))x^(n+1) + C (n≠-1)∫ (sinx)dx = -cosx + C∫ (cosx)dx = sinx + C∫ (sec^2x)dx = tanx + C∫ (csc^2x)dx = -cotx + C∫ (e^x)dx = e^x + C∫ (1/x)dx = ln,x, + C四、概率与统计公式1.事件的概率计算公式:设A为事件,P(A)表示事件A发生的概率,则有:P(A)=n(A)/n(S)其中,n(A)为事件A的样本点数,n(S)为样本空间的样本点数。
成人高考专升本高等数学公式大全

成人高考专升本高等数学公式大全1.代数基本公式:-平方差公式:$a^2-b^2=(a+b)(a-b)$-三角恒等式:- 正弦定理:$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$- 余弦定理:$c^2 = a^2 + b^2 - 2ab\cos C$- 正弦余弦定理:$\sin^2 A + \cos^2 A = 1$- 二项式定理:$(a + b)^n = \sum_{k=0}^{n}\binom{n}{k}a^{n-k}b^k$2.函数与极限公式:-导数的四则运算:- $(u \pm v)' = u' \pm v'$- $(uv)' = u'v + uv'$- $\left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2}$- 泰勒公式:$f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)(x - a)^2}{2!} + \cdots$-常用极限:- $\lim_{x \to 0}\frac{\sin x}{x} = 1$- $\lim_{x \to \infty}(1 + \frac{1}{x})^x = e$- $\lim_{x \to \infty}(1 + \frac{k}{x})^x = e^k$- $\lim_{n \to \infty}(1 + \frac{x}{n})^n = e^x$3.微分公式:-求导法则:-$(c)'=0$- $(x^n)' = nx^{n-1}$-$(e^x)'=e^x$- $(\ln x)' = \frac{1}{x}$-高阶导数:-$(f(x)g(x))''=f''(x)g(x)+2f'(x)g'(x)+f(x)g''(x)$-$(f(g(x)))''=f''(g(x))(g'(x))^2+f'(g(x))g''(x)$-微分运算法则:- $\frac{d(u \pm v)}{dx} = \frac{du}{dx} \pm \frac{dv}{dx}$ - $\frac{d(kv)}{dx} = k\frac{dv}{dx}$- $\frac{d(uv)}{dx} = u\frac{dv}{dx} + v\frac{du}{dx}$- $\frac{d(\frac{u}{v})}{dx} = \frac{v\frac{du}{dx} -u\frac{dv}{dx}}{v^2}$4.积分公式:-不定积分法则:- $\int k \,dx = kx + C$- $\int x^n \,dx = \frac{x^{n+1}}{n+1} + C, (n \neq -1)$- $\int e^x \,dx = e^x + C$- $\int \frac{1}{x} \,dx = \ln ,x, + C$-定积分法则:- $\int_a^b kf(x) \,dx = k\int_a^b f(x) \,dx$- $\int_a^b [f(x) + g(x)] \,dx = \int_a^b f(x) \,dx +\int_a^b g(x) \,dx$- $\int_a^b (f(x) - g(x)) \,dx = \int_a^b f(x) \,dx -\int_a^b g(x) \,dx$5.级数公式:-等比级数求和:$S_n = \frac{a(1-q^n)}{1-q}$,其中 $S_n$ 是前n 项和,a 是首项,q 是公比。
高等数学专升本公式集合

高等数学专升本公式集合摘要:一、高等数学专升本公式集合概述二、高等数学中的基本初等函数公式三、高等数学中的极限与导数公式四、高等数学中的积分与级数公式五、高等数学中的向量与矩阵公式六、高等数学中的多元函数微分法与积分公式正文:一、高等数学专升本公式集合概述高等数学专升本公式集合,是针对专升本高等数学学科的公式整理,主要包括初等函数、极限与导数、积分与级数、向量与矩阵、多元函数微分法与积分等方面的公式。
掌握这些公式对于学习高等数学课程有着至关重要的作用,可以帮助学生更好地理解高等数学的基本概念和方法,为解决实际问题提供有力工具。
二、高等数学中的基本初等函数公式高等数学中的基本初等函数包括幂函数、指数函数、对数函数、三角函数等。
这些函数在高等数学中有着广泛的应用,是学习高等数学的基础。
具体公式如下:1.幂函数:y = x^n(n 为实数)2.指数函数:y = a^x(a > 0 且a ≠ 1,x 为实数)3.对数函数:y = log_a(x)(a > 0 且a ≠ 1,x > 0)4.三角函数:y = sinx、y = cosx、y = tanx(x 为实数)三、高等数学中的极限与导数公式极限与导数是高等数学中的基本概念,其中导数是函数在某一点的切线斜率,极限是函数在某一点的邻域内的平均变化率。
具体公式如下:1.极限:lim(x->a) [f(x) - f(a)] / (x - a)(a 为实数)2.导数:f"(x) = lim(h->0) [f(x + h) - f(x)] / h(x 为实数)四、高等数学中的积分与级数公式积分与级数是高等数学中的基本运算,其中积分是求解函数在某一区间内的累积和,级数是求解无穷数列的和。
具体公式如下:1.不定积分:∫[f(x)] dx = F(x) + C(C 为常数)2.定积分:∫[f(x)] dx(a ≤ x ≤ b)= F(b) - F(a)(b、a 为实数)3.级数:Σ[a_n](n 从1 至∞) = a(a 为实数)五、高等数学中的向量与矩阵公式向量与矩阵是高等数学中的基本工具,其中向量是具有大小和方向的量,矩阵是具有特定行和列的量。
自考高等数学全部公式
变限求导公式
(1) [ f (t )dt ] f ( x) ;
a x
(2) [
b x
f (t )dt ] f ( x) ;
(3) [
(4) [
(5) [
(x)
a b
f (t )dt ] f [ ( x )] ( x ) ;
g( x)
f ( t )dt ] f [ g( x )] g( x ) ;
自由项 f ( x )
e x pm ( x )
方程 y ay by f ( x ) 的特解 y
(1) 不是特征根
(2) 是单特征根
y Qm ( x )e x
y x Qm ( x )e x
y x 2 Qm ( x )e x
(3) 是二重特征根
(1) α iβ 不是特征根
e
x
y ex [Ql ( x )cosx Rl ( x )sinx ]
y xex [Ql ( x )cosx
[ Pm ( x )cos x
Pn ( x )sin x ]
(2) α iβ 是特征根
Rl ( x )sinx] 其中lmax{ ,n} m
f ( x0 x ) f ( x0 ) f ( x ) f ( x0 ) y f ( x ) lim lim lim x 0 x x 0 x x0 x x x0
基本初等函数和常数的求导公式
(1)(c ) 0 ;
(2) ( x ) x 1 ;
1 1 x2 dx arcsinx C ;
(4)d(arctanx )
1 1 x 1
2
dx;
(5)d(arcsinx )
专升本高等数学公式全集

专升本高等数学公式全集在高等数学中,有许多重要的公式需要掌握。
下面是一些常用的高等数学公式全集:1.点与直线公式:1)点到直线的距离公式:设直线方程为Ax+By+C=0,点P(x0,y0)为直线外一点,则点P到直线的距离为d=,Ax0+By0+C,/√(A^2+B^2)。
2)点到直线的垂足坐标公式:设直线方程为Ax+By+C=0,点P(x0,y0)为直线外一点,点Q(x1,y1)为点P到直线的垂足,则x1=(B^2*x0-A*B*y0-A*C)/(A^2+B^2),y1=(-A*B*x0+A^2*y0-B*C)/(A^2+B^2)。
2.导数的四则运算:1)和差法则:(f+g)'=f'+g',(f-g)'=f'-g'。
2)积法则:(f*g)'=f'*g+f*g'。
3)商法则:(f/g)'=(f'*g-f*g')/g^24)复合函数法则:(f(g(x)))'=f'(g(x))*g'(x)。
3.不定积分的基本公式:1)幂函数不定积分公式:∫x^n dx = (x^(n+1)) / (n+1) + C,其中n不等于-12)指数函数不定积分公式:∫a^x dx = (a^x) / ln(a) + C,其中a为常数且a不等于13)三角函数不定积分公式:∫sin x dx = -cos x + C,∫cos x dx = sin x + C,∫sec^2 x dx = tan x + C。
4.定积分的基本公式:1)定积分的基本公式:∫[a, b]f(x) dx = F(b) - F(a),其中F(x)为f(x)的一个原函数。
2)分部积分公式:∫[a, b]u(x)v'(x) dx = u(x)v(x)∣[a, b] -∫[a, b]u'(x)v(x) dx。
5.泰勒级数展开:若函数f(x)在x=a处具有n阶导数,则泰勒级数展开可表示为f(x)=f(a)+f'(a)(x-a)+f''(a)(x-a)^2/2!+...+f^n(a)(x-a)^n/n!+Rn(x),其中Rn(x)为余项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等数学(工本)》公式第一章 空间解析几何与向量代数1. 空间两点间的距离公式21221221221)()()(z z y y x x p p -+-+-=2. 向量的投影3. 数量积与向量积:向量的数量积公式:设},,{},,,{z y x z y x b b b a a a == .1︒z z y y x x b a b a b a b a ++=⋅ .2︒b a ⊥的充要条件是:0=⋅b a.3︒b a =∧)cos(向量的数量积公式:.1︒k b a b a j b a b a i b a b a b b b a a a kj ib a x y y x z x x z y z z y zy xz y x)()()(-+-+-==⨯.2︒=ϕsin.3︒b a //的充要条件是0=⨯b a4. 空间的曲面和曲线以及空间中平面与直线平面方程公式: ),,(o o o o z y x M },,{C B A =点法式:0)()()(=-+-+-o o o z z C y y B x x A直线方程公式: },,{n m l S = ,),,(o o o o z y x M 点向式:nz z m y y l x x oo o -=-=-5. 二次曲面第二章 多元函数微分学6. 多元函数的基本概念,偏导数和全微分偏导数公式:.1︒),(),,(),,(y x v y x u v u f z ψϕ===x vv z x u u z x z ∂∂∂∂+∂∂∂∂=∂∂ yv v z y u u z y z ∂∂∂∂+∂∂∂∂=∂∂ .2︒设),(),,(),,(y x v y x u v u f z ψϕ===dxdvv z dx du u z dx dz ∂∂+∂∂=.3︒设0),,(=z y x FFzFyy z FzFx x z -=∂∂-=∂∂ 全微分公式:设),,(y x f z =dy yz dx x z dz ∂∂+∂∂= 7. 复合函数与隐函数的偏导数 8. 偏导数的应用:二元函数极值 9. 高阶导数第三章 重积分10. 二重积分计算公式:.1︒⎰⎰=DkA kd σ(A 为D 的面积).2︒⎰⎰⎰⎰⎰⎰==)()()()(1212),(),(),(y y cdDx x badx y x f dy dy y x f dx d y x f ϕϕϕϕσ.3︒⎰⎰⎰⎰=Drdr r r f d d y x f )()(12)sin ,cos (),(θϕθϕβαϑϑϑσ11. 三重积分计算公式:.1︒利用直角坐标系计算,Ω为⎪⎩⎪⎨⎧≤≤≤≤≤≤b x a x y y x y y x z z y x z )()(),(),(2121⎰⎰⎰⎰⎰⎰=Ω),(),()()(2121),,(),,(y x z y x z x y x y badz z y x f dy dx d z y x f σ.2︒利用柱面坐标计算:Ω为⎪⎩⎪⎨⎧===z y r y r x ϑϑsin cos⎰⎰⎰⎰⎰⎰=Ω),(),()()(212121),sin ,cos (),,(ϑϑϑϑϑϑϑϑr z r z r r dz z r r f rdr dx dv z y x f.3︒利用球面坐标计算:Ω为⎪⎩⎪⎨⎧===ϕϕϑϕϑcos sin sin sin cos r y r y r x⎰⎰⎰Ωdv z y x f ),,(⎰⎰⎰=),(),(2)()(2121sin )cos ,sin sin ,sin cos (ϑϕϑϕϑϕϑϕβαϕϕϕϑϕϑϕϑr r dr r r r r f d d12. 重积分的应用公式:.1︒曲顶柱体的体积:⎰⎰=Ddxdy y x f V ,),(曲面),(:y x f z =∑.2︒设V 为Ω的体积:⎰⎰⎰Ω=dv V.3︒设∑为曲面),(y x f z =曲面的面积为σd f f S Dy x ⎰⎰++=221第四章 曲线积分与曲面积分13. 对弧长的曲线积分(1)若L :b x a x f y ≤≤=),(,则⎰⎰+=baLdx x x x f dl y x f )(1)](,[),(2ϕϕ(2)若L :βαψϕ≤≤⎩⎨⎧==t t y t x ,)()(则⎰⎰'+'=βαψϕψϕdx t t t t f dl y x f L)()()](),([),(22(3)当1),(=y x f 时,曲线L 由B 的弧长为⎰=Ldl S 。
14. 对坐标的曲线积分(1)终点起点)()()(:)](,[),(b B a A x y L dx x x P dx y x P AB baL ABϕϕ==⎰⎰(2)[]终点起点)()()()(:)]()(),(),(βαψϕϕψϕβαB A t y t x L dt t t t P dx y x P AB L AB ⎩⎨⎧=='=⎰⎰15. 格林公式及其应用 格林公式:Qdy Pdx dxdy y Px Q LD+=∂∂-∂∂⎰⎰⎰)(其中L 是沿正向取的闭区域的边界曲线。
16. 姻亲的种类(P66) 17. 对面积的曲面积分⎰⎰⎰⎰++=∑Dxyy x dxdy z z y x z y x f ds z y x f 221)],(,,[),,(∑=),(:y x z z18. 对坐标的曲面积分⎰⎰⎰⎰±=∑Dxy dxdy y x z y x R dxdy z y x R )],(,,[),,( 下侧取负号上侧取正号∑=),(:y x z z第五章 常微分方程19. 微分方程基本概念 20. 三类一阶微分方程(1)一阶线性微分方程:)()(x Q y x p y =+'通解])([)()(C dx e x Q ey dx x p dxx p +=⎰⎰⎰-(2)二阶常系数线性齐次微分方程公式:0=+'+''qy y p y 特征方程:02=++q pr r.1︒21r r ≠实根:通解为x r x r e c e c y 2121+=.2︒21r r =实根:通解为x r e c c y 1)(21+=.3︒i r βα±=21,:通解为)sin cos (21x c c e y xββα+= (3) 二阶常系数线性非齐次微分方程公式:axm e x P qy y p y )(=+'+''通解为*y y y += y 为对应齐次方程的通解x m k e x Q x y α)(*= *y 为所求方程的一个特解0=k :a 不是特征方程的根 1=k :a 是特征方程的单根2=k :a 是特征方程的重根第六章 无穷级数21. 数项级数的基本概念以及基本性质22 22. 数项级数的审敛法审敛准则公式:.1︒比值判别法:⎪⎪⎪⎩⎪⎪⎪⎨⎧=∞><=∑∑∑∞=∞=∞=+∞→不定级数发散级数收敛级数1111,1),(1,1limn n n n n n nn n u u u q u u.2︒比较判别法:1)设n n v u ≤,而∑∞=1n nv收敛,则∑∞=1n nu收敛。
2)设n n v u ≥,而∑∞=1n nv发散,则∑∞=1n nu发散。
23. 幂级数以及函数的幂级数展开式幂级数的收敛半径和收敛区间 公式:.1︒收敛半径1lim +∞→=n nn a a R.2︒收敛区间:1)[-R,R] 2)[-R,R ) 3)(-R ,R]设发散,右边开收敛,右边闭∑∞==1:n nn R a R x发散,左边开收敛,左边闭)(∑∞=--=1:n nn R a R x.3︒R x x R x x R x x R x x x x a n n n -=-=-+==--∑∞=00001)令( 幂级数的展开式公式:.1︒+∞<<∞-+++++=x n x x x e nx!!212.2︒+∞<<∞--+-=x x x x x x !7!5!3sin 753.3︒+∞<<∞--+-=x x x x x !6!4!21cos 642.4︒11432)1ln(432≤<--+-=+x x x x x x.5︒1111132<<-+++=-x x x x x。
