专题4:立体几何中垂直关系的证明基础练习题
2022年高考数学备考中等生百日捷进提升系列 专题04立体几何解答题(理)(综合提升篇)解析版

2021中等生百日综合提升篇专题四 立体几何解答题(理)空间向量运算与利用向量证明平行、垂直的位置关系【背一背重点学问】1.用向量证明线面平行的方法主要有:①证明直线的方向向量与平面的法向量垂直;②证明可在平面内找到一个向量与直线的方向向量是共线向量;③利用共面对量定理,即证明直线的方向向量可用平面内两个不共线向量线性表示.2.面面平行:①证明两个平面的法向量平行;②转化为线面平行,线线平行.3.用向量证明线面垂直的方法有:①证明直线的方向向量与平行的法向量平行;②利用线面垂直的判定定理,转化为线线垂直.4.面面垂直的证明发法:①两个平面的法向量垂直;②转化为线面垂直,线线垂直. 【讲一讲提高技能】 必备技能:1.用向量证明空间中的平行关系①设直线1l 和2l 的方向向量分别为1v 和2v ,则1l ∥2l (或1l 与2l 重合)⇔ 1v ∥2v .②设直线l 的方向向量为v ,与平面α共面的两个不共线向量1v 和2v ,则l ∥α或l ⊂α⇔存在两个实数,x y ,使12v xv yv =+.③设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u . ④设平面α和β的法向量分别为1u ,2u ,则α∥β⇔1u ∥2u . 2.用向量证明空间中的垂直关系①设直线l 1和l 2的方向向量分别为1v 和2v ,则l 1⊥l 2⇔1v ⊥2v ⇔1v .2v =0. ②设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔v ∥u ③设平面α和β的法向量分别为1u 和2u ,则α⊥β⇔1u ⊥2u ⇔1u ·2u =0. 典型例题:例1如图,在四棱锥P ABCD -中,PD ⊥平面ABCD ,//AB CD ,090ADC ∠=,1PD AD AB ===,2DC =.(1)求证:BC ⊥平面PBD ; (2)求二面角A PB C --的大小. 【答案】(1)证明见解析;(2)56π. 【解析】例2如图,正方形CD AB 和四边形C F A E 所在平面相互垂直,C C E ⊥A ,F//C E A ,2AB =,C F 1E =E =.(1)求证:F//A 平面D B E ; (2)求证:CF ⊥平面D B E ; (3)求二面角D A-BE-的大小.【答案】(1)证明见解析;(2)证明见解析;(3)6π. 【解析】(2)证明:由于正方形CD AB 和四边形C F A E 所在的平面相互垂直,且C C E ⊥A , 所以C E ⊥平面CD AB .如图,以C 为原点,建立空间直角坐标系C xyz -. 则()C 0,0,0,)2,2,0A,()2,0B ,()D2,0,0,()0,0,1E ,22F ,22⎛⎫⎪ ⎪⎝⎭.22CF 2⎛⎫= ⎪ ⎪⎝⎭,()0,2,1BE =-,()D 2,0,1E =-.CF 0110⋅BE =-+=,CF D 1010⋅E =-++=,所以CF ⊥BE ,CF D ⊥E ,又D BE E =E ,所以CF ⊥平面D B E .(3)由(2)知,22CF ,22⎛⎫= ⎪ ⎪⎝⎭是平面D B E 的一个法向量.设平面ABE 的法向量(),,n x y z =,则0n ⋅BA =,0n ⋅BE =,即()()()(),,2,0,00,,0,2,10x y z x y z ⎧⋅=⎪⎨⋅-=⎪⎩,得0x =,且2z y =.令1y =,则2z =,()0,1,2n =.从而CF 3cos ,CF 2CFn n n ⋅==. 故二面角D A-BE-为锐角,故二面角D A-BE-的大小为6π. 【练一练提升力量】1已知在四棱锥P ABCD -中,底面ABCD 是矩形,且2AD =,1AB =,PA ⊥平面ABCD ,E 、F 分别是线段AB 、BC 的中点. (1)证明:PF FD ⊥(2)在线段PA 上是否存在点G ,使得EG ∥平面PFD ,若存在,确定点G 的位置;若不存在,说明理由. (3)若PB 与平面ABCD 所成的角为45,求二面角A PD F --的余弦值【解析】(Ⅱ)设平面PFD 的法向量为(),,n x y z =,由0n PF n DF ⎧⋅=⎪⎨⋅=⎪⎩,得00x y tz x y +-=⎧⎨-=⎩,令1z =,得:2t x y ==.∴,,122t t n ⎛⎫= ⎪⎝⎭.设G 点坐标为(0,0,)m ()0m t ≤≤,1,0,02E ⎛⎫⎪⎝⎭,则1(,0,)2EG m =-,要使EG ∥平面PFD ,只需0EG n =,即1()0102224t t tm m -⨯+⨯+⨯=-=,得14m t =,从而满足14AG AP =的点G 即为所求.2. 如图,四棱锥ABCD P -的底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,DC PD =,E 是PC 的中点. (Ⅰ)证明:PA //平面BDE ;(Ⅱ)求二面角C DE B --的平面角的余弦值;(Ⅲ)在棱PB 上是否存在点F ,使PB ⊥平面DEF ?证明你的结论.【解析】法二:(I )连接AC ,AC 交BD 于O ,连接OE .在PAC ∆中,OE 为中位线,∴OE //PAPA BDE ⊄又平面,∴PA //平面BDE .利用空间向量求空间角 【背一背重点学问】1.求两条异面直线所成的角,设b a ,分别是直线21,l l 的方向向量,则21,l l 所成角为θ,b a ,的夹角为><b a ,,则ba b a b a ⋅>=<=,cos cos θ2.求直线与平面所成的角,设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,ba n a n a ⋅=><=,cos sin θ.3. 设n m ,是二面角βα-l -的法向量,则n m ,的夹角大小就是二面角的平面角的大小,nm n m n m ⋅>=<=,cos cos θ,再依据平面是锐角还是钝角,最终确定二面角的平面角的大小.【讲一讲提高技能】 1.必备技能: 用法向量求角(1)用法向量求二面角如图,有两个平面α与β,分别作这两个平面的法向量1n 与2n ,则平面α与β所成的角跟法向量1n 与2n 所成的角2n 相等或互补,所以首先必需推断二面角是锐角还是钝角.(2)法向量求直线与平面所成的角要求直线a 与平面α所成的角θ,先求这个平面α的法向量n 与直线a 的夹角的余弦a n ,cos ,易知θ=a n ,或者a n ,2-π.2.典型例题:例1如图,在四棱锥P ABCD -中,底面ABCD 是菱形,且60DAB ∠=︒.点E 是棱PC 的中点,平面ABE 与棱PD 交于点F .F BD CP EA(1)求证://AB EF ;(2)若PA PD AD ==,且平面PAD ⊥平面ABCD ,求平面PAF 与平面AFE 所成的锐二面角的余弦值. 【答案】(1)详见解析;(2)1313. 【解析】试题分析:(1)首先证明//AB 面PCD ,再利用线面平行的性质即可得证;(2)建立空间直角坐标系,求得两个平面的法向量后即可求解.zyG AEP CDBF例2如图,四棱锥ABCD P -中,底面是以O 为中心的菱形,⊥PO 底面ABCD , 3,2π=∠=BAD AB ,M 为BC 上一点,且AP MP BM ⊥=,21. αβ1n(Ⅰ)求PO 的长;(Ⅱ)求二面角C PM A --的正弦值.分析:(Ⅰ)连结AC 、BD ,由于是菱形ABCD 的中心,ACBD O =,以O 为坐标原点,,,OA OB OP 的方向分别为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系,依据题设条件写出,,O A M 的坐标,并设出点P 的坐标()0,0,a ,依据空间两点间的距离公式和勾股定理列方程解出a 的值得到PO 的长;.(Ⅱ)设平面APM 的法向量为()1111,,n x y z =,平面PMC 的法向量为()2222,,n x y z =,首先利用向量的数量积列方程求出向量12,n n 的坐标,再利用向量的夹角公式求出12cos ,n n <>,进而求出二面角C PM A --的正弦值. 【解析】从而33,,044OM OB BM ⎛⎫=+=- ⎪ ⎪⎝⎭,即33,,0.44M ⎛⎫- ⎪ ⎪⎝⎭设()0,0,,0,P a a >,则()333,0,,,,.44AP a MP a ⎛⎫=-=-⎪ ⎪⎝⎭由于MP AP ⊥, 故0,MP AP ⋅=即2304a -+=,所以33,22a a ==-(舍去),即32PO =.【练一练提升力量】1. 如图,在长方体1111ABCD A B C D -中,11,2AD AA AB ===,点E 在棱AB 上移动.(Ⅰ)证明:11D E A D ⊥;(Ⅱ)当E 为AB 的中点时,求点E 到面1ACD 的距离; (Ⅲ)AE 等于何值时,二面角1D EC D --的大小为4π.【解析】2. 如图,四棱锥P —ABCD 中,PAB ∆为边长为2的正三角形,底面ABCD 为菱形,且平面PAB ⊥平面ABCD ,AB PC ⊥,E 为PD 点上一点,满足ED PE 21=(1)证明:平面ACE ⊥平面ABCD ;(2)求直线PD 与平面ACE 所成角正弦值的大小.【解析】E BACPABCDA 1B 1C 1D 1E解答题(共10题)1.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥底面ABCD ,AB AP =,E 为棱PD 的中点.(1)证明:AE CD ⊥;(2)求直线AE 与平面PBD 所成角的正弦值;(3)若F 为AB 中点,棱PC 上是否存在一点M ,使得FM AC ⊥,若存在,求出PMMC的值,若不存在,说明理由.【答案】(1)详见解析;(2)63;(3)13PM MC =.【解析】6cos ,3AE EF <>=所以,直线EF 与平面PBD 所成角的正弦值为63;(3)向量(2,2,2)CP =--,(2,2,0)AC =,(2,0,0)AB =.由点M 在棱PC 上,设(01)CM CP λλ=≤≤,故(12,22,2)FM FC CM λλλ=+=--,由FM AC ⊥,得0FM AC ⋅=, 因此(12)2(22)20λλ-⨯+-⨯=,解得34λ=,所以13PM MC =.2. 如图,在四棱柱ABCD -A 1B 1C 1D 1中,侧棱AA 1⊥底面ABCD ,AB ∥DC ,11AA =,3AB k =, 456(0)AD k BC k DC k k ===>,,.(Ⅰ)求证:CD ⊥平面ADD 1A 1;(Ⅱ)若直线AA 1与平面AB 1C 所成角的正弦值为67,求k 的值. 【解析】(Ⅱ)以D 为原点,DA ,DC ,1DD 的方向为x ,y ,z 轴的正方向建立如图所示的空间直角坐标系,3. 如图,在直三棱柱111ABC A B C -中,平面1A BC ⊥ 侧面11A ABB 且12AA AB ==.(Ⅰ)求证:AB BC ⊥;(Ⅱ)若直线AC 与平面1A BC 所成的角为6π,求锐二面角1A A C B --的大小. 【解析】(1)证明:如图,取1A B 的中点D ,连接AD ,因1AA AB =,则1AD AB ⊥ ,由平面1A BC ⊥侧面11A ABB ,且平面1A BC 侧面11A ABB 1A B =,得1AD A BC ⊥平面,又BC ⊂平面1A BC , 所以AD BC ⊥. 由于三棱柱111ABC A B C —是直三棱柱,则1AA ABC ⊥底面,所以1AA BC ⊥. 又1=AA AD A ,从而BC ⊥侧面11A ABB ,又AB ⊂侧面11A ABB ,故AB BC ⊥.解法二(向量法):由(1)知AB BC ⊥且1BB ABC ⊥底面,所以以点B 为原点,以1BC BA BB 、、所在直线分别为,,x y z 轴建立空间直角坐标系B xyz -,如图所示,且设BC a =,则(0,2,0)A ,(0,0,0)B ,(,0,0)C a ,1(0,2,2)A ,(,0,0)BC a =,1(0,2,2)BA =,(,2,0)AC a =-,1(0,0,2)AA = 设平面1A BC 的一个法向量1(,,)n x y z =,由1BC n ⊥, 11BAn ⊥ 得: 0220xa y z =⎧⎨+=⎩令1y = ,得 0,1x z ==-,则1(0,1,1)n =- 设直线AC 与1A BC 平面所成的角为θ,则6πθ=得12121sin6242AC n AC n a π-===+,解得2a =,即(2,2,0)AC =- 又设平面1A AC 的一个法向量为2n ,同理可得2(1,1,0)n =,设锐二面角1A A C B --的大小为α,则1212121cos cos ,2n n n n n n α=<>==,且(0,)2πα∈,得 3πα=∴ 锐二面角1A A C B --的大小为3π. 4. 在三棱柱111C B A ABC -中,侧面11A ABB 为矩形,2=AB ,221=AA ,D 是1AA 的中点,BD 与1AB 交于点O ,且CO ⊥平面11A ABB .(1)证明:1AB BC ⊥;(2)若OA OC =,求直线CD CD 与平面ABC 所成角的正弦值. 【答案】(1)证明见解析;(2)515. 【解析】又BC ⊂平面CBD ,∴BC AB ⊥1.5. 如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,BC =CD =2,AC =4,∠ACB =∠ACD =3π,F 为PC 的中点,AF ⊥PB.(1)求PA 的长;(2)求二面角B -AF -D 的正弦值. 【解析】(2)由(1)知()03,3,-=AD ,()03,3,=AB ,()320,,=AF .设平面FAD FAD 的法向量为()1111,z y x n =,平面FAB 的法向量为()2222,z y x n =.由0,011=⋅=⋅AF n AD n 得,⎪⎩⎪⎨⎧=+=+032033-1111z y y x 因此可取()2,3,31-=n .由0,022=⋅=⋅AF n AB n 得⎪⎩⎪⎨⎧=+=+0320332222z y y x 故可取()2,3,32-=n .从而法向量21,n n 的夹角的余弦值为81,cos 212121=⋅>=<n n n n n n .故二面角D AF B --正弦值为873. 6. 如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,60ABC ∠=E 、F 分别是PB 、CD 的中点,且4PB PC PD ===.(1)求证:PA ABCD ⊥平面;(2)求证://EF 平面PAD ; (3)求二面角A PB C --的余弦值.ADBCPE FBCADP EFN GH M【解析】(3)取AB 的中点,G 过G 作GH PB ⊥于点,H 连结,.HC GC 则,CG AB ⊥又,,CG PA PAAB A CG ⊥=∴⊥平面.PAB ,HC PB ∴⊥ GHC ∴∠是二面角A PB C --的平面角.在Rt PAB ∆中,2,4,2 3.AB PB PA ==∴= 又Rt BHG ∆∽Rt BAP ∆,3,2HG BG HG PA PB ∴=∴=.在Rt HGC ∆中,可求得153,,2GC HC =∴=5cos 5GHC ∴∠=, 故二面角A PB C --的余弦值为5.57. 直三棱柱111ABC A B C -中,11AA AB AC ===,,E F 分别是1,CC BC 的中点,11AE A B ⊥,D 为棱11A B 上的点.(1)证明:AC AB ⊥ ; (2)证明:DF AE ⊥;(3)是否存在一点D ,使得平面DEF 与平面ABC 所成锐二面角的余弦值为1414?若存在,说明点D 的位置,若不存在,说明理由.【答案】(1)证明见解析;(2)存在,点D 为11A B 中点. 【解析】试题解析:(1)证明:∵11AE A B ⊥,11//,A B AB AE AB ∴⊥,又∵11,AA AB AA AE A ⊥=∴AB ⊥面11A ACC .又∵AC ⊂面11A ACC ,∴AB AC ⊥,以A 为原点建立如图所示的空间直角坐标系A xyz -,则有()()()111110,0,0,0,1,,,,0,0,0,1,1,0,1222A E F A B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,设()111,,,D x y z A D A B λ=且()0,1λ∈,即(),,1(1,0,0)x y z λ-=,则11(,0,1),,,122D DF λλ⎛⎫∴=--⎪⎝⎭,∵1110,1,,0222AE DF AE ⎛⎫=∴⋅=-= ⎪⎝⎭,所以DF AE ⊥;8. 如图,在底面为直角梯形的四棱锥P -ABCD 中,AD ∥BC ,∠ABC =90°,P A ⊥平面ABCD ,P A =3,AD =2,AB =23,BC =6. (1)求证:BD ⊥平面P AC ; (2)求二面角P -BD -A 的大小.【解析】9. 如图1,直角梯形ABCD 中,AD ∥,BC 90ABC ∠=,BC AB AD 21==,E 是底边BC 上的一点,且BE EC 3=.现将CDE ∆沿DE 折起到DE C 1∆的位置,得到如图2所示的四棱锥,1ABED C -且AB A C =1.ABCDE 图1BE ADMC 1图2(1)求证:⊥A C 1平面ABED ;(2)若M 是棱E C 1的中点,求直线BM 与平面DE C 1所成角的正弦值. 【答案】(1)见解析;(2)49. 【解析】(2)由(1)知:⊥A C 1平面ABED 且AD AB ⊥,分别以1AC AD AB 、、为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系,如图:z xB EAD MC 1y则)0,1,0(),0,21,1(),1,0,0(),0,0,1(1D E C B10.在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,△PAD 是等边三角形,底面ABCD 是边长为2的菱形,∠BAD =60°,E 是AD 的中点,F 是PC 的中点.(1)求证:BE ⊥平面PAD ; (2)求证:EF ∥平面PAB ;(3)求直线EF 与平面PBE 所成角的余弦值. 【解析】(2)取PB 中点为H ,连接AH FH ,,则⎪⎪⎭⎫⎝⎛23,230,H ,⎪⎪⎭⎫ ⎝⎛-=23,231,EF ,()⎪⎪⎭⎫⎝⎛-=-⎪⎪⎭⎫ ⎝⎛=23,23100123,230,,,,AH , AH EF //∴, 又⊄EF 平面PAB ,⊂AH 平面PAB ,//EF ∴平面PAB .。
高中立体几何证明方法及例题

1.空间角与空间距离在高考的立体几何试题中,求角与距离是必考查的问题,其中最主要的是求线线角、线面角、面面角、点到面的距离,求角或距离的步骤是“一作、二证、三算”,即在添置必要的辅助线或辅助面后,通过推理论证某个角或线段就是所求空间角或空间距离的相关量,最后再计算。
2.立体几体的探索性问题立体几何的探索性问题在近年高考命题中经常出现,这种题型有利于考查学生归纳、判断等方面的能力,也有利于创新意识的培养。
近几年立体几何探索题考查的类型主要有:(1)探索条件,即探索能使结论成立的条件是什么?(2)探索结论,即在给定的条件下命题的结论是什么。
对命题条件的探索常采用以下三种方法:(1)先观察,尝试给出条件再证明;(2)先通过命题成立的必要条件探索出命题成立的条件,再证明充分性;(3)把几何问题转化为代数问题,探索出命题成立的条件。
对命题结论的探索,常从条件出发,再根据所学知识,探索出要求的结论是什么,另外还有探索结论是否存在,常假设结论存在,再寻找与条件相容还是矛盾。
(一)平行与垂直关系的论证由判定定理和性质定理构成一套完整的定理体系,在应用中:低一级位置关系判定高一级位置关系;高一级位置关系推出低一级位置关系,前者是判定定理,后者是性质定理。
1.线线、线面、面面平行关系的转化:面面平行性质α//βαI γ=a ,βI γ⎫⎬⇒a =b ⎭//baa //b⎫⎬ba ⊄α,b ⊂α⎭α⇒a //αa ⊂α,b ⊂αAb a I b =Aαaa //β,b //ββ⎫⎪⎬⎪⎭(a//b,b//c线线∥⇒a //c)公理4线面平行判定线面平行性质线面∥⇒α//β面面平行判定1面面∥面面平行性质面面平行性质1α//γ⎫β//γ⎭⎫⎪a ⊂β⎬αI β=b ⎪⎭a //α⇒a //bα//β⎫a ⊂α⎭⎬⎬⇒α//β⇒a //β2.线线、线面、面面垂直关系的转化:⎫⎪a Ib =O ⎬l ⊥a ,l ⊥b ⎪⎭a ,b ⊂α⇒l ⊥α⎫⎬⇒α⊥βa ⊂β⎭a ⊥α面面⊥三垂线定理、逆定理线线⊥PA ⊥α,AO 为PO 在α内射影a ⊂α则a ⊥OA ⇒a ⊥PO a ⊥PO ⇒a ⊥AOl ⊥α线面垂直判定1线面垂直定义线面⊥α⊥β面面垂直判定面面垂直性质,推论2⎫⎬a ⊂α⎭⇒l ⊥a⎫⎪αI β=b ⎬⇒a ⊥αa ⊂β,a ⊥b ⎪⎭α⊥γβ⊥γαI β⎫⎪⎬⇒a ⊥γ=a ⎪⎭面面垂直定义αI β=l ,且二面角α-l -β⎫成直二面角⎬⇒α⊥β⎭3.平行与垂直关系的转化:a //b ⎫a ⊥αa ⊥α⎫⇒b ⊥αa⎬⎭⎬⇒αa ⊥β⎭//β线线∥线面垂直判定2线面垂直性质2a ⊥α⎫线面⊥面面平行判定2面面平行性质3面面∥⎬⇒a //b b ⊥α⎭α//β⎫a ⊥α⎬a ⊥β⎭4.应用以上“转化”的基本思路——“由求证想判定,由已知想性质。
第8章立体几何专题4 垂直的证明-人教A版(2019)高中数学必修(第二册)常考题型专题练习

垂直的证明【方法总结】1、证明线面垂直的方法:①利用线面垂直定义:如果一条直线垂直于平面内任一条直线,则这条直线垂直于该平面;②用线面垂直判定定理:如果一条直线与平面内的两条相交直线都垂直,则这条直线与平面垂直;③用线面垂直性质:两条平行线中的一条垂直于一个平面,则另一条也必垂直于这个平面.2、证明线线(或线面)垂直有时需多次运用线面垂直的定义和线面垂直的判定定理,实现线线垂直与线面垂直的相互转化.3、证明面面垂直一般要先找到两个面的交线,然后再在两个面内找能与交线垂直的直线,最后通过证明线面垂直证明面面垂直。
【分类练习】考向一线面垂直例1、在四棱锥P ABCD -中,PA ⊥底面ABCD ,//AB CD ,AB BC ⊥,1AB BC ==,2DC =,点E 在PB 上求证:CA ⊥平面PAD ;【答案】(1)证明见解析;(2)2.【解析】(1)过A 作AF ⊥DC 于F ,则CF =DF =AF ,所以∠DAC =90°,即AC ⊥DA ,又PA ⊥底面ABCD ,AC ⊂面ABCD ,所以AC ⊥PA ,因为PA 、AD ⊂面PAD ,且PA ∩AD =A ,所以AC ⊥平面PAD .例2、如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;解析:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BE EC ⊥,所以BE ⊥平面11EB C .例3、如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB 的中点求证:AC ⊥平面BEF ;【解析】(1)在三棱柱111ABC A B C -中,∵1CC ⊥平面ABC ,∴四边形11A ACC 为矩形.又E ,F 分别为AC ,11A C 的中点,∴AC ⊥EF .∵AB BC =.∴AC ⊥BE ,∴AC ⊥平面BEF .例4、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,CD ⊥AD ,BC ∥AD ,12BC CD AD ==.(Ⅰ)求证:BD ⊥平面PAB ;【解析】因为PA ⊥平面ABCD ,BD ⊂平面ABCD ,所以BD ⊥PA .所以222AD AB BD =+,所以BD AB ⊥.因为PA AB A = ,所以BD ⊥平面PAB .【巩固练习】1、如图,在三棱柱ABC-A 1B 1C 1中,AB=AC,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.证明:A 1D⊥平面A 1BC;【答案】见解析【解析】证明:设E 为BC 的中点,连接A 1E,AE.由题意得A 1E⊥平面ABC,所以A 1E⊥AE.因为AB=AC,所以AE⊥BC.故AE⊥平面A 1BC.连接DE,由D,E 分别为B 1C 1,BC 的中点,得DE∥B 1B 且DE=B 1B,从而DE∥A 1A 且DE =A 1A,所以AA 1DE 为平行四边形.于是A 1D∥AE.因为AE⊥平面A 1BC,所以A 1D⊥平面A 1BC.2.(2019·上海格致中学高三月考)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD DC =,E 是PC 的中点,作EF PB ⊥交PB 于点F .(1)证明:PA ∥平面EDB ;(2)证明:PB ⊥平面EFD .【答案】(1)详见解析;(2)详见解析.【解析】(1)设AC 与BD 相交于O ,连接OE ,由于O 是AC 中点,E 是PC 中点,所所以PA ∥平面EDB .(2)由于PD ⊥底面ABCD ,所以PD BC ⊥,由于,BC CD PD CD D ⊥⋂=,所以BC ⊥平面PCD ,所以BC DE ⊥.由于DP DC =且E 是PC 中点,所以DE PC ⊥,而PC BC C ⋂=,所以DE ⊥平面PBC ,所以DE PB ⊥.依题意EF PB ⊥,DE EF E = ,所以PB ⊥平面EFD .3.(2019·江苏高三月考)如图,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,AC ,BD 相交于点O ,OP OC =,E 为PC 的中点,PA PD ⊥.(1)求证://PA 平面BDE ;(2)求证:PA ⊥平面PCD【答案】(1)详见解析(2)详见解析【解析】(1)连结OE .因为四边形ABCD 是平行四边形,AC ,BD 相交于点O ,所以O 为AC 的中点.因为E 为PC 的中点,所以//OE PA .因为OE ⊂平面BDE ,PA ⊄平面BDE ,所以//PA 平面BDE .(2)因为OP OC =,E 为PC 的中点,所以OE PC ⊥.由(1)知,//OE PA ,所以PA PC ⊥.因为PA PD ⊥,PC ,PD ⊂平面PCD ,PC PD P ⋂=,所以PA ⊥平面PCD .考向二面面垂直例1、如图,在四棱锥P ABCD -中,已知底面ABCD 为矩形,且AB =,1BC =,E ,F 分别是AB ,PC 的中点,PA DE ⊥.(1)求证://EF 平面PAD ;(2)求证:平面PAC ⊥平面PDE .【答案】(1)详见解析(2)详见解析【解析】证明:(1)取PD 中点G ,连AG ,FG ,F ,G 分别是PC ,PD 的中点又E 为AB 中点//AE FG ∴,AE FG=四边形AEFG 为平行四边形//EF AG ∴,又EF ⊄平面PAD ,AG ⊂平面PAD//EF ∴平面PAD(2)设AC DE H= 由AEH CDH ∆∆ 及E 为AB 中点又BAD ∠为公共角GAE BAC∴∆∆ 90AHE ABC ∴∠=∠=︒即DE AC ⊥又DE PA ⊥,PA AC A= DE ⊥平面PAC ,又DE ⊂平面PDE∴平面PAC ⊥平面PDE例2、如图,边长为2的正方形ABCD 所在的平面与半圆弧 CD所在平面垂直,M 是 CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;【解析】(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为 CD上异于C ,D 的点,且DC 为直径,所以DM ⊥CM .又BC CM =C ,所以DM ⊥平面BMC .而DM ⊂平面AMD ,故平面AMD ⊥平面BMC .例3、如图,在梯形ABCD 中,AB ∥CD ,AD=DC=CB=a ,∠ABC=3π,平面ACFE ⊥平面ABCD ,四边形ACFE 是矩形,AE=AD ,点M 在线段EF 上。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
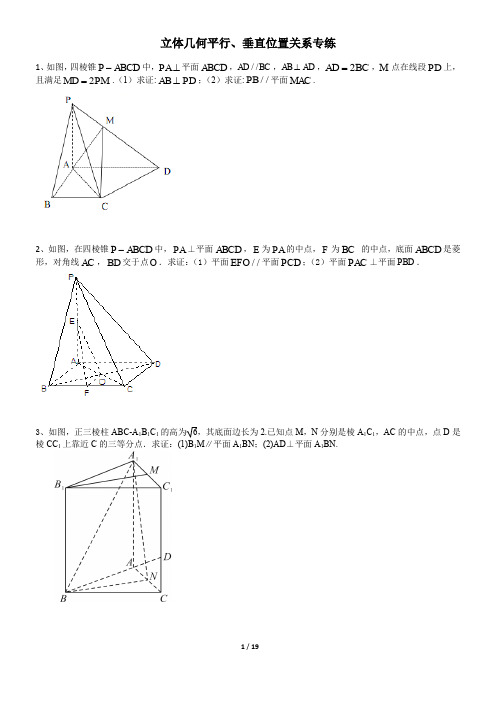
立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
高考数学复习—立体几何:(二)空间直线平面关系判断与证明—平行与垂直关系证明(试题版)
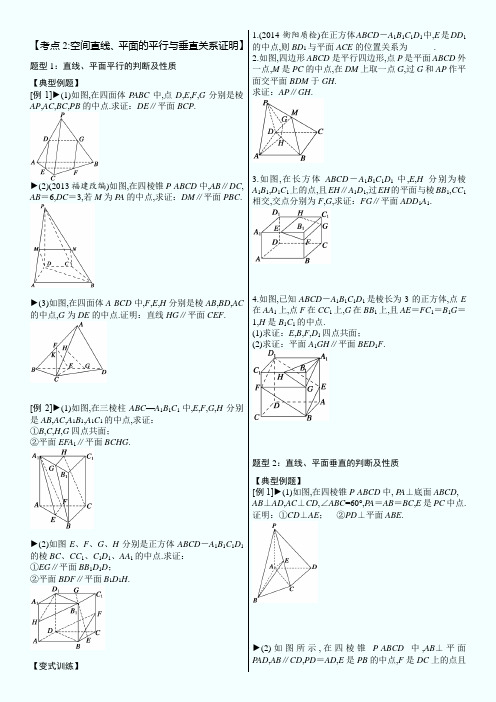
【考点2:空间直线、平面的平行与垂直关系证明】题型1:直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证:DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB=6,DC=3,若M为P A的中点,求证:DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明:直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:①B,C,H,G四点共面;②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:①EG∥平面BB1D1D;②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH .3.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.4.如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F .题型2:直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC中点. 证明:①CD⊥AE;②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=12AB,PH为△P AD中AD边上的高.①证明:PH⊥平面ABCD;②证明:EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(I)求证:EF⊥平面BCG;(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA1,D是棱AA1的中点.(I)证明:平面BDC1⊥平面BDC;(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.①求证:PC⊥BC;②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证:CE⊥平面P AD;(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A=PB=AB =BC,∠PBC=90°,D为AC的中点,AB⊥PD.(1)求证:平面P AB⊥平面ABC;(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.☆题型3:直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α∥β,l∥α,则l∥β;④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.(I)求证:平面ABE⊥平面B1BCC1;(II)求证:C1F∥平面ABE;(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A=6,BC=8,DF=5. 求证:(I)直线P A∥平面DEF;(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积;(II)证明:四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证:DE∥平面A1CB;(II)求证:A1F⊥BE;(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β=c.给出下列命题:①若a与b是异面直线,则c至少与a,b中的一条相交;②若a不垂直于c,则a与b一定不垂直;③若a∥b,则必有a∥c;④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证: (1)P A ⊥底面ABCD ; (2)BE ∥平面P AD ;(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB =BC=12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证:AP ∥平面BEF ; (2)求证:BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明:BC 1∥平面A 1CD ;(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证:BC ⊥平面P AC ; (2)设Q 为P A 的中点,G 为△AOC 的重心,求证:QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明:PB ∥平面AEC ;(2)设AP =1,AD =3,三棱锥P - ABD 的体积V =34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1.设AB 1的中点为D ,B 1C ∩BC 1=E . 求证:(1)DE ∥平面AA 1C 1C ; (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3. (1)证明:BC ∥平面PDA ; (2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值.16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE . (Ⅰ)证明:CD ⊥平面A 1OC ;(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值.17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置. (1)证明:AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′ABCFE 的体积.18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点. (1)证明MN ∥平面P AB ;(2)求四面体N -BCM 的体积.19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ; (2)若PA =PD =AB =DC ,∠ADP =90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
立体几何专题复习(自己精心整理)

专题一证明平行垂直问题题型一证明平行关系(1)如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD。
(2)在正方体AC1中,M,N,E,F分别是A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN∥平面EFDB.思考题1(1)如图所示,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,求证:平面EFG∥平面PBC.(2)如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=22,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.求证:PQ∥平面BCD。
题型二证明垂直关系(微专题)微专题1:证明线线垂直(1)已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC。
求证:PM⊥QN.(2)(2019·山西太原检测)如图,直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点,求证:DF⊥AE。
微专题2:证明线面垂直(3)在正方体ABCD-A1B1C1D1中,求证:BD1⊥平面ACB1.(4)(2019·河南六市一模)在如图所示的几何体中,ABC-A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.若AA1=AC,求证:AC1⊥平面A1B1CD。
微专题3:证明面面垂直(5)已知正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点,求证:平面DEA⊥平面A1FD1.(6)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=错误!PD,求证:平面PQC⊥平面DCQ。
思考题2(1)(2019·北京东城区模拟)如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥BP交BP于点F,求证:PB⊥平面EFD。
高考大题专项(四) 立体几何

| || |
所以异面直线 PC 与 BQ
=
2
,
3
2
所成角的余弦值为 3 .
解题心得用向量法求异面直线所成角的一般步骤
(1)选择三条两两垂直的直线建立空间直角坐标系.
(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量.
(3)利用向量的夹角公式求出向量夹角的余弦值.
(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值.
高考大题专项(四) 立体几何
【考情分析】
从近五年的高考试题来看,立体几何是历年高考的重点,约占整个试卷的
15%,通常以一大两小的模式命题,以中、低档难度为主.简单几何体的表面
积与体积、点、线、面位置关系的判定与证明以及空间角的计算是考查
的重点内容,前者多以客观题的形式命题,后者主要以解答题的形式命题考
【例题】 (2020安徽高三三模)如图,边长为2的等边三角形ABC所在平面与
菱形A1ACC1所在平面互相垂直,且BC∥B1C1,BC=2B1C1,A1C=
(1)求证:A1B1∥平面ABC;
(2)求多面体ABC-A1B1C1的体积.
3 1.
AC
(1)证明∵四边形A1ACC1是菱形,
∴AC∥A1C1.
对点训练2(2020辽宁高三三模)如图,在直棱柱ABCDA1B1C1D1中,底面ABCD为菱形,AB=BD=2,BB1=2,BD
与AC相交于点E,A1D与AD1相交于点O.
(1)求证:AC⊥平面BB1D1D;
(2)求直线OB与平面OB1D1所成的角的正弦值.
(1)证明∵底面ABCD为菱形,∴AC⊥BD.
查.着重考查推理论证能力和空间想象能力,而且对数学运算的要求有加强
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.证明见解析
【分析】
在等腰三角形PAB中, 是 的中点,可得 ,利用线面垂直的判定定理可证 平面 ,利用线面垂直的性质定理,即可得证.
【详解】
证明:∵ 是 的中点, ,
∴ ,
∵ 底面 ,
∴ ,
又∵ ,即
∴ 平面 ,
∴ ,
∵ 平面 , 平面 ,
∴ 平面 ,
∵ 平面 ,
∴ .
8.证明见解析
【分析】
由平面 ⊥平面 得到 ⊥平面 ,进一步得到 ⊥ ,再结合直径所对圆周角为直角得到 ⊥ , ⊥平面 ,从而得到证明.
【详解】
由题设知,平面 ⊥平面 ,交线为 .
因为 ⊥ , 平面 ,所以 ⊥平面 ,故 ⊥ .
因为 为 上异于 , 的点,且 为直径,所以 ⊥ .
又 = ,所以 ⊥平面 .
∴点O为三角形ABC的垂心,∴BO⊥AC
又因PO⊥AC,所以AC⊥PBO
故PB⊥AC
考点:证明异面直线垂直.
7.见解析
【分析】
由已知中P为正方形ABCD所在平面外一点,PA⊥面ABCD,结合正方形的几何特征,我们易得到BC⊥平面PAB,由线面垂直的性质得到BC⊥AE,结合已知中AE⊥PB,及线面垂直的判定定理,得到AE⊥平面PBC,最后再由线面垂直的判定定理,即可得到AE⊥PC.
【点睛】
此题考查线面垂直的性质和判定的综合应用,利用线面垂直得线线垂直.
5.证明见解析
【分析】
先证直线 平面 ,再证平面 ⊥平面 .
【详解】
证明:∵ 是圆的直径, 是圆上任一点, , ,
平面 , 平面 ,
,又 ,
平面 ,又 平面 ,
平面 ⊥平面 .
【点睛】
本题考查圆周角及线面垂直判定定理、面面垂直判定定理的应用,考查垂直关系的简单证明.
6.三棱锥P—ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证:
(1)AO⊥BC
(2)PB⊥AC
7.P为正方形ABCD所在平面外一点,PA⊥面ABCD,AE⊥PB,求证:AE⊥PC.
8.如图,边长为2的正方形 所在的平面与半圆弧 所在平面垂直, 是 上异于 , 的点.证明:平面 平面 .
专题4:立体几何中垂直关系的证明基础练习题
1.如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且 ,求证:CD⊥平面PAD.
2.如图所示, 是边长为 的正六边形 所在平面外一点, , 在平面 内的射影为 的中点 .证明 .
而 平面 ,故平面 ⊥平面定理进行证明即可
【详解】
证明:由已知得, 平面 ,
平面 ,
故 .
又 , ,
所以, 平面 .
10.证明见解析
【分析】
由等腰三角形的性质证明 ,由面面垂直的性质定理证明 平面 ,最后由线面垂直的性质得出PE⊥BC.
【详解】
∵ ,且 为 的中点,∴ .
9.如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1,证明:BE⊥平面EB1C1
10.如图,在四棱锥P−ABCD中,底面ABCD为平行四边形,平面PAD⊥平面ABCD,PA=PD,E为AD的中点.求证:PE⊥BC.
11.如图所示,四面体 中, 为 的中点, , ,求证: 平面 .
12.如图所示,在四棱锥 中,底面为直角梯形, , , 底面 ,且 , 、 分别为 、 的中点.求证: .
参考答案
1.证明见解析
【分析】
由PA⊥CD,AD⊥CD即可得出.
【详解】
因为PA⊥平面ABCD, 平面ABCD,
所以PA⊥CD,
又因为AD⊥CD,
所以CD⊥平面PAD.
2.证明见解析
【分析】
连结 ,则易知 与 的交点为 ,利用线面垂直的判定定理及性质定理,即可得证.
【详解】
证明:连结 ,则易知 与 的交点为 ,如图所示:
由正六边形的性质可得 ,
∵ , , ,
∴ 平面 ,
∵ 平面 ,
∴ .
3.详见解析.
【分析】
根据直线与平面垂直的判定定理可知,只需证明 与平面 内的两条相交直线垂直即可,而 , 满足定理条件.
【详解】
证明: C是底面圆周上异于A,B的任意一点,AB是圆柱底面圆的直径, ,
3.如图所示,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点,A1A=AB=2.求证:BC⊥平面A1AC.
4.如图,在三棱锥P-ABC中, ,垂足为D, 底面ABC,垂足为O,且O在CD上,求证: .
5.已知 是圆的直径, 垂直圆所在的平面, 是圆上任一点.求证:平面 ⊥平面 .
【详解】
证明:∵PA⊥面ABCD,
∴PA⊥AD
又∵BC∥AD
∴PA⊥BC
又由AB⊥BC,PA∩AB=A
∴BC⊥平面PAB
又AE⊂平面PAB
∴BC⊥AE
又由AE⊥PB,BC∩PB=B
∴AE⊥平面PBC
又∵PC⊂平面PBC
∴PC⊥AE
【点睛】
本题考查知识点是直线与平面垂直的判定及直线与平面垂直的性质,其中熟练掌握正方形的几何特征及线面垂直的判定定理和性质是解答本题的关键.
∵平面 平面 ,平面 平面
∴ 平面 .
∵ 面 ,∴PE⊥BC.
11.证明见解析
【分析】
在等腰三角形ABD中, 为 的中点,可得 ,分别求出AO,CO,AC的长,利用勾股定理,可得 ,利用线面垂直的判定定理,即可得证.
【详解】
证明:连接 ,∵ , ,
∴ ,
在 中,由已知可得 , , ,
∴ ,即 ,
∵ , 平面 , 平面 ,
平面 平面 , ,
平面 平面
平面 .
【点睛】
本题考查直线与平面垂直的判定,考查棱柱的性质,考查学生空间想象能力和推理论证能力,属于中档题.
4.证明见解析
【分析】
通过线面垂直证得 ,结合 得 平面POC,即可得证.
【详解】
证明: 底面ABC, 底面ABC, .
∵O在CD上, .
又 ,
平面POC. 平面POC, .
6.证明过程详见解析.
【解析】
试题分析:异面直线垂直往往是证明其中一条直线垂直另一条直线所在的平面,即由直线与平面垂直的性质证明直线与直线垂直.
试题解析:(如图)
(1)∵PO⊥面ABC,BC 平面ABC
∴PO⊥BC,又因PA⊥BC
∴BC⊥平面PAO
∴AO⊥BC.
由(1)知,AO⊥BC.同(1)证法,由PC⊥AB,可得CO⊥AB
