20100401101张锦锦
国家统计局辽宁调查队系统2010年公务员招考面试公告情况表

96.4 3月4日下午 98.8 调剂 调剂
沈阳市于洪区崇山东路8号 刘东 86906498 15998812611 金剑大厦(长客总站对面) 胡平 86906738 15998812655
99.5
3月5日上午
沈阳市于洪区崇山东路8号 刘东 86906498 15998812611 金剑大厦(长客总站对面) 胡平 86906738 15998812655
95.6
3月5日下午
沈阳市于洪区崇山东路8号 刘东 86906498 15998812611 金剑大厦(长客总站对面) 胡平 86906738 15998812655
铁岭调查队
朝阳调查队
绥中调查队
葫芦岛调查队
阜新调查队
李学成 张民 朱磊 邰娜 纪姝羽 付学先 沈达奇 杨靖 陈予昕 孔德新 张园元 贺亚丽 时健伦 李一 丛鹏君 张冠芳 宋士龙 柴冠林 刘杜成 薛利杰 张军 王龙华 张怀磊
99.4 98.7 102.2 102.1
3月5日上午
沈阳市于洪区崇山东路8号 刘东 86906498 15998812611 金剑大厦(长客总站对面) 胡平 86903月5日下午
沈阳市于洪区崇山东路8号 刘东 86906498 15998812611 金剑大厦(长客总站对面) 胡平 86906738 15998812655
706222018208 706221136217 706239493115 706221170727 706241243910 706212353522 706221180413 346243083425 335221126711 706221090621 706221051002 706237164710 706239633409 785245012506 335239431017 706221123523 706221139626 706211202428 706241165817 706239520523 706241243907 706241165826 706241165824 706221135409 706212270912 718243064714 706221191924 706221181325 706248100528 706261144505 706221086519 706237430118
中国服务业全球价值链参与度的测算及国际比较

Measurement and International Comparison of China’s Service Industry Participation in GVC 作者: 牛华[1];张梦锦[1]
作者机构: [1]对外经济贸易大学统计学院,北京100029
出版物刊名: 统计与决策
页码: 127-130页
年卷期: 2020年 第19期
主题词: 全球价值链;服务贸易;世界投入产出表;GDP分解
摘要:服务全球化已成为经济全球化进入新阶段的鲜明特征,服务业已成为支撑经济发展的重要动力、价值创造的主要源泉和国际竞争的主战场。
文章参照Wang等(2017)提出的GDP分解法,构建世界各国服务业全球价值链(GVC)参与程度的理论框架,并利用世界投入产出表测算了2000—2014年中国及主要经济体服务业全球价值链参与度指数。
结果发现:中国服务业生产的增加值中被复出口到世界各国的比例不足3%;在国际比较中,中国服务业GVC参与程度落后于德国、丹麦、爱尔兰及俄罗斯等国。
总体上看,我国服务业全球化参与水平还不高,这迫切需要加快转变理念和思路,着力在深化对外开放、营造良好贸易环境及促进贸易多元化发展上下功夫。
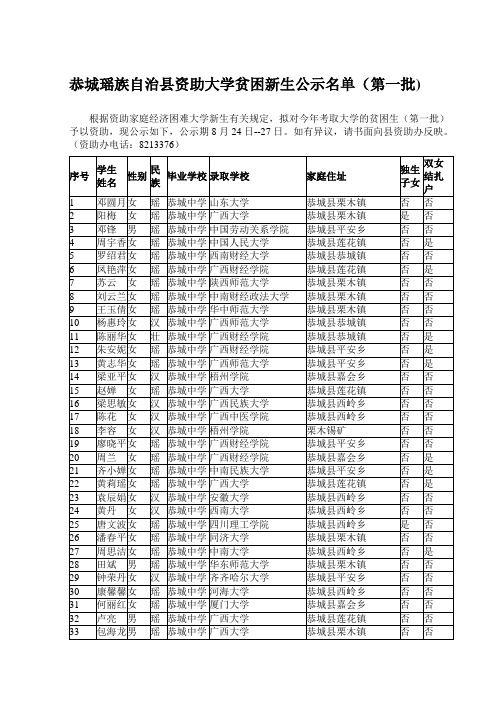
恭城瑶族自治县资助大学贫困新生公示名单(第一批)
否
是
185
邓亚云
女
汉
恭城中学
中国民航飞行学院
恭城西岭
否
否
186
莫存礼
男
壮
恭城中学
上海海事
阳朔高田
否
否
187
卢冬梅
女
瑶
恭城中学
台州学院
恭城莲花
否
是
188
陈宇
女
瑶
恭城中学
广西师范大学
恭城平安
否
否
189
陈思晖
男
汉
恭城中学
中国医科大学
恭城镇
是
否
190
周元浩
男
瑶
恭城中学
大连理工大学
恭城栗木
否
否
191
周玉斌
否
102
陈丹
女
瑶
恭城中学
广西大学预科
恭城县栗木镇
否
是
103
陈娅玲
女
瑶
恭城中学
广西财经学院
恭城县莲花镇
否
是
104
陈冬玲
女
瑶
恭城中学
河池学院
恭城县栗木镇
是
否
105
钟庆花
女
汉
恭城中学
右江民族医学院
平乐县沙子
否
否
106
周晨
女
瑶
恭城中学
百色学院
恭城县栗木镇
否
否
107
齐庆媛
女
汉
恭城中学
玉林师范学院
恭城镇
否
否
108
广西大学
恭城县栗木镇
否
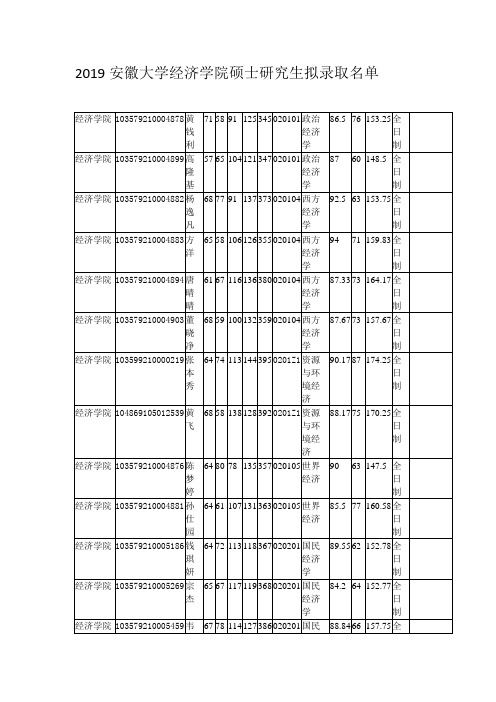
2019安徽大学经济学院硕士研究生拟录取名单
73 80 121 126 400 020205 产业 经济 学
73 80 115 125 393 020205 产业 经济 学
68 84 122 129 403 020205 产业 经济 学
78 62 122 121 383 020205 产业 经济 学
日
雪
学
制
经济学院 103579210004948 张 65 69 114 124 372 020206 国际 91.84 64 157.25 全
夏
贸易
日
男
学
制
经济学院 103579210004958 汤 62 64 104 134 364 020206 国际 86.07 61 152.87 全
培
贸易
经济学院 103579210005269 宗 杰
经济学院 103579210005459 韦
71 58 91 125 345 020101 政治 经济 学
57 65 104 121 347 020101 政治 经济 学
68 77 91 137 373 020104 西方 经济 学
65 58 106 126 355 020104 西方 经济 学
彬
学பைடு நூலகம்
制
经济学院 103579210005201 曾 71 73 120 116 380 020206 国际 86.07 69 156.2 全
芹
贸易
日
学
制
经济学院 103579210005349 王 63 64 126 119 372 020206 国际 86.27 60 154.8 全
希
贸易
初二年级期中生物成绩登统

11.15
地理 物理 总分 校名次 班名次
初二年级期中考试成绩登统
考号 2099 2100 2101 2102 2103 2104 2105 2106 2107 2108 2109 2110 2111 2112 2113 2114 2115 2116 2117 2118 2119 2120 2121 2122 2123 2124 2125 2126 2127 2128 2129 2130 2131 2132 2133 2134 2135 2136 2137 2138 2139 2140 2141 2142 2143 2144 2145 2146 2147 姓名 班级 王梦瑶 02 王雅婷 03 云婷婷 05 刘学敏 06 刘玉凤 07 房晓波 08 闫飞 09 那普豪 01 李元 02 杨嘉乐 04 王靖仙 05 段婧旭 06 苗源春 07 丁嘉蓉 08 李伟 09 徐丽娇 10 张媛 01 高洪涛 02 刘子政 03 马嘉欣 04 袁令卓 05 吕金鑫 07 邬尚亨 08 张雅楠 09 刘庭恺 10 马明曦 01 柯林 02 王克雄 07 边慧娟 06 赵艺宁 07 苏科 01 杨凯慧 02 鲁雅芝 02 张雨欣 09 闫旭 07 刘宇 02 张雨瑾 04 王妍婷 08 白笑证 01 倪阳 02 刘秦 06 张巧媛 04 单雅琪 06 王雨蒙 09 郭永旺 04 凌云子 06 王宁 08 杨茹媛 03 尹晴天 09 语文 数学 英语 政治 历史 生物 79.0 76.0 61.0 67.0 30.0 72.0 50.0 81.0 84.0 18.0 80.0 58.0 52.0 54.0 16.0 65.0 83.0 57.0 45.0 64.0 13.0 8.0 71.0 45.0 78.0 77.0 79.0 64.0 73.0 71.0 81.0 90.0 73.0 64.0 79.0 88.0 87.0 47.0 70.0 59.0 70.0 64.0 71.0 58.0 80.0 68.0 68.0 78.0 65.0
2013 北航3系研究生招生 录取名单

是否录取 是 是 是 是 是 是 是 是 是
导师 韩亮 陶飞 李妮 马耀飞 王江云 李妮 任磊 宋晓 林新
姓名 何雨洵 潘帆 莫昊 鲍乐庭 张亮 马良 李锦坤 袁珍 张小书 荣倩楠
初试成绩 407 377 379 373 348 360 335 346 348 342
复试总成绩 410.91 398.82 393.18 381.18 405.27 391.09 399.64 358.82 355.09 360.91
姓名 范文涛 张越 王少丹 翟刚 张翟 谭润祥 崔晋 周文 孙观楠
初试成绩 413 345 377 423 360 367 341 351 343
复试总成绩 375.36 426.73 386.45 339.27 384.82 376.09 394.18 382.27 374.73
总成绩 788.36 771.73 763.45 762.27 744.82 743.09 735.18 733.27 717.73
总成绩 817.91 775.82 772.18 754.18 753.27 751.09 734.64 704.82 703.09 702.91
是否录取 是 是 是 是 是 是 是 否 否 否
导师 张霖 张霖 龚光红 王江云 张霖 宋晓 刘丽
姓名 田杰荣
初试成绩 338
复试总成绩 342.45
总成绩 是否录取 680.45 是
导师 韩亮
奖学金 一等 二等 二等 二等 二等 二等 二等 二等 二等
备注 工学 工学 工学 工学 工学 工学 工学 工学 工学
奖学金 二等 二等 二等 二等 二等 二等 二等
备注 工程 工程 工程 工程 工程 技术; 考生编号 100063210000880 100063210000887 100063210000885 100063210000886 100063210000888 100063210502953 100063210501195 100063210000889 100063210500354 工程硕士 考生编号 100063210502958 100063210000930 100063210000927 100063210000891 100063210000957 100063210504969 100063210503637 100063210503625 100063210000877 100063210504058 强军硕士 考生编号 100063210002503
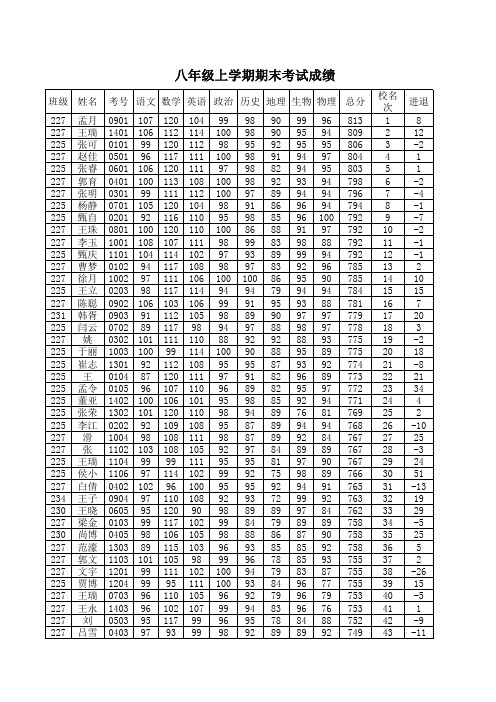
八年级上学期期末成绩
227 231 225 227 238 225 231 226 235 225 228 226 237 227 225 233 230 235 228 227 236 229 233 226 225 234 226 228 225 233 226 231 232 237 228 238 230 236 225 225 229 231 226 232 226 225 237
95 94 98 95 98 90 92 97 98 93 90 93 99 95 93 98 96 90 94 98 90 97 94 90 91 98 98 90 92 93 100 95 96 96 88 93 94 96 98 94 94 99 96 94 98 96 90
90 94 91 92 84 90 91 85 91 88 81 89 95 96 92 89 90 85 97 93 96 80 92 85 92 83 83 79 74 90 81 83 78 87 80 80 78 89 71 84 84 76 67 78 78 84 80
45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91
34 28 1 -22 9 -3 -29 -33 -19 43 20 -7 35 7 -19 -15 -17 6 -17 -14 1 -30 9 30 -13 54 23 14 22 8 2 36 10 -6 -10 8 -14 35 -52 6 41 15 -23 22 -5 3 18
101 100 90 92 99 95 99 91 100 92 85 85 90 100 92 88 98 94 103 81 87 99 90 96 96 80 93 93 95 84 91 98 90 88 98 91 94 88 88 97 95 90 92 86 104 96 98
2017国考广西国税局面试分数线及面试名单(柳州市)

莫纯丽
3月4日
陈海娟
黄志娟
柳州市融安县国家税务局科员(一)(0701051001)
105.6
张杨
3月5日
钟贻刚
莫若捷
柳州市融安县国家税务局科员(二)(0701051002)
115.4
路远梅
3月5日
黄后浪
周凌云
柳州市融安县国家税务局科员(三)(0701051003)
107.6
黄丽
3月4日
段祥涛
韦秋月
3月5日
韦如栋
侯惠娇
柳州市柳江县国家税务局科员(三)(0701048003)
118.1
谭秋金
3月4日
王宇欣
谭黄鲜
柳州市柳江县国家税务局科员(四)(0701048004)
144.9
陈兆瑜
3月4日
袁茂森
张华
柳州市柳江县国家税务局科员(五)(0701048005)1Fra bibliotek6.6马涛
3月4日
邓胜琳
蓝丽姣
柳州市柳城县国家税务局科员(一)(0701049001)
刘炫汝
柳州市鹿寨县国家税务局科员(一)(0701050001)
107.9
覃晓晓
3月5日
华泽英
黄静
陶玉婵
张巧青
韦雪冰
柳州市鹿寨县国家税务局科员(二)(0701050002)
130.1
邱俏梅
3月5日
汤晓钰
陈凯欣
柳州市鹿寨县国家税务局科员(三)(0701050003)
127.9
金星宇
3月4日
蓝云岑
邓海川
柳州市鹿寨县国家税务局科员(四)(0701050004)
135.9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信阳师范学院华锐学院本科毕业论文专业数学与应用数学专业年级2010级姓名张锦锦论文题目古典概型及其应用指导教师任园园职称讲师2014年4月22日目录摘要 (1)关键词 (1)Abstract (1)Key Words (1)引言 (1)1.古典概率思想的发展 (1)2.古典概率的定义与性质 (2)2.1概率的古典定义 (2)2.2古典概率的性质 (3)3.古典概率的计算 (4)3.1直接计算古典概率 (4)3.2间接计算古典概率 (5)3.3组合分析公式计算古典概率 (5)4.古典概型及其应用 (7)4.1彩票问题 (7)4.2配对问题 (9)4.3分房问题 (10)5.小结 (11)参考文献 (12)致谢 (13)古典概型及其应用学生姓名:张锦锦学号:20100401101数学与计算机科学系 2010数学与应用数学本科2班指导老师:任园园职称:讲师摘要:本文首先从发展、定义、性质三方面对古典概率进行了简析,然后介绍了古典概率的几种常用计算方法,如直接计算、间接计算、运用组合分析公式等方法,最后探讨了古典概率在彩票、配对、分房等方面的实际应用.关键词:古典概率;性质;计算;应用Abstract: Firstly, from the development, definition, nature three aspects of classical probability were analyzed briefly, and then introduces several common calculation method of classical probability, such as direct calculation, calculation, using the combination of indirect analysis formula method, finally discusses the practical application of classical probability in the lottery, paired, housing and so on.Key Words:Classical probability;Property; C alculate; Apply.引言在概率论中我们最先学到的知识就是古典概型,古典概型是概率论的起源,是一切概率问题的基础,它包括了许多实际问题,有很广泛的应用,本论文首先从定义、性质方面对古典概率进行了简析,然后介绍了古典概率的几种常用计算方法,如直接计算、间接计算、运用组合分析公式等方法,目的是更加深层次的理解古典概型的内涵与,找出解决问题的根本方法,通过了解古典概率的计算方法,使人们在解题过程中能正确分析题意,运用适当的方法获得准确的答案,从而提高分析问题和解决问题的能力,最后对概率中比较实际的古典概型问题如彩票问题、配对问题、分房问题进行了探讨,旨在说明古典概型在生活中具有广泛的应用.1.古典概率思想的发展为了了解古典概率思想的产生、发展和形成, 我们划分几个阶段对其进行探讨.萌芽时期:这一时期的代表人物和作品是文艺复兴时期意大利数学家卡尔达诺及其于1526 年写成, 但在他死后很长时间才在1663 年出版的遗著《论机会游戏》( 另译《游戏机遇的学说》) .正是在他的这部有关论赌博的著作中, 卡尔达诺首次给出了等可能性事件发生概率的一个粗略定义:一个特殊结果发生的概率等于得到这一结果的各种可能方式的数目除以“全范围”.由此可见, 卡尔达诺给出的定义正是拉普拉斯古典概率定义()nm A P =的原始形式. 计算时期:这一时期的主要代表人物是法国数学家帕斯卡和费马、荷兰数学家惠更斯 .帕斯卡和费马的主要工作是赌博中赌金的“公平”分配和计算.1654 年, 帕斯卡和费马通信讨论一些赌博中提出的问题,其中一个最有名的问题就是“点数问题”,此为帕斯卡的朋友梅累所提出,这一问题是古典概率的经典题例并影响日后古典概率思想的发展.惠更斯的工作主要是推广了帕斯卡和费马关于赌金分配的计算, 并于1657 年出版了《论赌博中的计算》一书, 该书被认为是概率论最早的论著.逻辑推理、公式推导与研究对象、应用的扩大时期:这一时期的重要代表著作有瑞士伯努利家族中的雅各布--伯努利于1713 年出版的遗著《猜度术》 ( 又译《推想的艺术》) 、其侄子尼古拉--伯努利于1709 年通过的博士论文《关于猜度术在法律中的用途》、法( 英) 数学家棣莫弗1711 年写成的《抽签的计量》和1718 年出版的《机会论》及《分析杂论》、辛普生的《论机会的性质与规律》、法国数学家蒲丰于1777 年发表的《或然性算术试验》等.全面总结与形成时期:这一时期的主要代表人物和著作是法国数学家、天文学家拉普拉斯和他的《概率的分析理论》( 1812 年第1版) , 以及1814 年《概率的分析理论》第2版增加了一个长达150 页的绪论, 该绪论同年刊印成单行本, 题为《概率的哲学导论》,《概率的哲学导论》论述概率论定义、发展历史、概率计算的一般原理与应用,在这部著作中, 拉普拉斯给出了概率论的七个一般原理, 这七个原理是现在概率教科书中古典概率部分的核心内容.2.古典概率的定义与性质2.1 概率的古典定义下面我们讨论一类最简单的随机试验.这种随机试验具有下列两个特征:(1)试验的所有样本点只有有限个(有限样本空间);(2)试验中每个样本点发生的可能性是相等的(等可能性).这类随机试验在概率论发展初期即被注意到,许多最初的概率论结果也是对它作出的,一般把这类随机试验的数学模型称为古典概型.古典概型在概率论中占有相当重要的地位.一方面,由于它简单,对它的讨论有助于直观地理解概率论的许多基本概念;另一方面,古典概型的计算在产品质量抽样检查等实际问题以及理论物理的研究中都有重要作用.定义2.1.1 对于给定的古典概型,若样本点总数为n ,事件A 包括其中的m 个,则定义事件A 的概率为()A P =nm =样本点总数包括的样本点数事件A =样本点总数的有利样本点数A . 常称之为古典概率(事件A 包括的样本点数,习惯上常常称为A 的有利样本点数). 例如 掷一枚匀称的骰子,观察正面朝上的点数,显然这是一个古典概型.令=i ω“掷出点数为i ”,6,,2,1 =i ,=B “掷出点数为偶数点”,则},,,,,{654321ωωωωωω=Ω,6=n ;},,{642ωωω=B ,3=m ,所以()B P =n m =样本点总数的有利样本点数B =63=21. 2.2 古典概率的性质古典概率具备以下基本性质:(1)非负性 ()10≤≤A P ;(2)正规性 ()1=ΩP (样本点全体所成的集合称为样本空间,记为Ω);(3)()0=ΦP (Φ为空集);(4)有限可加性 设事件m A A A ,,,21 互斥,则()()()()m m A P A P A P A A A P ++= 2121.古典概率作为概率的一类,还具有一些其他性质.性质2.2.1 对任一随机事件A ,有()()A P A P -=1.性质2.2.2 若B A ⊃,则()()()B P A P B A P -=-.推论 若B A ⊃,则()()B P A P ≥.性质2.2.3 对于任意两个事件A 、B ,都有()()()()AB P B P A P B A P -+= . 3.古典概率的计算古典概率是概率论发展初期的主要研究对象,在概率论的教程中至今仍占有很重要的地位,下面介绍几种计算古典概率的方法.在古典概型中,随机事件A 的概率()A P 的计算公式是:()A P =nm . 其中n 表示有限样本空间Ω中基本事件的总数,m 表示事件A 在Ω中所含的基本事件数,且各个基本事件发生的可能性是相等的.因此,对于古典概率计算问题来说,根据题意构造样本空间Ω是至关重要的;一旦样本空间构造出来,基本事件总数也就随之确定.若事件A 在Ω中所含的基本事件数易知,则事件A 的概率()A P 就迎刃而解了;初学概率的学生常感到解古典概率题难,首先就是难于构造样本空间;其次,难于准确地理解描述事件的一些术语的含义,如“至少”、“至多”、“恰有”、“指定”、“都”、“不都”、“都不”等;如果学生对其含义理解不清,那么在计算事件A 所含的基本事件数,或将A 表示为几个简单事件之和时,往往会发生错误,以致不能得到()A P 的正确结果.3.1 直接计算古典概率当问题比较简单时,可以直接计算m 和n .例1 从9,,2,1,0 十个数字中任取一个数字,求取得奇数数字的概率.解 基本事件的总数10=n ,设事件A 表示取得奇数数字,则它所含的基本事件数为5=m ,从而所求概率为()5.0105==A P .像这类总数不大的对象,有时可以采用枚举法.枚举法是指把对象一一列举出来进行计数的办法,关键是要做到枚举时不重复、不遗漏.枚举所有等可能的情况,计算出m ,n 的值以计算概率,这不失为一个朴素、有效地策略.3.2 间接的计算古典概率当直接计算有困难时,可以考虑利用概率的性质和定理,间接地计算事件的概率.例2 一批产品共有50个,其中45个是合格品,5个是次品,从这批产品中任取3个,求其中有次品的概率.解 设=A {取出的3个产品中有次品},=A {取出的3个产品全是正品},则事件A 与A 互为对立事件,而()724.0350345==C C A P , 从而所求事件的概率为()()276.01=-=A P A P .3.3 组合分析公式计算古典概率古典概率的计算经常要用到排列与组合公式,为此先复习一下有关知识.全部组合分析公式的推导基于下列两条原理:乘法原理 若一项工作需依次经过1A 和2A 两个过程,1A 过程有1n 种方法,2A 过程有2n 种方法,则完成该项工作共有21n n ⨯种方法.加法原理 若一项工作可以有两种不同的过程1A 和2A 来完成,1A 过程有1n 种方法,2A 过程有2n 种方法,则完成该项工作共有21n n +种方法.显然这两条原理可以拓广到多个过程的场合.(1)排列从包含有n 个元素总体中取出r 个来进行排列,这是既要考虑到取出的元素也要顾及到其排列顺序.这种排列可分为两类:第一种是有放回选取,这时每次选取都是在全体元素中进行,同一元素可被重复选中;另一种是无放回选取,这时一个元素一旦被取出,便立刻从总体中去除,因此每个元素至多被选一次,在后一种情况,必有n r ≤.①在有放回选取中,从n 个元素中取出r 个来进行排列,这种排列称为有重复排列,其总数为r n .②在无放回选取中,从n 个元素中取出r 个来进行排列,这种排列称为选排列,其总数为)1()2)(1(+---=r n n n n A r n ,特别当n r =时,称为全排列,此时!n A n n=. (2) 组合①从n 个元素中取出r 个而不考虑其顺序,称为组合,其总数为:)!(!!!)1()1(!r n r n r r n n n r A C r n rn-=+--== 这里r n C 称为组合数或二项系数,它是二项展开式∑=-=+n r r n r r n nb a C b a 0)((规定10=n C )中r n r b a -的系数.显然,组合数有以下性质:r n n r n C C -=,r n n r n C rn C --=1. ②若n r r r k =+++ 21,把n 个不同的元素分成k 个部分,其中第一部分1r 个,第二部分2r 个,…,第k 部分k r 个,则不同的分法有!!!!2111211k r r r n r r n r n r r r n C C C k k =----- 种,上式中的数称为多项系数,因为它是n k x x x )(21+++ 展开式中k r k r r x x x 2121的系数,当2=k 时,即为组合数.③若n 个元素有1n 个带足标“1”,2n 个带足标“2”,…,k n 个带足标“k ”,且n n n n k =+++ 21,从这n 个元素中取出r 个,使得带足标“i ”的元素有i r 个(k i ≤≤1),而r r r r k =+++ 21,这时不同取法的总数为k kr n r n r n C C C 2211这里当然要求i i n r ≤.例 3 已知一批产品共有N 件,其中有M 件次品,从中任取n 件,试求其中恰有k 件次品的概率.解 这是一个无顺序的问题,可用组合公式求解.设=A {所取n 件中恰有k 件次品}.样本点总数为n N C ,有利于A 的样本点数可这样考虑:N 件产品分成两类,“1”类是次品有M 件,“2”类是正品有M N -件,由组合公式③,A 的有利样本点数为k n M N k M C C --,从而()n Nk n M N k M C C C A P --=, 其中),min(,,2,1,0n M k =.这是古典概率计算中的一个典型问题,其概率称为超几何分布概率.它有着多方面的应用,特别是产品检验方面起很大作用.当然古典概率的题型千变万化,其解法也多种多样,但不管怎样,我们都发现这种题型往往离不开排列组合(虽然有可能不是最简单的),所以这就要求我们在解古典概率时,必须熟练掌握排列组合的相关知识,对题目认真分析,利用有关公式,寻求好的解题方法,从而得到正确结果.4.古典概型及其应用现实世界中许多事件的不确定性可以建立数学模型用概率知识进行判断与决策,如常见的抽样模型(放回抽样和不放回抽样)、球盒模型、配对问题、超几何分布等等,下面就实际问题中常见的一些问题应用古典概率知识作简要分析.4.1彩票问题在我国各省市发行者各种电脑彩票,花两元钱买一张彩票,就中几百万乃至几千万的巨额奖金,这大概是很多人梦寐以求的事,可是这样的机会具体有多大呢?我们以某省发行的“36选6+1”福利彩票为例.“36选6+1”方案是这样的:先从01—36个号码中一个一个的摇出6个基本号,再从剩下的30个号码中摇出一个特别号码;从01—36个号码中任选7个组成一注(不可重复),根据单注号码与中奖号码相符的个数多少确定相应的中奖等级,不考虑号码顺序.这两种方案的中奖等级如下:一等奖:7个号码全中(中6个基本号码及特殊号码);二等奖:中6个基本号码,特别号码未中;三等奖:中5个基本号码及特别号码;四等奖:中5个基本号码,特别号码未中;五等奖:中4个基本号码及特别号码;六等奖:中4个基本号码,特别号码未中;七等奖:中3个基本号码及特别号码.下面我们来计算一下每个中奖等级的中奖概率,以一注为单位,计算每注彩票的中奖概率.基本事件数:从36个数中任取7个,不考虑顺序,共有736C n =种取法.一等奖:七个号码全中,只有一种可能,故一等奖有利事件数11=k .因此一等奖中奖概率为=1P =n k 1=7361C 7101979.1-⨯. 二等奖:六个基本号码全中,特别号未中,故二等奖有利事件数129662C C k =.因此二等奖中奖概率为=2P =n k 2=73612966C C C 6104739.3-⨯. 三等奖:六个基本号码中五个,特别号中了,故三等奖有利事件数11129563C C C k =.因此三等奖中奖概率为=3P =n k 3=7361112956C C C C 5100843.2-⨯. 四等奖:六个基本号码中五个,特别号未中,故四等奖有利事件数229564C C k =.因此四等奖中奖概率为=4P =n k 4=73622956C C C 4109182.2-⨯. 五等奖:六个基本号码中四个,特别号中了,故五等奖有利事件数11229465C C C k =。
