平面力系的简化与平衡
合集下载
第二章2 平面任意力系的简化,平衡条件和平衡方程
FRy ' Fiy ' Fiy Fy
主矢大小 方向
2 2 FR ( Fix ) ( Fiy )
Fix cos( F 'R , i ) FR
Fiy cos( F 'R , j ) FR
作用点: 作用于简化中心 上
主矩
MO MO (Fi )
Fr Ft tan20 3.64P 1
F 0
x
FBx Fr 0
F
y
0
FBy P P2 Ft 0
FBy 32P 1
FBx 3.64P 1
取小轮，画受力图.
F 0 Fy 0 M 0
x
A
FAx Fr ' 0
FAy Ft 'P 1 0
将该力系中心的位置坐标 记为 xC
1 xC F qx 2 ql 2 dx l 3 0
l
l
y
q
Foy
O
xc
F
q
x
Fox
x l dx
FA
A
q
ql 2 l 2 3
最后，利用平面力系的平衡方程求 得 3 个未知的约束反力：
y
由： M Oz ( Fi ) 0
n i 1
xc
主矩：
M O M O ( F ) 3F1 1.5 P 1 3.9 P 2 2355kN m
（2）求合力其作用线位置：
M O M O FR x FRy y FRx x FR' y y FR' x
x 3.514
（3）求合力作用线方程：
工程力学第二章力系简化与平衡
一、平面任意力系的平衡方程
1 平衡条件
力系的主矢和对任意点的主矩都等于零
即 F 0 M 0
R
o
F R
(
F x
)2
(
F y
)2
M O
M
O
(
F i
)
2 平衡方程
Fx 0
X 0
Fy 0
或 Y 0
M o (F) 0
M o 0
M i
i1
二、 平面任意力系的简化研究
1、力的平移定理
作用在刚体上力F的作用线可等效 地平移到同一刚体上的任意一点，但 须附加一力偶，此附加力偶的矩值等 于原力F对平移点的力矩。
M M (F ) Fd
B
B
２ 力与力偶的合成 是力线平移的逆过程。
3、力线平移定理在简化中的应用
F F
解得 FC 28.28kN, FAx 20kN, FAy 10kN
例6 已知：P1 700kN, P2 200kN, 尺寸如图；
求：（1）起重机满载和空载时不翻倒，平衡载重P3； （2）P3=180kN，轨道AB给起重机轮子的约束力。
解： 取起重机，画受力图。 满载时，FA 0, 为不安全状况
（2）、求合力及其作用线位置。
d
Mo FR'
2355 3.3197m 709.4
x
d
3.514m
cos 900 70.840
（3）、求合力作用线方程
Mo Mo FR x FRy y FRx x FR'y y FR'x
即 2355 x670.1 y 232.9
建筑力学-第4章 平面力系的简化与平衡方程.
平面固定端约束
=
=
≠
=
3、 平面任意力系的简化结果分析
=
FR 0 M O 0
合力
合力作用线过简化中心
FR 0 M O 0
合力
合力作用线距简化中心M O
FR
其中
MO d FR
M o FRd
M o ( FR ) M O M O ( Fi )
FR FR FR
q 20 kN
求： 固定端A处约束力.
, l 1m; F 400kN, m
解： 取T型刚架，画受力图. 1 其中 F1 q 3l 30kN 2 Fx 0 FAx F1 F sin 600 0 解得 FAx 316.4kN
F Ay P F cos 60 0 Fy 0 解得 FAy 300kN
A
M
解得
0
12 FBy 10 P 6 P 1 4P 2 2 P 5F 0
FBy 77.5kN
iy
F
解得
0 FAy FBy 2 P P 1P 2 0
FAy 72.5kN
取吊车梁,画受力图.
M
解得
D
0
8FE' 4P 1 2P 2 0
Fx 0
Fy 0
FAx FB 0
FAy P 1P 2 0
M
解得
A
0
FB 5 1.5 P 1 3.5 P 2 0
FAy 50kN
FB 31kN
FAx 31kN
例4-4 已知： P, q, a, M pa; 求： 支座A、B处的约束力. 解：取AB梁，画受力图.
静力平衡方程应用—平面任意力系的简化与平衡
O
O′
O
d
d
FR″
d
MO FR '
FR O′
1.2 平面任意力系简化结果讨论
(4) FR =0，MO =0 原力系为平衡力系。
物体在此力系作用下处于平衡状态。
2.添平加面标题任意力系平衡方程
2. 平面任意力系平衡方程 2.1 基本形式平衡方程
平面任意力系平衡的必要和充分条件是：力系的主矢和对任一点的主矩都等于零。
n
M O M O (Fi ) i 1
平面任意力系向作用面内任一点O 简化，可得一个力和一个力偶。这个力 等于该力系的主矢，作用线通过简化中心O 。这个力偶的矩等于该力系对于点 O 的主矩。主矢与简化中心的位置无关，主矩与简化中心的位置有关。
1.2 平面任意力系简化结果讨论
(1) 平面任意力系简化为一个力偶的情形
2. 平面任意力系平衡方程 2.3三力矩式平衡方程
M A (Fi )=0 M B (Fi )=0
MC (Fi )=0
附加条件是：A、B、C 三点不共线。 注意：
以上格式分别有三个独立方程，只能求出三个未知数。
3添.平加面标题平行力系平衡方程
3. 平面平行力系平衡方程
力的作用线在同一平面且相互平行的力系称平面平行力系。 平面平行力系作为平面任意力系的特殊情况，当它平衡时，也应满足平
FR 0，MOΒιβλιοθήκη 0原力系与一个力偶等效，主矩与简化中心的位置无关。 (2) 平面任意力系简化为一个合力的情形
FR 0，MO =0
原力系与一个力等效，作用线恰好通过简化中心。
1.2 平面任意力系简化结果讨论
(3) FR 0，MO 0 原力系还可进一步简化为一合力。
建筑力学第三章 平面力系的平衡方程
刚体等效于只有一个力偶的作用，（因为力偶可以在刚 体平面内任意移动，故这时，主矩与简化中心O无关。）
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时， 简化结果就是合力（这个力系的合力）, FR FR'。（此时
与简化中心有关，换个简化中心，主矩不为零）
重庆大学出版社
建筑力学
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
重庆大学出版社
建筑力学
[例] 已知：Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求：
BC杆拉力和铰A处的支座反力？
解：（1）选AB梁为研究对象。
C
（2）画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
Байду номын сангаас
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
（3）列平衡方程，求未知量。
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
重庆大学出版社
建筑力学
物系平衡问题的特点： ①物体系统平衡，物系中每个单体也是平衡的。 ②每个单体可列3个（平面任意力系）平衡方程，整个系统
可列3n个方程（设物系中有n个物体）。
解物系问题的一般方法：
机构问题： 个体 个体
个体
“各个击破”
力系中各力对于同一点之矩的代数和。
重庆大学出版社
建筑力学
3.2平面力系的平衡方程及应用
FR=0， MO =0，力系平衡
FR =0 为力平衡
MO =0 为力偶也平衡 平面力系平衡的充要条件为：
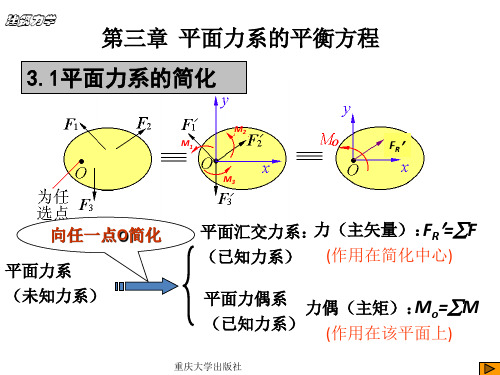
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时， 简化结果就是合力（这个力系的合力）, FR FR'。（此时
与简化中心有关，换个简化中心，主矩不为零）
重庆大学出版社
建筑力学
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
重庆大学出版社
建筑力学
[例] 已知：Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求：
BC杆拉力和铰A处的支座反力？
解：（1）选AB梁为研究对象。
C
（2）画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
Байду номын сангаас
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
（3）列平衡方程，求未知量。
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
重庆大学出版社
建筑力学
物系平衡问题的特点： ①物体系统平衡，物系中每个单体也是平衡的。 ②每个单体可列3个（平面任意力系）平衡方程，整个系统
可列3n个方程（设物系中有n个物体）。
解物系问题的一般方法：
机构问题： 个体 个体
个体
“各个击破”
力系中各力对于同一点之矩的代数和。
重庆大学出版社
建筑力学
3.2平面力系的平衡方程及应用
FR=0， MO =0，力系平衡
FR =0 为力平衡
MO =0 为力偶也平衡 平面力系平衡的充要条件为：
理论力学平面力系的简化和平衡
原力偶系的合力偶矩
n
M Mi i 1
只受平面力偶系作用的刚体平衡充要条件：
n
M Mi 0 i 1
对BC物块对B点取矩，以逆时针为正列方程应为：
M 2 M B (FC ) M FCY a FCx b M FC (b a) cos45 0
[例] 在一钻床上水平放置工件,在工件上同时钻四个等直径 的孔,每个钻头的力偶矩为 m1m2 m3 m4 15Nm 求工件的总切削力偶矩和A 、B端水平反力?
两轴不平行即 条件：x 轴不 AB
可，矩心任意
连线
mA (Fi ) 0 mB (Fi ) 0 mC (Fi ) 0
③三矩式 条件：A,B,C不在
同一直线上
上式有三个独立方程，只能求出三个未知数。
4. 平面一般力系的简化结果分析
简化结果： 主矢R ，主矩 MO ，下面分别讨论。 ① R =0， MO =0，则力系平衡,下节专门讨论。 ② R =0,MO≠0 即简化结果为一合力偶, MO=M 此时刚
解除约束，可把支反
力直接画在整体结构
的原图上）
解除约束
由
mA (Fi
)
0
P2a N B
3a0,
N B
2P 3
X 0 XA 0
Y 0 YB NB P0,
YA
P 3
2.5物体系统的平衡、静定与超静定问题
1、物体系统的平衡问题 物体系统（物系）：由若干个物体通过约束所组成的系统叫∼。 [例]
外力：外界物体作用于系统上的力叫外力。 内力：系统内部各物体之间的相互作用力叫内力。
N2个物体受平面汇交力系（或平面平行力系）
X 0 Y 0
2*n2个独立平衡方程
N3个物体受平 X 0 面任意力系 Y 0
第四章 平面力系简化平衡方程
第四章 平面力系的简化与平衡方程
工程实例：
厂房吊车梁实例：
平面任意力系：
本章任务：
（1）掌握平面任意力系向一点的简化---主矢 和主矩 （2）掌握平面任意力系的平衡条件· 平衡方程 （3）掌握物系的平衡问题（包括了解考虑摩 擦的物系平衡问题的处理）
一、平面一般力系向一点(简化中心O点)简化：
解（1）取整体为研究对 象，作受力图如图；
（2）列平衡方程， 求解未知力。 ∑X=0，XA +qL =0 XA A
1.5L
q
B
NB
L
X
∑Y=0，YA +NB
=0
YA
∑ mA（Fi）=0 1.5LNB -0.5L×qL =0
XA =-qL(←)
NB =qL/3
YA = -qL/3(↓)
[例4-4]十字交叉梁用三个链杆支座固定，如图所示。求在 水平力P的作用下各支座的约束反力。
[例4-1] 在边长为a=1m的正方形的四个顶点上，作用有 F1、 F2 、 F3 、F4等四个力，如图所示。已知F1=40N，F2=60N， F3=60N，F4=80N。试求该力系向A点简化的结果。
解：R′x=40cos45°+60cos45°+60cos60°-80sin30°=60.7N R′y=40sin45°-60sin45°-60sin60°- 80cos30°=-106.1N R′=√(R′ x)2+(R′ y)2=122.4N cos=60.7/122.4 , =60.27°
1.若R´=0，Mo=0，原力 系为平衡力系，物体处于 平衡状态。
平衡
2．若 R´=0，Mo≠0， 原力系与一力偶等效， 其力偶矩就是原力系 的 主矩。并且简化结 果与 简化中心位置无关。
工程实例：
厂房吊车梁实例：
平面任意力系：
本章任务：
（1）掌握平面任意力系向一点的简化---主矢 和主矩 （2）掌握平面任意力系的平衡条件· 平衡方程 （3）掌握物系的平衡问题（包括了解考虑摩 擦的物系平衡问题的处理）
一、平面一般力系向一点(简化中心O点)简化：
解（1）取整体为研究对 象，作受力图如图；
（2）列平衡方程， 求解未知力。 ∑X=0，XA +qL =0 XA A
1.5L
q
B
NB
L
X
∑Y=0，YA +NB
=0
YA
∑ mA（Fi）=0 1.5LNB -0.5L×qL =0
XA =-qL(←)
NB =qL/3
YA = -qL/3(↓)
[例4-4]十字交叉梁用三个链杆支座固定，如图所示。求在 水平力P的作用下各支座的约束反力。
[例4-1] 在边长为a=1m的正方形的四个顶点上，作用有 F1、 F2 、 F3 、F4等四个力，如图所示。已知F1=40N，F2=60N， F3=60N，F4=80N。试求该力系向A点简化的结果。
解：R′x=40cos45°+60cos45°+60cos60°-80sin30°=60.7N R′y=40sin45°-60sin45°-60sin60°- 80cos30°=-106.1N R′=√(R′ x)2+(R′ y)2=122.4N cos=60.7/122.4 , =60.27°
1.若R´=0，Mo=0，原力 系为平衡力系，物体处于 平衡状态。
平衡
2．若 R´=0，Mo≠0， 原力系与一力偶等效， 其力偶矩就是原力系 的 主矩。并且简化结 果与 简化中心位置无关。
平面力系-平面汇交力系的简化与平衡方程(常用版)
平面力系-平面汇交力系的简化与平衡方程（常用版）(可以直接使用，可编辑完整版资料，欢迎下载）第2章平面力系192.1 平面汇交力系的简化与平衡方程 (19)2.2 力对点之矩合力矩定理 (24)2.3 力偶及其性质 (27)2.4 平面力偶系的合成与平衡方程 (30)2.5 平面一般力系的简化与平衡方程 (32)2.6 物体系统的平衡 (40)*附录Ⅱ：机械应用实例 (49)第2章平面力系本章主要介绍平面力系的简化与平衡问题，平面状态下物系平衡问题的解法。
按照力系中各力的作用线是否在同一平面内，可将力系分为平面力系和空间力系。
若各力作用线都在同一平面内并汇交于一点，则此力系称为平面汇交力系。
按照由特殊到一般的认识规律，我们先研究平面汇交力系的简化与平衡规律。
2.1 平面汇交力系的简化与平衡方程2.1.1 概述设刚体上作用有一个平面汇交力系F1、F2、…、F n，各力汇交于A点（图2-1a）。
根据力的可传性，可将这些力沿其作用线移到A点，从而得到一个平面共点力系（图2-1b）。
故平面汇交力系可简化为平面共点力系。
a ）b ）图2-1连续应用力的平行四边形法则，可将平面共点力系合成为一个力。
在图2-1b 中，先合成力F 1与F 2（图中未画出力平行四边形），可得力F R1，即 F R1＝F 1+ F 2；再将F R1与F 3合成为力F R2，即F R2＝F R1+ F 3；依此类推，最后可得F R ＝F 1+ F 2+…+ F n ＝∑F i （2-1）式中 F R 即是该力系的合力。
故平面汇交力系的合成结果是一个合力，合力的作用线通过汇交点，其大小和方向由力系中各力的矢量和确定。
因合力与力系等效，故平面汇交力系的平衡条件是该力系的合力为零。
2.1.2力在坐标轴上的投影过F 两端向坐标轴引垂线（图2-2）得垂足a 、b 、a'、b'。
线段ab 和a'b'分别为F 在x 轴和y轴上投影的大小，投影的正负号规定为：从a 到b （或从a'到b'）的指向与坐标轴正向相同为正，相反为负。