2010-2011学年山东省德州一中高二(下)模块检测数学试卷(选修1-1、1-2)(文科)
山东省德州一中10-11学年高二下学期期中考试(数学)A

德州一中2010-2011学年第二学期高二年级模块检测数 学 试 题 (A 卷) 2011年4月本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至6页,共150分,考试时间120分钟。
第Ⅰ卷(共60分)一、选择题(本大题共12个小题,每个小题都有四个选项,其中,只有一个选项正确,请将正确选项的题号涂在答题卡的相应位置上,答对一个小题得5分)1、一质点运动方程()212s t gt =(29.8 /g m s =),则 3 t s =时的瞬时速度为( ) A . 20 B . 49.4 C . 29.4 D . 64.12、曲线2122y x x =-在点31,2⎛⎫- ⎪⎝⎭处的切线的倾斜角为( )A . -1B . 45°C . -45°D . 135°3、若()()0, 1, 1, 1, 1, 0a b =-=,且()a b a λ+⊥,则实数λ的值是( ) A . -1 B . 0 C . 1 D . -24、平面的一条斜线段长是它在平面内射影长的2倍,则斜线与平面所成的角的大小为( ) A . 30° B . 60° C . 45° D . 120°5、命题“二次方程2230x x a +-=有两个不等的实数根”的推理形式是( )A .三段论推理B .完全归纳推理C . 传递推理D .合情推理 6、若1123ln 2ax dx x ⎛⎫+=+ ⎪⎝⎭⎰,则a 的值是( )A . 6B . 4C . 3D . 27、函数()31f x ax x =++有极值的充要条件是( ) A . 0a > B . 0a ≥ C . 0a < D . 0a ≤ 8、已知()()()()212f x f x x N f x *+=∈+,()11f =,猜想()f x 的表达式为( ) A . ()422x f x =+ B . ()21f x x =+ C . ()11f x x =+ D . ()221f x x =+ 9、用反证法证明命题:若系数都为整数的一元二次方程()200ax bx c a ++=≠有有理根,那么,,a b c 中至少有一个是偶数。
高二数学(文科)(选修1—1)考试题
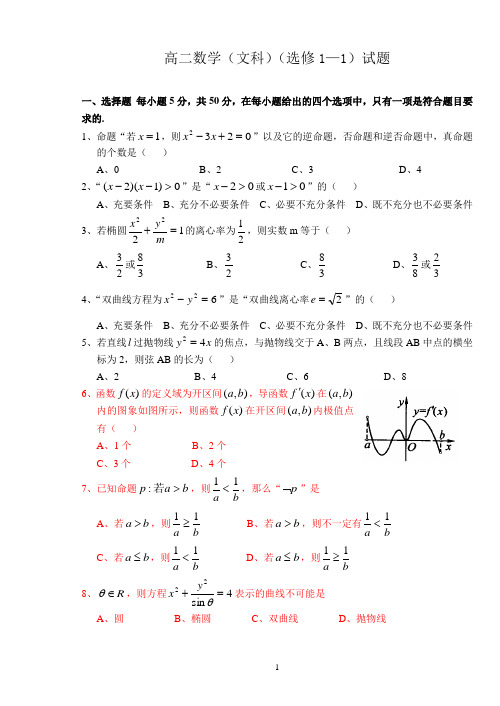
高二数学(文科)(选修1—1)试题一、选择题 每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1、命题“若1=x ,则0232=+-x x ”以及它的逆命题,否命题和逆否命题中,真命题的个数是( )A 、0B 、2C 、3D 、4 2、“0)1)(2(>--x x ”是“02>-x 或01>-x ”的( )A 、充要条件B 、充分不必要条件C 、必要不充分条件D 、既不充分也不必要条件3、若椭圆1222=+my x 的离心率为21,则实数m 等于( ) A 、23或38 B 、23 C 、38 D 、83或324、“双曲线方程为622=-y x ”是“双曲线离心率2=e ”的( )A 、充要条件B 、充分不必要条件C 、必要不充分条件D 、既不充分也不必要条件 5、若直线l 过抛物线x y 42=的焦点,与抛物线交于A 、B 两点,且线段AB 中点的横坐标为2,则弦AB 的长为( )A 、2B 、4C 、6D 、8 6、函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a内的图象如图所示,则函数)(x f 在开区间),(b a 内极值点有( )A 、1个B 、2个C 、3个D 、4个 7、已知命题b a p >若:,则ba 11<,那么“p ⌝”是 A 、若b a >,则b a 11≥ B 、若b a >,则不一定有b a 11< C 、若b a ≤,则b a 11< D 、若b a ≤,则ba 11≥ 8、R ∈θ,则方程4sin 22=+θy x 表示的曲线不可能是 A 、圆 B 、椭圆 C 、双曲线 D 、抛物线9、一物体作直线运动,其运动方程为23t t s -=,其中位移s 单位为米,时间t 的单位为秒,那么该物体的初速度为A 、0米/秒B 、—2米/秒C 、3米/秒D 、3—2t 米/秒 10、下列说法正确的是 ( )A 、函数在闭区间上的极大值一定比极小值大.B 、函数在闭区间上的最大值一定是极大值.C 、对于函数12)(23+++=x px x x f ,若6||<P ,则)(x f 无极值.D 、函数)(x f 在区间),(b a 上一定存在最值.二、填空题 本大题共5小题,每小题5分,共25分,把答案填在题中横线上.11、已知动点M ),(y x 满足|1243|)2()1(522++=-+-y x y x ,则M 点的轨迹曲线为 . 12、函数],2[,sin ππ∈-=x x x y 的最大值为 。
山东省德州一中10-11学年高二下学期期中考试(数学)B

德州一中10-11年度第二学期模块检测高二年级数学试题(B 卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟第Ⅰ卷(选择题 共60分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名,准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号除黑。
如需改动,用像皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
一、选择题(注意:每个题的四个选项中只有一个是正确的。
本大题满分5分1260⨯=分) 1.函数y =x 2co sx 的导数为 ( )22.'2co i .'2co i .'2i .'2i A y x sx x s nx B y x sx x s nx C y xs nxD y xs nx==+==--2.复数1i-的虚部是( ).1.1..A B C i D i --3.下面使用类比推理正确的是 ( ) A.“若33a b ⋅=⋅,则a b =”类推出“若00a b ⋅=⋅,则a b =” B.“若()a b c ac bc +=+”类推出“()a b c ac bc ⋅=⋅”C.“若()a b c ac bc +=+” 类推出“a b a bc c c+=+ (c ≠0)” D.“n n a a b =n (b )” 类推出“n n a a b +=+n(b )” 4.用反证法证明命题“如果220,a b a b >>>那么”时,假设的内容应是 ( )A 22a b =B 22a b <C 22a b ≤D 2222a b a b <=,且 5.设)()(,sin )('010x f x f x x f ==,'21()(),,f x f x ='1()()n n f x f x +=,n ∈N ,则2012()f x = ( ) A.sin xB.-sin xC.cos xD.-cos x6. 在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是 ( ) A.若2χ的观测值为6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病;C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系,是指有5% 的可能性使得推判出现错误;D.以上三种说法都不正确.7 曲线3()2f x x x =+-在0p 处的切线平行于直线41y x =-,则0p 点的坐标为( )A (1,0)B (2,8)C (1,0)和(1,4)--D (2,8)和(1,4)--8.设函数()y f x =可导,()y f x =的图象如图1所示,则导函数()y f x '=可能为( )911z z -+若=,则复数z 对应的点在 ( ) A.实轴上 B.虚轴上 C.第一象限 D.第二象限 10.将2005x =输入如图所示的程序框图得结果 ( ) A.2005- B.2005 C.0 D.200611、已知3)2(3123++++=x b bx x y 是R 上的单调增函数,则b 的取值范围是 ( ) A. 21>-<b b ,或 B. 21≥-≤b b ,或 C. 21<<-b D. 21≤≤-b12.()f x 是定义在(0,)+∞上的非负可导函数,且满足'()()0xf x f x -≤,对任意正数,a b ,若a b <,则必有( )ABCDA .()()af b bf a ≤B .()()bf a af b ≤C .()()af a f b ≤D .()()bf b f a ≤ 第二卷(共90分)二、填空题(本大题共4个小题,请将正确答案填在横线上,每个小题4分,满分共16分)13.曲线y =3x 5-5x 3共有___________个极值..14.若复数z =m 2-m -6m +3+(m 2-2m -15)i 是实数,则实数m=___________15.16.过原点作曲线y=e x 的切线,则切线的斜率为 .三、解答题(本大题共6个小题,请写出每个题的必要的解题过程,满分共74分)17、(本小题满分12分)设复数()()ii i z +-++=21312,若i b az z +=++12,求实数b a ,的值。
山东省德州一中10-11学年高二下学期期中考试(英语)

德州一中2010-2011学年第二学期高二年级模块检测英语试题2011年4月本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至6页,共150分,考试时间120分钟。
第Ⅰ卷(三部分共105分)第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What is the most probable relationship between the speakers?A. Husband and wife.B. Passenger and clerk.C. Friends.2.When must you turn on your TV if you want to watch the football program?A. 20:25.B. 21:30.C. 19:00.3. Where is the man going?A. To the bank.B. To the hotel. D. T o the Oxford Street.4. Which one of Mary’s arms was hurt?A. The left one.B. The right one.C. Both.5. Why doesn’t the woman buy the larger coat?A. It’s too big.B. It’s too tight.C. She doesn’t like the color.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
高二数学选修单元测试题

2010级高二数学选修1-1、2-1单元测试题班级______________姓名______________一、选择题1.双曲线122=+y mx 的虚轴长是实轴长的2倍,则m 等于 A .41-B .4-C . 4D .41 2.过双曲线的一个焦点2F 作垂直于实轴的弦PQ ,1F 是另一焦点,若∠21π=Q PF ,则双曲线的离心率等于 A .12-B .2C .12+D .22+3.双曲线22221x y a b-=(0a >,0b >)的左、右焦点分别是12F F ,,过1F 作倾斜角为30的直线交双曲线右支于M 点,若2MF 垂直于x 轴,则双曲线的离心率为ABC D .34.双曲线221102x y -=的焦距为A .B . B . D .5.若直线l 过点(3,0)与双曲线224936x y -=只有一个公共点,则这样的直线有 A .1条 B .2条 C .3条 D .4条6.与椭圆1422=+y x 共焦点且过点(2,1)Q 的双曲线方程是 A .1222=-y x B .1422=-y x C .13322=-y x D .1222=-y x 7.已知P 是双曲线22219x y a -=右支上的一点,双曲线的一条渐近线方程为30x y -=,设12F F 、分别为双曲线的左、右焦点, 若23PF =,则1PF =A . 5B .4C .3D .28.设1e ,2e 分别为有公共焦点1F ,2F 的椭圆和双曲线的离心率,P 为两曲线的一个公共点,且满足021=⋅PF PF ,则222111e e +的值为A .21 B .3 C .2 D .不确定9.已知双曲线12222=-by a x )0,0(>>b a 的右焦点为F ,若过点F 且倾斜角为30°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 A .) B .] C .∞) D .∞)10.已知双曲线中心在原点且一个焦点为F (7,0)直线y =x -1与其相交于M 、N 两点, MN 中点的横坐标为32-,则此双曲线的方程是 A .14322=-y x B .13422=-y x C .12522=-y x D .15222=-y x 11.双曲线C :116922=-y x 的渐近线方程为 A .430x y ±= B .340x y ±= C .450x y ±= D .540x y ±=12.双曲线的虚轴长为4,离心率21,26e F F ,=分别是它的左右焦点,若过1F 的直线与双曲线的左支交与A 、B 两点,且21,AF AF AB 是的等差中项,则1BF 等于 A .28 B .24 C .22 D .8二、填空题13.设点1F ,2F 是双曲线116922=-y x 的两个焦点,则||21F F =_________. 14.双曲线C 的焦点在x 轴上,离心率2=e ,且经过点)3 , 2(P ,则双曲线C 的标准方程是_________ .15.双曲线2288kx ky -=的一个焦点为(0,3),则k 的值为_____________.16.已知双曲线22221(0,0)x y a b a b -=>>的两条渐近线方程为3y x =±,若顶点到渐近线的距离为1,则双曲线方程为 .17.对于椭圆191622=+y x 和双曲线19722=-y x ,有下列命题: ① 椭圆的焦点恰好是双曲线的顶点;② 双曲线的焦点恰好是椭圆的顶点; ③ 双曲线与椭圆共焦点;④ 椭圆与双曲线有两个顶点相同;⑤ 椭圆的离心率与双曲线的离心率互为倒数. 其中所有真命题...的序号是 ____.三、解答题18.已知命题p :方程221215x y m m +=-表示焦点在y 轴上的椭圆;命题q :双曲线 22123y x m-=的离心率)3,2(∈e ;若p q ∨为真,且p q ∧为假,求实数m 的取值范围.19.已知离心率为53的双曲线与椭圆2214015x y +=有公共焦点,求双曲线的方程.20.中心在原点,焦点在x 轴上的椭圆与双曲线有共同的焦点1F 、2F ,且13221=F F ,椭圆的长半轴长与双曲线的实半轴长之差为4,椭圆的离心率与双曲线的离心率之比为 3:7.求该椭圆与双曲线的方程.21.已知双曲线22221(0,0)x y a b a b -=>>的虚轴长为212,F F 为双曲线的两个焦点.(Ⅰ)求双曲线的方程;(Ⅱ)若双曲线上有一点P ,满足01260F PF ∠=,求12FPF ∆的面积.22.点M 是圆422=+y x 上的一个动点,过点M 作MD 垂直于x 轴,垂足为D ,P 为线段MD 的中点。
高中数学 模块综合测试(一)(含解析)新人教A版高二选修1-1数学试题

选修1-1模块综合测试(一)(时间120分钟 满分150分)一、选择题(本大题共12小题,每小题5分,共60分) 1.若命题p :∀x∈R,2x 2+1>0,则¬p 是( ) A .∀x ∈R,2x 2+1≤0 B .∃x ∈R,2x 2+1>0 C .∃x ∈R,2x 2+1<0 D .∃x ∈R,2x 2+1≤0 解析:¬p :∃x ∈R,2x 2+1≤0. 答案:D2.不等式x -1x>0成立的一个充分不必要条件是( )A. -1<x <0或x >1B. x <-1或0<x <1C. x >-1D. x >1解析:本题主要考查充要条件的概念、简单的不等式的解法.画出直线y =x 与双曲线y =1x 的图象,两图象的交点为(1,1)、(-1,-1),依图知x -1x>0⇔-1<x <0或x >1 (*),显然x >1⇒(*);但(*)x >1,故选D.答案:D3.[2014·某某模拟]命题“若a >b ,则a +1>b ”的逆否命题是( ) A .若a +1≤b ,则a >b B .若a +1<b ,则a >b C .若a +1≤b ,则a ≤b D .若a +1<b ,则a <b解析:“若a >b ,则a +1>b ”的逆否命题为“若a +1≤b ,则a ≤b ”,故选C. 答案:C4.[2014·某某省日照一中模考]下列命题中,为真命题的是( ) A. ∀x ∈R ,x 2-x -1>0B. ∀α,β∈R ,sin(α+β)<sin α+sin βC. 函数y =2sin(x +π5)的图象的一条对称轴是x =45πD. 若“∃x 0∈R ,x 20-ax 0+1≤0”为假命题,则a 的取值X 围为(-2,2)解析:本题主要考查命题的判定及其相关知识的理解.因为x 2-x -1=(x -12)2-54,所以A 错误;当α=β=0时,有sin(α+β)=sin α+sin β,所以B 错误;当x =4π5时,y =0,故C 错误;因为“∃x 0∈R ,x 20-ax 0+1≤0”为假命题,所以“∀x ∈R ,x 2-ax +1>0”为真命题,即Δ<0,即a 2-4<0,解得-2<a <2,即a 的取值X 围为(-2,2).故选D.答案:D5.已知△ABC 的顶点B 、C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是( )A .2 3B .6C .4 3D .12解析:设椭圆的另一焦点为F ,由椭圆的定义知 |BA |+|BF |=23,且|CF |+|AC |=23, 所以△ABC 的周长=|BA |+|BC |+|AC | =|BA |+|BF |+|CF |+|AC |=4 3. 答案:C6.过点(2,-2)与双曲线x 2-2y 2=2有公共渐近线的双曲线方程为( ) A.x 22-y 24=1 B.x 24-y 22=1 C.y 24-x 22=1 D. y 22-x 24=1解析:与双曲线x 22-y 2=1有公共渐近线方程的双曲线方程可设为x 22-y 2=λ,由过点(2,-2),可解得λ=-2. 所以所求的双曲线方程为y 22-x 24=1.答案:D7.若双曲线x 2a 2-y 2b2=1(a >0,b >0)的右支上到原点和右焦点距离相等的点有两个,则双曲线离心率的取值X 围是( )A .e > 2B .1<e < 2C .e >2D .1<e <2解析:由题意,以原点及右焦点为端点的线段的垂直平分线必与右支交于两个点,故c2>a ,∴c a>2.答案:C8.把一个周长为12 cm 的长方形围成一个圆柱,当圆柱的体积最大时,该圆柱的底面周长与高的比为( )A. 1∶πB. 2∶πC. 1∶2D. 2∶1解析:设圆柱高为x ,底面半径为r ,则r =6-x 2π,圆柱体积V =π(6-x 2π)2x =14π(x 3-12x 2+36x )(0<x <6),V ′=34π(x -2)(x -6). 当x =2时,V 最大.此时底面周长为6-x =4, (6-x )∶x =4∶2=2∶1. 答案:D9.设双曲线x 2a 2-y 2b2=1(a >0,b >0)的渐近线与抛物线y =x 2+1相切,则该双曲线的离心率等于( )A. 3 B .2 C. 5D. 6解析:双曲线x 2a 2-y 2b 2=1的渐近线方程为y =±b ax ,因为y =x 2+1与渐近线相切,故x2+1±bax =0只有一个实根,∴b 2a 2-4=0,∴c 2-a 2a 2=4, ∴c 2a2=5,∴e = 5. 答案:C10.[2014·某某五校联考]设函数f (x )=e x(sin x -cos x )(0≤x ≤2012π),则函数f (x )的各极小值之和为( )A. -e 2π1-e2012π1-e 2πB. -e 2π1-e1006π1-eπC. -e 2π1-e1006π1-e2πD. -e 2π1-e2010π1-e2π解析:f ′(x )=(e x)′(sin x -cos x )+e x(sin x -cos x )′=2e xsin x ,若f ′(x )<0,则x ∈(π+2k π,2π+2k π),k ∈Z ;若f ′(x )>0,则x ∈(2π+2k π,3π+2k π),k ∈Z .所以当x =2π+2k π,k ∈Z 时,f (x )取得极小值,其极小值为f (2π+2k π)=e2k π+2π[sin(2π+2k π)-cos(2π+2k π)]=e2k π+2π×(0-1)=-e2k π+2π,k ∈Z .因为0≤x ≤2012π,又在两个端点的函数值不是极小值,所以k ∈[0,1004],所以函数f (x )的各极小值构成以-e 2π为首项,以e 2π为公比的等比数列,共有1005项,故函数f (x )的各极小值之和为S 1005=-e 2π-e 4π-…-e2010π=e2π1-e2010π1-e2π.答案:D11.已知抛物线C :y 2=8x 的焦点为F ,准线与x 轴的交点为K ,点A 在C 上且|AK |=2|AF |,则△AFK 的面积为( )A .4B .8C .16D .32解析:∵抛物线C :y 2=8x 的焦点为F (2,0),准线为x =-2,∴K (-2,0). 设A (x 0,y 0),如下图所示,过点A 向准线作垂线,垂足为B ,则B (-2,y 0).∵|AK |=2|AF |,又|AF |=|AB |=x 0-(-2)=x 0+2, ∴由|BK |2=|AK |2-|AB |2,得y 20=(x 0+2)2, 即8x 0=(x 0+2)2,解得x 0=2,y 0=±4.∴△AFK 的面积为12|KF |·|y 0|=12×4×4=8,故选B.答案:B12.[2013·某某高考]如图,F 1、F 2是椭圆C 1:x 24+y 2=1与双曲线C 2的公共焦点,A 、B 分别是C 1、C 2在第二、四象限的公共点.若四边形AF 1BF 2为矩形,则C 2的离心率是( )A. 2B. 3C. 32D.62解析:本题考查椭圆、双曲线的定义和简单的几何性质.设双曲线的方程为x 2a 2-y 2b2=1(a >0,b >0) ①,点A 的坐标为(x 0,y 0).由题意a 2+b 2=3=c 2②,|OA |=|OF 1|=3,∴⎩⎪⎨⎪⎧x 20+y 20=3x 20+4y 20=4,解得x 20=83,y 20=13,又点A 在双曲线C 2上,代入①得,83b 2-13a 2=a 2b2③,联立②③解得a =2,所以e =c a =62,故选D. 答案:D二、填空题(本大题共4小题,每小题5分,共20分)13.函数y =13ax 3-12ax 2(a ≠0)在区间(0,1)上是增函数,则实数a 的取值X 围是________.解析:y ′=ax 2-ax =ax (x -1),∵x ∈(0,1),y ′>0,∴a <0. 答案:a <014.已知命题p :∃x ∈R ,x 2+2ax +a ≤0,若命题p 是假命题,则实数a 的取值X 围是__________.解析:p 是假命题,则¬p 为真命题,¬p 为:∀x ∈R ,x 2+2ax +a >0,所以有Δ=4a 2-4a <0,即0<a <1.答案:(0,1)15.[2014·某某质检]已知a ∈R ,若实数x ,y 满足y =-x 2+3ln x ,则(a -x )2+(a +2-y )2的最小值是________.解析:(a -x )2+(a +2-y )2≥x -a +a +2-y22=x +x 2-3ln x +222.设g (x )=x+x 2-3ln x (x >0),则g ′(x )=1+2x -3x=2x +3x -1x,易知g (x )在(0,1)上为减函数,在(1,+∞)上为增函数,故g (x )≥g (1)=2,(a -x )2+(a +2-y )2≥2+222=8.答案:816.[2013·某某省某某一中月考]F 1、F 2分别是双曲线x 216-y 29=1的左、右焦点,P 为双曲线右支上一点,I 是△PF 1F 2的内心,且S △IPF 2=S △IPF 1-λS △IF 1F 2,则λ=________.解析:本题主要考查双曲线定义及标准方程的应用.设△PF 1F 2内切圆的半径为r ,则S △IPF 2=S △IPF 1-λS △IF 1F 2⇒12×|PF 2|×r =12×|PF 1|×r -12λ×|F 1F 2|×r ⇒|PF 1|-|PF 2|=λ|F 1F 2|,根据双曲线的标准方程知2a =λ·2c ,∴λ=a c =45.答案:45三、解答题(本大题共6小题,共70分)17.(10分)已知全集U =R ,非空集合A ={x |x -2x -3<0},B ={x |(x -a )(x -a 2-2)<0}.命题p :x ∈A ,命题q :x ∈B .(1)当a =12时,p 是q 的什么条件?(2)若q 是p 的必要条件,某某数a 的取值X 围. 解:(1)A ={x |x -2x -3<0}={x |2<x <3}, 当a =12时,B ={x |12<x <94},故p 是q 的既不充分也不必要条件.(2)若q 是p 的必要条件,即p ⇒q ,可知A ⊆B , 由a 2+2>a ,故B ={a |a <x <a 2+2},∴⎩⎪⎨⎪⎧a ≤2a 2+2≥3,解得a ≤-1或1≤a ≤2.18.(12分)已知c >0,设p :y =c x为减函数;q :函数f (x )=x +1x >1c 在x ∈[12,2]上恒成立,若“p ∨q ”为真命题,“p ∧q ”为假命题,求c 的取值X 围.解:由y =c x为减函数,得0<c <1.当x ∈[12,2]时,由不等式x +1x ≥2(x =1时取等号)知:f (x )=x +1x 在[12,2]上的最小值为2,若q 真,则1c <2,即c >12.若p 真q 假,则0<c <1且c ≤12,所以0<c ≤12.若p 假q 真,则c ≥1且c >12,所以c ≥1.综上:c ∈(0,12]∪[1,+∞).19.(12分)[2014·海淀期末]已知函数f (x )=(x +a )e x,其中a 为常数. (1)若函数f (x )是区间[-3,+∞)上的增函数,某某数a 的取值X 围; (2)若f (x )≥e 2在x ∈[0,2]时恒成立,某某数a 的取值X 围. 解:(1)f ′(x )=(x +a +1)e x,x ∈R .因为函数f (x )是区间[-3,+∞)上的增函数,所以f ′(x )≥0,即x +a +1≥0在[-3,+∞)上恒成立. 因为y =x +a +1是增函数,所以满足题意只需-3+a +1≥0,即a ≥2. (2)令f ′(x )=0,解得x =-a -1,f (x ),f ′(x )的变化情况如下:f (0)≥e 2,解得a ≥e 2,所以此时a ≥e 2;②当0<-a -1<2,即-3<a <-1时,f (x )在[0,2]上的最小值为f (-a -1), 若满足题意只需f (-a -1)≥e 2,求解可得此不等式无解, 所以a 不存在;③当-a -1≥2,即a ≤-3时,f (x )在[0,2]上的最小值为f (2),若满足题意只需f (2)≥e 2,解得a ≥-1,所以此时a 不存在.综上讨论,所某某数a 的取值X 围为[e 2,+∞).20.(12分)已知椭圆x 29+y 25=1,F 1、F 2分别是椭圆的左、右焦点,点A (1,1)为椭圆内一点,点P 为椭圆上一点.求|PA |+|PF 1|的最大值.解:由椭圆的定义知|PF 1|+|PF 2|=2a =6, 所以|PF 1|=6-|PF 2|,这样|PA |+|PF 1|=6+|PA |-|PF 2|.求|PA |+|PF 1|的最大值问题转化为6+|PA |-|PF 2|的最大值问题, 即求|PA |-|PF 2|的最大值问题, 如图在△PAF 2中,两边之差小于第三边,即|PA |-|PF 2|<|AF 2|,连接AF 2并延长交椭圆于P ′点时, 此时|P ′A |-|P ′F 2|=|AF 2|达到最大值, 易求|AF 2|=2,这样|PA |-|PF 2|的最大值为2, 故|PA |+|PF 1|的最大值为6+ 2.21.(12分)已知椭圆M 的对称轴为坐标轴,且抛物线x 2=-42y 的焦点是椭圆M 的一个焦点,又点A (1,2)在椭圆M 上.(1)求椭圆M 的方程;(2)已知直线l 的方向向量为(1,2),若直线l 与椭圆M 交于B 、C 两点,求△ABC 面积的最大值.解:(1)由已知抛物线的焦点为(0,-2),故设椭圆方程为y 2a 2+x 2a 2-2=1.将点A (1,2)代入方程得2a 2+1a 2-2=1,整理得a 4-5a 2+4=0,解得a 2=4或a 2=1(舍去). 故所求椭圆方程为y 24+x 22=1.(2)设直线BC 的方程为y =2x +m , 设B (x 1,y 1),C (x 2,y 2),代入椭圆方程并化简得4x 2+22mx +m 2-4=0, 由Δ=8m 2-16(m 2-4)=8(8-m 2)>0, 可得m 2<8.由x 1+x 2=-22m ,x 1x 2=m 2-44,故|BC |=3|x 1-x 2|=3×16-2m22.又点A 到BC 的距离为d =|m |3,故S △ABC =12|BC |·d =m216-2m24≤142×2m 2+16-2m22= 2.因此△ABC 面积的最大值为 2.22.(12分)[2014·某某质检]已知函数f (x )=x -1+ae x (a ∈R ,e 为自然对数的底数).(1)若曲线y =f (x )在点(1,f (1))处的切线平行于x 轴,求a 的值; (2)求函数f (x )的极值;(3)当a =1时,若直线l :y =kx -1与曲线y =f (x )没有公共点,求k 的最大值. 解:(1)由f (x )=x -1+a e x ,得f ′(x )=1-aex ,又曲线y =f (x )在点(1,f (1))处的切线平行于x 轴,所以f ′(1)=0,即1-ae =0,解之得a =e.(2)f ′(x )=1-aex ,①当a ≤0时,f ′(x )>0,f (x )为(-∞,+∞)上的增函数,所以函数f (x )无极值. ②当a >0时,令f ′(x )=0,得e x=a ,x =ln a .当x ∈(-∞,ln a )时,f ′(x )<0;当x ∈(ln a ,+∞)时,f ′(x )>0, 所以f (x )在(-∞,ln a )上单调递减,在(ln a ,+∞)上单调递增, 故f (x )在x =ln a 处取得极小值,且极小值为f (ln a )=ln a ,无极大值.综上,当a ≤0时,函数f (x )无极值;当a >0时,f (x )在x =ln a 处取得极小值ln a ,无极大值.(3)当a =1时,f (x )=x -1+1e x .令g (x )=f (x )-(kx -1)=(1-k )x +1ex ,则直线l :y =kx -1与曲线y =f (x )没有公共点,等价于方程g (x )=0在R 上没有实数解.当k >1时,g (0)=1>0,g (1k -1)=-1+1e 1k -1<0, 又函数g (x )的图象在定义域R 上连续,由零点存在定理,可知g (x )=0至少有一实数解,与“方程g (x )=0在R 上没有实数解”矛盾,故k ≤1.当k =1时,g (x )=1e x >0,知方程g (x )=0在R 上没有实数解.所以k 的最大值为1.。
最新人教版高二数学选修1-1模块考试题带答案

A.
x2 y2 1 16 9
B.
C.
D.
9.设曲线 y ax 2 在点(1, a )处的切线与直线 2 x y 6 0 平行,则 a (
A. 1 B.
)
1 2
C.
1 2
D. 1
)
D. y x e )
7.已知椭圆的长轴长是短轴长的 2 倍,则椭圆的离心率等于(
高二数学(文科) 第 1 页( 共 9 页)
A.
3 2
B.
3 3
C.
1 2
D.
1 3
8.已知两点 F1 (1,0) 、 F (1,0) ,且 F1 F2 是 PF1 与 PF2 的等差中项,则动点 P 的轨 迹方程是( )
11 .25 升.
高二数学(文科) 第 8 页( 共 9 页)
21(本小题满分 10 分) 解:(Ⅰ)由已知 c 2 及点 P(3, 7 ) 在双曲线 C 上得
a 2 b2 4 2 ( 7 )2 3 1 b2 a2
解得 a 2 2, b 2 2
所以,双曲线 C 的方程为
)
3 2 3.命题“对任意的 x R,x x 1 ≤ 0 ”的否定是(
)
3 2
A.不存在 x R,x x 1 ≤ 0 C.存在 x R,x x 1 0
3 2
3
2
B.存在 x R,x x 1 ≤ 0 D.对任意的 x R,x x 1 0
1 10.抛物线 y x 2 的准线方程是 8
A. x
(
C. y
2010-2011学年高二数学综合测试卷 新人教A版选修1

2010-2011学年高二数学选修1-2综合测试卷一、填空题:本大题共14小题,每小题5分,共70分.1.下列命题:①x R ∀∈,220x +>;②x N ∀∈,41x ≥;③x Z ∃∈,31x <;④x Z ∀∈,23x ≠;其中假命题的序号是 .2.曲线sin y x =在(,32p π处的切线斜率是 3. 抛物线2x ay =(0a ≠)的准线方程是 . 4. 函数ln y x x =的单调递减区间为 .5. 若双曲线的渐近线方程为3y x =±,它的一个焦点是,则双曲线的方程为 . 6. 一物体作直线运动,其运动方程为43215243S t t t =-+(S 的单位为m ,t 的单位为s ),则物体速度为0的时刻是 .7.如果方程22123x yk k+=--表示椭圆,则k 的取值范围是 . 8. 要建造一座跨度为16米,拱高为4米的抛物线拱桥,建桥时每隔4米用一根支柱支撑,两边的柱长应为 .9.已知双曲线22221x y a b-=(0a >,0b >)的右焦点为F ,若过点F 且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线的离心率的取值范围是 .10.已知点F 为双曲线191622=-y x 右焦点,M 是双曲线右支上的一动点,()4,5A ,则MA MF 54-的最大值为11. 已知曲线3114:333C y x x =-+,曲线229:2C y x x m =-+,若当[]2,2x ∈-时,曲线1C 在曲线2C 的下方,则实数m 的取值范围是 .12.函数32()f x x ax bx c =+++,[]2,2x ∈-,表示的曲线过原点,且在1x =±处的切线的斜率均为1-,有以下命题:①()f x 的解析式是3()4f x x x =-,[]2,2x ∈-;②()f x 的极值点有且只有1个; ③()f x 的最大值与最小值之和为0; 其中真命题的序号是 .13. 与双曲线22142x y -=有相同的焦点,且过点(2,1)Q 的圆锥曲线方程为 . 14. 已知函数)(x f 是定义在R 上的奇函数,0)1(=f ,0)()(2>-'xx f x f x )(0>x ,则不等式0)(2>x f x 的解集是 .二、解答题:本大题共5小题,共90分.解答应写出文字说明、证明过程或演算步骤. 15.(12分)设p :实数x 满足22430x ax a -+<,其中0a <,q :实数x 满足260x x --≤或2280x x +->,且p ⌝是q ⌝的必要不充分条件,求a 的取值范围.16.(14分)抛物线的顶点在原点,它的准线过椭圆22221x y a b+=(0a b >>)的一个焦点1F ,且垂直于椭圆的长轴,又抛物线与椭圆的一个交点是226(,)3M ,求抛物线与椭圆方程.17.(14分)已知函数3()f x ax x =-,其中13a ≤. (Ⅰ)当1a =时,求曲线()y f x =在点(2(2))f ,处的切线方程;(Ⅱ)求函数()f x 在[1,1]-上的最大值.18.(16分)设双曲线22213y x a -=的两个焦点分别为1F 、2F ,离心率为2. (I )求双曲线的渐近线方程;(II )过点(1,0)N 能否作出直线l ,使l 与双曲线C 交于P 、Q 两点,且0OP OQ •=,若存在,求出直线方程,若不存在,说明理由.19.(16分)设1F 、2F 分别是椭圆2222:162x y C m m +=(0m >)的左、右焦点. (I )当p C ∈,且120pF pF •=,124pFpF •=时,求椭圆C 的左、右焦点1F 、2F 的坐标.(II )1F 、2F 是(I )中的椭圆的左、右焦点,已知2F 的半径是1,过动点Q 作的切线QM(M为切点),使得1QF =,求动点Q 的轨迹.20.(18分)如图,有一块半椭圆形钢板,其长半轴为2r ,短半轴为r ,计划将此钢板切割成等腰梯形的形状,下底AB 是半椭圆的短轴,上底CD 的端点在椭圆上,记2CD x =,梯形面积为S .(I )求面积S 关于变量x 的函数表达式,并写出定义域;(II )求面积S 的最大值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010-2011学年山东省德州一中高二(下)模块检测数学试卷(选
修1-1、1-2)(文科)
(扫描二维码可查看试题解析)
一、选择题(注意:每个题的四个选项中只有一个是正确的.本大题满分60分)
2
2.(5分)(2009•重庆模拟)复数的虚部是()
=+
4.(5分)(2013•杨浦区校级模拟)用反证法证明命题“如果a>b>0,那么a>b”时,假设的内容应是()
5.(5分)(2010秋•天心区校级期末)设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,
6.(5分)(2014春•菏泽期末)在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是
7.(5分)(2011•福州一模)曲线f(x)=x+x﹣2在p0处的切线平行于直线y=4x﹣1,则p0点的坐标为()
导函数y=f′(x)可能为()
C
D
11.(5分)(2013秋•荔城区校级期末)已知y=x 3
+bx 2
+(b+2)x+3是R 上的单调增函数,
则b 的取值是( )
二、填空题(本大题共4个小题,请将正确答案填在横线上,每个小题4分,满分共16分) 13.(4分)曲线y=3x 5
﹣5x 3
共有 个极值. 14.(4分)若复数z=
+(m 2
﹣2m ﹣15)i 是实数,则实数m= .
15.(4分)(2013春•雨城区校级期中)比较大小:
+.
16.(4分)(2014春•新城区校级期中)过原点作曲线y=e x
的切线,则切线的斜率为 .
三、解答题(本大题共6个小题,请写出每个题的必要的解题过程,满分共74分)
17.(12分)(2014春•陵县期中)设复数z=,若z2+az+b=1+i,求实数a,b的值.
18.(12分)(2010•云南模拟)设复数z满足|z|=1,且(3+4i)•z是纯虚数,求.
19.(12分)(2013春•象山县校级期中)设f(x)=x3﹣﹣2x+5
(1)求函数f(x)的极值;
(2)当x∈[﹣1,2]时,f(x)<m恒成立,求实数m的取值范围..
20.(12分)(2013春•雨城区校级期中)已知a,b,c∈R+,a+b+c=1,求证:.
21.(12分)(2006•福建)统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y
(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:x+8(0<
x≤120).已知甲、乙两地相距100千米.
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
22.(14分)(2014•漳州模拟)已知函数f(x)=ax+lnx(a∈R).
(Ⅰ)若a=2,求曲线y=f(x)在x=1处切线的斜率;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=x2﹣2x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
2010-2011学年山东省德州一中高二(下)模块检测数学试卷(选修1-1、1-2)(文科)
一、选择题(注意:每个题的四个选项中只有一个是正确的.本大题满分60分)
1.A 2.B 3.C 4.C 5.A 6.D 7.D 8.D 9.B 10.D 11.D 12.A
二、填空题(本大题共4个小题,请将正确答案填在横线上,每个小题4分,满分共16分)13.2 14.5 15.>16.1
三、解答题(本大题共6个小题,请写出每个题的必要的解题过程,满分共74分)17.18.19.20.21.22.。
