七年级数学(上册)导学案(全)
七年级数学上册导学案(全集)
七年级数学上册导学案第1章基本的几何图形1.1我们身边的图形世界一、导入激学:满天星斗的夜空,形形色色的建筑群,各式各样的交通工具和道路,五彩缤纷的自然界……只要你注意观察,就会发现我们生活在一个丰富多彩的图形世界里。
二、导标引学学习目标:1.认识不同的几何体,初步体会几何研究的对象、方法、并感悟抽象的数学思想。
2.了解从物体抽象出来的几何体、平面、曲面等概念的定义。
3.知道正方体、圆柱、圆锥、球等都是几何体,能认识表示它们的图形。
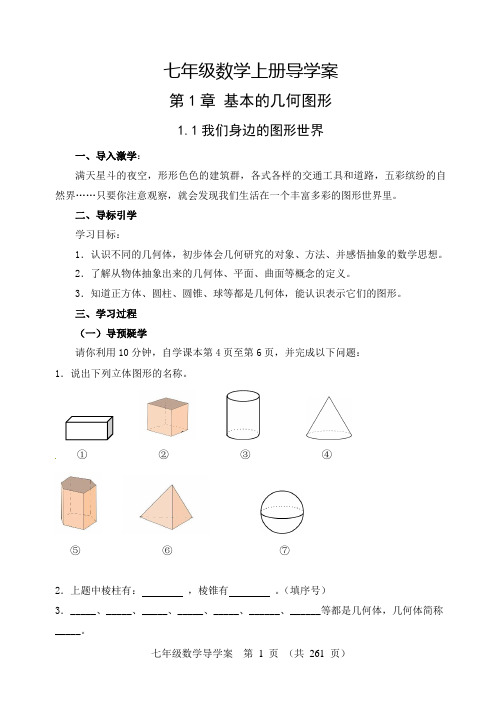
三、学习过程(一)导预疑学请你利用10分钟,自学课本第4页至第6页,并完成以下问题:1.说出下列立体图形的名称。
①②③④⑤⑥⑦2.上题中棱柱有:,棱锥有。
(填序号)3._____、_____、_____、_____、_____、______、______等都是几何体,几何体简称_____。
4.观察下列实物图片,它们的形状分别类似于哪种几何体?①②③④⑤(二)导问互学问题:棱柱与圆柱、棱锥与圆锥的区别与联系:顶点棱侧面底面棱柱圆柱棱锥圆锥解决问题评价:(三)导根典学在下图中的三幅图案中,你分别看到了哪些图形?它们是怎样组合而成的?(四)导标达学1.下列几何体,是由一个曲面和两个平面围成的是_____。
A B C D2. 一个以下说法中正确的是。
A.正方体是棱柱。
B.电视机的形状类似于球体。
C.生活中应用的六角螺母的形状类似于圆柱。
D.鸡蛋的形状类似于圆锥。
3.一个七棱柱共有个面,条棱,个顶点,形状和面积完全相同的只有个面.4.图中的的几何体由几个面围成,面与面相交成几条线?它们是直的还是曲的?5.下列几何体中不是多面体的是( )A、立方体B、长方体C、三棱锥D、圆柱6.下列几何体没有曲面的是()A、圆柱B、圆锥C、球D、棱柱7.下列图案是由哪些简单的几何图形组成的?8.请你用两个圆、两个三角形和两条线段组合几幅新奇、有趣的图形,并给出文字说明。
反馈评价:四、导法慧学1.将所学知识纳入知识体系.2.本节解决问题的具体方法是怎样的?据此请总结此类问题的解题思路.3.还有没有更好的解法?你还有疑问吗?设计人:王望中学王志海1.2 几何图形一、导入激学:我们学过的长方体有几个面?几个顶点?几条棱?二、导标引学学习目标:1.认识点、线、面、体,初步感受“点动成线、线动成面、面动成体”的生活实例。
新人教版七年级数学-上册导学案(全册)

新人教版七年级数学上册导学案课题:1.1 正数和负数(1)学习目标:1、掌握正数和负数概念;2、会区分两种不同意义的量,会用符号表示正数和负数;3、体验数学发展是生活实际的需要,激发学生导学数学的兴趣。
学习重点及难点:重点:正数和负数概念难点:负数概念知识链接:1、小学里学过哪些数请写出来:、、。
2、阅读课本P1和P2三幅图(重点是三个例子,边阅读边思考)回答下面提出的问题:3、在生活中,仅有整数和分数够用了吗?有没有比0小的数?如果有,那叫做什么数?学法指导:自主学习、合作探究学习过程一、自主学习1、正数与负数的产生(1)、生活中具有相反意义的量如:运进5吨与运出3吨;上升7米与下降8米;向东50米与向西47米等都是生活中遇到的具有相反意义的量。
请你也举一个具有相反意义量的例子:。
(2)负数的产生同样是生活和生产的需要二、合作探究【探究一】1、正数和负数的表示方法(1)一般地,我们把上升、运进、零上、收入、前进、高出等规定为正的,而与它相反的量,如:下降、运出、零下、支出、后退、低于等规定为负的。
正的量就用小学里学过的数表示,有时也在它前面放上一个“+”(读作正)号,如前面的5、7、50;负的量用小学学过的数前面放上“—”(读作负)号来表示,如上面的—3、—8、—47。
(2)活动两个同学为一组,一同学任意说意义相反的两个量,另一个同学用正负数表示.(3)阅读P3练习前的内容三、达标检测1.小明的姐姐在银行工作,她把存入3万元记作+3万元,那么支取2万元应记作_______,-4万元表示________________。
2.已知下列各数:51-,432-,3.14,+3065,0,-239;则正数有_____________________;负数有____________________。
3.下列结论中正确的是…………………………………………()A.0既是正数,又是负数B.O是最小的正数C .0是最大的负数D .0既不是正数,也不是负数4.给出下列各数:-3,0,+5,213-,+3.1,21-,2004,+2010;其中是负数的有 ……………………………………………………( ) A .2个B .3个C .4个D .5个四、课堂小结及作业布置 小结:正数、负数的概念:(1)大于0的数叫做 ,小于0的数叫做 。
七年级数学上册导学案

七年级数学上册导学案班级: __________________ 姓名:___________________课题:第二章复习课(典型题归纳)_____________________学习目标:系统复习第二章前七节,掌握基本知识,对典型题的做法清楚,明了。
重点:会在掌握基本知识的基础上,对第二章的典型题的解法有清晰的认识。
难点:简便方法的应用方法:教师引导,师生合作探究学习过程:(一)知识回顾本章基本概念:有理数,数轴,绝对值,有理数加法/减法/乘法法则,相反数,倒数(二)师生合作探索由学生自主回答本章所学知识可能会有有哪些题型,根据学生回答情况,补充一下。
并让学生回答哪些题是有难度的,作为典型题目来讲解这些类型的题目。
典型题:①计算题中的简便算法②去绝对值号③判断正负典型题做法的总结:①计算题中的简便算法例1:计算(1) -19.25+38+(-17)+19.25+62-82;(2)(-8.25)+(-7)+100+(-0.25)+12;(3)(-4)×5×(-0.25)×12×20;(4) 67×78×57×33×0×24;总结:加减法简算:乘法简算:②去绝对值号例2:数a,b,c在数轴上对应位置如图,化简:| a + b | + | b + c | —| c–a |.例3:已知| x+ 5| + | y+ 2 |=0;求x+y+2总结去绝对值号的方法③判断正负思考:用“>”“<”“=”号填空(1)如果a>0,b>0,那么a·b____0.(2)如果a>0 b<0, 那么a·b____0.(3)如果a<0, b<0 , 那么a·b____0 .(4)如果a=0, b≠0, 那么a·b____0(若b=0或者a=b=0该怎样判断)例4:当a,b是什么有理数时,下式成立:a×b=| a×b|(分类讨论)例5:当a是有理数时,判断a+ |a|的符号怎样判断正负:当堂总结:知识巩固:1.若| a-3|与| b+2|互为相反数,求a+b+5的值;2.计算(1) (-125) ×(-2) ×(-8)(2) 15+(-65)-(-85)+233.用“>”“<”“=”号填空(1)如果a>0,b<0,那么a-b_________0;(2)如果a<0,b>0,那么a-b_________0;(3)如果a>0,b>0, | a| >| b|,那么a-b________0;(4)如果a<0,b<0, | a|<| b|,那么a-b_________0;。
七年级数学上册导学案全册

七年级数学上册导学案全册导学案-七年级数学上册注意:本导学案旨在帮助学生预习和复习七年级数学上册的内容,提供课前准备和课后巩固的指导,请密切配合教材使用。
第一章分数一、概念引入1.1 了解分数的定义和常用表示方法;1.2 掌握分数在数轴上的位置及其大小关系。
二、分数的基本运算2.1 分数的加法和减法:同分母、异分母情境下的计算;2.2 分数的乘法:分数乘以整数的计算;2.3 分数的除法:计算除法表达式,化简答案。
三、混合运算3.1 掌握混合数的概念及相互转化;3.2 掌握带分数的加减法运算;3.3 灵活运用所学知识解决实际问题。
第二章代数式一、代数式的概念1.1 了解代数式的定义和构成要素;1.2 了解代数式的计算方法。
二、代数表达式的分解和合并2.1 分解代数式为因式的乘积;2.2 合并同类项简化代数式。
三、代数式的应用3.1 运用代数式解决实际问题;3.2 利用代数式建立数学模型。
第三章图形的初步认识一、几何基本概念1.1 了解点、线、面的概念,认识线段、射线、直线、角等基本几何要素;1.2 掌握正方形、矩形、三角形、圆的定义和性质。
二、图形的相似和全等2.1 了解相似和全等的概念;2.2 掌握判断图形相似和全等的条件;2.3 运用相似和全等的性质解决实际问题。
三、平面镶嵌3.1 了解平面镶嵌的概念和方法;3.2 探索平面镶嵌的规律。
第四章线性方程一、方程的概念1.1 了解方程的定义及解的概念;1.2 掌握等式的性质。
二、解一元一次方程2.1 书写一元一次方程;2.2 运用等式性质解一元一次方程。
三、实际问题与方程3.1 将实际问题转化为方程;3.2 运用方程解决实际问题。
第五章数据与概率一、统计图与数据1.1 了解条形图、折线图的表示方法;1.2 能够读取和分析各类统计图。
二、概率初步2.1 了解概率的定义和常用表示方式;2.2 进行简单事件的概率计算;2.3 利用概率解决实际问题。
三、收集与处理数据3.1 学会收集和整理数据;3.2 运用统计学方法分析数据。
七年级数学(上册)导学案参考答案.doc

七年级数学(上册)导学案参考答案第一章有理数P2.课堂练习2.-2力'元;支取4力'元1 33.正数有3. 14, +3065;负数有,- 2—, -239;5 44. D5. B拓展训练1.-15°C; -4°C2.甲;丙3.甲比乙小3岁4.潜水艇高度:-40米;鲨鱼的高度-30米;P4拓展训练1 > - 17 °C 2、9.05 (mm); 8.95 (mm );P6拓展训练1. CP8拓展训练1. 42. AP10拓展训练2. 1.6 ; -2x; b-a3. 0;负数4. 13;5.4 ; 6 ;・9 5・5;P12拓展训练1. c2. ±7;± 7 ;3・a-3;a-3 ;4・c 5. BP14拓展训练1.对;错;错;错2.10 ;-10; 6;・6P16拓展训练1. 5 ; - ;21; 062.>;<;>;<;3.3250P30 拓展训练 A ; B17;P32拓展训2. -16;- 273.-25; - 3. 08X 10P18 拓展训练 1. 10; -69; -297; 3.9; -1.25 2. 5; 1;P20 拓展训练 1. -30;P22 拓展训练 1. a 、b 都为正; 2. ・6; P24 拓展训练 ―、1. c 2. B 3. B 55 —、1. — 2. —38P26 拓展训练 10 1. —;173;11;P28 拓展训练P34拓展训练 1. -11;拓展训练(6) 7. 805X 101. ( 1) 4. 65X 10(2) 1. 2X 10 (3) 1. 000001 X 10(4) -7. 89P38 拓展训练 1. ( 1) 0. 036; (2) (3) 3. 9; ( 4) 0. 057; (5) 0. 29; ( 6) 0. 290;6, 4, 9;(2)百位;3; 2,3, 6;(3) 力'位;2;5, 7; P40拓展训练1. C2. c3. ±7;P42 拓展训练1.3.4X 105 2. 3.40 X 104 3. 5或1;4. C ;10 15.4—13 84;3, ±7;P43,P443.40 X 1052. (1)万位; 4. c ; 5.第一章有理数检测试卷 1. B 2.A 3.B 4. B 5.B 6. D 7. D8. B 2. a 2 < 丄;3. 10 月 1 a日2:00, 4.65.4; 5;1. 四 1.2.3. 6. -1 -2 2. (1) 第二章 711 — 16守门员回到了原来的位置;(2) 12 米;(3) 54米;(1)-- 7 a=2,b 二1; 整式加减 P46 拓展训练 1. B 2. c8 9 20082009 (2 ) --------- ; 0 ;20101. D2.c3.—;1;——a2b ;3 4b;4.1.2;3.-32x6 y;(-2)叫(-2)叫n+11.17;2.-0.001.2.B;3.5xy21. c 2.3.-271.三;四; 2. (m+2 )3. -X2+5X~3;4.4;5.6.他的说法有道理,原式为7 . a=-2;b二1;8.这个数是11 (a +6.11;-2.75(2) 2. 5 17. 原式为-2b+b+3;P48拓展训练P50拓展训练P52拓展训练P54拓展训练P56拓展训练P60拓展训练9. 6.5m-4.5n;29;10. 6bc~9ac;P61; P62第二章整式加减检测试卷2 12一、1. x-2; 2. —一;2; 3•二;三;2; 4. 2;2; 5. 1;57.-4 a2+ab+10b2;8.4(a+20); 3(a-20);二、9. B 10. c 11. D 12. c 13. c 14. D三、15. ( 1) 6m2-3m;(2) 2x2-2y2-7xy;16.(2. 60千米/时1.(1)错;3x 二-(2)错;2x-x=-(3)对;2. 15, 16, 22,23;第三章一元一次方程 P64 拓展训练 1. 500; P66 拓展训练2.设小华要x 分钟才能完成;列方程700+50x=2000; x=26P68 拓展训练3. x=・5 ; x=9 ; P70 拓展训练 1. x ;3x ;5x ;3x+5x=32;8x=32;x=4; 12; 20; 2. x ; — x+2; 丄 x ・l ; (— x+2)+ (丄 x ・ l)+23=x ;3 2 3 2 P72 拓展训练P74 拓展训练 1.8, 10, 12;P76 拓展训练 1.当学生16人时,两家公司一样; 当学生数大于16人时,甲公司省钱; 当学生数小于16人时,乙公司省钱; P78 拓展训练 (1) x 二0;( 2 ) x= —; (3) y=10;7P80拓展训练1.安排16天生产甲种零件;安排14天生产乙种零件;P82拓展训练9(1) x=- ;(2) x=-20;5P84拓展训练1. 28 人P86拓展训练1.该股民在这次交易中是亏损,亏损150元;2.书费大于91元时,办卡划算;书费小于91元时,不办卡划算;3.这件商品的成本价是200元;P88拓展训练1.此工厂原计划生产零件700个,预定期限是30天;P90拓展训练1.该队胜了4场;2.(1)小华答对了50题;(2)小胡这个说法正确,因为小胡只要答对54题;P94拓展训练1.(1) y=3;(2) x=—;82.这种鞋的标价是105元,优惠价是84元;3.原来甲水池有30吨水,原来乙水池有200吨水;4.他选对23题;现有500名学生参加考试,没有得83分的同学;P95 ;P96第三章一元一次方程检测试题一、1.B 2. D 3. B 4. A 5. B 6. A二、7. 3x-7=2x+5 : 8. 2;9.2 ;10. 4;11. -1;12. 4;三、(1) x=8; (2) y=0; (3) x=55; (4) y=3;四、1. m=2,x=-4,代数式(X +3)2010=1;2.这种商品的进价为5000元;3.共有多320宿舍,有2565住宿生;第四章图形认识初步P98拓展训练1. D;P100拓展训练1. CP102拓展训练1. D;2. D;P104拓展训练1.线,点动成线;2.面;线;点;3.线;面;体;4. B;P106拓展训练1. 6 条2. 10 种;20 种;P108拓展训练1•两点之间,线段最短;2.线段DE=8cm;P110 拓展训练1. (37. 145) 0 度生分 42 秒;98°30' 18' ' = 98. 50 5 度;2. B ;3. CD 与CE 垂直; P112 拓展训练1. ZDOE=90°; P114 拓展训练1. 这个角的度数是75°;2. Za=70°; ,0=2"; P116 拓展训练1. Z1=Z3;理由:等角的余角相等; P120 拓展训练1. (1) AAOD 的补角 ZBOZ), ZBOE 的补角 ZAOE ; (2) Z COZ)=34°; ZEOC=56°; (3) ZCOD+ZEOC=90°;2. (1) 10; 15; (2);2P121; P122第四章图形认识初步检测试卷一、1.长方形; 2.49°45 <3.60°; 4.10; 5. 1; 6.两;两点确定一条直线;7. 22; 30;8. 12. 4;9. 15 ;二、 10. B 11. C12. A13. D14. A三、15.(略);16.(略);17.ZB0F=56°;ZE0F=90°;18. (1) MN=5 (cm) ;(2)+ ");(3) MN=1 (cm);。
人教版七年级数学上册导学案(全)

七年级数学“先学后教”导学案第一章 有理数§1.1 正数和负数一.学习目标1、通过实际例子,感受引入负数的必要性;2、知道什么是正数,什么是负数;会用正负数表示实际问题的数量。
二、阅读指导1、我们以前学过的数:1、2、3……0 21、32、53…… 这三类数是如何产生的,请同学们在课本上找一下,并在小组读一遍。
2、课本中出现了新数:-3、-2、-2.7%,这些数和以前学习的数有什么区别?课本上结合实际对它们的意义做了说明,你有其他说法吗? 请想一想在组内说一说。
3、把一组旧数和新数放在一起:3、2、1、1.8%、+6、+3.2、-3、-2、-2.7%、0,请同学们根据课本知识把它们分类一下,并读出来。
4、归纳什么是正数:什么是负数:5、正数、0、负数结合实际后都能表示一定的意义,在课本中都举出哪些可用正数、0、负数表示的例子,请找出来并写在课本的空白处。
三、尝试练习课本P3页的练习1、2、3、4;P4页练习。
课本P5页习题1.1第1、2、3题.四、交流展示1、在组内讲解阅读思考,并交流。
2、在组内指定同学报答案,答案不同的先记下,最后交流展示。
3、教师巡视各组学习情况,并适时点拨或启发五、当堂反馈1、课本P5页习题1.1第4-8题.2、(1)若规定向南为正,则向北50米记作(2)若+101元表示收入101元,则-100元表示3、2008年我国花生产量比上年增长1.8%,油菜籽产量比上年增长-2.7%,这里的1.8%,-2.7%分别代表什么意思?六、反思小结为什么要引入负数?举例说明正数、负数在表示相反意义的量时的作用。
§1.2.1 有理数一、学习目标理解有理数的意义,知道什么是有理数,会将有理数进行分类。
二、阅读指导1、至今为此我们学过的数有哪些? 其中对正分数和负分数的理解,你有什么疑问?2、正数包含:负数包含:3、有理数包含:4、正整数、0、负整数统称为正分数和负分数统称为整数和分数统称为三、尝试练习1、课本P8页练习;课本P14页习题1.2第1题。
七年级数学上册导学案全册

(4)6x2+x-2=0 (5)1+2=3 (6) - -m=11
2.下列式子哪些是一元一次方程?不是一元一次方程的,要说明理由.
(1)9x=2 (2)x+2y=0 (3)x2-1=0
(4) x=0 (5) =2 (6) ax=b(a、b是常数)
(5)某班有x名学生,要求平均每人展出4枚邮票,实际展出的邮票量比要求数多了15枚,问该班共展出多少枚邮票?
三、学习小结
四、作业
习题3.1第1、5题。
第二课时3.1.1一元一次方程(2)
班级姓名__小组__评价__
学习目标
根据实际问题中的数量关系,设未知数,列出一元一次方程。
知道方程的解和解方程是两个不同的概念。
(5)如果-2x=6,那么x=________.
2、若 ,则a=___;若(c2+1)x=2(c2+1),则x=____.
3、若c=2a+1,b=3a+6,且c=b则a=____.
4、下列等式的变形中,不正确的是()
A.若x=y,则x+5=y+5 B.若 (a≠0),则x=y
C.若-3x=-3y,则x=y D.若mx=my,则x=y
3.等式的性质2 ____________________________________________
如果a=b ,那么ac=________
如果a=b (c≠0),那么 =_______
[提示]等式除了以上两条性质外,还有其他的一些性质。
(1)对称性:等式的左、右两边交换位置,所得的结果仍是等式。如果a=b,那么b=a .
七年级上册数学导学案全册

七年级上册数学导学案全册一、整数的概念和运算在本节课中,我们将学习整数的概念和运算。
整数包括正整数、负整数和零。
在进行整数运算时,我们需要掌握加法、减法、乘法和除法的规则,并注意运算的顺序。
下面是一些例题来帮助我们理解整数的概念和运算。
例题1:计算下列各式的值:1) 5 + (-3)2) (-4) - 73) 6 × (-2)4) (-12) ÷ 3例题2:先计算括号内的值,再计算整体的值:1) 3 × (4 + (-2))2) (-5) × (-3 + 7) ÷ 2二、分数的运算与表示在本节课中,我们将学习分数的概念、运算与表示。
分数由分子和分母组成,表示了部分与整体的关系。
我们需要掌握分数的加法、减法、乘法和除法的规则,并能灵活地运用它们。
例题1:计算下列各式的值:1) 1/2 + 2/32) 5/6 - 1/33) 3/4 × 2/54) 3/5 ÷ 1/4例题2:化简分数:1) 4/8化简为最简分数2) 12/15化简为最简分数三、代数表达式在本节课中,我们将学习代数表达式的概念和运算。
代数表达式由变量、常数和运算符组成,用来表示数与数之间的关系。
我们需要掌握代数表达式的加法、减法、乘法和除法的规则,并能灵活地运用它们。
例题1:计算下列各式的值,其中a=2,b=-3,c=5:1) 2a + b - c2) a × (b + c) - 3b3) c ÷ (a + b)例题2:根据题意写出代数表达式:1) 一个数加上3的两倍2) 七的3倍减去4四、平方根与立方根在本节课中,我们将学习平方根与立方根的概念和运算。
平方根是指一个数的平方等于给定数的非负实数解,立方根则是指一个数的立方等于给定数的解。
我们需要掌握平方根和立方根的计算方法,并能应用到实际问题中。
例题1:计算下列各式的值:1) √162) ∛273) √(4 × 9)4) ∛64 ÷ 2例题2:根据题意写出平方根与立方根的表达式:1) 一个数的平方根减去32) 八的立方根加上2五、四边形的特征与性质在本节课中,我们将学习四边形的特征与性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章有理数课题:1.1 正数和负数(1)【学习目标】:1、掌握正数和负数概念;2、会区分两种不同意义的量,会用符号表示正数和负数;3、体验数学发展是生活实际的需要,激发学生学习数学的兴趣。
【重点难点】:正数和负数概念【导学指导】:一、知识链接:1、小学里学过哪些数请写出来:、、。
2、阅读课本P1和P2三幅图(重点是三个例子,边阅读边思考)回答下面提出的问题:3、在生活中,仅有整数和分数够用了吗?有没有比0小的数?如果有,那叫做什么数?二、自主学习1、正数与负数的产生(1)、生活中具有相反意义的量如:运进5吨与运出3吨;上升7米与下降8米;向东50米与向西47米等都是生活中遇到的具有相反意义的量。
请你也举一个具有相反意义量的例子:。
(2)负数的产生同样是生活和生产的需要2、正数和负数的表示方法(1)一般地,我们把上升、运进、零上、收入、前进、高出等规定为正的,而与它相反的量,如:下降、运出、零下、支出、后退、低于等规定为负的。
正的量就用小学里学过的数表示,有时也在它前面放上一个“+”(读作正)号,如前面的5、7、50;负的量用小学学过的数前面放上“—”(读作负)号来表示,如上面的—3、—8、—47。
(2)活动两个同学为一组,一同学任意说意义相反的两个量,另一个同学用正负数表示.(3)阅读P3练习前的内容3、正数、负数的概念1)大于0的数叫做,小于0的数叫做。
2)正数是大于0的数,负数是的数,0既不是正数也不是负数。
【课堂练习】:1. P3第一题到第四题(直接做在课本上)。
2.小明的姐姐在银行工作,她把存入3万元记作+3万元,那么支取2万元应记作_______,-4万元表示________________。
3.已知下列各数:51-,432-,3.14,+3065,0,-239; 则正数有_____________________;负数有____________________。
4.下列结论中正确的是 …………………………………………( ) A .0既是正数,又是负数 B .O 是最小的正数C .0是最大的负数D .0既不是正数,也不是负数5.给出下列各数:-3,0,+5,213-,+3.1,21-,2004,+2010; 其中是负数的有 ……………………………………………………( ) A .2个B .3个C .4个D .5个【要点归纳】:正数、负数的概念:(1)大于0的数叫做 ,小于0的数叫做 。
(2)正数是大于0的数,负数是 的数,0既不是正数也不是负数。
【拓展训练】:1.零下15‴,表示为_________,比O‴低4‴的温度是_________。
2.地图上标有甲地海拔高度30米,乙地海拔高度为20米,丙地海拔高度为-5米,其中最高处为_______地,最低处为_______地.3.“甲比乙大-3岁”表示的意义是______________________。
4.如果海平面的高度为0米,一潜水艇在海水下40米处航行,一条鲨鱼在潜水艇上方10米处游动,试用正负数分别表示潜水艇和鲨鱼的高度。
【总结反思】:课题:1.1正数和负数(2)【学习目标】:1、会用正、负数表示具有相反意义的量;2、通过正、负数学习,培养学生应用数学知识的意识;【学习重点】:用正、负数表示具有相反意义的量;【学习难点】:实际问题中的数量关系;【导学指导】一、知识链接.通过上节课的学习,我们知道在实际生产和生活中存在着两种不同意义的量,为了区分它们,我们用__________ 和___________ 来分别表示它们。
问题:“零”为什么即不是正数也不是负数呢?引导学生思考讨论,借助举例说明。
参考例子:温度表示中的零上,零下和零度。
二.自主探究问题:(课本第4页例题)先引导学生分析,再让学生独立完成例(1)一个月内,小明体重增加2kg,小华体重减少1kg,小强体重无变化,写出他们这个月的体重增长值;2)2001年下列国家的商品进出口总额比上一年的变化情况是:美国减少6.4%, 德国增长1.3%,法国减少2.4%, 英国减少3.5%,意大利增长0.2%, 中国增长7.5%.写出这些国家2001年商品进出口总额的增长率;解:(1)这个月小明体重增长__________ ,小华体重增长_________ ,小强体重增长_________ ;2)六个国家2001年商品进出口总额的增长率:美国___________ 德国__________法国___________ 英国__________意大利__________ 中国__________【课堂练习】1.课本第4页练习2、阅读思考(课本第8页)用正负数表示加工允许误差;问题:直径为30.032mm和直径为29.97的零件是否合格?【要点归纳】1、本节课你有那些收获?2、还有没解决的问题吗?【拓展训练】1)甲冷库的温度是-12°C,乙冷库的温度比甲冷酷低5°C,则乙冷库的温度是;2)一种零件的内径尺寸在图纸上是9〒0.05(单位:mm),表示这种零件的标准尺寸是9mm,加工要求最大不超过标准尺寸多少?最小不小于标准尺寸多少?【总结反思】:课题:1.2.1 有理数【学习目标】:1、掌握有理数的概念,会对有理数按一定标准进行分类,培养分类能力;2、了解分类的标准与集合的含义;3、体验分类是数学上常用的处理问题方法;【学习重点】:正确理解有理数的概念【学习难点】:正确理解分类的标准和按照一定标准分类【导学指导】一、温故知新1、通过两节课的学习,,那么你能写出3个不同类的数吗?.(4名学生板书)__________________________________________二、自主探究问题1:观察黑板上的12个数,我们将这4位同学所写的数做一下分类;该分为几类,又该怎样分呢?先分组讨论交流,再写出来分为类,分别是:引导归纳:统称为整数,统称为有理数。
问题2:我们是否可以把上述数分为两类?如果可以,应分为哪两类?师生共同交流、归纳2、正数集合与负数集合所有的正数组成集合,所有的负数组成集合【课堂练习】1、P8练习(做在课本上)2.把下列各数填入它所属于的集合的圈内:15, -1, -5,2,813, 0.1, -5.32, -80, 123, 2.333;正整数集合负整数集合正分数集合负分数集合【要点归纳】: 有理数分类⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 或者 ⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数【拓展训练】1、下列说法中不正确的是……………………………………………( ) A .-3.14既是负数,分数,也是有理数 B .0既不是正数,也不是负数,但是整数c .-2000既是负数,也是整数,但不是有理数 D .O 是正数和负数的分界2、在下表适当的空格里画上“√”号【总结反思】:课题:1.2.2数轴【学习目标】:1、掌握数轴概念,理解数轴上的点和有理数的对应关系;2、会正确地画出数轴,利用数轴上的点表示有理数;3、领会数形结合的重要思想方法;【重点难点】:数轴的概念与用数轴上的点表示有理数;【导学指导】一、知识链接1、观察下面的温度计,读出温度.分别是°C、°C、°C;2、在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一汽车站请同学们分小组讨论,交流合作,动手操作二、自主探究1、由上面的两个问题,你受到了什么启发?能用直线上的点来表示有理数吗?2、自己动手操作,看看可以表示有理数的直线必须满足什么条件?引导归纳:1)、画数轴需要三个条件,即、方向和长度。
2)数轴【课堂练习】1、请你画好一条数轴2、利用上面的数轴表示下列有理数 1.5, —2, 2, —2.5,92, 23-, 0; 3、 写出数轴上点A,B,C,D,E 所表示的数:三、寻找规律1、观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,由此你有什么发现?2、每个数到原点的距离是多少?由此你又有什么发现?3、进一步引导学生完成P9归纳【要点归纳】:画数轴需要三个条件是什么?【拓展练习】1、在数轴上,表示数-3,2.6,53-,0,314,322-,-1的点中,在原点左边的点有 个。
2、在数轴上点A 表示-4,如果把原点O 向正方向移动1个单位,那么在新数轴上点A 表示的数是( )A.-5,B.-4C.-3D.-23、你觉得数轴上的点表示数的大小与点的位置有什么关系?【总结反思】:课题:1.2.3 相反数【学习目标】:1、掌握相反数的意义;2、掌握求一个已知数的相反数;3、体验数形结合思想;【学习重点】:求一个已知数的相反数;【学习难点】:根据相反数的意义化简符号。
【导学指导】一、温故知新1、数轴的三要素是什么?在下面画出一条数轴:2、在上面的数轴上描出表示5、—2、—5、+2 这四个数的点。
3、观察上图并填空:数轴上与原点的距离是2的点有个,这些点表示的数是;与原点的距离是5的点有个,这些点表示的数是。
从上面问题可以看出,一般地,如果a是一个正数,那么数轴上与原点的距离是a的点有两个,即一个表示a,另一个是,它们分别在原点的左边和右边,我们说,这两点关于原点对称。
二、自主学习自学课本第10、11的内容并填空:1、相反数的概念像2和—2、5和—5、3和—3这样,只有不同的两个数叫做互为相反数。
2、练习(1)、2.5的相反数是,—115和是互为相反数,的相反数是2010;(2)、a和互为相反数,也就是说,—a是的相反数例如a=7时,—a=—7,即7的相反数是—7.a=—5时,—a=—(—5),“—(—5)”读作“-5的相反数”,而—5的相反数是5,所以,—(—5)=5你发现了吗,在一个数的前面添上一个“—”号,这个数就成了原数的(3)简化符号:-(+0.75)= ,-(-68)= ,-(-0.5 )= ,-(+3.8)= ;(4)、0的相反数是 .3、数轴上表示相反数的两个点和原点的距离。
【课堂练习】P11第1、2、3题【要点归纳】:1、本节课你有那些收获?2、还有没解决的问题吗?【拓展训练】1.在数轴上标出3,-1.5,0各数与它们的相反数。
2.-1.6的相反数是,2x的相反数是,a-b的相反数是;3. 相反数等于它本身的数是,相反数大于它本身的数是;4.填空:(1)如果a=-13,那么-a=;(2)如果-a=-5.4,那么a=;(3)如果-x=-6,那么x=;(4)-x=9,那么x=;5.数轴上表示互为相反数的两个数的点之间的距离为10,求这两个数。
