2015届高三南师数学模考
南京市、盐城市2015届高三年级第二次模拟考试数学试题word版本

南京市、盐城市2015届高三年级第二次模拟考试数 学一、填空题1、函数x x x f cos sin )(=的最小正周期为 。
2、已知复数)31)(2(i i z +-=,其中i 是虚数单位,则复数z 在复平面上对应的点位 于第 象限。
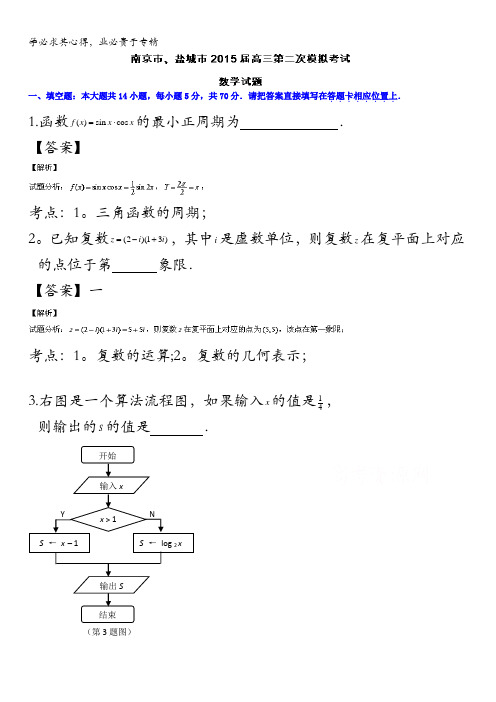
3、右图是一个算法流程图,如果输入x 的值是41,则输出S 的值是。
4、某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重, 所得数据均在区间[96,106]中,其中频率分布直方图如图所示,则在抽测的100件产品中,净重在区[100,104]上的产品件数是 。
若红球,得2分,摸出黑球,得1分,则3次摸球所得总分至少是4分的概率是 。
6、如图,在平面四边形ABCD 中,AC,BD 相交于点O ,E 为线段AO 的中点,若μλ+=(R ∈μλ,),则 =+μλ 7、已知平面α,β,直线n m ,,给出下列命题: ①若//m α,//,n m n β⊥,则βα⊥,②若//αβ,//,//m n αβ,则||m n , ③若,,m n m n αβ⊥⊥⊥,则αβ⊥, ④若βα⊥, ,m n αβ⊥⊥,则m n ⊥.其中是真命题的是 。
(填写所有真命题的序号)。
8、如图,在ABC ∆中,D 是BC 上的一点。
已知060=∠B ,BDACO E第6题图BACD 第8题图2,AD AC ===AB= 。
9、在平面直角坐标系xoy 中,已知抛物线C :24x y =的焦点为F ,定点)0,22(A ,若射线FA 与抛物线C 相交于点M ,与抛物线C 的准线相交于点N ,则FM :MN= 。
10、记等差数列{}n a 的前n 项和为n S ,已知12a =,且数列{}nS 也为等差数列,则13a = 。
11、已知知函数1()||1x f x x +=+,x R ∈,则不等式2(2)(34)f x x f x -<-的解集是 。
12、在平面直角坐标系xoy 中,已知⊙C:22(1)5x y +-=,A为⊙C与x 负半轴的交点,过A 作⊙C的弦AB ,记线段AB 的中点为M.则直线AB 的斜率为 。
江苏省南京市、盐城市2015届高三年级第二次模拟考试数学试题 含解析
一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1.函数()sin cos f x x x =⋅的最小正周期为 . 【答案】考点:1。
三角函数的周期;2。
已知复数(2)(13)z i i =-+,其中i 是虚数单位,则复数z 在复平面上对应的点位于第 象限. 【答案】一考点:1。
复数的运算;2。
复数的几何表示;3.右图是一个算法流程图,如果输入x 的值是14,则输出的S 的值是 .输入x开始 x > 1S ← x - 1S ← log 2 x输出S 结束 (第3题图)N Y【答案】-2 【解析】试题分析:x =14时,114>不成立,所以21log 24S ==-;考点:1。
算法流程图;2。
判断结构;4。
某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间中,其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间[100,104)上的产品件数是 .【答案】55考点:1。
频率分布直方图;5。
袋中有大小、质地相同的红、黑球各一个,现有放回地随机摸取3次,每次摸取一个球,若摸出红球,得2分,摸出黑球,得1分,则3次摸球所得总分至少是4分的概率是 .【答案】780.150 0.125 0.100 0.075 0.050(第4题图)频率/组距(克)考点:1.古典概型;2。
互斥事件与对立事件;6.如图,在平面四边形ABCD 中,AC ,BD 相交于点O ,E 为线段AO 的中点。
若BE BA BD λμ=+(,R λμ∈),则λμ+= .【答案】34考点:1。
平面向量的运算;2.平面向量基本定理; 7.已知平面α,β,直线,m n .给出下列命题: ① 若mα,,nm nβ,则αβ; ② 若αβ,,mn αβ,则mn;③ 若,,m n m n αβ⊥⊥⊥,则αβ⊥; ④ 若αβ⊥,,m n αβ⊥⊥,则m n ⊥。
江苏省南京市2015届高考全真模拟数学试题

江苏省南京市2015届高考全真模拟数学试题注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页,包含填空题(第1题——第14题)、解答题(第15题——第20题)。
本卷满分160分,考试时间为120分钟。
考试结束后,请将本卷和答题卡一并交回。
2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.请在答题卡上按照晤顺序在对应的答题区域内作答,在其他位置作答一律无效。
作答必须用0.5毫米黑色墨水的签字笔。
请注意字体工整,笔迹清楚。
5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗。
6.请保持答题卡卡面清洁,不要折叠、破损。
一、填空题:本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.1、复数1i1i 2等于___ ★ ___ 2、函数sin(2)6π=-y x 的最小正周期为___ ★ ___ 3、已知集合⎭⎬⎫⎩⎨⎧-==24x x y x A ,(]a B ,∞-=,若A B ⊆,则实数a 的取值范围是___ ★ ___4、为了保证信息安全传输必须使用加密方式,有一种方式其加密、解密原理如下: 明文 密文 密文 明文已知加密为2-=xa y (x 为明文、y 为密文),如果明文“3”通过加密后得到密文为“6”, 再发送,接受方通过解密得到明文“3”,若接受方接到密文为“14”,则原发的明文 是___ ★ ___5、为了在运行下面的程序之后得到输出y =25,键盘输入x 应该是___ ★ ___ Input xIf x<0 theny=(x+1)*(x+1) Elsey=(x-1)*(x-1)End ifPrint y End6、已知向量 1),θ=a ,(1 cos ),θ=b ,则⋅a b 的最大值为___ ★ ___7、在区间[-π,π]内随机取两个数分别记为a ,b ,则使得函数22()2π=+-+f x x ax b 有零点的概率为___ ★ ___解密 加密 发送8、若函数123+++=mx x x y 是R 上的单调函数,则实数m 的取值范围是___ ★ ___ 9、设0)()(0,,),1(log )(223≥+≥++++=b f a f b a b a x x x x f 是则对任意实数的___ ★ ___条件。
南师附中2015届高三数学备战市一模试题

南师附中2015届高三数学备战市一模试题2015.12已知数列{a n}是各项均不为0的等差数列,公差为d,S n为其前n项和,且满足a n2=S2n-1,n ∈N*,数列{b n}满足,T n为数列{b n}的前n项和,(1)求a1、d和T n;(2)若对任意的n∈N*,不等式λT n<n+8·(-1)n恒成立,求实数λ的取值范围;(3)是否存在正整数m,n(1<m<n),使得T1,T m,T n成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由。
解:(1)在中,令n=1,n=2,得,解得,∴,,∴。
(2)①当n为偶数时,要使不等式恒成立,即需不等式恒成立,,等号在n=2时取得,∴此时λ需满足λ<25;②当n为奇数时,要使不等式恒成立,即需不等式恒成立,是随n的增大而增大,∴n=1时,取得最小值-6,∴此时λ需满足λ<-21;综合①、②可得λ的取值范围是λ<-21。
(3),若成等比数列,则,由,即,∴,又m∈N,且m>1,所以m=2,此时n=12,因此,当且仅当m=2,n=12时,数列{T n}中的成等比数列2.设实数数列{a n}的前n项和S n满足S n+1=a n+1S n(n∈N*)。
(1)若a1,S2,-2a2成等比数列,求S2和a3;(2)求证:对k≥3有0≤a k+1≤a k≤。
解:(1)由题意得由S2是等比中项知S2≠0因此S2=-2由解得。
(2)由题设条件有故S n≠1,a n+1≠1且从而对k≥3有①因且,由①得a k≥0 要证由①只要证即证即(a k-1-2)2≥0,此式明显成立因此(k≥3)最后证若不然又因a k≥0,故即(a k-1)2<0,矛盾因此a k+1≤a k(k≥3)。
3已知数列{a n}满足:(n∈N*,a∈R,a为常数),数列{b n}中,.(1)求a1,a2,a3;(2)证明:数列{b n}为等差数列;(3)求证:数列{b n}中存在三项构成等比数列时,a为有理数.解:(1)由已知,得,,.(2),∴b n+1﹣b n=1,又b1=a3=a,∴数列{b n}是首项为a,公差为1的等差数列.(3)证明:由(2)知b n=a+n﹣1,若三个不同的项a+i,a+j,a+k成等比数列,i、j、k为非负整数,且i<j<k,则(a+j)2=(a+i)(a+k),得a(i+k﹣2j)=j2﹣ik,若i+k﹣2j=0,则j2﹣ik=0,得i=j=k,这与i<j<k矛盾.若i+k﹣2j≠0,则,∵i、j、k为非负整数,∴a是有理数.4. 商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b-a),这里,x被称为乐观系数。
江苏省南京师大附中2015届高三12月段考数学试卷

江苏省南京师大附中2015届高三12月段考数学试卷2014.12.30注意事项:本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答卷纸相应位置上.........1.在复平面内,复数-3+i 和1-i 对应的点间的距离为 ▲ .2.在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(圆中阴影部分)中的概率是 ▲ .3.对某种花卉的开放花期追踪调查,调查情况如下:则这种花卉的平均花期为 ▲ 天.4.若sin α=35,α∈⎝⎛⎭⎫-π2,π2,则cos ⎝⎛⎭⎫α+5π4= ▲ .5.直线x cos α+3y +2=0(α∈R)的倾斜角的范围是 ▲ .6.设函数f (x )是奇函数且周期为3,f (-1)=-1, 则f (2014)= ▲7.阅读右面的程序框图,运行相应的程序, 则输出i 的值为 ▲ .8.若等边三角形ABC 的边长为23,平面内一点M 满足1263CM CB CA =+,则MA MB ⋅= ▲ .9.有下面四个判断:①命题“设a 、b ∈R ,若a +b ≠6,则a ≠3或b ≠3”是一个假命题; ②若“p 或q ”为真命题,则p 、q 均为真命题;③命题“∀a 、b ∈R ,a 2+b 2≥2(a -b -1)”的否定是“∃a 、b ∈R ,a 2+b 2≤2(a -b -1)”; ④若函数f (x )=ln ⎝⎛⎭⎫a +2x +1的图象关于原点对称,则a =3.其中正确的有 ▲ 个.10.若双曲线x 2a 2-y 23=1的一条渐近线被圆(x -2)2+y 2=4所截得的弦长为2,则该双曲线的实轴长为▲ .11.设n 为正整数,f (n )=1+12+13+…+1n ,计算得f (2)=32,f (4)>2,f (8)>52,f (16)>3,观察上述结果,可推测一般的结论为 ▲ .12.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为 ▲ .13.设函数f (x )=ax 3-3x +1(x ∈R ),若对于任意x ∈[-1,1],都有f (x )≥0成立,则实数a 的值为 ▲ .14.已知f (x )是定义在R 上不恒为零的函数,对于任意的x ,y ∈R ,都有f (x ·y )=xf (y )+yf (x ) 成立.数列{a n }满足a n =f (2n )(n ∈N *),且a 1=2.则数列的通项公式a n = ▲ .二、解答题:本大题共6小题,共90分.请在答卷纸指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)设△ABC 的内角A ,B ,C 的对边长分别为a ,b ,c ,且b 2=12ac .(1)求证:cos B ≥34;(2)若cos(A -C )+cos B =1,求角B 的大小.16.(本小题满分14分)如图,在直三棱柱ABC -A 1B 1C 1中,已知∠ACB =90°,BC =CC 1,E ,F 分别为AB ,AA 1的中点. (1)求证:直线EF ∥平面BC 1A 1;(2)求证:EF ⊥B 1C .17.(本小题满分14分)经市场调查,某旅游城市在过去的一个月内(以30天计),日旅游人数()f t (万人..)与时间t (天)的函数关系近似满足1()4f t t=+,人均消费()g t (元.)与时间t (天)的函数关系近似满足()115|15|g t t =--. (Ⅰ)求该城市的旅游日收益()w t (万元..)与时间(130,)t t t N ≤≤∈的函数关系式; (Ⅱ)求该城市旅游日收益的最小值(万元..).18.(本小题满分16分)已知抛物线D 的顶点是椭圆C :x 216+y 215=1的中心,焦点与该椭圆的右焦点重合.(1)求抛物线D 的方程;(2)过椭圆C 右顶点A 的直线l 交抛物线D 于M 、N 两点. ① 若直线l 的斜率为1,求MN 的长;② 是否存在垂直于x 轴的直线m 被以MA 为直径的圆E 所截得的弦长为定值?如 果存在,求出m 的方程;如果不存在,说明理由. 19.(本小题满分16分)设函数1()ln ().f x x a x a R x=--∈ (1)讨论()f x 的单调性;(2)若()f x 有两个极值点12x x 和,记过点1122(,()),(,())A x f x B x f x 的直线的斜率为k ,问:是否存在a ,使得2?k a =-若存在,求出a 的值,若不存在,请说明理由.20.(本小题满分16分)记数列{}n a 的前n 项和为n S (n ∈N*),若存在实常数A ,B ,C ,对于任意正整数n ,都有2n n a S An Bn C +=++成立.(1)已知0A B ==,10a ≠,求证:数列{}n a (n ∈N*)是等比数列;(2)已知数列{}n a (n ∈N*)是等差数列,求证:3A C B +=; (3)已知11a =,0B >且1B ≠,2B C +=.设λ为实数,若n ∀∈N*,1nn a a λ+<, 求λ的取值范围.南京师大附中2015届高三12月段考试卷数 学 2014.12.30注意事项:本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答卷纸相应位置上.........1.在复平面内,复数-3+i 和1-i 对应的点间的距离为 ▲ . 解析 -3+i -1+i|=|-4+2i|=(-4)2+22=20=2 5. 答案 2 52.在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(圆中阴影部分)中的概率是 ▲ .解析 设正方形的边长为2,则豆子落在正方形内切圆的上半圆中的概率为12π×124=π8.答案 π83.对某种花卉的开放花期追踪调查,调查情况如下:则这种花卉的平均花期为 ▲ 天.解析 x =1100(12×20+15×40+18×30+21×10)=15.9(天).答案 15.94.若sin α=35,α∈⎝⎛⎭⎫-π2,π2,则cos ⎝⎛⎭⎫α+5π4= ▲ . 解析 因为α∈⎝⎛⎭⎫-π2,π2,sin α=35,所以cos α=45, 所以cos ⎝⎛⎭⎫α+5π4=-22(cos α-sin α)=-210. 答案 -2105.直线x cos α+3y +2=0(α∈R)的倾斜角的范围是 ▲ . 解析:由x cos α+3y +2=0得直线斜率k =-33cos α. ∵-1≤cos α≤1,∴-33≤k ≤33. 设直线的倾斜角为θ,则-33≤tan θ≤33. 结合正切函数在⎣⎡⎭⎫0,π2∪⎝⎛⎭⎫π2,π上的图象可知,0≤θ≤π6或5π6≤θ<π. 6.设函数f (x )是奇函数且周期为3,f (-1)=-1,则f (2014)= ▲ .解析 因为f (-x )=-f (x ),f (x +3)=f (x ),f (-1)=-1,所以f (1)=1,f (2 014)=f (3×671+1)=f (1)=1. 答案 17.阅读下面的程序框图,运行相应的程序, 则输出i 的值为 ▲ . 解析 第一次运行结束:i =1,a =2; 第二次运行结束:i =2,a =5; 第三次运行结束:i =3,a =16;第四次运行结束:i =4,a =65,故输出i =4. 答案 48.若等边三角形ABC 的边长为23,平面内一点M 满足1263CM CB CA =+,则MA MB ⋅= ▲ .3),则M ⎝⎛⎭⎫332,12,解析 建立直角坐标,由题意,设C (0,0),A (23,0),B (3,MA MB ⋅=⎝⎛⎭⎫32,-12·⎝⎛⎭⎫-32,52=-2.答案 -29.有下面四个判断:①命题“设a 、b ∈R ,若a +b ≠6,则a ≠3或b ≠3”是一个假命题; ②若“p 或q ”为真命题,则p 、q 均为真命题;③命题“∀a 、b ∈R ,a 2+b 2≥2(a -b -1)”的否定是“∃a 、b ∈R ,a 2+b 2≤2(a -b -1)”; ④若函数f (x )=ln ⎝⎛⎭⎫a +2x +1的图象关于原点对称,则a =3.其中正确的有 ▲ 个.解析 对于①:此命题的逆否命题为“设a 、b ∈R ,若a =3且b =3,则a +b =6”,此命题为真命题,所以原命题也是真命题,①错误;“p 或q ”为真,则p 、q 至少有一个为真命题,②错误;“∀a 、b ∈R ,a 2+b 2≥2(a -b -1)”的否定是“∃a 、b ∈R ,a 2+b 2<2(a -b -1)”,③错误;对于④:若f (x )的图象关于原点对称,则f (x )为奇函数,则f (0)=ln(a +2)=0,解得a =-1,④错误. 答案 010.若双曲线x 2a 2-y 23=1的一条渐近线被圆(x -2)2+y 2=4所截得的弦长为2,则该双曲线的实轴长为▲ . 答案 2解析 双曲线x 2a 2-y 23=1的渐近线方程为y =±3a x ,即3x ±ay =0,圆(x -2)2+y 2=4的圆心为C (2,0),半径为r =2,如图,由 圆的弦长公式得弦心距|CD |=22-12=3,另一方面,圆心 C (2,0)到双曲线x 2a 2-y 23=1的渐近线3x -ay =0的距离为d =|3×2-a ×0|3+a 2=233+a 2,所以233+a 2=3,解得a 2=1,即a =1,该双曲线的实轴长为2a =2.11.设n 为正整数,f (n )=1+12+13+…+1n ,计算得f (2)=32,f (4)>2,f (8)>52,f (16)>3,观察上述结果,可推测一般的结论为 ▲ .解析 由前四个式子可得,第n 个不等式的左边应当为f (2n ),右边应当为n +22,即可得一般的结论为f (2n )≥n +22. 答案 f (2n )≥n +2212.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为 ▲ . 答案26解析 由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍. 在三棱锥O -ABC 中,其棱长都是1,如图所示, S △ABC =34×AB 2=34,高OD =12-⎝⎛⎭⎫332=63, ∴V S -ABC =2V O -ABC =2×13×34×63=26.13.设函数f (x )=ax 3-3x +1(x ∈R ),若对于任意x ∈[-1,1],都有f (x )≥0成立,则实数a 的值为 ▲ . 解析 若x =0,则不论a 取何值,f (x )≥0显然成立;当x >0,即x ∈(0,1]时,f (x )=ax 3-3x +1≥0可化为a ≥3x 2-1x 3.设g (x )=3x 2-1x 3,则g ′(x )=3(1-2x )x 4,所以g (x )在区间⎝⎛⎦⎤0,12上单调递增,在区间⎣⎡⎦⎤12,1上单调递减,因此g (x )max =g ⎝⎛⎭⎫12=4,从而a ≥4.当x <0,即x ∈[-1,0)时,同理a ≤3x 2-1x 3.g (x )在区间[-1,0)上单调递增, ∴g (x )min =g (-1)=4,从而a ≤4, 综上可知a =4. 答案 414.已知f (x )是定义在R 上不恒为零的函数,对于任意的x ,y ∈R ,都有f (x ·y )=xf (y )+yf (x ) 成立.数列{a n }满足a n =f (2n )(n ∈N *),且a 1=2.则数列的通项公式a n = ▲ . 解析 由a n +1=f (2n +1)=2f (2n )+2n f (2)=2a n +2n +1,得a n +12n +1=a n 2n +1,所以⎩⎨⎧⎭⎬⎫a n 2n 是首项为1,公差为1的等差数列,所以a n2n =n ,a n =n ·2n .答案 n ·2n二、解答题:本大题共6小题,共90分.请在答卷纸指定.....区域内...作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)设△ABC 的内角A ,B ,C 的对边长分别为a ,b ,c ,且b 2=12ac .(1)求证:cos B ≥34;(2)若cos(A -C )+cos B =1,求角B 的大小.解 (1)因为cos B =a 2+c 2-b 22ac ……………2分=a 2+c 2-12ac 2ac ≥2ac -12ac2ac =34,所以cos B ≥34 ……6分(2)因为cos(A -C )+cos B =cos(A -C )-cos(A +C )=2sin A sin C =1, 所以sin A sin C =12.……………8分又由b 2=12ac ,得sin 2B =12sin A sin C =14, ……………10分又B ∈(0,π),且cos B ≥34>0,知B 为为锐角 ……………12分故sin B =12,得B =π6.……………14分16.(本小题满分14分)如图,在直三棱柱ABC -A 1B 1C 1中,已知∠ACB =90°,BC =CC 1,E ,F 分别为AB ,AA 1的中点. (1)求证:直线EF ∥平面BC 1A 1; (2)求证:EF ⊥B 1C .证明 (1)由题知,EF 是△AA 1B 的中位线, 所以EF ∥A 1B ……………2分由于EF ⊄平面BC 1A 1,A 1B ⊂平面BC 1A 1,所以EF ∥平面BC 1A 1. ……………6分(2)由题知,四边形BCC 1B 1是正方形,所以B 1C ⊥BC 1. ……8分 又∠A 1C 1B 1=∠ACB =90°,所以A 1C 1⊥C 1B 1.在直三棱柱ABC -A 1B 1C 1中,CC 1⊥平面A 1C 1B 1,A 1C 1⊂平面A 1C 1B 1,从而A 1C 1⊥CC 1, 又CC 1∩C 1B 1=C 1,CC 1,C 1B 1⊂平面BCC 1B 1,所以A 1C 1⊥平面BCC 1B 1 又B 1C ⊂平面BCC 1B 1,所以A 1C 1⊥B 1C . . ……………10分因为A 1C 1∩BC 1=C 1,A 1C 1,BC 1⊂平面BC 1A 1,所以B 1C ⊥平面BC 1A 1. ……………12分 又A 1B ⊂平面BC 1A 1,所以B 1C ⊥A 1B .又由于EF ∥A 1B ,所以EF ⊥B 1C . ……………14分17.(本小题满分14分)经市场调查,某旅游城市在过去的一个月内(以30天计),日旅游人数()f t (万人..)与时间t (天)的函数关系近似满足1()4f t t=+,人均消费()g t (元.)与时间t (天)的函数关系近似满足()115|15|g t t =--. (Ⅰ)求该城市的旅游日收益()w t (万元..)与时间(130,)t t t N ≤≤∈的函数关系式; (Ⅱ)求该城市旅游日收益的最小值(万元..). 解:(Ⅰ)由题意得,1()()()(4)(115|15|)w t f t g t t t=⋅=+-- ………5分(Ⅱ)因为**1(4)(100),(115,)()1(4)(130),(1530,)t t t N tw t t t t N t ⎧++≤<∈⎪⎪=⎨⎪+-≤≤∈⎪⎩…………………7分①当115t ≤<时,125()(4)(100)4()401w t t t t t=++=++4401441≥⨯=当且仅当25t t=,即5t =时取等号 …………………10分 ②当1530t ≤≤时,1130()(4)(130)519(4)w t t t t t =+-=+-,可证()w t 在[15,30]t ∈上单调递减,所以当30t =时,()w t 取最小值为14033……………………13分由于14034413<,所以该城市旅游日收益的最小值为14033万元 ………14分18.(本小题满分16分)已知抛物线D 的顶点是椭圆C :x 216+y 215=1的中心,焦点与该椭圆的右焦点重合.(1)求抛物线D 的方程;(2)过椭圆C 右顶点A 的直线l 交抛物线D 于M 、N 两点. ① 若直线l 的斜率为1,求MN 的长;② 是否存在垂直于x 轴的直线m 被以MA 为直径的圆E 所截得的弦长为定值?如 果存在,求出m 的方程;如果不存在,说明理由. 解:(1)由题意,可设抛物线方程为()022>=p px y . 由13422=-=-b a ,得1=c .∴抛物线的焦点为()0,1,2=∴p . ∴抛物线D 的方程为x y 42=…………… 4分(2)设()11,y x A ,()22,y x B .① 直线l 的方程为:4-=x y , 联立⎩⎨⎧=-=xy x y 442,整理得:016122=+-x x)522,526(),522,526(++--A A AB ∴=()()221221y y x x ---104=9分② 设存在直线a x m =:满足题意,则圆心114,22x y E +⎛⎫⎪⎝⎭,过E 作直线a x =的垂线,垂足为F ,设直线m 与圆E 的一个交点为G .可得: 222,FG EG FE =- ……………11分即222FGEA FE=-=()2121212444⎪⎭⎫ ⎝⎛-+-+-a x y x =()()()21212121444441a x a x x y -+++--+=()211144a x a x x -++-=()2143a a x a -+-……………………………… 14分当3=a 时, 23FG =,此时直线m 被以AP 为直径的圆M 所截得的弦长恒为定值32. 因此存在直线3:=x m 满足题意 ……………………………………16分 19.(本小题满分16分) 设函数1()ln ().f x x a x a R x=--∈ (1)讨论()f x 的单调性;(2)若()f x 有两个极值点12x x 和,记过点1122(,()),(,())A x f x B x f x 的直线的斜率为k ,问:是否存在a ,使得2?k a =-若存在,求出a 的值,若不存在,请说明理由.解:(1)()f x 的定义域为(0,).+∞22211'()1a x ax f x x x x-+=+-=……………………………………2分 令2()1,g x x ax =-+其判别式D =a 2-4.当||2,0,'()0,a f x ≤≤≥时故()(0,)f x +∞在上单调递增.……………………………………3分当2a <-时,>0,g(x)=0的两根都小于0,在(0,)+∞上,'()0f x >,故()(0,)f x +∞在上单调 递增.……………………………………5分当2a >时,>0,g(x)=0的两根为12x x == 当10x x <<时, '()0f x >;当12x x x <<时, '()0f x <;当2x x >时, '()0f x >,故()f x 分别 在12(0,),(,)x x +∞上单调递增,在12(,)x x 上单调递减.………………8分(2)由(1)知,2a >. 因为1212121212()()()(ln ln )x x f x f x x x a x x x x --=-+--,所以 1212121212()()ln ln 11f x f x x x k a x x x x x x --==+--- 又由(1)知,121x x =.于是1212ln ln 2x x k ax x -=--……………………………………10分 若存在a ,使得2.k a =-则1212ln ln 1x x x x -=-.……………………………………12分 即1212ln ln x x x x -=-. 亦即222212ln 0(1)(*)x x x x --=> 再由(1)知,函数1()2ln h t t t t=--在(0,)+∞上单调递增,而21x >, 所以222112ln 12ln10.1x x x -->--=与(*)式矛盾.故不存在a ,使得2.k a =-.…16分20.(本小题满分16分)记数列{}n a 的前n 项和为n S (n ∈N*),若存在实常数A ,B ,C ,对于任意正整数n ,都有2n n a S An Bn C +=++成立.(1)已知0A B ==,10a ≠,求证:数列{}n a (n ∈N*)是等比数列;(2)已知数列{}n a (n ∈N*)是等差数列,求证:3A C B +=;(3)已知11a =,0B >且1B ≠,2B C +=.设λ为实数,若n ∀∈N*,1n n a a λ+<,求λ的取值范围. 解:(1)由0A B ==,得n n a S C +=(n ∈N*), ①从而11n n a S C +++=. ② ………2分 ②-①式得12n n a a +=,又10a ≠,所以数列{}n a 为等比数列. ………4分(2)由数列{}n a 是等差数列,可令公差为d ,则11(1)(1),2n n n n a a n d S na d -=+-=+. 于是由2n n a S An Bn C +=++得1221()22d d n a n a n B C d A n ++++=+-. 由正整数n 的任意性得11,2,2.d A d B a C a d ⎧=⎪⎪⎪=+⎨⎪=-⎪⎪⎩………6分 从而得113223d d a a B A d C +-=+==+. ………8分 (3)由11a =,2B C +=,及2n n a S An Bn C +=++,得12a A B C =++,即2A B C =++, 则有0A =. ………9分于是(2)n n a S Bn B +=+-,从而11(1)(2)n n a S B n B +++=++-,相减得12n n a a B +-=,11()2n n a B a B +-=-, 又11a =,1B ≠,则10a B -≠, 所以111()2n n a B a B --=-,即11(1)2n n a B B -=-+. ………12分 于是111(1)121(1)2(11)2n n n n n B B B B BB a B a -+-+=--+-=++.由0B >且1B ≠,下面需分两种情形来讨论.(i )当01B <<时,10B ->,则式子1(1)2n B B B --+的值随n 的增大而减小, 所以,对n ∀∈N *,1n n a a +的最大值在1n =时取得,即max 12()111(1)2n n n a B B B B a +--+==+=+.于是,对于n ∀∈N *,121n n a a B +≤+,又1n n a a λ+<,21B λ∴>+. ………14分 (ii )当1B >时,由(1)2(1)210n B B B B B -+≥-+=+>,2221n B B B ≥>-, 得110(1)2n B B B--<<-+.所以,对于n ∀∈N *, 11011(1)2n n n a B a B B+-<=+<-+. ① 假设1λ<,则有0λ>,且111(1)2n n n a B a B B λ+-=+<-+, 得(1)(2)2(1)n B B λλ--<-,即2(1)(2)log (1)B n Bλλ--<-, 这表明,当n 取大于等于2(1)(2)log (1)B B λλ---的正整数时,1n n a a λ+<不成立, 与题设不符,矛盾.所以1λ≥.又由①式知1λ≥符合题意. 故1B >时,1λ≥.综上所述,当01B <<时,21Bλ>+;当1B >时,1λ≥. ……16分。
南京师大附中2015届高三数学模拟考试试卷

2015高考数学模拟题(1)南师大《数学之友》一. 填空题1. 在ABC ∆中,已知2=AC ,3=BC ,54cos -=A ,则=+)62sin(πB ▲ .2.已知中心为O 的正方形ABCD 的边长为2,点M 、N 分别为线段BC 、CD 上的两个1≤,则⋅的取值范围是 ▲ .3. 若函数f (x )=xx 2+a (a >0)在[1,+∞)上的最大值为22,则a 的值为___▲_____.4.设 x 、y 均为正实数,且33122x y+=++,以点),(y x 为圆心,xy R =为半径的圆的 面积最小时圆的标准方程为 ▲ .5. 任给实数,a b ,定义,0,0ab ab a b a ab b≥⎧⎪*=⎨<⎪⎩,设函数()ln f x x x =*. {}n a 是公比大于0的等比数列,且51a =,()()()()()187321a a f a f a f a f a f =+++++ ,则1a = ▲ . 6. 已知函数()11--=x x f ,如果关于x 的方程()m x f =()R m ∈恰有4个互不相等的实 数根1x ,2x ,3x ,4x ,则4321x x x x 的取值范围是 ▲ .二、解答题7. 某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段.已知跳水板AB 长为m 2,跳水板距水面CD 的高BC 为3m ,5CE m =,m CF 6=.为安全和空中姿态优美,训练时跳水曲线应在离起跳点A 处水平距h m (1≥h )时达到距水面最大高度4m .规定:以CD 为横轴,BC 为纵轴建立直角坐标系. (1)当h =1时,求跳水曲线所在的抛物线方程;(2)若跳水运动员在区域EF 内入水时才能达到压水花的训练 要求,求达到压水花的训练要求时,h 的取值范围.8. 已知椭圆C :22221(0)x y a b a b +=>>,点A 、B 分别是椭圆C 的左顶点和上顶点,直线AB 与圆G : 2224c x y +=(c 是椭圆的半焦距)相离,P 是直线AB 上一动点,过点P作圆G 的两切线,切点分别为M 、N .(1)若椭圆C 经过点,离心率35=e ,求椭圆C 的方程; (2)若存在点P 使得△PMN 为正三角形,试求椭圆离心率e 的取值范围.9. 已知等比数列}{n a 的首项20151=a ,公比21-=q ,数列}{n a 前n 项和记为n S . (1)证明:21n S S S ≤≤;(2)证明:若数列}{n a 中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若 所有这些等差数列的公差按从大到小的顺序依次记为n d d d ,,,21 ,则数列}{n d 为等 比数列.10.对于函数)(x f y =,若存在开区间D ,同时满足:①存在D a ∈,当a x <时,函数)(x f 单调递减,当a x >时,函数)(x f 单调递增; ②对任意0>x ,只要D x a x a ∈+-,,都有)()(x a f x a f +>-. 则称)(x f y =为D 内的“勾函数”.(1)证明:函数x y ln =为),0(+∞内的“勾函数”. (2)对于给定常数λ,是否存在m ,使函数122131)(3223+--=x x x x h λλλ在),(+∞m 内为“勾函数”?若存在,试求出m 的取值范围,若不存在,说明理由.理科加试11. 如图,在直三棱柱111ABC A B C -中,90BAC ∠=︒,12AB AC AA ===,E 是BC 的中点. (1)若棱1AA 上存在一点M ,满足11B M C E ⊥,求AM 的长; (2)求平面1AEC 与平面11ABB A 所成锐二面角的余弦值.12.在数列}{n a 和}{n b 中,nn a a =,b n a b n ++=)1(, ,3,2,1=n ,其中2≥a 且*N a ∈,R b ∈.设},,,{321 a a a A =,},,,{321 b b b B =,试问在区间],1[a 上是否存在实数b 使得φ≠=B A C .若存在,求出b 的一切可能的取值及相应的集合C ;若不存在,试说明理由.1B参考答案一、填空题1. 答案:.5017712+ 解:在ABC ∆中,.53)54(1cos 1sin 22=--=-=A A 由正弦定理,,sin sin B AC A BC =所以.525332sin sin =⨯=⋅=A BC AC B 又因为54cos -=A ,所以A ∠为钝角,从而B ∠为锐角,于是,521)52(1sin 1cos 22=-=-=B B ,25171)521(21cos 22cos 22=-⨯=-=B B .21254521522cos sin 22sin =⨯⨯==B B B .501771221251723252146sin 2cos 6cos 2sin 62sin +=⨯+⨯=+=+πππB B B )(2. 答案:)2⎡⎣. 解:以O 为原点,平行于AB 的直线为x 轴作平面直角坐标系(如图1),不妨设),1(y M 、)1,(x N .由题意知1≤,故 ⎪⎩⎪⎨⎧+=⋅≤-+-yx y x 1)1()1(22,其中10≤≤x ,10≤≤y .在41圆PRQ 中找一点),(y x 使y x +取最大最小.设目标函数为y x z +=.①由图2可知,当直线0=-+z y x 与在41圆PRQ 相切于点R 时,z 取得最小值,即y x =,得1)1(22=-x ,21)1(2=-x ,由于10≤≤x ,故122+-=x . 因此min z 22)122(2-=+-=.由图2可知,当直线0=-+z y x 经过点C 时,即1==y x ,z 取得最大值,最大值为211=+=z ,但是由题意知M 、N 是两个不同点,故最大值2取不到.综上可得,OM ON ⋅的取值范围是)2⎡⎣.图 1 图 2 3. 答案:12-.解:f (x )=x x 2+a=1x +a x(x ≥1),当a ≥1时,f (x )的最大值为12a=22,得a =21<1(舍去);当0<a <1时,f (x )的在[1,+∞)上单调递减,其最大值为11+a =22,得a =12-. 所以a 的值为12-.4. 答案: 256)4()4(22=-+-y x .解:由12323=+++y x 得:18-+=y yx .182-+=∴y yy xy .令1-=y z ,则1+=z y .zz z z xy 88122++++=∴z z z 9102++=109+⎪⎭⎫ ⎝⎛+=z z . 6929≥⋅≥+z z z z ,当且仅当zz 9=时,等号成立. 此时xy 最小,即圆的面积最小,此时3=z ,4=y ,4=x , ∴圆的标准方程:256)4()4(22=-+-y x . 5. 答案:e .解:5()(1)0f a f ==,设数列{}n a 公比为q , 551()()()()0ii i i f a f a f f q q-++=+=, 所以 283746()()()()()()0f a f a f a f a f a f a +=+=+=, 因此11()f a a =.当11a ≥时,1111ln ,a a a a e *==, 当11a <时,111ln a a a =无解. 6. 答案:()0,3-.解:函数11)(--=x x f 的图像如右图所示: 由图可知,若()m x f =的四个互不相等的实数根,则()1,0∈m ,且1x ,2x ,3x ,4x 分别为:m x =1,m x -=22,23+=m x ,m x -=4,所以,4321x x x x ()()222+--=m m m()4222--=m ()0,3-∈.二、解答题7.解:由题意可知最高点为)1)(4,2(≥+h h .可设抛物线方程为4)]2([2++-=h x a y .(1)当1=h 时,最高点为)4,3(,方程为4)3(2+-=x a y . 将)3,2(A 代入,得抛物线方程为562-+-=x x y . (2)将点)3,2(A 代入4)]2([2++-=h x a y ,得12-=ah . 由题意,得方程2[(2)]40a x h -++=在区间]6,5[内有一解. 令2221(x)[(2)]4[(2)]4f a x h x h h =-++=--++,则04)3(1)5(22≥+--=h hf ,且 221(6)(4)40f h h =--+≤,解得341≤≤h . 所以要达到压水花的训练要求h 的取值范围为]34,1[.8. 解:(1)椭圆为22194x y +=. (2)由直线AB 与圆G : 2224c x y +=(c 是椭圆的焦半距)相离,2c >,即222224()a b c a b >+,2222224()(2)a a c c a c ->-, 得42640e e -+>因为01e <<,所以203e <<连接,,,ON OM OP 若存在点P 使PMN ∆为正三角形,则在Rt OPN ∆中, 22OP ON r c ===,所以,点O 到直线AB 的距离不大于cc ≤,∴22222()a b c a b ≤+,222222()(2)a a c c a c -≤-,得42310e e -+≤因为01e <<21e ≤<,②23e ≤<e ≤< 9.(1)证明:12111111[1()]112[1()]1321()2n n n a S S S a S ----=+=---≤--,当1=n 时,等号成立.23222121[1()]112[1()]621()2n n n a S S S a S ----=+=+--≥--,当2=n 时,等号成立.∴21n S S S ≤≤.(2)证明: 1)21(2015--=n n a ,∴n a 随n 增大而减小,n a 奇数项均正,偶数项均负.①当k 是奇数时,}{n a 中的任意相邻三项按从小到大排列为1k a +,2k a +,k a , 则kk kk k a a a a a 2)21()21(11111=-+-=+-+,k k k a a a 2)21(221112=-=++, ∴122k k k a a a +++=,因此k k k a a a ,,21++成等差数列,公差11111223])21()21[(++++=---=-=k k k k k k a a a a d .②当k 是偶数时,设}{n a 中的任意相邻三项按从小到大排列为k a ,2k a +,1k a +,则1111111()()222k k k k ka a a a a -++=-+-=-,1121122()22k k k a a a ++=-=-, ∴122k k k a a a +++=,因此k k k a a a ,,21++成等差数列,公差111211311[()()]222k k k k k k a d a a a +-++=-=---=.综上可知,}{n a 中的任意相邻三项按从小到大排列,总可以使其成等差数列,且1123+=k k a d ,211=+n n d d ,∴数列}{n d 为等比数列. 10. 证明:(1)①存在1=a ,当x x f x ln )(),1,0(-=∈为减函数, 当x x f x ln )(),,1(=+∞∈为增函数;②对任意0>x ,当01>-x 时,),1ln()1ln()1(x x x f --=-=- ).1ln()1ln()1(x x x f +=+=+所以,0)1ln()1ln()1ln()1()1(2>--=+---=+--x x x x f x f 即).1()1(x f x f +>-所以函数x y ln =为),0(+∞内的“勾函数”.(2)①当0=λ时,1)(=x h ,不存在m 使函数)(x h 在),(+∞m 内为“勾函数”; ②当0<λ时,).2)((2)(322'λλλλλλ-+=--=x x x x x h 当),2(λλ-∈x 时,0)('>x h ,)(x h 为增函数; 当),(+∞-∈λx 时,0)('<x h ,)(x h 为减函数,因此不存在m 及常数0x ,使函数)(x h 在),(0x m 为减函数,同时在),(0+∞x 为增函数. 所以不存在m 使函数)(x h 在),(+∞m 内为“勾函数”.③当0>λ时,)(x h 在)2,(λλ-为减函数,在),2(+∞λ为增函数.当)2,[λλ-∈m ,则在),(+∞m 上存在λ2=a ,使)(x h 在),(a m 内为减函数,在),(+∞a 内为增函数.当0>x ,),(,+∞∈+-m x a x a 时, 因为)()(x a h x a h +--)]2()2[(2])2()2[(21])2()2[(31322233x x x x x x +---+---+--=λλλλλλλλλ .0323<-=x λ所以)()(x a h x a h +<-.所以也不存在m 使函数)(x h 在),(+∞m 内为“勾函数”.综上所述,不论常数λ取何值,都不存在m ,使函数)(x h 在),(+∞m 内为“勾函数”.理科加试11. 解:(1)如图,建立直角坐标系.则1A (0,0,2),B (2,0,0),1(2,0,2)B ,(0,2,0)C ,1(0,2,2)C ,(1,1,0)E ,(0,0,)M m , 1B M=(2,0,2)m --,1C E =()2,1,1--.因为11B M C E ⊥,所以11B M C E ⋅=22(2)m ---=0. 解得1m =所以1AM =. (2)AE =(1,1,0),1(0,2,2)AC =, 设平面1AEC 的法向量n=(,,)x y z ,则:10220n AE x y n AC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,令1y =-,则1x =,1z =.(1,1,1)n =- . 因为1AA AC ⊥,BA AC ⊥,所以AC ⊥平面11ABB A , AC 为平面11ABB A 的法向量,AC=(0,2,0).c o s ,A C n <> =AC n AC n ⋅⋅.所以平面1AEC 与平面11ABB A. 12.解:设存在实数],1[a b ∈,使φ≠=B A C ,设C m ∈0,则0m A ∈,且0m B ∈.设)(*0N t a m t∈=,)()1(*0N S b S a m ∈++=,则(1)ta a Sb =++,所以1+-=a ba S t ,因为*,,N s t a ∈,且2≥a ,所以b a t -能被1+a 整除.① 当1=t 时,因为],1[a b ∈,]1,0[-∈-a b a ,所以*1a bS N a -=∉+; ② 当)(2*N n n t ∈=时,b a C a b a b a n n n n -++-++=--+=-1)1()1(]1)1[(12222 , 由于],1[a b ∈,所以]1,0[1-∈-a b ,110+<-≤a b ,所以,当且仅当1=b 时,b a t-能被1+a 整除.③ 当*21()t n n N =+∈时,212121121[(1)1](1)(1)1n n n n a b a b a C a b ++++-=+--=++++-- ,由于],1[a b ∈,所以]1,2[1+∈+a b ,所以,当且仅当11+=+a b ,即a b =时,b a t-能被1+a 整除.综上,在区间],1[a 上存在实数b ,使φ≠=B A C 成立.当1=b 时,},{*2N n a y y C n ∈==;当a b =时,21*{,}n C y y a n N +==∈.2015高考数学模拟题(2)南师大《数学之友》一. 填空题1. 已知),2(ππα∈且53cos -=α,则)42tan(πα-的值为 ▲ . 2. 在平面直角坐标系xOy 中,设A 是曲线1C :31(0)y ax a =+>与曲线2C :2252x y +=的一个公共点,若1C 在A 处的切线与2C 在A 处的切线互相垂直,则实数a 的值是 ▲ .3. 椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,若椭圆上恰好有6个不同的点P ,使得12F F P ∆为等腰三角形,则椭圆C 的离心率的取值范围是 ▲ .4. 已知2,3,60,2,(1),(0,1)AB AC BAC CD BC AE xAD x AB x ==∠===+-∈,则AE 在AC上的投影的取值范围是 ▲ .5. 设函数⎩⎨⎧≤-≤≤--=20,102,1)(x x x x f <, 若函数ax x f x g -=)()(,]2,2[-∈x 为偶函数,则实数a 的值为 ▲ .6. 各项为实数的等差数列的公差为4,其首项的平方与其余各项之和不超过100,这样的数列至多有 ▲ 项.二、解答题7. 在平面直角坐标系xOy 中,已知圆O :x 2+y 2=64,圆O 1与圆O 相交,圆心为O 1(9,0). (1) 经过1O 作圆O 的切线,求切线方程;(2) 过定点()0,6P 作动直线l 与圆O ,圆1O 都相交,且直线l 被圆O ,圆1O 截得的弦长分别为d ,1d .若d 与1d 的比值总等于同一常数λ,求λ的值和圆1O 的方程.8. 某港湾的平面示意图如图所示,直线1l 、2l 是两条海岸线,点O 为1l 、2l 交点,A 位于O 的正南方向6km 处,B 位于O 的北偏东︒60方向10km 处.(1) 求集镇A ,B 间的距离;(2) 随着经济的发展,为缓解集镇O 的交通压力,拟在海岸线1l ,2l 上分别修建码头N M 、,开辟水上航线.勘测时发现:以O 为圆心,3km 为半径的扇形区域为浅水区,不适宜 船只航行.请确定码头N M 、的位置,使得N M 、之间的直线航线最短.9. 有n 个首项都是1的等差数列,设第m 个数列的第k 项为mk a (,1,2,3,,, 3)m k n n = ≥,公差为m d ,并且123,,,,n n n nn a a a a 成等差数列. (1)证明()()2112d m d m d m -+-=; (2)设3,121==d d ,当6≥n 时,不等式n n d n >-+12)32(501恒成立.10.已知函数x b xx a x f ln )1()(--=(R b a ∈,),2)(x x g =.(1) 若1=a ,曲线)(x f y =在点))1(,1(f 处的切线与y 轴垂直,求b 的值; (2) 在(1)的条件下,求证2ln 2)()(->x f x g ;(3) 若2b =,函数)(x f 与)(x g 在其公共点处是否存在公切线.若存在,求出a 值的个数;若不存在,说明理由.理科加试11. 在正方体1111D C B A ABCD -中,O 是AC 的中点,E 是线段O D 1上一点,且 EO E D λ=1.(1)若1=λ,求异面直线DE 与1CD 所成角的余弦值; (2)若平面CDE ⊥平面O CD 1,求λ的值.12. 如图,椭圆1C :1422=+y x 的离心率为23,x 轴被曲线2C :12-=x y 截得的线段长等于1C 的长半轴长.设2C 与y 轴的交点为M ,过坐标原点O 的直线l 与2C 相交于点A ,B ,直线MA ,MB 分别与1C 相交于点D ,E .(1)证明:ME MD ⊥;(2) 记MAB ∆,MDE ∆的面积分别为1S ,2S ,问:是否存在直线l ,使得21S S 3217=成立?请说明理由.A C 1参考答案一. 填空题1.答案:31. 解:224παπ<<,12cos2cos 2-=αα,∴21cos 25α=,552cos =α,5522sin =α, 22tan=α,tan112tan()2431tan2ααπα--==+. 2.答案: 4.解:设()00,y x A ,所以1C 在A 处的切线斜率为()200'3ax x f =,2C 在A 处的切线斜率为001y x k OA -=-,又1C 在A 处的切线与2C 在A 处的切线互相垂直, 所以,132000-=⋅⎪⎪⎭⎫ ⎝⎛-ax y x ,即3003ax y =. 又1030-=y ax ,故230=y .代入25:222=+y x C ,得210±=x ,将210±=x ,230=y 代入()013>+=a ax y ,得4=a . 3.答案:111(,)(,1)322⋃.解:422111232c a c e e c a>-⎧⇒<<≠⎨≠⎩且,故离心率范围为111(,)(,1)322⋃. 4.答案:[]7,1.解:如图,(3,0),(1(7,C B D -.(61,AE x =+-,3(61)cos 61,(0,1)361[1,7]AE AC x AE EAC x x ACx ∙+∠===+∈∴+∈5.答案:21. 解:由题设,⎩⎨⎧≤--≤≤---=20,1)1(02,1)(x x a x ax x g <,则⎩⎨⎧≤-<--≤-≤--=-20,1)1(02,1)(x x a x ax x g ⎩⎨⎧≤≤-≤----=20.1,02,1)1(x ax x x a < 因为)(x g 为偶函数,故)()(x g x g -=. 则1)1(1--=-x a ax 对于]2,2[-∈x 恒成立,从而有a a -=1,得21=a . 6.答案: 8.解:设n a a a a ,,,,321 是公差为4的等差数列, 则1003221≤++++n a a a a , 即()()[]()100121441121≤-⋅-++++n n a a a ,=∆ ()()010*******1≤--+-+n n a n a , 因此,=∆0401672≤--n n , 解得21n n n ≤≤, 其中()028163711<-=n ,≤897281632<+=n , 所以,自然数n 的最大值为8,故这样的数列至多有8项. 故答案为:8.二、解答题7.解:(1)设切线的斜率为k ,则由题意可得切线方程为 09=+-k kx y ,由圆心O )0,0(到切线的距离为圆O 的半径得:219kk +8=,解得817±=k . 所以切线方程为8179817-=x y 或8179817+-=x y . (2) 当直线l 的斜率存在时,设直线l 为)6(-=x k y ,即06=+-k kx y .则点O ,O 1到直线l 的距离分别为216kk h +=,h 1=213kk +,设圆1O 的半径为r ,从而22136642k k d +-=,2221192kk r d +-=. 由d d 1=λ,得2122d d λ=. 所以64-22136k k +=)19(2222kk r +-λ. 整理得:064)928(222222=+-+-r k r λλλ. 由题意,知上式对于任意实数k 恒成立,所以⎪⎩⎪⎨⎧=+-=+-064092822222r r λλλ.解得λ=2(负根舍去),162=r .综上所述,λ=2.圆1O 的标准方程为16)9(22=+-y x .8. 解:(1) 在ABO ∆中,6=OA ,10=OB ,︒=∠120AOB ,︒⨯⨯⨯-+=120cos 2222OB OA OB OA AB 19621106210622=⎪⎭⎫⎝⎛-⨯⨯⨯-+=.14=∴AB ,即A ,B 间的距离为14km .(2) 依题意,直线MN 与圆O 相切,设切点为C ,连接OC ,则MN OC ⊥. 设x OM =,y ON =,u MN =, 在OMN ∆中,OC MN ON OM ⋅⋅=⋅⋅⋅︒2160sin 21, 即u xy 32=.由余弦定理,︒-+=120cos 2222xy y x u xy y x ++=22xy 3≥.所以,u u 362≥,36≥u ,当且仅当6==y x 时,u 取得最小值. 答:N M 、建在距离O 点均为km 6处航线最短.9. 证明:(1)因为123,,,,n n n nn a a a a 成等差数列,所以2322212,......,,,n a a a a 成等差数列.)1()1()1()1()1()1(12312-+-+==+-+=+-+∴n n d d d d d d即12312--==-=-n n d d d d d d ,所以,}{n d 成等差数列,公差为12d d -, 所以12112(1)()(2)(1)m d d m d d m d m d =+--=-+-. (2)由题知,12-=n d n ,2)32(5011n n d n >-+ 即 1(23)250(21)n n n +->-. 即为不等式1(23)250(21)0n n n +--->的解,考虑函数1()(23)250(21)n f n n n +=---, 由于]502)12[(2)()1(-+=-+nn n f n f , 当3≥n 时,(1)()f n f n +>. 即 <<<<)6()5()4()3(f f f f , 而(6)9(12850)1006020f =--=>, 所以,当6n ≥时,有()0f n >.因此当6n ≥时,1(23)250(21)n n n +->-恒成立,即n n d n >-+12)32(501恒成立. 10. 解:(1)1=a ,1()ln f x x b x x =--,222'111)(x bx x x b x x f +-=-+=,依题意,02)1('=-=b f .∴2=b . (2)由(1)得1()2ln f x x x x=--,),0(+∞∈x . 要证2ln 2)()(->x f x g ,只须证02ln 2ln 212>+++-x xx x . 设21(x)2ln 2ln 2F x x x x=-+++(0>x ). 222232')1)(12(2122112)(x x x x x x x x x x x F +-=+--=+--= .令'()0F x =,得21=x . 当210<<x 时,'()0F x <;当21>x 时,'()0F x >.所以,当12x =时,)(x F 取极小值,也是最小值,047)21()(min >==F x F .因此()0F x >,2ln 2)()(->x f x g .(3)设函数)(x f 与)(x g 的图像在其公共点),(00y x 处存在公切线.1()()2ln f x a x x x =--,2'22()ax x a f x x-+=,x x g 2)('=. 由)()(0'0'x g x f =,可得到0202022x x a x ax =+-,即02202030=-+-a x ax x , 200(2)(1)0x a x -+=,得20ax =.)(x f 的定义域为(0,)+∞. 当0≤a 时,0(0,)2ax =∉+∞.函数)(x f 与)(x g 在其公共点处没有公切线; 当0a >时,令)2()2(a g a f =,22412ln 2221a a a =--,即)2ln(882aa =-. 02ln 88ln 82=-+-a a .设2()8ln 88ln 2h x x x =-+-(0>x ),x xx h 28)('-=.令'()0h x =,得2=x . 当(0,2)x ∈时,'()0h x >,)(x h 递增;当(2,)x ∈+∞时,'()0h x <,)(x h 递减. 所以04)2()(max >==h x h .22224()8ln ()88ln 20h e e e e -=-+-=<,在(0,2)上存在唯一1x ,使得0)(1=x h ; 又082ln 8)2(2<-=h ,在(2,)+∞上存在唯一2x ,2()0h x =.综上,0≤a 时,不存在公切线;0a >时,存在公切线,适合题意的a 值有两个.理科加试11. 解:(1)不妨设正方体的棱长为1,以1,,DD DC DA 为单位正交基底建立如图所示的空间直角坐标系xyz D -,由题设,E 为O D 1的中点,则 )0,0,1(A ,)0,21,21(O ,)0,1,0(C , )1,0,0(1D ,)21,41,41(E , 于是)21,41,41(=DE ,)1,1,0(1-=CD ,)0,21,21(-=CO ,由63,cos 1=>=<CD . 所以异面直线AE 与1CD 所成角的余弦值为63. (2)设平面O CD 1的法向量为),,(111z y x =m ,由0=⋅m ,01=⋅CD m ,得⎪⎩⎪⎨⎧=+-=-,0,021211111z y y x 取11=x ,得111==z y ,即)1,1,1(=m .由EO E D λ=1, 得)11,)1(2,)1(2(λλλλλ+++E ,1(,,)2(1)2(1)1DE λλλλλ=+++ . 又设平面CDE 的法向量为),,(222z y x =n ,由0=⋅CD n ,0=⋅DE n ,得⎪⎩⎪⎨⎧=+++++=,0)1(2)1(2)1(2,02222λλλλλλz y x y 取22=x ,得λ-=2z ,即),0,2(λ-=n . 因为平面CDE ⊥平面1CD E ,所以0=⋅n m ,得2=λ.12. 解:(1) 由题意知,直线l 的斜率存在,设为k ,则直线l 的方程为kx y =.由⎩⎨⎧-==12x y kxy 得012=--kx x .设),(11y x A ,),(22y x B ,则1x ,2x 是上述方程的两个实根, 于是k x x =+21,21x x 1-=.又点M 的坐标)1,0(-,所以 =⋅MB MA k k 111x y +221x y +⋅2121)1)(1(x x kx kx ++= 21212121)(x x x x k x x k +++=1122-++-=k k 1-=.故ME MD ⊥.(2) 设直线MA 的斜率为1k ,则直线MA 的方程为11-=x k y , 由⎩⎨⎧-=-=1121x y x k y 解得⎩⎨⎧-==10y x 或⎩⎨⎧-==1211k y k x .故点A 的坐标为)1,(211-k k . 又直线MB 的斜率为11k -,同理可得点B 的坐标为)11,1(211--k k . 于是1S MB MA ⋅=21121121111121k k k k -+⋅⋅+=12121k k +=, 由⎩⎨⎧=-+-=0441221y x x k y 得08)41(1221=-+x k x k .解得⎩⎨⎧-==10y x 或⎪⎪⎩⎪⎪⎨⎧+-=+=21212114114418k k y k k x , 故点D 的坐标为)4114,418(2121211k k k k +-+, 又直线ME 的斜率为11k -,同理可得点E 的坐标为)44,48(2121211k k k k +-+-,于是2S ME MD ⋅=21)4)(41()1(322121121++⋅+=k k k k .因此)1744(641212121++=k k S S 由题意知,)1744(641212121++=k k S S 3217=, 解得421=k 或4121=k .又由点A ,B 的坐标可知,11212111k k k k k +-==111k k -,所以23±=k . 故满足条件的直线l 存在,且有两条,其方程分别为x y 23=,x y 23-=. 当a b =时,21*{,}n C y y a n N +==∈.。
南京市、盐城市2015届高三第一次模拟考试数学试题_含答案

i ←1 S ←0 While i <8 i ←i + 3 S ←2i + SEnd While Print S第6题图南京市、盐城市2015届高三年级第一次模拟考试数 学 试 题(总分160分,考试时间120分钟)参考公式:样本数据x 1,x 2,…,x n 的方差2211()n i i s x x n ==-∑,其中11n i i x x n ==∑锥体的体积公式:13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 圆锥的侧面积公式:rl s π=,其中是圆锥的r 底面半径,l 为母线长一、 填空题:本大题共14小题,每小题5分,计70分。
不需写出解答过程,请把答案写在答题纸的指定位置。
1.设集合{}2,0,M x =,集合{}0,1N =,若N M ⊆,则x = ▲ . 2.若复数a iz i+=(其中i 为虚数单位)的实部与虚部相等,则实数a = ▲ . 3.在一次射箭比赛中,某运动员5次射箭的环数依次是9,10,9,7,10,则该组数据的 方差是 ▲ .4.甲、乙两位同学下棋,若甲获胜的概率为0.2,甲、乙下和棋的概率为0.5,则乙获胜的 概率为 ▲ . 5.若双曲线222(0)x y a a -=>的右焦点与抛物线24y x =的焦点重合,则a = ▲ . 6.运行如图所示的程序后,输出的结果为 ▲ .7.若变量,x y 满足202300x y x y x -≤⎧⎪-+≥⎨⎪≥⎩,则2x y+的最大值为 ▲ .8.若一个圆锥的底面半径为1,侧面积是底面积的2倍,则该圆锥的体积为 ▲ . 9.若函数()sin()(0)6f x x πωω=+>图象的两条相邻的对称轴之间的距离为2π,且该函数图象关于点0(,0)x 成中心对称,0[0,]2x π∈,则0x = ▲ .10.若实数,x y 满足0x y >>,且22log log 1x y +=,则22x y x y+-的最小值为 ▲ .11.设向量(sin 2,cos )θθ=a ,(cos ,1)θ=b ,则“//a b ”是“1tan 2θ=”成立的 ▲ 条件 (选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”) .12.在平面直角坐标系xOy 中,设直线2y x =-+与圆222(0)x y r r +=>交于,A B 两点,O 为坐标原点,若圆上一点C 满足5344OC OA OB =+,则r = ▲ .13.已知()f x 是定义在[2,2]-上的奇函数,当(0,2]x ∈时,()21xf x =-,函数2()2g x x x m =-+. 如果对于1[2,2]x ∀∈-,2[2,2]x ∃∈-,使得21()()g x f x =,则实数m 的取值范围是 ▲ .14.已知数列{}n a 满足11a =-,21a a >,*1||2()n n n a a n N +-=∈,若数列{}21n a -单调递减,数列{}2n a 单调递增,则数列{}n a 的通项公式为n a = ▲ .二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,并把答案写在答题纸的指定区域内)15.在平面直角坐标系xOy 中,设锐角α的始边与x 轴的非负半轴重合,终边与单位圆交于点11(,)P x y ,将射线OP 绕坐标原点O 按逆时针方向旋转2π后与单位圆交于点22(,)Q x y . 记12()f y y α=+. (1)求函数()f α的值域;(2)设ABC ∆的角,,A B C 所对的边分别为,,a b c ,若()2f C =2a =1c =,求b .16.(本小题满分14分)如图,在正方体1111ABCD A B C D -中,,O E 分别为1,B D AB 的中点. (1)求证://OE 平面11BCC B ; (2)求证:平面1B DC ⊥平面1B DE .xy PQOα 第15题图BACDB 1A 1C 1D 1E第16题图O17.在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的右准线方程为4x =,右顶点为A ,上顶点为B ,右焦点为F ,斜率为2的直线l 经过点A ,且点F 到直线l 的距离为25.(1)求椭圆C 的标准方程;(2)将直线l 绕点A 旋转,它与椭圆C 相交于另一点P ,当,,B F P 三点共线时,试确定直线l 的斜率.18.某地拟模仿图甲建造一座大型体育馆,其设计方案侧面的外轮廓线如图乙所示:曲线AB 是以点E 为圆心的圆的一部分,其中(0,)E t (025t <≤,单位:米);曲线BC 是抛物线250(0)y ax a =-+>的一部分;CD AD ⊥,且CD 恰好等于圆E 的半径. 假定拟建体育馆的高50OB =米.(1)若要求30CD =米,AD =245米,求t 与a 的值;(2)若要求体育馆侧面的最大宽度DF 不超过75米,求a 的取值范围;(3)若125a =,求AD 的最大值.(参考公式:若()f x a x =-,则()2f x a x'=--)FPOxAly B第17题图·第18题-甲 xy O ABCD 第18题-乙E ·F19.设数列{}n a 是各项均为正数的等比数列,其前n 项和为n S ,若1564a a =,5348S S -=.(1)求数列{}n a 的通项公式;(2)对于正整数,,k m l (k m l <<),求证:“1m k =+且3l k =+”是“5,,k m l a a a 这三项经适当排序后能构成等差数列”成立的充要条件;(3)设数列{}n b 满足:对任意的正整数n ,都有121321n n n n a b a b a b a b --++++13246n n +=⋅--,且集合*|,n n b M n n N a λ⎧⎫=≥∈⎨⎬⎩⎭中有且仅有3个元素,试求λ的取值范围.20.已知函数()xf x e =,()g x mx n =+.(1)设()()()h x f x g x =-.① 若函数()h x 在0x =处的切线过点(1,0),求m n +的值;② 当0n =时,若函数()h x 在(1,)-+∞上没有零点,求m 的取值范围; (2)设函数1()()()nx r x f x g x =+,且4(0)n m m =>,求证:当0x ≥时,()1r x ≥.南京市、盐城市2015届高三年级第一次模拟考试数学参考答案一、填空题:本大题共14小题,每小题5分,计70分. 1. 1 2. -1 3. 654. 0.3 5.2 6. 42 7. 889. 512π10. 4 11.要不充分 1213. [5,2]-- 14. (2)13n --( 说明:本答案也可以写成21,321,3n nn n ⎧--⎪⎪⎨-⎪⎪⎩为奇数为偶数12解读:方法1:(平面向量数量积入手)22225325539244164416OC OA OB OA OA OB OB⎛⎫=+=+⋅⋅+ ⎪⎝⎭,即:222225159+cos 16816r r r AOB r =∠+,整理化简得:3cos 5AOB ∠=-,过点O 作AB 的垂线交AB 于D ,则23cos 2cos 15AOB AOD ∠=∠-=-,得21cos 5AOD ∠=,又圆心到直线的距离为OD ==所以222212cos 5OD AOD r r ∠===,所以210r =,r =.方法2:(平面向量坐标化入手)设()11,A x y ,()22,B x y ,(),C x y ,由5344OC OA OB=+得125344x x x =+,125344y y y =+,则22222222121211112222535325251525251544441616816168x y x x y y x y x y x y x y ⎛⎫⎛⎫+=+++=+++++ ⎪ ⎪⎝⎭⎝⎭由题意得,()222112225251516168r r r x y x y =+++,联立直线2y x =-+与圆222(0)x y r r +=>的方程,由韦达定理可解得:10r =.方法3:(平面向量共线定理入手)由5344OC OA OB =+得153288OC OA OB =+,设OC与AB 交于点M ,则A M B 、、三点共线。
南京市2015届高三第三次模拟考试数学试题及答案

南京市2015届高三年级第三次模拟考试注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、班级、学校写在答题纸上.试题的答案写在答题纸...上对应题目的答案空格内.考试结束后,交回答题纸. 参考公式样本数据x 1,x 2,…,x n 的方差s 2=1n i =1∑n (x i --x )2,其中-x =1n i =1∑n x i .锥体的体积公式:V =13Sh ,其中S 为锥体的底面积,h 为锥体的高.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题纸相应位置.......上. 1.已知复数z =2i 1-i-1,其中i 为虚数单位,则z 的模为 ▲ .2.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:则该营业窗口上午9点钟时,至少有2人排队的概率是 ▲ .3.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤2,x ≥1,y ≥0,则z =2x +y 的最大值是 ▲ .4.下图是一个算法流程图,则输出k 的值是 ▲ .5.如图是甲、乙两位射击运动员的5次训练成绩(单位:环)的茎叶图,则成绩较为稳定(方差较小)的运动员是 ▲ .6.记不等式x 2+x -6<0的解集为集合A ,函数y =lg(x -a )的定义域为集合B .若“x ∈A ”是“x ∈B ”的充分条件,则实数a 的取值范围为 ▲ .7.在平面直角坐标系xOy 中,过双曲线C :x 2-y 23=1的右焦点F 作x 轴的垂线l ,则l 与双曲线C 的两条渐近线所围成的三角形的面积是 ▲ .8.已知正六棱锥P -ABCDEF 的底面边长为2,侧棱长为4,则此六棱锥的体积为 ▲ . 9.在△ABC 中, ABC =,BA =2,BC =3,D ,E 是线段AC 的三等分点,则BD ·BE的值为 ▲ .10.记等差数列{a n }的前n 项和为S n .若S k -1=8,S k =0,S k +1=-10,则正整数k = ▲ . 11.若将函数f (x )=∣sin(-6)∣(>0)的图象向左平移9个单位后,所得图象对应的函数为偶函数 ,则实数的最小值是 ▲ . 12.已知x ,y 为正实数,则4x 4x +y +y x +y的最大值为 ▲ . 13.在平面直角坐标系xOy 中,圆C 的方程为(x -1)2+(y -1)2=9,直线l :y =kx +3与圆C 相交于A ,B 两点,M 为弦AB 上一动点,以M 为圆心,2为半径的圆与圆C 总有公共点,则实数k 的取值范围为 ▲ .14.已知a ,t 为正实数,函数f (x )=x 2-2x +a ,且对任意的x ∈[0,t ],都有f (x )∈[-a ,a ].若对每一个正实数a ,记t 的最大值为g (a ),则函数g (a )的值域为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a cos C +c cos A =2b cos A .(1)求角A的值;(2)求sin B+sin C的取值范围.16.(本小题满分14分)在四棱锥P-ABCD中,BC∥AD,P A⊥PD,AD=2BC,AB=PB,E为P A的中点.(1)求证:BE∥平面PCD;(2)求证:平面P AB⊥平面PCD.17.(本小题满分16分)在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.(1)已知点(62,1)在椭圆C上,求实数m的值;(2)已知定点A(-2,0).①若椭圆C 上存在点T ,使得TATF 1=2,求椭圆C 的离心率的取值范围;②当m =1时,记M 为椭圆C 上的动点,直线AM ,BM 分别与椭圆C 交于另一点P ,Q ,若AM → =λAP →,BM →=BQ →,求证:λ+为定值.18.(本小题满分16分)已知函数f (x )=x 2-x +t ,t ≥0,g (x )=ln x . (1)令h (x )=f (x )+g (x ),求证:h (x )是增函数;(2)直线l 与函数f (x ),g (x )的图象都相切.对于确定的正实数t ,讨论直线l 的条数,并说明理由.19.(本小题满分16分)已知数列{a n }的各项均为正数,其前n 项的和为S n ,且对任意的m ,n ∈N*,都有(S m +n +S 1)2=4a 2m a 2n .(1)求a 2a 1的值;(2)求证:{a n }为等比数列;(3)已知数列{c n },{d n }满足|c n |=|d n |=a n ,p (p ≥3)是给定的正整数,数列{c n },{d n }的前p 项的和分别为T p ,R p ,且T p =R p ,求证:对任意正整数k (1≤k ≤p ),c k =d k .南京市2015届高三年级第三次模拟考试数学附加题注意事项:1.附加题供选修物理的考生使用. 2.本试卷共40分,考试时间30分钟.3.答题前,考生务必将自己的姓名、班级、学校写在答题纸上.试题的答案写在答题..纸.上对应题目的答案空格内.考试结束后,交回答题纸. 20.选做题:在A 、B 、C 、D 四小题中只要选做2题,每小题10分,共计20分.请在答.卷纸指定区域内.......作答.解答应写出文字说明、证明过程或演算步骤. A .选修4—1:几何证明选讲如图,AB ,AC 是⊙O 的切线,ADE 是⊙O 的割线,求证:BE · CD =BD · CE .B .选修4-2:矩阵与变换已知矩阵A =⎣⎡⎦⎤a 11a ,直线l :x -y +4=0在矩阵A 对应的变换作用下变为直线l :x -y +2a =0.(1)求实数a 的值; (2)求A 2.C . 选修4-5:不等式选讲已知实数x ,y 满足x >y ,求证:2x +1x 2-2xy +y 2≥2y +3.必做题:第22题、第23题,每题10分,共计20分.请在答卷纸指定区域内........作答.解答应写出文字说明、证明过程或演算步骤.21.(本小题满分10分)如图,四棱锥P -ABCD 中,P A 平面ABCD ,AD ∥BC ,AB AD ,BC =233,AB =1,BD =P A =2.(1)求异面直线BD 与PC 所成角的余弦值; (2)求二面角A -PD -C 的余弦值.23.(本小题满分10分)已知集合A 是集合P n ={1,2,3,…,n } (n ≥3,n ∈N*)的子集,且A 中恰有3个元素,同时这3个元素的和是3的倍数.记符合上述条件的集合A 的个数为f (n ). (1)求f (3),f (4);(2)求f (n )(用含n 的式子表示).南京市2015届高三第三次模拟考试数学参考答案及评分标准说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题:本大题共14小题,每小题5分,共70分.1. 5 2.0.74 3.4 4.6 5.甲 6.(-∞,-3] 7.4 3 8.12 9.119 10.911.32 12. 43 13.[-34,+∞) 14.(0,1)∪{2}二、解答题:本大题共6小题,共90分.15.解:(1)因为a cos C +c cos A =2b cos A ,所以sin A cos C +sin C cos A =2sin B cos A ,即sin(A +C )=2sin B cos A .因为A +B +C =π,所以sin(A +C )=sin B .从而sin B =2sin B cos A . ………………………… 4分 因为sin B ≠0,所以cos A =12.因为0<A <π,所以A =π3. ………………………… 7分(2)sin B +sin C =sin B +sin(2π3-B )=sin B +sin 2π3cos B -cos 2π3sin B=32sin B +32cos B =3sin(B +π6). ………………………… 11分 因为0<B <2π3,所以π6<B +π6<5π6.所以sin B +sin C 的取值范围为(32,3]. ………………………… 14分16.证明:(1)取PD 的中点F ,连接EF ,CF .因为E 为P A 的中点,所以EF ∥AD ,EF =12AD .因为BC ∥AD ,BC =12AD ,所以EF ∥BC ,EF =BC . 所以四边形BCFE 为平行四边形.所以BE ∥CF . ………………………… 4分 因为BE 平面PCD ,CF 平面PCD ,所以BE ∥平面PCD . ………………………… 6分 (2)因为AB =PB ,E 为P A 的中点,所以P A ⊥BE .因为BE ∥CF ,所以P A ⊥CF . ………………………… 9分 因为P A ⊥PD ,PD 平面PCD ,CF 平面PCD ,PD ∩CF =F ,所以P A ⊥平面PCD . ………………………… 12分 因为P A 平面P AB ,所以平面P AB 平面PCD . ………………………… 14分17. 解:(1)设椭圆C 的方程为x 2a 2+y2b 2=1(a >b >0). 由题意,得⎩⎪⎨⎪⎧a 2c =m +1,(m +1)-c =m , 解得⎩⎪⎨⎪⎧a 2=m +1,b 2=m ,c =1.所以椭圆方程为x 2m +1+y 2m =1.因为椭圆C 过点(62,1),所以32(m +1)+1m=1, 解得m =2或m =-12(舍去).所以m =2. ………………………… 4分 (2)①设点T (x ,y ).由TATF 1=2,得(x +2)2+y 2=2[(x +1)2+y 2],即x 2+y 2=2. ………………… 6分 由⎩⎪⎨⎪⎧x 2+y 2=2,x 2m +1+y 2m=1, 得y 2=m 2-m .因此0≤m 2-m ≤m ,解得1≤m ≤2. 所以椭圆C 的离心率e =1m +1∈[33,22]. ………………………… 10分②(方法一)设M (x 0,y 0),P (x 1,y 1),Q (x 2,y 2). 则AM =(x 0+2,y 0),AP =(x 1+2,y 1). 由AM =AP , 得 ⎩⎨⎧x 0+2=(x 1+2),y 0=1.从而⎩⎨⎧x 0=1+2(-1),y 0=1.………………………… 12分因为x 022+y 02=1,所以[1+2(-1)]22+(1)2=1.即2(x 122+y 12)+2(-1)x 1+2(-1)2-1=0.因为 x 122+y 12=1,代入得2(-1)x 1+32-4+1=0.由题意知,≠1, 故x 1=-3-12,所以x 0=-32. 同理可得x 0=-+32. ………………………… 14分因此-32=-+32, 所以+=6. ………………………… 16分 (方法二)设M (x 0,y 0),P (x 1,y 1),Q (x 2,y 2). 直线AM 的方程为y =y 0x 0+2(x +2).将y =y 0x 0+2(x +2)代入x 22+y 2=1,得(12(x 0+2)2+y 20)x 2+4y 20x +4y 20-(x 0+2)2=0(*). 因为x 022+y 02=1,所以(*)可化为(2x 0+3)x 2+4y 20x -3x 20-4x 0=0. 因为x 0x 1=-3x 20+4x 02x 0+3,所以x 1=-3x 0+42x 0+3.同理x 2=3x 0-42x 0-3. ………………………… 14分因为AM =AP ,BM →=BQ →,所以+=x 0+2x 1+2+x 0-2x 1-2=x 0+2-3x 0+42x 0+3+2+x 0-23x 0-42x 0-3-2=(x 0+2)(2x 0+3)x 0+2+(x 0-2)(2x 0-3)-x 0+2=6.即λ+为定值6. ………………………… 16分 18.解:(1)由h (x )=f (x )+g (x )=x 2-x +t +ln x ,得h' (x )=2x -1+1x,x >0.因为2x +1x≥22x ·1x=22,所以h' (x )>0, 从而函数h (x )是增函数. ………………………… 3分 (2)记直线l 分别切f (x ),g (x )的图象于点(x 1,x 12-x 1+t ),(x 2,ln x 2),由f'(x )=2x -1,得l 的方程为y -(x 12-x 1+t )=(2x 1-1)(x -x 1),即y =(2x 1-1)x -x 12+t .由g'(x )=1x ,得l 的方程为y -ln x 2=1x 2(x -x 2),即y =1x 2· x +ln x 2-1.所以⎩⎪⎨⎪⎧ 2x 1-1=1x 2,-x 12+t =ln x 2-1.(*) 消去x 1得ln x 2+(1+x 2)24x 22-(t +1)=0 (**). ………………………… 7分令F (x )=ln x +(1+x )24x 2-(t +1),则F'(x )=1x -1+x 2x 3=2x 2-x -12x 3=(2x +1)(x -1)2x 3,x >0.由F'(x )=0,解得x =1.当0<x <1时,F'(x )<0,当x >1时,F'(x )>0, 所以F (x )在(0,1)上单调递减,在(1,+∞)上单调递增,从而F (x )min =F (1)=-t . ………………………… 9分 当t =0时,方程(**)只有唯一正数解,从而方程组(*)有唯一一组解,即存在唯一一条满足题意的直线; ………………………… 11分 当t >0时,F (1)<0,由于F (e t +1)>ln(e t +1)-(t +1)=0,故方程(**)在(1,+∞)上存在唯一解; ………………………… 13分 令k (x )=ln x +1x -1(x ≤1),由于k' (x )=1x -1x 2=x -1x 2≤0,故k (x )在(0,1]上单调递减,故当0<x <1时,k (x )>k (1)=0,即ln x >1-1x ,从而ln x +(1+x )24x 2 -(t +1)>(12x -12)2-t . 所以F (12(t +1))>(t +12)2-t =t +14>0,又0<12(t +1)<1,故方程(**)在(0,1)上存在唯一解.所以当t >0时,方程(**)有两个不同的正数解,方程组(*)有两组解. 即存在两条满足题意的直线.综上,当t =0时,与两个函数图象同时相切的直线的条数为1;当t >0时,与两个函数图象同时相切的直线的条数为2.………………………… 16分19.解:(1)由(S m +n +S 1)2=4a 2n a 2m ,得(S 2+S 1)2=4a 22,即(a 2+2a 1)2=4a 22.因为a 1>0,a 2>0,所以a 2+2a 1=a 2,即a 2a 1=2. ………………………… 3分证明:(2)(方法一)令m =1,n =2,得(S 3+S 1)2=4a 2a 4,即(2a 1+a 2+a 3)2=4a 2a 4, 令m =n =2,得S 4+S 1=2a 4,即2a 1+a 2+a 3=a 4. 所以a 4=4a 2=8a 1.又因为a 2a 1=2,所以a 3=4a 1. ………………………… 6分由(S m +n +S 1)2=4a 2n a 2m ,得(S n +1+S 1)2=4a 2n a 2,(S n +2+S 1)2=4a 2n a 4. 两式相除,得(S n +2+S 1)2(S n +1+S 1)2=a 4a 2,所以S n +2+S 1S n +1+S 1=a 4a 2=2. 即S n +2+S 1=2(S n +1+S 1), 从而S n +3+S 1=2(S n +2+S 1).所以a n +3=2a n +2,故当n ≥3时,{a n }是公比为2的等比数列. 又因为a 3=2a 2=4a 1,从而a n =a 1·2 n -1,n ∈N*.显然,a n =a 1·2 n-1满足题设,因此{a n }是首项为a 1,公比为2的等比数列. ………………………… 10分 (方法二)在(S m +n +S 1)2=4a 2n a 2m 中,令m =n ,得S 2n +S 1=2a 2n . ① 令m =n +1,得S 2n +1+S 1=2a 2n a 2n +2 , ② 在①中,用n +1代n 得,S 2n +2+S 1=2a 2n +2. ③ ②-①,得a 2n +1=2a 2n a 2n +2-2a 2n =2a 2n (a 2n +2-a 2n ), ④ ③-②,得a 2n +2=2a 2n +2-2a 2n a 2n +2=2a 2n +2(a 2n +2-a 2n ), ⑤ 由④⑤得a 2n +1=a 2n a 2n +2. ⑥………………………… 8分⑥代入④,得a 2n +1=2a 2n ;⑥代入⑤得a 2n +2=2a 2n +1, 所以a 2n +2a 2n +1=a 2n +1a 2n =2.又a 2a 1=2,从而a n =a 1·2 n -1,n ∈N*.显然,a n =a 1·2 n-1满足题设,因此{a n }是首项为a 1,公比为2的等比数列. ………………………… 10分 (3)由(2)知,a n =a 1·2 n -1.因为|c p |=|d p |=a 1·2p -1,所以c p =d p 或c p =-d p .若c p =-d p ,不妨设c p >0,d p <0,则T p ≥a 1·2p -1-(a 1·2p -2+a 1·2p -3+…+a 1)=a 1·2p -1-a 1·(2p -1-1)=a 1>0.R p ≤-a 1·2p -1+(a 1·2p -2+a 1·2p -3+…+a 1)=-a 1·2p -1+a 1·(2p -1-1)=-a 1<0.这与T p =R p 矛盾,所以c p =d p . 从而T p -1=R p -1.由上证明,同理可得c p -1=d p -1.如此下去,可得c p -2=d p -2,c p -3=d p -3.…,c 1=d 1. 即对任意正整数k (1≤k ≤p ),c k =d k . ………………………… 16分南京市2015届高三第三次模拟考试数学附加题参考答案及评分标准 2015.0520.选做题:在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共20分. A .选修4—1:几何证明选讲证明:因为AB 是⊙O 的切线,所以ABD =AEB .又因为BAD =EAB ,所以△BAD ∽△EAB .所以BD BE =ABAE . ………………………… 5分同理,CD CE =AC AE..因为AB ,AC 是⊙O 的切线,所以AB =AC .因此BD BE =CDCE ,即BE · CD =BD · CE . ………………………… 10分B .选修4—2:矩阵与变换解:(1)设直线l 上一点M 0(x 0,y 0)在矩阵A 对应的变换作用下变为l上点M (x ,y ),则⎣⎢⎡⎦⎥⎤x y =⎣⎡⎦⎤a 11a ⎣⎢⎡⎦⎥⎤x 0y 0=⎣⎢⎡⎦⎥⎤ax 0+y 0x 0+ay 0, 所以⎩⎨⎧x =ax 0+y 0,y =x 0+ay 0.………………………… 3分代入l 方程得(ax 0+y 0)-(x 0+ay 0)+2a =0, 即(a -1)x 0-(a -1)y 0+2a =0. 因为(x 0,y 0)满足x 0-y 0+4=0,所以2a a -1=4,解得a =2. ………………………… 6分(2)由A =⎣⎡⎦⎤2112,得A 2=⎣⎡⎦⎤2112⎣⎡⎦⎤2112=⎣⎡⎦⎤5445. ………………… 10分C .选修4—5:不等式选讲证明:因为x >y ,所以x -y >0,从而左边=(x -y )+(x -y )+1(x -y )2+2y≥33(x -y )(x -y )1(x -y )2+2y =2y +3 =右边.即原不等式成立. ………………………… 10分 21.解:(1)因为P A 平面ABCD ,AB 平面ABCD ,AD 平面ABCD ,所以P A AB ,P A AD . 又AD AB ,故分别以AB ,AD ,AP 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系. 根据条件得AD =3.所以B (1,0,0),D (0,3,0),C (1,233,0),P (0,0,2).从而BD =(-1,3,0),PC =(1,233,-2).………………………… 3分设异面直线BD ,PC 所成角为x , 则cos x =|cos <→BD ,→PC >|=|BDPC ∣BD ∣∣PC ∣|=|(-1,3,0)·(1,233,-2)2×193|=5738.即异面直线BD 与PC 所成角的余弦值为5738. ………………………… 5分 (2)因为AB 平面P AD ,所以平面P AD 的一个法向量为 AB =(1,0,0).设平面PCD 的一个法向量为n =(x ,y ,z ), 由nPC ,nPD ,PC =(1,233,-2),PD =(0,3,-2),得⎩⎪⎨⎪⎧x +233y -2z =0,3y -2z =0, 解得⎩⎨⎧x =23z ,y =233z .不妨取z =3,则得n =(2,23,3). ………………………… 8分 设二面角A -PD -C 的大小为, 则cos =cos <AB ,n >=AB · n∣AB ∣×∣n ∣=(1,0,0)·(2,23,3)1×5=25.即二面角A -PD -C 的余弦值为25. ………………………… 10分22.解:(1)f (3)=1,f (4)=2; ………………………… 2分 (2)设A 0={m ∣m =3p ,p ∈N*,p ≤n 3},A 1={m ∣m =3p -1,p ∈N*,p ≤n +13}, A 2={m ∣m =3p -2,p ∈N*,p ≤n +23},它们所含元素的个数分别记为∣A 0∣,∣A 1∣,∣A 2∣.……………………… 4分 ①当n =3k 时,则∣A 0∣=∣A 1∣=∣A 2∣=k . k =1,2时,f (n )=(C 1k)3=k 3;k ≥3时,f (n )=3C 3k +(C 1k )3=32k 3-32k 2+k .从而 f (n )=118n 3-16n 2+13n ,n =3k ,k ∈N*. ………………………… 6分②当n =3k -1时,则∣A 0∣=k -1,∣A 1∣=∣A 2∣=k . k =2时,f (n )=f (5)=2×2×1=4; k =3时,f (n )=f (8)=1+1+3×3×2=20;k >3时,f (n )=C 3k -1+2C 3k +C 1k -1 (C 1k )2=32k 3-3k 2+52k -1;从而 f (n )=118n 3-16n 2+13n -49,n =3k -1,k ∈N*. ………………………… 8分③当n =3k -2时,∣A 0∣=k -1,∣A 1∣=k -1,∣A 2∣=k . k =2时,f (n )=f (4)=2×1×1=2; k =3时,f (n )=f (7)=1+3×2×2=13;k >3时,f (n )=2C 3k -1+C 3k +(C 1k -1)2 C 1k =32k 3-92k 2+5k -2;从而 f (n )=118n 3-16n 2+13n -29,n =3k -2,k ∈N*.所以f (n )=⎩⎨⎧118n 3-16n 2+13n ,n =3k ,k ∈N*,118n 3-16n 2+13n -49,n =3k -1,k ∈N*,118n 3-16n 2+13n -29,n =3k -2,k ∈N*. …………………… 10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015高考数学模拟题(1)南师大《数学之友》一. 填空题1. 在ABC ∆中,已知2=AC ,3=BC ,54cos -=A ,则=+)62sin(πB ▲ .2.已知中心为O 的正方形ABCD 的边长为2,点M 、N 分别为线段BC 、CD 上的两个1≤,则⋅的取值范围是 ▲ .3. 若函数f (x )=xx 2+a (a >0)在[1,+∞)上的最大值为22,则a 的值为___▲_____.4.设 x 、y 均为正实数,且33122x y+=++,以点),(y x 为圆心,xy R =为半径的圆的 面积最小时圆的标准方程为 ▲ .5. 任给实数,a b ,定义,0,0ab ab a b a ab b≥⎧⎪*=⎨<⎪⎩,设函数()ln f x x x =*. {}n a 是公比大于0的等比数列,且51a =,()()()()()187321a a f a f a f a f a f =+++++ ,则1a = ▲ . 6. 已知函数()11--=x x f ,如果关于x 的方程()m x f =()R m ∈恰有4个互不相等的实 数根1x ,2x ,3x ,4x ,则4321x x x x 的取值范围是 ▲ .二、解答题7. 某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段.已知跳水板AB 长为m 2,跳水板距水面CD 的高BC 为3m ,5CE m =,m CF 6=.为安全和空中姿态优美,训练时跳水曲线应在离起跳点A 处水平距h m (1≥h )时达到距水面最大高度4m .规定:以CD 为横轴,BC 为纵轴建立直角坐标系. (1)当h =1时,求跳水曲线所在的抛物线方程;(2)若跳水运动员在区域EF 内入水时才能达到压水花的训练 要求,求达到压水花的训练要求时,h 的取值范围.8. 已知椭圆C :22221(0)x y a b a b +=>>,点A 、B 分别是椭圆C 的左顶点和上顶点,直线AB 与圆G : 2224c x y +=(c 是椭圆的半焦距)相离,P 是直线AB 上一动点,过点P作圆G 的两切线,切点分别为M 、N .(1)若椭圆C 经过点(1,3,离心率35=e ,求椭圆C 的方程; (2)若存在点P 使得△PMN 为正三角形,试求椭圆离心率e 的取值范围.9. 已知等比数列}{n a 的首项20151=a ,公比21-=q ,数列}{n a 前n 项和记为n S . (1)证明:21n S S S ≤≤;(2)证明:若数列}{n a 中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若 所有这些等差数列的公差按从大到小的顺序依次记为n d d d ,,,21 ,则数列}{n d 为等 比数列.10.对于函数)(x f y =,若存在开区间D ,同时满足:①存在D a ∈,当a x <时,函数)(x f 单调递减,当a x >时,函数)(x f 单调递增; ②对任意0>x ,只要D x a x a ∈+-,,都有)()(x a f x a f +>-. 则称)(x f y =为D 内的“勾函数”.(1)证明:函数x y ln =为),0(+∞内的“勾函数”. (2)对于给定常数λ,是否存在m ,使函数122131)(3223+--=x x x x h λλλ在),(+∞m 内为“勾函数”?若存在,试求出m 的取值范围,若不存在,说明理由.理科加试11. 如图,在直三棱柱111ABC A B C -中,90BAC ∠=︒,12AB AC AA ===,E 是BC 的中点. (1)若棱1AA 上存在一点M ,满足11B M C E ⊥,求AM 的长; (2)求平面1AEC 与平面11ABB A 所成锐二面角的余弦值.12.在数列}{n a 和}{n b 中,nn a a =,b n a b n ++=)1(, ,3,2,1=n ,其中2≥a 且*N a ∈,R b ∈.设},,,{321 a a a A =,},,,{321 b b b B =,试问在区间],1[a 上是否存在实数b 使得φ≠=B A C .若存在,求出b 的一切可能的取值及相应的集合C ;若不存在,试说明理由.1B参考答案一、填空题1. 答案:.5017712+ 解:在ABC ∆中,.53)54(1cos 1sin 22=--=-=A A 由正弦定理,,sin sin B AC A BC =所以.525332sin sin =⨯=⋅=A BC AC B 又因为54cos -=A ,所以A ∠为钝角,从而B ∠为锐角,于是,521)52(1sin 1cos 22=-=-=B B ,25171)521(21cos 22cos 22=-⨯=-=B B .21254521522cos sin 22sin =⨯⨯==B B B .501771221251723252146sin 2cos 6cos 2sin 62sin +=⨯+⨯=+=+πππB B B )(2. 答案:)2⎡⎣. 解:以O 为原点,平行于AB 的直线为x 轴作平面直角坐标系(如图1),不妨设),1(y M 、)1,(x N .由题意知1≤,故 ⎪⎩⎪⎨⎧+=⋅≤-+-yx y x 1)1()1(22,其中10≤≤x ,10≤≤y .在41圆PRQ 中找一点),(y x 使y x +取最大最小.设目标函数为y x z +=.①由图2可知,当直线0=-+z y x 与在41圆PRQ 相切于点R 时,z 取得最小值,即y x =,得1)1(22=-x ,21)1(2=-x ,由于10≤≤x ,故122+-=x . 因此min z 22)122(2-=+-=. 由图2可知,当直线0=-+z y x 经过点C 时,即1==y x ,z 取得最大值,最大值为211=+=z ,但是由题意知M 、N 是两个不同点,故最大值2取不到.综上可得,OM ON ⋅的取值范围是)2⎡⎣.图 1 图 2 3. 答案:12-.解:f (x )=x x 2+a=1x +a x(x ≥1),当a ≥1时,f (x )的最大值为12a =22,得a =21<1(舍去);当0<a <1时,f (x )的在[1,+∞)上单调递减,其最大值为11+a =22,得a =12-. 所以a 的值为12-.4. 答案: 256)4()4(22=-+-y x .解:由12323=+++y x 得:18-+=y yx .182-+=∴y yy xy .令1-=y z ,则1+=z y .z z z z xy 88122++++=∴ z z z 9102++=109+⎪⎭⎫⎝⎛+=z z .6929≥⋅≥+z z z z ,当且仅当zz 9=时,等号成立. 此时xy 最小,即圆的面积最小,此时3=z ,4=y ,4=x , ∴圆的标准方程:256)4()4(22=-+-y x . 5. 答案:e .解:5()(1)0f a f ==,设数列{}n a 公比为q , 551()()()()0i i i i f a f a f f q q-++=+=, 所以 283746()()()()()()0f a f a f a f a f a f a +=+=+=, 因此11()f a a =.当11a ≥时,1111ln ,a a a a e *==, 当11a <时,111ln a a a =无解. 6. 答案:()0,3-.解:函数11)(--=x x f 的图像如右图所示: 由图可知,若()m x f =的四个互不相等的实数根,则()1,0∈m ,且1x ,2x ,3x ,4x 分别为:m x =1,m x -=22,23+=m x ,m x -=4,所以,4321x x x x ()()222+--=m m m()4222--=m ()0,3-∈.二、解答题7.解:由题意可知最高点为)1)(4,2(≥+h h .可设抛物线方程为4)]2([2++-=h x a y .(1)当1=h 时,最高点为)4,3(,方程为4)3(2+-=x a y将)3,2(A 代入,得抛物线方程为562-+-=x x y . (2)将点)3,2(A 代入4)]2([2++-=h x a y ,得12-=ah . 由题意,得方程2[(2)]40a x h -++=在区间]6,5[内有一解. 令2221(x)[(2)]4[(2)]4f a x h x h h =-++=--++,则04)3(1)5(22≥+--=h hf ,且 221(6)(4)40f h h =--+≤,解得341≤≤h . 所以要达到压水花的训练要求h 的取值范围为]34,1[.8. 解:(1)椭圆为22194x y +=. (2)由直线AB 与圆G : 2224c x y +=(c 是椭圆的焦半距)相离,2c >,即222224()a b c a b >+,2222224()(2)a a c c a c ->-, 得42640e e -+>因为01e <<,所以203e <<连接,,,ON OM OP 若存在点P 使PMN ∆为正三角形,则在Rt OPN ∆中, 22OP ON r c ===,所以,点O 到直线AB 的距离不大于cc ≤,∴22222()a b c a b ≤+,222222()(2)a a c c a c -≤-,得42310e e -+≤因为01e <<21e ≤<,②由①②,2332e ≤<122e ≤< 9.(1)证明:12111111[1()]112[1()]1321()2n n n a S S S a S ----=+=---≤--,当1=n 时,等号成立.23222121[1()]112[1()]621()2n n n a S S S a S ----=+=+--≥--,当2=n 时,等号成立.∴21n S S S ≤≤.(2)证明: 1)21(2015--=n n a ,∴n a 随n 增大而减小,n a 奇数项均正,偶数项均负.①当k 是奇数时,}{n a 中的任意相邻三项按从小到大排列为1k a +,2k a +,k a , 则kk kk k a a a a a 2)21()21(11111=-+-=+-+,k k k a a a 2)21(221112=-=++, ∴122k k k a a a +++=,因此k k k a a a ,,21++成等差数列,公差11111223])21()21[(++++=---=-=k k k k k k a a a a d .②当k 是偶数时,设}{n a 中的任意相邻三项按从小到大排列为k a ,2k a +,1k a +,则1111111()()222k k k k ka a a a a -++=-+-=-,1121122()22k k k a a a ++=-=-, ∴122k k k a a a +++=,因此k k k a a a ,,21++成等差数列,公差111211311[()()]222k k k k k k a d a a a +-++=-=---=.综上可知,}{n a 中的任意相邻三项按从小到大排列,总可以使其成等差数列,且1123+=k k a d ,211=+n n d d ,∴数列}{n d 为等比数列. 10. 证明:(1)①存在1=a ,当x x f x ln )(),1,0(-=∈为减函数, 当x x f x ln )(),,1(=+∞∈为增函数;②对任意0>x ,当01>-x 时,),1ln()1ln()1(x x x f --=-=- ).1ln()1ln()1(x x x f +=+=+所以,0)1ln()1ln()1ln()1()1(2>--=+---=+--x x x x f x f 即).1()1(x f x f +>-所以函数x y ln =为),0(+∞内的“勾函数”.(2)①当0=λ时,1)(=x h ,不存在m 使函数)(x h 在),(+∞m 内为“勾函数”;②当0<λ时,).2)((2)(322'λλλλλλ-+=--=x x x x x h当),2(λλ-∈x 时,0)('>x h ,)(x h 为增函数; 当),(+∞-∈λx 时,0)('<x h ,)(x h 为减函数,因此不存在m 及常数0x ,使函数)(x h 在),(0x m 为减函数,同时在),(0+∞x 为增函数. 所以不存在m 使函数)(x h 在),(+∞m 内为“勾函数”.③当0>λ时,)(x h 在)2,(λλ-为减函数,在),2(+∞λ为增函数.当)2,[λλ-∈m ,则在),(+∞m 上存在λ2=a ,使)(x h 在),(a m 内为减函数,在),(+∞a 内为增函数.当0>x ,),(,+∞∈+-m x a x a 时, 因为)()(x a h x a h +--)]2()2[(2])2()2[(21])2()2[(31322233x x x x x x +---+---+--=λλλλλλλλλ .0323<-=x λ所以)()(x a h x a h +<-.所以也不存在m 使函数)(x h 在),(+∞m 内为“勾函数”.综上所述,不论常数λ取何值,都不存在m ,使函数)(x h 在),(+∞m 内为“勾函数”.理科加试11. 解:(1)如图,建立直角坐标系.则1A (0,0,2),B (2,0,0),1(2,0,2)B ,(0,2,0)C ,1(0,2,2)C ,(1,1,0)E ,(0,0,)M m , 1B M =(2,0,2)m --,1C E =()2,1,1--.因为11B M C E ⊥,所以11B M C E ⋅=22(2)m ---=0. 解得1m =所以1AM =.(2)AE =(1,1,0),1(0,2,2)AC =, 设平面1AEC 的法向量n =(,,)x y z ,则:1220n AE x y n AC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,令1y =-,则1x =,1z =.(1,1,1)n =-.因为1AA AC ⊥,BA AC ⊥,所以AC ⊥平面11ABB A , AC 为平面11ABB A 的法向量,AC =(0,2,0). c o s,A C n <>=AC n AC n⋅⋅=. 所以平面1AEC 与平面11ABB A . 12.解:设存在实数],1[a b ∈,使φ≠=B A C ,设C m ∈0,则0m A ∈,且0m B ∈.设)(*0N t a m t ∈=,)()1(*0N S b S a m ∈++=,则(1)t a a S b =++,所以1+-=a ba S t ,因为*,,N s t a ∈,且2≥a ,所以b a t -能被1+a 整除.① 当1=t 时,因为],1[a b ∈,]1,0[-∈-a b a ,所以*1a bS N a -=∉+; ② 当)(2*N n n t ∈=时,b a C a b a b a n n n n -++-++=--+=-1)1()1(]1)1[(12222 , 由于],1[a b ∈,所以]1,0[1-∈-a b ,110+<-≤a b ,所以,当且仅当1=b 时,b a t-能被1+a 整除.③ 当*21()t n n N =+∈时,212121121[(1)1](1)(1)1n n n n a b a b a C a b ++++-=+--=++++--,由于],1[a b ∈,所以]1,2[1+∈+a b ,所以,当且仅当11+=+a b ,即a b =时,b a t-能被1+a 整除.综上,在区间],1[a 上存在实数b ,使φ≠=B A C 成立.当1=b 时,},{*2N n a y y C n ∈==;当a b =时,21*{,}n C y y a n N +==∈.2015高考数学模拟题(2)南师大《数学之友》一. 填空题1. 已知),2(ππα∈且53cos -=α,则)42tan(πα-的值为 ▲ . 2. 在平面直角坐标系xOy 中,设A 是曲线1C :31(0)y ax a =+>与曲线2C :2252x y +=的一个公共点,若1C 在A 处的切线与2C 在A 处的切线互相垂直,则实数a 的值是 ▲ .3. 椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,若椭圆上恰好有6个不同的点P ,使得12F F P ∆为等腰三角形,则椭圆C 的离心率的取值范围是 ▲ .4. 已知2,3,60,2,(1),(0,1)AB AC BAC CD BC AE xAD x AB x ==∠===+-∈, 则AE 在AC 上的投影的取值范围是 ▲ .5. 设函数⎩⎨⎧≤-≤≤--=20,102,1)(x x x x f <, 若函数ax x f x g -=)()(,]2,2[-∈x 为偶函数,则实数a 的值为 ▲ .6. 各项为实数的等差数列的公差为4,其首项的平方与其余各项之和不超过100,这样的数列至多有 ▲ 项.二、解答题7. 在平面直角坐标系xOy 中,已知圆O :x 2+y 2=64,圆O 1与圆O 相交,圆心为O 1(9,0). (1) 经过1O 作圆O 的切线,求切线方程;(2) 过定点()0,6P 作动直线l 与圆O ,圆1O 都相交,且直线l 被圆O ,圆1O 截得的弦长分别为d ,1d .若d 与1d 的比值总等于同一常数λ,求λ的值和圆1O 的方程.8. 某港湾的平面示意图如图所示,直线1l 、2l 是两条海岸线,点O 为1l 、2l 交点,A 位于O 的正南方向6km 处,B 位于O 的北偏东︒60方向10km 处.(1) 求集镇A ,B 间的距离;(2) 随着经济的发展,为缓解集镇O 的交通压力,拟在海岸线1l ,2l 上分别修建码头N M 、,开辟水上航线.勘测时发现:以O 为圆心,3km 为半径的扇形区域为浅水区,不适宜 船只航行.请确定码头N M 、的位置,使得N M 、之间的直线航线最短.9. 有n 个首项都是1的等差数列,设第m 个数列的第k 项为mk a (,1,2,3,,, 3)m k n n =≥,公差为m d ,并且123,,,,n n n nn a a a a 成等差数列.(1)证明()()2112d m d m d m -+-=; (2)设3,121==d d ,当6≥n 时,不等式n n d n >-+12)32(501恒成立.10.已知函数x b xx a x f ln )1()(--=(R b a ∈,),2)(x x g =.(1) 若1=a ,曲线)(x f y =在点))1(,1(f 处的切线与y 轴垂直,求b 的值; (2) 在(1)的条件下,求证2ln 2)()(->x f x g ;(3) 若2b =,函数)(x f 与)(x g 在其公共点处是否存在公切线.若存在,求出a 值的个数;若不存在,说明理由.理科加试11. 在正方体1111D C B A ABCD -中,O 是AC 的中点,E 是线段O D 1上一点,且 EO E D λ=1.(1)若1=λ,求异面直线DE 与1CD 所成角的余弦值; (2)若平面CDE ⊥平面O CD 1,求λ的值.12. 如图,椭圆1C :1422=+y x 的离心率为23,x 轴被曲线2C :12-=x y 截得的线段长等于1C 的长半轴长.设2C 与y 轴的交点为M ,过坐标原点O 的直线l 与2C 相交于点A ,B ,直线MA ,MB 分别与1C 相交于点D ,E .(1)证明:ME MD ⊥;(2) 记MAB ∆,MDE ∆的面积分别为1S ,2S ,问:是否存在直线l ,使得21S S 3217=成立?请说明理由.A C 1参考答案一. 填空题1.答案:31. 解:224παπ<<,12cos2cos 2-=αα,∴21cos 25α=,552cos =α,5522sin =α, 22tan=α,tan112tan()2431tan2ααπα--==+. 2.答案: 4.解:设()00,y x A ,所以1C 在A 处的切线斜率为()200'3ax x f =,2C 在A 处的切线斜率为001y x k OA -=-,又1C 在A 处的切线与2C 在A 处的切线互相垂直, 所以,132000-=⋅⎪⎪⎭⎫ ⎝⎛-ax y x ,即3003ax y =. 又1030-=y ax ,故230=y .代入25:222=+y x C ,得210±=x ,将210±=x ,230=y 代入()013>+=a ax y ,得4=a . 3.答案:111(,)(,1)322⋃.解:422111232c a c e e c a>-⎧⇒<<≠⎨≠⎩且,故离心率范围为111(,)(,1)322⋃. 4.答案:[]7,1.解:如图,(3,0),(1(7,C B D -.(61,AE x =+-,3(61)cos 61,(0,1)361[1,7]AE AC x AE EAC x x ACx ∙+∠===+∈∴+∈5.答案:21. 解:由题设,⎩⎨⎧≤--≤≤---=20,1)1(02,1)(x x a x ax x g <,则⎩⎨⎧≤-<--≤-≤--=-20,1)1(02,1)(x x a x ax x g ⎩⎨⎧≤≤-≤----=20.1,02,1)1(x ax x x a < 因为)(x g 为偶函数,故)()(x g x g -=. 则1)1(1--=-x a ax 对于]2,2[-∈x 恒成立,从而有a a -=1,得21=a . 6.答案: 8.解:设n a a a a ,,,,321 是公差为4的等差数列, 则1003221≤++++n a a a a , 即()()[]()100121441121≤-⋅-++++n n a a a ,=∆ ()()010*******1≤--+-+n n a n a , 因此,=∆0401672≤--n n , 解得21n n n ≤≤, 其中()028163711<-=n ,≤897281632<+=n , 所以,自然数n 的最大值为8,故这样的数列至多有8项. 故答案为:8.二、解答题7.解:(1)设切线的斜率为k ,则由题意可得切线方程为 09=+-k kx y ,由圆心O )0,0(到切线的距离为圆O 的半径得:219kk +8=,解得817±=k .所以切线方程为8179817-=x y 或8179817+-=x y . (2) 当直线l 的斜率存在时,设直线l 为)6(-=x k y ,即06=+-k kx y .则点O ,O 1到直线l 的距离分别为216kk h +=,h 1=213kk +,设圆1O 的半径为r ,从而22136642k k d +-=,2221192k k r d +-=.由d d 1=λ,得2122d d λ=. 所以64-22136k k +=)19(2222k k r +-λ. 整理得:064)928(222222=+-+-r k r λλλ. 由题意,知上式对于任意实数k 恒成立,所以⎪⎩⎪⎨⎧=+-=+-064092822222r r λλλ.解得λ=2(负根舍去),162=r .综上所述,λ=2.圆1O 的标准方程为16)9(22=+-y x .8. 解:(1) 在ABO ∆中,6=OA ,10=OB ,︒=∠120AOB ,︒⨯⨯⨯-+=120cos 2222OB OA OB OA AB 19621106210622=⎪⎭⎫⎝⎛-⨯⨯⨯-+=. 14=∴AB ,即A ,B 间的距离为14km .(2) 依题意,直线MN 与圆O 相切,设切点为C ,连接OC ,则MN OC ⊥. 设x OM =,y ON =,u MN =,在OMN ∆中,OC MN ON OM ⋅⋅=⋅⋅⋅︒2160sin 21, 即u xy 32=.由余弦定理,︒-+=120cos 2222xy y x u xy y x ++=22xy 3≥.所以,u u 362≥,36≥u ,当且仅当6==y x 时,u 取得最小值. 答:N M 、建在距离O 点均为km 6处航线最短.9. 证明:(1)因为123,,,,n n n nn a a a a 成等差数列,所以2322212,......,,,n a a a a 成等差数列.)1()1()1()1()1()1(12312-+-+==+-+=+-+∴n n d d d d d d即12312--==-=-n n d d d d d d ,所以,}{n d 成等差数列,公差为12d d -, 所以12112(1)()(2)(1)m d d m d d m d m d =+--=-+-. (2)由题知,12-=n d n ,2)32(5011n n d n >-+即 1(23)250(21)n n n +->-. 即为不等式1(23)250(21)0n n n +--->的解, 考虑函数1()(23)250(21)n f n n n +=---, 由于]502)12[(2)()1(-+=-+nn n f n f , 当3≥n 时,(1)()f n f n +>. 即 <<<<)6()5()4()3(f f f f , 而(6)9(12850)1006020f =--=>, 所以,当6n ≥时,有()0f n >.因此当6n ≥时,1(23)250(21)n n n +->-恒成立, 即n n d n >-+12)32(501恒成立. 10. 解:(1)1=a ,1()ln f x x b x x =--,222'111)(x bx x x b x x f +-=-+=,依题意,02)1('=-=b f .∴2=b .(2)由(1)得1()2ln f x x x x=--,),0(+∞∈x . 要证2ln 2)()(->x f x g ,只须证02ln 2ln 212>+++-x xx x . 设21(x)2ln 2ln 2F x x x x=-+++(0>x ). 222232')1)(12(2122112)(xx x x x x x x x x x F +-=+--=+--= . 令'()0F x =,得21=x . 当210<<x 时,'()0F x <;当21>x 时,'()0F x >.所以,当12x =时,)(x F 取极小值,也是最小值,047)21()(min >==F x F .因此()0F x >,2ln 2)()(->x f x g .(3)设函数)(x f 与)(x g 的图像在其公共点),(00y x 处存在公切线.1()()2ln f x a x x x =--,2'22()ax x a f x x -+=,x x g 2)('=.由)()(0'0'x g x f =,可得到0202022x x a x ax =+-,即02202030=-+-a x ax x , 200(2)(1)0x a x -+=,得20ax =.)(x f 的定义域为(0,)+∞. 当0≤a 时,0(0,)2ax =∉+∞.函数)(x f 与)(x g 在其公共点处没有公切线; 当0a >时,令)2()2(a g a f =,22412ln 2221a a a =--,即)2ln(882aa =-. 02ln 88ln 82=-+-a a .设2()8ln 88ln 2h x x x =-+-(0>x ),x xx h 28)('-=.令'()0h x =,得2=x . 当(0,2)x ∈时,'()0h x >,)(x h 递增;当(2,)x ∈+∞时,'()0h x <,)(x h 递减. 所以04)2()(max >==h x h .22224()8ln ()88ln 20h e e e e -=-+-=<,在(0,2)上存在唯一1x ,使得0)(1=x h ; 又082ln 8)2(2<-=h ,在(2,)+∞上存在唯一2x ,2()0h x =.综上,0≤a 时,不存在公切线;0a >时,存在公切线,适合题意的a 值有两个.理科加试11. 解:(1)不妨设正方体的棱长为1,以1,,DD DC DA 为单位正交基底建立如图所示的空间直角坐标系xyz D -,由题设,E 为O D 1的中点,则 )0,0,1(A ,)0,21,21(O ,)0,1,0(C , )1,0,0(1D ,)21,41,41(E , 于是)21,41,41(=,)1,1,0(1-=CD ,)0,21,21(-=CO ,由63,cos 1=>=<CD . 所以异面直线AE 与1CD 所成角的余弦值为63. (2)设平面O CD 1的法向量为),,(111z y x =m ,由0=⋅m ,01=⋅CD m ,得⎪⎩⎪⎨⎧=+-=-,0,021211111z y y x 取11=x ,得111==z y ,即)1,1,1(=m .由EO E D λ=1, 得)11,)1(2,)1(2(λλλλλ+++E ,1(,,)2(1)2(1)1DE λλλλλ=+++. 又设平面CDE 的法向量为),,(222z y x =n ,由0=⋅n ,0=⋅n ,得⎪⎩⎪⎨⎧=+++++=,0)1(2)1(2)1(2,02222λλλλλλz y x y 取22=x ,得λ-=2z ,即),0,2(λ-=n . 因为平面CDE ⊥平面1CD E ,所以0=⋅n m ,得2=λ.12. 解:(1) 由题意知,直线l 的斜率存在,设为k ,则直线l 的方程为kx y =.由⎩⎨⎧-==12x y kxy 得012=--kx x .设),(11y x A ,),(22y x B ,则1x ,2x 是上述方程的两个实根, 于是k x x =+21,21x x 1-=.又点M 的坐标)1,0(-,所以 =⋅MB MA k k 111x y +221x y +⋅2121)1)(1(x x kx kx ++=21212121)(x x x x k x x k +++=1122-++-=k k 1-=.故ME MD ⊥.(2) 设直线MA 的斜率为1k ,则直线MA 的方程为11-=x k y , 由⎩⎨⎧-=-=1121x y x k y 解得⎩⎨⎧-==10y x 或⎩⎨⎧-==1211k y k x .故点A 的坐标为)1,(211-k k . 又直线MB 的斜率为11k -,同理可得点B 的坐标为)11,1(211--k k . 于是1S MB MA ⋅=21121121111121k k k k -+⋅⋅+=12121k k +=, 由⎩⎨⎧=-+-=0441221y x x k y 得08)41(1221=-+x k x k .解得⎩⎨⎧-==10y x 或⎪⎪⎩⎪⎪⎨⎧+-=+=21212114114418k k y k k x , 故点D 的坐标为)4114,418(2121211k k k k +-+, 又直线ME 的斜率为11k -,同理可得点E 的坐标为)44,48(2121211k k k k +-+-,于是2S ME MD ⋅=21)4)(41()1(322121121++⋅+=k k k k .因此)1744(641212121++=k k S S 由题意知,)1744(641212121++=k k S S 3217=, 解得421=k 或4121=k .又由点A ,B 的坐标可知,11212111k k k k k +-==111k k -,所以23±=k . 故满足条件的直线l 存在,且有两条,其方程分别为x y 23=,x y 23-=.当a b =时,21*{,}n C y y a n N +==∈.。
