海门市2010年中考数学二模试卷(含答案)
2010年中考模拟数学卷参考答案

2010年中考模拟试卷 数学参考答案及评分标准三、解答题(本题有8小题,第17~19题每题6分,第20~21题8分,第22~23题每题10分,第24题12分,共66分) 17、(本题满分6分) 解:∵方程2233x mx x -=--无解∴方程2233x mx x -=--有增根x=3------------2分∴方程两边同乘以(x-3),得:26x m -=------------2分∴当x=3时,m =分 18、(本题满分6分)解:过C 点作BA 的延长线交于点E ,------------1分∵AB =AC =10,∠B =022.5 ∴∠EAC =045∴△EAC 为等腰直角三角形------------1分设AE =EC =X,则AB =AC =10∴x =∴111022S A B E C ∆=⋅=⨯⨯=≈35.42m ------------2分又∵53.610⨯2cm =362m >35.42m ------------1分 ∴预订草皮够用------------1分19、(本题满分6分)解:答案不唯一,酌情给分。
20、(本题满分8分)解:(1)18 0.55------------各1分(2)图略--------------共4分(虚设组不设各扣1分)(3)0.55±0.1均为正确------------2分 21、(本题满分8分) 解:(1)正确的结论:①②③------------2分(2)错误理由:当a >0时,只有1x >2x >0或2x <1x <0时,1y <2y 而2x <0<1x 时,1y >2y ------------4分 改正:当a >0时,在同一象限内,函数a y x=,y 随x 增大而减小-----2分22、(本题满分10分)解:(1)如右图------------共6分(030,045角,线段a 各1分,余酌情给分)(2)设AB =x,则R t △ABC 中,OB =x ,由题意得:6+ x ------------1分得,1)x =≈8米------------2分 答:旗杆高度约为8米。
2010年初中数学中考模拟试卷.doc
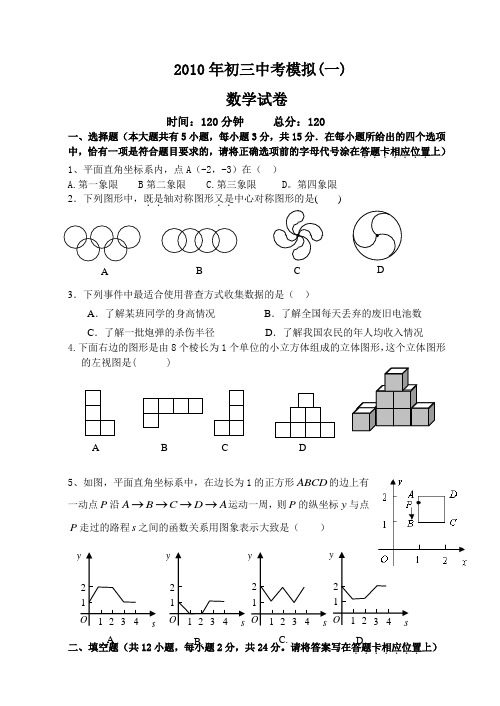
2010年初三中考模拟(一)数学试卷时间:120分钟 总分:120一、选择题(本大题共有5小题,每小题3分,共15分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号涂在答题卡相应位置.......上) 1、平面直角坐标系内,点A (-2,-3)在( )A.第一象限 B 第二象限 C.第三象限 D 。
第四象限 2.下列图形中,既是..轴对称图形又是..中心对称图形的是( )3.下列事件中最适合使用普查方式收集数据的是( )A .了解某班同学的身高情况B .了解全国每天丢弃的废旧电池数C .了解一批炮弹的杀伤半径D .了解我国农民的年人均收入情况 4.下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的左视图是( )5、如图,平面直角坐标系中,在边长为1的正方形ABCD 的边上有一动点P 沿A B C D A →→→→运动一周,则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是( )二、填空题(共12小题,每小题2分,共24分。
请将答案写在答题卡相应位置.......上)1 2 3 412ys O 1 2 3 4 1 2 y s O s 1 2 3 4 1 2 y sO 1 2 3 4 1 2 y O A B .C .D . DC B A A B C DABC DE 第16题图6计算:2332x x ∙ ,()322x。
7、分解因式:228x -= 。
8、已知数据:2,1-,3,5,6,5,则这组数据的众数是 ,极差是 。
9 函数21+=x y 中,自变量x 的取值范围是 .10.如图5,∠1,∠2,∠3,∠4是五边形ABCDE 的外角,且∠1=∠2=∠3=∠4=070,则∠AED 的度数是_________________ .第10题 第12题 第13题 11、已知双曲线xky =过点(-2,3),则k = 。
12、AB ∥CD ,AC ⊥BC ,∠BAC =65°,则∠BCD =______________度。
江苏省海门市第二学期调研考试试卷九年级数学(中考数学二模)

九年级数学注 意 事 项考生在答题前请认真阅读本注意事项1.本试卷共6页,满分为150分,考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、考试证号用0.5毫米黑色字迹的签字笔填写在试卷及答题卡指定的位置.3.答案必须按要求填涂、书写在答题卡上,在试卷、草稿纸上答题一律无效. 一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置.......上. 1.3的倒数是【▲】A .3B .3-C .13D .13- 2.计算23x x -⋅的结果是【▲】A .5x B .5x - C .6x D .6x -3.如图,一把矩形直尺沿直线断开并错位,点E 、D 、 B 、F 在同一条直线上,若∠ADE =128°, 则∠DBC 的度数为【▲】A .52°B .62°C .72°D .128°4.从 - 3,- 2,- 1,4,5中任取2个数相乘,所得积中的最大值为a ,最小值为b ,则ab 的值为【▲】 A .43- B .12- C .13 D .2035.在平面直角坐标系中,平行四边形OABC 的顶点为O (0,0)、A (1,2)、B (4,0),则顶点C 的坐标是 【▲】 A .(-3,2) B .(5,2) C .(-4,2) D .(3,-2) 6.某小组7名同学积极参加支援“希望工程” 的捐书活动,他们捐书的册数分别是(单位:本):10,12,10,13,10,15,17,这组数据的众数和中位数分别是【▲】 A .10,1 B .10,13 C .10,10 D .17,107.已知粉笔盒里只有2支黄色粉笔和3支红色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,则取出黄色粉笔的概率是【▲】 A .15 B .25 C .35D . 238. 如图,扇形OAB 是圆锥的侧面展开图,点O 、A 、B 分别是格点.已知小正方形方格的边长为1cm ,则这个圆锥的底面半径为 【▲】(第3题)OA .cm D .12cm 9. 不等式组221x x -⎧⎨-<⎩≤的整数解共有【▲】A .3个B .4个C .5个10.如图,点P 在y 轴正半轴上运动,点C 在x 轴上运动,过点P 且平行于x 轴的直线分别交函数4y x=- 和2y x=于A 、B 两点,则△ABC 的面积等于【▲】 A .3 B .4 C .5 D .6二、填空题:本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答题卡相应位置.......上. 11.在函数y 中,自变量x 的取值范围是 ▲ . 12.一个长方体的主视图和左视图如图所示(单位:cm ),则其俯视图的面积是 ▲ cm 2.13.如图,A 、B 、C 三点在正方形网格线的交点处,若将△ABC 绕着点A 逆时针旋转得到△AB 1C 1,则tan B 1的 值为 ▲ .14.若将7个数按照从小到大的顺序排成一列,中间的数恰是这7个数的平均数,前4个数的平均数是25,后 4个数的平均数是35,则这7个数的和为 ▲ .15.设a 为实数,点P (m ,n ) (m >0)在函数y =x 2+ ax -3的图象上,点P 关于原点的对称点Q 也在此函数的图 象上,则m 的值为 ▲ . 16.已知αβ,为方程2420x x ++=的两实根,则=+-542βα ▲ .17.如图,在△ABC 中,AD 为BC 边上的中线.已知AC =5,AD =4,则AB 的取值范围是 ▲ .18.在直角坐标系中,已知两点A (8,3)-、B (4,5)-以及动点C (0,)n 、D (,0)m ,则当以点A 、 B 、C 、D 为顶点的四边形的周长最小时,比值mn为 ▲ . 三、解答题:本大题共10小题,共96分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.(第10题) (第12题)(第13题)ABDCABB 1C 1 C(第17题)19.(本小题满分10分)(1)计算:20|31|22sin 602010--+-︒+-(π).(2)先化简,再求值:141151--÷⎪⎭⎫ ⎝⎛--+x x x x ,其中425-=x .20.(本小题满分6分)解方程:2111=-+-xx x . 21.(本小题满分8分)“一方有难,八方支援”.雅安地震牵动着全国人民的心,我市某医院准备从甲、乙、丙三位医生和A 、B 两名护士中选取一位医生和一名护士支援雅安.(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果; (2)求恰好选中甲医生和护士A 的概率. 22.(本小题满分8分)国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.某中学为了了解学生体育活动情况,随机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”.以下是根据所得的数据制成的统计图的一部分.根据以上信息,解答下列问题:(1)该校随机抽查的学生中每天在校锻炼时间超过1小时的人数是 ; (2)请将图2补充完整;(3)2013年该市初中毕业生约为6.4万人,请你估计今年该市初中毕业生中每天锻炼时间超过1小时的学生约有多少万人?23.(本小题满分8分)已知关于x 的一元二次方程()011222=-+-+k x k x 有两个不相等的实数根.图1 图2(1)求实数k 的取值范围;(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由; (3)若此方程的两个实数根的平方和为30,求实数k .24.(本小题满分10分)如图,防洪大堤的横断面是梯形,背水坡AB 的坡比i =1:3(指坡面的铅直高度与水平宽度的比),且AB =20m .身高为1.7m 的小明站在大堤A 点,测得髙压电线杆顶端点D 的仰角为30°.已知地面CB 宽30m ,求髙压电线杆CD 的髙度(结果保留三个有效数字,3≈1.732).25.(本小题10分) 五一假期中,小明和小亮相约晨练跑步.小明比小亮早1分钟离开家门,3分钟后迎面遇到从家跑来的小亮.两人沿滨江路并行跑了2分钟后,决定进行直线长跑比赛,比赛时小明的速度始终是250米/分,小亮的速度始终是300米/分.下图是两人之间的距离y (米)与小明离开家的时间x (分钟)之间的函数图象,根据图象回答下列问题:(1)请直接写出小明和小亮比赛前的速度,并说出图中点A (1,500)的实际意义;(2)请在图中的( )内填上正确的值,并求两人比赛过程中y 与x 之间的函数关系式;(3)若小亮从家出门跑了11分钟时,立即按原路以比赛时的速度返回,则小亮再经过多少分钟时两人相距75米?26.(本小题满分10分)已知二次函数2y ax bx c =++中,其函数y 与自变量x 之间的部分对应值如下表所(第24题) y (米)600500 135x (分)7( )OA示:(1)当=-1时,的值为 ▲ ;(2)点A (1x ,1y )、B (2x ,2y )在该函数的图象上,则当112,x <<234x <<时,1y 与2y 的大小关系是 ▲ ;(3)若将此图象沿x 轴向右平移3个单位,请写出平移后图象所对应的函数关系式:▲ ; (4)设点P 1(m ,y 1)、P 2(m +1,y 2)、P 3(m +2,y 3)都在二次函数2y ax bx c =++的图象上,问:当m <-3时,y 1、y 2、y 3的值一定能作为同一个三角形三边的长吗?为什么?27.(本小题满分12分)如图,矩形ABCD 中, AB =4,BC =2,点P 是射线DA 上的一动点,DE ⊥CP ,垂足为E ,EF ⊥BE 与射线DC 交于点F . (1)若点P 在边DA 上(与点D 、点A 不重合).①求证:△DEF ∽△CEB ;②设AP =x ,DF =y ,求y 与x 的函数关系式,并写出x 的取值范围; (2)当△EFC 与△BEC 面积之比为3︰16时,线段AP 的长为多少?(直接写出答 案,不必说明理由).28.(本小题满分14分)如图,一次函数34y mx m =++(m <0)的图象经过定点A ,与x 轴交于点B ,与y 轴交于点E ,AD ⊥y 轴于点D ,将射线AB 沿直线AD 翻折,交y 轴于点C .(1)用含m 的代数式分别表示点B ,点E 的坐标;B C A D E F P B C A D (备用图)(2)若△ABC中AC边上的高为5,求m的值;(3)若点P为线段AC中点,是否存在m的值,使△APD与△ABD相似?若存在,请求出m(第28题)参考答案一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置.......上.1.C 2.B 3.A 4.A 5.D 6.A 7.B 8.C 9.C 10.A二、填空题:本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答题卡相应位置.......上. 11.x ≥3 12.6 13.3114.210 15.3 16.19 17.3<AB <13 18.23-三、解答题:本大题共10小题,共96分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 19.(本小题满分10分) (1)解:原式=12324113+⨯-+-……………………………………………4分 =41………………………………………………5分 (2)解:原式=14115112--÷⎪⎪⎭⎫ ⎝⎛----x x x x x ……………………………………………1分=411162--⋅--x x x x ………………………………………………………2分 =411)4)(4(--⋅--+x x x x x ………………………………………………3分=4+x …………………………………………………………………4分 当425-=x 时, 原式=4425+-=25…………………………………………………5分 20.(本小题满分6分) 解:去分母,得)1(21-=-x x ……………………………………………………………………3分 解得 1=x ………………………………………………………………………4分检验:当1=x 时,0111=-=-x ……………………………………………5分∴1=x 不是原方程的解∴原方程无解.……………………………………………………………………6分 21.(本小题满分8分) 解:(1)∴共有6种可能出现的结果:甲A 、甲B 、乙A 、乙B 、丙A 、丙B …5分 (2)P=61∴恰好选中甲医生和护士A 的概率是61…………………………………8分 22.(本小题满分8分) 解:(1)390…………………………………………………………………………2分 (2)…………………………4分(3)6.4万×360270=6.4万×43=4.8万…………………………………………7分 答:估计今年该市初中毕业生中每天锻炼时间超过1小时的学生约有4.8万人.………………………………………………………8分23.(本小题满分8分)解:(1)由题意得:△=[])1(14)1(222-⨯⨯--k k >0………………………1分解得:k <1∴实数k 的取值范围为k <1.……………………………………………2分 (2)0可能是方程的一个根,…………………………………………………3分 把x =0代入原方程中,012=-k ∴1±=k∵k <1 ∴1-=k ……………………………………………………4分 此时方程为042=-x x 解得01=x ,42=x∴它的另一个根是4.…………………………………………………5分医生 护士 甲 A B 乙 A B 丙 A B 图270(3)设此方程的两个实数根为1x ,2x则 )1(221--=+k x x ,1221-=⋅k x x ……………………………6分∵302221=+x x ∴302)(21221=-+x x x x∴[]30)1(2)1(222=----k k 整理得 01242=--k k解得 21-=k ,62=k ………………………………………………7分 ∵k <1 ∴2-=k ………………………………………………………8分 24.(本小题满分10分)解:过点M 作MN ⊥DC ,垂足为N ,延长MA 交CB 延长线于点Q . 在Rt△AQB 中,AB =20m , ∵i =BQ AQ =31=33,∴tan∠ABQ =33, ∴∠ABQ =30°.……………………………1分 ∴AQ =21AB =10m ,∴BQ =22AQ AB -=310m .……………………3分 ∵MA =1.7m ,∴MQ = MA + AQ =11.7m ,∴NC =11.7m .……………………4分 ∵BC =30m ,∴CQ = BC + BQ =30+310(m),∴MN = CQ =30+310(m).…6分 在Rt△DNM 中,∠DNM =90°,∠DMN =30°, ∴NMDN= tan30°=33,∴DN =MN ×33=33)31030(⨯+=10310+,…8分∴DC = DN + NC =10310++11.7≈10×1.732+10+11.7≈39.0(m).…………9分 答:髙压电线杆CD 的髙度约39.0 m .………………………………………10分25.(本小题10分) 解:(1)比赛前小明的速度为100米/分…………………………………………1分 比赛前小亮的速度为150米/分…………………………………………2分点A (1,500)的实际意义是:小明出发1分钟时两人相距500米.或小亮从家跑出时,小明已出发了1分钟,且与小明相距500米.………………3分(2)100.………………………………………………………………………4分(第24题)Q设b kx y +=.∵过点(5,0)和(7,100), ∴⎩⎨⎧=+=+100705b k b k ,解得⎩⎨⎧-==25050b k ,∴25050-=x y .……………………………………………………6分 (3)当12111=+=x 时,3502501250=-⨯=y .…………………7分 设小亮再经过x 分钟两人相距75米.则75350)300250(-=+x 或75350)300250(+=+x ,解得21=x 或2217=x .(只考虑1种情况得1分) ………………9分 答:小亮再经过21或2217分钟时两人相距75米.…………………10分26.(本小题满分10分) 解:(1)9……………………………………………………………………………2分 (2)1y <2y ……………………………………………………………………4分 (3)25102+-=x x y 或2)5(-=x y ………………………………………6分 (4)当m <-3时,y 1、y 2、y 3的值一定能作为同一个三角形三边的长.…7分理由:由上可知二次函数的解析式为2)2(-=x y ,∴21)2(-=m y ,22)1(-=m y ,23m y =.∵m <-3,∴1y >2y >3y >0,……………………………………………………8分3+m <0,1-m <-4<0,∵)1)(3(32)2()1(2222132-+=-+=--+-=-+m m m m m m m y y y∴132y y y -+>0, ∴32y y +>1y ……………………………9分 ∴当m <-3时,y 1、y 2、y 3的值一定能作为同一个三角形三边的长.…10分 27.(本小题满分12分)(1)①证明:∵四边形ABCD 为矩形,∴AD ∥BC ,∠ADC =90°,∴∠ECB =∠DPE ,∠PDE +∠CDE =90°.………………………1分∵DE ⊥CP ,∴∠DEP =∠DEC =90°,∴∠PDE +∠DPE =90°,∴∠DPE =∠CDE .………………………………………………2分∵∠ECB =∠DPE ,∴∠ECB =∠EDF .…………………………3分∵∠DEC =90°,∴∠DEF +∠FEC =90°.∵EF ⊥BE ,∴∠CEB +∠FEC =90°,∴∠DEF =∠CEB ,………………………………………………4分∴△DEF ∽△CEB .………………………………………………5分②解:∵△DEF ∽△CEB ,∴DF DE CB CE=.………………………………6分 ∵DF =y ,BC =2,AP =x , AB =4,∴2y DE CE=,DP =2x -,CD =4.…………………………………7分 由∠PDC =90°,DE ⊥CP ,易证△DPC ∽△EDC ,∴24DE DP x CE DC -==,∴224y x -=,∴112y x =-+,………8分 x 的取值范围为0<x <2.……………………………………9分(2)AP 长为2-+2+或212分28.(本小题满分14分)解:(1)当y =0时,340mx m ++=,∴43m x m +=-,∴B (43m m+-,0).…2分 当x =0时,y =34m +,∴E (0,34m +).…………………………4分 (2)由直线34y mx m =++经过定点A ,∴定点A (-4,3).…………5分 又∵AD ⊥y 轴,∴D (0,3).由翻折可知:CD =ED =3(43)m -+=4m -,∴CE =2CD =8m -.………………………………………………………6分 当点B 在原点右边时,S △ABC = S △ACE + S △BCE =1()2CE AD OB ⋅⋅+ =143(8)4()2m m m +⎡⎤⨯-⨯+-⎢⎥⎣⎦=13(8)()2m m ⨯-⨯-=12. 当点B 在原点左边时,S △ABC = S △ACE -S △BCE =143(8)42m m m +⎡⎤⨯-⨯-⎢⎥⎣⎦=13(8)()2m m ⨯-⨯-=12.∴S △ABC =12是不变化的.……………………………………………7分 ∵AC 边上的高为5,∴152AC ⋅⋅=12,∴AC =245.………………………………………8分 ∵AD =4,∠ADC =90°,CD =4m -,∴22224(4)4()5m -+=,解得 m =±,……………………9分又∵m <0,∴5m =-.…………………………………………10分(3)存在m 的值,使△APD 与△ABD 相似.……………………………11分 ①当点B 在原点右边时,只有△APD ∽△ADB 一种情形.由AP =PD 可得AD =DB =4.∵OD =3,∴OB ,∴43m m +-,解得 m =.②当点B 在原点左边时,若△APD ∽△ABD 时,AB =DB ,∴43m m +-=-2,解得 32m =-.若△APD ∽△ADB 时,AD =DB =4,∵OD =3,∴OB ,∴43m m +-=,解得 m =.∴存在m 的值,使△APD 与△ABD 相似,m 的值为43或32-或43-.……………………………14分。
2010年江苏省南通市中考数学试题答案

2010年南通市中考数学试卷答案1、D2、A3、B4、C5、D6、A7、C8、D9、C 10、B 11、-2 12、1:2 13、ax(x-1) 14、21 15、(2,4) 16、50°17、34 18、8 19、⑴4 ⑵3+a a20、34 21、⑴ m=-1,k=2 ;⑵ (-1,-2);⑶经过点B 22、⑴ ①4000 ②80<x ≤90 ③108°; ⑵ 符合要求,合格率=5.97975.040001172171==--%>97%23、)13(50-m 24、分配给甲、乙两船的任务数分别是210吨和280吨 25、略 26、⑴根据题意,设36+x+y=20k(k 为整数) 则x+y=20k-36∵0≤x+y ≤18∴0≤20k-36≤18 1.8≤k ≤2.7 ∵k 为整数∴k=2∴x+y=20×2-36=4 ⑵小沈一次拨对小陈手机号码的概率是5127、解:(1)∵EF ⊥DE ,∴∠DEF =90°,∴∠BEF +∠CED =90°∵∠BEF +∠BFE =90°,∴∠BFE =∠CED 又∵∠B =∠C =90°,∴△BEF ∽△CDE ∴BE BF =CD CE ,即x y -8=mx∴y =-m 1x2+m8x ·························································································· 4分 (2)若m =8,则y =-81x2+x =-81( x -4)2+2∴当x =4时,y 的值最大,y 最大=2 ······························································· 7分(3)若y =m 12,则-m 1x2+m8x =m 12∴x2-8x +12=0,解得x 1=2,x 2=6 ····························································· 8分 ∵△DEF 为直角三角形,∴要使△DEF 为等腰三角形,只能DE =EF 又DE 2=CD 2+CE 2=m2+x2,EF 2=BE 2+BF 2=( 8-x )2+y2=( 8-x )2+2144m∴m2+x2=( 8-x )2+2144m ,即m2+16x -64-2144m =0 当x =2时,m 2-32-2144m=0,即m 4-32m2-144=0解得m2=36或m2=-4(舍去)∵m >0,∴m =6 ···························································································· 10分当x =6时,m2+32-2144m=0,即m4+32m2-144=0解得m2=-36(舍去)或m2=4∵m >0,∴m =2 ···························································································· 12分28、解:(1)设直线AB 的解析式为y =px +q则⎩⎪⎨⎪⎧3=-4p +q0=2p +q 解得⎩⎪⎨⎪⎧p =-21q =1∴直线AB 的解析式为y =-21x +1 ······················································································· 2分 ∵当x =3和x =-3时,这条抛物线上对应点的纵坐标相等∴抛物线的对称轴为y 轴,∴b =0,∴y =ax2+c把A (-4,3)、B (2,0)代入,得:⎩⎪⎨⎪⎧3=16a +c 0=4a +c 解得⎩⎪⎨⎪⎧a =41c =-1∴抛物线的解析式为y =41x2-1 ··············································· 4分 (2)∵A (-4,3),∴AO =2243+=5,即⊙A 的半径为∵经过点C (0,-2)的直线l 与x 轴平行∴直线l 的解析式为y =-2,∴点A 到直线l 的距离为5∴直线l 与⊙A 相切 ························································································· 8分 (3)把x =-1代入y =-21x +1,得y =23,∴D (-1,23) 过点P 作PH ⊥直线l 于H ,则PH =n +2,即41m2+1 又∵PO =22n m+=222141)(-m m+=41m2+1 ∴PH =PO ……10分∵DO 的长度为定值,∴当PD +PO 即PD +PH 最小时,△当D 、P 、H 三点在一条直线上时,PD +PH 最小 ∴点P 的横坐标为-1,代入抛物线的解析式,得n =-43 ∴P (-1,-43) 12分 此时四边形CODP 的面积为: S 四边形CODP=S △PDO +S △PCO=21×( 23+43)×1+21×2×1=817 14分。
2010年中考模拟试卷数学卷s

新世纪教育网精选资料版权所有@新世纪教育网2010 年中考模拟试卷数学参照答案及评分标准一、仔一号0案二、真填一填11 . x≤ 7/212. 10/313.不可以1n 114.6 或 315 .0≤ s≤ 1/216.3417. 解 :(2)三.全面答一答18. (1) 由意, q=3k-12⋯⋯⋯⋯⋯⋯⋯⋯ 1 分因正比率函数,因此 3k-12=0k=4⋯⋯⋯⋯⋯⋯⋯⋯1分(2)因抛物与 x 的交点 A1(-2m/3 , 0),A2(4, 0),与 y 的交点 B(0,-8m)⋯⋯⋯⋯⋯⋯⋯⋯ 1 分若 S△OBA1 =4,; 4= 12m.8m ,m= 6 ⋯⋯⋯⋯⋯⋯⋯⋯ 1 分23若 S△OB A2=4,; 4= 14.8m, m=1 24因此当,足条件,抛物的分析式与坐的交点26A(,0),B(0,-8 6 )或3A(2,0),B(0,-4)LAB:y=-12x-8 6 或y=2x-4⋯⋯⋯⋯⋯⋯⋯⋯1分象 A,B两点的一次函数的特点数( -12 , -8 6 ) 或( 2,-4 )⋯⋯⋯1分19. 作法: (1) 作∠ MAN=∠ α .⋯⋯⋯⋯⋯⋯⋯⋯ 2 分(2)作∠ MAN的均分 AE⋯⋯⋯⋯⋯⋯⋯⋯ 1 分(3) 在 AM上截取 AB=c,在 AE上截取 AD=b. ⋯⋯⋯⋯⋯⋯⋯⋯ 1 分(4)BD,并延交AN于点C. ⋯⋯⋯⋯⋯⋯⋯⋯1 分△ABC就是所画的三角形 .( 如 ) ⋯⋯⋯⋯⋯⋯⋯⋯ 1 分20. 解 : ( 1)丙同学提出的方案最 合理 ⋯⋯⋯⋯⋯⋯⋯⋯2 分(2)如 ⋯⋯⋯⋯⋯⋯⋯⋯4 分( 每 各 2 分 , 涂 " 基本不参加 " ,暗影只假如两个扇形均可)(3) 220 人 ⋯⋯⋯⋯⋯⋯⋯⋯ 2 分21. 解( 1) A ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分 ( 2)①相像比 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分②相像比的平方 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分 ③相像比的立方⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分x1.70(3) 他的体重是xkg , 依据 意得191.23⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分得 x = 54.02 ( kg )⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分20xx 2200503x 250020x5022. 解:( 1)依据 意得:解得:360 x68 2解得:11∵ x 正整数∴ x 可取 60, 61,62, 63,64, 65,66, 67,6811xx∵ 3也必要是整数∴ 3可取 20, 21, 22∴有三种 方案:方案一:成人票 60 ,小孩票 20 :方案二:成人票 63 ,小孩票 21 :方案一:成人票66 ,小孩票 22 :⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分(2)在( 1)中,方案一 的 数目最少,因此 用最少最少 用 : 60×20+20×50=220⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分(3) 用( 2)中的最少 用最多 能够多 小孩票数目y ,20 90%(60 3 y) 50 80%(20y)y3 19y 3192200 解得:47∵ y 正整数∴ 足47的最大正整数3∴多 的小孩票 :3 y 9(根)⋯⋯⋯⋯⋯⋯3 分答:用( 2)中的最少 用最多 能够多9 成人票和 3 小孩票⋯⋯⋯⋯⋯⋯⋯1 分23.∵△ DCB 等腰三角形, PE⊥AB , PF⊥ CD, AC ⊥BD ,∴ PE+PF=AC 。
2010年初中数学中考模拟题测试卷及答案

C. x1 = 2,x2 = −2
5、如图(3),已知 AB 是半圆 O 的直径,∠BAC=32º,D 是弧 AC 的中点,那么∠DAC 的度数是( ) A、25º B、29º C、30º D、32°
D C
6. 下列函数中, 自变量 x 的取值范围是 x > 2 的函数是 ( A. y =
)
A
O
B
x−2
(第 23 题)
, − 2b) . 24.已知:抛物线 y = x 2 + (b − 1) x + c 经过点 P ( −1
(1)求 b + c 的值; (2)若 b = 3 ,求这条抛物线的顶点坐标; ( 3 ) 若 b > 3 , 过 点 P 作直线 PA ⊥ y 轴 , 交 y 轴 于 点 A , 交 抛 物 线 于 另 一 点 B , 且
B. y =
1 x−2 1 2x −1
)
C. y =
2x −1
D. y =
7.在平行四边形 ABCD 中, ∠B = 60o ,那么下列各式中,不能 成立的是( .. A. ∠D = 60o B. ∠A = 120o C. ∠C + ∠D = 180o D. ∠C + ∠A = 180o
8.在四川抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前
PDF 文件使用 "pdfFactory Pro" 试用版本创建
跑到 400 米以外的安全区域. 已知导火线的燃烧速度是 1.2 厘米/秒, 操作人员跑步的速度是 5 米/秒.为了保证操作人员的安全,导火线的长度要超过( ) A.66 厘米 B.76 厘米 C.86 厘米 D.96 厘米 二、填空题(每小题 3 分,共 24 分) 9. 2008 年北京奥运圣火在厦门的传递路线长是 17400 米, 用科学记数法表示为 10.一组数据:3,5,9,12,6 的极差是 . 11.计算: 3 × 2 = 12.不等式组 .
2010年中考模拟试卷sa
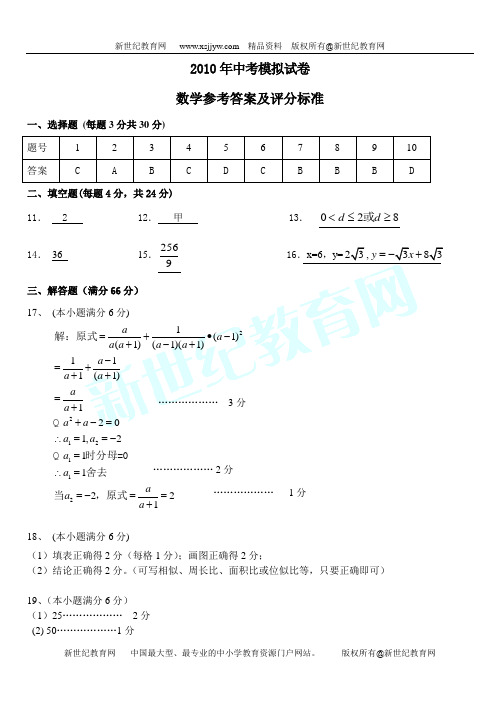
22121121(1)(1)(1)(1)111(1)1201,211221a a a a a a a a a a a a a a a a a a a a =+∙-+-+-=+++=++-=∴==-=∴==-==+解:原式 时分母=0舍去 当,原式2010年中考模拟试卷 数学参考答案及评分标准一、选择题 (每题3分共30分) 题号 1 2 3 4 5 6 7 8 9 10 答案CABCDCBBBD二、填空题(每题4分,共24分)11. 2 12. 甲 13. 820≥≤<d d 或14. 36 15.9256 16.x=6,y=23,383y x =-+三、解答题(满分66分)17、 (本小题满分6分)……………… 3分……………… 2分……………… 1分18、 (本小题满分6分)(1)填表正确得2分(每格1分);画图正确得2分; (2)结论正确得2分。
(可写相似、周长比、面积比或位似比等,只要正确即可) 19、(本小题满分6分) (1)25……………… 2分 (2) 50………………1分A DC BE F 图(略)……………1分(3)5人(要有过程) ………………2分20、(本小题满分8分)解 :(1)真命题是:已知:如图①AC ⊥BD ;②AC 平分对角线BD ;③AD ∥BC ; 则有四边形ABCD 为菱形 ………… 2分 证明:∵AC ⊥BD ,AC 平分对角线BD ∴ AB=AD,BC=CD,BAO DAO ∠=∠ ………… 1分 ∵AD ∥BC∴OAD BCO ∠=∠ ∴BCO BAO ∠=∠ ∴AB=BC ………… 1分 ∴AB=BC=CD=DA∴四边形ABCD 为菱形………… 1分(2)假命题是:已知②AC 平分对角线BD ③AD ∥BC ;④∠OAD=∠ODA. 求证:四边形ABCD 为菱形…………… 2分 反例:如矩形………… 1分21、(本小题满分8分)解:(1)在R t △BCD 中,cos40o CB CD=,∴52033cos 404o CB CD ===≈6.7,…………3分(2)在R t △BCD 中, BC =5, ∴ BD =5 tan400=4.2. …………1分过E 作AB 的垂线,垂足为F ,在R t △AFE 中,AE =1.6, ∠EAF =180O -120O =60O , AF =12AE =0.8………… 2分∴FB =AF +AD +BD =0.8+2+4.20=7米-…………1分答:钢缆CD 的长度为6.7米,灯的顶端E 距离地面7米. …………1分CBADO22、(本小题满分10分)解:(1)设A 种类型店面的数量为x 间,则B 种类型店面的数量为(80-x )间,根据题意,得: ⎩⎨⎧⨯≤-+⨯≥-+%.852400)80(2028%,802400)80(2028x x x x ………………………………………………3分解之,得⎩⎨⎧≤≥.55,40x x∴A 种类型店面的数量为40≤x ≤55,且x 为整数. ……………………………3分(2) 设应建造A 种类型的店面x 间,则店面的月租费为: W =400×75%·x +360×90%·(80-x )=-24x +25920, …………………………………………………………………………2分 ∵-24<0,40≤x ≤55,∴为使店面的月租费最高,应建造A 种类型的店面40间.…………………2分 23.(本小题满10分) 解:(1)连接AP∵四边形ODPC 为矩形∴PD ⊥AB∴AD=BD=1/2AB=1/2×6=3 …………………………1分又∵抛物线y=ax 2+bx +4经过A , B , C 三点 ∴C (0,4) …………………………1分 即OC=4∴PD=OC=4∴有勾股定理得AP=5 …………………………1分 ∴⊙P 的半径R 的长为5 (2)∵OD=CP=AP=5∴A(2,0) B(8,0)求得函数解析式为 y=1/4(x-2)(x-8) …………………………2分抛物线与⊙P 的第四个交点E 的坐标为(10,4)…………………………1分 (3)连接BF∵AB 为⊙D 的直径∴∠AFB=900=∠COA 又∵∠CAO=∠BAF∴△AOC ∽△AFB∴ ---------------------2分∵AO=2 AC=52422222=+=+CO OA AB=6 …1分∴∴AF= --------1分24.(本小题12分) (1)方案①211(120)(60)180022y x x x =⨯⨯-=--+当x=60时,y 最大值=1800; ……………4分(2)方案②过点B 作BE ⊥AD 于E,CF ⊥AD 于F, 设AB=CD=xcm ,梯形的面积为2scm , 则BC=EF=(120-2x )cm , AE=DF=12x ,BE=CF=32x ,AD=120-x , ∴S=1322x ⨯(240-3x ) 当x=40,S 最大值= 12003, S 最大值>y 最大值;……………4分方案:①正八边形一半,②正十边形一半,③半圆等(作出两个即可)……………4分CABCABABCDFE 30 135° 135° 135°30 3030 半径=π60 6522=AF 556AB ACAF OA =。
江苏海门中学2009-2010八年级(上)期中数学试卷

2009—2010八年级第一学期期中考试数学试卷1.①两角及一边对应相等 ②两边及其夹角对应相等 ③两边及一边所对的角对应相等 ④两角及其夹边对应相等,以上条件能判断两个三角形全等的是( )A .①③B .②④C .②③④D .①②④2. 如图,已知AB =DC ,AD =BC ,E.F 在DB 上两点且BF =DE ,若∠AEB =120°,∠ADB =30°, 则∠BCF= ( )A. 150°B.40°C.80°D. 90°3.如图,△ABC 中,AB =AC ,BD ⊥AC 于D ,CE ⊥AB 于E ,BD 和CE 交于点O ,AO 的延长线交BC 于F ,则图中全等直角三角形的对数为( )A.5对B.6对C.7对D.8对O FEC BA第2题图 第3题图 第4题图 第5题图4.如图,在△ABC 中,D 、E 分别是边AC 、BC 上的点,若△EAB ≌△EDB ≌△EDC ,则∠C=( ).A .36°B .30°C .25°D .15°5.如图,AE =AF ,AB =AC ,EC 与BF 交于点O ,∠A =600,∠B =250,则∠EOB 的度数为( ) A .600 B .700C .750D .8506.△ABC 是等边三角形,M 是AC 上一点, N 是BC 上的一点,且AM=BN ,∠MBC =25°,AN 与BM 交于点O, 则∠MON=( )A.130°B. 120°C.110°D. 85°7.下列说法: ①无限小数都是无理数;②无理数都是无限小数;③带根号的数都是无理数;④不带根号的数一定是有理数;⑤有理数和数轴上的点一一对应;⑥负数没有立方根。
其中正确的有( )A.1个B.2个C.3个D.4个 8.如图: ,那么a b - 的结果是( )A .-2bB .2bC .―2aD .2a 二、细心填一填(本大题8小题,每小题3分,共24分)1. 2)4(±的算术平方根是,36的平方根是 . 327-= 2. 若52=x,则=x ;若22)3(-=x ,则=x ;若16)1(2=-x ,=x ; 3. 比较大小:23- 23-; 4.已知:如图,∠ABC =∠DEF ,AB =DE ,要说明△ABC ≌△DEF ,(1)若以“SAS ”为依据,还须添加的一个条件为________________.班级: 姓名: 座号:(2)若以“ASA ”为依据,还须添加的一个条件为________________. (3)若以“AAS ”为依据,还须添加的一个条件为________________.5.已知△ABC ≌△DEF ,且∠A=90°,AB=6,AC=8,BC=10,△DEF 中最大边长是 , 最大角是 度.6.如图,已知BD 是∠ABC 的内角平分线,CD 是∠ACB 的外角平分线,由D 出发,作点D 到BC 、AC 和AB 的垂线DE 、DF 和DG ,垂足分别为E 、F 、G ,则DE 、DF 、DG 的关系是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中 考 模 拟 试 卷
数 学
总分:150分.答卷时间:120分钟.
注意事项:
1.本试卷的选择题和非选择题都在答题卡上作答,不能..
答在试卷上. 2.答卷前,考生务必将自己的姓名、考生号、试室号、座位号、考卷类型用铅笔涂写在
答题卡上.
3.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,
用橡皮擦干净后,再选涂其他答案.
4.非选择题必须在指定的区域内,用黑色字迹的签字笔或钢笔作答,不能超出指定区域
或在非指定区域作答,否则答案无效.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,恰.有一项...
是符合题目要求的, 1.在两个不同时刻,对同一水池中的水位进行测量,记录如下:上升3cm ,下降6cm . 如 果上升3cm 记为+3cm ,那么下降6cm 记为
A .6cm
B .+6cm
C .-6cm
D .-6 2.25的算术平方根是
A . 5
B .±5
C .5
D .±5 3.计算432)2(b a -的结果是
A .12
816b a B .12
88b a C .12
88b a - D .12
816b a - 4.已知∠α与∠β互余,若∠α=43°26′,则∠β的度数是 A .56°34′ B .47°34′ C .136°34′ D .46°34′ 5.如图(1)放置的一个机器零件,若其主视图如图(2),则其俯视图是
6.如图,将两根钢条'AA 、'BB 的中点O连在一起,使'AA 、
'BB 可以绕着点0自由转动,就做成了一个测量工件,则 ''A B 的长等于内槽宽AB ,那么判定△AOB ≌△''A OB 的 理由是
A .边角边
B .角边角
C .边边边
D .角角边
A B C
D
(2)
(1)
(第5题)
A .
2 B .
3 C .
4 D . 5
9.已知某村今年的荔枝总产量是p 吨(p 是常数),设该村荔枝的人均产量为y (吨),
人口总数为x (人),则y 与x 之间的函数图象是
10.如图,是一个工件的三视图,则此工件的全面
积是
A .85πcm 2
B .90πcm 2
C .155πcm 2
D .165πcm 2
二、填空题:共8小题,每小题3分,共30分.
11.比较大小:2- ▲ 3.
(填“>,=或<”) 12.水星的半径为2 440 000m ,用科学记数法表示水星的半径是 ▲ m . 13.方程
11
2
=-x 的解为 ▲ . 14.如图,在△ABC 中,点D 、E 分别是边AB 、AC 的中点,
已知DE =6cm ,则BC =___▲___cm . 15.分解因式:x x +-3
= ▲ .
16.摩托车生产是某市的支柱产业之一,不少品牌的摩托车畅销国内外.下表是该市某摩
托车厂今年1至5月份摩托车销售量的统计表:(单位:辆)
则这5个月销售量的中位数是 ▲ 辆.
17.为了测量一个圆形铁环的半径,某同学采用了如下办法:将 铁环平放在水平桌面上,用一个锐角为30°的三角板和一 个刻度尺,按如图所示的方法得到相关数据,进而可求得铁 环的半径,若测得P A =5cm ,则铁环的半径是 ▲ cm .
(第7题) (第14题)
(第10题)
(第17题)
18.在Rt ABC △中,∠BAC =90°,AB =3,M 为
边BC 上的点,连接AM (如图所示).如果将 ABM △沿直线AM 翻折后,点B 恰好落在边 AC 的中点处,那么点M 到AC 的距离是 ▲ . 三、解答题:本大题共10小题,共96分.
解答时应写出文字说明、证明过程或演算步骤. 19.(本小题10分) (1)计算:25)4080(-+÷-;
(2)化简:)2(2
a
b ab a a b a --÷-. 20.(本小题8分)解方程:0)32()32)(32(=+--+x x x x 。
21.(本小题8分)热气球的探测器显示,从热气球看一栋高楼
顶部的仰角为30°,看这栋高楼底部的俯角为60°,热 气球与高楼的水平距离为120m ,问这栋高栋有多高? (结果精确到0.1m )
22.(本小题8分)如图,⊙O 的直径AB 为10cm ,
弦AC 为6cm ,∠ACB 的平分线交⊙O 于D , 求BC ,AD ,BD 的长.
23.(本小题8分)有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中
平均一个人传染了几个人? 24.(本小题8分)如图,过点P (2,2)作x 轴的平行线交y 轴于点A ,交双曲线k y x
= (0x >)于点N ,作PM AN ⊥交双曲线k
y x
=(0x >)于点M ,连结AM .已 知4PN =.
(1)求k 的值;
(2)设直线MN 解析式为b ax y +=,
求不等式x
k
≥b ax +的解集;
(3)试判断△AMN 的形状?并说明理由.
(第18题)
(第21题)
(第24题)
A B C
O · (第22题)
25.(本小题10分)2008年北京奥运会后,同学们参与体育锻炼的热情高涨.为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下的频数分布表和扇形统计图.
根据上述信息解答下列问题:
(1)m=______,n=_________;
(2)在扇形统计图中,D组所占圆心角的度数为_____________;
(3)全校共有3000名学生,估计该校平均每周体育锻炼时间不少于6小时的学生约有多少名?
26.(本小题10分)某企业获准生产“上海世博会”纪念徽章,若生产A种款式的纪念徽章125件,B种款式的纪念徽章150件,需生产成本700元;若生产A种款式的纪念徽章100件,B种款式的纪念徽章450件,需生产成本1550元.已知A、B两种纪念徽章的市场零售价分别为2.3元,3.5元.
(1)求每个A、B两种款式的纪念徽章的成本是多少元?
(2)随着上海世博会的开幕,为了满足市场的需要,该企业现在每天要生产A、B两种款式的纪念徽章共4500件,若要求每天投入成本不超过1万元,并且每天生产
的B种款式的纪念徽章不少于A种款式纪念徽章的
1
4
.那么每天最多获利多少元,最少获利多少元?获利最多的方案如何设计?
27.(本小题12分)如图,矩形ABCD中,AB=4,AD=8,P是对角线AC上一动点,连
接PD,过点P作PE⊥PD交线段
..BC于E,设AP=x.
(1)求PD︰PE的值;
(2)设2
DE=y,试求出y与x的函数关系式,并求x取何值时,y有最小值;
(3)当△PCD为等腰三角形时,求AP的长.
P
A D
28.(本小题14分)如图,在平面直角坐标系中,直线AB :1
12
y x =-
-与x 轴交于点A ,与y 轴交于点B .点C 为AB 延长线上一点且BC =AB ,抛物线23y ax bx =+-过点A 、点C .
(1)求点A 、B 、C 的坐标.
(2)求抛物线的解析式及顶点坐标.
(3)抛物线的对称轴与x 轴交于点M ,将△ABO 绕点M 旋转,使得点A 的对应点落在
抛物线上,试求出A 的对应点的坐标.(直接写出结果)
(4)△ABO 绕平面内的某一点旋转180°后,是否存在A 、B 的对应点同时落在抛物线
上?若存在,求出对应点A '、B '和旋转中心的坐标;若不存在,请说明理由.
(第28题)。
