扭转的概念和实例§3-2 扭转内力的计算
合集下载
扭转—扭转的概念和实例(建筑力学)
扭转
扭转
学习目标：
1. 弄清扭转轴的受力特点和变形特点。 2. 应用截面法熟练计算扭转轴的内力，并能正确绘制扭矩图 3.了解剪切胡克定律和剪应力互等定理。 4. 掌握圆轴扭转时横截面上的切应力计算公式，明确切应力 的分布规律。 5. 掌握扭转轴的强度和刚度计算。 6.了解矩形截面杆件扭转时的切应力计算。
两横截面间相对转动的角度称为扭转角，用φ表示。 凡以扭转变形为主的杆件，通常称为轴。
扭转
在实际工程中，在扭转的同时常伴有其他变形，如雨篷梁 等，发生扭转的同时还受到弯曲变形。
重点：
扭转轴的内力计算和扭矩图的绘制，以及圆扭转时横截面 上的切应力计算和强度计算
பைடு நூலகம்转
第一节 扭转的概念和实例
在工程实际中，以扭转变形为主的杆件是很多的。
汽车方向盘的操纵杆 搅拌器的主轴 钻探机的钻杆
扭转
构件的受力特点：在垂直杆件轴线的两平面内，作用一 对大小相等、转向相反的力偶。
在这种受力情况下，杆件任意两横截面都绕杆的轴线发 生相对转动。这种变形形式称为扭转变形。
扭转
学习目标：
1. 弄清扭转轴的受力特点和变形特点。 2. 应用截面法熟练计算扭转轴的内力，并能正确绘制扭矩图 3.了解剪切胡克定律和剪应力互等定理。 4. 掌握圆轴扭转时横截面上的切应力计算公式，明确切应力 的分布规律。 5. 掌握扭转轴的强度和刚度计算。 6.了解矩形截面杆件扭转时的切应力计算。
两横截面间相对转动的角度称为扭转角，用φ表示。 凡以扭转变形为主的杆件，通常称为轴。
扭转
在实际工程中，在扭转的同时常伴有其他变形，如雨篷梁 等，发生扭转的同时还受到弯曲变形。
重点：
扭转轴的内力计算和扭矩图的绘制，以及圆扭转时横截面 上的切应力计算和强度计算
பைடு நூலகம்转
第一节 扭转的概念和实例
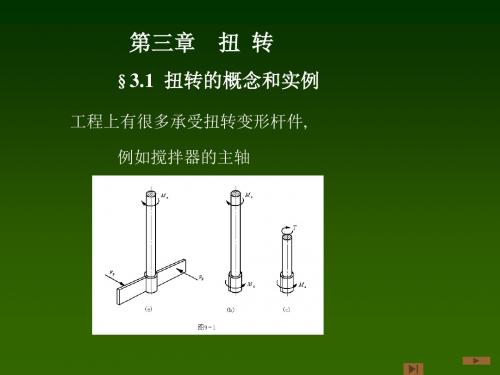
在工程实际中，以扭转变形为主的杆件是很多的。
汽车方向盘的操纵杆 搅拌器的主轴 钻探机的钻杆
扭转
构件的受力特点：在垂直杆件轴线的两平面内，作用一 对大小相等、转向相反的力偶。
在这种受力情况下，杆件任意两横截面都绕杆的轴线发 生相对转动。这种变形形式称为扭转变形。
第三章 扭转
46
三、切应变 剪切胡克定律 1、切应变 l
a
´
c
´
b
d t
为扭转角 r0 l
r0 即
l
纵轴 T——
T
2r02t
纯剪切单元体的相对两侧面 发生微小的相对错动，
使原来互相垂直的两个棱边 的夹角改变了一个微量γ；
横轴
r0
l
47
2、剪切虎克定律
做薄壁圆筒的扭转试验可得
在弹性范围内切应力 与切应变成正比关系。
切应力与扭矩同向的顺流
51
切应变的变化规律：
Me
pq
Me
pq p
q
d
a
d
c
a' O b
R
p
b′ q
dx
_ 扭转角（rad）
x
d _ dx微段两截面的
相对扭转角
边缘上a点的错动距离：
aa' Rd dx
边缘上a点的切应变：
R d
dx
发生在垂直于半径的平面内。
52
p
q
d
ae
d
c
a ' e′O b
③ 结论：①圆筒表面的各圆周线的形状、大小和间距均未改 变，只是绕轴线作了相对转动。
②各纵向线均倾斜了同一微小角度 ,仍为直线。
③所有矩形网格均歪斜成同样大小的平行四边形。
40
表明： 当薄壁圆筒扭转时，其横截面和包含轴线的纵向截
面上都没有正应力； 横截面上便只有切于截面的切应力；
41
2、切应力分布规律假设
Me2
Me1
n
Me3
从动轮
主动轮
从动轮
求： 作用在该轮上的外力偶矩Me。
三、切应变 剪切胡克定律 1、切应变 l
a
´
c
´
b
d t
为扭转角 r0 l
r0 即
l
纵轴 T——
T
2r02t
纯剪切单元体的相对两侧面 发生微小的相对错动，
使原来互相垂直的两个棱边 的夹角改变了一个微量γ；
横轴
r0
l
47
2、剪切虎克定律
做薄壁圆筒的扭转试验可得
在弹性范围内切应力 与切应变成正比关系。
切应力与扭矩同向的顺流
51
切应变的变化规律：
Me
pq
Me
pq p
q
d
a
d
c
a' O b
R
p
b′ q
dx
_ 扭转角（rad）
x
d _ dx微段两截面的
相对扭转角
边缘上a点的错动距离：
aa' Rd dx
边缘上a点的切应变：
R d
dx
发生在垂直于半径的平面内。
52
p
q
d
ae
d
c
a ' e′O b
③ 结论：①圆筒表面的各圆周线的形状、大小和间距均未改 变，只是绕轴线作了相对转动。
②各纵向线均倾斜了同一微小角度 ,仍为直线。
③所有矩形网格均歪斜成同样大小的平行四边形。
40
表明： 当薄壁圆筒扭转时，其横截面和包含轴线的纵向截
面上都没有正应力； 横截面上便只有切于截面的切应力；
41
2、切应力分布规律假设
Me2
Me1
n
Me3
从动轮
主动轮
从动轮
求： 作用在该轮上的外力偶矩Me。
材料力学-扭转问题解读
d1 86.4mm
4.直径d2的选取 按强度条件:
3 3
d1
A
M e1
C
M e2
d2
B M e3
16T 16 4580 d2 π[ ] π 70106 69.3 103 m 69.3mm
4580 N m 7640 N m
按刚度条件 :
32T 180 32 4580 180 3 d2 76 10 m 76mm 2 9 2 Gπ [ ] 80 10 π 1
§3.7 非圆截面杆扭转 矩形截面杆扭转
变 形 特 征
T Wt
T
12100
x
max
Wt
D 3
16
T [ ]
-1590
D3
16 Mn
58.7 mm
刚度条件：
T 180 G Ip
D 4 T 180 Ip 32 G
32 Mn 180 D4 49mm G
4
圆轴扭转的强度条件:
max
T T T R I Ip Wt p R Wt 抗扭截面系数
Wt Wt
D 3
16 16
实心圆
4
D 3
1
d 空心圆 D
d
对阶梯轴，因各段的Wt不同 ,最大切应 力不一定在最大T所在截面，须综合考 虑T和Wt，确定T/ Wt极值。
1 G1 2 G2
2) 在下述三种情况下的切应力分布情况： （1）G1 > G2; （2） G1=G2 ; （3） G1<G2
G2Ip2
R2
G1Ip1
材料力学第四版课件 第三章 扭转
2
例1：图示空心圆轴外径D=100mm,内径 图示空心圆轴外径D=100mm,内径 d=80mm, M1=6kN·m, M2=4kN·m, 材料的切变 =6kN· 模量 G=80GPa. （1） 试画轴的扭矩图； 试画轴的扭矩图； （2） 求轴的最大切应力,并指出其位置. 求轴的最大切应力,并指出其位置.
平面假设：圆轴扭转后各横截面仍保持为平面， 平面假设：圆轴扭转后各横截面仍保持为平面， 各横截面如同刚性平面仅绕轴线作相对转动。 各横截面如同刚性平面仅绕轴线作相对转动。
横截面上无σ 1）横截面上无σ 2）横截面上只有τ
F O1 a d dφ d1 dx O2
dd1 ρdφ γ ρ ≈ tanγ ρ = = ad dx
4
πd
3 0
(
)
16T ∴d0 ≥ 3 = 76.3mm 4 π (1−α )[τ ]
取 d0 = 76.3mm、 、 (3)比较空心轴与实心轴的重量 比较空心轴与实心轴的重量 积之比： 二者重量之比等于横截面 积之比：
π (d − di ) 4 = 0.395 β= 2 4 πd
2 0 2
可见空心轴比实心轴的重量轻 可见空心轴比实心轴的重量轻
任一点处的切应变 切应变与到 距圆心为 ρ 任一点处的切应变与到 成正比。 圆心的距离ρ成正比。
2. 物理方面
dφ γρ = ρ dx
dφ τ ρ = Gρ dx
3. 静力学方面
dφ 2 T = ∫ ρτ ρ dA = G ∫ ρ dA dx A A
Ip = ∫ ρ dA 称为极惯性矩
2 A
ρ
dA
MB
1
MC
MA
2 2
A
3
MD
例1：图示空心圆轴外径D=100mm,内径 图示空心圆轴外径D=100mm,内径 d=80mm, M1=6kN·m, M2=4kN·m, 材料的切变 =6kN· 模量 G=80GPa. （1） 试画轴的扭矩图； 试画轴的扭矩图； （2） 求轴的最大切应力,并指出其位置. 求轴的最大切应力,并指出其位置.
平面假设：圆轴扭转后各横截面仍保持为平面， 平面假设：圆轴扭转后各横截面仍保持为平面， 各横截面如同刚性平面仅绕轴线作相对转动。 各横截面如同刚性平面仅绕轴线作相对转动。
横截面上无σ 1）横截面上无σ 2）横截面上只有τ
F O1 a d dφ d1 dx O2
dd1 ρdφ γ ρ ≈ tanγ ρ = = ad dx
4
πd
3 0
(
)
16T ∴d0 ≥ 3 = 76.3mm 4 π (1−α )[τ ]
取 d0 = 76.3mm、 、 (3)比较空心轴与实心轴的重量 比较空心轴与实心轴的重量 积之比： 二者重量之比等于横截面 积之比：
π (d − di ) 4 = 0.395 β= 2 4 πd
2 0 2
可见空心轴比实心轴的重量轻 可见空心轴比实心轴的重量轻
任一点处的切应变 切应变与到 距圆心为 ρ 任一点处的切应变与到 成正比。 圆心的距离ρ成正比。
2. 物理方面
dφ γρ = ρ dx
dφ τ ρ = Gρ dx
3. 静力学方面
dφ 2 T = ∫ ρτ ρ dA = G ∫ ρ dA dx A A
Ip = ∫ ρ dA 称为极惯性矩
2 A
ρ
dA
MB
1
MC
MA
2 2
A
3
MD
材料力学-扭转
扭转角（ 扭转角（ϕ）：任意两截面绕轴线相对转动的角度。又称为角 位移。通常用ϕ表示。ϕB − A表示B截面相对A截面转过的角度。 剪应变（ 剪应变（γ）： 剪应变又叫角应变或切应变，它是两个相互垂直方 向上的微小线段在变形后夹角的改变量（以弧度表示， 角度减小时为正） O ϕ B m
A m
γ
第二节 杆受扭时的内力计算
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
实心圆截面： 实心圆截面：
2
I p = ∫ ρ d A = ∫ ρ (2 πρ d ρ )
2
ρ
d O
dρ
A
d 2 0
= 2 π(
ρ
4
d /2
4
)
0
πd = 32
4
d A = 2 πρ d ρ
πd 3 Wp = = d / 2 16 Ip
空心圆截面： 空心圆截面：
T T = ρ max = IP IP T = WP
ρ max
Ip—截面的极惯性矩， 截面的极惯性矩，单位： 单位：m 4 , mm 4 Ip 3 3 WP —抗扭截面模量， WP = 抗扭截面模量，单位：m , mm .
ρ max
整个圆轴上——等直杆： 等直杆： τ max
Tmax = WP
三、公式的使用条件： 公式的使用条件： 1、等直的圆轴， 等直的圆轴， 2、弹性范围内工作。 弹性范围内工作。
Tmax Wp
πD 3 实心, 16 T max W = 2）设计截面尺寸: 设计截面尺寸:WP ≥ 3 P [τ ] πD (1 − α 4 ) 空心. 16 ≤ ⇒ m 3）确定外荷载: 确定外荷载: Tmax WP ⋅ [τ ]
≤
材料力学第3章扭转
试问：纵向截面里的切应力是由什么内力平衡的？
§3.8 薄壁杆件的自由扭转
薄壁杆件：杆件的壁厚远小于截面的其它尺寸。 开口薄壁杆件：杆件的截面中线是不封闭的折线或曲
线，例如：工字钢、槽钢等。 闭口薄壁杆件：杆件的截面中线是封闭的折线或曲线，
例如：封闭的异型钢管。
一、开口薄壁杆的自由扭转
＝ Tl
GI t
变形特点：截面发生绕杆轴线的相对转动 本章主要研究圆截面等直杆的扭转
§3.2 外力偶矩的计算 扭矩和扭矩图
功率： P(kW) 角速度：ω 外力偶矩：Me
P = Meω
转速：n(r/min)
2n/ 60
Me
1000 P＝9549
P n
(N
m)
内力偶矩：扭矩 T 求法：截面法
符号规则： 右手螺旋法则 与外法线同向“ + ” 与外法线反向“－”
max
T max
It
It
1 3
hi
3 i
二、闭口薄壁杆的自由扭转
max
T
2 min
TlS
4G 2
其中：ω截面为中线所围的面积
S 截面为中线的长度
闭口薄壁杆的应力分布：
例： 截面为圆环形的开口和闭口薄壁杆件如图所 示，设两杆具有相同平均半径 r 和壁厚δ，试 比较两者的扭转强度和刚度。
开＝3 r 闭 开＝3( r )2 闭
8FD3n Gd 4
C
ห้องสมุดไป่ตู้
Gd 4 8D3n
F C
§3.7 矩形截面杆扭转的概念
1) 翘曲
变形后杆的横截面不再保持为平面的现象。
2) 自由扭转和约束扭转
自由扭转：翘曲不受限制的扭转。 各截面翘曲程度相同，纵向纤维无伸缩， 所以，无正应力，仅有切应力。
扭转的概念和实例
第三章 扭 转§3.1 扭转的概念和实例§3.2 外力偶矩的计算，扭矩和扭矩图 §3.3 纯剪切§3.4 圆轴扭转时的应力 §3.5 圆轴扭转时的变形§3.6 圆柱形密圈螺旋弹簧的应力和变形 §3.7 非圆截面杆扭转的概念§3.1 扭转的概念和实例1．实例如：车床的光杆 反应釜的搅拌轴 汽车转向轴2．扭转：在杆件的两端作用等值，反向且作用面垂直于杆件轴线的一对力偶时，杆的任意两个横截面都发生绕轴线的相对转动，这种变形称为扭转变形。
§3.2 外力偶矩的计算，扭矩和扭矩图1．M e 、m 、 P 之间的关系 M e ——外力偶矩（N ∙m ） n ——转速（r/min ）P ——功率（kW ）（1kW=1000N ∙m/s ）（马力）（1马力=735.5W ） 每秒钟内完成的功力P nM e 1000602 ·=π或P nM e 5.735602 ·=π{}{}{}{}{}{}min/7024min/kW9549..r n P M r n P M mN e m N e 马力==2．扭矩和扭矩图（1）截面法、平衡方程 ΣM x =0T-M e =0T =M e（2）扭矩符号规定：为无论用部分I 或部分II 求出的同一截面上的扭矩不但数值相同且符号相同、扭矩用右手螺旋定则确定正负号。
（3）扭矩图例1 主动轮A 输入功率P A =50kW ，从动轮输出功率P B =P C =15kW ，P D =20kW ，n =300r/min ，试求扭矩图. 解：（1）15913005095499549=⨯==n P M eA m N ⋅ mN 637mN 477300159549⋅=⋅=⨯==eD eC eB M M M （2）求TΣM x =0 T 1+M eB =0 T 1=-M eB =-477T 2-M eA +M eB =0 T 2=1115NT 3-M eD =0 T 3=M ed =63T例2 主动轮与从动轮布置合理性的讨论主动轮一般应放在两个从动轮的中间，这样会使整个轴的扭矩图分布比较均匀。
扭转
反之为负。
第3章 扭转
外力偶矩的计算 扭矩和扭矩图
M
T
扭矩的大小由平衡方程求得：
mx 0
二、扭矩图
T M 0
x
T M
表示杆件轴线上的各横截面上的扭矩变化情况
扭矩图的画法步骤与轴力图基本相同，具体如下：
第3章
外力偶矩的计算 扭矩和扭矩图
扭矩图的画法步骤：
扭转
1.画一条与杆的轴线平行且与杆等长的直线作为基线
满足强度条件
（2）按刚度校核
1
T1 GI P1
180
32 600
80109 404
1012
180
1.71o
/m
2
T2 GI P 2
180
32 800
80109 704
1012
180
0.24o
/m
max 1 1.71o /m>[ ] 不满足刚度条件
圆杆扭转时的变形
第3章 扭转
（3）两端相对扭转角
② 各纵向线长度不变，但均倾斜了同一微小角度γ
③ 所有矩形网络均歪斜成同样大小的平行四边形
纯剪切
第3章 扭转
一、薄壁筒扭转时的切应力
薄壁圆筒扭转时，因长度不变，故横截面上没有 正应力，只有切应力；因筒壁很薄，切应力沿薄壁厚 分布可视作均匀的，切应力沿圆周切线方向与扭矩转 向一致
A
dA r0
T
r0 A dA r0 2 r0 t T
max
d D
84.91 2Leabharlann 42.45MPaD
圆杆扭转时的变形
第3章 扭转
单位长度扭转角
d T
dx GIP
l T dx 0 GIP
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Me2
Me1
n
Me3
从动轮
主动轮
从动轮
Me—作用在轴上的力偶矩( N · m ) n—轴的转速( r/min ) P—轴传递的功率(kW)
11
二、内力的计算 (Calculation of internal force)
1.求内力(Calculating internal force) 截面法 (Method of sections) 在n-n 截面处假想将轴截开取 左侧为研究对象 Me Me
一、工程实例(Example problems)(视频 2)
拧瓶盖。
螺丝刀
5
一、连轴器
高铁高速转向架 —— 传动机构
7
二、受力特点(Character of external force)
杆件的两端作用两个大小相等、方向相反、且作用平面垂直
于杆件轴线的力偶.
三、变形特点(Character of deformation)
杆件的任意两个横截面都发生绕轴线的相对转动.
Me
Me
§3-2 扭转的内力的计算 (Calculating internal force of torsion)
一、外力偶矩的计算 (Calculation of external moment)
P kW M e Nm 9 549 nr / min
计算 CA 段内任横一截面 2-2
截面上的扭矩. 假设 T 2为正值.
由平衡方程
Me2 B Me2
Me3 2 C 2 Me3 T 2 C
Me1
Me4 D
Mx 0
M e 2 M e 3 T2 0
A x
T2 M e 2 M e 3 9549N m
结果为负号, 说明T 2 应是负值扭矩
4774.5 N· m
9549 N· m
6366 N· m
+
Tmax 9549 N m
Chapter 3 Torsion
第三章
扭
转 (Torsion)
§3-1 扭转的概念和实例 (Concepts and example problem of torsion) §3-2 扭转内力的计算 (Calculating internal force of torsion) §3-3 薄壁圆筒的扭转 (Torsion in thin—wall circular tube) §3-4 圆轴扭转的应力分析及强度条件 (Analyzing stress of circular bars & strength condition)
§3-5 圆杆在扭转时的变形 ·刚度条件 (Torsional deformation of circular bars & stiffness condition) §3-6 密圈螺旋弹簧的应力和变形 (Calculation of the stress and deformation in close-coiled helical springs)
B Me2
T1
x
同理,在 BC 段内
Me2 1 Me3
B 1 C T1
Me1 3 Me4 A T3 3 D Me4
T1 M e 2 4774.5 N m
在 AD 段内
T3 M e 4 6366 N m
注意：若假设扭矩为正值,
Me2
则扭矩的实际符号与计算符号相同. 作出扭矩图 从图可见, 最大扭矩在 CA段内. _
§3-7 非圆截面杆的扭转 (Torsion of noncircular prismatic bars)
§3-8 开口和闭合薄壁截面杆的自由扭转 (Free torsion of open and closed thinwalled members)
3
§3-1 扭转的概念及实例 (Concepts and example problem of torsion)
x
横截面的位置; 用垂直于杆轴线的
坐标 T 表示横截面上的扭矩, 正的 扭矩画在 x 轴上方, 负的扭矩画在 x 轴下方. T +
_
x
例题1 一传动轴如图所示,其转速 n = 300 r/min , 主动轮A输入 的功率为P1 = 500 kW . 若不计轴承摩擦所耗的功率, 三个从动轮
输出的功率分别为P2 = 150 kW , P3 = 150 kW , P4 = 200 kW.
试作扭矩图. Me1 Me2
Me3
n
Me4
B
C
A
D
Me1
Me2 Me3 n Me4
B 解: 计算外力偶矩
C
A
D
M e1 15915 N m M e 4 6366 N m
pkw M e 9 549 nr / min
M e 2 M e 3 4774.5 N m
Mx 0
T Me
Me T
12
2.扭矩符号的规定 (Sign convention for torque) 采用右手螺旋法则, 当力偶矩 矢的指向背离截面时扭矩为正, 反 之为负. 3.扭矩图(Torque diagram) 用平行于杆轴线的坐标 x 表示
Me
n
Me • x
n Me T • x Me • T •