6 统计(1)

合集下载

2018-2019学年度六年级语文上册期中测试成绩统计(1)

25
26
27
28
29
30
31
32
33
34
35
36Hale Waihona Puke 373839
40
41
42
43
44
45
46
47
48
49
50
51
毕海波张吉缘吴继鹏王玉婷陈非非黄鑫吴兴娟
67.5 71.5 54 65 54.5 53.5 53.5 4242.5
48 47 54 31 34 52 19 4274.5
52 46 56 36 37 14 37 3787 65.29
167.5 164.5 164 132 125.5 119.5 109.5
52
53
54
55
56
57
58
73.14655 73.69828
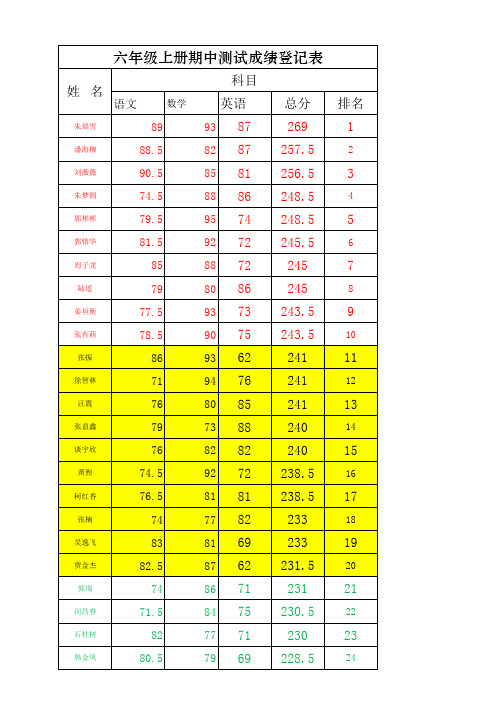
六年级上册期中测试成绩登记表
姓名
语文
朱瑞雪潘海柳刘薇薇朱梦圆郭彬彬郭镕华周子龙陆遥姜垣衡张有萌张振徐智林汪震张益鑫谈宇欣黄煦柯红香张楠吴逸飞贾金杰郭瑞闵昌睿石桂树韩金凤
科目
数学
英语
93 82 85 88 95 92 88 80 93 90 93 94 80 73 82 92 81 77 81 87 86 84 77 79
87 87 81 86 74 72 72 86 73 75 62 76 85 88 82 72 81 82 69 62 71 75 71 69
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

小学-数学-苏教版(2014秋)-苏教版六下第7单元《统计》测试卷(1)

苏教版六下第7单元《统计》测试卷（1）一、填空题1、我们已学过的统计图有条形统计图、折线统计图和______统计图.要对3月份全校学生课外阅读量变化情况进行统计，最好选用______统计图.2、第30届奥运会我国共获得______枚奖牌.3、下图是某景区近年来游客人数统计图. 图中每格代表______万人. 2018年的游客人数比2016年的游客人数多______万人.4、下面是四（三）班喜欢的体育项目统计图. 由图可知，喜欢______项目的人数最多，喜欢______项目的人数最少.5、看图填空. 上半年比下半年少销售______瓶；全年平均每月销售______瓶.第三季度的销售量是第四季度的______倍.6、由图可知，甲、乙两地温差最大的是______月.7、前进小学六年级学生喜欢的运动项目统计如下图，其中喜欢足球的有40人，那么喜欢踢毽的占总人数的______%；前进小学六年级一共有______人；喜欢乒乓球的人数比喜欢足球的人数多______%.8、下图是某工厂2019年每季度完成产值情况的统计图. 已知第三季度完成总产值500万元，那么全年完成总产值______万元，第四季度完成产值______万元.二、选择题9、为了解班里的同学最喜欢的课外小组情况，下面收集数据的方式不合理的是（）.A. 每个同学写出自己最喜欢的一个小组B. 询问班里的一组同学C. 举手数出最喜欢每个小组的人数10、要反映中国1996～2016年在各届奥运会上获得的奖牌的变化情况，应选择（）.A. 条形统计图B. 折线统计图C. 扇形统计图D. 复式统计表11、下面是二（1）班同学喜欢的季节统计表.喜欢冬季的比喜欢夏季的少（）.A. 8人B. 3人C. 5人12、某足球队想从队员中选一个人做前锋，下表是甲、乙、丙三名运动员最近5个赛季进球数统计表（“/”表示这个赛季没有参加比赛，单位：个），选（）运动员比较合适.A. 甲B. 乙C. 丙13、优品超市甲、乙两种品牌的矿泉水1月份至3月份销售情况如下表，那么这几个月中，（）品牌的矿泉水销售得更多.A. 甲B. 乙14、强强前3次打靶的平均数为5环，要使前4次的平均数不低于6环，则第4次至少应该打出（）.A. 8环B. 9环C. 10环15、下面是科技小组的同学绘制的某日气温统计图.从统计图中可以看出，科技小组的同学每隔（）小时测量一次气温.A. 1B. 2C. 4D. 816、今天有8节课，其中有2节语文课，则统计图中表示语文课的应是扇形（）.A. 甲B. 乙C. 丙D. 丁17、某市九月份的天气情况如下图，本月的雨天有（）.A. 21天B. 6天C. 3天18、某公司有员工700人参加元旦庆祝活动，参加各种活动的情况统计图如下图，规定每人只参加一项，那么不下围棋的共有（）人.A. 259B. 441C. 438D. 700三、判断题19、条形统计图不仅可以表示数量的多少，还可以表示数量增减变化的情况. （）20、折线统计图和条形统计图都能够表示数量的多少，但扇形统计图不能表示出数量的多少.（）21、小明要统计全校各年级的人数情况，应选用折线统计图；要统计一昼夜气温的变化情况，应选用条形统计图. （）22、扇形统计图中，所有扇形的百分比之和必须小于1. （）四、解答题23、下面是某校课外活动期间参加各项活动的人数统计表.（1）踢球比跳绳的多多少人？（2）跑步和踢球的一共有多少人？24、甲、乙两个村2008~2016年家庭汽车拥有量统计如下图：（1）2014年乙村家庭汽车拥有量是2008年的几倍？（2）2016年甲村家庭汽车拥有量是2008年的几倍？（3）你还能得到什么信息？有什么感受？25、六（1）班共有40人，下面是他们最喜欢的饮料统计图，请问每种饮料各有多少人最喜欢？26、读图，完成下列问题(1)西陵超市第二季度每个月销售的情况如图2．已知六月份销售额是150万元，请分别计算出四月份与五月份的销售额．(2)根据以上数据完成统计图1.参考答案1、【答案】扇形,折线【分析】本题考查的是统计图的认识和选择．【解答】我们学过条形统计图、折线统计图、扇形统计图三种统计图，其中折线统计图可以直观地看出统计数量变化情况.故本题的答案是扇形，折线．2、【答案】88【分析】共获得的奖牌数量＝获得的金牌数量＋获得的银牌数量＋获得的铜牌数量. 【解答】由表可知，第30届奥运会我国获得38枚金牌，27枚银牌，23枚铜牌，一共获得奖牌：38＋27＋23＝88（枚）.故本题的答案是88.3、【答案】2,8【分析】本题考查的是从条形统计图获取信息.【解答】由图可知，图中每格代表2万人，2018年的游客人数为18万人，2016年的游客人数为10万人，所以2018年的游客人数比2016年的游客人数多：18－10＝8（万人）.故本题的答案是2，8.4、【答案】跳绳,足球【分析】本题考查的是从复式条形统计图中获取信息.【解答】由图可知，喜欢乒乓球的人数是14＋2＝16（人）；喜欢足球的人数是4＋3＝7（人）；喜欢跑步的人数是3＋5＝8（人）；喜欢跳绳的人数是10＋9＝19（人）.所以喜欢跳绳的人数最多，喜欢足球的人数最少.故本题的答案是跳绳，足球.5、【答案】200,250,3【分析】本题考查的是从折线统计图中获取信息.【解答】(1)通过折线统计图可知，上半年的销售量为：500＋900＝1400（瓶），下半年的销售量为：1200＋400＝1600（瓶），所以上半年比下半年少销售：1600－1400＝200（瓶）.（2）全年的销售量是500＋900＋1200＋400＝3000（瓶），所以全年平均每月的销售量为：3000÷12＝250（瓶）.（3）第三季度的销售量为1200瓶，第四季度的销售量为400瓶，求第三季度的销售量是第四季度的多少倍用除法：1200÷400＝3.故本题的答案是200，250，3.6、【答案】2【分析】本题考查的是根据复式折线统计图解决问题.【解答】复式折线统计图上同一竖线上的不同折点距离越大，表示它们代表的数据差距越大.由图可知，2月份的甲地区和乙地区的温度折点之间的距离最大，所以2月份甲答案第1页，共6页乙两地温差最大.故本题的答案是2.7、【答案】8,200,50【分析】把六年级的总人数看作单位“1”，用1减去喜欢足球、跳绳、乒乓球、其他人数所占的百分比就是喜欢踢毽人数所占的百分比.根据百分数除法的意义，用喜欢足球的人数除以所占的百分比就是六年级的总人数.用喜欢乒乓球比喜欢足球多的占总人数的百分比除以喜欢足球占总人数所占的百分比即可.【解答】1－20%－19%－30%－23%＝8%，所以喜欢踢毽的占总人数的8%.40÷20%＝200（人），所以前进小学六年级一共有200人.（30%－20%）÷20%＝50%，所以喜欢乒乓球的人数比喜欢足球的人数多50%.故本题的答案是8，200，50.8、【答案】2000,800【分析】由图可知：把总产值看成单位“1”，第一季度的产值占总产值的15%；第二季度的产值占总产值的20%；第三季度的产值占总产值的25%；剩下的是第四季度的产值；500万元对应的百分数是25%，由此用除法求出全年的总产值；先求出第四季度的产值占全年总产值的百分之几，再用全年的总产值乘这个百分数即可.【解答】500÷25%＝2000（万元），所以全年完成产值是2000万元.2000(115%20%25%)200040%800()⨯---=⨯=万元所以第四季度完成产值800万元.故本题的答案是2000、800.9、【答案】B【分析】本题考查的是收集数据的方式.【解答】在收集数据时要保证数据的普遍性，只询问班里的一组同学得到的数据不具有普遍性，所以不合理.选B.10、【答案】B【分析】条形统计图能很容易看出数量的多少；折线统计图不仅容易看出数量的多少，而且能反映数量的增减变化情况；扇形统计图能反映部分与整体的关系；由此根据情况选择即可．【解答】根据统计图的特点可知：要反映中国1996～2016年在各届奥运会上获得的奖牌的变化情况，应选择折线统计图.选B.11、【答案】B【分析】本题考查的是用画“正”字的方法统计数据.“正”字的每一笔都代表一个数据，一个“正”字代表5个数据.【解答】由统计表可知，喜欢冬季的人数是：5＋2＝7（人），喜欢夏季的有2个“正”字，代表的是5×2＝10（人），求喜欢冬季的比喜欢夏季的少几人，列式计算为：10－7＝3（人）.选B.12、【答案】B【分析】本题考查的是求平均数.【解答】求甲运动员成绩的平均数，列式计算为：（23＋17＋18＋24＋23）÷5＝21（个）；求乙运动员成绩的平均数，列式计算为：（26＋22＋24）÷3＝24（个）；求丙运动员成绩的平均数，列式计算为：（30＋12＋26＋20）÷4＝22（个）.因为24＞22＞21，乙运动员成绩的平均数比较高，所以选乙运动员比较合适.选B.13、【答案】B【分析】本题考查的是根据复式统计表解决实际问题.【解答】1－3月份甲品牌共销售矿泉水：130＋90＋70＝290（箱），乙品牌共销售矿泉水：80＋110＋140＝330（箱）.因为290＜330，所以乙品牌的矿泉水销售得更多.选B.14、【答案】B【分析】本题考查的是平均数的应用.第4次打出的环数＝前4次打出的总环数－前3次打出的总环数.【解答】强强前3次打靶的平均数为5环，一共3×5＝15（环）.要使前4次平均数不低于6环，即总环数要不低于4×6＝24（环），则第4次至少应该打出：24－15＝9（环）.选B.15、【答案】A【分析】本题考查的是认识折线统计图.【解答】由图可知，科技小组的同学每2个小时测量2次气温，也就是每隔1个小时测量一次气温.选A.16、【答案】A【分析】一共有8节课，语文课有2节，那么语文课的节数就占总节数的2÷8＝25%，那么语文课的节数的扇形的圆心角是360°的25%，由此求出表示语文课节数的扇形的圆心角即可.【解答】2÷8＝25%，360×25%＝90°，甲的圆心角是90°，所以统计图中表示语文课的应是扇形甲.选A.17、【答案】C【分析】把九月份的总天数看作“1”，即100%，根据扇形统计图提供的信息，用九月份的天数乘雨天所占的百分率就是九月份的雨天数.答案第3页，共6页【解答】30×10%＝3（天），所以本月的雨天有3天.选C.18、【答案】B【分析】把总人数用单位“1”表示，1－下围棋的百分率＝不下围棋的百分率，用总人数乘不下围棋人数占的百分率，即可求出不下围棋的人数.【解答】700(137%)=70063%=441()⨯-⨯人所以不下围棋的共有441人，选B.19、【答案】×【分析】本题考查的是认识条形统计图的特点.【解答】条形统计图可以表示数量的多少，但不能表示数量增减变化的情况.故本题错误.20、【答案】✓【分析】本题考查的是认识各种统计图的特点.【解答】条形统计图能形象地表示出数量的多少，扇形统计图能清楚地表示出数量与总数之间的关系；折线统计图不仅能表示出数量的多少，还能清楚地表示出数量的增减变化情况.故本题正确.21、【答案】×【分析】本题考查的是选择合适的统计图.【解答】折线统计图能直观地表示数据的增减变化，条形统计图能直观地表示各个年级的人数.要统计全校各年级的人数情况，应选用条形统计图；要统计一昼夜气温的变化情况，应选用折线统计图.故本题错误.22、【答案】×【分析】根据扇形统计图的概念和意义可知圆代表整体，即单位“1”，各个扇形代表部分.【解答】绘制扇形统计图时，把圆看作一个单位“1”，所以所有的百分比之和必须等于1.故本题错误.23、【答案】（1）踢球比跳绳的多26人.（2）跑步和踢球的一共有54人.【分析】本题考查的是根据统计表回答问题.【解答】根据表格可知，参加踢球的有34人，参加跑步的有20人，参加跳绳的有8人.（1）34－8＝26（人）答：踢球比跳绳的多26人.（2）34＋20＝54（人）答：跑步和踢球的一共有54人.24、【答案】（1）2014年乙村家庭汽车拥有量是2008年的4倍.（2）2016年甲村家庭汽车拥有量是2008年的13倍.（3）从2008年到2016年购买汽车的辆数逐步增多，人民的生活逐渐富裕，逐步改善生活条件.（答案不唯一，合理即可）【分析】（1）求2014年乙村家庭汽车拥有量是2008年的几倍，根据除法的意义列式为12÷3；（2）求2016年甲村家庭汽车拥有量是2008年的几倍，根据除法的意义列式为26÷2；（3）从2008年到2016年购买汽车的辆数逐步增多，人民的生活逐渐富裕.【解答】（1）2008年乙村家庭汽车拥有量是3辆，2014年乙村家庭汽车拥有量是12辆.12÷3＝4答：2014年乙村家庭汽车拥有量是2008年的4倍.（2）2008年甲村家庭汽车拥有量是2辆，2016年甲村家庭汽车拥有量是26辆.26÷2＝13答：2016年甲村家庭汽车拥有量是2008年的13倍.（3）从2008年到2016年购买汽车的辆数逐步增多，人民的生活逐渐富裕，逐步改善生活条件.25、【答案】最喜欢橙汁的有12人，最喜欢矿泉水的有4人，最喜欢牛奶的有16人，最喜欢可乐的有8人.【分析】把总人数看作单位“1”，根据总人数和各部分所占的百分比，利用百分数乘法的意义列式解答即可.【解答】最喜欢橙汁的有：40×30%＝12（人）；最喜欢矿泉水的有：40×10%＝4（人）；最喜欢牛奶的有：40×40%＝16（人）；最喜欢可乐的有：40×20%＝8（人）.答：最喜欢橙汁的有12人，最喜欢矿泉水的有4人，最喜欢牛奶的有16人，最喜欢可乐的有8人.26、【答案】（1）四月份的销售额是160万元，五月份的销售额是190万元.答案第5页，共6页（2）【分析】（1）全部的销售额是单位“1”，它的30%对应的销售额是150万元，用除法求出全部的销售额；再根据四月份和五月份占的百分数分别求出它们的数量；（2）根据四、五、六月份的销售额画出条形统计图即可．【解答】（1）150÷30%＝500（万元）500×32%＝160（万元）500×38%＝190（万元）答：四月份的销售额是160万元，五月份的销售额是190万元.（2）画图见答案.答案第6页，共6页。

冀教版二年级数学上册第六单元《第1课时认识象形统计图和统计表》教学设计

第六单元象形统计图和统计表
第1课时认识象形统计图和统计表
教学目标：
1.经历数菊花、用涂色的方块表示数量和借助象形统计图比较树叶多少的过程。

2.认识象形统计图和统计表，能用象形统计图表示简单的数据。

3.积极参与数学活动，感受分类和用图表表示的直观性，培养初步的数据整理意识。

教学重点：认识象形统计图和统计表，能用象形统计图表示简单的数
据。

教学难点：能用象形统计图表示简单的数据。

教学设计：
一、创设情境
出示情境图：引导学生观察情境图。

说一说是什么花？还见过什么样的花？自己喜欢什么颜菊花？
二、探究与体验
1.学生数一数每种菊花各有多少？
要求：找一种容易数的形式，并提出“做一做”。

2.集体进行订正。

3.出示第二幅情境图：
学生仿上活动。

4.说一说：每种水果各是多少？哪种水果多？
5.你还能提出哪些问题？
6.班上交流同学们的问题。

三、小结
同学们，今天你们有什么收获？学生谈一谈自己的收获。

板书
统计（1）
梨最多，桃子最少。

临武县2013年下期楚江小学六(5)班期末成绩统计表(1)

79 99 96 100 80 76 90 99 86 82 88 99 61 87 76 82 79 86 74 87 92 98 68 98
黄葵雷丽春雷思玲贺威鹏王欣谭跃发袁周星杨军强艾梅王珊邓湘云袁心宇雷科翔成玉琳
82 87 78 79 71 66 27 51 79 70 86 88 13 72
刘玉林王琳晶王临娟钟丽苹刘桂芳王佳菲王源力邓丽华王乔兰王馨萍钟文雄王芬王彩娟邓梦雨王江华王小燕钟申云刘雨轩刘美风刘吓伟王苗刘巧林钟玲凤钟城军
邓玲艳王佳辉邓叶玲谭玉君贺孔欢李静邓树青卢桂莹王甜甜黄涛黄思雲雷安平成松谭玉媛雷美琼雷艳雷鸿鸣黄章威黄富康邓少林黄锦艾玄真黄孝鹏王贤总分人平分及格人数
王艳霞黄志军黄佳鹏黄瑞黄佳豪刘永芳黄娟雷志鹏邓德宝谭勋豪艾三霞黄丽婷欧幸增谭美青邓元涛何益峰
贺彪敏黄京艾欣武邓杜军邓新伟黄理鹏艾双强欧水清邓华芳王远珠雷明涛谭琳蜂陈华斌王田福王田霞邓旺钟展鹏李云轩邓帅雷金君邓凯军邓旭靓刘攀蒋华威总分人平分及格人数
贺孔翔王会婷王盘黄梦霞雷云谭玉宣黄丹丽李卫萍谭素娇邓永顺邓文斌雷娟兰刘兰芳邓欣竹邓倩欣
及格率%
优秀人数
优秀率%
学校
Xm 姓名 Zgf01 语文 Zgf02 数学 Zgf03 英语 Zgf04 品德
2013年下期小学教师任教班期末教学质量监测成绩登记表（三）楚江中心小学年级六班次 4
Zgf05 科学 Zgf06 国学 Xm 姓名 Zgf01 语文 Zgf02 数学 Zgf03 英语 Zgf04 品德 Zgf05 科学 Zgf06 国学 Xm 姓名

新人教版六年级上册《第6章_统计》小学数学-有答案-单元测试卷(1)

新人教版六年级上册《第6章统计》单元测试卷（1）一、填空．1. 从条形统计图中，很容易看出________．2. 在一幅条形统计图上，纵轴用1厘米长表示30万元，表示150万元的直条应画________厘米长，一条直条长2.5厘米，它表示________万元。

3. 用统计表表示的数量，还可以用________来表示。

4. 护士记录病人一天的体温应选用________统计图。

5. 常用的统计图有：________、________、________．二、仔细分析统计表、图，回答问题．某小组学生2分钟的跳绳次数情况统计如下表：（1）这个小组学生2分钟的跳绳总成绩是________次。

（2）这个小组跳绳次数是100次的学生有________人。

（3）跳绳次数是100的人数比跳绳次数是85的多________%．（4）这个小组一共有________人。

（5）这个小组跳绳次数最多的人数占全组人数的________%．（6）这个小组跳绳次数是90次与85次的人数比是________．下面是宿州百丽鞋业一车间中三个小组男、女工人数统计图。

（1）男工人数最多的是________小组，最少的是________小组；女工人数最多的是________小组，最少的是________小组；从图上可以看出________小组人数最多，________小组人数最少。

（2）通过计算，知道第一小组是________人，人数最少；第二小组是________人，人数最多；第三小组是________人。

（3）第一小组男工人数是女工人数的________倍。

（4）第二小组男工人数占女工人数的________．．（5）全车间共有工人________人，其中女工________人，占()()（6）第一小组女工人数比男工人数少________%．下面是某超市毛衣、衬衫的销售情况统计图。

（1）下半年的毛衣销售量平均每月是多少件？（2）十二月份毛衣的销售量比衬衫的销售量多百分之几？（3）看图描述下半年毛衣和衬衫销售量是如何变化的。

统计学六个指数的概念

统计学六个指数的概念统计学是一门研究数据收集、整理、分析和解释的学科，它提供了一系列指数来衡量和总结数据。

下面我将详细介绍六个重要的统计学指数。

1. 算术平均数：算术平均数是数据集中所有数值的总和除以数据个数。

它是最常用的统计指数之一，用来衡量数据集的集中趋势。

算术平均数对异常值非常敏感，因为它把所有数据都纳入计算中。

2. 中位数：中位数是将数据集按升序排列后，位于中间位置的数值。

如果数据集的个数为奇数，中位数就是中间位置的数值；如果数据集的个数为偶数，中位数就是中间两个数值的平均值。

中位数对于数据集中的异常值不敏感，它能更好地反映数据集的典型值。

3. 众数：众数是数据集中出现次数最多的数值。

一个数据集可以有一个或多个众数，也可以没有众数。

众数适用于描述分类数据和定性数据的分布情况。

4. 方差：方差是衡量数据集分散程度的指标。

它衡量了每个数据点与算术平均数的偏离程度。

方差越大，数据点相对于平均值的偏离就越大，数据分布越分散。

5. 标准差：标准差是方差的平方根，它是最常用的衡量数据集分散程度的指标之一。

标准差的计算相对方差来说更易于解释和理解，因为它与原始数据集的单位一致。

6. 相关系数：相关系数是衡量两个变量之间关联程度的指标。

相关系数介于-1和1之间，如果相关系数为正值，表示两个变量具有正相关关系；如果相关系数为负值，表示两个变量具有负相关关系；如果相关系数接近0，表示两个变量之间没有线性关系。

相关系数的绝对值越接近1，说明相关性越强。

总结：以上六个统计学指数涵盖了许多统计分析的要点，不同的指数适用于不同类型的数据和分析目的。

了解和使用这些指数可以帮助我们更好地理解和解释数据，提取其中的信息，并作出更明智的决策。

第六章数理统计的基本概念(1)

(k 1, M1就是X )
XK
1 n
n i 1
X
k i
（4）样本k阶中心矩：
1 n
n i 1
(Xi
X )k
（5）顺序统计量： X(1) X(2) X(n) . 其中 X(k) 为将 X1, X2 , , Xn 从小到大排列第 k 位值.
18 September 2020
概率论与数理统计
理学院数学系
2、离散型设总体X的分布律为 P{ X x} p( x)
则样本X1, X2 ,的, 联Xn合分布律为 P{ X1 x1, X2 x2 ,, Xn xn } p( x1 ) p{ x2 ) p( xn )
18 September 2020
概率论与数理统计
理学院数学系
样本分布
第六章数理统计的基本概念
（1）样本均值：
X
1 n
n i 1
Xi
（2）样本方差：
Sn2
1 n
n
(Xi
i 1
X )2
修正样本方差：
Sn*2
1 n1
n i 1
(Xi
X )2
nSn2 (n 1)Sn*2
18 September 2020
概率论与数理统计
理学院数学系
第六章数理统计的基本概念
第22页
（3）样本k阶原点矩：
第13页
1、样本的联合分布函数设总体 X 的分布函数为 FX (., ), (X1, X2 ,
则样本的联合分布函数为
, Xn ) 为样本.
FX1,X2 , ,Xn ( x1, x2 , , xn ; ) FX ( x1, )FX ( x2 , ) FX ( xn , )

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

不会。在卖出的服装中，出现次数最多的是型号为100厘米的服装，所以应该进这一型号的衣服。
归纳
众数的定义
在一个样本中，出现次数最多的数据叫做这个样本的众数。
例：求下列各样本的众数：（）10 9 7 8 9 10 9 8 9 6
75 （2）7 5 5 8 6 6
解：（1）在上述样本中，9出现了4次，是出现次数最多的，所以9是这个样本的众数。
每组人数是否应相同？时间分别是多少？优化：在同一时间内打电话的人越多，用去的时间越少。
假设分成三组。子方案一：每组都是5人。模型：
时间： 7分钟。
子方案二：每组人数不同，如分别是6、5、4 人（还可变化）。模型：
时间： 6分钟。
假设分成五组：子方案一：每组都是3人。模型：
时间： 7分钟。
习题答案
1.（1）中位数30，众数31。（2）10人 2.（1）甲：平均数9.6，众数9.5。乙：平均数
86.2，众数10。（2）甲去更好，甲的平均成绩高。 3.（1）中位数98，众数110。（2）4天
1.（1）男生平均身高高于女生。 2.（1）一年温度是先由低到高，再变为由高到低。（2）甲。 3.（1）14岁（2）体重和身高都是逐年增加。
中国代表团历届奥运会金牌获奖情况统计图
美国代表团历届奥运会金牌获奖情况统计表
将美国代表团历届奥运会金牌获奖情况绘制成条形统计图。
美国代表团历届奥运会金牌获奖情况统计图
怎样才能更方便比较两国金牌数的变化？
23~28届奥运会中国和美国获金牌情况统计图
下面是我国6~12岁小学男、女生平均身高的统计图。
中国代表团历届奥运会金牌获奖情况统计图
1.画轴 2.定高 3.成形
直观生动地反映每个项目的具体数目
1.画轴 2.描点 3.连线
清楚地反映各数据变化的走向
打电话
活动目标：设计合理的方案，使整个时间最短。方案一：教师挨个通知15名学生（单层结构）：相当于分成15组。时间：15分钟。方案二：教师通知组长，再由组长通知组员（分层）。问题：分多少组比较合适？
子方案二：每组人数不同，如分别是5、4、 3、2、1人。
模型：
时间： 5分钟。
方案三：每个队员接到通知后马上通知别人（多层结构）。模型：
时间： 4分钟。
课堂小结
1.众数：在一个样本中，出现次数最多的数据叫做这个样本的众数。 2.复式折线统计图：复式折线图在分析数据时更直接清晰。
课堂练习
1.某商店上周销售各种尺码男式皮鞋的情况如下表。
在这组数据中，哪种尺码是众数？为什么？这个众数对商家进货有帮助吗？说说你的想法。
2. 2008年奥运会前对参加射击的两名运动员选拔成绩如下：
甲：9.5、10、 9.3 、 9.5 、 9.6 、 9.5 、9.2 、 9.5、9.42
乙：10、9、8.3、9.8、9.5、10、9.8、8.7、9.9
众数的意义及特点
小明的妈妈开了一家服装店。在一段时间内销售了200件某种品牌的服装，其中各种型号服装的销售量如下表：
小明算出平均数为95 （厘米），建议他妈妈下次进货时型号为95 （厘米）的多进些。
1、你知道小明求平均数的方法吗？
（80+90+95+100+105）÷5=95
2、你认为他妈妈会采纳他的建议吗？
从图中你知道了哪些信息？与大家交流。
归纳
折线统计图是用一个单位长度表示一定的数量，根据数量的多少描出各点，然后把各点用线段顺次连接起来，折线统计图不但可以表示数量的多少，而且能够清楚地表示出数量增减变化的情况。
复式折线图在分析数据时更直接清晰。
条形统计图和折线统计图的比较
中国代表团历届奥运会金牌获奖情况统计图
（1）甲乙成绩的平均数、众数分别是多少？甲：平均数：9.50 众数：9.5 乙：平均数：9.44 众数：10和9.8
（2）你认为谁去参加比赛更合适？为什么？甲去更合适。
中国体育代表团在第25~28届奥运会上获得奖牌数如下。
根据表格中的数据绘制拆线统计图。
中国体育代表团在第25~28届奥运会上获得奖牌数
（2）在上述样本中，5和6都出现了2次，是出现次数最多的，所以5和6是这个样本的众数。
归纳
1.众数能反映一组数据的集中情况。 2.众数是样本中出现次数最多的数据，是样本中的原数据，而不是相应的次数。 3.样本中的众数有时不止一个。
复式折线统计图
中国代表团历届奥运会金牌获奖情况统计表
将中国代表团历届奥运会金牌获奖情况绘制成条形统计图。
导入新课
你喜欢哪个季节呢？
我喜欢数学我喜欢语文
我喜欢英语
你喜欢哪一学科呢？你们班喜欢哪一学科
的人最多呢？
教学目标
1. 理解众数的含义，学会求一组数据的众数，理解众数在统计学上的意义。
2. 根据数据的具体情况，选择适当的统计量表示数据的不同特征。
3. 认识复式折线统计图，了解其特点，能根据需要，选择条形、折线统计图直观、有效地表示数据，并能对数据进行简单的分析和预测。
4.（1）A种产品总销量高（2）折线图，因为折线图便于比较。（3）A种产品1、2、3月份热销。
5.（1）条形统计图。（2）折线统计图。