从Hlog ∞到混合范数空间的Volterra复合算子
一类卷积型Volterra积分方程解的存在性和吸引性

一类卷积型Volterra积分方程解的存在性和吸引性张艳艳;简伟刚【摘要】根据非紧性测度和吸引性的定义,利用经典的Shauder不动点原理,对如下一类带有卷积型的Volterra积分方程:u(t)=p(t)+g(t,u(t))∫t0 a(t-s)f(t,s,u(s))ds,t∈R+(1)进行了研究,其中a∈L1loc(R+)是标量核,函数p,g和f满足定理2.1中的某些条件,得出了方程式(1)存在具有一致局部吸引性的解.【期刊名称】《江西科学》【年(卷),期】2017(035)006【总页数】4页(P848-851)【关键词】Volterra积分方程;非紧性测度;Shauder不动点原理;一致局部吸引性【作者】张艳艳;简伟刚【作者单位】江西师范大学数学与信息科学学院,330022,南昌;豫章师范学院自然科学系,330103,南昌【正文语种】中文u(t)=p(t)+g(t,u(t))a(t-s)f(t,s,u(s))ds,t∈R+进行了研究,其中是标量核,函数p,g和f满足定理2.1中的某些条件,得出了方程式(1)存在具有一致局部吸引性的解。
早在1985年,Deimling在文献[1]中研究了二次积分方程形如:x(t)=f(t,x(t))u(t,s,x(s))ds,t∈[0,1]的解的存在性和渐近稳定性。
2003年,Banas在文献[2]中将方程(2)中的t∈[0.1]的推广到了t≥0。
x(t)=f(t,x(t))u(t,s,x(s))ds,t≥0并研究了其解的存在性和渐近稳定性。
同年,Banas和Rzepka在文献[3]中给出了一致局部吸引性和渐近稳定性的概念一致。
在2008年,Banas和O′Regan在文献[4]中研究了包含式(3)在内的二次Volterra积分方程:x(t)=p(t)+ds,t≥0的解的存在性和吸引性。
在式(4)的基础上,本文将主要研究a(t)=·且0<α<1的情况。
【国家自然科学基金】_volterra级数_基金支持热词逐年推荐_【万方软件创新助手】_20140730
53 54 55 56 57 58 59 60
volterra自适应滤波器 volterra series svm) qpso) gfrf flash模数转换器 cfd/csd cascode放大器
1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 volterra级数 气动弹性 故障诊断 volterra核 非线性系统 非线性 非定常气动力 零阶保持 隐markov模型(hmm) 降阶模型 陀螺漂移预测 递推最小二乘算法 转子裂纹 超定方程 自适应预测 自适应辨识 自适应 系统辨识 短期交通流预测 相空间重构 混沌理论 混沌 气动力降阶模型 正交频分复用 模式识别 李雅诺夫指数 提升小波 小波 子空间 大坝位移 分阶 光载无线电链路 作物蒸发蒸腾量 交通工程 α 稳定分布 volterra级数滤波器 volterra滤波器 haar尺度函数 ap算法
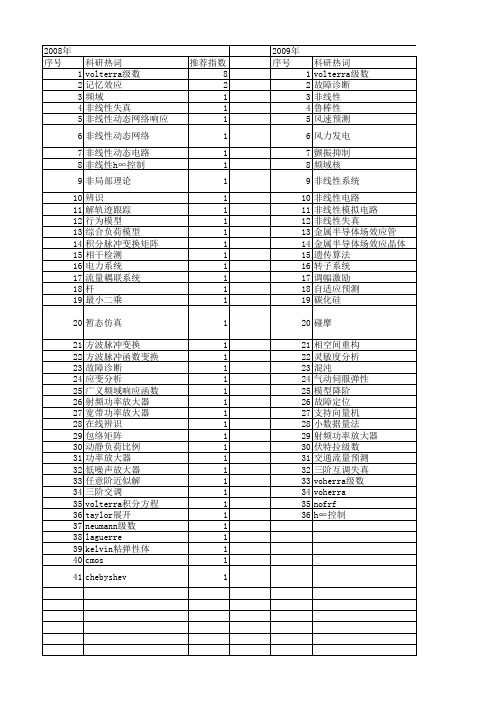
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
科研热词 volterra级数 记忆效应 频域 非线性失真 非线性动态网络响应 非线性动态网络 非线性动态电路 非线性h∞控制 非局部理论 辨识 解轨迹跟踪 行为模型 综合负荷模型 积分脉冲变换矩阵 相干检测 电力系统 流量耦联系统 杆 最小二乘 暂态仿真 方波脉冲变换 方波脉冲函数变换 故障诊断 应变分析 广义频域响应函数 射频功率放大器 宽带功率放大器 在线辨识 包络矩阵 动静负荷比例 功率放大器 低噪声放大器 任意阶近似解 三阶交调 volterra积分方程 taylor展开 neumann级数 laguerre kelvin粘弹性体 cmos chebyshev
单位球上不同privalov空间之间的复合算子

复合算子在很多应用中都有着重要的作用。
在球上不同Privalov空间之间的复合算子就起着这样的作用。
这里,Privalov空间指的是一种特殊的运动学模型,它由一个最大的半圆和三个小的半圆(称为半圆数)组成。
这三个小的半圆与最大的半圆的调和函数有关,其中,最大的半圆的调和函数取决于半径的大小。
复合算子的作用是将这三个小的半圆数与最大的半圆数融合成一个整体。
它可以将每一个点在调和函数上联系起来,并将其映射到最大的半圆上。
这样可以使球上不同Privalov空间之间的运动更加有利。
此外,复合算子还可以用来计算球上不同空间之间的半径差。
这是因为在求解这些问题的过程中都要进行拉格朗日变换,这个变换十分有效。
另外,复合算子还可以用来测定抛物线和匀旋曲线(hyperbola)上不同半径处的角度。
复合算子还可以用来构建全球定义的曲线。
这是因为它可以将每一个点在调和函数上映射到一个连续的曲线上。
这些曲线可以用来分析不同表面上的层状结构,例如椭圆和环形。
总之,复合算子在球上不同Privalov空间之间发挥着重要作用。
它可以将每一个点在调和函数上映射到最大的半圆上,这样可以使球上不同Privalov空间之间的运动更加有利。
此外,它还可以用来测量不同半径处的角度,以及用来构造全局定义的曲线。
基于线性空间投影的计算Volterra级数高阶核的方法

响应 , 频域核是广义频 率响应 ) 。基 于 V hr o e a级数 的 以上优 r
点, 一百多年以来 , 很多人选用具有成熟 数学理论基础 的 V l o— t r 级数来进行非线性时不变动态系统的辨 识。但用 V lr ea r oe a t
第 2 第 1 期 5卷 1
20 0 8年 1 1月
计 算 机 应 用 研 究
Ap l a in Re e r h o mp t  ̄ p i t s a c fCo u e c o
Vo . 5 No 1 12 . 1 NO . 2 0 V 08
基于线性空间投影的计算 V l r .t r o e a级数高 阶核 的方法
Ab ta t s r c :T i p p r rp s d a n v lmeh d t d n i otra k r eso o l e r y a c y tms h e n w n t n h s a e o o e o e t o oi e t y V l r e n l f ni a l d n mia s se .T e o i s p f e n n y l o d v lp d a lme tt n o c u aea d e c e t o p r merca g r h rt ei e t ia in o h r e e f r es e eo e n i e n ai f c rt n f in n aa t lo i msf ni c t f mp o a i n i t o h d f o Vo er s r so d r a i o u o a btay d g e s C mp tt n ls lt n s o st e v l i n f ce c f h lo t m. p t r i r e r e . o u ai a i a i h w h ai t a d e in y o e ag r h r o mu o dy i t i Ke r s:n n i e rs se y wo d o l a yt m;Vot ra sre ;l e rs a e;k r e ;fn t n l n l r e s i a p c e i n e l u ci a n o
Banach空间及其相关定理

课程论文课程现代分析基础学生姓名学号院系专业指导教师二O一五年十二月四日目录1 绪论 (1)2 Banach空间基本概念 (1)2.1拟范数定义及例子 (1)2.2 Banach空间 (2)2.3 Banach空间中线性变换及其性质 (3)3 一致有界定理及其推论 (4)3.1问题 (4)3.2基本概念 (4)3.3一致有界定理及其推论 (5)3.4一致有界性定理及其推论的应用 (6)4 Hahn-Banach定理与凸集分离定理 (7)4.1实线性空间上的Hahn-Banach定理 (7)4.2复线性空间上的Hahn-Banach定理 (8)4.3赋范线性空间上的Hahn-Banach定理 (8)4.4有关Hahn-Banach定理的一些推论 (9)4.5 Hahn-Banach定理的几何形式:凸集分离定理 (9)5 Banach空间中开映射、闭图像定理以及逆算子定理 (9)5.1开映射定理 (10)5.2逆算子定理 (11)5.3闭图像定理 (12)6 总结 (14)参考文献 (16)Banach空间及其相关定理南京理工大学自动化学院,江苏南京摘要:本文的主要是介绍了Banach空间以及其相关定理。
首先,本文讲了Banach空间产生的背景以及应用领域。
然后本文介绍了Banach空间的基本概念及其相关性质。
最后本文开始从一致有界定理开始,将Banach空间中Hahn-Banach定理、开映射、闭图像以及逆算子定理这几个重要定理逐一做出介绍并给出相应定理的证明。
关键词:Banach空间;一致有界定理;Hahn-Banach定理;开映射、闭图像、逆算子定理1 绪论巴拿赫空间(Banach space)是一种赋有“长度”的线性空间,泛函分析研究的基本对象之一。
数学分析各个分支的发展为巴拿赫空间理论的诞生提供了许多丰富而生动的素材。
从魏尔斯特拉斯,K.(T.W.)以来,人们久已十分关心闭区间[a,b]上的连续函数以及它们的一致收敛性。
代数中常用英语词汇

(0,2) 插值||(0,2) interpolation0#||zero-sharp; 读作零井或零开。
0+||zero-dagger; 读作零正。
1-因子||1-factor3-流形||3-manifold; 又称“三维流形”。
AIC准则||AIC criterion, Akaike information criterionAp 权||Ap-weightA稳定性||A-stability, absolute stabilityA最优设计||A-optimal designBCH 码||BCH code, Bose-Chaudhuri-Hocquenghem codeBIC准则||BIC criterion, Bayesian modification of the AICBMOA函数||analytic function of bounded mean oscillation; 全称“有界平均振动解析函数”。
BMO鞅||BMO martingaleBSD猜想||Birch and Swinnerton-Dyer conjecture; 全称“伯奇与斯温纳顿-戴尔猜想”。
B样条||B-splineC*代数||C*-algebra; 读作“C星代数”。
C0 类函数||function of class C0; 又称“连续函数类”。
CA T准则||CAT criterion, criterion for autoregressiveCM域||CM fieldCN 群||CN-groupCW 复形的同调||homology of CW complexCW复形||CW complexCW复形的同伦群||homotopy group of CW complexesCW剖分||CW decompositionCn 类函数||function of class Cn; 又称“n次连续可微函数类”。
Cp统计量||Cp-statisticC。
谱图傅里叶变换与谱图小波变换基分析研究

收稿日期:2020-02-17 修回日期:2020-06-22基金项目:海南省自然科学基金资助项目(619MS076)作者简介:李社蕾(1979-),女,副教授,研究方向为智能算法、人工智能。
谱图傅里叶变换与谱图小波变换基分析研究李社蕾1,2,杨博雄1,2,陆娇娇1,2(1.三亚学院信息与智能工程学院,海南三亚572022;2.三亚学院陈国良院士工作站,海南三亚572022)摘 要:卷积神经网络在欧氏数据上取得巨大成功之后,开始在图结构、几何流行等非欧数据上泛化。
当前图卷积神经已成为研究热点。
在数字图像去噪、压缩、增强、融合以及加密方面傅里叶变换与小波变换是不可或缺的处理手段,在图卷积神经中有卷积定理将傅里叶变换用于实现图上的卷积运算,谱图小波变换也只是实现了卷积的快速算法,都是围绕如何在图结构上做卷积而展开的研究,没有真正发挥其作用,大大限制了图卷积神经网络性能的发挥。
该文对谱图傅里叶变换与谱图小波变换基进行分析研究,同时研究基与图结构之间的关系。
实验表明通过谱图傅里叶变换和谱图小波变换可以获取图结构的特征信息,为谱图小波变换和谱图傅里叶变换更深入地与图卷积神经网络结合提供了参考。
关键词:谱图;小波变换;图卷积神经网络;傅里叶变换;卷积定理;本征函数;拉普拉斯算子中图分类号:TN911.30-39 文献标识码:A 文章编号:1673-629X(2021)05-0085-05doi:10.3969/j.issn.1673-629X.2021.05.015AnalysisandStudyofSpectralFourierTransformandSpectralWaveletTransformBasisLIShe-lei1,2,YANGBo-xiong1,2,LUJiao-jiao1,2(1.SchoolofInformation&IntelligenceEngineering,UniversityofSanya,Sanya572022,China;2.ChenGuoliangAcademicianWorkstation,UniversityofSanya,Hainan572022,China)Abstract:AfterachievinggreatsuccessinEuclideandata,convolutionalneuralnetworkbegantogeneralizeonnon-Euclideandatasuchasgraphstructureandgeometricpopularity.Atpresent,thegraphconvolutionalnervehasbecomearesearchhotspot.Inthedigitalimagedenoising,compression,enhancement,fusionandencrypted,Fouriertransformandwavelettransformareindispensablemeansofprocessing.ThereisaconvolutiontheoreminthegraphconvolutionalnervetorealizetheconvolutionoperationonthegraphbyspectralFouriertransformandfastconvolutionalgorithmbyspectralwavelettransform.Thestudyisoverhowtoconvolutionsonthegraphstructure,whichdoesnotreallyplayitsroleandgreatlylimitstheperformanceofthegraphconvolutionalneuralnetwork.Therefore,weanalyzeandstudytheFouriertransformandwavelettransformbasisofspectrogramandalsotherelationshipbetweenthebasisandgraphstructure.TheexperimentshowsthatthecharacteristicinformationofthegraphstructurecanbeobtainedbytheFouriertransformandwavelettransformofthespectrum,whichprovidesareferenceforthedeepercombinationofthewavelettransformandFouriertransformofthespectrumwiththeconvolutionalneuralnetworkofthegraph.Keywords:spectral;wavelettransform;graphconvolutionalneuralnetwork;Fouriertransform;convolutiontheorem;eigenfunction;Laplaceoperator0 引 言在现实世界中,大量数据是以图或者网络的形式存在的,比如社交网络、知识图谱、蛋白质相互作用网、世界贸易网等等。
从B αlog空间到Qk空间的复合算子

文献 [ ]引人 了 D上 加权 Boh空 间和小 加权 1 lc
Boh空 间 , le 其定 义 为 : = { ∈ /( :I J B f / - o) I l flo
( I l)o - lg z { ∈ ( . / D)
.
Q s』/ I(z)L ) ∞ u『 ) g ,)( < , = gl (a c ) 4
的一种Байду номын сангаас新的刻画.
空间到 空间的复合算子 , 利用 K—C r sn al o 测度刻画了 曰 e : 空间到 Q 空 间的
复合算子 , 得到 了该算子 为有界 和紧的充要条件 ; 此结果是 Boh型空 间到 空间上复合算子 为有 界和 紧 lc
关键词 : 复合算子 ; 加权 Boh空间 ;Q lc 空间 ; K—C r sn测度 al o e
联系作者简介 : 伍鹏程 ( 95 ) 男 , 15 一 , 教授 , 主要从事 函数论 的研究
第 6期
龙 见仁 , : S 等 从 , 空间到 Q 2 空间的复合算 子
项式 在 嚣 中稠密.
义以q为符号的复合算子 为:j = 。 , b c f 其中/
∈H( . D) 常通过 描述 的 函数性 质 来 刻 画 复合 算
子 的有 界性 和 紧性.
定 义
设 K:0,。 一 [ , ) 右 连续 的 [ 。) 0∞ 是
非减 函数 , 果f ∈H( 如 D)满足
设 l =l 0 l I 则 在该 范数 意 义下 l 州 ) +l 川
为 B n c 间. a a h空 另外定 义
. l D. ^ ) g ,) ( = } 0 厂 = ∈ ) I I (a a z 0 . ) 4 ) 1 f f
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定 义如 下 :
1
,
z=f )
-
' 1 3
()m () , 红 ) g拓 。 ∈
研究了从对数型空间的% 到混合范数空间上 V hr 复合算子 , oe a r 的有界性及 紧性。
关 键 词 : oer 合 算 子 ; 数 型 空 间 ; 合 范 数 空 间 Vhr a复 对 混 中图 分 类 号 :0 7 . 6 14 5 文 献标 识 码 : A 文章 编 号 :0 6— 4 X(00)5— 0 5~ 3 10 6 2 2 1 0 00 0
并 且 研 究 了该 算 子 从 广 义 加 权 B rm n空 间 到 eg a
I l f l 1
( () d < , ) f r ∞ ( 0 ) 2
Boh l 型空间的有界性及 紧性 。文 [2 1 ] c 1 ,3 研究 了 V hr oer a复合 算 子 , Boh空 间 以及 对 数 Boh 在 l c l c
算 子 首 次 出现在 文 [ ] 被 称为 广义 Csr 算 2, eao 子 ( Re an—Si js 子 ) 或 im n the 算 e 。文 [ 4~l] 究 了 O研 算子 在某 些 函数空 间上 的性质 。
[ , ) s以及 t0<s<t 满 足 ( 见 [ , ] : 01 , , , 参 1 2 )
∞,
义 了如下 的 V l r o er t a复合算 子 :
,
则称 在 [ ,) 0 1 上是正规 的。 设 0< , 。 ∈ ( , 在 [ ,) 是 正规 p q<。 B) 01 上
的。 如果
z= ( ) ( - E, ) ) [ td ( ) gz B 4 ), - t  ̄
从 g 混 合 范 数 空 间的 V h r 复 合 算 子 到 oe a r
古 定 桂
( 嘉应学 院 数学 学院 , 广东 梅 州 5 4 1 ) 10 5
摘 要 : B表示 cI 用 .中的复单位球 , 表示 的边界 , B) . s 日( 表示 B上的一 纯函数全体 。设/ g∈H( , , B) 妒是 上的全纯 自映射 , oer Vlr t a复合算子
的 主要 结论 。
基金项 目 : 广东省 自然科学基金 资助项 目(7 0 70 。 00 6 0 ) 作者简 介 : 古定桂 (9 3一) 男 , 16 , 广东梅州人 , 教授 , 副 主要 研
究方 向 : 函数 论 。
定理 1 设 g∈H( , B上 的全纯 自映射 , B)p是
的算 子 , 称 不 复合 算 子 。 由[ ] C 3 可知 单 位 圆盘 上 H ry空 间 与 B r n 空 间 上 的 复 合 算 子 是 有 ad eg ma
界 的。
设厂 ( , ∈ B) 如果
I l‰: _ I z t <∞ l = fl f ) ( 。
一
() 1
-- .得 1
( ( g)1 i J ( lg i [ 嗜 i 1 ( ) o
r ( 一 ) d <∞ ; ) 1 r r
) (∥ d) )
() 5
a O
(I( Io_ J g )( ( g= 1南
g∈H( 是 在8) 递 的 且 每 0 复合设 f, 义B),Do算B上 的全纯,自映射]。结 合 [ 上 减, ,是 并 1 , 算 子与广 Ce‘r 子 的定 义 文 [1 首 次定 s h 1
在 [ ,) 61 上是 递 增 的 , 且 l 并 i m
l上 一 r J 一 I l — rJ
第2 8卷
第 5期
嘉应学 院学报 ( 自然 科 学 ) J U N LO I Y N N V R IY( a rl c ne O R A FJ I G U IE ST N t a Si c ) A u e
V0 . No. 128 5
21 0 0年 5月
Ma 0 0 y2 1
0< , <∞, 在 [ , ) pq ( b 0 1 上是正规的。则下列断言 等价 :
6
嘉 应 学 院学 报 (自然 科 学 )
21 00年 5月
() , 吒 ( ,,) i : pg咖 是有界算子;
(i .: i ) ( g 咖) 紧算子 ; p,, 是
g
设 g, fEH( , 义算 子 如 下 : B) 定
1 J‘
则称 厂属 于对 数型 空 间 嚣, 记厂∈日盂。易 知在 范数
z=f )
) () g 半,z B () ∈, 3
f.f 下 , 是一个 Bnc 空间。 I I % % aah
设 是 [ 1 上 的 正 连 续 函 数 。若 存 在 8∈ 0, ]
空 间上 的性质 。
则 称 厂属 于 混 合 范 数 空 间 日( g 咖)( , P, , B) 记
本文主要给出 Vhr oea复合算子 . % 一 r :
H( , , 的有界 性及 紧性刻 画 , 面 的定 理是 本文 p q ) 下
收 稿 日期 :00— 3—1 21 0 2
0 引 言
记 B为 C 中 的 复 单 位 球 , . s为 B 的 边 界 , 日( 为 B上 全 体 解 析 函数 所 构 成 的空 间 。设 f∈ )
厂∈H( , , p q )= ( , , ( , 中 P q 咖) B) 其
, r 、
( ,f l o  ̄ } ( -
设 是 到 B 的全 纯 自映 射 , 所 有 的 厂∈ 对
() ) 芝 譬( 表 厂 径 导 , 用 : 弓 示 的 向 数。 )
| U
Ⅳ( , 等式 c 厂 j=。 定义了一个从 H( ) H B) B到 (
