2017年广州市海珠区中考一模数学试卷(含答案)
2017年广州市中考数学试卷(含答案)
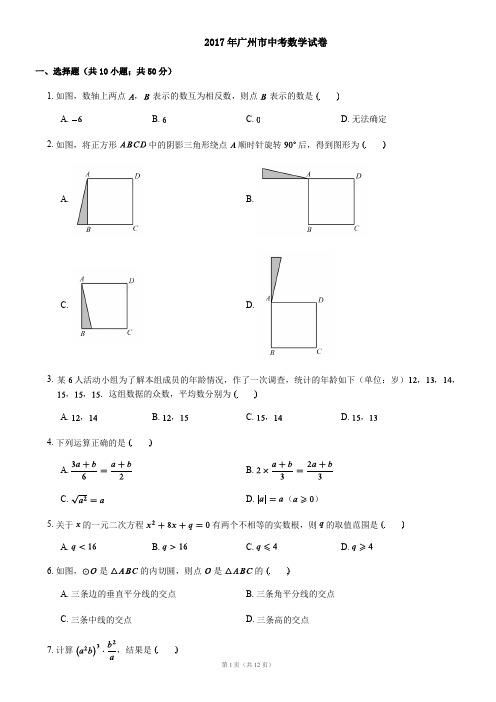
2017年广州市中考数学试卷一、选择题(共10小题;共50分)1.如图,数轴上两点,表示的数互为相反数,则点表示的数是B. C. D. 无法确定2.如图,将正方形中的阴影三角形绕点顺时针旋转后,得到图形为A. B.C. D.3. 某人活动小组为了解本组成员的年龄情况,作了一次调查,统计的年龄如下(单位:岁),,,,,.这组数据的众数,平均数分别为A. ,B. ,C. ,D. ,4. 下列运算正确的是A. B.C.()5.关于的一元二次方程有两个不相等的实数根,则的取值范围是A. B. C. D.6. 如图,是的内切圆,则点是的A. 三条边的垂直平分线的交点B. 三条角平分线的交点C. 三条中线的交点D. 三条高的交点7. 计算,结果是A. B. C. D.8. 如图,,分别是平行四边形的边,上的点,,,将四边形沿翻折,得到,交于点,则的周长为A. B. C. D.9. 如图,在中,是直径,是弦,,垂足为,连接,,,则下列说法中正确的是A. B.C. D.10.,函数与在同一直角坐标系中的大致图象可能是A. B.C. D.二、填空题(共6小题;共30分)11. 如图,四边形中,,,则.12. 分解因式:.13. 当时,二次函数有最小值.14. 如图,中,,,.15. 如图,圆锥的侧面展开图是一个圆心角为的扇形,若圆锥的底面圆半径是,则圆锥的母线.16. 如图,平面直角坐标系中是原点,平行四边形的顶点,的坐标分别是,,点,把线段三等分,延长,分别交,于点,,连接,则下列结论:①是的中点;②与相似;③四边形的面积是;其中正确的结论是.(填写所有正确结论的序号)三、解答题(共9小题;共117分)17. 解方程组:18. 如图,点,在上,,,.求证:.19. 某班为了解学生一学期做义工的时间情况,对全班名学生进行调查,按做义工的时间(单位:小时),将学生分成五类:A类,B类,C类,D类,E类.绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:(1)E 类学生有人,补全条形统计图;(2)D 类学生人数占被调查总人数的;(3)从该班做义工时间在的学生中任选人,求这人做义工时间都在中的概率.20. 如图,在中,,,.(1)利用尺规作线段的垂直平分线,垂足为,交于点:(保留作图痕迹,不写作法);(2)若的周长为,先化简,再求的值.21. 甲、乙两个工程队均参与某筑路工程,先由甲队筑路公里,再由乙队完成剩下的筑路工程,已知乙队倍,甲队比乙队多筑路天.(1)求乙队筑路的总公里数;(2)若甲、乙两队平均每天筑路公里数之比为,求乙队平均每天筑路多少公里.22. 将直线向下平移个单位长度,得到直线,若反比例函数的图象与直线相交于点,且点的纵坐标是.(1)求和的值;(2)结合图象求不等式的解集.23.已知抛物线,直线,的对称轴与交于点,点与的顶点的距离是.(1)求的解析式;(2)若随着的增大而增大,且与都经过轴上的同一点,求的解析式.24. 如图,矩形的对角线,相交于点,关于的对称图形为.(1)求证:四边形是菱形;(2)连接,若,.①求的值;②若点为线段上一动点(不与点重合),连接,一动点从点出发,以的速度沿线段匀速运动到点,再以的速度沿线段匀速运动到点,到达点后停止运动,当点沿上述路线运动到点所需要的时间最短时,求的长和点走完全程所需的时间.25. 如图,是的直径,,,连接.(1)求证:;(2)若直线为的切线,是切点,在直线上取一点,使,所在的直线与所在的直线相交于点,连接.①试探究与之间的数量关系,并证明你的结论;②是否为定值?若是,请求出这个定值;若不是,请说明理由.答案第一部分1. B2. A3. C4. D5. A6. B7. A8. C9. D 10. D第二部分11.12.13. ;14.15.16. ①③第三部分17.得:将代入得方程组的解是18. 因为,所以,,即,在和中,所以,.19. (1) E 类:(人),统计如图所示(2)(3)设人分别为,,,,,画树状图:所以这人做义工时间都在中的概率为.20. (1)如下图所示:(2),,,,,所以.21. (1)乙队筑路的总公里数:(公里).(2)设甲队每天筑路公里,乙队每天筑路公里.根据题意得:解得:经检验是原方程的解且符合题意.乙队每天筑路:答:乙队平均每天筑路公里.22. (1)由向下平移一个单位长度而得,,点纵坐标为且在上,点坐标为,点在反比例函数上,.(2)与的图象如图所示,由图可知当或.23.(1)的对称轴与的交点为,的对称轴为直线顶点坐标为,,,,,或.(2)①当时,与轴交点为,,随的增大而增大,,(ⅰ)当经过点,时,则有得(舍去),(ⅱ)当经过点,时,则有得.②当时,令,则,得,与轴交于点,,(ⅰ)当经过点,时,则有得(ⅱ)当经过点,时,则有得,综上,的解析式为:或.24. (1)因为四边形为矩形,所以,因为与交于点,且与关于对称,所以,,,所以,所以四边形是菱形.(2)①连接,使直线分别交于点,交于点,因为关于的对称图形为,所以,因为,,所以,,因为四边形是菱形,所以,.又矩形中,.所以为的中位线,所以,因为,,所以,所以,又,所以,,所以因为,所以,所以.②过点作交于点,因为由①可知:,所以点以的速度从到所需时间等同于以的速度从运动到所需时间.即:所以由运动到所需的时间就是的值.因为如图,当运动到,即时,所用时间最短,所以,在中,设,则,,所以,解得:或(舍去),所以所以当点点沿题述路线运动到点所需时间最短时,的长为,点走完全程所需要的时间为.25. (1)如图,连接,是的直径,.,,.(2)①.如图所示,作于,连接,由()可知为等腰直角三角形.又是的中点,,,为等腰直角三角形,,为的切线,,又,四边形为矩形,,.,,.,.,,,..当为钝角时,如图所示,同理,得,易得,.,,,.②如图,当在左侧时,过点作交于点,由()①知,,.又,,.中,,,.当在右侧时,如图,过作于,由()①知,,,.,.,,在中,,.。
2017年广东广州海珠区初三一模数学试卷答案

20
10
21. 某小区为更好的提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示 牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元. (1) 问购买1个温馨提示牌和1个垃圾箱各需多少元?
答案 解析
2018/12/04 购买1个温馨提示牌需要60元,购买1个垃圾箱需要100元.
17. 解答下列问题:
(1) 解不等式组{
x−1 < 0
.
8 + 3(x − 1) ⩾ −4
答 案 . −3 ⩽ x < 1
解析
① x − 1 < 0
{
② 8 + 3(x − 1) ⩾ −4
解不等式①得:x < 1
解不等式②得:x ⩾ −3
此不等式组的解集为:−3 ⩽ x < 1 .
(2) 解方程 2 = 1 .
答案
7.
10
解 析 树状图如下:
学生版
教师版
答案版
编辑
目录
选择题(本大题共10小题,每小题3分,… 填空题(本大题共6小题,每小题3分,… 解答题(本大题共9小题,共102分)
由树状图可以,抽取2名学生,共有20种等可能的结果,其中至少有1名女生的结果有14种P (2名学生
中至少有1名女生)= 14 = 7 .
C、不是中心对称图形,本选项错误;
D、是中心对称图形,本选项正确.
故选D.
3.
如图,点A、B、C 在⊙D上,∠ABC
=
,则 ∘
70
∠ADC
的度数为(
).
A. ∘ 100
B. ∘ 140
C.
∘ 35
(word完整版)2017年广州市中考数学试卷(含答案),推荐文档
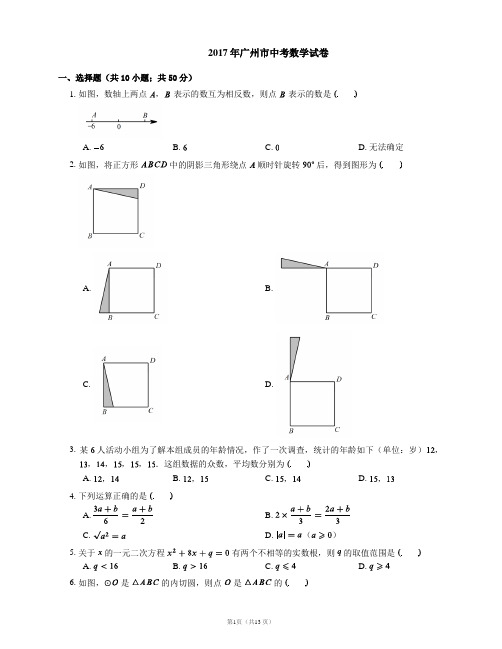
2017年广州市中考数学试卷一、选择题(共10小题;共50分)1.如图,数轴上两点,表示的数互为相反数,则点表示的数是B. C. D. 无法确定2.如图,将正方形中的阴影三角形绕点顺时针旋转后,得到图形为A. B.C. D.3. 某人活动小组为了解本组成员的年龄情况,作了一次调查,统计的年龄如下(单位:岁),,,,,.这组数据的众数,平均数分别为A. ,B. ,C. ,D. ,4. 下列运算正确的是A. B.C. ()5.关于的一元二次方程有两个不相等的实数根,则的取值范围是A. B. C. D.6.如图,是的内切圆,则点是的A. 三条边的垂直平分线的交点B. 三条角平分线的交点C. 三条中线的交点D. 三条高的交点7.计算,结果是A. B. C. D.8. 如图,,分别是平行四边形的边,上的点,,,将四边形沿翻折,得到,交于点,则的周长为A. B. C. D.9. 如图,在中,是直径,是弦,,垂足为,连接,,,则下列说法中正确的是A. B.C. D.10.,函数与在同一直角坐标系中的大致图象可能是A. B.C. D.二、填空题(共6小题;共30分)11. 如图,四边形中,,,则.12. 分解因式:.13. 当时,二次函数有最小值.14. 如图,中,,,.15. 如图,圆锥的侧面展开图是一个圆心角为的扇形,若圆锥的底面圆半径是,则圆锥的母线.16. 如图,平面直角坐标系中是原点,平行四边形的顶点,的坐标分别是,,点,把线段三等分,延长,分别交,于点,,连接,则下列结论:①是的中点;②与相似;③四边形的面积是④;其中正确的结论是.(填写所有正确结论的序号)三、解答题(共9小题;共117分)17. 解方程组:18. 如图,点,在上,,,.求证:.19. 某班为了解学生一学期做义工的时间情况,对全班名学生进行调查,按做义工的时间(单位:小时),将学生分成五类:A类,B类,C类,D类,E类.绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:(1)E 类学生有人,补全条形统计图;(2)D(3)从该班做义工时间在的学生中任选人,求这人做义工时间都在中的概率.20. 如图,在中,,,.(1)利用尺规作线段的垂直平分线,垂足为,交于点:(保留作图痕迹,不写作法);(2)若的周长为,先化简,再求的值.21. 甲、乙两个工程队均参与某筑路工程,先由甲队筑路公里,再由乙队完成剩下的筑路工程,已知乙队筑路总公里数是甲队筑路总公里数的倍,甲队比乙队多筑路天.(1)求乙队筑路的总公里数;(2)若甲、乙两队平均每天筑路公里数之比为,求乙队平均每天筑路多少公里.22. 将直线向下平移个单位长度,得到直线,若反比例函数的图象与直线相交于点,且点的纵坐标是.(1)求和的值;(2)结合图象求不等式的解集.23. 已知抛物线,直线,的对称轴与交于点,点与的顶点的距离是.(1)求的解析式;(2)若随着的增大而增大,且与都经过轴上的同一点,求的解析式.24. 如图,矩形的对角线,相交于点,关于的对称图形为.(1)求证:四边形是菱形;(2)连接,若.①求的值;②若点为线段上一动点(不与点重合),连接,一动点从点出发,以的速度沿线段匀速运动到点,再以的速度沿线段匀速运动到点,到达点后停止运动,当点沿上述路线运动到点所需要的时间最短时,求的长和点走完全程所需的时间.25. 如图,是的直径,,,连接.(1)求证:;(2)若直线为的切线,是切点,在直线上取一点,使,所在的直线与所在的直线相交于点,连接.①试探究与之间的数量关系,并证明你的结论;②是否为定值?若是,请求出这个定值;若不是,请说明理由.答案第一部分1. B2. A3. C4. D5. A6. B7. A8. C9. D 10. D第二部分11.12.13. ;14.15.16. ①③第三部分17.得:将代入得方程组的解是18. 因为,所以,,即,在和中,所以,.19. (1) E 类:(人),统计如图所示(2)(3)设人分别为,,,,,画树状图:所以这人做义工时间都在中的概率为.20. (1)如下图所示:(2),,,,,所以.21. (1)乙队筑路的总公里数:(公里).(2)设甲队每天筑路公里,乙队每天筑路公里.根据题意得:解得:经检验是原方程的解且符合题意.乙队每天筑路:(公里),答:乙队平均每天筑路公里.22. (1)由向下平移一个单位长度而得,,点纵坐标为且在上,点坐标为,点在反比例函数上,.(2)与的图象如图所示,由图可知当或.23. (1)的对称轴与的交点为,的对称轴为直线顶点坐标为,,,,,或.(2)①当时,与轴交点为,,随的增大而增大,,(ⅰ)当经过点,时,则有得(舍去),(ⅱ)当经过点,时,则有得.②当时,令,则,得,与轴交于点,,(ⅰ)当经过点,时,则有得(舍去),(ⅱ)当经过点,时,则有得,综上,的解析式为:或.24. (1)因为四边形为矩形,所以,因为与交于点,且与关于对称,所以,,,所以,所以四边形是菱形.(2)①连接,使直线分别交于点,交于点,因为关于的对称图形为,所以,因为,,所以,,因为四边形是菱形,所以,.又矩形中,.所以为的中位线,所以,因为,,所以,所以,又,所以,,所以因为,所以,所以②过点作交于点,因为由①可知:,所以点以的速度从到所需时间等同于以的速度从运动到所需时间.即:所以由运动到所需的时间就是的值.因为如图,当运动到,即时,所用时间最短,所以,在中,设,则,,所以,解得:或所以所以当点点沿题述路线运动到点所需时间最短时,的长为,点走完全程所需要的时间为.25. (1)如图,连接,是的直径,.,,.(2)①.如图所示,作于,连接,由()可知为等腰直角三角形.又是的中点,,,为等腰直角三角形,,为的切线,,又,四边形为矩形,,.,,.,.,,,..当为钝角时,如图所示,同理,得,易得,.,,,.②如图,当在左侧时,过点作交于点,由()①知,,.又,,.中,,,.当在右侧时,如图,过作于,由()①知,,,.,.,,在中,,.。
2017年广州市海珠区中考一模数学试卷(含答案)

广州市海珠区2017年中考一模数学试卷第一部分选择题〔共30分〕一、选择题〔此题共10 个小题,每题 3 分,总分值30 分.下面每题给出的四个选项中,只有一个是正确的.〕1.如果向东走50m 记为50m,那么向西走30m 记为〔〕A.-30mB. |-30| mC.-〔-30〕mD.m2.以下图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是〔〕A.B.C.D.3.如图,点A.B.C 在⊙D 上,∠ABC=70°,则∠ADC 的度数为〔〕A.110°B.140°C.35°D.130°第3题图4.如下图的几何体是由一些小立方块搭成的,则这个几何体的俯视图是A. B. C. D.5.以下计算正确的选项是〔〕A.3x2 ·4x2 =12x2B.=(y)C. D.6.以下命题中,假命题...是〔 〕 A.对角线互相平分的四边形是平行四边形B.两组对角分别相等的四边形是平行四边形C.一组对边平行,另一组对边相等的四边形是平行四边形D.对角线相等的平行四边形是矩形7.以下函数中,y 随 x 的增大而增大的是〔 〕 A. B. x+5 C. D.8.如图,在R t ABC 中,∠B =90°,∠A =30°,DE 垂直平分斜边AC ,交AB 于点D ,点E 是垂足,连接CD . 假设BD =1,则AC 的长是〔 〕A . 2 3B .2C . 4 3D .4 9.已知抛物线y 的图象如下图,顶点为〔4,6〕,则以下说法错误的选项是〔 A . b 2 >4ac B .6C . 假设点〔2,m 〕〔5,n 〕在抛物线上,则m >nD . 8a +b = 0〕10.如图,在平面直角坐标系中,R t OAB 的顶点A 在x 轴的正半轴上,顶点B 的坐标为( 2, 2),点 C 的坐标为〔1,0〕,点P 为斜边OB 上的一动点,则P A +PC 的最小值为〔 〕第 8 题图 第 9 题图 第 10 题图 A . 2 B . 3 C . 2 D . 3 2第二部分非选择题〔共120分〕二、填空题〔此题共6 个小题,每题 3 分,共18 分.〕11.在不透明口袋内有形状.大小.质地完全一样的5 个小球,其中红球3 个,白球2 个,随机抽取一个小球是红球的概率是________.12.分解因式:3x2 -6xy =_________.13.某饮料店为了解本店一种罐装饮料上半年的销售情况,随机调查了6 天该种饮料的日销售情况,结果如下〔单位:罐〕:33,28,32,25,24,30,这 6 天销售量的中位数是________.14.某公司制作毕业纪念册的收费如下:设计费与加工费共1000元,另外每册收取材料费4 元,则总收费y与制作纪念册的册数x的函数关系式为___________.15.如图,AB是⊙O的直径,AC.BC是⊙O的弦,直径DE⊥BC于⌒上,AC=8,BC=6,则EM=_______.点M. 假设点E在优弧AB第15题图16.假设一元二次方程0 有两个相同的实数根,则a2 -b2 +5的最小值为__________.三、解答题〔此题共9 个小题,共102 分,解答要求写出文字说明,证明过程或计算步骤.〕17.〔共9 分〕〔1〕解不等式组〔2〕解方程18. 〔共9 分〕如图,AC是菱形ABCD的对角线,点E.F分别在AB、AD上,且AE=AF.求证:△ACE≌△ACF.19.〔共10 分〕已知A= ( )·〔1〕化简A;〔2〕假设x满足x2 -2x -8 =0,求A的值.20.〔共10 分〕中央电视台举办的“中国诗词大会”节目受到中学生的广泛关注.某中学为了解该校九年级学生对观看“中国诗词大会”节目的喜爱程度,对该校九年级部分学生进行了随机抽样调查,并绘制出如下图的两幅统计图.在条形图中,从左向右依次为:A 级〔非常喜欢〕,B 级〔较喜欢〕,C 级〔一般〕,D 级〔不喜欢〕.请结合两幅统计图,答复以下问题:〔1〕本次抽样调查的样本容量是__________,表示“D级〔不喜欢〕”的扇形的圆心角为__________°;〔2〕假设该校九年级有200 名学生.请你估计该年级观看“中国诗词大会”节目B 级〔较喜欢〕的学生人数;〔3〕假设从本次调查中的A 级〔非常喜欢〕的5 名学生中,选出2 名去参加广州市中学生诗词大会比赛,已知A 级学生中男生有3 名,请用“列表”或“画树状图”的方法求出所选出的2 名学生中至少有1 名女生的概率.21.〔共12 分〕某小区为更好的提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,假设购买3 个温馨提示牌和4 个垃圾箱共需580 元,且每个温馨提示牌比垃圾箱廉价40 元.〔1〕问购买1 个温馨提示牌和 1 个垃圾箱各需多少元?〔2〕如果需要购买温馨提示牌和垃圾箱共100 个,费用不超过8000 元,问最多购买垃圾箱多少个?22.〔共12 分〕如图,在ABC 中,∠C=90°〔1〕利用尺规作∠B 的角平分线交AC于D,以BD为直径作 O交AB于E〔保留作图痕迹,不写作法〕;〔2〕综合应用:在〔1〕的条件下,连接DE ①求证:CD=DE;②假设si nA=,AC=6,求AD.23.〔共12 分〕如图,在平面直角坐标系中,一次函数y1 =ax+b 〔a ≠ 0〕的图象与y轴相交于点A,与反比例函数y2 〔c ≠0〕的图象相交于点B〔3,2〕、C〔-1,n〕.〔1〕求一次函数和反比例函数的解析式;〔2〕根据图象,直接写出y1> y2时x的取值范围;〔3〕在y轴上是否存在点P,使P AB为直角三角形,如果存在,请求点P的坐标,假设不存在,请说明理由.24.〔共14 分〕抛物线y =ax2 +c与x轴交于A、B两点〔A在B的左边〕,与y轴交于点C,抛物线上有一动点P.〔1〕假设A〔-2,0〕,C〔0,-4〕,①求抛物线的解析式;②在①的情况下,假设点P在第四象限运动,点D〔0,-2〕,以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围;〔2〕假设点P在第一象限运动,且 a 0,连接AP、BP分别交y轴于点E、F,则问是否与a、c有关?假设有关,用a、c表示该比值;假设无关,求出该比值.25.〔共14 分〕如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4.〔1〕证明:AD2 = AE·AF ;〔2〕延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB 交DF于点G,连接EG,设∠ACB =α,BG= x, EG =y .①当α=900时,探索EG与BD的大小关系?并说明理由;②当α=1200时,求y与x的关系式,并用x的代数式表示y .。
广州市海珠区中考一模数学试卷含答案

广州市海珠区2017年中考一模数学试卷第一部分选择题(共30分)一、选择题(本题共10 个小题,每小题 3 分,满分30 分.下面每小题给出的四个选项中,只有一个是正确的.)1.如果向东走50m 记为50m,那么向西走30m 记为()A.-30mB. |-30| mC.-(-30)m 1 302.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是()A.B.C.D.3.如图,点在⊙D 上,∠ABC=70°,则∠ADC 的度数为()°°°°第3题图4.如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是A. B. C. D.5.下列计算正确的是()·4x2 =12x2 B.x2y2=xy(y≠0)C.2√x+3√y=5√xy(x≥0,y≥0)D. xy2÷12y=2xy3(y≠0)6.下列命题中,假命题...是( ) A.对角线互相平分的四边形是平行四边形 B.两组对角分别相等的四边形是平行四边形C.一组对边平行,另一组对边相等的四边形是平行四边形D.对角线相等的平行四边形是矩形7.下列函数中,y 随 x 的增大而增大的是( )A. y =− 3xB. y =−x+5C. y =12x D. y =12x 28.如图,在R t ABC 中,∠B =90°,∠A =30°,DE 垂直平分斜边AC ,交AB 于点D ,点E 是垂足,连接CD . 若BD =1,则AC 的长是( )3 C .4 39.已知抛物线y =ax 2+bx +c 的图象如图所示,顶点为(4,6),则下列说法错误的是( A . b 2 >4acB . ax 2+bx +c ≤6C . 若点(2,m )(5,n )在抛物线上,则m >nD . 8a +b = 0)10.如图,在平面直角坐标系中,R t OAB 的顶点A 在x 轴的正半轴上,顶点B 的坐标为( 2, 2),点 C 的坐标为(1,0),点P 为斜边OB 上的一动点,则P A +PC 的最小值为()第 8 题图第 9 题图 第 10 题图A . 2B . 3C . 2D .32第二部分 非选择题(共120分)二、填空题(本题共 6 个小题,每小题 3 分,共 18 分.)11.在不透明口袋内有形状.大小.质地完全一样的 5 个小球,其中红球 3 个,白球 2 个,随机抽取一个小球是红球的概率是________. 12.分解因式:3x 2 -6xy =_________.13.某饮料店为了解本店一种罐装饮料上半年的销售情况,随机调查了 6 天该种饮料的日销售情况,结果如下(单位:罐):33,28,32,25,24,30,这 6 天销售量的中位数是________.14.某公司制作毕业纪念册的收费如下:设计费与加工费共 1000 元,另外每册收取材料费 4 元,则总收费y 与制作纪念册的册数x 的函数关系式为___________.15.如图,AB 是⊙O 的直径,是⊙O 的弦,直径DE ⊥BC 于点M . 若点E 在优弧上,AC =8,BC =6,则EM =_______.第15题图16.若一元二次方程ax 2+bx +1=0 有两个相同的实数根, 则a 2 -b 2 +5的最小值为__________.三、解答题(本题共 9 个小题,共 102 分,解答要求写出文字说明,证明过程或计算步骤.)17.(共 9 分)(1)解不等式组 {x −1<0 8+3(x −1)≥−4(2)解方程 2x−3=1x+118. (共9 分)如图,AC是菱形ABCD的对角线,点分别在AB、AD上,且AE=AF.求证:△ACE≌△ACF.19.(共10 分)已知A= (x+2x2−2x−x−2x2−4x+4)·x2−4x+2(1)化简A;(2)若x满足x2 -2x -8 =0,求A的值.20.(共10 分)中央电视台举办的“中国诗词大会”节目受到中学生的广泛关注.某中学为了解该校九年级学生对观看“中国诗词大会”节目的喜爱程度,对该校九年级部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为:A 级(非常喜欢),B 级(较喜欢),C 级(一般),D 级(不喜欢).请结合两幅统计图,回答下列问题:(1)本次抽样调查的样本容量是__________,表示“D级(不喜欢)”的扇形的圆心角为__________°;(2)若该校九年级有200 名学生.请你估计该年级观看“中国诗词大会”节目B 级(较喜欢)的学生人数;(3)若从本次调查中的 A 级(非常喜欢)的5 名学生中,选出2 名去参加广州市中学生诗词大会比赛,已知 A 级学生中男生有 3 名,请用“列表”或“画树状图”的方法求出所选出的 2 名学生中至少有1 名女生的概率.21.(共12 分)某小区为更好的提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买 3 个温馨提示牌和 4 个垃圾箱共需580 元,且每个温馨提示牌比垃圾箱便宜40 元.(1)问购买1 个温馨提示牌和 1 个垃圾箱各需多少元?(2)如果需要购买温馨提示牌和垃圾箱共100 个,费用不超过8000 元,问最多购买垃圾箱多少个?22.(共12 分)如图,在ABC 中,∠C=90°(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作 O交AB于E(保留作图痕迹,不写作法);(2)综合应用:在(1)的条件下,连接DE ①求证:CD=DE;②若si nA=,AC=6,求AD.23.(共12 分)如图,在平面直角坐标系中,一次函数y1 =ax+b (a ≠ 0)的图象与y轴相交于点A,与反比例函数y2 =kx(c ≠0)的图象相交于点B(3,2)、C(-1,n).(1)求一次函数和反比例函数的解析式;(2)根据图象,直接写出y1> y2时x的取值范围;(3)在y轴上是否存在点P,使P AB为直角三角形,如果存在,请求点P的坐标,若不存在,请说明理由.24.(共 14 分)抛物线y =ax 2 +c 与x 轴交于A 、B 两点(A 在B 的左边),与y 轴交于点C ,抛物线上有一动点P .(1)若A (-2,0),C (0,-4), ①求抛物线的解析式;②在①的情况下,若点P 在第四象限运动,点D (0,-2),以BD 、BP 为邻边作平行四边形BDQP ,求平行四边形BDQP 面积的取值范围;(2)若点P 在第一象限运动,且a <0,连接AP 、BP 分别交y 轴于点E 、F ,则问S △AOE + S △BOF S △ABC是否与a 、c 有关?若有关,用a 、c 表示该比值;若无关,求出该比值.25.(共14 分)如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4.(1)证明:AD2 = AE·AF ;(2)延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB 交DF于点G,连接EG,设∠ACB =α,BG= x, EG =y .①当α=900时,探索EG与BD的大小关系?并说明理由;②当α=1200时,求y与x的关系式,并用x的代数式表示y .。
2017年广州中考数学一模应用题汇编——参考答案

2017一模应用题汇编——参考答案【例题分析】例题1、(白云区一模)(本小题满分12分)解:设轮船的日速为x 千米/日,…………………………………………………1分由题意,得11025249x -×3=1.611025x⨯,…………………………………………7分 解此分式方程,得x =392,……………………………………………………9分 经检验,x =392是原分式方程的解,………………………………………10分 2x -49=735.……………………………………………………………11分 答:列车的速度为735千米/日;轮船的速度为392千米/日.………12分例题2、(从化区一模)(1)解:甲、乙两同学从家到学校的距离之比是 10:7,甲同学的家与学校的距离为 3000 米. ∴乙同学的家与学校的距离: 1073000⨯= 2100 (米);答:乙同学的家与学校的距离为 2100 米. ……………3分(2)设乙骑自行车的速度为 x 米/分钟,则公交车的速度为 2 x 米/分钟。
……………4分依题意得:2230002100=-xx ……………………………………………7分 解得: x = 300 ……………………………………………10分经检验, x = 300 是方程的根 …………………………………………11分 答:乙骑自行车的速度为 300 米/分钟. ………………………………………12分例题3(海珠区一模)解:设购买1个温馨提示牌需要x 元,购买1个垃圾箱需要y 元,依题意得:3458040x y x y +=⎧⎨=-⎩,解得:60100x y =⎧⎨=⎩ 答:购买1个温馨提示牌需要60元,购买1个垃圾箱需要100元。
(2)6分解:设购买垃圾箱m 个,则购买温馨提示牌(100-m )个,依题意得:60(100)100800050m m m -+≤≤答:最多购买垃圾箱50个。
例题4、(天河区一模)解:延长PQ 交AB 的延长线于H ,则PH ⊥AB,由题意得,∠QBH=30°,∠PBH=60°,∴∠BQH=60°,∠PBQ=30°,∴∠BPQ=∠BQH -∠PBQ=30°,即∠BPQ=∠PBQ∴PQ=BQ,即△BPQ 是等腰三角形…………………4分设PQ=BQ=x ,∵∠QBH=30°∴QH=21BQ=21x ,BH=x 23………………6分 ∵∠A=45° ∴21236+=+x x ………………10分 解得:9632≈+=x答:该电线杆PQ 的高度约为9m………………12分【强化训练】1、(二中一模)解:(1)如图所示,过点C 作CE ⊥AB 于点E ,可得∠CBD=45°,∠CAD=60°,设CE=x ,在Rt △CBE 中,BE=CE=x ,在Rt △CAE 中,AE=x ,∵1)AB =海里,∴x+x=60(13+),解得:x=603,则AC=x=120, BC=x=606,答:A 与C 的距离为120海里,B 与C 的距离为606海里;(2)如图所示,过点D 作DF ⊥AC 于点F ,在△ADF 中,∵AD=100,∠CAD=60°,∴DF=ADsin60°=100×23≈86.6>80, 故海监船沿AC 前往C 处盘查,无触礁的危险.2、(南沙区一模)解:(1)设每张门票原定的票价x 元,由题意得: …………………1分 5036004000-=x x ……………………………4分 解得 500=x .经检验,500=x 是原方程的解. …………………………5分答:每张门票原定的票价600元. ……………………………6分(2)设平均每次降价的百分率为y ,由题意得: ……………………………7分500(1-y )2 =405 ……………………………10分解得y 1=0.1,y 2=1.9(不合题意,舍去) .……………………………11分答:平均每次降价10%. ……………………………12分3、(增城区一模)解:设原来每天改造管道 x 米, ......………………1分依题意得 27)%201(360900360=+-+x ……………………………6分解得: x = 30 ……………………………10分经检验: x = 30 是所列方程的解 ……………………………11分答:引进新设备前工程队每天改造管道 30 米. ……………………………12分4、(花都区一模)解:(1)设一根A 型跳绳的售价是x 元,一根B 型跳绳的售价是y 元,则: ……………………………1分………………………4分 解得: ………………………5分 答:一根A 型跳绳的售价是10元,一根B 型跳绳的售价是36元. ………6分(2)设购进A 型跳绳x 根,总费用为y 元,则: ………………7分 1036(50)261800y x x x =+-=-+ ………………………8分 ∵260-<∴y 随x 的增大而减小. ………………………9分 又∵x≤3(50-x ),解得:x≤37.5,且x 为正整数 ………………………10分 ∴当x=37时,y 最小 ………………………11分 {256282x y x y +=+={1036x y ==此时50-37=13.答:当购进A型跳绳37根,A型跳绳13根时,最省钱.………………12分【课后训练】1、(省实一模)解:(1)在Rt△ABD中,AD=24m,∠B=31°,∴tan31°=,即BD==40m,在Rt△ACD中,AD=24m,∠ACD=50°,∴tan50°=,即CD==20m,∴BC=BD﹣CD=40﹣20=20m,则B,C的距离为20m;(2)根据题意得:20÷2=10m/s<15m/s,则此轿车没有超速.2、(省实一模)解:(1)设该快递公司投递快递总件数的月平均增长率为x,根据题意得:10×(1+x)2=12.1,解得:x1=10%,x2=﹣210%.答:该快递公司投递快递总件数的月平均增长率为10%.(2)12.1×(1+10%)=13.31(万件),26×0.6=15.6(万件).∵15.6>13.31,∴该公司现有的26名快递投递业务员能完成今年6月份的快递投递任务.3、(广雅一模)解:(1)设甲单独完成需x 天,则乙队单独完成需要的时间是1.5x 天,由题意,得 16)5.111=⨯+xx ( 解得:x=10,经检验,x=10是原方程的根,∴乙队单独完成需要的时间是15天.答:甲单独完成需10天,则乙队单独完成需要的时间是15天;(2)设乙每天工程费为y 元,则甲队每天的工程费为(y+4000)元,由题意,得 6(y+y+4000)=385200,解得:y=30100.∴甲队每天的费用为:30100+4000=34100元.乙队的总费用为30100×15=451500(元),甲队的总费用为:(30100+4000)×10=341000(元).∵341000元<451500元,∴应选甲队.4、(广铁一模)解:(1)设A 型学习用品单价x 元,根据题意得:=,解得:x=20,经检验x=20是原方程的根,x+10=20+10=30.答:A 型学习用品20元,B 型学习用品30元;(2)设可以购买B 型学习用品a 件,则A 型学习用品(1000﹣a )件,由题意,得: 20(1000﹣a )+30a ≤28000,解得:a ≤800.答:最多购买B 型学习用品800件.5、(越秀一模)解:设小王骑自行车的速度为x千米/时,则小英的速度为1.2x千米/时,根据题意,得,即,两边同乘以6x去分母,得75+x=90,解得x=15.经检验,x=15是该分式方程的根.答:小王的速度为15千米/时.。
广州市海珠区2017年中考综合练习数学含答案

本试卷分选择题和非选择题两部分,共三大题 25 小题,共 4 页,满分 150 分,考试时间 120 分 钟, 可以使用计算器. 注意事项院 1.答卷前,考生务必在答题卡第 1 面、第 3 面、第 5 面上用黑色字迹的钢笔或签字笔填写自己的学校、 班级、姓名、座位号、考号;再用 2B 铅笔把对应号码的标号涂黑. 2.选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题号的答案标号涂黑;如需改动,用橡皮擦干净 后,再选涂其他答案标号;不能答在试卷上. 3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用 2B 铅笔画图.答案必须写在答 题卡各题指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;改动的答案也 不能超出指定的区域.不准使用铅笔、圆珠笔和涂改液,不按以上要求作答的答案无效. 4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回. 第一部分 选择题 (共 30 分) 一、 选择题 (本题有 10 个小题, 每小题 3 分, 满分 30 分, 下面每小题给出的四个选项中,只 有一个是正确的) 1. 某种药品说明书上标明保存温度是 (20±3)0C,则该药品在 ( ) 范围内保存最合适. A. 170C~200C B. 200C ~230C C. 170C ~230C D. 170C ~240C 2. 一个几何体的三视图如图所示,则这个几何体可能是 ( ) .
1 x+b 与 ABC 的边有交点时,b 的取值范围是 ( ) . 2 1 1 3 3 A. -2 ≤b ≤2 B. ≤b ≤2 C. ≤ b≤ D. ≤b≤2 2 2 2 2
当直线 y= 10.
正方形 A BCD 中,对角线 A C、BD 相交于点 O,DE 平分∠A DO 交 AC 于点 E ,把 A DE 沿 AD
2017广州中考数学试卷真题(含答案)

2017年广州市初中毕业生考试数学第一部分选择题(共30分)一、选择题(本大题共10小题,每小题3分,满分30分。
在每个小题给出的四个选项中,只有一项是符合题目要求的.)1、如图1,数轴上两点A、B表示的数互为相反数,则点B表示的数为()A、-6B、6C、0D、无法确定2、如图2,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为()A B C D3、某6人活动小组为了了解本组成员的年龄情况,作了一次调查,统计的年龄如下(单位:岁):12,13,14,15,15,15.这组数据中的众数、平均数分别为()A、12,14B、12,15C、15,14D、15,134、下列运算正确的是()A、3a+b6=a+b2B、2×a+b2=2a+b3C、2、|a|=a(a≥0)5、关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,则q的取值范围是()A、q<16B、q>16C、q≤4D、q≥46、如图3,圆O是△ABC的内切圆,则点O是△ABC的()A、三条边的垂直平分线B、三条角平分线的交点C、三条中线的交点D、三条高的交点7、计算(a2b)3·b2a,结果是()A、a5b5B、a4b5C、a b2D、a5b58、如图4,E、F分别是平行四边形ABCD的边AD,BC边上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到E’F’C’D’, ED’交BC于点G,则△GEF的周长为()A、6B、12C、18D、249、如图5,在圆O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是()A、AD=2OBB、CE=EOC、∠OCE=40°D、∠BOC=2∠BAD10、a≠0,函数y=ax 与y=-a x2+a在同一直角坐标系中的大致图像可能是B C D( )第二部分 非选择题(共120分) 二、填空题11、如图6,四边形ABCD 中,AD ∥BC ,∠A=110°,则∠B= .12、分解因式:x y 2-9x= .13、当x= 时二次函数y=x 2-2x+6有最小值 . 14、如图7,R t△ABC 中,∠C=90°,BC=15,tanA=158,则AB= .15、如图8,圆锥的侧面展开图是一个圆心角为120°的扇形,若圆锥的底面半径是5,则圆锥的母线l= .16、如图9,平面直角坐标系中O 是原点,平行四边形OABC 的顶点A ,C 的坐标分别是(8,0),(3,4),点D ,E 把线段OB 三等分,延长OA,AB 于点F ,G ,连接FG ,则下列结论: ①F 是OA 的中点;②△OFD 与△BEG 相似; ③四边形DEGF 的面积是203; ④OD=4√53其中正确的结论是 .(填写所有正确结论的序号)三、 解答题(本大题共9小题,满分102分,解答应写出文字说明,证明过程或演算步骤) 17、(本小题满分9分) 解方程组{x +y =52x +3y =1118、(本小题满分9分)如图10,点E 、F 在AB 上,AD=BC ,∠A=∠B,AE=BF ,求证: △ADF≌△BCE. 19、(本小题满分10分)某班为了学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t (单位:小时),将学生分成五类;A 类(0≤t ≤2)B 类(2<t ≤4)C 类(4<t≤6)D 类(6<t ≤8)E 类(t >8),绘制成尚不完整的条形统计图如图根据以上信息,解答下列问题;(1)E 类学生有 人,补全条形统计图; (2)D 类学生人数占被调查人数的 %;(3)从该班做义工时间在0≤t ≤4的学生中任选2人,求这2人做义工时间都在2<t ≤4中的概率. 20、(本小题满分10分)图11如图12,在R t△ABC中,∠B=90°,∠A=30°,AC=2√3.(1)利用迟归作线段AC的垂直平分线DE,垂足为E,交AB于点D;(保留作图痕迹,不写作法)(2)若△ADE的周长为a,先化简T=(a+1)2−a(a−1),再求T的值.21、(本小题满分12分)甲乙两个工程队均参与某筑路工程,先由甲队筑路60公里,再由乙队完成剩下的筑路工程,已知乙队筑路总公里数是甲队筑路总公里数的43倍,甲队比乙队多筑路20天.(1)求乙队筑路的总公里数;(2)若甲、乙两队平均每天筑路公里数之比为5:8,求乙队平均每天筑路多少公里.22(本小题满分12分)将直线y=3x+1向下平移1个单位长度,得到直线y=3x+m,若反比例函数y=kx的图像与直线y=3x+m相交于点A,且点A的纵坐标是3,(1)求m和k的值;(2)结合图像求不等式3x+m>kx的解集.23、(本小题满分12分)已知抛物线y1=-x2+mx+n,直线y2=kx+b, y1的对称轴与y2交于点A(-1,5),点A与y1的顶点B的距离是4.(1)求y1的解析式(2) 若y 2随着x 的增大而增大,且y 1与y 2都经过x 轴上一点,求y 2的解析式.24、(本小题14分)如图13,矩形ABCD 的对角线AC ,BD 相交于点O ,△COD 关于CD 的对称图形为△CEO.(1) 求证:四边形OCED 是菱形; (2) 连接AE ,若AB=6cm ,BC=√5cm.①求sin∠EAD 的值;②若点P 为线段AE 上一动点(不与点A 重合),连接OP.一动点Q 从点O 出发,以1cm/s 的速度沿线段OP 匀速运动到点P ,再以1.5cm/s 的速度沿线段PA 匀速运动到点A ,到达A 点后停止运动,当点Q 沿上述路线运动到点A 所需要的时间最短时,求AP 的长和点Q 走完全程所需要的时间.25、(本小题满分14分)如图14,AB 是圆O 的直径,弧AC=弧BC ,AB=2,连接AC. (1) 求证:∠CAB =45°;(2) 若直线l 为圆O 的切线,C 是切点,在直线l 上取一点D ,使BD=AB,BD 所在的直线与AC 所在的直线相交于点E ,连接AD.①试探究AE 与AD 之间的数量关系,并证明你的结论;②EB是否为定值?若是,请求出这个定值;若不是,请说明理由.CD解析&唐老师碎碎念:1、选B,不解释;2、选A,注意图2在最右边,我就真的肯定有同学会吧A选项看成原图,不认真审题的悲剧;3、选C,众数就是出现最多次数的那个,为15,平均数就不用教了吧,为14;4、选D,这题我猜选C的同学也不少,这个选项没有说明a>0啊喂!!!;5、选A,用根的判别式△>0就可以求出来啦,不能等于0,人家说的是“两个不相等的实数根”;6、选B,内切圆的圆心就是角平分线的交点啦,再送你一条,外接圆的圆心是垂直平分线的交点!;7、选A,不解释;8、选C,△EFG是个等边三角形,应该不难证吧,∠DEF=60°,翻折说明∠FEG=60°,那∠AEG=60°,根据两直线平行内错角相等,∠EGF=∠EFG不就都为60°了吗?;9、选D,根据垂径定理可得出弧BC=弧BD,∠BAD和∠COB分别为相等的弧长所对的圆周角和圆心角,两倍关系,搞定!;10、选D,二次函数中的二次项系数加了个负号,肯定搞得很多同学晕头转向了吧,注意符号问题,一次函数中的a表示反比例函数中的k值,如果大于0,图像在一、三象限,如果小于0,图像在二、四象限,二次函数中的-a表示二次项系数,大于0,图像开口向上,小于0,图像开口向下,二次函数中的第二个a表示与y轴的交点,大于0,交于y轴正半轴,小于0,交于y轴负半轴;11、70°,两直线平行,同旁内角互补;12、x(y+3)(y-3),不解释;13、第一空填1,第二空填5,把二次函数一般形式化简为顶点式,利用配方法,或直接代入顶点公式求解;14、17,根据tanA=15/8,BC=15,可求出AC=8,再用勾股定理就能求出AB的大小;15、3根号5,扇形的弧长公式和圆锥的底面周长公式联立即可求解,这两者关系式相等的哦;16、①③;过程太麻烦了,懒得写;17、x=4,y=1,不解释;18、用(SAS)证明,AE+EF=BF+EF,所以AF=BE,剩下的不用我说了吧;19、(1)5,用总人数减去A、B、C、D就求出来啦(2)36,18÷50=36%(3)3/10,列树状图,设存在5个人参与A1、A2、B1、B2、B3,剩下的自己体会吧;20、(1)画垂直平分线么毛病吧,如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州市海珠区2017年中考一模数学试卷
第一部分选择题(共30分)
一、选择题(本题共10 个小题,每小题 3 分,满分30 分.下面每小题给出的四个
选项中,只有一个是正确的.)
1.如果向东走50m 记为50m,那么向西走30m 记为()
A.-30m
B. |-30| m
C.-(-30)m
D.m
2.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是
()
A.B.C.D.
3.如图,点A.B.C 在⊙D 上,∠ABC=70°,则∠ADC 的度数为()
A.110°
B.140°
C.35°
D.130°第3题图
4.如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是
A. B. C. D.
5.下列计算正确的是()
A.3x2 ·4x2 =12x2
B.=(y)
C. D.
6.下列命题中,假命题
...是()
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.对角线相等的平行四边形是矩形
7.下列函数中,y 随x 的增大而增大的是()
A. B.x+5 C. D.
8.如图,在R t ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于点D,点E是垂足,连接CD. 若BD=1,则AC的长是()
A.2 3
B.2
C. 4 3
D.4
)9.已知抛物线y的图象如图所示,顶点为(4,6),则下列说法错误的是(
A. b2 >4ac
B.
6
C. 若点(2,m)(5,n)在抛物线上,则m>n
D. 8a+b = 0
10.如图,在平面直角坐标系中,R t OAB的顶点A在x轴的正半轴上,顶点B的坐标为( 2, 2),点C的坐标为(1,0),点P为斜边OB上的一动点,则P A+PC的最小值为()
第 8 题图
第 9 题图 第 10 题图
第二部分 非选择题(共120分)
二、填空题(本题共 6 个小题,每小题 3 分,共 18 分.)
11.在不透明口袋内有形状.大小.质地完全一样的 5 个小球,其中红球 3 个,白球 2 个,随机抽取一个小球是红球的概率是________.
12.分解因式:3x 2 -6xy =_________.
13.某饮料店为了解本店一种罐装饮料上半年的销售情况,随机调查了 6 天该种饮料的日销售情况,结果如下(单位:罐):33,28,32,25,24,30,这 6 天
销售量的中位数是________.
14.某公司制作毕业纪念册的收费如下:设计费与加工费共 1000
元,另外每册收取材料费 4 元,则总收费y 与制作纪念册的册数x
的函数关系式为___________.
15.如图,AB 是⊙O 的直径,AC .BC 是⊙O 的弦,直径DE ⊥BC 于点M . 若点E 在优弧AB
⌒ 上,AC =8,BC =6,则EM =_______. 第15题图
16.若一元二次方程0 有两个相同的实数根, 则a 2 -b 2 +5的最小值为__________.
三、解答题(本题共 9 个小题,共 102 分,解答要求写出文字说明,证明过程或计算步骤.)
A . 2
B . 3
C . 2
D . 3
2
17.(共9 分)(1)解不等式组(2)解方程
18. (共9 分)如图,AC是菱形ABCD的对角线,点E.F分别
在AB、AD上,且AE=AF.求证:△ACE≌△ACF.
19.(共10 分)已知A= ( )·
(1)化简A;
(2)若x满足x2 -2x -8 =0,求A的值.
20.(共10 分)中央电视台举办的“中国诗词大会”节目受到中学生的广泛关注.某中学为了解
该校九年级学生对观看“中国诗词大会”节目的喜爱程度,对该校九年级部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为:A 级(非常喜欢),B 级(较喜欢),C 级(一般),D 级(不喜欢).请结合两幅统计图,回答下列问题:
(1)本次抽样调查的样本容量是__________,表示“D级(不喜欢)”的扇形的圆心角为__________°;(2)若该校九年级有200 名学生.请你估计该年级观看“中国诗词大会”节目B 级(较喜欢)的学生人数;
(3)若从本次调查中的 A 级(非常喜欢)的5 名学生中,选出2 名去参加广州市中学生诗词大会比赛,已知 A 级学生中男生有 3 名,请用“列表”或“画树状图”的方法求出所选出的 2 名学生中至少有1 名女生的概率.
21.(共12 分)某小区为更好的提高业主垃圾分类的意识,管理处决定在小区内安装垃圾
分类的温馨提示牌和垃圾箱,若购买 3 个温馨提示牌和 4 个垃圾箱共需580 元,且每个温馨提示牌比垃圾箱便宜40 元.
(1)问购买1 个温馨提示牌和 1 个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共100 个,费用不超过8000 元,问最多购买垃圾箱多少个?
22.(共12 分)如图,在ABC 中,∠C=90°
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作 O交AB于E (保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE ①求证:CD=DE;
②若si nA=,AC=6,求AD.
23.(共12 分)如图,在平面直角坐标系中,一次函数y1 =ax+b (a ≠ 0)的图象与y轴相交于点A,
与反比例函数y2 (c ≠0)的图象相交于点B(3,2)、C(-1,n).(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1> y2时x的取值范围;
(3)在y轴上是否存在点P,使P AB为直角三角形,如果存在,请求点P的坐标,若不存在,请说明理由.
24.(共14 分)抛物线y =ax2 +c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线
上有一动点P.
(1)若A(-2,0),C(0,-4),
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,-2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围;
(2)若点P在第一象限运动,且 a 0,连接AP、BP分别交y轴于点E、F,则问
是否与a、c有关?若有关,用a、c表示该比值;若无关,求
出该比值.
25.(共14 分)如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4.
(1)证明:AD2 = AE·AF ;
(2)延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB 交DF于点G,连接EG,设∠ACB =α,BG= x, EG =y .
①当α=900时,探索EG与BD的大小关系?并说明理由;
②当α=1200时,求y与x的关系式,并用x的代数式表示y .。
