华师大版八年级数学上册第14章勾股定理PPT教学课件
合集下载
最新华师版八年级数学上第14章《勾股定理》小结与复习ppt公开课优质课件

∴△ABC是直角三角形,
∴∠B=90°.
方法总结 勾股定理及其逆定理均体现了数形结合思想 . 勾股定理是 由图形的特征(三角形中有一个角是直角)得到数量之间的关 系(三角形的三边长 a , b , c 满足 a2+b2=c2 ) ; 勾股定理的逆定
理由数量之间的关系(a2+b2=c2)得到图形的特征(以a,b,c
第14章 勾股定理
小结与复习
要点梳理
考点讲练
课堂小结
课后作业
要点梳理
1.勾股定理 勾股定理:直角三角形两条直角边的平方和等于斜边的 平方 . 即:对于任意的直角三角形,如果它的两条直角边分别 为a、b,斜边为c ,那么一定有 a2+b2=c2 . 勾股定理表达式的常见变形:a2=c2-b2, b2=c2-a2, .a 2 c a 2 b2 , a c 2 b2 , b c 2 勾股定理分类计算:如果已知直角三角形的两边是a、 b(且a>b),那么,当第三边c是斜边时,c=_________ a 2 b2 ; a 2 b2 . 当a是斜边时,第三边c=_________ [注意] 只有在直角三角形里才可以用勾股定理,运用时要 分清直角边和斜边.
解:①在 Rt△ABC1 中, 2 2 2 2 2 AC2 1 =AB + BC 1=4 + 3 =5 , ∴AC1 = 25. ②在 Rt△ACC1 中, 2 2 2 2 AC2 1 = AC + CC 1=6 +1 =37, ∴AC1 = 37. ③在 Rt△AB1 C1 中, 2 2 2 2 AC2 1 = AB 1+ B1 C1 =5 +2 =29, ∴AC1 = 29. ∵25<29<37, ∴沿图①的方式爬行路线最短,最短路线长是 5.
1 ∴4× 2ab+(b-a)2=c2,
华东师大版八年级上册14.反证法课件(共23张)

王戎是怎样知道李子是苦的呢?他运用了
怎样的推理方法?
王戎的推理方法是:
假设李子不苦 则因树在“道”边,李子早就被别人采摘, 这与“多子”产生矛盾. 所以假设不成立,李为苦李.
生活实例: 妈妈:小华,听说邻居小芳全家这几天在外 地旅游. 小华:不可能,我上午还在学校碰到了她和 她妈妈呢!
上述对话中,小华要告知妈妈的命题是什么?
课后作业
1、已知:一个整数的平方能被2整除.
求证:这个数是偶数.
2、已知a≠0,证明x的方程ax=b有且只有一个根.
3、已知x>0,y>0,x+y>2.
求证:1+x y
,1+y x
中至少有一个小于2.
4、求证: 2 是无理数.
5、求证:在三角形的内角中,至少有一个角大于 或等于60º. 6、证明:等腰三角形的两底角必定是锐角. 7、证明:两直线平行,同旁内角互补. 8、如图,已知AB∥CD,
当∠B是_钝__角__时,则_∠__B_+__∠__C_>__1_8_0_°
这与__三__角__形__的__三__个__内__角__和__等__于__1_8_0_°_矛盾; 综上所述,假设不成立. ∴∠B一定是锐角.
强调 用反证法证题时,应注意的事项 : (1)周密考察原命题结论的否定事项, 防止否定不当或有所遗漏; (2)推理过程必须完整,否则不能说 明命题的真伪性; (3)在推理过程中,要充分使用已知条 件,否则推不出矛盾,或者不能断 定推出的结果是错误的。
P
a
证明: 假设c与b不相交,
则c∥b.
b c
∵ a∥b,
∴ a∥c,
这与“c、a相交于点P”矛盾, ∴ 假设不成立,故c与b相交.
变式练习
怎样的推理方法?
王戎的推理方法是:
假设李子不苦 则因树在“道”边,李子早就被别人采摘, 这与“多子”产生矛盾. 所以假设不成立,李为苦李.
生活实例: 妈妈:小华,听说邻居小芳全家这几天在外 地旅游. 小华:不可能,我上午还在学校碰到了她和 她妈妈呢!
上述对话中,小华要告知妈妈的命题是什么?
课后作业
1、已知:一个整数的平方能被2整除.
求证:这个数是偶数.
2、已知a≠0,证明x的方程ax=b有且只有一个根.
3、已知x>0,y>0,x+y>2.
求证:1+x y
,1+y x
中至少有一个小于2.
4、求证: 2 是无理数.
5、求证:在三角形的内角中,至少有一个角大于 或等于60º. 6、证明:等腰三角形的两底角必定是锐角. 7、证明:两直线平行,同旁内角互补. 8、如图,已知AB∥CD,
当∠B是_钝__角__时,则_∠__B_+__∠__C_>__1_8_0_°
这与__三__角__形__的__三__个__内__角__和__等__于__1_8_0_°_矛盾; 综上所述,假设不成立. ∴∠B一定是锐角.
强调 用反证法证题时,应注意的事项 : (1)周密考察原命题结论的否定事项, 防止否定不当或有所遗漏; (2)推理过程必须完整,否则不能说 明命题的真伪性; (3)在推理过程中,要充分使用已知条 件,否则推不出矛盾,或者不能断 定推出的结果是错误的。
P
a
证明: 假设c与b不相交,
则c∥b.
b c
∵ a∥b,
∴ a∥c,
这与“c、a相交于点P”矛盾, ∴ 假设不成立,故c与b相交.
变式练习
1勾股定理(第3课时)PPT课件(华师大版)

讲授新课
现在再回到勾股定理:直角三角形两直角边的平方和等于斜边 的平方.即“在△ABC中,如果AB=c,BC=a,CA=b,且∠C=90°, 那么a2+b2=c2”是一个真命题. 思考:在△ABC中,如果AB=c,BC=a,CA=b,且∠C≠90°, 那么a2+b2≠c2是真命题吗?
先思考作什么假设, 再用反证法写出推理 过程.
讲授新课
证明:假设两条相交直线l1与l2不止一个交点,不妨假设l1与l2有两 个交点A和B.
这样过点A和点B就有两条直线l1与l2.这与两点确定一条直线,即经 过点A和点B的直线只有一条的基本事实矛盾.
所以假设不成立,因此两条直线相交只有一个交点.
讲授新课
练一练
1、求证:在一个三角形中,至少有一个内角小于或等于60°. 已知:△ABC. 求证:△ABC至少有一个内角小于或等于60°.
讲授新课
典例精析
【例1】求证:两条直线相交只有一个交点。 已知:如图两条相交直线a、b。 求证:a与b只有一个交点。
证明:假设a与b不止一个交点,不妨假设有
两个交点A和A’。
a
● A,
因为两点确定一条直线,即经过点A和A’
●
A
的直线有且只有一条,这与已知两条直线矛
盾,假设不成立。
b
所以两条直线相交只有一个交点。
数学(华东师大版)
八年级 上册
第14章 勾股定理
14.1 勾股定理 第3课时 反证法
学习目标
1、了解反证法的证明步骤,体会反证法证明问题的思想,并能 够运用反证法来证明一些问题; 2、理解并体会反证法的思想内涵; 3、通过反证法的学习,培养辩证唯物主义观念;
温故知新
如图,在△ABC中,AB=c,BC=a,AC=b,(a≤b≤c)有关系a2 +b2 =c2时,
华师大版八年级数学上册第十四章勾股定理PPT教学课件全套

解: 在 Rt△ABC 中, 斜边不确定, 这就需要分情况讨论: 若 AB 是斜边,则 AB2=AC2+BC2=152+82=289,从 而 AB=17; 若 AB 不是斜边,由 AC>BC,知 AC 为斜边,此时 AC2 =AB2+BC2,即 AB2=AC2-BC2=152-82=161,从而 AB = 161. 综上所述,AB 边的长为 17 或 161.
图 14-1-3
14.1.1
探索直角三角形三边的关系
重难互动探究
探究问题一 理解勾股定理 (1)求出如图 14-1-4 所示直角三角形中未知边的长度; (2)在直角三角形 ABC 中, ∠C = 90°, BC = 12, AC = 9,求 AB 的长; (3)已知:图 14-1-5 的正方形是以直角三角形的边长为 边的正方形,那么正方形 A 的面积是多少? (4)已知:图 14-1-6 的正方形是以直角三角形的边长为 边的正方形,那么正方形 B 的边长是多少?
图 14-1-4
图 14-1-5
图 14-1-6
14.1.1
探索直角三角形三边的关系
解:(1)如图 14-1-4,在 Rt△ABC 中,∠C=90°,AC =15, BC=8.由勾股定理, 得 AB2=AC2+BC2=152+82=289, ∴ AB=17. (2)∵∠C = 90°,BC = 12,AC = 9 ,∴ AB2=BC2 +AC2=122+92=225, ∴AB=15. (3) 由勾股定理可知:直角三角形的两条直角边上的正方 形的面积和等于斜边上的正方形的面积,故可以求得正方形 A 的面积是 37+63=100. (4)由勾股定理可知: 直角三角形的两条直角边上的正方形 的面积和等于斜边上的正方形的面积, 故可以求得正方形 B 的 面积是 100-36=64,所以边长是 8.
华师大版初中八年级数学上册第14章《勾股定理》PPT课件

D
A
B
图1
CD
13
C
5
4
12
A3 B
图2
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角. 在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角. 因此,这个零件符合要求.
例4 已知△ABC,AB=n²-1,BC=2n,AC=n²+1(n为大于
1的正整数).试问△ABC是直角三角形吗?若是,哪一条 边所对的角是直角?请说明理由
x=15, 15+9=24(m). 答:旗杆原来高24 m.
课堂小结
认识勾 股定理
如果直角三角形两直角边长 分别为a,b,斜边长为 c , 那么a2+b2=c2
利用勾股定理进行计算
第14章 勾股定理
14.1 勾股定理 第2课时
学习目标
情境引入
1.了解直角三角形的判定条件.(重点) 2.能够运用勾股数解决简单实际问题.(难点)
A 2 E 2 D △FCB均为直角三角形. 1 F 由勾股定理,知
4
BE2=22+42=20,EF2=22+12=5,
3 BF2=32+42=25,
B
4
C ∴BE2+EF2=BF2. ∴ △BEF是直角三角形.
课堂小结
一定是直 角三角形
勾股定理的逆定理:如果三角形的 三边长a,b,c满足a2+b2=c2,那么 这个三角形是直角三角形.
如图,在△ABC中,AB=c,BC=a,AC=b,(a≤b≤c)
有关系a2 +b2 =c2时,这个三角形一定是直角三角形吗?
解析:由a2 +b2 =c2 ,根据勾股定理的逆
1勾股定理(第2课时)教学PPT课件(华师大版)
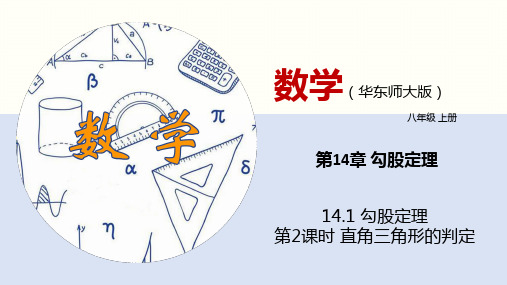
C. a 1, 2a,a 1
D. a 1, 2a,a 1
当堂检测
5.若三角形ABC的三a,b,c满足a2+b2+c2+50=6a+8b+10c. 试判断
△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c ∴ a2-6a+9+b2-8b+16+c2-10c+25=0. 即 (a-3)²+ (b-4)²+ (c-5)²=0. ∴ a=3, b=4, c=5 即 a2+b2+c2.
“直角三角形”为条件,数量关系a2+ b2= c2 数量关系a2+ b2= c2为条件,“直角三角形”
为结论. 是直角三角形的性质.
为结论. 是直角三角形的判定.
联系
都与直角三角形有关,都与三边数量关系a2 + b2 = c2有关
讲授新课
典例精析
【例1】下面以a、b、c为边长的三角形是不是直角三角形?若是,请指
∴△ABC直角三角形.
当堂检测
6.一艘在海上朝正北方向航行的轮船,在航行240海里时方位仪坏了,凭经
验,船长指挥船左传90°,继续航行70海里,则距出发地250海里,你能判
断船转弯后,是否沿正西方向航行?
解:由题意画出相应的图形AB=240海里,BC=70海里,AC=250 海里; 在△ABC中AC2-AB2=2502-2402 =4900=702 =BC2 即AB2+BC2=AC2 ∴△ABC是Rt△ 答:船转弯后,是沿正西方向航行的。
解:因为a2=c2-b2,所以a2+b2=c2,所以这个三角形是直角三角形.
华师大版八年级上册数学课件(第14章 勾股定理)

试一试
观察图14. 1. 2,如果每一小方格表示1平 方厘米, 那么可以得到: 正方形P的面积= 平方厘米;
知1-导
正方形Q的面积=
正方形R的面积=
平方厘米;
平方厘米.
我们发现,正方形P、Q、R的面积之间的关系是 . 由此,我们得出Rt△ABC的三边长度之间存在的关 系
是
.
知1-导
做一做
画出两条直角边分别为5 cm、12 cm的直角三角形, 然后用刻度尺量 出斜边的长,并验证上述关系对这个直角 三角形是否成立.
第14章 勾股定理
14.1 勾股定理
第 1 课时
直角三角形三边的关系 --- 认识勾股定理
1
课堂讲解 课时流程
逐点 导讲练
勾股定理 勾股定理与面积的关系
2
课堂 小结
作业 提升
你知道2002年在北京召开的国际数学家大会(ICM-
2002)吗?在这次大 会上,到处可以看到一个简洁优美、
远看像旋转的纸风车的图案,它就是大 会的会标. 会标采用了 1700多年前中国古代数学家赵爽用来证 明勾股定理的弦图.
2
,S2=π•
π•
AB 1 2 2
2
BC 1 2 2
2
,S3=
,另外由勾股定理可知AC2+BC2
=AB2,所以S1+S2=S3;
(3)阴影部分的面积=两个小半圆形的面积和+直
角三角形的面积-大半圆形的面积,由(2)可知 两个小半圆形的面积和=大半圆形的面积,所
∴由勾股定理,得(2b)2+b2=52,解得b= 5.
知1-讲
例3 已知直角三角形的两边长分别为3,4,求第 三边的长.
错解:第三边的长为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
底部12 m处.旗杆原来有多高?
9 m
12 m
解:设旗杆顶部到折断处的距离为x m,根据勾股 定理,得
92 122 x 2
x=15, 15+9=24(m). 答:旗杆原来高24 m.
课堂小结
如果直角三角形两直角边长 分别为a,b,斜边长为 c , 那么a2+b2=c2 认识勾 股定理
利用勾股定理进行计算
讲授新课
做一做
用四个全等的直角三角形,还可以拼成如图所示的图形,
你能否根据这一图形,证明勾股定理.
大正方形的面积可以表示为 (a+b)2 ;
b a b
a
也可以表示为
c2 +4•ab/2
.
c c
a
c c
b
b a
∵ (a+b)2 = c2 + 4•ab/2
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
八年级数学上(HS) 教学课件
第14章 勾股定理
14.1 勾股定理
1.直角三角形三边的关系
导入新课 讲授新课 当堂练习 课堂小结
学习目标
法.(重点)
情境引入
1.掌握勾股定理及其简单应用,理解定理的一般探究方 2.通过利用方格纸计算面积的方法探索勾股定理,经历 观察、归纳、猜想和验证的数学发现过程,发展数形结合
是否等于斜边的平方呢?
试一试
A
Q
C
R
B
P的面 Q的面 R的面 积(单 积(单 积(单 位长度) 位长度) 位长度)
图2 图3
A
9 9
16 4
25 13
Pபைடு நூலகம்
R P
B
Q
C
P、Q、 R面积 关系
直角三 角形三 边关系
SP+SQ=SR BC2+AC2=AB2 BC2+AC2=AB2
(每一小方格表示1平方厘米)
Q
P
R
R Q P
把R看作是四个直角三角形的面积+小正方形面积.
Q P
R
S正方形R
1 7 4 3 4 2
2
R Q P
25
把R看作是大正方形面积减去四个直角三角形的面积.
做一做
分别以5cm、12cm为直角三角形的直角边作出一个直
角三角形ABC,测量斜边的长度,然后验证上述关系对这
A
R
P
C Q B
(3)正方形R的面积是
2
平方厘米.
(图中每一格代表一平方厘米)
上面三个正方形的面积之间有什么关系? SP+SQ=SR
等腰直角三角形ABC三边长度之间存在什么关系吗? Sp=AC2 SQ=BC2 SR=AB2 AC2+BC2=AB2
想一想
这说明在等腰直角三角形ABC中,两直角边的平 方和等于斜边的平方 那么,在一般的直角三角形中,两直角边的平方和
5.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶
上方4 km处,过了15 s,飞机距离这个男孩头顶5 km.这一
过程中飞机飞过的距离是多少千米? 解:在Rt△ABC中, C B
BC2 =52 -42 =9, BC>0 BC=3(km)
4 4
答:飞机飞过的距离是3km.
A
6.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆
八年级数学上(HS) 教学课件
第14章 勾股定理
14.1 勾股定理
2.直角三角形的判定
导入新课 讲授新课 当堂练习 课堂小结
学习目标 情境引入
1.了解直角三角形的判定条件.(重点)
2.能够运用勾股数解决简单实际问题.(难点)
导入新课
问题:同学们你们知道古埃及人用什么方法得到直角? 据说,古埃及人曾用下面的方法画直角: 他们用13个等距离的结把一根绳子分成等长的12段,一个 工匠同时握住绳子的第1个结和第13个结,两个助手分别握住 第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其 直角在第4个结处. 你想知道这是什么道理吗?
c
C
∟
b
A
赵爽弦图
c a b
b-a
证明: S大正方形=c2
S小正方形=(b-a)2 S大正方形=4· S三角形+S小正方形
1 即 c =4× ab+(b-a)2, 2 c2=2ab+a2-2ab+b2 所以 a2+b2=c2
2
温馨提示:上述这种验证勾股定理的方法是用面积法 “赵爽弦图”表现了我国古人对数学的钻研精神和聪明 才智,它是我国古代数学的骄傲.因为,这个图案被选为2002 年在北京召开的国际数学大会的会徽.
方法小结:我们利用拼图的方法,将形的问题与数的问题结 合起来,再进行整式运算,从理论上验证了勾股定理.
练一练
求下列图形中未知正方形的面积或未知边的长度(口答):
100 225
x
17 15
?
已知直角三角形两边,求第三边.
当堂练习
1.图中阴影部分是一个正方形,则此正方形的面积
为
64 cm² .
15 cm
* (12) (11) (2) * * * (10) (3) * (9) * * (4) * * * * (7) * (8) (5) (6)
(1) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13)
(13)
* * * * * * * * * * * * *
的数学思想.(难点)
导入新课 问题情境
某楼房三楼失火,消防队员赶来救火,了解到每层楼高
3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基
的距离是2.5米,请问消防队员能否进入三楼灭火?
讲授新课
直角三角形三边的关系
观察正方形瓷砖铺成的地面. (1)正方形P的面积是 (2)正方形Q的面积是 1 1 平方厘米; 平方厘米;
17 cm
2.判断题
①△ABC的两边AB=5,AC=12,则BC=13 (
②△ABC的a=6,b=8,则c=10 ( 3.填空题
)
)
在△ABC中, ∠C=90°,AC=6,CB=8,则△ABC面积为_____, 24 4.8 斜边为上的高为 ______. A D
C
B
4.一高为2.5米的木梯,架在高为2.4米的墙上(如图), 这时梯脚与墙的距离是多少? A 解:在Rt△ABC中,根据勾 股定理,得: BC2=AB2-AC2 =2.52-2.42 =0.49, C B 所以BC=0.7.
个直角三角形是否成立.
A 13 5
C
12
B
归 纳
由前面的探索可以发现:对于任意的直角三角形,如
果它的两条直角边分别为a、b,斜边为c,那么一定有
a2+b2=c2 勾股定理:直角三角形两直角边的平方和等于斜边的平方. 几何语言: ∵在Rt△ABC中 ,∠C=90°, ∴a2+b2=c2(勾股定理). 勾股定理揭示了直角三角形三边之间的关系. B a
