SolidWorks中“方程式驱动的曲线”工具的应用
solidworks用方程式驱动曲线

solidworks用方程式驱动曲线SolidWorks自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系)下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的X 值以后,Y值会随着X值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X值表达式中含有变量T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转换到笛卡尔坐标系,以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWorks 帮助文件详细了解使用方法。
一、显式方程1.类型:正弦函数(1)函数解析式:。
其中,正弦曲线是一条波浪线,是常数(k 、ω、φ∈R,ω≠0);A是振幅、(ωx+φ)是相位、φ是初相;k是偏距,是反应图像沿Y轴整体的偏移量;且(2)目标:模拟交流电的瞬时电压值得到正弦曲线图像,周期(3)操作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如下方程。
(4)方程式:(5)函数图像:如图1所示,使用尺寸标注工具得出图像关键点对应的数值。
2.类型:一次函数(1)函数解析式:。
其中一次函数是一条直线,y值与对应x值成正比例变化,比值为k ;k 、b 是常数,x ∈R。
(2)目标:模拟速度—位置曲线,其中k=4,b=0。
(3)操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程。
sw中方程式驱动的曲线

sw中方程式驱动的曲线曲线是数学中一个非常重要的概念,它在各个领域中都有广泛的应用。
在计算机科学中,曲线也是一个常见的概念。
在计算机图形学领域中,曲线是一种通过一组点计算出来的几何形状。
在本文中,我将介绍一种常见的曲线表示方法——方程式驱动的曲线。
方程式驱动的曲线是通过一个或多个方程来定义的。
这些方程通常包含一些参数,通过调整这些参数可以改变曲线的形状。
方程式驱动的曲线可以是二维的或三维的,可以表示平面上的曲线或者空间中的曲线。
方程式驱动的曲线可以分为两类:显式曲线和参数曲线。
显式曲线是通过一个或多个方程显式给出的,可以直接计算出曲线上的点的坐标。
参数曲线是通过一个或多个参数方程给出的,通过改变参数的取值可以得到曲线上的不同点。
在计算机图形学中,方程式驱动的曲线通常用于表示三维模型的曲线、路径动画的路径等。
通过调整参数或方程,我们可以方便地改变曲线的形状,从而达到需要的效果。
在二维图形学中,最常见的方程式驱动的曲线是直线、圆和椭圆等。
直线的方程通常写作y = ax + b,其中a和b是常数,可以通过改变a和b的取值来改变直线的斜率和截距。
圆的方程通常写作(x - h)² + (y - k)² = r²,其中(h, k)是圆心的坐标,r是半径。
椭圆的方程通常写作(x - h)²/a² + (y - k)²/b² = 1,其中(h, k)是椭圆中心的坐标,a和b是椭圆在x和y轴上的半轴长度。
在三维图形学中,方程式驱动的曲线可以更复杂。
例如,一个常见的三维曲线表示方法是贝塞尔曲线。
贝塞尔曲线是通过一组控制点来定义的,通过调整控制点的坐标可以改变曲线的形状。
贝塞尔曲线可以是一阶、二阶、三阶等不同阶数的曲线,不同阶数的曲线拥有不同的平滑度和曲线形状。
除了贝塞尔曲线,还有许多其他方程式驱动的曲线可以用于表示三维模型。
例如,NURBS曲线是一种广泛应用于计算机图形学中的曲线表示方法。
SolidWorks中“方程式驱动的曲线”工具的应用

SolidWorks中“方程式驱动的曲线”工具的应用在曲线精度、绘制效率和修改参数等方面都极大地方便了用户SolidWords自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系) 下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确的数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的X 值以后,Y 值会随着X 值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X值表达式中含有变量T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线的关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转化到笛卡尔坐标系以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWords帮助文件详细了解使用方法。
(一)显式方程类型:正弦函数函数解析式:Yx=A×si n( ωx+φ)+k正弦曲线是一条波浪线,k、ω和φ是常数(k、ω、φ∈R,ω≠0)A——振幅、(ωx+φ)——相位、φ——初相k——偏距、反应图像沿Y轴整体的偏移量ω=□(2π/T)目标:模拟交流电的瞬时电压值得正玄曲线图像,周期□(T=2π/3),φ=π/2,A=2操作:新建零件文件◊工具◊选择绘图基准面◊方程式驱动的曲线,键入如下方程。
方程式: Yx=2*sin〖(3*x+〗 pi/2)X1= - pi/2,X2= pi/2函数图像:如图1-1 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-1类型:一次函数函数解析式: Yx=kx+b一次函数是一条直线 , y值与对应x值成正比例变化,比值为kk、b是常数, x∈R目标:模拟速度—位置曲线,k=4,b=0操作:新建零件文件◊选择基准面◊驱动的曲线,键入如下方程方程式: Yx=4*x+0函数图像:如图1-2 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-2类型:二次函数函数解析式: Yx=ax^2+bx+c平面内,到一个定点F和不过F的一条定直线L距离相等的点的轨迹(或集合)称之为抛物线。
SW方程式驱动曲线圆柱上创建波浪凹槽

SW方程式驱动曲线圆柱上创建波浪凹槽
文底图中的扫描切除,需要用到的核心功能是“方程式驱动曲线”,本文会用该模型的绘制方法逐步讲解方程式驱动曲线的功能。
1. 需要建立在3D草图的基础上
从切割的路径上就能判断出2D草图是无法满足功能需要的,因此,首先需要建立3d草图环境。
2. 方程式驱动曲线的应用
找功能可以在软件界面右上角搜索栏中输入方程式,若要经常使用,可以自定义界面,把搜索出的功能拖拽到command manager上(也就是功能面板上,图中红框处)。
点击该功能后,功能面板如下图:
具体参数含义如下:
① 方程式采用“笛卡尔坐标系”;
② Xt中的50代表半径,由于被切割的圆柱直径是φ100,因此切割路径需要R50,故Xt中是50*,“*”代表乘号。
Xt和Yt分别代表曲线的x和y方向的半径,若X取50,Y取100,则X方向的半径值是50,Y方向半径值是100,过渡部分会连接(大家可自行测试);
③ sin和cos函数规定了曲线的走向(即正弦、余弦函数),其中,参数t1、t2是取值范围,会分别代入Xt、Yt的t中;
④ Zt代表曲线的纵方向信息,其中20代表波幅(上下分别20mm,故总的是40,下图中可以看到参考线长度接近40mm)。
6*t中的6代表波数;
⑤ 若想围成一个正圆,需分两段方程式曲线画,且在一个3d草图内。
t1t2取值从0~pi,更改为pi~2pi,pi代表π(即圆周);
3. 提升曲线的鲁棒性
样条曲线完成后,可以使用套合样条曲线提升曲线的鲁棒性。
最后使用拉伸切除即可。
完成。
(理解运用方程式驱动曲线,有助于提高此类模型的建模速度,值得学习拥有)
以上!。
SolidWorks方程式的使用
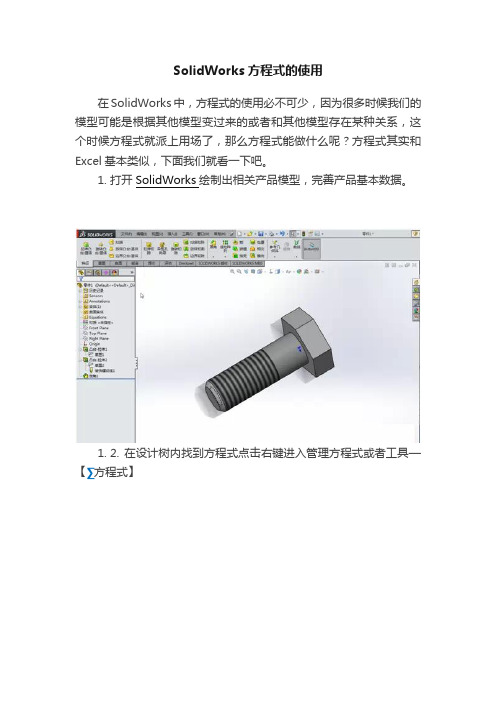
SolidWorks方程式的使用
在SolidWorks中,方程式的使用必不可少,因为很多时候我们的模型可能是根据其他模型变过来的或者和其他模型存在某种关系,这个时候方程式就派上用场了,那么方程式能做什么呢?方程式其实和Excel基本类似,下面我们就看一下吧。
1. 打开SolidWorks绘制出相关产品模型,完善产品基本数据。
1. 2. 在设计树内找到方程式点击右键进入管理方程式或者工具—【∑方程式】
1. 3. 在方程式内找到需要使用条件的尺寸
1. 4. 键入你需要的条件,例:如果草图1的尺寸小于65,那么螺栓长度为100,否则为120(D1@凸台-拉伸=IIF(”D1@草图1”<65,”100”,”120”))
1. 5.如果D1@草图1=60,相对应的螺栓长度就应该为100
上述是if语句,其实在SolidWorks 方程式里面还能进行方程式讲特征压缩:
我们也可以通过用if语句的方式给特征进行条件压缩/解压缩,当然有人要问了这个压缩和在设计树里压缩有什么不同,可以告诉你肯定是不同的,首先是有条件给他压缩,切条件在,在设计树里就不能进行解除压缩。
大家可以试验一下。
SolidWorks不仅支持条件语句还提供更多的选择,如三角函数等,大家都可以根据自己的需要来选择,能让设计者能更方便和快捷的来设计。
solidworks用方程式驱动曲线

solidworks用方程式驱动曲线SolidWorks自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系)下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的X 值以后,Y值会随着X值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X值表达式中含有变量T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转换到笛卡尔坐标系,以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWorks 帮助文件详细了解使用方法。
一、显式方程1.类型:正弦函数(1)函数解析式:。
其中,正弦曲线是一条波浪线,是常数(k 、ω、φ∈R,ω≠0);A是振幅、(ωx+φ)是相位、φ是初相;k是偏距,是反应图像沿Y轴整体的偏移量;且(2)目标:模拟交流电的瞬时电压值得到正弦曲线图像,周期(3)操作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如下方程。
(4)方程式:(5)函数图像:如图1所示,使用尺寸标注工具得出图像关键点对应的数值。
2.类型:一次函数(1)函数解析式:。
其中一次函数是一条直线,y值与对应x值成正比例变化,比值为k ;k 、b 是常数,x∈R。
(2)目标:模拟速度—位置曲线,其中k=4,b=0。
(3)操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程。
solidworks 方程式草图复习课程

SolidWorks中“方程式驱动的曲线”工具的应用潘思达SolidWords自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系) 下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确的数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的 X 值以后,Y 值会随着 X 值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X 值表达式中含有变量 T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线的关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转化到笛卡尔坐标系以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWords帮助文件详细了解使用方法。
(一)显式方程类型:正弦函数函数解析式:1正弦曲线是一条波浪线,k、ω和φ是常数(k、ω、φ∈R,ω≠0)2A——振幅、(ωx+φ)——相位、φ——初相3k——偏距、反应图像沿Y轴整体的偏移量4ω目标:模拟交流电的瞬时电压值得正玄曲线图像,周期,φ=,A=2操作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如下方程。
方程式:X1=- ,X2=函数图像:如图 1-1 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-1类型:一次函数函数解析式:Yx=1一次函数是一条直线 , y值与对应x值成正比例变化,比值为k 2k、b是常数,x∈R目标:模拟速度—位置曲线,k=4,b=0操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程方程式: Yx=4*x+0函数图像:如图 1-2 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-2类型:二次函数函数解析式:Yx=1平面内,到一个定点F和不过F的一条定直线L距离相等的点的轨迹(或集合)称之为抛物线。
solidworks用方程式驱动曲线

solidworks用方程式驱动曲线SolidWorks自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系)下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的X 值以后,Y值会随着X值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X值表达式中含有变量T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转换到笛卡尔坐标系,以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWorks 帮助文件详细了解使用方法。
一、显式方程1.类型:正弦函数(1)函数解析式:。
其中,正弦曲线是一条波浪线,是常数(k 、ω、φ∈R,ω≠0);A是振幅、(ωx+φ)是相位、φ是初相;k是偏距,是反应图像沿Y轴整体的偏移量;且(2)目标:模拟交流电的瞬时电压值得到正弦曲线图像,周期(3)操作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如下方程。
(4)方程式:(5)函数图像:如图1所示,使用尺寸标注工具得出图像关键点对应的数值。
2.类型:一次函数(1)函数解析式:。
其中一次函数是一条直线,y值与对应x值成正比例变化,比值为k ;k 、b 是常数,x∈R。
(2)目标:模拟速度—位置曲线,其中k=4,b=0。
(3)操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程。
