矩阵论简明教程(徐仲等编著)思维导图
行列式的简单总结(思维导图)
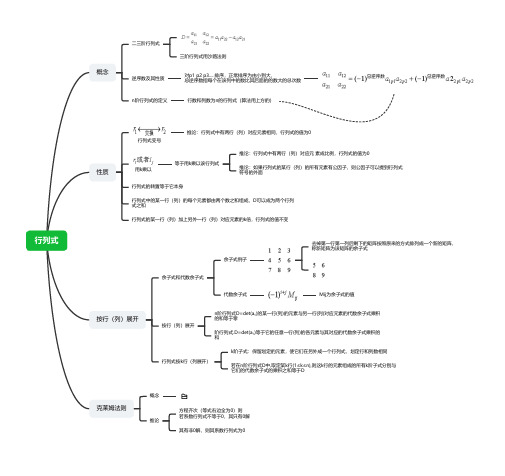
行列式概念
二三阶行列式
三阶行列式用沙路法则
逆序数及其性质对p1 p2 p3.....排序,正常排序为由小到大,
总逆序数指每个在该列中的数比其后面的的数大的总次数
n阶行列式的定义行数和列数为n的行列式(算法用上方的)
性质
行列式变号
推论:行列式中有两行(列)对应元素相同,行列式的值为0
用k乘以
等于用k乘以该行列式
推论:行列式中有两行(列)对应元 素成比例,行列式的值为0
推论:如果行列式的某行(列)的所有元素有公因子,则公因子可以提到行列式
符号的外面
行列式的转置等于它本身
行列式中的某一行(列)的每个元素都由两个数之和组成,D可以成为两个行列
式之和
行列式的某一行(列)加上另外一行(列)对应元素的k倍,行列式的值不变
按行(列)展开
余子式和代数余子式
余子式例子
去掉第一行第一列后剩下的矩阵按照原来的方式排列成一个新的矩阵,
称新矩阵为该矩阵的余子式
代数余子式Mij为余子式的值
按行(列)展开
n阶行列式 D=det(aᵢⱼ) 的某一行(列)的元素与另一行(列)对应元素的代数余子式乘积
的和等于零
阶行列式. D=det(aᵢⱼ) 等于它的任意一行(列)的各元素与其对应的代数余子式乘积的
和
行列式按k行(列展开)
k阶子式:保留划定的元素,使它们在另外成一个行列式,划定行和列数相同
若在n阶行列式D中,取定某k行(1≤k≤n),则这k行的元素组成的所有k阶子式分别与
它们的代数余子式的乘积之和等于D
克莱姆法则
概念
推论
方程齐次(等式右边全为0)则
若系数行列式不等于0,其只有0解
其有非0解,则其系数行列式为0。
中大控制工程矩阵论习题总结

矩阵论简明教程---徐仲(共计10道题)1、 求矩阵的Jordan 标准形和相应的相似变换矩阵。
1115211762621⎛⎫⎪- ⎪ ⎪--⎝⎭解答:A I -λ=)1(2+λλ=D 3(λ), λI -A 有2阶子式172111----λ=λ-4λ-4不是D 3(λ)的因子, 所以D 2(λ)=D 1(λ)=1, A 的初等因子为λ-1,2λ. A 的Jordan 标准形为J =⎪⎪⎪⎭⎫ ⎝⎛-000100001 设A 的相似变换矩阵为P=(p 1,p 2,p 3), 则由AP=PJ 得⎪⎩⎪⎨⎧==-=23211pAp Ap p Ap 0解出P=⎪⎪⎪⎭⎫ ⎝⎛-----2412311112.试将计算:8542234A A A A I -++-,其中A=102011010⎛⎫ ⎪- ⎪ ⎪⎝⎭解答:设f (λ)=4322458-++-λλλλ. A 的最小多项式为12)(3+-=λλλA m ,作带余除法,得f (λ)=(149542235-+-+λλλλ),)(λA m =1037242+-λλ, 于是f (A)=I A A 1037242+-=⎪⎪⎪⎭⎫ ⎝⎛----3461061950264833.求矩阵的最小多项式126103114⎛⎫-- ⎪⎪⎪--⎝⎭解答:λI -A=⎪⎪⎪⎭⎫ ⎝⎛---+41131621λλλ,标准形⎪⎪⎪⎭⎫ ⎝⎛--2)1(00010001λλ, A 的最小多项式为2)1(-λ;4.下列矩阵A 是否正规矩阵?若是,试求出酉矩阵U ,使得1U AU -为对角矩阵:A=222254245⎛⎫- ⎪- ⎪ ⎪--⎝⎭解答:A 是实对称矩阵. A I -λ=2)1)(10(--λλ,A 有特征值 10, 1, 1. 当λ=10时. 对应的齐次线性方程组 (10I -A)x=0的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--542452228~⎪⎪⎪⎭⎫ ⎝⎛000110102 由此求出特征向量p 1=(-1, -2, 2)T , 单位化后得e 1= (32,32,31--)T. 当λ=1时, 对应的齐次线性方程组 (I -A)x=0的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛-----442442221~⎪⎪⎪⎭⎫ ⎝⎛-000000221 由此求出特征向量 p 2=(-2, 1, 0)T, p 3=(2, 0, 1)T. 单位化后得e2=(0,51,52-)T , e 3=(535,534,532)T . 令U=⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---53503253451325325231, 则U 1-AU=⎪⎪⎪⎭⎫⎝⎛11105.设A ∈C 是Hermite 矩阵,证明A 是Hermite 正定矩形阵的充分必要条件是,存在Hermite 正定矩阵B ,使得2A B -证明:若A 是Hermit 正定矩阵,则由定理1.24可知存在n 阶酉矩阵U, 使得U H AU=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n λλλ21, i λ﹥0, I=1, 2, , n. 于是A=U⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n λλλ21UH= U⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n λλλ21UHU⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n λλλ21U H ,令B=U ⎪⎪⎪⎪⎪⎭⎫⎝⎛n λλλ21U H ,则A=B 2.6.证明:对nxn C 上的任一矩阵范数∙ 均有n I ≥1证明:因为I n ≠O, 所以n I >0.从而利用矩阵范数的相容性得:n n n I I I =≦nI n I ,即n I ≧17.设U 是n 阶酉矩阵,证明2U =1 利用定理2.12得122H 2===nI UU U8.设∙为nxn C 上的矩阵范数,λ为A ∈nxn C 的特征值,证明λ≤m m A 解答:设x 是对应于λ的特征向量, 则A x x m m λ=.又设v ⋅是C n 上与矩阵范数⋅相容的向量范数,那么vm vm v mx A x x ==λλ≦v m x A因v x >0, 故由上式可得mλ≦m A ⇒λ≦m m A .9.求矩阵130230206A ⎛⎫⎪= ⎪ ⎪-⎝⎭的Doolittle 分解与Crout 分解。
第1章-1 线性空间与线性变换

对∀α、β 、γ ∈ R 2,∀k、l ∈ R, 成立 (A1) 加法交换律: α + β = β + α,
(A2) 加法结合律: (α + β ) + γ = α + ( β + γ ),
1
矩阵分析简明教程
(A3) 具有加法单位元(零向量)θ ∈ R 2 ,使得 α +θ = α (A4) 具有加法逆元(负向量) −α ∈ R 2 ,使得 α + ( −α ) = θ (M1) 数乘的结合律:k ( lα ) = ( kl )α (M2) 数乘的单位元: 1⋅α = α (D1) 分配律1: k (α + β ) = kα + k β (D2) 分配律2: ( k + l )α = kα + lα
º span{α1 , α2 , , αr }
线性无关。
则必有 α r +1 ∈ V 且α r +1 ∉ W ,使得
定理1.1.2 定理 1.1.2 (基的扩张定理) 数域 F 上的 n 维线 性空间 V 中的任意一个线性无关向量组 中的任意 个线性无关向量组
α1 , α2 , , αr , αr+1
x1 = (α1 , , α n ) = (α1 , , α n ) x xn
= [ β1 , , β n ] y = (α 1 , , α n ) Px
项式按照多项式的加法以及数与多项式的乘法也构 成 F上的线性空间吗?
N ( A) ≡ { x ∈ R n | Ax = θ ,
A ∈ R m×n }
Ker ( A)
问:S ≡ { x ∈ R n | Ax = b, b ≠ 0, A ∈ R m×n } ?
简明线性代数教程(第三版)(柴伟文主编)思维导图

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
线性代数总结(西工大徐仲老师总结精华)

线性代数总结一、课程特点特点一:知识点比较细碎。
如矩阵部分涉及到了各种类型的性质和关系,记忆量大而且容易混淆的地方较多。
特点二:知识点间的联系性很强。
这种联系不仅仅是指在后面几章中用到前两章行列式和矩阵的相关知识,更重要的是在于不同章节中各种性质、定理、判定法则之间有着相互推导和前后印证的关系。
复习线代时,要做到“融会贯通”。
“融会”——设法找到不同知识点之间的内在相通之处;“贯通”——掌握前后知识点之间的顺承关系。
二、行列式与矩阵第一章《行列式》、第二章《矩阵》是线性代数中的基础章节,有必要熟练掌握。
行列式的核心内容是求行列式,包括具体行列式的计算和抽象行列式的计算,其中具体行列式的计算又有低阶和阶两种类型;主要方法是应用行列式的性质及按行\列展开定理化为上下三角行列式求解。
对于抽象行列式的求值,考点不在求行列式,而在于、、等的相关性质,及性质(其中为矩阵的特征值)。
矩阵部分出题很灵活,频繁出现的知识点包括矩阵运算的运算规律、、、的性质、矩阵可逆的判定及求逆、矩阵的秩的性质、初等矩阵的性质等。
三、向量与线性方程组向量与线性方程组是整个线性代数部分的核心内容。
相比之下,行列式和矩阵可视作是为了讨论向量和线性方程组部分的问题而做铺垫的基础性章节;后两章特征值、特征向量、二次型的内容则相对独立,可以看作是对核心内容的扩展。
向量与线性方程组的内容联系很密切,很多知识点相互之间都有或明或暗的相关性。
复习这两部分内容最有效的方法就是彻底理顺诸多知识点之间的内在联系,因为这样做首先能够保证做到真正意义上的理解,同时也是熟练掌握和灵活运用的前提。
解线性方程组可以看作是出发点和目标。
线性方程组(一般式)还具有两种形式:(Ⅰ)矩阵形式,其中,,(Ⅱ)向量形式,其中,向量就这样被引入了。
1)齐次线性方程组与线性相关、无关的联系齐次线性方程组可以直接看出一定有解,因为当时等式一定成立;印证了向量部分的一条性质“零向量可由任何向量线性表示”。
高等工程数学——中山大学

1) 特征向量法
设 AC
nn
, 如果 i 是 A 的单特征值, 则对应一
阶Jordan块 J i i ; 如果 i 是 A 的 ri ri 1 重特征
值, 则对应 i 有几个线性无关的特征向量, 就有几个 以 i 为对角元素的Jordan块, 这些Jordan块的阶数 之和等于 ri . 由 A 的所有特征值对应的Jordan块构成 的Jordan矩阵即为 A 的Jordan标准形. 2) 初等变换法 3) 行列式因子法
利用内积可以定义向量的长度和正交:
定义: 设 x 1 , 2 ,, n C n , 令
T
x
2
x, x k
k 1
n
2
称 x 2 为向量 x的长度或2范数. 定理 1.19: 设 x, y C , C , 则
n
(1) 当 x 0时, x 2 0 ; 当 x 0 时, x 2 0 (2) x x 2
i
1 i r r i i
的矩阵称为 ri 阶Jordan块. 由若干个Jordan块构成
的分块对角阵 J diagJ 1 , J 2 ,, J s 称为Jordan矩阵.
定理1.9(Jordan): 设 A C nn 则 A 一定与一个 , Jordan矩阵 J 相似. 且这个Jordan矩阵 J 除Jordan 块的排列顺序外由 A 唯一决定. 将方阵 A C nn 相似变换为Jordan标准形的方法:
答案: 正规矩阵
定义: 设 A C nn , 若 A 满足 AH A AAH ,
则称 A 为正规矩阵.
酉矩阵, 正交阵; Hermite阵, 实对称阵; 反Hermite
高等无机化学答案陈慧兰

高等无机化学答案陈慧兰【篇一:高等无机化学陈慧兰 7.3节】t>固体的导电性是由于固体中载流子的运动。
对于金属导体载流子是电子,半导体的载流子是电子或空穴。
固体电解质(solid electrolytes)具有与强电解质水溶液相当的导电性(见表 7-4)。
这类固体通过其中的离子迁移进行电荷传递,载流子是离子,故又称为固体离子导体 (solid ionic conductors)、快离子导体(fastionic conductors)或超离子导体( superionic conductors)。
早在1834年faraday就发现第一个固体电解质pbf2 ,其电导率随温度升高而连续增大,这种现象被称faraday相变。
1913年,发现agi在400 ℃以上离子电导率可以与液体电解质相比。
1961年合成了agi和ag2s 的固溶体ag3si,1967年发现了 rbag4i5 ,它们的室温离子电导率与液体电解质相当。
现在发现的固体电解质材料已达到数百种之多。
表7-5列出一些重要的固体电解质,它们大部分是氧化物或卤化物,晶格中存在着缺陷或可提供离子迁移的通道,部分离子处于无序状态。
如agcl晶体中,可能存在着schottiky和 frenkel两类缺陷,其中ag+ 离子在晶格中迁移方式(图7-27)可以按以下两种机制:(ⅰ)空穴机制,这种模式涉及晶格中空穴的运动,当晶体中出现空穴时,其附近的离子跃入该空穴,原来填充离子的位置出现新的空穴。
(ⅱ)空隙机制。
空隙的ag+ 离子跃入相邻的空隙空穴。
实际的固体电解质也可以是(ⅰ)和(ⅱ)的协同,可称为堆填子机制。
由于室温下原子或离子在固体中的扩散通常比气体、液体中的扩散慢得多,只有温度升高,缺陷的浓度增大,离子有足够的能量在体晶格中迁移,出现较大的离子导电现象。
ea是缺陷形成和运动所需激活能。
对于碱金属卤化物,ea值较高,因此只有在接近。
而一些在低温或室温下使用的固体电解质有较低活化能,电导率可与液体电解质相当。
