勾股定理的逆定理同步练习
勾股定理的逆定理-习题训练(含答案)

勾股定理的逆定理一、基础·巩固1.满足下列条件的三角形中,不是直角三角形的是( )A.三内角之比为1∶2∶3B.三边长的平方之比为1∶2∶3C.三边长之比为3∶4∶5D.三内角之比为3∶4∶52.如图18-2-4所示,有一个形状为直角梯形的零件ABCD ,AD ∥BC ,斜腰DC 的长为10 cm ,∠D=120°,则该零件另一腰AB 的长是________ cm (结果不取近似值).图18-2-4 图18-2-5 图18-2-63.如图18-2-5,以Rt △ABC 的三边为边向外作正方形,其面积分别为S 1、S 2、S 3,且S 1=4,S 2=8,则AB 的长为_________.4.如图18-2-6,已知正方形ABCD 的边长为4,E 为AB 中点,F 为AD 上的一点,且AF=41AD ,试判断△EFC 的形状.5.一个零件的形状如图18-2-7,按规定这个零件中∠A 与∠BDC 都应为直角,工人师傅量得零件各边尺寸:AD=4,AB=3,BD=5,DC=12 , BC=13,这个零件符合要求吗?图18-2-76.已知△ABC 的三边分别为k 2-1,2k ,k 2+1(k >1),求证:△ABC 是直角三角形.二、综合·应用7.已知a、b、c是Rt△ABC的三边长,△A1B1C1的三边长分别是2a、2b、2c,那么△A1B1C1是直角三角形吗?为什么?8.已知:如图18-2-8,在△ABC中,CD是AB边上的高,且CD2=AD·BD.求证:△ABC是直角三角形.图18-2-89.如图18-2-9所示,在平面直角坐标系中,点A、B的坐标分别为A(3,1),B(2,4),△OAB是直角三角形吗?借助于网格,证明你的结论.图18-2-910.阅读下列解题过程:已知a、b、c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.解:∵a2c2-b2c2=a4-b4,(A)∴c2(a2-b2)=(a2+b2)(a2-b2),(B)∴c2=a2+b2,(C)∴△ABC是直角三角形.问:①上述解题过程是从哪一步开始出现错误的?请写出该步的代号_______;②错误的原因是______________;③本题的正确结论是__________.11.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.12.已知:如图18-2-10,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3.求:四边形ABCD的面积.图18-2-10参考答案一、基础·巩固1.思路分析:判断一个三角形是否是直角三角形有以下方法:①有一个角是直角或两锐角互余;②两边的平方和等于第三边的平方;③一边的中线等于这条边的一半.由A 得有一个角是直角;B 、C 满足勾股定理的逆定理,所以应选D.答案:D2.解:过D 点作DE ∥AB 交BC 于E, 则△DEC 是直角三角形.四边形ABED 是矩形,∴AB=DE.∵∠D=120°,∴∠CDE=30°.又∵在直角三角形中,30°所对的直角边等于斜边的一半,∴CE=5 cm.根据勾股定理的逆定理得,DE=3551022=- cm.∴AB=3551022=- cm.3.思路分析:因为△ABC 是Rt △,所以BC 2+AC 2=AB 2,即S 1+S 2=S 3,所以S 3=12,因为S 3=AB 2,所以AB=32123==S . 答案:324.思路分析:分别计算EF 、CE 、CF 的长度,再利用勾股定理的逆定理判断即可.解:∵E 为AB 中点,∴BE=2.∴CE 2=BE 2+BC 2=22+42=20.同理可求得,EF 2=AE 2+AF 2=22+12=5,CF 2=DF 2+CD 2=32+42=25.∵CE 2+EF 2=CF 2,∴△EFC 是以∠CEF 为直角的直角三角形.5.分析:要检验这个零件是否符合要求,只要判断△ADB 和△DBC 是否为直角三角形即可,这样勾股定理的逆定理就可派上用场了.解:在△ABD 中,AB 2+AD 2=32+42=9+16=25=BD 2,所以△ABD 为直角三角形,∠A =90°.在△BDC 中,BD 2+DC 2=52+122=25+144=169=132=BC 2.所以△BDC 是直角三角形,∠CDB =90°.因此这个零件符合要求.6.思路分析:根据题意,只要判断三边之间的关系符合勾股定理的逆定理即可.证明:∵k2+1>k2-1,k2+1-2k=(k-1)2>0,即k2+1>2k,∴k2+1是最长边.∵(k2-1)2+(2k)2=k4-2k2+1+4k2=k4+2k2+1=(k2+1)2,∴△ABC是直角三角形.二、综合·应用7.思路分析:如果将直角三角形的三条边长同时扩大一个相同的倍数,得到的三角形还是直角三角形(例2已证).8.思路分析:根据题意,只要判断三边符合勾股定理的逆定理即可.证明:∵AC2=AD2+CD2,BC2=CD2+BD2,∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2.∴△ABC是直角三角形.9.思路分析:借助于网格,利用勾股定理分别计算OA、AB、OB的长度,再利用勾股定理的逆定理判断△OAB是否是直角三角形即可.解:∵ OA2=OA12+A1A2=32+12=10,OB2=OB12+B1B2=22+42=20,AB2=AC2+BC2=12+32=10,∴OA2+AB2=O B2.∴△OAB是以OB为斜边的等腰直角三角形.10.思路分析:做这种类型的题目,首先要认真审题,特别是题目中隐含的条件,本题错在忽视了a有可能等于b这一条件,从而得出的结论不全面.答案:①(B) ②没有考虑a=b这种可能,当a=b时△ABC是等腰三角形;③△ABC是等腰三角形或直角三角形.11.思路分析:(1)移项,配成三个完全平方;(2)三个非负数的和为0,则都为0;(3)已知a、b、c,利用勾股定理的逆定理判断三角形的形状为直角三角形.解:由已知可得a2-10a+25+b2-24b+144+c2-26c+169=0,配方并化简得,(a-5)2+(b-12)2+(c-13)2=0.∵(a-5)2≥0,(b-12)2≥0,(c-13)2≥0.∴a -5=0,b -12=0,c -13=0.解得a=5,b=12,c=13.又∵a 2+b 2=169=c 2,∴△ABC 是直角三角形.12.思路分析:(1)作DE ∥AB ,连结BD ,则可以证明△ABD ≌△EDB (ASA );(2)DE=AB=4,BE=AD=3,EC=EB =3;(3)在△DEC 中,3、4、5为勾股数,△DEC 为直角三角形,DE ⊥BC ;(4)利用梯形面积公式,或利用三角形的面积可解.解:作DE ∥AB ,连结BD ,则可以证明△ABD ≌△EDB (ASA ),∴DE=AB=4,BE=AD=3.∵BC=6,∴EC=EB=3.∵DE 2+CE 2=32+42=25=CD 2,∴△DEC 为直角三角形.又∵EC=EB=3,∴△DBC 为等腰三角形,DB=DC=5.在△BDA 中AD 2+AB 2=32+42=25=BD 2,∴△BDA 是直角三角形.它们的面积分别为S △BDA =21×3×4=6;S △DBC =21×6×4=12. ∴S 四边形ABCD =S △BDA +S △DBC =6+12=18.。
人教版初中数学八年级下册第十七章《172勾股定理的逆定理》同步练习题(含答案).docx

《17・2勾股定理的逆定理》同步练习题一、选择题(每小题只有一个正确答案)1.下列各组数是勾股数的是()A. 3, 4, 5B. 7, 8, 9C.9, 41, 47D. 52, 122, 1322.AABC中,ZA, ZB, ZC的对边分别记为a, b, c,由下列条件不能判定AABC为直角三角形的是()A. ZA+ZB二ZCB. ZA: ZB: ZC=1: 2: 3C. a2=c2 - b2D. a: b: c=3: 4: 63.在厶ABC中,AB=1, AC=2, BC=領,则该三角形为()A.锐角三角形B.直角三角形C.钝角三角形D.等腰直角三角形4.在ZiABC 屮,AB=A/2 , BC=V5 , AoJL 贝】J ()A. ZA二90°B. ZB二90°C. ZC二90°D. ZA二ZB5.已矢Fl AD 为AABC 的中线,且AB = 17, BC = 16, AD = 15,则AC 等于()A. 15B. 16C. 17D. 186.给出长度分别为7cm, 15cm, 20cm, 24cm, 25cm的五根木棒,分别取其中的三根首尾连接,最多可以搭成的直角三角形的个数为()A. 1个B. 2个C. 3个D. 4个127.如图,\咏中,AU3, BU 5, ADIBC^BC^^ D, AD=—f延长BC 至E 使得5CE二BC,将MBC沿AC翻折得到MFC,连接EF,则线段EF的长为A. 6B.832 32C. —D.—5 3二、填空题8.若|a・7| +心-24+ (c-25)?二0,则以a、b、c为三边的三角形的形状是___________ .9.一个三角形的三边之比为5: 12: 13,它的周长为60,则它的面积是 ____________ .10.木工师傅做一个长方形桌面,量得它的长为80分米,宽为60分米,对角线为100 分米,则这个桌面_•(填“合格〃或"不合格〃)□.如图所示的一块地,ZADC = 90° , AD = 4f CD = 3, AB = 13, BC = 12, 求这块地的面积 .12.____________________________________________________________ 如图所示,ABLBC, AB = 2运,CD二5, AD=3, BC=2,则ZA二_______________________ 度.三、解答题13.已知:在AABC中,ZA, ZB, ZC的对边分别是a, b, c,三边分別为下列长度, 判断该三角形是不是直角三角形,并指出哪一个角是直角.(1)a=V3, b = 2匹,c=V5;(2)a=5, b=7, c=9;(3)a=2, b=V3, c=V7;(4)a=5, b=2V6, c=l.14.如图,在△ ABC 中,AB = 8cm, AC = 6cm, BC=10cm,点D在AB ±,且BD = CD, 求ABDC的面积.15.如图,在RtAABC 中,CD丄AB,垂足为D,如果CD=12, 4D=16, BD=9,那么AABC 是直角三角形吗?请说明理由.C16.如图是一个零件的示意图,测量AB=4 cm, BC=3 cm, CD=12 cm, AD=13 cm, ZABC=90°,根据这些条件,你能求!l!ZACD的度数吗?试说明理由.参考答案I.A2. D3. B4. A5. C6・ B7. A&直角三角形9.12010.合格II.2412.6013.解析:(1) *.* a=V3» b=2V2, c=V5»a2=3, b2=8, C2=5,13+5=8,:.a2+c2=b2,•••△ABC是直角三角形,ZB=90°;(2)*.*a=5, b=7, c=9,Aa2=25, b2=49, c2=81.•・• 25+49=74邦1,・・・此三角形不是直角三角形;(3)a=2, b=V3, c=V7,a2=4, b2=3, C2=7.V4+3=7,a2+b2=c2,A A ABC是直角三角形,ZC=90°;(4)*.*a=5, b=2V6, c=l,a2=2 5, b2=24, c2= 1.V24+1=25,b2+c2=a2,A A ABC是直角三角形,ZA=90°.13.—cm24解析:*• AB— 8cm, AC— Gem, BC= 10cm,:.AB2+AC1 = BC1i・・・ZBAC=90。
人教版八年级下册 第十七章 勾股定理 17.2 勾股定理的逆定理 同步练习(包含答案)

勾股定理的逆定理同步练习一、选择题1、下列各组数中,能构成直角三角形的是()。
A. 4,5,6 B. 1,1, C. 6,8,11 D. 5,12,232、下列各组数中不能作为直角三角形的三边长的是()A. 2, 3,4;B. 7, 24, 25;C. 6, 8, 10;D. 9, 12, 15.3、△ABC的三边为a、b、c,且,则( )A、△ABC是锐角三角形;B、c边的对角是直角;C、△ABC是钝角三角形;D、a边的对角是直角;4、在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为()A、 B、C、D、5、用长度分别为7,15,20,24,25的五根小木棒首尾相连搭成两个直角三角形,正确的是()6、已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且,四边形ABCD的面积是()A.18cm2 B.36cm2 C.72cm2 D.90cm27、已知,如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,△ABD中,∠ADB=90°,DA=DB,则△ADB的面积是()A. 24B. 50C. 25D. 208、一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,则木板的面积是()A.24 B.60 C. 30 D.129、小丽和小芳二人同时从公园去图书馆,都是每分钟走50米,小丽走直线用了10分钟,小芳先去家拿了钱去图书馆,小芳到家用了6分,从家到图书馆用了8分,小芳从公园到图书馆拐了个( )角.A、锐角B、直角C、钝角D、不能确定10、如图,在梯形ABCD中,AB//DC,∠D=90o,AD=DC=4,AB=2,F为AD的中点,则点F到BC的距离是()A. B. C.2 D.11、下列命题①如果a、b、c为一组勾股数,那么4a、4b、4c仍是勾股数;②含有30°角的直角三角形的三边长之比是3:4:5;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2∶b2∶c2=2∶1∶1.其中正确的是()A.①② B.①④ C.①③ D.②④12、如图,用四个螺丝将四条不可弯曲的木条围成一个木框ABCD,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则现在A、C相对的螺丝的距离的最大值,以及现在B、D相对的螺丝的距离的最大值分别为()A. 5和7B. 10和7C. 5和8D. 10和813、如图,长方形ABCD中,AD=8cm,CD=4cm.点P是边AD上的一个点,PA=PC,Q是AB边上的一个点,, △PCQ 是()A. 直角三角形B. 等腰三角形C. 锐角三角形D. 钝角三角形14、如图,南北向MN为我国领域,即MN以西为我国领海,以东为公海.上午9时50分,我反走私A艇发现正东方向有一走私艇C以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C两艇的距离是13海里,A、B两艇的距离是5海里;反走私艇测得离C艇的距离是12海里.若走私艇C的速度不变,最早会在什么时间进入我国领海?()A. 10时41分 B. 10时30分 C. 10时51分 D. 11时二、填空题15、已知三角形的三边长分别为3,5,,则该三角形最长边上的高为16、如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为.17、如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD=18、如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10,AB=20.求∠A的度数.19、如图,在直角△ABC中,∠C=90°,AC=6,BC=8,P,Q分别为边BC,AB上的两个动点,若要使△APQ是等腰三角形且△BPQ是直角三角形,则AQ=_ .20、如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为cm2.三、简答题21、已知:如图,AB=3,AC=4,AB⊥AC,BD=12,CD=13.(1)求BC的长度;(2)线段BC与线段BD的位置关系是什么?说明理由.22、如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断AD与AB是否垂直?请说明理由.23、已知△ABC中,a2+b2+c2=10a+24b+26c-338,试判定△ABC的形状,并说明你的理由.24、如图所示,在△ABC中,AB=20,AC=12,BC=16,把△ABC折迭,使AB落在直线AC上,求重迭部分(阴影部分)的面积.25、如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D、E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.(1)求证:BH=AC;(2)求证:BG2-GE2=EA2.参考答案一、选择题1、B;2、A;3、D;;4、B;5、C;6、B;7、C;8、A;9、B;10、A;11、B;12、a;13、A;14、A;二、填空题15、16、1417、1318、∠A=30°.19、或20、18三、简答题21、解:(1)∵AB=3,AC=4,AB⊥AC,∴BC==5;(2)BC⊥BD,理由如下:∵BC=5,BD=12,CD=13,∴BC2+BD2=25+144=169=132=CD2,∴∠CBD=90°,∴BC⊥BD.22、解:与会互相垂直。
人教版八年级数学下册172_勾股定理的逆定理同步习题+答案
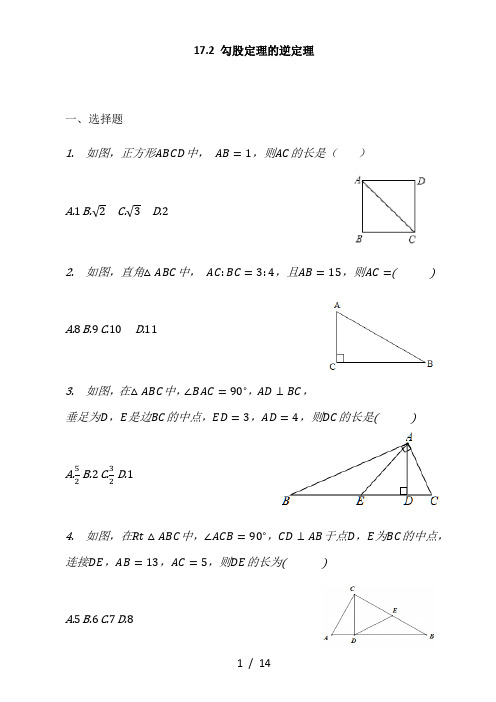
17.2 勾股定理的逆定理一、选择题1. 如图,正方形ABCD中,AB=1,则AC的长是()A.1B.√2C.√3D.22. 如图,直角△ABC中,AC:BC=3:4,且AB=15,则AC=()A.8B.9C.10D.113. 如图,在△ABC中,∠BAC=90∘,AD⊥BC,垂足为D,E是边BC的中点,ED=3,AD=4,则DC的长是()A.5 2B.2C.32D.14. 如图,在Rt△ABC中,∠ACB=90∘,CD⊥AB于点D,E为BC的中点,连接DE,AB=13,AC=5,则DE的长为()A.5B.6C.7D.85. 在△ABC中,∠A、∠B、∠C的对应边分别是a、b、c,若∠A+∠C=90∘,则下列等式中成立的是()A.a2+b2=c2B.b2+c2=a2C.a2+c2=b2D.c2−a2=b26. 若直角三角形的三边长为6,8,m,则m2的值为()A.10B.100C.28D.100或287. 如图,在平行四边形ABCD中,两内角的平分线交于点P,PB=5,PC=2,则AD的长是()A.8B.√29C.√21D.10.58. 如图,在Rt△ABC中,∠A=90∘,BC=2.5cm,AC=1.5cm,则AB的长为()A.3.5cmB.2cmC.3cmD.4cm9. 如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF 等于()A.2 3B.1C.32D.210. 如图,在△ABC中,∠BAC=90∘,AB=3,AC=4,AD平分∠BAC交于点D,则CD的长为()A.125B.157C.207D.12711. 如图,正方形A、B、C的边长分别为直角三角形的三边长,若正方形A,B的边长分别为3和5,则正方形C的面积为()A.16B.12C.15D.1812. 在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+2S2+2S3+S4=()A.5B.4C.6D.、10二、填空题13. 一直角三角形的两边长分别为4和5,则第三边的长为________.14. 如图所示:是一段楼梯,高BC是3m,斜边AC是5m,如果在楼梯上铺上地毯,那么地毯至少需要长_______m.15. 如图,在矩形ABCD中,AB=3,AD=4.过点A作AG⊥BD于G,则AG等于________.16. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为________.三、解答题17. 如图,在四边形ABCD中,AB=4,BC=3,CD=12,AD=13,∠B=90∘,求四边形ABCD的面积.18. 如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知该纸片宽AB=3cm,长BC=5cm.求EC的长.17.2 勾股定理的逆定理一、选择题1.【答案】B【解答】解:∵ABCD为正方形,∴AB=BC=1,∴在Rt△ABC中,AC=√AB2+BC2=√12+12=√2.故选B.2.【答案】B【解答】解:设AC=3k,则BC=4k.在Rt△ABC中,AC=3k,BC=4k,AB=15,根据勾股定理,得(3k)2+(4k)2=152,解得k=3,∴AC=3k=3×3=9.3.【答案】B【解答】解:由勾股定理,得:AE=√AD2+DE2=√42+32=5.∵∠BAC=90∘,E是边BC的中点,∴BC=2AE=10,∴EC=5,∴DC=EC−ED=2.故选B.4.【答案】B【解答】解:由题设在Rt△ACB中,∵AB=13,AC=5,∴BC=√AB2−AC2=√132−52=12.∵CD⊥AB,E是CB中点,CB=6.∴DE=12故选B.5.【答案】C【解答】∵在△ABC中,∠A+∠C=90∘,∴∠B=90∘,∴△ABC为直角三角形,则根据勾股定理得:a2+c2=b2.6.【答案】D【解答】解:①当边长为8的边是直角边时,m2=62+82=100;②当边长为8的边是斜边时,m2=82−62=28;综上所述,m2的值为100或28.故选D.7.【答案】B【解答】解:在平行四边形ABCD中,∠ABC+∠BCD=180∘,又因为两内角的平分线交于点P,所以∠PBC+∠PCB=90∘,所以∠BPC=90∘,故在Rt△BPC中,BP2+PC2=BC2,故AD=BC=√BP2+PC2=√29.故选B.8.【答案】B【解答】解:∵BC=2.5cm,AC=1.5cm,∠A=90∘,根据勾股定理:AB=2−1.52=2cm.故选B.9.【答案】C【解答】∵四边形ABCD是矩形,∴AD=BC=5,∠D=∠B=∠C=90∘,∵AF平分∠DAE,EF⊥AE,∴DF=EF,由勾股定理得:AE2=AF2−EF2,AD2=AF2−DF2,∴AE=AD=5,在△ABE中由勾股定理得:BE=2−AB2=3,∴EC=5−3=2,∵∠BAE+∠AEB=90∘,∠AEB+∠FEC=90∘,∴∠BAE=∠FEC,∴△ABE∽△ECF,∴ABCE =BECF,∴42=3CF,∴CF=32.10.【答案】C【解答】过D作DN⊥AC于N,DM⊥AB于M,则∠DNA=∠CAB=∠DMA=90∘,∵AD平分∠CAB,∴DN=DM,∴四边形AMDN是正方形,设正方形的边长是x,则AN=DN=x,∴DN // AB,∴△CND∽△CAB,∴DNAB =CNAC,∴x3=4−x4,解得:x=127,在Rt△CND中,CN=4−127=167,DN=127,由勾股定理得:CD=207,11.【答案】A【解答】如图所示:正方形A、B的边长分别为3和5,DF=5EF=3DE=√52−32=4故县方形C的面积为412.【答案】C【解答】如图,∵ 图中的四边形为正方形,∴ ∠ABD =90∘,AB =DB ,∴ ∠ABC +∠DBE =90∘,∵ ∠ABC +∠CAB =90∘,∴ ∠CAB =∠DBE ,∵ 在△ABC 和△BDE 中,{∠ACB =∠BED ∠CAB =∠EBD AB =BD,∴ △ABC ≅△BDE(AAS),∴ AC =BE ,∵ DE 2+BE 2=BD 2,∴ ED 2+AC 2=BD 2,∵ S 1=AC 2,S 2=DE 2,BD 2=1,∴ S 1+S 2=1,同理可得S 2+S 3=2,S 3+S 4=3,∴ S 1+2S 2+2S 3+S 4=1+2+3=6.二、 填空题 13.【答案】√41或3【解答】解:当4和5都是直角边时,则第三边是2+52=√41;当5是斜边时,则第三边是3.故答案为:√41或3.14.【答案】7【解答】解:∵△ABC是直角三角形,BC=3m,AC=5m,∴AB=√AC2−BC2=√52−32=4(m),∴如果在楼梯上铺地毯,那么至少需要地毯为AB+BC=4+3=7(m).故答案为:7.15.【答案】________、125【解答】解:四边形ABCD是矩形,加BAD=90∘.BD=2+AD2=√32+42=5由三角形的面积公式得,S△ABD=12BD⋅AG=12AB⋅AD…AG=AB⋅ADBD =125故答案为:12516.【答案】9【解答】此题暂无解答三、解答题(本题共计 2 小题,每题10 分,共计20分)17.【答案】24【解答】解:连接AC,∠B=90∘AC=√42+32=5=5.AC=90∘…四边形ABCD的面积=12×5×12−12×3×4=24________DA________18.【答案】EC=−3【解答】解:由折叠可知|AD=AF=5cm,DE=EF∠B=90∘AB2+BF2=AF2∵AB=3cm,AF=5cmBF=4cmBC =5cmFC=1cm∠C=90∘∴EC2+F2=EF2设EC=x,则DE=EF=3−x(3−x)2=12+x2x=4 3即EC=43。
《17.2勾股定理的逆定理》同步练习测试及答案解析

《17.2勾股定理的逆定理》同步练习测试及答案解析(第1课时)A.3,4,5 B.6,8,10 C,2, D.5,12,13 C.如果,那么D.等边三角形的三个角都等于600C的逆命题是:如果,那么;3.已知三角形三边长为,如果,则的形状是().A.以为斜边的直角三角形B.以为斜边的直角三角形C.以为斜边的直角三角形 D.不是直角三角形解析:将式子左边变形得: ,因为,,,所以,,,即,,,又因为,所以,所以是以为斜边的直角三角形.解析:因为,所以该三角形为直角三角形且两条直角边分别为5cm、12cm,所以面积=.5.已知为的三边长,且满足,则它的形状为.解析:因为式子可变形为即,所以或,即或,所以为直角三角形或等腰三角形.6.有下列判断:①△ABC中,,则△ABC不是直角三角形;②△ABC是直角三角形,∠C=900,则;③若△ABC中,,则△ABC是直角三角形;④若△ABC是直角三角形,则,以上判断正确的是(填序号).解析:根据勾股定理的逆定理,一个三角形中两条较小边长的平方和等于最大边长的平方,那么这个三角形是直角三角形,①中三边大小关系未知,或有可能成立,故①是错误的;根据勾股定理②是正确的;③中可变形为,④中变形为即,所以③和④都正确;所以正确的序号是②③④.7.已知是的三边长,根据下列条件,判断是不是直角三角形.解析:①∵a>c>b,,∴∵b>c>a,,∴8.在中,,,,其中是正整数,且.试判断是否是直角三角形.答案: 是直角三角形.解析:因为是正整数,且,,所以,,即,因为,又因为,所以,所以是直角三角形.《17.2勾股定理的逆定理》同步练习测试及答案解析(第2课时)一、精心选一选(每小题只有一个正确选项,请把正确选项的代号填在题后的括号内).1.下列四组数据:①8,17,17;②9,12,15;③1.2;1.5,2;④7,24,25,其中是勾股数的有().A.1组 B.2组 C.3组 D.4组A.∠A=∠B-∠C B.a:b:c=1::2C.∠A:∠B:∠C=3:4:5 D.A选项中关系式∠A=∠B-∠C变形为∠A+∠C=∠B,因为∠A+∠C+∠B=180°,所以求得∠B=90°,所以△ABC为直角三角形;B选项中设,则即,所以为直角三角形;C选项中设的度数分别为,则,,所以,,,所以不是直角三角形;D选项变形为,所以为直角三角形.故答案是C.分别8,8,16,④中三边长平方分别为10,13,17,⑤中三边长平方分别为13,13,26,⑥中三边长平方分别为10,13,17.由勾股定理的逆定理可知①③⑤是直角三角形,由勾股定理可知②④⑥均不是直角三角形.答案:或5.解析:当斜边长为4时,第三边长=;当第三边是斜边时,第三边长=.解析:小明所走的三段路程看成是三条线段,三条线段围成一个三角形且三边长度分别是80m,60m,100m,因为,所以这个三角形是直角三角形,所以小明向东走80m后,又走60m的方向是与原方向垂直的方向,所以答案是向南或向北.6.已知的三边分别为,且,,,则的形状是.解析:,,,,即,又因为,所以,所以为直角三角形.7.如图所示的一块地,,,,,,求这块地的面积.答案:.解析:连接,将题目中不规则的四边形面积转化成两个直角三角形的面积差.连,∵∴∵,,∴∴∴这块地的面积为.8.如图,在港有甲、乙两艘渔船,若甲船沿北偏东600方向,以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度前进,1小时后甲船到达岛,乙船到达岛,且岛与岛相距17海里,你能知道乙船沿哪个方向航行吗?,,∵,∴∴∴。
勾股定理的逆定理 同步练习(含答案)

7.4勾股定理的逆定理1.下列各组数据中,不能作为直角三角形三边长的是( ) A.9,12,15 B.43,1,45 C.0.2,0.3,0.4 D.40,41,9 2.满足下列条件的三角形中,不是直角三角形的是( ) A.三个内角比为1∶2∶1 B.三边之比为1∶2∶5 C.三边之比为3∶2∶5 D. 三个内角比为1∶2∶33.已知三角形两边长为2和6,要使这个三角形为直角三角形,则第三边的长为( ) A.2 B.102 C.10224或 D.以上都不对4. 五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )715242520715202425157252024257202415(A)(B)(C)(D)5. △ABC 的三边分别是7、24、25,则三角形的最大内角的度数是 .6.三边为9、12、15的三角形,其面积为 .7.已知三角形ABC 的三边长为c b a ,,满足18,10==+ab b a ,8=c ,则此三角形为 三角形.8.在三角形ABC 中,AB=12cm ,AC=5cm ,BC=13cm ,则BC 边上的高为AD= cm . 9. 如图,已知四边形ABCD 中,∠B =90°,AB =3,BC =4,CD =12,AD =13, 求四边形ABCD 的面积.10. 如图,E 、F 分别是正方形ABCD 中BC 和CD 边上的点,且AB =4,CE =41BC ,F 为CD 的中点,连接AF 、AE ,问△AEF 是什么三角形?请说明理由.11. 如图,AB 为一棵大树,在树上距地面10m 的D 处有两只猴子,它们同时发现地面上的C 处有一筐水果,一只猴子从D 处上爬到树顶A 处,利用拉在A 处的滑绳AC ,滑到C 处,另一只猴子从D 处滑到地面B ,再由B 跑到C ,已知两猴子所经路程都是15m ,求树高AB .12. 观察下列勾股数:第一组:3=2×1+1, 4=2×1×(1+1), 5=2×1×(1+1)+1; 第二组:5=2×2+1, 12=2×2×(2+1), 13=2×2×(2+1)+1; 第三组:7=2×3+1, 24=2×3×(3+1), 25=2×3×(3+1)+1; 第三组:9=2×4+1, 40=2×4×(4+1), 41=2×4×(4+1)+1; ……观察以上各组勾股数的组成特点,你能求出第七组的c b a ,,各应是多少吗?第n 组呢?BE参考答案1.C ;2.C ;3.C ,提示:当已经给出的两边分别为直角边时,第三边为斜边=;1026222=+当6为斜边时,第三边为直角边=242622=-;4. C ;5.90°提示:根据勾股定理逆定理得三角形是直角三角形,所以最大的内角为 90°.6.54,提示:先根基勾股定理逆定理得三角形是直角三角形,面积为.5412921=⨯⨯ 7.直角,提示:2222222864182100,1002,100)(c b a ab b a b a ===⨯-=+=++=+得;8.1360,提示:先根据勾股定理逆定理判断三角形是直角三角形,再利用面积法求得AD ⨯⨯=⨯⨯132151221; 9.解:连接AC ,在Rt △ABC 中, AC 2=AB 2+BC 2=32+42=25, ∴ AC =5. 在△ACD 中,∵ AC 2+CD 2=25+122=169, 而 AB 2=132=169,∴ AC 2+CD 2=AB 2,∴ ∠ACD =90°. 故S 四边形ABCD =S △ABC +S △ACD =21AB ·BC +21AC ·CD =21×3×4+21×5×12=6+30=36.10. 解:由勾股定理得AE 2=25,EF 2=5, AF 2=20,∵AE 2= EF 2 +AF 2, ∴△AEF 是直角三角形11. 设AD =x 米,则AB 为(10+x )米,AC 为(15-x )米,BC 为5米,∴(x +10)2+52=(15-x )2,解得x =2,∴10+x =12(米)12. 解:第七组,.1131112,112)17(72,15172=+==+⨯⨯==+⨯=c b a 第n 组,1)1(2),1(2,12++=+=+=n n c n n b n a。
勾股定理的逆定理专题训练(含答案)

勾股定理的逆定理专题训练(含答案)
1.三角形ABC的两边分别为5和12,另一边c为奇数,并且a+b+c是3的倍数。
求c的值和三角形的类型。
2.三角形中两条较短的边为a+b和a-b(a>b),求第三条边使得三角形为直角三角形。
3.已知三角形ABC的三边a,b,c满足a²+b²+c²+50=2(m-1)余m+1,求三角形的类型。
4.已知三角形ABC中,BC=6,BC边上的高为7,求AC 边上的高。
5.已知一个三角形的三边分别为3k,4k,5k(k为自然数),求三角形的类型和理由。
6.已知一个三角形的三边分别为7cm,24cm,25cm,求三角形的面积。
7.给出几组数,判断哪组能构成直角三角形的三边长。
8.给出几组数,判断哪组能构成直角三角形的三边长。
9.等边三角形的三条高把这个三角形分成直角三角形的个数是多少?
10.已知四边形ABCD中,AB=3,BC=4,CD=12,
AD=13,求四边形的面积。
11.已知三角形ABC中,AC=17,AD=8,CD=15,
AB=10,求三角形的类型和面积。
12.已知三角形ABC中,AB=17cm,BC=30cm,求三角形的类型和面积。
13.判断一个机器零件是否符合要求。
14.已知四边形ABCD中,∠B=90,BC上的中线
AD=8cm,判断三角形ABC的类型和理由。
15.为了庆祝红宝石婚,XXX和XXX举办了一场数学竞赛,其中包括了勾股定理的逆定理的专题训练。
勾股定理逆定理练习题

勾股定理逆定理练习题一、选择题1. 在直角三角形中,如果已知两条直角边的长度分别为a和b,那么斜边的长度为:A. √(a^2 + b^2)B. a + bC. a * bD. a / b2. 如果三角形的三边长分别为3,4,5,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定3. 勾股定理逆定理指出,如果一个三角形的三边长满足a^2 + b^2 = c^2,那么这个三角形是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形4. 在一个三角形中,如果最长边的平方等于其他两边平方和,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不是三角形5. 如果三角形的三边长满足a^2 + c^2 = b^2,那么这个三角形的最长边是:A. aB. bC. cD. 不能确定二、填空题6. 在直角三角形中,如果已知斜边长度为13,一条直角边长度为5,那么另一条直角边的长度是________。
7. 勾股定理逆定理可以用来判断一个三角形是否是________。
8. 如果一个三角形的三边长分别为7,24,25,根据勾股定理逆定理,这个三角形是________。
9. 在一个三角形中,如果两边长分别为8和15,要使这个三角形是直角三角形,第三边的长度至少是________。
10. 如果三角形的三边长满足x^2 + y^2 = z^2,其中z是最长边,那么这个三角形是________。
三、解答题11. 已知三角形ABC的三边长分别为AB=9,BC=12,AC=15,判断三角形ABC是否是直角三角形,并说明理由。
12. 在三角形DEF中,DE=8,EF=15,DF=17,使用勾股定理逆定理判断三角形DEF是否是直角三角形。
13. 一个三角形的三边长分别为a、b和c,如果a^2 + b^2 = c^2,求证这个三角形是直角三角形。
14. 已知三角形GHI的三边长分别为GH=7,HI=24,IG=25,求证三角形GHI是直角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
18.2 勾股定理的逆定理二
◆回顾归纳
1.如果△ABC的三边长a,b,c满足a2+b2=c2,则△ABC是______三角形,_____=90°,•这个定理叫做_______.
2.一个命题成立,那么它的逆命题_______成立.
◆课堂测控
测试点一勾股定理的逆定理
1.已知△ABC的三边长a,b,c分别为6,8,10,则△ABC______(•填“是”或“不是”)直角三角形.
2.△ABC中,AB=7,AC=24,BC=25,则∠A=______.
3.△ABC的三边分别为下列各组值,其中不是直角三角形三边的是()
A.a=41,b=40,c=9 B.a=1.2,b=1.6,c=2
C.a=1
2,b=1
3
,c=1
4
D.a=3
5
,b=4
5
,c=1
4.(分析判断题)在解答“判断由长为6
5,2,8
5
的线段组成的三角形
是不是直角三角形”一题中,小明是这样做的:
解:设a=6
5,b=2,c=8
5
.
因为a2+b2=(6
5)2+22=13664
2525
=c2.
所以由a,b,c组成的三角形不是直角三角形,你认为小明的解答正确吗?•请说明理由.
测试点二逆命题与逆定理
5.下列各命题都成立,写出它们的逆命题,这些逆命题成立吗?(1)内错角相等,两直线平行;
(2)对顶角相等;
(3)全等三角形的对应角相等;
(4)如果两个实数相等,那么它们的绝对值相等.
◆课后测控
1.以下列数组为三角形的边长:(1)5,12,13;(2)10,12,13;
(3)7,24,25;(4)6,8,10,其中能构成直角三角形的有()A.4组B.3组C.2组D.1组
2.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是()
3.下列命题中,真命题是()
A.如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B.如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C.若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D.如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为ab
c
4.下列命题的逆命题是真命题的是()
A.若a=b,则a2=b2B.全等三角形的周长相等
C.若a=0,则ab=0 D.有两边相等的三角形是等腰三角形5.△ABC中,BC=n2-1,AC=2n,AB=n2+1(n>1),则这个三角形是______.
6.如果三角形的三边长为1.5,2,2.5,那么这个三角形最短边上的高为______.
7.A,B,C三地的位置及两两之间的距离如图所示,则点C•在点B•的方位是_____
8.如图所示,四边形ABCD中,BA⊥DA,AB=2,AD=2CD=3,BC=5,求∠ADC的度数.
9.写出下列命题的逆命题,并判断真假.
(1)如果a=0,那么ab=0;
(2)如果x=4,那么x2=16;
(3)面积相等的三角形是全等三角形;
(4)如果三角形有一个内角是钝角,则其余两个角是锐角;(5)在一个三角形中,等角对等边.
10.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q 从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,问过3秒时,△BPQ的面积为多少?
◆拓展创新
11.能够成为直角三角形三边长的三个正整数,我们称之为一组勾股数,•观察下列表格所给出的三个数a,
b,c,a<b<c.
(1)试找出它们的共同点,并证明你的
结论.
9,40,41
(2)写出当a=17时,b,c的值.
答案
回顾归纳
1.直角,∠C,勾股定理的逆定理
2.不一定
课堂测控
1.是2.90°点拨:BC2=AB2+AC2
3.C 点拨:计算两短边的平方和与最长边的平方比较.
4.不正确.因为6
5<2,8
5
<2,且(6
5
)2+(8
5
)2=22,即a2+c2=b2,
所以此三角形为直角三角形.5.(1)两直线平行,内错角相等.成立.
(2)如果两个角相等,那么它们是对顶角,不成立.
(3)如果两个三角形的对应角相等,则它们全等.不成立.
(4)如果两个实数的绝对值相等,那么它们相等,不成立.课后测控
1.B 点拨:有(1)(3)(4)三组.
2.C 3.D 4.D
5.直角三角形点拨:BC2+AC2=AB2.
6.6
7.正南方向
5
8.∵AB⊥AD,AB=2,
∴BD=,
∴AB=1
BD,∠ADB=30°,
2
∵BD2+DC2=42+32=52,
∴BD2+DC2=BC2.
∴∠BDC=90°,∴∠ADC=120°.
9.(1)的逆命题是:如果ab=0,那么a=0,它是一个假命题.(2)的逆命题是:如果x2=16,那么x=4,它是一个假命题.(3)的逆命题是:全等三角形的面积相等.它是一个真命题.(4)的逆命题是:如果三角形有两个内角是锐角,那么另一个内角是钝角,它是一个假命题.
(5)的逆命题是:在一个三角形中,等边对等角,它是一个真命题.
10.先求AB=9,BC=12,AC=15,由AB2+BC2=AC2可得△ABC
是直角三角形.
所以S△PBQ=1
2BP·BQ=1
2
×(9-3)×6=18cm2.
拓展创新
11.(1)以上各组数的共同点可以从以下方面分析:
①以上各组数均满足a2+b2=c2;
②最小的数(a)是奇数,其余的两个数是连续的正整数;
③最小奇数的平方等于另两个连续整数的和,
如32=9=4+5,52=25=12+13,72=49=24+25,92=81=40+41…
由以上特点我们可猜想并证明这样一个结论:
设m为大于1的奇数,将m2拆分为两个连续的整数之和,即m2=n+(n+1),
则m,n,n+1就构成一组简单的勾股数.
证明:∵m2=n+(n+1)(m为大于1的奇数),
∴m2+n2=2n+1+n2=(n+1)2,
∴m,n,(n+1)是一组勾股数.
(2)运用以上结论,当a=17时,
∵172=289=144+145,∴b=144,c=145.。
