人教版必修四重难点全梳理2
2020届(人教版必修四)高考政治一轮总复习资料:《生活与哲学》重难点知识速记

《生活与哲学》重难点知识速记1. 理解“哲学”的概念①哲学是关于世界观的学问。
②哲学是对自然、社会和思维知识的概括和总结。
③哲学是系统化、理论化的世界观。
④哲学是世界观和方法论的统一。
哲学既是关于世界观的学说,又是关于方法论的学说。
注意:“哲学就是世界观”“哲学就是关于世界观的科学”“哲学是科学世界观和方法论的统一”等说法都是错误的。
2. 把握哲学的基本问题及其内容①哲学的基本问题是思维和存在的关系问题,简单地说,就是意识和物质的关系问题。
②思维和存在的关系问题的内容包括:一是思维和存在何者为第一性的问题;二是思维和存在有没有同一性的问题。
3.正确理解唯物主义①基本观点:物质是本原,先有物质后有意识,物质决定意识。
②基本形态:古代朴素唯物主义、近代形而上学唯物主义、辩证唯物主义和历史唯物主义。
③划分基本形态的依据:对物质的理解不同。
古代朴素唯物主义把物质归结为具体的物质形态。
近代形而上学唯物主义把物质归结为自然科学上的物质。
辩证唯物主义和历史唯物主义认为物质是不依赖于人的意识,并能为人的意识所反映的客观实在。
4.正确理解唯心主义①基本观点:意识是本原的,物质依赖于意识,不是物质决定意识,而是意识觉得物质。
②基本形态:主观唯心主义和客观唯心主义。
③划分基本形态的依据:对意识的理解不同。
主观唯心主义把意识理解为人的主观精神。
客观唯心主义把意识理解为客观精神。
5.全面理解哲学的作用①哲学是指导人们生活得更好的艺术。
真正的哲学可以使我们正确地看待自然、社会和人生的变化与发展,用睿智的眼光看待生活和实践,正确看待社会进步与个人发展,正确对待集体利益与个人利益的关系,正确对待进与退、得与失、名与利,从而为生活和实践提供积极有益的指导。
②哲学是社会变革的先导。
首先体现在它可以通过对旧制度和旧思想的批判,更新人的观念,解放人的思想。
其次体现在它可以预见和指明社会的前进方向,提出社会发展的理想目标,指引人们追求美好的未来;动员和掌握群众,从而转化为变革社会的巨大物质力量。
(人教版)高中数学必修四教学三维目标重难点

第一章三角函数1.1任意角和弧度制1.1.1任意角一、教学目标:1、知识与技能(1)推广角的概念、引入大于360︒角和负角;(2)理解并掌握正角、负角、零角的定义;(3)理解任意角以及象限角的概念;(4)掌握所有与α角终边相同的角(包括α角)的表示方法;(5)树立运动变化观点,深刻理解推广后的角的概念;(6)揭示知识背景,引发学生学习兴趣.(7)创设问题情景,激发学生分析、探求的学习态度,强化学生的参与意识.2、过程与方法通过创设情境:“转体720︒,逆(顺)时针旋转”,角有大于360︒角、零角和旋转方向不同所形成的角等,引入正角、负角和零角的概念;角的概念得到推广以后,将角放入平面直角坐标系,引入象限角、非象限角的概念及象限角的判定方法;列出几个终边相同的角,画出终边所在的位置,找出它们的关系,探索具有相同终边的角的表示;讲解例题,总结方法,巩固练习.3、情态与价值通过本节的学习,使同学们对角的概念有了一个新的认识,即有正角、负角和零角之分.角的概念推广以后,知道角之间的关系.理解掌握终边相同角的表示方法,学会运用运动变化的观点认识事物.二、教学重、难点重点: 理解正角、负角和零角的定义,掌握终边相同角的表示法.难点: 终边相同的角的表示.三、学法与教学用具之前的学习使我们知道最大的角是周角,最小的角是零角.通过回忆和观察日常生活中实际例子,把对角的理解进行了推广.把角放入坐标系环境中以后,了解象限角的概念.通过角终边的旋转掌握终边相同角的表示方法.我们在学习这部分内容时,首先要弄清楚角的表示符号,以及正负角的表示.另外还有相同终边角的集合的表示等.教学用具:电脑、投影机、三角板1.1任意角和弧度制1.1.2弧度制一、教学目标:1、知识与技能(1)理解并掌握弧度制的定义;(2)领会弧度制定义的合理性;(3)掌握并运用弧度制表示的弧长公式、扇形面积公式;(4)熟练地进行角度制与弧度制的换算;(5)角的集合与实数集R之间建立的一一对应关系.(6) 使学生通过弧度制的学习,理解并认识到角度制与弧度制都是对角度量的方法,二者是辨证统一的,而不是孤立、割裂的关系.2、过程与方法创设情境,引入弧度制度量角的大小,通过探究理解并掌握弧度制的定义,领会定义的合理性.根据弧度制的定义推导并运用弧长公式和扇形面积公式.以具体的实例学习角度制与弧度制的互化,能正确使用计算器.3、情态与价值通过本节的学习,使同学们掌握另一种度量角的单位制---弧度制,理解并认识到角度制与弧度制都是对角度量的方法,二者是辨证统一的,而不是孤立、割裂的关系.角的概念推广以后,在弧度制下,角的集合与实数集R之间建立了一一对应关系:即每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应,为下一节学习三角函数做好准备.二、教学重、难点重点: 理解并掌握弧度制定义;熟练地进行角度制与弧度制地互化换算;弧度制的运用.难点: 理解弧度制定义,弧度制的运用.三、学法与教学用具在我们所掌握的知识中,知道角的度量是用角度制,但是为了以后的学习,我们引入了弧度制的概念,我们一定要准确理解弧度制的定义,在理解定义的基础上熟练掌握角度制与弧度制的互化.教学用具:计算器、投影机、三角板1.2 任意角的三角函数1.2.1任意角的三角函数(一)一、教学目标:1、知识与技能(1)掌握任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);(2)理解任意角的三角函数不同的定义方法;(3)了解如何利用与单位圆有关的有向线段,将任意角α的正弦、余弦、正切函数值分别用正弦线、余弦线、正切线表示出来;(4)掌握并能初步运用公式一;(5)树立映射观点,正确理解三角函数是以实数为自变量的函数.2、过程与方法初中学过:锐角三角函数就是以锐角为自变量,以比值为函数值的函数.引导学生把这个定义推广到任意角,通过单位圆和角的终边,探讨任意角的三角函数值的求法,最终得到任意角三角函数的定义.根据角终边所在位置不同,分别探讨各三角函数的定义域以及这三种函数的值在各象限的符号.最后主要是借助有向线段进一步认识三角函数.讲解例题,总结方法,巩固练习.3、情态与价值任意角的三角函数可以有不同的定义方法,而且各种定义都有自己的特点.过去习惯于用角的终边上点的坐标的“比值”来定义,这种定义方法能够表现出从锐角三角函数到任意角的三角函数的推广,有利于引导学生从自己已有认知基础出发学习三角函数,但它对准确把握三角函数的本质有一定的不利影响,“从角的集合到比值的集合”的对应关系与学生熟悉的一般函数概念中的“数集到数集”的对应关系有冲突,而且“比值”需要通过运算才能得到,这与函数值是一个确定的实数也有不同,这些都会影响学生对三角函数概念的理解.本节利用单位圆上点的坐标定义任意角的正弦函数、余弦函数.这个定义清楚地表明了正弦、余弦函数中从自变量到函数值之间的对应关系,也表明了这两个函数之间的关系.二、教学重、难点重点: 任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);终边相同的角的同一三角函数值相等(公式一).难点: 任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号);三角函数线的正确理解.三、学法与教学用具任意角的三角函数可以有不同的定义方法,本节利用单位圆上点的坐标定义任意角的正弦函数、余弦函数.表明了正弦、余弦函数中从自变量到函数值之间的对应关系,也表明了这两个函数之间的关系.另外,这样的定义使得三角函数所反映的数与形的关系更加直接,数形结合更加紧密,这就为后续内容的学习带来方便,也使三角函数更加好用了.教学用具:投影机、三角板、圆规、计算器第二课时任意角的三角函数(二)【复习回顾】1、三角函数的定义;2、三角函数在各象限角的符号;3、三角函数在轴上角的值;4、诱导公式(一):终边相同的角的同一三角函数的值相等;5、三角函数的定义域.要求:记忆.并指出,三角函数没有定义的地方一定是在轴上角,所以,凡是碰到轴上角时,要结合定义进行分析;并要求在理解的基础上记忆.【探究新知】1.引入:角是一个图形概念,也是一个数量概念(弧度数).作为角的函数——三角函数是一个数量概念(比值),但它是否也是一个图形概念呢?换句话说,能否用几何方式来表示三角函数呢?2.[边描述边画]以单位长度1为半径画一个圆,这个圆就叫做单位圆(注意:这个单位长度不一定就是1厘米或1米).当角α为第一象限角时,则其终边与单位圆必有一个交点(,)⊥轴交x轴于点M,则请你观P x y,过点P作PM x察:根据三角函数的定义:|||||sin|OM xα====;|||||cos|MP yα随着α在第一象限内转动,MP、OM是否也跟着变化?3.思考:(1)为了去掉上述等式中的绝对值符号,能否给线段MP、OM规定一个适当的方向,使它们的取值与点P的坐标一致?(2)你能借助单位圆,找到一条如MP、OM一样的线段来表示角α的正切值吗?我们知道,指标坐标系内点的坐标与坐标轴的方向有关.当角α的终边不在坐标轴时,以O为始点、M为终点,规定:当线段OM与x轴同向时,OM的方向为正向,且有正值x;当线段OM与x轴反向时,OM的方向为负向,且有正值x;其中x为P点的横坐标.这样,无论那种情况都有==cosOM xα同理,当角α的终边不在x轴上时,以M为始点、P为终点,规定:当线段MP与y轴同向时,MP的方向为正向,且有正值y;当线段MP与y轴反向时,MP的方向为负向,且有正值y;其中y为P点的横坐标.这样,无论那种情况都有==MP yαsin4.像MP OM、这种被看作带有方向的线段,叫做有向线段(direct line segment).5.如何用有向线段来表示角α的正切呢?如上图,过点(1,0)A 作单位圆的切线,这条切线必然平行于轴,设它与α的终边交于点T ,请根据正切函数的定义与相似三角形的知识,借助有向线段OA AT 、,我们有tan y AT xα== 我们把这三条与单位圆有关的有向线段MP OM AT 、、,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线.6.探究:(1)当角α的终边在第二、第三、第四象限时,你能分别作出它们的正弦线、余弦线和正切线吗?(2)当α的终边与x 轴或y 轴重合时,又是怎样的情形呢?7.例题讲解例1.已知42ππα<<,试比较,tan ,sin ,cos αααα的大小.处理:师生共同分析解答,目的体会三角函数线的用处和实质.8.练习19P 第1,2,3,4题9学习小结(1)了解有向线段的概念.(2)了解如何利用与单位圆有关的有向线段,将任意角α的正弦、余弦、正切函数值分别用正弦线、余弦线、正切线表示出来.(3)体会三角函数线的简单应用.【评价设计】1. 作业:比较下列各三角函数值的大小(不能使用计算器)(1)sin15︒、tan15︒ (2)'cos15018︒、cos121︒ (3)5π、tan 5π2.练习三角函数线的作图.1.2任意角的三角函数1.2.2同角三角函数的基本关系一、教学目标:1、知识与技能(1) 使学生掌握同角三角函数的基本关系;(2)已知某角的一个三角函数值,求它的其余各三角函数值;(3)利用同角三角函数关系式化简三角函数式;(4)利用同角三角函数关系式证明三角恒等式;(5)牢固掌握同角三角函数的三个关系式并能灵活运用于解题,提高学生分析,解决三角问题的能力;(6)灵活运用同角三角函数关系式的不同变形,提高三角恒等变形的能力,进一步树立化归思想方法;(7)掌握恒等式证明的一般方法.2、过程与方法由圆的几何性质出发,利用三角函数线,探究同一个角的不同三角函数之间的关系;学习已知一个三角函数值,求它的其余各三角函数值;利用同角三角函数关系式化简三角函数式;利用同角三角函数关系式证明三角恒等式等.通过例题讲解,总结方法.通过做练习,巩固所学知识.3、情态与价值通过本节的学习,牢固掌握同角三角函数的三个关系式并能灵活运用于解题,提高学生分析,解决三角问题的能力;进一步树立化归思想方法和证明三角恒等式的一般方法.二、教学重、难点重点:公式1cos sin 22=+αα及αααtan cos sin =的推导及运用:(1)已知某任意角的正弦、余弦、正切值中的一个,求其余两个;(2)化简三角函数式;(3)证明简单的三角恒等式.难点: 根据角α终边所在象限求出其三角函数值;选择适当的方法证明三角恒等式.三、学法与教学用具利用三角函数线的定义, 推导同角三角函数的基本关系式: 1cos sin 22=+αα及αααtan cos sin =,并灵活应用求三角函数值,化减三角函数式,证明三角恒等式等.教学用具:圆规、三角板、投影第二章 平面向量第1课时§2.1 平面向量的实际背景及基本概念教学目标:1.了解向量的实际背景,理解平面向量的概念和向量的几何表示;掌握向量的模、零向量、单位向量、平行向量、相等向量、共线向量等概念;并会区分平行向量、相等向量和共线向量.2.通过对向量的学习,使学生初步认识现实生活中的向量和数量的本质区别.3.通过学生对向量与数量的识别能力的训练,培养学生认识客观事物的数学本质的能力.教学重点:理解并掌握向量、零向量、单位向量、相等向量、共线向量的概念,会表示向量.教学难点:平行向量、相等向量和共线向量的区别和联系.学法:本节是本章的入门课,概念较多,但难度不大.学生可根据在原有的位移、力等物理概念来学习向量的概念,结合图形实物区分平行向量、相等向量、共线向量等概念.教具:多媒体或实物投影仪,尺规授课类型:新授课第2课时§2.2.1 向量的加法运算及其几何意义教学目标:1、掌握向量的加法运算,并理解其几何意义;2、会用向量加法的三角形法则和平行四边形法则作两个向量的和向量,培养数形结合解决问题的能力;3、通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,并会用它们进行向量计算,渗透类比的数学方法;教学重点:会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.教学难点:理解向量加法的定义.学法:数能进行运算,向量是否也能进行运算呢?数的加法启发我们,从运算的角度看,位移的合成、力的合成可看作向量的加法.借助于物理中位移的合成、力的合成来理解向量的加法,让学生顺理成章接受向量的加法定义.结合图形掌握向量加法的三角形法则和平行四边形法则.联系数的运算律理解和掌握向量加法运算的交换律和结合律. 教具:多媒体或实物投影仪,尺规第3课时§2.2.2 向量的减法运算及其几何意义教学目标:1.了解相反向量的概念;2.掌握向量的减法,会作两个向量的减向量,并理解其几何意义;3.通过阐述向量的减法运算可以转化成向量的加法运算,使学生理解事物之间可以相互转化的辩证思想.教学重点:向量减法的概念和向量减法的作图法.教学难点:减法运算时方向的确定.学法:减法运算是加法运算的逆运算,学生在理解相反向量的基础上结合向量的加法运算掌握向量的减法运算;并利用三角形做出减向量.教具:多媒体或实物投影仪,尺规授课类型:新授课2.3平面向量的基本定理及坐标表示第4课时§2.3.1 平面向量基本定理教学目的:(1)了解平面向量基本定理;(2)理解平面里的任何一个向量都可以用两个不共线的向量来表示,初步掌握应用向量解决实际问题的重要思想方法;(3)能够在具体问题中适当地选取基底,使其他向量都能够用基底来表达.教学重点:平面向量基本定理.教学难点:平面向量基本定理的理解与应用.授课类型:新授课教具:多媒体、实物投影仪第5课时§2.3.2—§2.3.3 平面向量的正交分解和坐标表示及运算教学目的:(1)理解平面向量的坐标的概念;(2)掌握平面向量的坐标运算;(3)会根据向量的坐标,判断向量是否共线.教学重点:平面向量的坐标运算教学难点:向量的坐标表示的理解及运算的准确性.授课类型:新授课教具:多媒体、实物投影仪第6课时§2.3.4 平面向量共线的坐标表示教学目的:(1)理解平面向量的坐标的概念;(2)掌握平面向量的坐标运算;(3)会根据向量的坐标,判断向量是否共线.教学重点:平面向量的坐标运算教学难点:向量的坐标表示的理解及运算的准确性授课类型:新授课教具:多媒体、实物投影仪§2.4平面向量的数量积第7课时一、平面向量的数量积的物理背景及其含义教学目的:1.掌握平面向量的数量积及其几何意义;2.掌握平面向量数量积的重要性质及运算律;3.了解用平面向量的数量积可以处理有关长度、角度和垂直的问题;4.掌握向量垂直的条件.教学重点:平面向量的数量积定义教学难点:平面向量数量积的定义及运算律的理解和平面向量数量积的应用授课类型:新授课教具:多媒体、实物投影仪第8课时二、平面向量数量积的运算律教学目的:1.掌握平面向量数量积运算规律;2.能利用数量积的5个重要性质及数量积运算规律解决有关问题;3.掌握两个向量共线、垂直的几何判断,会证明两向量垂直,以及能解决一些简单问题.教学重点:平面向量数量积及运算规律.教学难点:平面向量数量积的应用授课类型:新授课教具:多媒体、实物投影仪内容分析:启发学生在理解数量积的运算特点的基础上,逐步把握数量积的运算律,引导学生注意数量积性质的相关问题的特点,以熟练地应用数量积的性质.教学过程:第9课时三、平面向量数量积的坐标表示、模、夹角教学目的:⑴要求学生掌握平面向量数量积的坐标表示⑵掌握向量垂直的坐标表示的充要条件,及平面内两点间的距离公式.⑶能用所学知识解决有关综合问题.教学重点:平面向量数量积的坐标表示教学难点:平面向量数量积的坐标表示的综合运用授课类型:新授课教具:多媒体、实物投影仪第三章三角恒等变换3.1.1 两角差的余弦公式一、教学目标掌握用向量方法建立两角差的余弦公式.通过简单运用,使学生初步理解公式的结构及其功能,为建立其它和(差)公式打好基础.二、教学重、难点1. 教学重点:通过探索得到两角差的余弦公式;2. 教学难点:探索过程的组织和适当引导,这里不仅有学习积极性的问题,还有探索过程必用的基础知识是否已经具备的问题,运用已学知识和方法的能力问题,等等.三、学法与教学用具1. 学法:启发式教学2. 教学用具:多媒体§3.1.2 两角和与差的正弦、余弦、正切公式一、教学目标理解以两角差的余弦公式为基础,推导两角和、差正弦和正切公式的方法,体会三角恒等变换特点的过程,理解推导过程,掌握其应用.二、教学重、难点1. 教学重点:两角和、差正弦和正切公式的推导过程及运用;2. 教学难点:两角和与差正弦、余弦和正切公式的灵活运用.三、学法与教学用具学法:研讨式教学§3.1.3 二倍角的正弦、余弦和正切公式一、教学目标以两角和正弦、余弦和正切公式为基础,推导二倍角正弦、余弦和正切公式,理解推导过程,掌握其应用.二、教学重、难点教学重点:以两角和的正弦、余弦和正切公式为基础,推导二倍角正弦、余弦和正切公式;教学难点:二倍角的理解及其灵活运用.三、学法与教学用具学法:研讨式教学四3.2 简单的三角恒等变换(3个课时)一、课标要求:本节主要包括利用已有的十一个公式进行简单的恒等变换,以及三角恒等变换在数学中的应用.二、编写意图与特色本节内容都是用例题来展现的.通过例题的解答,引导学生对变换对象目标进行对比、分析,促使学生形成对解题过程中如何选择公式,如何根据问题的条件进行公式变形,以及变换过程中体现的换元、逆向使用公式等数学思想方法的认识,从而加深理解变换思想,提高学生的推理能力.三、教学目标通过例题的解答,引导学生对变换对象目标进行对比、分析,促使学生形成对解题过程中如何选择公式,如何根据问题的条件进行公式变形,以及变换过程中体现的换元、逆向使用公式等数学思想方法的认识,从而加深理解变换思想,提高学生的推理能力.四、教学重点与难点教学重点:引导学生以已有的十一个公式为依据,以推导积化和差、和差化积、半角公式的推导作为基本训练,学习三角变换的内容、思路和方法,在与代数变换相比较中,体会三角变换的特点,提高推理、运算能力.教学难点:认识三角变换的特点,并能运用数学思想方法指导变换过程的设计,不断提高从整体上把握变换过程的能力.五、学法与教学用具学法:讲授式教学《三角恒等变换》复习课(2个课时)一、教学目标进一步掌握三角恒等变换的方法,如何利用正、余弦、正切的和差公式与二倍角公式,对三角函数式进行化简、求值和证明:二、知识与方法:1. 11个三角恒等变换公式中,余弦的差角公式是其它公式的基础,由它出发,用-β代替±ββ、2π代替β、α=β等换元法可以推导出其它公式。
人教版高中语文必修四第二单元知识梳理

人教版高中语文必修四第二单元知识梳理第二单元【知识梳理】《柳永词两首》《苏轼词两首》《辛弃疾词两首》《李清照词两首》《柳永词两首》1、《望海潮》是描写北宋时期杭州繁盛景象的词。
词的上片描写杭州的自然风光和都市的繁华。
词的下片描写杭州人民和平宁静的生活景象。
词作以铺叙见长。
首先,以“东南形胜,三吴都会,钱塘自古繁华”总领全篇,概括介绍杭州的自然风光和都市的繁华。
然后分别从“形胜”“都会”和“繁华”三个方面铺开叙述:“烟柳画桥”之中家家户户安居乐业,人烟阜盛;“云树”“堤沙”之外惊涛拍岸,汹涌壮观;都市街衢,珠宝遍陈,普通人家,披罗着锦,满目奢华景象。
过片(下片起句)之后,先描写西湖水碧山青、桂子飘香的景象,后叙羌笛横吹、菱歌互答的欢愉场景。
由民众忘情山水之乐引出官员宴饮之乐,一路铺叙下,但又不是平铺直叙,很见裁减功力。
这是一篇投赠之作。
作者路经杭州,想谒见当时出任两浙转运使的孙何,便写了这首词。
词作一方面反映了北宋结束五代分裂割据局面后,经过真宗、仁宗两朝的休养生息,确实呈现了繁荣的景象,但收笔也流露了粉饰太平、献宠官僚的味道,有唐朝干谒诗的遗风。
2、《雨霖铃》是描写作者在长亭与情人话别的词。
词作主要采用了情景交融的艺术手法。
其一,用哀景写悲情。
词作开篇用“寒蝉”“长亭”“骤雨”等意象,烘托离别时凄冷沉郁的气氛。
其二,以无情衬有情。
离人难舍难分,而无情的舟子却催促起航,有情人只得以泪相向,“无语凝噎”。
其三,以想象未之景诉悲情。
作者用一“念”字引出离别后行人消失在烟波浩淼的楚地江天,极目远眺,一片茫然,不觉悲从中。
“良辰美景”原为欢乐愉快的场景,但是随后而的“虚设”二字顷刻间就使欢乐之情顿然消失,而沉入到无边无际的愁伤之中,所以,这里也是“乐景写悲情”。
积累运用1、下列诗句的节拍划分有误的一项()A.东南 / 形胜,三吴 / 都会,钱塘 / 自古 / 繁华。
B.有 / 三秋 / 桂子,十里 / 荷花。
必修4 数学最全 知识点梳理(完整版)

高中数学必修4 知识点总结第一章:三角函数§1.1.1、任意角1、 正角、负角、零角、象限角的概念.2、 与角α终边相同的角的集合:{}Z k k ∈+=,2παββ.§1.1.2、弧度制1、 把长度等于半径长的弧所对的圆心角叫做1弧度的角.2、 rl =α. 3、弧长公式:R Rn l απ==180. 4、扇形面积公式:lR R n S 213602==π.§1.2.1、任意角的三角函数1、 设α是一个任意角,它的终边与单位圆交于点()y x P ,,那么:xyx y ===αααtan ,cos ,sin 2、 设点(),A x y为角α终边上任意一点,那么:(设r =sin y r α=,cos x r α=,tan y xα= 3、 αsin ,αcos ,αtan 在四个象限的符号和三角函数线的画法.正弦线:MP; 余弦线:OM; 正切线:AT 4、 特殊角0°,30°,45°,60°,§1.2.2、同角三角函数的基本关系式 1、 平方关系:1cos sin 22=+αα. 2、 商数关系:αααcos sin tan =. §1.3、三角函数的诱导公式(概括为“奇变偶不变,符号看象限”Z k ∈)1、 诱导公式一: ()()().tan 2tan ,cos 2cos ,sin 2sin απααπααπα=+=+=+k k k (其中:Z k ∈) 2、 诱导公式二: ()()().tan tan ,cos cos ,sin sin ααπααπααπ=+-=+-=+3、诱导公式三: ()()().tan tan ,cos cos ,sin sin αααααα-=-=--=- 4、诱导公式四: ()()().tan tan ,cos cos ,sin sin ααπααπααπ-=--=-=-5、诱导公式五: .sin 2cos ,cos 2sin ααπααπ=⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛- 6、诱导公式六: .sin 2cos ,cos 2sin ααπααπ-=⎪⎭⎫⎝⎛+=⎪⎭⎫⎝⎛+§1.4.1、正弦、余弦函数的图象和性质 1、记住正弦、余弦函数图象:2、能够对照图象讲出正弦、余弦函数的相关性质:定义域、值域、最大最小值、对称轴、对称中心、奇偶性、单调性、周期性. 3、会用五点法作图.sin y x =在[0,2]x π∈上的五个关键点为: 30010-12022ππππ(,)(,,)(,,)(,,)(,,).§1.4.3、正切函数的图象与性质12、能够对照图象讲出正切函数的相关性质:定义域、值域、对称中心、奇偶性、单调性、周期性.周期函数定义:对于函数()x f ,如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有()(),那么函数()x f 就叫做周期函数,非零常数T 叫做这个函数的周期.图表归纳:正弦、余弦、正切函数的图像及其性质§1.5、函数()ϕω+=x A y sin 的图象 1、对于函数:()()sin 0,0y A x B A ωφω=++>>有:振幅A ,周期2T πω=,初相ϕ,相位ϕω+x ,频率πω21==Tf .2、能够讲出函数x y sin =的图象与()sin y A x B ωϕ=++的图象之间的平移伸缩变换关系.① 先平移后伸缩:sin y x = 平移||ϕ个单位 ()sin y x ϕ=+(左加右减) 横坐标不变 ()sin y A x ϕ=+纵坐标变为原来的A 倍纵坐标不变 ()sin y A x ωϕ=+横坐标变为原来的1||ω倍平移||B 个单位 ()sin y A x B ωϕ=++(上加下减)② 先伸缩后平移:sin y x = 横坐标不变 sin y A x =纵坐标变为原来的A 倍 纵坐标不变 sin y A x ω=横坐标变为原来的1||ω倍()sin y A x ωϕ=+平移||B 个单位()sin y A x B ωϕ=++(上加下减)3、三角函数的周期,对称轴和对称中心函数sin()y x ωϕ=+,x ∈R 及函数cos()y x ωϕ=+,x ∈R(A,ω,ϕ为常数,且A ≠0)的周期2||T πω=;函数tan()y x ωϕ=+,,2x k k Z ππ≠+∈(A,ω,ϕ为常数,且A ≠0)的周期||T πω=. 对于sin()y A x ωϕ=+和cos()y A x ωϕ=+来说,对称中心与零点相联系,对称轴与最值点联系. 求函数sin()y A x ωϕ=+图像的对称轴与对称中心,只需令()2x k k Z πωϕπ+=+∈与()x k k Z ωϕπ+=∈解出x 即可.余弦函数可与正弦函数类比可得.4、由图像确定三角函数的解析式 利用图像特征:max min 2A =,max min2y y B +=. ω要根据周期来求,ϕ要用图像的关键点来求.§1.6、三角函数模型的简单应用 1、 要求熟悉课本例题.第三章、三角恒等变换§3.1.1、两角差的余弦公式记住15°的三角函数值:§3.1.2、两角和与差的正弦、余弦、正切公式 1、()βαβαβαsin cos cos sin sin +=+ 2、()βαβαβαsin cos cos sin sin -=- 3、()βαβαβαsin sin cos cos cos -=+ 4、()βαβαβαsin sin cos cos cos +=-5、()tan tan 1tan tan tan αβαβαβ+-+=. 6、()tan tan 1tan tan tan αβαβαβ-+-=.§3.1.3、二倍角的正弦、余弦、正切公式 1、αααcos sin 22sin =, 变形: 12sin cos sin 2ααα=. 2、ααα22sin cos 2cos -=1cos 22-=α α2sin 21-=. 变形如下:升幂公式:221cos 22cos 1cos 22sin αααα⎧+=⎪⎨-=⎪⎩ 降幂公式:221cos (1cos 2)21sin (1cos 2)2αααα=+=-⎧⎪⎨⎪⎩ 3、ααα2tan 1tan 22tan -=.4、sin 21cos 2tan 1cos 2sin 2ααααα-==+ §3.2、简单的三角恒等变换1、 注意正切化弦、平方降次.2、辅助角公式)sin(cos sin 22ϕ++=+=x b a x b x a y(其中辅助角ϕ所在象限由点(,)a b 的象限决定,tan baϕ= ).第二章:平面向量§2.1.1、向量的物理背景与概念1、 了解四种常见向量:力、位移、速度、加速度.2、 既有大小又有方向的量叫做向量. §2.1.2、向量的几何表示1、 带有方向的线段叫做有向线段,有向线段包含三个要素:起点、方向、长度.2、 向量的大小,也就是向量的长度(或称模),记作AB ;长度为零的向量叫做零向量;长度等于1个单位的向量叫做单位向量.3、 方向相同或相反的非零向量叫做平行向量(或共线向量).规定:零向量与任意向量平行. §2.1.3、相等向量与共线向量1、 长度相等且方向相同的向量叫做相等向量. §2.2.1、向量加法运算及其几何意义1、 三角形加法法则和平行四边形加法法则.2++.§2.2.2、向量减法运算及其几何意义1、 与a 长度相等方向相反的向量叫做a 的相反向量.2、 三角形减法法则和平行四边形减法法则.§2.2.3、向量数乘运算及其几何意义1、 规定:实数λ与向量a 的积是一个向量,这种运算叫做向量的数乘.记作:a λ,它的长度和方向规定如下:⑴= ⑵当0>λ时, a λ的方向与a 的方向相同;当0<λ时, a λ的方向与a 的方向相反. 2、 平面向量共线定理:向量()≠与 共线,当且仅当有唯一一个实数λ,使λ=. §2.3.1、平面向量基本定理1、 平面向量基本定理:如果21,e e 是同一平面内的两个不共线向量,那么对于这一平面内任一向量,有且只有一对实数21,λλ,使2211e e a λλ+=. §2.3.2、平面向量的正交分解及坐标表示 1、 ()y x y x ,=+=. §2.3.3、平面向量的坐标运算1、 设()()2211,,,y x b y x a ==,则: ⑴()2121,y y x x b a ++=+,⑵()2121,y y x x --=-, ⑶()11,y x λλλ=, ⑷1221//y x y x =⇔. 2、 设()()2211,,,y x B y x A ,则: ()1212,y y x x AB --=. §2.3.4、平面向量共线的坐标表示 1、设()()()332211,,,,,y x C y x B y x A ,则⑴线段AB 中点坐标为()222121,y y x x ++, ⑵△ABC 的重心坐标为()33321321,y y y x x x ++++.§2.4.1、平面向量数量积的物理背景及其含义1、 θ=⋅.2、 在θcos .3、 2=.4、=.5、 0=⋅⇔⊥.§2.4.2、平面向量数量积的坐标表示、模、夹角 1、 设()()2211,,,y x y x ==,则:⑴2121y y x x b a +=⋅2121y x +=⑶121200a b a b x x y y ⊥⇔⋅=⇔+= ⑷1221//0a b a b x y x y λ⇔=⇔-= 2、 设()()2211,,,y x B y x A ,则:()()212212y y x x -+-=.3、 两向量的夹角公式 2cos a b a bx θ⋅==+4、点的平移公式平移前的点为(,)P x y (原坐标),平移后的对应点为(,)P x y '''(新坐标),平移向量为(,)PP h k '=,则.x x hy y k '=+⎧⎨'=+⎩函数()y f x =的图像按向量(,)a h k =平移后的图像的解析式为().y k f x h -=-§2.5.1、平面几何中的向量方法 §2.5.2、向量在物理中的应用举例知识链接:空间向量空间向量的许多知识可由平面向量的知识类比而得.下面对空间向量在立体几何中证明,求值的应用进行总结归纳.1、直线的方向向量和平面的法向量 ⑴.直线的方向向量:若A 、B 是直线l 上的任意两点,则AB 为直线l 的一个方向向量;与AB 平行的任意非零向量也是直线l 的方向向量. ⑵.平面的法向量:若向量n 所在直线垂直于平面α,则称这个向量垂直于平面α,记作n α⊥,如果n α⊥,那么向量n 叫做平面α的法向量.⑶.平面的法向量的求法(待定系数法): ①建立适当的坐标系.②设平面α的法向量为(,,)n x y z =.③求出平面内两个不共线向量的坐标123123(,,),(,,)a a a a b b b b ==. ④根据法向量定义建立方程组00n a n b ⎧⋅=⎪⎨⋅=⎪⎩.⑤解方程组,取其中一组解,即得平面α的法向量. (如图)2 用向量方法判定空间中的平行关系设直线12,l l 的方向向量分别是a b 、,则要证明1l ∥2l ,只需证明a ∥b ,即()a kb k R =∈. 即:两直线平行或重合两直线的方向向量共线.⑵线面平行①(法一)设直线l 的方向向量是a ,平面α的法向量是u ,则要证明l ∥α,只需证明a u ⊥,即0a u ⋅=. 即:直线与平面平行直线的方向向量与该平面的法向量垂直且直线在平面外②(法二)要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可. ⑶面面平行若平面α的法向量为u ,平面β的法向量为v ,要证α∥β,只需证u ∥v ,即证u v λ=. 即:两平面平行或重合两平面的法向量共线. 3、用向量方法判定空间的垂直关系 ⑴线线垂直设直线12,l l 的方向向量分别是a b 、,则要证明12l l ⊥,只需证明a b ⊥,即0a b ⋅=. 即:两直线垂直两直线的方向向量垂直.⑵线面垂直①(法一)设直线l 的方向向量是a ,平面α的法向量是u ,则要证明l α⊥,只需证明a ∥u ,即a u λ=.②(法二)设直线l 的方向向量是a ,平面α内的两个相交向量分别为m n 、,若0,.0a m l a n α⎧⋅=⎪⊥⎨⋅=⎪⎩则 即:直线与平面垂直直线的方向向量与平面的法向量共线直线的方向向量与平面内两条不共线直线的方向向量都垂直. ⑶面面垂直若平面α的法向量为u ,平面β的法向量为v ,要证αβ⊥,只需证u v ⊥,即证0u v ⋅=. 即:两平面垂直两平面的法向量垂直. 4、利用向量求空间角 ⑴求异面直线所成的角A ,C 与B ,D 分别是,a b 上的任意两点,,a b 所成的角为θ,则cos .AC BD AC BDθ⋅=⑵求直线和平面所成的角①定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角②求法:设直线l 的方向向量为a ,平面α的法向量为u ,直线与平面所成的角为θ,a 与u 的夹角为ϕ, 则θ为ϕ的余角或ϕ的补角 的余角.即有:cos s .ina ua uϕθ⋅==①定义:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面二面角的平面角是指在二面角βα--l 的棱上任取一点O ,分别在两个半平面内作射线l BO l AO ⊥⊥,,则AOB ∠为二面角βα--l 的平面角.如图:②求法:设二面角l αβ--的两个半平面的法向量分别为m n 、,再设m n 、的夹角为ϕ,二面角l αβ--的平面角为θ,则二面角θ为m n 、的夹角ϕ或其补角.πϕ- 根据具体图形确定θ是锐角或是钝角: ◆如果θ是锐角,则cos cos m n m nθϕ⋅==;◆ 如果θ是钝角,则cos cos m n m nθϕ⋅=-=-.5、利用法向量求空间距离⑴点Q 到直线l 距离若Q 为直线l 外的一点,P 在直线l 上,a 为直线l 的方向向量,b =PQ ,则点Q 到直线l 距离为1(||||h a b a =⑵点A 到平面α的距离若点P 为平面α外一点,点M 为平面α内任一点,平面α的法向量为n ,则P 到平面α的距离就等于MP 在法向量n 方向上的投影的绝对值.即cos ,d MP n MP =n MP MP n MP⋅=⋅n MP n⋅=⑶直线a 与平面α之间的距离当一条直线和一个平面平行时,直线上的各点到平面的距离相等.由此可知,直线到平面的距离可转化为求直线上任一点到平面的距离,即转化为点面距离.即.n MP d n⋅=⑷两平行平面,αβ之间的距离利用两平行平面间的距离处处相等,可将两平行平面间的距离转化为求点面距离.即.n MP d n⋅=⑸异面直线间的距离高中数学必修四 知识梳理 10设向量n 与两异面直线,a b 都垂直,,,M a P b ∈∈则两异面直线,a b 间的距离d 就是MP 在向量n 方向上投影的绝对值.即.n MP d n⋅=6、三垂线定理及其逆定理⑴三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直推理模式:,,PO O PA A a PA a a OA αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭概括为:垂直于射影就垂直于斜线.⑵三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直推理模式:,,PO O PA A a AO a a AP αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭概括为:垂直于斜线就垂直于射影.7、三余弦定理设AC 是平面α内的任一条直线,AD 是α的一条斜线AB 在α内的射影,且BD ⊥AD ,垂足为D.设AB 与α (AD)所成的角为1θ, AD 与AC 所成的角为2θ, AB 与AC 所成的角为θ.则12cos cos cos θθθ=.8、 面积射影定理已知平面β内一个多边形的面积为()S S 原,它在平面α内的射影图形的面积为()S S '射,平面α与平面β所成的二面角的大小为锐二面角θ,则'cos =.S S S S θ=射原9、一个结论长度为的线段在三条两两互相垂直的直线上的射影长分别为123l l l 、、,夹角分别为123θθθ、、,则有2222123l l l l =++222123cos cos cos 1θθθ⇔++= 222123sin sin sin 2θθθ⇔++=.(立体几何中长方体对角线长的公式是其特例).。
人教版政治必修四
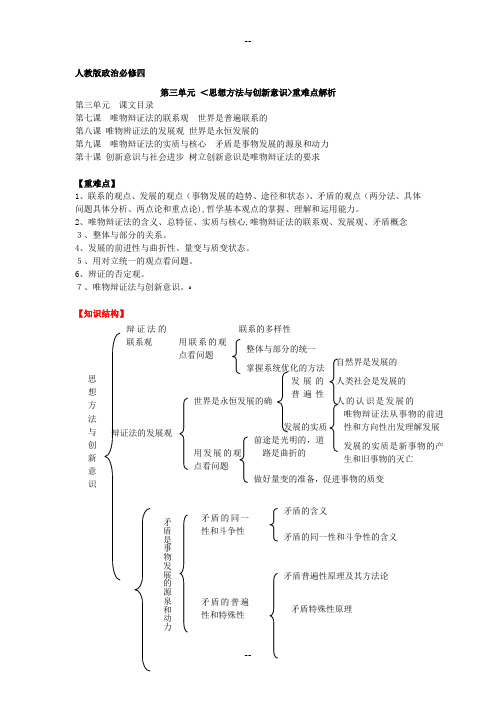
人教版政治必修四第三单元<思想方法与创新意识>重难点解析第三单元课文目录第七课唯物辩证法的联系观世界是普遍联系的第八课唯物辨证法的发展观世界是永恒发展的第九课唯物辩证法的实质与核心矛盾是事物发展的源泉和动力第十课创新意识与社会进步树立创新意识是唯物辩证法的要求【重难点】1、联系的观点、发展的观点(事物发展的趋势、途径和状态)、矛盾的观点(两分法、具体问题具体分析、两点论和重点论),哲学基本观点的掌握、理解和运用能力。
2、唯物辩证法的含义、总特征、实质与核心,唯物辩证法的联系观、发展观、矛盾概念3、整体与部分的关系。
4、发展的前进性与曲折性、量变与质变状态。
5、用对立统一的观点看问题。
6、辨证的否定观。
7、唯物辩证法与创新意识。
ﻩ【知识结构】思想方法与创新意识辩证法的联系观辩证法的发展观用联系的观点看问题联系的多样性整体与部分的统一掌握系统优化的方法世界是永恒发展的确发展的普遍性自然界是发展的人类社会是发展的人的认识是发展的发展的实质唯物辩证法从事物的前进性和方向性出发理解发展发展的实质是新事物的产生和旧事物的灭亡用发展的观点看问题前途是光明的,道路是曲折的做好量变的准备,促进事物的质变矛盾是事物发展的源泉和动力矛盾的同一性和斗争性矛盾的普遍性和特殊性矛盾的含义矛盾的同一性和斗争性的含义矛盾普遍性原理及其方法论矛盾特殊性原理【要点详解】 一、唯物辩证法的联系观一、世界是不普遍联系的(一)、联系的普遍性1、联系的含义及所谓联系,就是事物之间以及事物内部诸要素之间的相互影响、相互制约和相互作用。
2、联系的普遍性 联系是普遍的。
(1)世界上一切事物都与周围其他事物有着这样或那样的联系。
(2)任何事物都处在联系之中。
每一个事物内部的各个部分、要素之间是相互联系的。
(3)世界是一个普遍联系的有机整体,没有一个事物是孤立存在的。
◇补充:联系具有普遍性,并不意味着任何两个事物之间都具有联系,还应明确事物之间的联系是有条件的。
2023年高考英语总复习第一部分教材考点梳理 必修四Unit 2 Working the land

for us to refresh our mind.
3.“be+adj.+with”高频短语集锦
①be satisfied with 对……感到满意
②be content with 对……满意
③be strict with
对……严格要求
④be familiar with 对……熟悉
⑤be patient with 对……有耐心
(三)仿写用活句式——造佳句·表达高 句式背诵 句型1 if so状语从句的省略形式 If so,what did you do to grow them? 如果是这样的话,你做了些什么来种植这些植物? 句型2 the+序数词+名词+to do sth. In 1973,he became the first agricultural pioneer in the world to grow rice that has
·会积累 联想拓展·
1.“因此”家族
①therefore adv.
因此;所以
②so conj.
因此;所以
③thus adv.
因此;于是
④consequently adv. 所以;因此
⑤as a result
结果;因此
2.“扩展”动词知多少 ①expand 使变大;伸展 ②extend 延伸;扩展 ③spread 展开,传播 ④enlarge 扩大;扩展 ⑤broaden 使变宽
必修四政治第四单元知识点梳理

必修四政治第四单元知识点梳理篇一:高中政治必修四(人教版)知识体系___每个单元的总体框架《生活与哲学》全册知识体系构建图表第一单元线索:什么是哲学→哲学的基本问题→哲学的派别→真正的哲学→马克思主义哲学含义:关于世界观的学说,是世界观与方法论的统一;是对自然、社会和思维知识的概括和总结基本问题:思维(意识)与存在(物质)的关系问题哲基本观点:物质是本原的,意识是派生的。
先有物质后有意唯物物质决定意识。
学主义基本古代朴素唯物主义进步性基本形态近代形而上学唯物主义局限性概派别辩证唯物主义和历史唯物主义唯心基本观点:意识是本原的,物质依赖于意识,不是物质决定意识,论主义而是意识决定物质。
形态真正的哲学是自己时代的精神上的精华哲学与时代↓哲学对社会变革的作用(思想、方向)科学的世界观与方法论产生的历史条件:阶级基础、自然科学基础、直接理论来源基本特征实现了实践基础上的科学性和革命性的统一马克思体系辩证唯物主义:辨证唯物论、唯物辨证法、认识论主义哲学构成历史唯物主义:历史观、人生观、价值观毛泽东思想:精髓、活的灵魂中国化的重大理论成果中国特色“三个代表”主题社会主义重要思想本质理论体系科学发展观:主题、提出意义1《生活与哲学》全册知识体系构建图表2一、辩证唯物论(世界的本质是什么)二、认识论(怎样了解物质世界的存在)4三、唯物辩证法(世界怎样存在)唯物辩证法线索图:总特征(基本观点):联系的观点、发展的观点概根本观点:矛盾的观点论实质和核心:对立统一规律与形而上学的分歧:具体主张的分歧、根本分歧(是否承认矛盾,是否承认事物的内部矛盾是事物发展的源泉。
)* 唯物辩证法的联系、发展、全面的观点和对立统一规律,要求我们把握科学发展观的科学内涵和精神实质,把科学发展观贯彻落实到经济社会发展的各个方面。
5篇二:政治必修四生活与哲学第四单元课本知识点梳理总结第四单元认识社会与价值选择第十一课寻觅社会的真谛社会发展的规律社会存在和社会意识的辩证关系:⒈社会存在决定社会意识:① 什么样决定什么样② 变化发展决定变化发展⒉社会意识具有相对独立性:① 具有不完全同步性② 对社会存在具有反作用生产力与生产关系的矛盾(关系、规律)经济基础与上层建筑的矛盾(关系、规律)矛盾生产关系一定要适合生产力状况的规律,上层建筑一定要适合经济基础状况的规律,是在任何社会中都起作用的普遍规律。
人教版高中英语必修四Book4Unit2重难点练习

高中英语学习材料madeofjingetieji13-14新课标Book4Unit2重难点练习Ⅰ. 在空格处写出该短语的汉语意思。
1. thanks to2. rid… of3. be satisfied with4. would rather5. build up6. lead to7. keep … free from / of8. care about9. rich in10. with the hope ofⅡ. 用以上短语的适当形式填空。
1. the police’s help, the little girl finally found her parents.2. A chance conversation with the famous businessman a brilliant career for the young man who had just graduated from university.3. He be poor than get money by dishonest methods.4. This European country is natural resources. However, it is short of labour force.5. Here are some tips to you some of your bad studying habits.6. Every morning he spends 45 minutes doing exercise to his health.7. Having graduated from college, Mr. Liu returned to his hometown leading the whole village to richness.8. the result of the exam, Jim’s father sent him a new bag.9. Children should be those bad video games, for most of them may be addicted(沉溺于) to them.10. She thinks only of herself; she doesn’t other people.Ⅲ. 根据括号里的汉语和句末括号内的英语提示,补全下列句子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版必修四重难点全梳理(Unit2)Unit 2 Working the land重点单词1. struggle(1) vt. & vi. 奋斗;挣扎;努力She struggled to keep back her tears.她努力地忍住泪水。
The poor had to struggle for life.穷人必须为生活而努力。
They had to struggle with/against all kinds of difficulties.他们必须和各种各样的困难作斗争。
The lion made a sudden angry noise and struggled to its feet.狮子突然发出一阵怒吼,挣扎着站了起来。
(2) n. 搏斗;斗争;努力;奋斗It was a hard struggle to get my work done on time.为使工作按时完成, 我做了一番努力。
2. hunger(1) n. 饥饿;欲望Many people die of hunger before liberation.解放前很多人死于饥饿。
His hunger for/after excitement got him into a lot of trouble.他寻求刺激的欲望给他添了许多麻烦。
(2)vt. & vi.(使)饥饿;渴望There is no food; they have to hunger the children.没有食物了,他们不得不让孩子们挨饿。
All the time she hungered for/after news from her youngest son.她每时每刻都在渴望得到她小儿子的消息。
3. disturbing adj. 令人烦恼的;令人不安的It is disturbing that there has been an increase in crime in the last six months.过去六个月里犯罪案件的增加令人非常不安。
知识拓展disturbed adj. 心烦的;不安的disturb vt. 打扰;扰乱;妨碍;使(人)心神不宁I felt disturbed to hear of your illness.听说你生病了,我感到不安。
Don’t disturb me while I am reading.我读书的时候不要打扰我。
4. therefore adv. 因此,所以,因而We have a growing population and therefore we need more food.我们的人口在日益增长,所以我们需要更多的食物。
There is still much to discuss. We shall, therefore, discuss it at our next meeting.要讨论的问题还很多,所以,我们将在下一次会议上讨论这个问题。
5. equip vt. & vi. 配备;装备; 使胜任equipment n. [U] 装备;设备Your education will equip you to earn a good living.你所受的教育会使你过上富裕的生活。
Your training will equip you for your future job.你的训练使得你能够胜任将来的工作。
He equipped his bike with a head light.他给自行车装上了前灯。
Our lab is well/poorly equipped.我们的实验室配备良好/简陋。
6. confuse vt. 使困惑,使迷惑;混淆They asked so many questions that they confused me.他们问了许多问题,都把我弄糊涂了。
I confused her with/and her sister because they were so alike.我把她和她妹妹弄混了,因为她们长得太像了。
We are confused by a lot of information.我们被大量的信息搞糊涂了。
知识拓展confused adj. 困惑的confusing adj. 令人费解的;使人困惑的confusion n. 困惑,糊涂I am still a bit confused about what happened.我对发生的事仍有点困惑。
The instructions on the box are very confusing.盒子上的使用说明令人费解。
7. regret(1) vt. 遗憾;后悔He regretted his carelessness.他对自己的粗心大意感到懊悔。
I regret that I shall not be able to come.很遗憾,我不能来。
They regretted not having taken/not taking his advice.他们后悔没有听他的建议。
I regretted to tell you you hadn’t passed the driving test.我很遗憾地告诉你你没有通过驾驶执照的考试。
(2)n. 懊悔;遗憾He told me with regret that he couldn’t come to the party.他很抱歉地对我说他不能参加这个聚会了。
I felt great regret about /for what I had said to him.我真后悔对他说了那样的话。
Much to my regret, I am unable to accept your invitation.非常抱歉,我不能接受你的邀请。
8. reduce vt. 减少,缩小;降低reduction n. 减少,缩小;减少的量They’ve reduced the prices in the shop, so it’s a good time to buy.商店已经降低了商品的价格,看来现在是买东西的好时候。
The number of the students in our school reduces by 20% this year.今年我们学校学生的数量减少了20%。
She reduced her weight to 45 kilograms.她的体重减轻到45公斤。
9. focus(1) vt. & vi. 集中(注意力、精力等);聚焦Focus your camera. 把照相机的焦距调准。
He focused the sun’s rays on a paper with a burning glass.他用一面凸透镜把阳光聚焦在纸上。
Today we’re going to focus on the question of homeless people.今天,我们主要讨论无家可归者的问题。
You must focus/fix/concentrate your attention on your work.你必须把注意力集中到你的工作上。
All eyes were focused on him when he came in.他进来时大家都注视着他。
(2)n. 焦点;(活动、注意力、兴趣等的)中心She was the focus of everyone’s attention at the party.她是聚会上大家注意的焦点。
10. comment(1) vi. & vt. 表达意见;作出评论He commented that she was not fit for the job.他评论说她不称职。
I won’t comment on what people say.对人们说的话我不作评论。
(2) n. 评论;议论The scandal caused a lot of comment. 这件丑闻遭到很多议论。
He made several favorable comments about/on their candidates.他对他们的候选人发表了一些有利的评论。
重点短语1. Thanks to his research, the UN has more tools in the battle to rid the world of hunger.多亏了他的研究,联合国在消除世界饥饿的战斗中有了更多的方法。
△thanks to幸亏;由于;因为Thanks to your help, much trouble was saved.多亏你的帮助,减少了许多麻烦。
Thanks to the bad weather, the match had been cancelled.因为天气不好, 比赛被取消了。
知识拓展英语中表示“由于;因为”这一意思的其他短语还有:because of/owing to/due to/on account of/as a result ofThe team’s success was largely due to her efforts.该队的成功在很大程度上是由于她的努力。
Owing to the rain, the meeting has to be put off.会议因雨而推迟了。
△rid sb./sth. of... 使某人/某物摆脱……;从……中解脱You should rid yourself of the bad habit.你应该改掉那个坏习惯。
I tried all kinds of ways to rid the kitchen of mice.我使用各种各样的方法除去厨房的老鼠。
2. Dr. Yuan is quite satisfied with his life. 袁博士对自己的生活非常满足。
△be satisfied with…= be content with…对……感到满足或满意I’m sure you’ll be satisfied with our product.我相信您会满意我们的产品的。
One shouldn’t be satisfied with only a little success.一个人不应该只因一点小成就而感到满足。
知识拓展△satisfy vt. 使满意;满足Nothing satisfies him—he is always complaining.什么事情都不能让他满意—他总是在抱怨。
