2019-2020届初三 中考复习 三视图 综合题 专项练习(含答案解析)教学提纲
2019-2020届初三 中考复习 三视图 综合题 专项练习(含答案解析)教学提纲
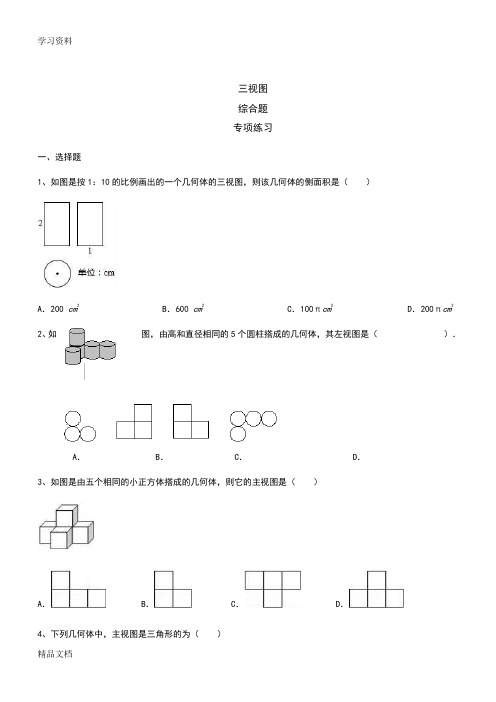
三视图综合题专项练习一、选择题1、如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是()A.200 cm2 B.600 cm2 C.100πcm2 D.200πcm2 2、如图,由高和直径相同的5个圆柱搭成的几何体,其左视图是().A. B. C. D.3、如图是由五个相同的小正方体搭成的几何体,则它的主视图是()A. B. C. D.4、下列几何体中,主视图是三角形的为()A. B. C. D.5、观察下列几何体,主视图、左视图和俯视图都是矩形的是()A. B. C. D.6、如图是某几何体的三视图及相关数据,则判断正确的是()A.a>c B.b>c C.4a2+b2=c2 D.a2+b2=c27、如图是由一些相同的小正方体搭成的几何体的三视图,搭成这个几何体的小正方体个数是( ) A.2个B.3个C.4个D.6个8、如图所示的几何体的俯视图是()9、如图是一个由5个相同的正方体组成的立体图形,它的三视图是()A. B.C. D.10、已知某几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.二、填空题11、如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:cm),计算出这个立体图形的表面积是________cm2.12、如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为________.13、如图是由几个相同的小立方块组成的三视图,小立方块的个数是 .14、长方体的主视图与俯视图如图297,则这个长方体的体积是________.图29715、三棱柱的三视图如图6226,在△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为____________cm.16、.图11-1是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm).将它们拼成如图11-2的新几何体,则该新几何体的体积为_______________cm3.(计算结果保留)17、一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆在课桌上成如图6形式,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为______.18、一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是_______________.19、如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数是个.20、如图所示是用小立方块搭成的几何体的主视图、俯视图,它最少需要___________个小立方块,最多需要_____________个小立方块.三、简答题21、一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),(1)这个零件是什么几何体?(2)求这个零件的表面积、体积(结果保留π)22、某几何体的主视图、左视图和俯视图分别如图,试求该几何体的体积.23、由6个相同的小立方块搭成的几何体如图所示,请画出从三个方向看所得到的形状图.24、如图,下列是一个机器零件的毛坯,请将这个机器零件的三视图补充完整.25、已知图为一几何体从不同方向看的图形:(1)写出这个几何体的名称;(2)任意画出这个几何体的一种表面展开图;(3)若长方形的高为10厘米,三角形的边长为4厘米,求这个几何体的侧面积.26、画图:(1)画出圆锥的三视图.已知∠AOB,用直尺和圆规作∠A′O′B′=∠AOB(要求:不写作法,保留作图痕迹)27、如图是一个几何体的二视图(左图为正视图,右图为俯视图),求该几何体的体积(л取3.14).28、由一些大小相同的小正方体组成的简单几何体的主视图和俯视图(如图11). (1)请你画出这个几何体的一种左视图;(2分)(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.(4分)29、如图是一个由若干个棱长相等的正方体构成的几何体的三视图。
三视图练习题及答案

三视图练习题及答案三视图是工程设计、制图等领域中常用的表达方式之一,它能够以三个不同的视角展示一个物体的外观和内部结构,帮助人们更好地理解和分析物体的形状和构造。
为了提高对三视图的理解和应用能力,下面将给出一些三视图练习题及答案,希望对读者有所帮助。
1. 请根据给出的三视图,画出物体的立体图。
答案:根据三视图,我们可以确定物体的形状和尺寸,然后利用透视法将其转化为立体图。
在绘制过程中,需要注意比例和透视关系,以保证立体图的准确性。
2. 给出一个物体的立体图,请根据立体图绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察立体图中的各个面,然后根据其相对位置和大小来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意比例和尺寸的准确性,以确保三视图能够准确地表达立体图的形状和结构。
3. 请根据给出的三视图,判断物体的形状是什么?答案:通过观察三视图中的线条和面,我们可以判断物体的形状。
例如,如果正视图中的线条是直的,侧视图中的线条是弯曲的,那么物体可能是一个圆柱体。
通过观察三视图中的特征,我们可以逐步推断出物体的形状。
4. 给出一个物体的形状,请根据形状绘制出相应的三视图。
答案:在绘制三视图时,我们需要观察物体的形状和结构,然后根据其特征来绘制对应的正视图、俯视图和侧视图。
在绘制过程中,需要注意线条的粗细和长度,以确保三视图能够准确地表达物体的形状和结构。
通过以上的练习题和答案,我们可以提高对三视图的理解和应用能力。
练习三视图不仅可以帮助我们更好地理解和分析物体的形状和结构,还可以提高我们的制图能力和空间想象力。
在实际工程设计和制图中,三视图是非常重要的表达方式,掌握好三视图的绘制和解读技巧对于工程师和设计师来说是非常必要的。
总之,通过不断地练习和应用,我们可以提高对三视图的掌握程度,为工程设计和制图提供更准确、更有效的表达方式。
希望以上的练习题和答案能够对读者有所帮助,进一步提高对三视图的理解和应用能力。
2019-2020学年浙教版九年级数学下学期第三章 三视图与表面展开图单元测试题(含答案)

浙教版九年级数学下第三章三视图与表面展开图单元检测第Ⅰ卷(选择题)一.选择题(共10小题,3*10=30)1.如图是由四个相同的小正方体组成的几何体,则这个几何体的主视图是()A B C D2.某时刻两根木棒在同一平面内的影子如图所示,此时,第三根木棒的影子表示正确的是()3.一个几何体的三视图如图所示,这个几何体的侧面积为()A.2π cm2B.4π cm2C.8π cm2D.16π cm24.小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为()A.上午12时B.上午10时C.上午9时30分D.上午8时5.如图,一个空心圆柱体,其主视图正确的是()A B C D6.下列命题正确的是()A.三视图是中心投影B.三视图等价于投影C.球的三视图均是半径相等的圆D.阳光从矩形窗子里照射到地面上,得到的投影仍是矩形7.如图,某厂生产横截面直径为7 cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()A.π4cm B.7π4cm C.7π2cm D.7π cm8.如图是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数有()A.3个B.4个C.5个D.6个9.如图,从一块直径为24 cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是() A.12 cm B.6 cm C.3 2 cm D.2 3 cm10.如图,夜晚,小亮从A经过路灯C的正下方沿直线走到点B,他的影子y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为()第Ⅱ卷(非选择题)二.填空题(共6小题,4*6=24)11.有一个圆柱,它的高等于12 cm,底面半径等于3 cm,如图9所示,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,则它沿圆柱侧面爬行的最短路程是_______ cm(π取3).12.为了在平面上表示空间物体,人们常用数学上的“投影”方法,即把物体从不同的方向投射到平面上,然后通过这些平面的投影图形去想象空间立体图形.这是人类征服空间所表现出的伟大智慧!如图是某一物体的三个方向的影像图.它相当于光线从正面、侧面和上面照射时,该物体留下的影子,那么这个几何体可能是____________.13.如图11所示是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是__________.14.一个几何体的三视图如图所示(其中标注的a,b,c为相应的边长),则这个几何体的体积是___________.15.如图13是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是___________.16.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的表面积是___________mm2.三.解答题(共6小题,46分)17.(8分)画出如图所示物体的三视图.18.(8分)如图,已知圆锥底面半径r=10 cm,母线长为40 cm.(1)求它的侧面展开图的圆心角和面积;(2)若一甲虫从点A出发沿着圆锥侧面绕行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?19.(10分)一位同学想利用有关知识测旗杆的高度,如图,他在某一时刻测得高为0.5 m 的小木棒的影子长为0.3 m,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子CD=1.0 m,又测地面部分的影长BC=3.0 m,你能根据上述数据帮他测出旗杆的高度吗?20.(10分)如图,有一直径是 2 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形BAC.(1)求AB的长;(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为多少米.21.(10分)如图,不透明圆锥体DEC放在水平面上,在A处灯光照射下形成影子.设BP过圆锥底面的圆心,已知圆锥的高为2 3 m,底面半径为2 m,BE=4 m.(1)求∠B的度数;(2)若∠ACP=2∠B,求光源A距水平面的高度.(答案用含根号的式子表示)22.(10分)如图是一粮仓,其顶部是一圆锥,底部是一圆柱.(1)画出粮仓的三视图;(2)若圆柱的底面圆的半径为1 m,高为2 m,求圆柱的侧面积;(3)假设粮食最多只能装到与圆柱同样高,则最多可以存放多少立方米的粮食?23.(10分)为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计的方案新颖,构思巧妙.(1)甲生的方案:如图1,将视力表挂在墙ABEF和墙ADGF的夹角处,被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由;(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可计算得到:测试线应画在距离墙ABEF________米处;(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?参考答案 1-5 CDBDB 6-10 CBBCA 11.1512. 一个倒立的圆锥 13. 5 14. abc_ 15. 左视图 16. 20017. 解:如答图所示.18. 解:(1)nπ×40180=2π×10,解得n =90.∴圆锥侧面展开图的圆心角为90°,圆锥侧面展开图的面积为π×10×40=400π(cm 2);(2)如图,由圆锥的侧面展开图可见,甲虫从A 点出发沿着圆锥侧面绕行到母线SA 的中点B 所走的最短路线是线段AB 的长.在Rt △ASB 中,SA =40 cm ,SB =20 cm ,∴AB =20 5 cm.∴甲虫走的最短路线的长度是20 5 cm.19. 解:作DE⊥AB于点E,那么四边形BCDE是矩形,∴BE=CD=1.0 m,DE=BC=3.0 m,∴AEDE=0.50.3,∴AE=5(m),∴AB=AE+BE=6(m)20. 解:(1)如图,连结BC.∵∠BAC=90°,∴BC为⊙O的直径,即BC= 2 m,∴AB=22BC=1(m);(2)设所得圆锥的底面圆的半径为r(m),由题意,得2πr=90×π×1180,解得r=14.答:圆锥的底面圆的半径为14m.21. 解:(1)在Rt△DOB中,OB=BE+OE=4+2=6(m),∴tanB=DOBO=236=33.∴∠B=30°(2)过点A作AF⊥BP,垂足为点F.∵∠B=30°,∴∠ACP=2∠B=60°.又∠ACP =∠B+∠BAC,∴∠B=∠BAC.∴AC=BC=BE+CE=8(m).在Rt△ACF中,AF=AC·sin∠ACF=8sin60°=43(m).故光源离水平面的高度为4 3 m22. 解:(1)粮仓的三视图如图所示:(2)S圆柱侧=2π·1×2=4π m2(3)V=π×12×2=2π(m3),即最多可存放2π m3的粮食23. 解:(1)甲生的方案可行.理由如下:根据勾股定理得AC2=AD2+CD2=3.22+4.32,∵3.22+4.32>52,∴AC2>52,即AC>5,∴甲生的方案可行;(2)设测试线应画在距离墙ABEFx米处,根据平面镜成像可得x+3.2=5,解得x=1.8,∴测试线应画在距离墙ABEF1.8米处;(3)∵△ADF∽△ABC,∴FDBC=ADAB,即FD3.5=35,∴FD=2.1(cm).答:小视力表中相应“E”的长是2.1cm.。
精品 九年级数学 中考专题 三视图 综合练习题

三视图综合练习题一、选择题:1.如图,甲、乙、丙、丁四人分坐在一方桌的四个不同方向上,看到桌面上的图案呈“A”种形状的是() A. 甲 B. 乙 C. 丙 D. 丁2. 如图,一个空间几何体的主视图和左视图都是边长为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是()3. 将如右图所示的Rt△ABC绕直角边AC旋转一周,所得几何体的主视图是()4. 如图①是一些大小相同的小正方形组成的几何体,其主视图如图②所示,则其俯视图是()5. 如图,圆锥的侧面积恰好等于其底面积的2倍,则该圆锥侧面展开图所对应扇形圆心角的度数为()A. 600B. 900C. 1200D. 18006. 如图,是由相同小正方形组成的立体图形,它的左视图是()7.将一个正方体沿某些棱展开后,能够得到的平面图形是()8. 由一些完全相同的小立方块搭成的几何体的三视图如图所示,那么搭成这个几何体所用的小立方块的个数是( ) A. 8 B. 7 C. 6 D. 59. 如图,是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体最多块数是( ) A. 9 B. 10 C. 11 D. 1210. 一个几何体由一些大小相同的小正方体组成,如图是它的主视图和俯视图,那么组成该几何体所需小正方体的个数最少为( )A.3B. 4C. 5D.611.如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的个数是( )A .2个或3个B .3个或4个C .4个或5个D .5个或6个12. 如图,它需要再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四个同学补画,其中正确的是( )13.图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN 的度数为( ) A .30º B .36º C .45º D .72º14.如图,晚上小亮在路灯下散步,在小亮由A 处径直走到B 处这一过程中,他在地上的影子( )A .逐渐变短B .先变短后变长C .先变长后变短D .逐渐变长15.如图,三角形ABC 是一个圆锥的左视图,其中AB=AC=5,BC=8,则这个圆锥的侧面积是( )A.12πB. 16πC. 20πD. 36π16. 如图,桌面上的模型由20个棱长为a 的小正方体组成,现将该模型露在外面的部分涂上涂料,则涂上涂料部分的总面积为( )A .220aB .230aC .240aD .250a17.如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去了7个小正方体),所得到的几何体的表面积是( )A .78B .72C .54D .4818.一个画家有14个边长为1m 的正方体,他在地面上把它们摆成如图8所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )A. 19m 2B. 21m 2C. 33m 2D. 34m 2二、填空题:19.三角尺在灯泡O 的照射下在墙上形成影子(如图6所示).现测得20cm 50cm OA OA '==,,这个三角尺的周长与它在墙上形成的影子的周长的比是 .20.如图,光源P 在横杆AB 的正上方,AB 在灯光下的影子为CD ,AB ∥CD ,AB =2m ,CD =6m ,点P 到CD的距离是2.7m ,则AB 与CD 间的距离是__________m .21.如图,一根直立于水平地面上的木杆AB 在灯光下形成影子,当木杆绕A 按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB 垂直于地面时的影长为AC (假定AC >AB ),影长的最大值为m ,最小值为n ,那么下列结论:①m >AC ;②m =AC ;③n =AB ;④影子的长度先增大后减小.其中,正确的结论的序号是 .22.如图都是由边长为1的正方体叠成的图形。
中考三视图练习题

中考三视图练习题一、选择题1. 下列哪个选项是正确的主视图?A. 左视图B. 俯视图C. 右视图D. 仰视图2. 三视图包括哪三个视图?A. 俯视图、左视图、右视图B. 主视图、俯视图、左视图C. 仰视图、俯视图、左视图D. 仰视图、右视图、左视图3. 观察一个物体时,哪个视图可以提供物体的宽度信息?A. 主视图B. 俯视图C. 左视图D. 仰视图4. 下列哪个选项是正确的俯视图?A. 显示物体的顶面形状B. 显示物体的侧面形状C. 显示物体的正面形状D. 显示物体的底面形状5. 当物体的主视图和左视图都相同,且都是矩形时,该物体可能是:A. 立方体B. 圆柱体C. 长方体D. 球体二、填空题6. 在三视图中,______视图显示物体的正面形状。
7. 当物体的主视图和俯视图都是圆形时,该物体可能是______。
8. 一个物体的三视图可以提供物体的______、______和______三个方向的信息。
9. 俯视图通常显示物体的______面形状。
10. 如果一个物体的主视图和左视图都是正方形,那么该物体可能是______。
三、判断题11. 一个物体的主视图和左视图可能完全不同。
()12. 三视图中的任何一个视图都不能单独表示物体的全部信息。
()13. 俯视图可以提供物体的高度信息。
()14. 物体的三视图是相互独立的,没有联系。
()15. 一个物体的三视图可以完全相同的情况是不存在的。
()四、简答题16. 请简述三视图在工程制图中的应用意义。
17. 描述如何通过三视图来确定一个物体的形状。
五、绘图题18. 根据以下描述,绘制一个物体的三视图:- 主视图:一个矩形,长为10cm,宽为5cm。
- 俯视图:一个矩形,长为8cm,宽为6cm。
- 左视图:一个矩形,长为10cm,宽为8cm。
19. 假设你面前有一个立方体,其边长为4cm,请绘制其三视图。
六、综合应用题20. 你是一名工程师,需要根据客户提供的三视图来制作一个零件。
2020年中考数学复习专项训练:三视图与展开图(含答案)
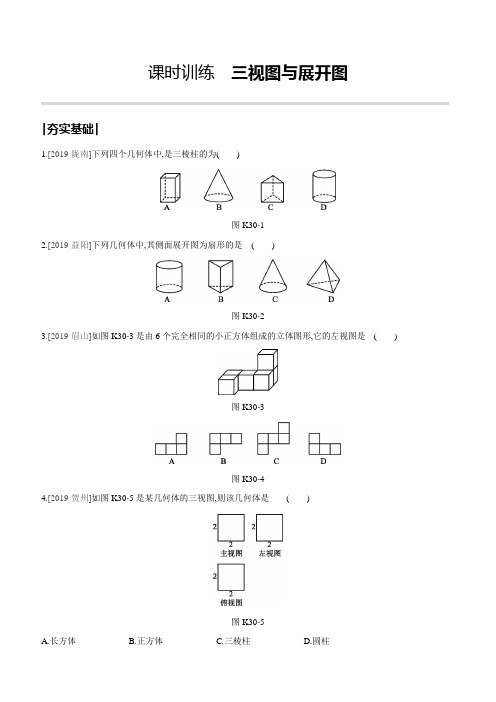
课时训练三视图与展开图|夯实基础|1.[2019·陇南]下列四个几何体中,是三棱柱的为()图K30-12.[2019·益阳]下列几何体中,其侧面展开图为扇形的是()图K30-23.[2019·眉山]如图K30-3是由6个完全相同的小正方体组成的立体图形,它的左视图是()图K30-3图K30-44.[2019·贺州]如图K30-5是某几何体的三视图,则该几何体是()图K30-5A.长方体B.正方体C.三棱柱D.圆柱5.[2019·聊城]如图K30-6所示的几何体的左视图是 ()图K30-6图K30-76.[2019·淄博]下列几何体中,其主视图、左视图和俯视图完全相同的是()图K30-87.[2018·烟台]由5个棱长为1的小正方体组成的几何体如图K30-9放置,一面着地,两面靠墙.如果将露出的部分涂色,则涂色部分的面积为()图K30-9A.9B.11C.14D.188.[2019·大庆]一个“粮仓”的三视图如图K30-10所示(单位:m),则它的体积是()图K30-10A.21π m3B.30π m3C.45π m3D.63π m39.[2019·深圳]下列哪个图形是正方体的展开图 ()图K30-1110.[2019·齐齐哈尔]如图K30-12是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图,则搭建这个几何体所需要的小正方体的个数至少为()图K30-12A.5B.6C.7D.811.[2018·济宁]一个几何体的三视图如图K30-13所示,则该几何体的表面积是()图K30-13A.24+2πB.16+4πC.16+8πD.16+12π12.[2019·北京]在如图K30-14所示的几何体中,其三视图中有矩形的是.(写出所有正确答案的序号)图K30-1413.[2019·甘肃]已知某几何体的三视图如图K30-15所示,其中俯视图为等边三角形,则该几何体的左视图的面积为.图K30-1514.已知一个底面为菱形的直棱柱,高为10 cm,体积为150 cm3,则这个棱柱的下底面面积为cm2;若该棱柱侧面展开图的面积为200 cm2,记下底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为cm.15.已知一个几何体的三视图如图K30-16,请描述该几何体的形状,并根据图中标注的尺寸(单位:cm)求它的侧面积.图K30-16|拓展提升|16.如图K30-17①是上、下底面为全等的正六边形的礼盒,其主视图与左视图均由矩形构成,测得相关数据如图②所示,左视图包含两个全等的矩形,如果用彩色胶带如图①所示包扎礼盒,所需胶带长度至少为cm. (若结果带根号,则保留根号)图K30-17,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再17.[2017·十堰]如图K30-18,已知圆柱的底面直径BC=6π沿另一面爬回C点,则小虫爬行的最短路程为()图K30-18A.3√2B.3√5C.6√5D.6√2【参考答案】1.C2.C3.D4.B5.B6.D7.B[解析]分别从正面、右面、上面观察可得该几何体的三视图如图.其中主视图面积为4,右视图面积为3,俯视图面积为4,从而露出的部分涂色面积为:4+3+4=11.故选B.8.C[解析]由图可知“粮仓”是由一个圆锥和一个圆柱组成的,其中,底面直径为6 m,圆柱的高为4 m,圆锥的高π×32×3=45π(m3),故选C.为3 m,所以体积=π×32×4+139.B10.B11.D[解析]由这个几何体的三视图可知,这个几何体是底面半径为2,高为4的圆柱体的一半,其表面积为上下两个相同的半径为2的半圆的面积,底面半径为2,高为4的圆柱侧面一半的面积以及边长为4的正方形的面积之和,其面积分别为4π,8π和16,则该几何体的表面积是16+12π,因此,本题应该选D.12.①②13.3√3cm2[解析]该几何体是一个三棱柱,底面等边三角形边长为2 cm,高为√3cm,三棱柱的高为3,所以,其左视图的面积为3×√3=3√3(cm2).14.151或915.解:这个几何体是底面为梯形的直四棱柱.侧面积=[3+6+4.5+√4.52+(6-3)2]×9(cm2).=243+27√13216.(120√3+90)17.D[解析]将已知圆柱侧面展开得到如图所示的矩形,小虫从C点爬到A点,然后再沿另一面爬回C点经过的,所以此圆柱的底面周长为6,则展开图中CB=C'B=3,又AB=3,所以最短路程为2AC.因为圆柱的底面直径BC=6πAC=3√2,所以小虫爬行的最短路程为6√2,故选D.。
九年级数学三视图专项测试(含答案)

学生做题前请先回答以下问题问题1:观察一个几何体的形状通常从三个方面看,从_____看(主视图),从____看(____),从______看(____).问题2:正方形的展开图有哪几种?三视图专项测试一、单选题(共7道,每道14分)1.如图是由若干个大小相同的小正方体堆砌而成的几何体.那么其三种视图中面积最小的是( )A.主视图B.左视图C.俯视图D.三种一样答案:B解题思路:试题难度:三颗星知识点:几何体的三视图2.如图是由若干个同样大小的立方体搭成的几何体的俯视图,小正方形中的数字表示该位置立方体的个数,则这个几何体的左视图是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:几何体的三视图3.一个铁制零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )A. B.C. D.解题思路:试题难度:三颗星知识点:简单几何体的三视图4.如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面上的字是( )A.中B.钓C.鱼D.岛答案:C解题思路:试题难度:三颗星知识点:正方体的展开图5.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体中与“着”字相对的面上的汉字是( )A.冷B.静C.应D.考解题思路:试题难度:三颗星知识点:正方体展开图---相对面6.如图所示的正方体的展开图可能是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:正方体的展开与折叠7.长方体的主视图与左视图如图所示(单位:m),则其俯视图的面积是( )A.12m2B.8m2C.6m2D.4m2答案:A解题思路:试题难度:三颗星知识点:三视图的面积应用。
2019-2020北师大版九年级上册 投影和视图专题(含答案)

2019-2020北师大版九年级上册投影与视图专题(含答案)一、单选题1.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是()A.主视图B.俯视图C.左视图D.一样大2.由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有()A.3块B.4块C.6块D.9块3.一个几何体由若干个相同的正方体组成,其主视图和俯视图如图所示,则这个几何体中正方体的个数最多是()A.3 B.4 C.5 D.64.一个几何体的三视图如图所示,则该几何体的表面积是()A.24+2πB.16+4πC.16+8πD.16+12π5.如图是一个几何体的主视图和俯视图,则这个几何体是()A.三棱柱B.正方体C.三棱锥D.长方体6.如图所示的几何体,它的左视图是()A.B.C.D.7.如图所示的支架(一种小零件)的两个台阶的高度和宽度相等,则它的左视图为()A. B. C. D.8.如图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数不可能是()A.3B.4C.5D.69.下面是几个一样的小正方体摆出的立体图形的三视图,由三视图可知小正方体的个数为()A.6个B.5个C.4个D.3个10.某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有()A.4个B.5个C.6个D.7个11.如图所示,是一个空心正方体,它的左视图是()A. B. C. D.12.如图,在下列四个几何体中,从正面、左面、上面看不完全相同的是()A.①②B.②③C.①④D.②④13.如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为()A.10B.12C.15D.18二、填空题14.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.15.如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m,已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为____m.三、解答题16.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.17.晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).参考答案1.C【解析】如图,该几何体主视图是由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,故三种视图面积最小的是左视图,故选C.2.B【解析】分析:从俯视图中可以看出最底层小正方体的个数及形状,从主视图和左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.解答:解:从俯视图可得最底层有3个小正方体,由主视图可得有2层上面一层是1个小正方体,下面有2个小正方体,从左视图上看,后面一层是2个小正方体,前面有1个小正方体,所以此几何体共有四个正方体.故选B.3.C【解析】【分析】易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由主视图可得第二层立方体的可能的个数,相加即可.【详解】结合主视图和俯视图可知,左边上层最多有2个,左边下层最多有2个,右边只有一层,且只有1个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三视图
综合题
专项练习
一、选择题
1、如图是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是()
A.200 cm2 B.600 cm2 C.100πcm2 D.200πcm2 2、如图,由高和直径相同的5个圆柱搭成的几何体,其左视图是().
A. B. C. D.
3、如图是由五个相同的小正方体搭成的几何体,则它的主视图是()
A. B. C. D.
4、下列几何体中,主视图是三角形的为()
A. B. C. D.
5、观察下列几何体,主视图、左视图和俯视图都是矩形的是()
A. B. C. D.
6、如图是某几何体的三视图及相关数据,则判断正确的是()
A.a>c B.b>c C.4a2+b2=c2 D.a2+b2=c2
7、如图是由一些相同的小正方体搭成的几何体的三视图,搭成这个几何体的小正方体个数是( ) A.2个B.3个C.4个D.6个
8、如图所示的几何体的俯视图是()
9、如图是一个由5个相同的正方体组成的立体图形,它的三视图是()
A. B.
C. D.
10、已知某几何体的三视图如图所示,则该几何体的体积为()
A. B. C. D.
二、填空题
11、如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:cm),计算出这个立体图形的表面积是________cm2.
12、如图,方桌正上方的灯泡(看作一个点)发出的光线照射方桌后,在地面上形成阴影(正方形)示意图,已知方桌边长1.2 m,桌面离地面1.2 m,灯泡离地面3.6 m,则地面上阴影部分的面积为________.
13、如图是由几个相同的小立方块组成的三视图,小立方块的个数
是 .
14、长方体的主视图与俯视图如图297,则这个长方体的体积是________
.
图297
15、三棱柱的三视图如图6226,在△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为____________cm.
16、
.图11-1是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm).将它们拼成如图
11-2的新几何体,则该新几何体的体积为_______________cm3.(计算结果保留)
17、一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆在课桌上成如图6形式,然后他把露出的表面都涂上不同的颜色,则被他涂上颜色部分的面积为______.
18、一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是_______________.
19、如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方
体的个数是
个.
20、如图所示是用小立方块搭成的几何体的主视图、俯视图,它最少需要___________个小立方块,最多需要_____________个小立方块.
三、简答题
21、一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),
(1)这个零件是什么几何体?
(2)求这个零件的表面积、体积(结果保留π)
22、某几何体的主视图、左视图和俯视图分别如图,试求该几何体的体积.
23、由6个相同的小立方块搭成的几何体如图所示,请画出从三个方向看所得到的形状图.
24、如图,下列是一个机器零件的毛坯,请将这个机器零件的三视图补充完整.
25、已知图为一几何体从不同方向看的图
形:
(1)写出这个几何体的名
称;
(2)任意画出这个几何体的一种表面展开
图;
(3)若长方形的高为10厘米,三角形的边长为4厘米,求这个几何体的侧面积.
26、画图:
(1)画出圆锥的三视图.已知∠AOB,用直尺和圆规作∠A′O′B′=∠AOB(要求:不写作法,保留作图痕迹)
27、如图是一个几何体的二视图(左图为正视图,右图为俯视图),求该几何体的体积(л取3.14).
28、由一些大小相同的小正方体组成的简单几何体的主视图和俯视图(如图11). (1)请你画出这个几何体的一种左视图;(2分)
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.(4分)
29、如图是一个由若干个棱长相等的正方体构成的几何体的三视图。
(1)请写出构成这个几何体的正方体个数;
(2)请根据图中所标的尺寸,计算这个几何体的表面积。
四、计算题
30、如图是某工件的三视图,指出该工件是什么几何图形,并求此工件的全面积.
31、如下图,是一个食品包装盒的侧面展开图。
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积。
32、下图是某几何体的展开图.
(1)这个几何体的名称是;(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(取3.14)
参考答案
一、选择题
1、D分析】首先判断出该几何体,然后计算其面积即可.
【解答】解:观察三视图知:该几何体为圆柱,高为2,底面直径为1,侧面积为:πdh=2×π=2π,
∵是按1:10的比例画出的一个几何体的三视图,
∴原几何体的侧面积=100×2π=200π,
故选:D.
【点评】本题考查了由三视图判断几何体及圆柱的计算,解题的关键是首先判断出该几何体.
2、.C
3、D.
4、B【考点】U1:简单几何体的三视图.
【分析】根据主视图的观察角度,从物体的正面观察,即可得出答案.
【解答】解:A、其三视图是矩形,故此选项错误;
B、其三视图是三角形,故此选项正确;
C、其三视图是矩形,故此选项错误;
D、其三视图是正方形形,故此选项错误;
故选:B.
5、B【考点】简单几何体的三视图.
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:A、主视图为矩形,俯视图为圆,错误;
B、主视图为矩形,俯视图为矩形,正确;
C、主视图为等腰梯形,俯视图为圆环,错误;
D、主视图为三角形,俯视图为有对角线的矩形,错误.
故选B.
【点评】本题重点考查了三视图的定义考查学生的空间想象能力.
6、D【解答】解:根据勾股定理,a2+b2=c2.
7、C
8、C
9、A【考点】简单组合体的三视图.
【分析】找到从正面、左面、上看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
【解答】解:此几何体的主视图有两排,从上往下分别有1,3个正方形;
左视图有二列,从左往右分别有2,1个正方形;
俯视图有三列,从上往下分别有3,1个正方形,
故选:A.
【点评】本题考查了三视图的知识,关键是掌握三视图所看的位置.
10、A
二、填空题
11、200 点拨:由三视图可知立体图形由上下两个长方体构成,上面长方体长4、宽2、高4,下面长方体长8,宽6、高2,去掉重合部分,立体图形表面积为:6×8×2+8×2×2+6×2×2+4×4×2+4×2×2=200(cm2).
12、3.24 m2
13、
14、24
15、6
16、60
17、33分米2 ;
18、6
19、4或5
20、9,13
三、简答题
21、【考点】由三视图判断几何体.
【分析】(1)根据三视图可得这个零件是圆柱体;
(2)根据表面积等于侧面积+上下两个底面的面积,体积=底面积×高,进而可得答案.【解答】解:(1)这个零件是圆柱体;
(2)表面积是:π×52×2+15×π×10=200π(平方厘米);
体积:π×52×15=375π(立方厘米),
答:表面积是200π平方厘米;体积是375π立方厘米.
22、(立方单位);
23、【解答】解:如图所示:
.
24、【考点】作图-三视图.
【分析】利用已知几何体的形状进而补全几何体的三视图.
【解答】解:如图所示:
【点评】此题主要考查了画几何体的三视图,注意三视图中实线与虚线.
25、【考点】由三视图判断几何体;几何体的展开
图.
【分析】(1)只有棱柱的主视图和左视图才能出现长方形,根据俯视图是三角形,可得到此几何体为三棱柱;
(2)应该会出现三个长方形,两个三角
形;
(3)侧面积为3个长方形,它的长和宽分别为10,4,计算出一个长方形的面积,乘3即
可.
【解答】解:(1)正三棱
柱;
(2)
;
(3)3×10×
4=120cm2.
【点评】用到的知识点为:棱柱的侧面都是长方形,上下底面是几边形就是几棱
柱.
26、【考点】作图-三视图;作图—基本作图.
【分析】(1)结合三视图的作法,分别从正面,左面,上面观察图形得出答案;结合作一角等于已知角的作法得出答案即可.
【解答】解:(1)如图所示:
;如图所示:
.
【点评】此题主要考查了三视图的作法以及作一角等于已知角,正确掌握基本作图方法是解题关键.
27、41248cm3.
28、(1)等
(2)n=8,9,10,11
29、解:(1)5个
(2)或
四、计算题
30、解:此工件为圆锥体
31、解:(1)这个多面体是六棱柱;
(2)侧面积为。
32、(1)圆柱;
(2)三视图为:
(3)体积为:==1570.。
