10.1.2立方根
立方根口诀表初中

立方根口诀表初中立方根,初中数学中的一个重要概念,是数学中的一个基础知识点。
立方根口诀表可以帮助初中生更好地记忆立方根的计算规则。
下面就来总结一下立方根口诀表。
1. 1-10的立方根口诀为了方便记忆,我们可以使用1至10的立方根口诀表,如下所示:•\(1^3\)等于1•\(2^3\)等于8•\(3^3\)等于27•\(4^3\)等于64•\(5^3\)等于125•\(6^3\)等于216•\(7^3\)等于343•\(8^3\)等于512•\(9^3\)等于729•\(10^3\)等于10002. 特殊的立方根口诀除了1至10的立方根口诀外,还有一些特殊的立方根口诀需要记忆,如下所示:•\(11^3\)等于1331•\(12^3\)等于1728•\(13^3\)等于21973. 简单计算立方根的小窍门在计算立方根时,有一个小窍门可以帮助我们快速计算,即将给定的数进行分解,如下所示:•对于一个二位数,我们可以将它分解为十位数和个位数,再进行计算。
•对于一个三位数,我们可以将它分解为百位数、十位数和个位数,再进行计算。
4. 立方根的性质在进一步学习立方根的过程中,我们还需要了解一些立方根的性质,如下所示:•对于正数a和b,\( \sqrt[3]{a} \times \sqrt[3]{b} = \sqrt[3]{a \times b} \)•对于任意的正整数n,都存在一个整数m,使得\(m^3 \leq n < (m+1)^3\)。
通过以上的立方根口诀表和小窍门,相信初中生们可以更好地掌握立方根的计算方法,提高数学能力。
希望这些内容对你有所帮助!。
实用的平方根表立方根表.pdf

,检查合同的履行情况;
4.5.4 保管法人代表授权委托书、合同专用章,并按编号归口使用;
4.5.5 建立合同管理台帐,对合同文本资料进行编号统计管理;
4.5.6 组织对法规、制度的学习和贯彻执行,定期向有关领导和部门报告工作;
4.5.7 在总经理领导下,做好合同管理的其他工作,
4.6 工程技术部:专职合同管理员及材料、燃料供应部兼职合同管理员履行以下职责:
4.2 工程部:是发电厂建设施工安装等工程合同签订管理部门;负责签订管理基建、安装、人工技术的工程合同。
4.3 经营部:是合同签订管理部门,负责管理设备、材料、物资的订购合同。
4.5 合同管理部门履行以下职责:
4.5.1 建立健全合同管理办法并逐步完善规范;
4.5.2 参与合同的洽谈、起草、审查、签约、变更、解除以及合同的签证、公证、调解、诉讼等活动,全程跟踪和检查合同的履行质量; 4.5.3 审查、登记合同对方单位代表资格及单位资质,包括营业执照、经营范围、技术装备、信誉、越区域经营许可等证件及履约能力(必要时要求对方提供担保)
立方根 √3 1 = 1 √ 2 = 1.260 √ 3 = 1.442 √ 4 = 1.587 √ 5 = 1.710 √ 6 = 1.817 √ 7 = 1.913 √8 = 2 √ 9 = 2.080 √ 10 = 2.154 √ 11 = 2.224 √ 12 = 2.289 √ 13 = 2.351 √ 14 = 2.410 √ 15 = 2.466 √ 16 = 2.520 √ 17 = 2.571 √ 18 = 2.621 √ 19 = 2.668 √ 20 = 2.714
平方根 √1=1 √2= 1.414 √3= 1.732 √4=2 √5= 2.236 √6= 2.449 √7= 2.646 √8= 2.828 √9=3 √10=3.162 √11 = 3.317 √12 = 3.464 √13 = 3.606 √14 = 3.742 √15 = 3.873 √16 = 4 √17 = 4.123 √18 = 4.243 √19 = 4.359 √20 = 4.472
立方根及乘方开方表

?cm1-3 立方根及乘方開方表一、重點整理你知道2的三次方等於8,但你知道什麼數的三次方等於2嗎?有沒有這樣的數?這個數怎 麼表示?它到底是多少?用心學過這個單元之後,這些疑惑就可以迎刃而解了。
(1) 正數的立方根體積是125立方公分的正方體,它的邊長是多少公分? 這個問題就是找一個正數,使這個正數的立方(三次方) 等於125。
12555553=⨯⨯=,即12553=5的立方是125,我們就稱5是125的立方根。
例題:(1)1的立方是1,即113=,1是1的立方根。
(2)2的立方是8,即823=,2是8的立方根。
(3)3的立方是27,即2733=,3是27的立方根。
(2) 負數的立方根 125)5()5()5()5(3-=-⨯-⨯-=-,即125)5(3-=-5-的立方是125-,我們就稱5-是125-的立方根。
例題:1. (1)1)1()1()1()1(3-=-⨯-⨯-=-,所以1-是1-的立方根。
(2)8)2()2()2()2(3-=-⨯-⨯-=-,所以2-是8-的立方根。
(3)27)3()3()3()3(3-=-⨯-⨯-=-,所以3-是27-的立方根。
(4)64)4()4()4()4(3-=-⨯-⨯-=-,所以4-是64-的立方根。
例題:2. (1)問3是不是27的立方根?(2)問3-是不是27的立方根?解:(1)因為2733333=⨯⨯=,所以3是27的立方根。
(2)因為2727)3()3()3()3(3≠-=-⨯-⨯-=-,所以3-不是27的立方根。
答:(1)是;(2)不是(3) 立方根的表示法 1. 正數的立方根是正的,零的立方根是零,負數的立方根是負的。
2. 表示法: 以3a (讀作三次跟號a )表示a 的立方根說明:平方跟號就是2讀作“二次根號”。
例1: (1) 823=∴2是8的立方根,記作283=(2) 8)2(3-=-∴2-是8-的立方根,記作283-=-例2: (1)3273= (2) 3273-=-(3) 0=(4) 乘方開方表我們也可以用乘方開方表來查平方根與立方根。
华师大版-数学-八年级上册-11.1.2 立方根 教案

11.1.2 立方根教学目标1.了解立方根的概念,会用根号表示一个数的立方根.2.会用立方运算求一个数的立方根,了解开立方与立方互为逆运算.3.了解立方根的性质.4.区分立方根与平方根的不同.教学重点立方根的概念及计算.教学难点立方根的求法,立方根与平方根的联系及区别.教法学法教学方法:类比法.教学过程一、创设问题情境:一个正方体的体积为216,那么它的棱长是多少啊?如果是64呢?是x 呢?(通过实际情境引入,让学生感受新知学习的必要性,激发学生的求知欲望.在思考问题的同时,学生既感受了数学的应用价值,激发了学生的学习热情,有很快将问题归结为如何确定一个数,从而顺利引入新课.)二、类比学习新知一般地,如果一个数的立方等于a ,那么这个数就叫做a 的立方根( 也叫做三次方根).如:2是8的立方根,的立是--273,0是0的立方根.(学生通过回顾上节课的学习内容,为进一步研究立方根的概念及性质做好铺垫,同时 突出平方根与立方根的对比,以利于学生类比学习法学习立方根知识.)三、应用新知:1.做一做:怎样求下列括号内的数?各题中已知什么数?求什么数?(1)27=) (3 ; (2)27=-) (3 ; (3)0 3=)(.【答案】(1)3; (2)-3; (3)0.2议一议:(1)正数有几个立方根?(2)0有几个立方根(3)负数呢?3.概括:(1)正数的立方根是正数;0的立方根是0;负数的立方根是负数.(2)数a 的立方根,记为“3a ”,读作“三次根号a”.a 是被开方数,3是根指数. (3)求一个数的立方根的运算叫做开立方(extrction of cubic root) , 开立方与立方互为逆运算.四、应用举例:例1:求下列各数的立方根:(1)27; (2)125-; (3)278; (4)008.0-;解:(1)因为2733=,所以27的立方根是3,即3273=.(2)因为()12553-=-,所以125-的立方根是5-,即51253-=-. (3)因为278323=⎪⎪⎭⎫ ⎝⎛,所以278的立方根是32,即322783=. (4)因为()008.02.03-=-,所以008.0-的立方根是2.0-,即2.0008.03-=-.五、巩固练习:求下列各数的立方根:(1)27-; (2)1258 ; (3)833 ; (4)216.0 ; (5)5-.解:(1)因为2733=-)(-,所以27-的立方根是3-,即3273=--;(2)因为1258523=⎪⎭⎫ ⎝⎛,所以1258的立方根是52,即5212583=; (3)因为833827233==)(,所以833的立方根是23,即238333=; (4)因为216.06.03=)(,所以216.0的立方根是6.0,即6.0216.03=;(5)5-的立方根是35-.六、巩固提高:用计算器求下列各数的立方根:(1)1331; (2)9.263(精确到0.01)解:(1)在计算器上依次键入SHIFT1331=显示结果为1111=(2)在计算器上依次键入SHIFT9.263=显示结果为2.10 2.10≈七、课堂小结:1.了解立方根的概念,会用三次根号表示一个数的立方根,能用立方运算求一个数的立方根.2.在学习中应注意以下5点:(1)符号3a中根指数“3”不能省略;(2)对于立方根,被开方数没有限制,正数、零、负数都有一个立方根;(3)平方根和立方根的区别:正数有两个平方根,但只有一个立方根;负数没有平方根,但却有一个立方根;(4)灵活运用公式:(3a)3=a,aa=33,3a-=3a-;(5)立方与开立方也互为逆运算.我们也可以用立方运算求一个数的立方根,或检验一个数是不是另一个数的立方根.八、课堂作业习题。
1到10的立方根口诀表

1到10的立方根口诀表
1到10的立方根口诀表
立方根口诀表是一个口头算术的数学知识表格,用来帮助记忆1到10的立方根。
下面就给大家介绍1到10的立方根口诀表是什么样子的以及它的重要性。
1到10的立方根口诀表如下:
1的立方根是1;
2的立方根是1.26;
3的立方根是1.44;
4的立方根是1.58;
5的立方根是1.70;
6的立方根是1.81;
7的立方根是1.91;
8的立方根是2.00;
9的立方根是2.08;
10的立方根是2.16。
由此可见,立方根口诀表是用来记忆1到10的立方根的一种非常有效的方法。
这样,读者可以轻松记忆下1到10的立方根,而不必费心去计算它们。
此外,立方根口诀表也能帮助人们更容易地理解更高级的立方根的概念。
比如,在计算更复杂的数学运算时,只要有1到10的立方根口诀表,必要的计算就可以
得出最终的结果。
总之,立方根口诀表就是一个非常重要的数学语言,它可以帮助我们在计算立
方根时节省许多时间。
当然,这个口诀表也可以作为一种数学应用解决更复杂的立方根问题。
无论如何,1到10的立方根口诀表对很多人来说都非常有用,它可以
为我们提供解决立方根问题的解决方案。
华东师范大学出版社初中数学八年级上册 11.1.2立方根PPT

情境引入
思考:故事中的人们遇到什么难题?你能把这个 难题抽象成数学问题吗?
情境引入
边长(?) 体积( 2)
立方
建模
类比学习
类比
牛刀小试
小组讨论归纳立方根的性质
探究1 立方根的性质
同号性
的立方根是正数正数
的立方根是0
0
分类
讨论
的立方根是负数负数
唯一性:一个数的立方根只有一个.
立方根的表示
课堂练习
探究2 正负数的立方根的关系
一般性结论
=
两个互为相反数 的立方根也互为 相反数!!
探究2 正负数的立方根的关系
课堂练习
区别与联 系
表示
区 别性
质
联系
正数 (一个)
互为相反数 (两个)
正数(一个)
0
0
0
没有
没有 负数(一个)
开方运算的结果
课堂练习
新知应用
立方运算 课堂小实际结问题互逆建模开立方运算
立方根
正数的立方根是正数; 负数的立方根是负数; 零的立方根是零
分类 讨论
唯一性
平方根
类比
一个数的立
方根只有一 个
同号性
1.判断下列说课法堂是否练正习确,并说明理由
x x x x
√
课后思考
再见
Adiós
谢谢
9.试着把光芒留给别人,不用太在意那些有的没的,你会更快乐。 80.懦夫把困难举在头顶,英雄把困难踩在脚下。 50.总有些事,管你愿不愿意,它都要发生,你只能接受;总有些东西,管你躲不躲避,它都要来临,你只能面对。 66.天下无难事,只怕有心人。 10.不要抱怨,不要总是觉得自己怀才不遇,这种状况大部分是自己造成的。 92.这个世界不会因为你的付出就必须给予回报,也不会因为你以怎样的方式对待别人,就要求他人同等对待你。人活在这世上,最难的就是 保持一份谦卑和平和,而这份谦卑,来源于内心的真诚和踏实的努力。
立方根表1到100

立方根表1到100在数学中,立方根是指一个数的立方的倒数。
计算立方根常常在科学、工程和数学领域中使用,因此,我将为您提供1到100的立方根表。
计算方法要计算一个数的立方根,可以使用以下的数学公式:cbrt(x) = x^(1/3) = x^(0.333...)其中,cbrt(x)表示x的立方根。
立方根表下面是1到100的立方根表:数字立方根112 1.263 1.444 1.595 1.716 1.827 1.91 829 2.0810 2.1511 2.2212 2.2913 2.3514 2.4115 2.4616 2.5217 2.5718 2.6219 2.6720 2.7121 2.7622 2.8023 2.8424 2.8825 2.9226 2.96 27328 3.0429 3.0730 3.1131 3.1432 3.1733 3.2134 3.2435 3.2736 3.3037 3.3338 3.3639 3.3940 3.4241 3.4542 3.4843 3.5144 3.5345 3.5646 3.5947 3.6148 3.6449 3.6650 3.6951 3.7152 3.7453 3.7654 3.7955 3.8156 3.8357 3.8658 3.8859 3.9060 3.9261 3.9562 3.9763 3.99 64465 4.0266 4.0567 4.0768 4.0969 4.1170 4.1371 4.1672 4.1873 4.2074 4.2275 4.2476 4.2677 4.2978 4.3179 4.3380 4.3581 4.3782 4.3983 4.4184 4.4385 4.4586 4.4787 4.4988 4.5189 4.5390 4.5591 4.5792 4.5993 4.6194 4.6395 4.6596 4.6797 4.6998 4.7199 4.72100 4.74请注意,立方根的计算结果保留两位小数。
实用的平方根表立方根表
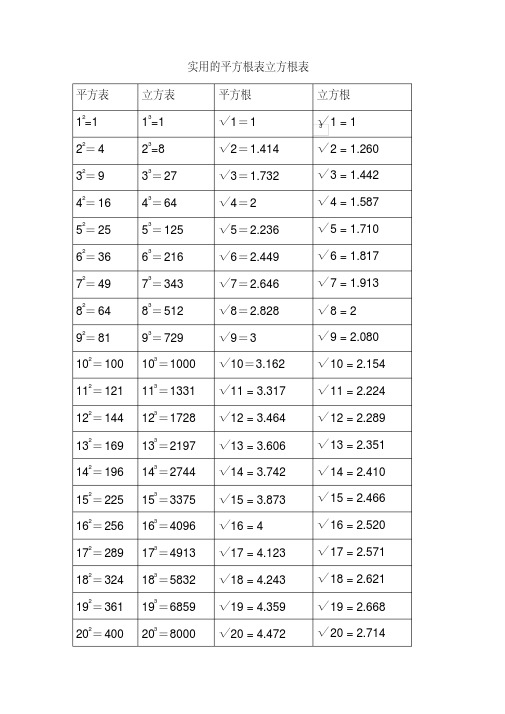
3 实用的平方根表立方根表平方表立方表平方根立方根12=1 13=1 √1=1 √1 = 1 22=4 23=8 √2=1.414 √2 = 1.260 32=9 33=27 √3=1.732 √3 = 1.442 42=16 43=64 √4=2 √4 = 1.587 52=25 53=125 √5=2.236 √5 = 1.710 62=36 63=216 √6=2.449 √6 = 1.817 72=49 73=343 √7=2.646 √7 = 1.913 82=64 83=512 √8=2.828 √8 = 2 92=81 93=729 √9=3 √9 = 2.080 102=100 103=1000 √10=3.162 √10 = 2.154 112=121 113=1331 √11 = 3.317 √11 = 2.224 122=144 123=1728 √12 = 3.464 √12 = 2.289 132=169 133=2197 √13 = 3.606 √13 = 2.351 142=196 143=2744 √14 = 3.742 √14 = 2.410 152=225 153=3375 √15 = 3.873 √15 = 2.466 162=256 163=4096 √16 = 4 √16 = 2.520 172=289 173=4913 √17 = 4.123 √17 = 2.571 182=324 183=5832 √18 = 4.243 √18 = 2.621 192=361 193=6859 √19 = 4.359 √19 = 2.668 202=400203=8000√20 = 4.472√20 = 2.7143√0 = 0(表示根号0等于0,下平方根表立方根表√1 = 1√2 = 1.414√3 = 1.732√4 = 2√5 = 2.236√6 = 2.449√7 = 2.646√8 = 2.828√9 = 3√10 = 3.162√11 = 3.317√12 = 3.464√13 = 3.606√14 = 3.742√15 = 3.873√16 = 4√17 = 4.123√18 = 4.243√19 = 4.359√20 = 4.472其中专业理论知识内容包括:保安理论知识、消防业务知识、职业道德、法律常识、保安礼仪、救护知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
( 8) 2
的平方根为
.
(7) 512 的立方根为
.
授课完
请大家认真完成作业
3
a a
3
也就是说,求一个负数的立方根,可以先 求出这个负数的绝对值的立方根,然后再取它 的相反数。
例2:求下列各式的值。 3 3 3 (1) 8 ;(2) 8 ;(3)
0.125
64 3 (4) 3 3 (5) 3 125 8 3 解:(1) 8 2
( 2) ( 3)
定义
立方根
举例
如果一个数X的 如果一个数X的 平方等于a,即X2=a, 立方等于a,即 那么,这个数X就叫 X3=a,那么,这个数 做a的平方根。 X就叫做a的立方根。 ∵( ± 2)2=4, 3=-8, ∵ ( -2 ) ∴ ± 2是4的平方根。 ∴ -2是-8的立方根。
2、立方根的性质与表示
平方根
立方根
性质
一个正数有 每个数都只有 两个平方根,它 一个立方根。正 们互为相反数; 数的立方根是正 0只有一个平方 数;0的立方根是 根,它是0本身; 0;负数的立方根 是负数。 负数没有平方根。
表示
a的平方根表示 为
a的立方根表示为:
3
a
a
3、开立方
开平方 定 义 认 识
求一个数a的 平方根的运算, 叫做开平方。
3
a 1
2
小结:
1、什么叫一个数的立方根?怎样 用符号表示 数a的立方根?任何数都有 立方根吗?
2、数的立方根与数的平方根有什么 区别?
作业:
(1)1的平方根是____;立方根为____;算术 平方根为__. (2)平方根是它本身的数是____. (3)立方根是其本身的数是____. (4)算术平方根是其本身的数是____. (5) 64 的立方根为 . (6)
开立方
求一个数a的立 方根的运算,叫 做开立方。
①它与平方互 ①它与立方 为逆运算; 互为逆运算; ②它是一种运 ②它是一种 算,而不是结果, 运算,而不是结 它的结果是平方 果,它的结果是 根。 立方根。
“平方根”与“立方根”的比 较
例1 用计算器求下列各数的立方根:
(1) 1 331;(2) -343;(3) 9.263.
3 用式子表示为:
125 5
注意:3
a
的根指数 3 不能省略,要写在根
号的左上角,而且要写得小一些,不能写成 3
a
求一个数的立方根(三次方根)的运算,叫 做开立方,开立方运算的结果就是立方根。 因为开立方与立方互为逆运算。 所以我们可以运用立方运算来求一个数的立 方根。
1、立方根的定义:
平方根
10.1.2 立方根
问题
现有一只体积为 216 cm3 的正方体纸 盒,它的每一条棱长是多少? 思考
这个实际问题,在数学上提出怎样的 一个计算问题?类比“平方根”的概念, 你可以抽象出一个什么数学概念?
概括
上面所提出的问题,实质上就是要找 一 个 数 x , 这 个 数 x 的 立 方 等 于 216. 即 x3=216。
3 3
8 8 2 0.125 0.5
3
解:(4)
3 27 3 3 3 3 8 8 2 64 64 4 3 3 125 125 5
( 5)
问:
一个自然数的算术平方根是a, 那么与这个自然数相邻的下一 个自然数的平方根是_________; 2 立方根是 a 1 ________.
显示结果为 2.100151161,
如果要求精确到0.01,那么所以 : 3 9.263 ≈ 2.10
例1:求下列各数的立方根。
(1)-27; (2)27; (3)-0.216;
( 4) 0;
解:∵
(3) 27
3
8 ( 5) 125
∴ -27的立方根是-3。
即 3
27 3
问题:
分析: 用计算器求一个有理数的立方根,只 需要直接按书写顺序按键. 解: (1) 在计算器上依次键入 显示结果为11,所以 :
3
1331 11
若被开方数为负数,“-”号的输入可以按 也可以按 。 ,
(2) 在计算器上依次键入:
3 . 显示结果为 -7,所以 :
343 7
(3) 在计算器上依次键入:
因为63=216,
所以正方体的棱长应为6 cm.
像平方根那样,6是216的立方根。 即:如果一个数的立方等于a,那么这个 数就叫做a的立方根.
数
a 的立方根用符号
3
a
表示。
读作:“三次根号 方数,3 是根指数。
a
”,其中
a
叫被开
例如:∵
5 125
3
∴ 5 是125 的立方根。 也可以说,125 的立方根是 5 。
正数有立方根吗?如果有,有几个。
负数呢? 零呢? 从上面的例1可知:一个正数有一个正的立 方根;一个负数有一个负的立方根,零的立方根 是零。
从上面的例题可知:
3
27 3
3பைடு நூலகம்
27 3
3
由此可得出: 3
27 27
也就是把根号里的“负号”直接从根号里 面提到了根号“外面” 。
由此得出求一个负数的立方根的一般方法:
