哈夫曼树的构造
哈夫曼树结点数和叶子结点数的关系
哈夫曼树结点数和叶子结点数的关系哈夫曼树是一种用来压缩信息的数据结构，它的关键在于能够将出现频率高的字符用较短的编码表示，从而达到节省空间的目的。
在构造哈夫曼树时，我们需要知道它的结点数和叶子结点数之间的关系，这是本文将要探讨的问题。
一、哈夫曼树的定义哈夫曼树（Huffman Tree）又称最优二叉树，是一种带权路径长度最短的树。
它的构造基于贪心算法，通过不断合并权值最小的两个子树来构造出最终的哈夫曼树。
在哈夫曼树中，树的每一个叶子结点都对应着一个字符，并且权值越大的叶子结点距离根结点越近。
二、哈夫曼树的结点数对于给定的n个字符（字符的出现概率已知），构造哈夫曼树时所需要的结点数是2n-1个。
这个结论可以通过归纳法证明。
首先，当n=1时，哈夫曼树只有一个结点，结论成立。
其次，当n=2时，哈夫曼树有3个结点。
假设当n=k时结论成立，考虑当n=k+1时的情况。
我们先对n个字符进行排序，找出权值最小的两个字符，将它们的权值相加得到一个新的权值，并构造一棵新的子树。
这样就将原来的n 个字符缩减成了n-1个字符，并且引入了一个新的结点。
在接下来的n-2次合并中，每次都引入了一个新的结点，所以总共需要2n-3个结点来构造出这n个字符对应的哈夫曼树。
此时，还需要引入一个新的根结点，作为两个结点（n个字符对应的两个子树）的父结点，并将两个子树连接到这个新的根结点上。
因此，总结点数为2n-3+1=2n-2。
最后，将新的根结点变为虚拟结点，并将n个叶子结点作为其子结点，就得到了结点数为2n-1的哈夫曼树。
三、哈夫曼树的叶子结点数在哈夫曼树中，每个叶子结点都对应着一个字符，因此叶子结点数就等于字符的个数n。
这个结论显然成立。
综上所述，哈夫曼树的结点数和叶子结点数之间存在如下关系：- 结点数 = 2n-1- 叶子结点数 = n这个结论可以帮助我们更好地理解哈夫曼树的构造过程，并且可以在实际应用中帮助我们提前估算哈夫曼树的大小。
wpl怎么算
wpl怎么算
wpl怎么算：wpl=∑Wκ•lκ(n,i=1)
哈夫曼树的构造
每次把最小的两棵二叉树合并。
将数据储存在最小堆中，每次找出最小的并从最小堆中删除。
这其实是一个找出数列其中最小的两个数，作为叶子，然后从数列中删除这两个数。
用这两个数的和sum作为叶子的根，再将根值插入数列中。
其过程为：
1.在堆中找出最小两个数a,b
2.从数列中删除a,b。
并求和a+b=sum
3.建立哈夫曼树，a,b作为叶子结点，sum作为叶子的父节点
4.再将sum插入数列中
5.循环
给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman tree)。
哈夫曼树也可以是k叉的，只是在构造k叉哈夫曼树时需要先进行一些调整。
构造哈夫曼树的思想是每次选k个权重最小的元素来合成一个新的元素，该元素权重为k个元素权重之和。
但是当k大于2时，按照这个步骤做下去可能到最后剩下的元素少于k个。
解决这个问题的办法是假设已经有了一棵哈夫曼树(且为一棵满k叉树)，则可以计算出其叶节点数目为(k-1)nk+1,式子中的nk表示子节点数目为k的节点数目。
于是对给定的n个权值构造k叉哈夫曼树时，
可以先考虑增加一些权值为0的叶子节点，使得叶子节点总数为(k-1)nk+1这种形式，然后再按照哈夫曼树的方法进行构造即可。
数据结构第六章 哈夫曼树
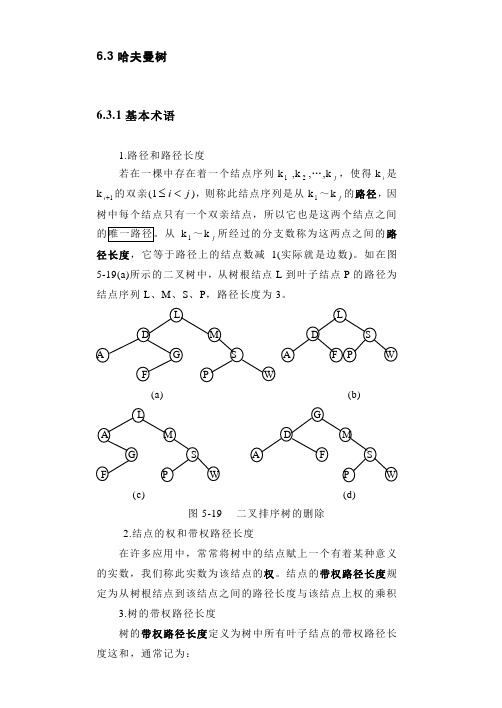
6.3哈夫曼树6.3.1基本术语1.路径和路径长度若在一棵中存在着一个结点序列k1 ,k2,…,kj，使得ki是k1+i 的双亲(1ji<≤)，则称此结点序列是从k1～kj的路径，因树中每个结点只有一个双亲结点，所以它也是这两个结点之间k 1～kj所经过的分支数称为这两点之间的路径长度，它等于路径上的结点数减1(实际就是边数)。
如在图5-19(a)所示的二叉树中，从树根结点L到叶子结点P的路径为结点序列L、M、S、P，路径长度为3。
(a) (b)(c) (d)图5-19 二叉排序树的删除2.结点的权和带权路径长度在许多应用中，常常将树中的结点赋上一个有着某种意义的实数，我们称此实数为该结点的权。
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积3.树的带权路径长度树的带权路径长度定义为树中所有叶子结点的带权路径长度这和，通常记为：2 WPL = ∑=n i i i lw 1其中n 表示叶子结点的数目，i w 和i l 分别表示叶子结点i k 的权值和根到i k 之间的路径长度 。
4.哈夫曼树哈夫曼(Huffman)树又称最优二叉树。
它是n 个带权叶子结点构成的所有二叉树中，带权路径长度 WPL 最小的二叉树。
因为构造这种树的算法是最早由哈夫曼于1952年提出的，所以被称之为哈夫曼树。
例如，有四个叶子结点a 、b 、c 、d ，分别带权为9、4、5、2，由它们构成的三棵不同的二叉树（当然还有其它许多种）分别如图5-20(a)到图5-20(c)所示。
b ac a b cd d c a b d(a) (b) (c)图5-20 由四个叶子结点构成的三棵不同的带权二叉树 每一棵二叉树的带权路径长度WPL 分别为：(a) WPL = 9×2 + 4×2 + 5×2 + 2×2 = 40(b) WPL = 4×1 + 2×2 + 5×3 + 9×3 = 50(c) WPL = 9×1 + 5×2 + 4×3 + 2×3 = 37其中图5-20(c)树的WPL 最小，稍后便知，此树就是哈夫曼树。
哈夫曼树空指针域
哈夫曼树空指针域
哈夫曼树是一种数据结构，通常用于实现二叉搜索树的某些特定操作。
它是一种树状数据结构，由若干个节点组成，每个节点包含了两个子节点，这些节点也被称为左右子节点。
空指针域是哈夫曼树的一个非常重要的特征。
在普通二叉搜索树中，空指针域通常是空的，而在哈夫曼树中，空指针域不仅可以存储根节点，还可以存储若干个左子节点和若干个右子节点。
哈夫曼树的构建过程如下。
首先，将根节点作为哈夫曼树的根节点，然后将根节点的左子节点和右子节点都设为空。
接着，从根节点开始，依次将左子节点和右子节点设为空，并将当前节点设置为有意义的节点。
这个过程一直持续到所有节点都被设置为有意义的节点。
在哈夫曼树的左子树和右子树中，空指针域通常是成对出现的。
也就是说，在左子树中，空指针域通常是（根节点，空），而在右子树中，空指针域通常是（根节点，空）。
哈夫曼树的空指针域可以用来存储任意数量的左子节点和任意数量的右子节点。
通过这种方式，我们可以将哈夫曼树表示成一个二叉树结构，其中包含一个根节点和若干个左子节点和右子节点。
空指针域在哈夫曼树中的作用非常重要。
它可以帮助我们实现一些非常有趣的数据结构，如计数器、优先队列等。
此外，在实际应用中，空指针域也可以用来优化哈夫曼树的构建过程，从而提高搜索效率。
总之，哈夫曼树是一种非常有趣的数据结构，其空指针域可以帮助我们实现许多有用的功能。
哈夫曼树.ppt
n
w i pi
最小，其中
i 1
Wi是第i个字符的使用频度，而Pi是第i个字符的编码长度， 这正是度量报文的平均长度的式子。
2020/3/5
21
例2：要传输的电文是{CAS；CAT；SAT；AT}
要传输的字符集是 D={C，A，S，T， ；}
每个字符出现的频率是W={ 2，4， 2，3， 3 }
PL=0+1+1+2+2=6
2020/3/5
9
问题2：什么样的带权树路径长度最小？
例如：给定一个权值序列{2,3,4,7}，可构造的多种 二叉树的形态。
2
3
4
7
2 34 7
(a) WPL=2×2＋2×3+2×4+2×7=32 (b) WPL=1×2＋2×3+3×4+3×7=41
2020/3/5
7
4
3
2
(c) WPL=1×7＋2×4+3×3+3×2=30
10
哈夫曼树的构造
例：给定权值{7，5，2，4}，构造哈夫曼树。
6
方法： 75 2 4
75
（1）a 初始b化：由c 原始d数据生成森林a ； b c
d
（次2小）的找二最叉小(树a树) 作：为在左森右林子中树选构取造两一棵棵根新结的点二权叉值树最(，小b)其的根和
A）先序遍历
B）中序遍历
C）后序遍历
D）从根开始进行层次遍历
2、某二叉树的先序序列和后序序列正好相反，则该二叉
树一定是（ B ）的二叉树。
A）空或只有一个结点
B）高度等于其结点数
C）任一结点无左孩子
D）任一结点无右孩子
数据结构(C语言版)第2版的习题集答案—严蔚敏(简化版).doc
第2章线性表1．选择题（1）顺序表中第一个元素的存储地址是100，每个元素的长度为2，则第5个元素的地址是（）。
A．110 B．108 C．100 D．120答案：B解释：顺序表中的数据连续存储，所以第5个元素的地址为：100+2*4=108。
（3）向一个有127个元素的顺序表中插入一个新元素并保持原来顺序不变，平均要移动的元素个数为（）。
A．8 B．63.5 C．63 D．7答案：B解释：平均要移动的元素个数为：n/2。
（4）链接存储的存储结构所占存储空间（）。
A．分两部分，一部分存放结点值，另一部分存放表示结点间关系的指针B．只有一部分，存放结点值C．只有一部分，存储表示结点间关系的指针D．分两部分，一部分存放结点值，另一部分存放结点所占单元数答案：A（5）线性表若采用链式存储结构时，要求内存中可用存储单元的地址（）。
A．必须是连续的B．部分地址必须是连续的C．一定是不连续的D．连续或不连续都可以答案：D（6）线性表Ｌ在（）情况下适用于使用链式结构实现。
A．需经常修改Ｌ中的结点值Ｂ．需不断对Ｌ进行删除插入C．Ｌ中含有大量的结点Ｄ．Ｌ中结点结构复杂答案：B解释：链表最大的优点在于插入和删除时不需要移动数据，直接修改指针即可。
（7）单链表的存储密度（）。
A．大于1 B．等于1 C．小于1 D．不能确定答案：C解释：存储密度是指一个结点数据本身所占的存储空间和整个结点所占的存储空间之比，假设单链表一个结点本身所占的空间为D，指针域所占的空间为N，则存储密度为：D/(D+N)，一定小于1。
（8）将两个各有n个元素的有序表归并成一个有序表，其最少的比较次数是（）。
A．n B．2n-1 C．2n D．n-1答案：A解释：当第一个有序表中所有的元素都小于（或大于）第二个表中的元素，只需要用第二个表中的第一个元素依次与第一个表的元素比较，总计比较n次。
（9）在一个长度为n的顺序表中，在第i个元素（1≤i≤n+1）之前插入一个新元素时须向后移动（）个元素。
数据结构哈夫曼树PPT课件
例：
W（权）={2,4,2,3,3}，叶子结点个数,m=5 试设计Huffman树。
14
6
3
3
8
4
4
22
构造的 Huffman树
第12页/共21页
三、哈夫曼树的应用(哈夫曼编码)
在远程通讯中，要将待传字符转换成由二进制组成 的字符串：
设要传送的字符为： 若编码为：A—00 (等长) B—01
重码 000011010
关键：要设计长度不等的编码，则必须使任一字符的编码都不 是另一个字符的编码的前缀。这种编码称作最优前缀编码。
第14页/共21页
设要传送的字符为：
若编码为 ：A—0
B—110
C用二叉树设 计二进制前缀
编码
0
1
C0
1
BD
第15页/共21页
ABACCDA
C—10 D---11
ABACCDA
若将编码设计为长度不等的二进制编码，即让待传字符串中出 现次数较多的字符采用尽可能短的编码，则转换的二进制字符 串便可能减少。
第13页/共21页
设要传送的字符为：ABACCDA 若编码为： A—0
B—00 C—1 D---01
ABACCDA
但： 0000 AAAA ABA BB
二、构造哈夫曼树 1．哈夫曼树的定义
在一棵二叉树中，若带权路径长度达到最小，称这样的 二叉树为最优二叉树，也称为哈夫曼树(Huffman tree)。
第3页/共21页
例 有4个结点，权值分别为7，5，2，4，构造有4个叶子结点的二叉树
4d
a 7
n
c
2
WPL
WK LK
k 1
哈夫曼树
字符序列：DATA TRERTER ARE AREA ART 用0、1组合进行编码，希望01串长度最短。 字符集为{A，D，T，R，E}，各字母出现的次 数为{6，1，4，6，4} 高频字符，译码尽可能短
一个方案
– – – – – A:10 D:010 T:011 R:11 E:00
基本术语
结点的权
– 在许多实际应用中，常常将树中的某些结 点赋上一个具有一定意义的实数，这个实 数称为该结点的权
结点的带权路径
– 从根结点到结点的路径长度*结点的权
树的带权路径WPL
– 树中所有叶子结点的带权路径长度之和
基本术语
对所有叶子结点i计算 Wi Li
计算WPL
哈夫曼树
最优树/哈夫曼树
（1）与n个权对应的结点构成具有n棵二叉 树的森林F={T1,T2,…,Tn}，其中每棵二叉 树Ti都只有一个根结点，左右子树均空 （2）从F中选出根结点权值最小的两棵树 作为一棵树的左右子树，且置新树的根 结点权值为左右子树根结点权值之和 （3）从F中删除这两棵树，将新树加入F （4）重复(2)、(3)，直到F中只含一棵树
哈夫曼树
哈夫曼（haffman)树又称为最优二叉树， 它是n个带权叶子结点构成的二叉树中 WPL最小的二叉树。 ？？
ቤተ መጻሕፍቲ ባይዱ
– 所有叶子结点的权值均为1（或相等），构 成的二叉树形式？ – 在哈夫曼树中叶子结点的权与路径长度的关 系？ – 叶子数目已知，结点总数=？ – 唯一性？
哈夫曼树—构造（贪心）
ht[m].codify:=“”; for i:=m downto n+1 do begin p:=ht[i].lchild; if p<>0 then ht[p].codify:=ht[i].codify+”0” p:=ht[i].rchild; if p<>0 then ht[p].codify:=ht[i].codify+”1” end;
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
45
0
1
19
0
1
26
0
1
9
10
11 15
A0
1 B0
1
55
7
8
C 0
1D
E
2
3
F
G
谢谢学习
主讲教师：尹红丽
0
1
a
0
1
c
0
1
b
d
约定左分支表示字符‘0’
右分支表示字符‘1’
3
哈夫曼编码
例：一组字符{A, B, C, D, E, F, G}出现的频率分别是{9, 11, 5, 7, 8, 2, 3}，
设计最经济的编码方案。 编码：
A： 00 B ： 10 C ： 010 D： 110 E ： 111 F ： 0110 G ： 0111
ABCD 00 01 10 11
不等长编码： 为了缩短传送信息的总长度，让出现频率高的字符具有
较短的编码，出现频率低的字符具有较长的编码
ABCD
1 10 0 01 发送：A B A C C C C D A B
1 10 1 0 0 0 0 01 1 10—长度为13 1101可以译为AACA、ABA、AAD 为此引入前缀编码的概念
2 34 7
2
3 47
7
4 23
WPL=2×2+3×2+4×2+7×2 =32
WPL=2×1+3×2+4×3+7×3 =41
WPL=2×3+3×3+4×2+7×1 =30
特点：权值越大的叶子结点越靠近根结点，权值越小的叶子结点越远离根结点。
2 哈夫曼树的构造
给定4个叶子结点，其权值分别为{2，4，5 ，3} 构造一棵哈夫曼树
《数据结构》 课程 哈夫曼树及其应用
主讲教师：尹红丽
目录 CONTENTS
1 哈夫曼树的定义 2 哈夫曼树的构造 3 哈夫曼编码
1
哈夫曼树的定义
路径：从一个结点到另一个结点间的分支
路径长度：路径上的分支数目。 A→E的路径长度＝2
结点的权：结点被赋予的有着某种意义的实数
A
B
C
结点的带权路径长度：从根到该结点间的路径长度与该 D
第1步：初始化 第2步：选取与合并 第3步：删除与加入
24 5 3
5
23
45
5
23
2 哈夫曼树的构造
W＝{2，4，5 ，3} 哈夫曼树的构造过程 ⑷ 重复⑵、⑶两步，当 重复第2步：选取与合并 集合F中只剩下一棵二叉树 时，这棵二叉树便是哈夫 曼树。
重复第3步：删除与加入
45
5
23 9
45
9
5
4 52 3
3
哈夫曼编码
前缀编码：任一字符的编码都不能是其他字符编 码的前缀的不等长编码。
利用二叉树进行前缀编码
从根结点到叶子结点的路径上以分支字符组成的 字符串作为叶子节点的编码——前缀编码
哈夫曼编码：以字符出现的频率作权，构造一棵 哈夫曼树，由此得到的前缀编码称哈夫曼编码— —总长最短的二进制前缀编码
2 哈夫曼树的构造
W＝{2，4，5 ，3} 哈夫曼树的构造过程
⑷ 重复⑵、⑶两步，当 重复第2步：选取与合并 集合F中只剩下一棵二叉树 时，这棵二叉树便是哈夫 曼树。
9
5
4 52 3 14
9
5
4 52 3 14
重复第3步：删除与加入
9
5
4 52 3：A B A C C C C D A B 00 01 00 10 10 10 10 11 00 01—长度为20
3
结点的权的乘积。 D结点的带权路径长度=2×3=6
EF G
24 5
二叉树的带权路径长度：二叉树中所有叶子结点的带权
路径长度之和。
WPL=2×3+2×2+2×4+2×5 =28
1
哈夫曼树的定义
哈夫曼树：给定一组具有确定权值的叶子结点，带权路径长度最小的二叉树。
例：给定4个叶子结点，其权值分别为{2，3，4，7}，可以构造出形状不同的多 个二叉树。
⑴⑵⑶初选删始取除化与与：合由加并给入：定：在的在F中nF个选中 权构取两删两值造根棵除棵{nw结 二棵作二1，点叉只为叉w有的树左树2一，权分、，个…值别右并，根最作子将w结为小树新n点} 左的的建 的、立二右的叉子二树叉树，树构从加造而入一得到棵到F一中新；的 二叉树，这棵新二叉树 个的二根叉结树点集的合权F＝值{T为1，其T左2 ，、…右，子Tn树}；根 结 点 的 权 值 之和；