哈夫曼树讲解
哈夫曼树定义

哈夫曼树定义
哈夫曼树是一种二叉树,它用来表示一组符号权值的最优编码。
它应用于编码论,通常用来代表数据权值的树。
哈夫曼树是指一种最短带宽传输时能够有效工作的最优编码树。
哈夫曼树是每个节点都包含一个权值的二叉树。
它的定义如下:每一个权值所构成的数据集合,其最优树形式是每一个数据项的权值都比它的子节点的权值大,最终形成一个哈夫曼树。
哈夫曼树的构建一般是以权值的大小为基础进行的,权值越大,在哈夫曼树上就越靠近根节点,在结点之间的路径越短,这样便可以减少树的总长度,可以加快数据的传输速度。
此外,哈夫曼树还可以用于实现多种额外的功能。
哈夫曼树的构建有一种特别的方法,叫做“哈夫曼编码”,它采用“编码”和“解码”的方法来把一个数据集分成不同的组,这些组就是哈夫曼树的节点。
每组的数据都含有一个权值,当这些组被组合到一起时,它们就构成了一棵哈夫曼树。
哈夫曼树的建立是低耗时的,最优建立方式是将权值数组排序,然后依次添加,添加过程为:先将最小的两个数字添加到根节点,再将它们的和也添加到根节点,重复此过程,直到所有数字都被添加完为止。
哈夫曼树在编码的时候,如果一个字符出现的次数越多,它的权值就越大,它就越接近根节点。
哈夫曼树构造原理

哈夫曼树构造原理哈夫曼树,又称最优二叉树,是由美国数学家哈夫曼于1952年提出的一种树形编码方法。
它的构造原理简单而有效,被广泛应用于数据压缩、文件传输和网络传输等领域。
哈夫曼树的构造过程是基于一个重要的原则:频率越高的字符,其编码越短。
这个原则保证了编码后的数据具有最小的存储空间和传输带宽。
下面我们来详细介绍哈夫曼树的构造原理。
我们需要统计待编码的字符出现的频率。
在实际应用中,这通常是通过扫描文件或数据流来完成的。
统计结果存储在一个字符频率表中,包含了字符和对应的频率。
然后,我们将频率表中的每个字符作为一个叶子节点构造一棵二叉树,节点的权重即为字符的频率。
接下来,我们需要合并这些二叉树,生成一棵更大的二叉树。
合并过程中,我们选择权重最小的两棵二叉树进行合并,生成一棵新的二叉树。
合并后,新生成的二叉树的权重为两棵二叉树的权重之和,且左子树权重小于等于右子树权重。
这个过程一直持续,直到所有的二叉树都合并为一棵哈夫曼树。
在合并的过程中,我们需要使用一种数据结构来存储和管理这些二叉树。
通常情况下,我们使用优先队列或最小堆来实现。
这样可以保证每次选择权重最小的两棵二叉树进行合并,提高了合并的效率。
当所有的二叉树都合并为一棵哈夫曼树后,我们就可以为每个字符生成对应的哈夫曼编码了。
从根节点开始,向左走表示编码为0,向右走表示编码为1。
通过遍历哈夫曼树的路径,可以得到每个字符的编码。
哈夫曼编码具有前缀码的特点,也就是说任意一个字符的编码不是另一个字符编码的前缀。
这个特性保证了编码的唯一性,解码时可以根据编码逐位向下匹配,不会出现歧义。
通过哈夫曼树的构造,我们可以将原始数据压缩成最优的编码形式。
在数据传输和存储过程中,我们可以使用哈夫曼编码来减少存储空间和传输带宽,提高传输效率。
总结一下,哈夫曼树的构造原理是基于字符频率的统计和权重的合并。
通过合并权重最小的二叉树,构造出一棵最优二叉树,然后根据哈夫曼树的路径生成对应的编码。
6-10+哈夫曼树

哈夫曼--编码
按A B C D E F G H 这八个字母出现的频率构造哈夫曼树。
A:0110,B:10,C:1110,D:1111, E:110,F:00,G:0111,H:010
树的带权路径长度的含义是各个字符的编码长与 其出现次数的乘积之和,也就是电文的代码总长, 所以采用哈夫曼树构造的编码是一种能使电文代码 总长最短的不等长编码。
对于同一组给定叶结点所构造的哈夫曼树,树的形状可 能不同,但带权路径长度值是相同的,一定是最小的
哈夫曼树—示例 叶结点权值集合为W = W = {7,5,3,1}构造哈夫曼树三种形态:
给定n个权值,需经过n-1次合并最终能得到一棵哈夫曼树。 经过n-1次合并得到n-1个新结点,这n-1个新结点都是具有两个孩子结点的分支 结点。也就是说哈夫曼树中没有度为1的结点。 构造的哈夫曼树共有2n-1个结点。
这样的编码不能保证译码的唯一性,我们称之为具有二义性的译码。
哈夫曼--编码
哈夫曼树可用于构造使电文的编码总长最短的编码方案,且不会产生二义性。
设需要编码的字符集合为{d1,d2,…,dn}, 它们在电文中出现的次数或频率集合为{w1,w2,…,wn}, 以d1,d2,…,dn作为叶结点,w1,w2,…,wn作为它们的权值, 构造一棵哈夫曼树,然后,规定哈夫曼树中的左分支代表0,右分支代表1, 则从根结点到每个叶结点所经过的路径分支组成的0和1的序列便为该结点对应 字符的编码,我们称之为哈夫曼编码。
哈夫曼树--基本概念
给定一组权值,用以作为叶结点可以构造出不同形状的二叉树。 例如,设有4个权值分别为1,3,5,7,作为4个叶结点,构造二叉树。
(a)
(b)
(c)
(d)
(e)
【算法总结】哈夫曼树

【算法总结】哈夫曼树在⼀棵树中,从任意⼀个结点到达另⼀个结点的通路被称为路径,该路径上所需经过的边的个数被称为该路径的长度。
若树中结点带有表⽰某种意义的权值,那么从根结点到达该节点的路径长度再乘以该结点权值被称为该结点的带权路径长度。
树所有的叶⼦结点的带权路径长度和为该树的带权路径长度和。
给定 n 个结点和它们的权值,以它们为叶⼦结点构造⼀棵带权路径和最⼩的⼆叉树,该⼆叉树即为哈夫曼树,同时也被称为最优树。
给定结点的哈夫曼树可能不唯⼀,所以关于哈夫曼树的机试题往往需要求解的是其最⼩带权路径长度和。
回顾⼀下我们所熟知的哈夫曼树求法(原理很容易理解,就是把⼩的往下放)。
1.将所有结点放⼊集合 K。
2.若集合 K 中剩余结点⼤于 2 个,则取出其中权值最⼩的两个结点,构造他们同时为某个新节点的左右⼉⼦,该新节点是他们共同的双亲结点,设定它的权值为其两个⼉⼦结点的权值和。
并将该⽗亲结点放⼊集合 K。
重复步骤 2 或 3。
3.若集合 K 中仅剩余⼀个结点,该结点即为构造出的哈夫曼树数的根结点,所有构造得到的中间结点(即哈夫曼树上⾮叶⼦结点)的权值和即为该哈夫曼树的带权路径和。
为了⽅便快捷⾼效率的求得集合 K 中权值最⼩的两个元素,我们需要使⽤堆数据结构。
它可以以 O(logn)的复杂度取得 n 个元素中的最⼩元素。
为了绕过对堆的实现我们使⽤标准模板库中的相应的标准模板——优先队列。
:有4 个结点 a, b, c, d,权值分别为 7, 5, 2, 4,试构造以此 4 个结点为叶⼦结点的⼆叉树。
根据给定的n个权值{w1,w2,…,wn}构成⼆叉树集合F={T1,T2,…,Tn},其中每棵⼆叉树Ti中只有⼀个带权为wi的根结点,其左右⼦树为空.在F中选取两棵根结点权值最⼩的树作为左右⼦树构造⼀棵新的⼆叉树,且置新的⼆叉树的根结点的权值为左右⼦树根结点的权值之和.在F中删除这两棵树,同时将新的⼆叉树加⼊F中.重复,直到F只含有⼀棵树为⽌.(得到哈夫曼树)利⽤语句priority_queue<int> Q;建⽴⼀个保存元素为 int 的堆 Q,但是请特别注意这样建⽴的堆其默认为⼤顶堆,即我们从堆顶取得的元素为整个堆中最⼤的元素。
数据结构第六章 哈夫曼树
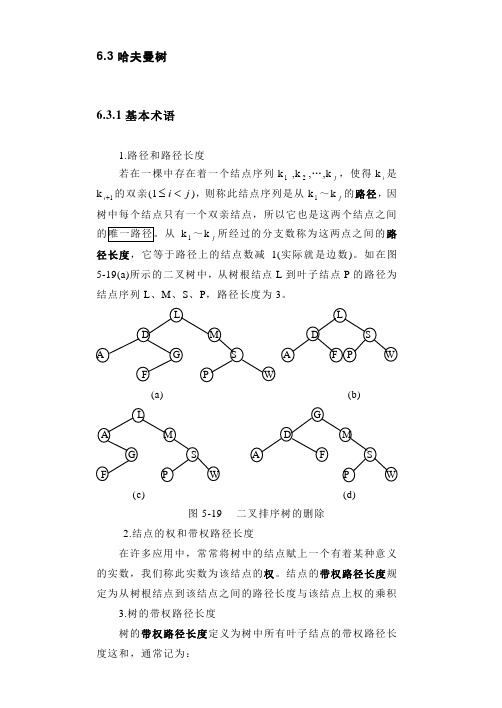
6.3哈夫曼树6.3.1基本术语1.路径和路径长度若在一棵中存在着一个结点序列k1 ,k2,…,kj,使得ki是k1+i 的双亲(1ji<≤),则称此结点序列是从k1~kj的路径,因树中每个结点只有一个双亲结点,所以它也是这两个结点之间k 1~kj所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1(实际就是边数)。
如在图5-19(a)所示的二叉树中,从树根结点L到叶子结点P的路径为结点序列L、M、S、P,路径长度为3。
(a) (b)(c) (d)图5-19 二叉排序树的删除2.结点的权和带权路径长度在许多应用中,常常将树中的结点赋上一个有着某种意义的实数,我们称此实数为该结点的权。
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积3.树的带权路径长度树的带权路径长度定义为树中所有叶子结点的带权路径长度这和,通常记为:2 WPL = ∑=n i i i lw 1其中n 表示叶子结点的数目,i w 和i l 分别表示叶子结点i k 的权值和根到i k 之间的路径长度 。
4.哈夫曼树哈夫曼(Huffman)树又称最优二叉树。
它是n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
因为构造这种树的算法是最早由哈夫曼于1952年提出的,所以被称之为哈夫曼树。
例如,有四个叶子结点a 、b 、c 、d ,分别带权为9、4、5、2,由它们构成的三棵不同的二叉树(当然还有其它许多种)分别如图5-20(a)到图5-20(c)所示。
b ac a b cd d c a b d(a) (b) (c)图5-20 由四个叶子结点构成的三棵不同的带权二叉树 每一棵二叉树的带权路径长度WPL 分别为:(a) WPL = 9×2 + 4×2 + 5×2 + 2×2 = 40(b) WPL = 4×1 + 2×2 + 5×3 + 9×3 = 50(c) WPL = 9×1 + 5×2 + 4×3 + 2×3 = 37其中图5-20(c)树的WPL 最小,稍后便知,此树就是哈夫曼树。
c语言哈夫曼树的构造及编码

c语言哈夫曼树的构造及编码一、哈夫曼树概述哈夫曼树是一种特殊的二叉树,它的构建基于贪心算法。
它的主要应用是在数据压缩和编码中,可以将频率高的字符用较短的编码表示,从而减小数据存储和传输时所需的空间和时间。
二、哈夫曼树的构造1. 哈夫曼树的定义哈夫曼树是一棵带权路径长度最短的二叉树。
带权路径长度是指所有叶子节点到根节点之间路径长度与其权值乘积之和。
2. 构造步骤(1) 将待编码字符按照出现频率从小到大排序。
(2) 取出两个权值最小的节点作为左右子节点,构建一棵新的二叉树。
(3) 将新构建的二叉树加入到原来排序后队列中。
(4) 重复上述步骤,直到队列只剩下一个节点,该节点即为哈夫曼树的根节点。
3. C语言代码实现以下代码实现了一个简单版哈夫曼树构造函数:```ctypedef struct TreeNode {int weight; // 权重值struct TreeNode *leftChild; // 左子节点指针struct TreeNode *rightChild; // 右子节点指针} TreeNode;// 构造哈夫曼树函数TreeNode* createHuffmanTree(int* weights, int n) {// 根据权值数组构建节点队列,每个节点都是一棵单独的二叉树TreeNode** nodes = (TreeNode**)malloc(sizeof(TreeNode*) * n);for (int i = 0; i < n; i++) {nodes[i] = (TreeNode*)malloc(sizeof(TreeNode));nodes[i]->weight = weights[i];nodes[i]->leftChild = NULL;nodes[i]->rightChild = NULL;}// 构建哈夫曼树while (n > 1) {int minIndex1 = -1, minIndex2 = -1;for (int i = 0; i < n; i++) {if (nodes[i] != NULL) {if (minIndex1 == -1 || nodes[i]->weight < nodes[minIndex1]->weight) {minIndex2 = minIndex1;minIndex1 = i;} else if (minIndex2 == -1 || nodes[i]->weight < nodes[minIndex2]->weight) {minIndex2 = i;}}}TreeNode* newNode =(TreeNode*)malloc(sizeof(TreeNode));newNode->weight = nodes[minIndex1]->weight + nodes[minIndex2]->weight;newNode->leftChild = nodes[minIndex1];newNode->rightChild = nodes[minIndex2];// 将新构建的二叉树加入到原来排序后队列中nodes[minIndex1] = newNode;nodes[minIndex2] = NULL;n--;}return nodes[minIndex1];}```三、哈夫曼编码1. 哈夫曼编码的定义哈夫曼编码是一种前缀编码方式,它将每个字符的编码表示为二进制串。
数据结构哈夫曼树PPT课件
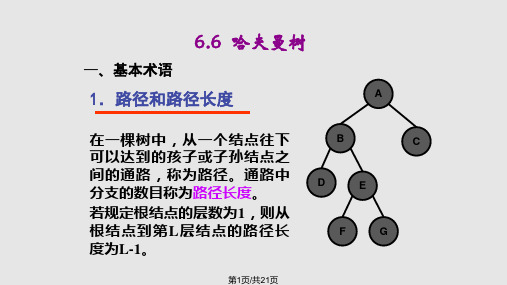
例:
W(权)={2,4,2,3,3},叶子结点个数,m=5 试设计Huffman树。
14
6
3
3
8
4
4
22
构造的 Huffman树
第12页/共21页
三、哈夫曼树的应用(哈夫曼编码)
在远程通讯中,要将待传字符转换成由二进制组成 的字符串:
设要传送的字符为: 若编码为:A—00 (等长) B—01
重码 000011010
关键:要设计长度不等的编码,则必须使任一字符的编码都不 是另一个字符的编码的前缀。这种编码称作最优前缀编码。
第14页/共21页
设要传送的字符为:
若编码为 :A—0
B—110
C用二叉树设 计二进制前缀
编码
0
1
C0
1
BD
第15页/共21页
ABACCDA
C—10 D---11
ABACCDA
若将编码设计为长度不等的二进制编码,即让待传字符串中出 现次数较多的字符采用尽可能短的编码,则转换的二进制字符 串便可能减少。
第13页/共21页
设要传送的字符为:ABACCDA 若编码为: A—0
B—00 C—1 D---01
ABACCDA
但: 0000 AAAA ABA BB
二、构造哈夫曼树 1.哈夫曼树的定义
在一棵二叉树中,若带权路径长度达到最小,称这样的 二叉树为最优二叉树,也称为哈夫曼树(Huffman tree)。
第3页/共21页
例 有4个结点,权值分别为7,5,2,4,构造有4个叶子结点的二叉树
4d
a 7
n
c
2
WPL
WK LK
k 1
计算机数据结构知识点梳理 哈夫曼(Huffman)树和哈夫曼编码

(3)在集合F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入 到集合F中;
(4)重复(2)(3)两步,当F中只剩下一棵二叉树时,这棵二叉树便是所要 建立的哈夫曼树。
(3)深度为h的哈夫曼树,其叶子结点的最大编码长度为h-1。
[题1]若度为m的哈夫曼树,其叶子结点个数为n,则非叶子结点 的个数为( )。
A.n-1 B.[n/m]-1 C.[(n-1)/(m-1)] D.[n/(m-1)]-1
分析:在构造度为m的哈夫曼树过程中,每次把m个子结点合并 为一个父结点(第一次合并可能少于m个子结点),每次合并 减少m-1个结点,从n个叶子结点减少到最后只剩一个父结点共 需[(n-1)/(m-1)]次合并,每次合并增加一个非叶子结点。
5、对哈夫曼树编码的总结
(1)哈夫曼编码是能使电文代码总长最短的编码方式。此结论由哈夫曼树是带 权路径长度最小的树的特征可得。
(2)哈夫曼编码是一种前缀编码,保证其在译码时不会产生歧义。因为,在哈 夫曼编码中,每个字符都是叶子结点,而叶子结点不可能从根结点到其他叶 子结点的路径上,所以一个字符的哈夫曼编码不可能是另一个字符的哈夫曼 编码的前缀。
知识点10:哈夫曼(HUFFMAN)树和哈夫曼编码
1、哈夫曼树(又称最优二叉树),是指对于一 组带有确定权值的叶结点,构造的具有最小带
权路径长度的二叉树。
2、哈夫曼树的构造方法的基本思想
(1)由给定的n个权值{W1,W2,…,Wn}构造n棵只有一个叶结点的二叉树, 从而得到一个二叉树的集合F={T1,T2,…,Tn};
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Hu Junfeng
/*哈夫曼树结点的结构*/
18
哈夫曼树的表示3 哈夫曼树的表示
• struct HtTree /*哈夫曼树类型*/ { int m; /*外部结点的个数*/ int root; /* 哈夫曼树根在数组中的位置 */ struct HtNode *ht; /*存放2m-1个结点的数组*/ }; typedef struct HtTree *PHtTree; /* 哈夫曼树类型的指针类型 */
Hu Junfeng
15
哈夫曼树的构造过程
23
2
3
12
6
5
12
6
11 5
6
12
11 5
2 3 6
12
2
3 2 3
4棵只有根的二叉树
2、3合并得到3棵二叉树 合并得到3
5、6合并得到2棵二叉树 合并得到2
11、12合并得到1 11、12合并得到1棵二叉树 合并得到
左右选择不同,得到的 树形态不同, 相同。 左右选择不同,得到的HuffMan树形态不同,但WPL相同。 树形态不同 相同
Y Y
100 内部节点
智
N
体
Y
N
70 18
德
N
5
Hu Junfeng
9
哈夫曼树(构建算法) 哈夫曼树(构建算法)
给定m个权值{ w1 , w2 ,…, wm }
① 构造由m棵二叉树组成的树林F = {T1,T2,…,Tm},其中每棵树Ti
只有一个根结点,且根结点的权值为wi;
② 在树林中选取两棵根结点权值最小的和次小的二叉树作为左右子
WPL
=
∑
i =1
w ili
• 其中,wi是第i个外部结点的权值,li为从根到第i个外部结点的 路径长度,m为外部结点的个数。
Hu Junfeng
8
哈夫曼树: 哈夫曼树:
• 对于一组非负实数{w1 , w2 , w3 ,…, wm}, 存在一棵以wi(i = 1,2,…,m)为权的m个 外部结点的扩充的二叉树,使得带权的外部 路径长度WPL最小。这棵二叉树就称为哈夫 哈夫 曼树或最优二叉树 曼树 最优二叉树。 最优二叉树 • WPL = 1 x 70 + 2 x 18 + 3 x 5 + 3 x 7 = 70 + 36 + 15 +21 = 142 7
Hu Junfeng
16
哈夫曼树的存储实现
• 存储结构可以有多种,如二叉链表、三叉链表等。下面给出 一种顺序结构(一维数组),结点结构:
ww parent llink rlink
– ww: 以该结点为根的子树中所有外部结点的加权和。 – parent: 父结点在数组中的存储位置(下标),根无父,设为-1。 – llink: 左孩子存储位置,对于外部结点,无孩子,设为-1。 – rlink: 右孩子存储位置,对于外部结点,无孩子,设为-1。
Hu Junfeng
4
哈夫曼树及其应用
• 哈夫曼树 • 哈夫曼算法 • 哈夫曼编码
Hu Junfeng
5
扩充二叉树的概念
•
– – –
把原二叉树的结点都变为 度数为2的分支结点
如果原结点的度数为2,则不 变 度数为1,则增加一个分支, 度数为0(树叶),则增加两 个分支。 内部节点
100
Y Y
德
N
Hu Junfeng
17
哈夫曼树的表示2 哈夫曼树的表示
• 假定外部结点个数为m,则内部结点个数必为m-1,因此 最后得到的HuffMan树必定有2m-1个结点。因此,用2m-1 个元素的一维数组就可以存储该HuffMan树。每个元素表 示一个结点,前m个存储外部结点,后m-1个用于内部结 点。 • struct HtNode
Hu Junfeng
22
信息编码1 信息编码
• 定长编码 – 所有的字符都具有相同的编码长度 • 如26个字符:A, B, C, D, …, Z A: B: C: D: 00000 00001 00010 00011 …… Z: 11001
线路传输 信息发送
ABB…
Hu Junfeng
信息接收
编码: 编码:00000 00001 00001 译码: 译码:00000 00001 00001 A B B
Y Y
德
N
智
N
N
5 70
体
Y
7
18
外部路径
Hu Junfeng
7
两个概念
• “外部路径长度” E:在扩充的二叉树里从根到每个外部结点的 m 路径长度之和。 E = ∑ li
i=1
• 其中,li为从根到第i个外部结点的路径长度,m为外部结点的 个数。 • 设扩充二叉树具有m个带权值的外部结点,那么从根结点到各 个外部结点的路径长度与相应结点权值的乘积的和,叫做扩充 二叉树的带权的外部路径长度。 m
树构造一棵新的二叉树,其根结点的权值为左右子树根结点权值 之和。
③ 将新的二叉树加入到树林F中,去除原两棵权值最小的树; ④ 重复2、3步骤,直至F中只剩一棵树为止。
Hu Junfeng
10
给定权值 {7,5,2,4},构造哈夫曼树 , , , ,
7 5 2 4 6
a
b (a)
c
d
7
5 c
18
d (b)
哈夫曼树 与 树的应用
2008/04/08
Hu Junfeng
非第归 后根遍历二叉树
• 先左子树 • 后右子树 • 然后根
B
A
C
D
E
F
G
H
I
Hu Junfeng
2
非第归 后根遍历二叉树
H D
3
Hu Junfeng
B
I E A F C G G
Heap中删除最小元素 中删除最小元素
2 3 9 14 12 11 10 16 7 5 4 8
struct HtTree /*哈夫曼树类型 哈夫曼树类型*/ 哈夫曼树类型 { struct HtNode ht[MAXNODE]; /* 哈夫曼树根在数组中的位置 */ int root; }; typedef struct HtTree *PHtTree; /* 哈夫曼树类型的指针类型 */
Hu Junfeng
h i
Hu Junfeng
4
4 4 28 28
j
改进的办法
•按一种周游次序在数组中存放结点,依次存放树的先根序列 按一种周游次序在数组中存放结点, 按一种周游次序在数组中存放结点
Hu Junfeng
29
29
Hu Junfeng
12
哈夫曼算法(初始化) 哈夫曼算法(初始化)
Hu Junfeng
13
哈夫曼算法(构造树) 哈夫曼算法(构造树)
思考:如何用堆结构实现huffman算法
Hu Junfeng
14
哈夫曼算法 —— 构造一棵பைடு நூலகம்夫曼树
① 根 据 给 定 的 n 个 权 值 {w1,w2,…,wn} , 构 成 n 棵 二 叉 树 的 集 合 F={T1,T2,…,Tn},其中每一棵二叉树Ti中只有一个带权为wi的 根结点,其左右子树为空。 ② 在F中选取两棵权值最小的树作为左右子树以构造一棵新的二叉 树,且新二叉树的根结点的权值为其左右子树根结点权值之和。 ③ 在F中删除这两棵树,同时将新得到的二叉树加入F中。 ④ 重复(2)和(3),直到F中只含一棵树为止。
0 1
0
145
0
120 50
65
80
50
• 互不为子串?
Hu Junfeng
24
树和树林的存储表示
• 选择存储表示方法原则:结点本身+结点之间的 关系 树的存储表示(三种链表结构)
– – – 父指针表示法 [双亲表示法] 子表表示法 [孩子表示法] 长子-兄弟表示法 [孩子兄弟表示法]
•
•
树林的存储表示
智
N
•
空二叉树的扩充二叉树规 定为只有一个外部结点组 成的二叉树。
7
N
5 70
体
Y
18
Hu Junfeng
6
加权路径: 加权路径:
WPL = ∑ wi li
i =1 m
100 内部节点
– wi是第i个外部结点的权值 – li为从根到第i个外部结点的路径长度 – m为外部结点的个数。 – WPL = 1 x 5 + 2 x 70 + 3 x 18 + 3 x 7 = 5 + 140 + 54 + 21 = 220
23
哈夫编码:在概率意义上平均码长最短 哈夫编码:
{ (hot,50), (warm,65),(mild,120), (cold,80), (very cold,50)} 365 hot warm mild cold very cold 111 01 10 00 110 100
1 0 1
1 220
Hu Junfeng
26
26
树的类型定义为:
struct ParTree { int MAXNUM; int n; /* 树中结点的个数 */ struct ParTreeNode *nodelist; /* 存放树中的结点 */ }; typedef struct ParTree *PParTree; /* 树类型的指针类型 */ struct ParTree { struct ParTreeNode nodelist[MAXNUM]; /* 存放树中的结点 */ int n; /* 树中结点的个数 */ }; typedef struct ParTree *PParTree; /* 树类型的指针类型 */ 2727
