哈夫曼树
哈夫曼树定义

哈夫曼树定义
哈夫曼树是一种二叉树,它用来表示一组符号权值的最优编码。
它应用于编码论,通常用来代表数据权值的树。
哈夫曼树是指一种最短带宽传输时能够有效工作的最优编码树。
哈夫曼树是每个节点都包含一个权值的二叉树。
它的定义如下:每一个权值所构成的数据集合,其最优树形式是每一个数据项的权值都比它的子节点的权值大,最终形成一个哈夫曼树。
哈夫曼树的构建一般是以权值的大小为基础进行的,权值越大,在哈夫曼树上就越靠近根节点,在结点之间的路径越短,这样便可以减少树的总长度,可以加快数据的传输速度。
此外,哈夫曼树还可以用于实现多种额外的功能。
哈夫曼树的构建有一种特别的方法,叫做“哈夫曼编码”,它采用“编码”和“解码”的方法来把一个数据集分成不同的组,这些组就是哈夫曼树的节点。
每组的数据都含有一个权值,当这些组被组合到一起时,它们就构成了一棵哈夫曼树。
哈夫曼树的建立是低耗时的,最优建立方式是将权值数组排序,然后依次添加,添加过程为:先将最小的两个数字添加到根节点,再将它们的和也添加到根节点,重复此过程,直到所有数字都被添加完为止。
哈夫曼树在编码的时候,如果一个字符出现的次数越多,它的权值就越大,它就越接近根节点。
数据结构哈夫曼树和哈夫曼编码权值

数据结构哈夫曼树和哈夫曼编码权值一、引言在计算机领域,数据结构是非常重要的一部分,而哈夫曼树和哈夫曼编码是数据结构中非常经典的部分之一。
本文将对哈夫曼树和哈夫曼编码的权值进行全面评估,并探讨其深度和广度。
通过逐步分析和讨论,以期让读者更深入地理解哈夫曼树和哈夫曼编码的权值。
二、哈夫曼树和哈夫曼编码的基本概念1. 哈夫曼树哈夫曼树,又称最优二叉树,是一种带权路径长度最短的二叉树。
它的概念来源于一种数据压缩算法,可以有效地减少数据的存储空间和传输时间。
哈夫曼树的构建过程是基于给定的权值序列,通过反复选择两个最小权值的节点构建出来。
在构建过程中,需要不断地重排权值序列,直到构建出一个满足条件的哈夫曼树。
2. 哈夫曼编码哈夫曼编码是一种变长编码方式,它利用了哈夫曼树的特点,对不同的字符赋予不同长度的编码。
通过构建哈夫曼树,可以得到一套满足最优存储空间的编码规则。
在实际应用中,哈夫曼编码经常用于数据压缩和加密传输,能够有效地提高数据的传输效率和安全性。
三、哈夫曼树和哈夫曼编码的权值评估1. 深度评估哈夫曼树和哈夫曼编码的权值深度值得我们深入探究。
从构建哈夫曼树的角度来看,权值决定了节点在树中的位置和层次。
权值越大的节点往往位于树的底层,而权值较小的节点则位于树的高层。
这种特性使得哈夫曼树在数据搜索和遍历过程中能够更快地找到目标节点,提高了数据的处理效率。
而从哈夫曼编码的角度来看,权值的大小直接决定了编码的长度。
权值越大的字符被赋予的编码越短,可以有效地减少数据传输的长度,提高了数据的压缩率。
2. 广度评估另哈夫曼树和哈夫曼编码的权值也需要进行广度评估。
在构建哈夫曼树的过程中,权值的大小直接影响了树的结构和形状。
当权值序列较为分散时,哈夫曼树的结构会更加平衡,节点的深度差异较小。
然而,当权值序列的差异较大时,哈夫曼树的结构也会更不平衡,而且可能出现退化现象。
这会导致数据的处理效率降低,需要进行额外的平衡调整。
6-10+哈夫曼树

哈夫曼--编码
按A B C D E F G H 这八个字母出现的频率构造哈夫曼树。
A:0110,B:10,C:1110,D:1111, E:110,F:00,G:0111,H:010
树的带权路径长度的含义是各个字符的编码长与 其出现次数的乘积之和,也就是电文的代码总长, 所以采用哈夫曼树构造的编码是一种能使电文代码 总长最短的不等长编码。
对于同一组给定叶结点所构造的哈夫曼树,树的形状可 能不同,但带权路径长度值是相同的,一定是最小的
哈夫曼树—示例 叶结点权值集合为W = W = {7,5,3,1}构造哈夫曼树三种形态:
给定n个权值,需经过n-1次合并最终能得到一棵哈夫曼树。 经过n-1次合并得到n-1个新结点,这n-1个新结点都是具有两个孩子结点的分支 结点。也就是说哈夫曼树中没有度为1的结点。 构造的哈夫曼树共有2n-1个结点。
这样的编码不能保证译码的唯一性,我们称之为具有二义性的译码。
哈夫曼--编码
哈夫曼树可用于构造使电文的编码总长最短的编码方案,且不会产生二义性。
设需要编码的字符集合为{d1,d2,…,dn}, 它们在电文中出现的次数或频率集合为{w1,w2,…,wn}, 以d1,d2,…,dn作为叶结点,w1,w2,…,wn作为它们的权值, 构造一棵哈夫曼树,然后,规定哈夫曼树中的左分支代表0,右分支代表1, 则从根结点到每个叶结点所经过的路径分支组成的0和1的序列便为该结点对应 字符的编码,我们称之为哈夫曼编码。
哈夫曼树--基本概念
给定一组权值,用以作为叶结点可以构造出不同形状的二叉树。 例如,设有4个权值分别为1,3,5,7,作为4个叶结点,构造二叉树。
(a)
(b)
(c)
(d)
(e)
8哈夫曼树

b d e c
2 3 4 5 6 7 b c d e
d
e f g f g h
f
g
h
8
h
25
3、用孩子兄弟表示法来存储
思路:用二叉链表来表示树,但链表中的两个 指针域含义不同。 左指针指向该结点的第一个孩子; 右指针指向该结点的下一个兄弟结点。
firstchild data nextsibling
100
40
21 32 g e 17 7 a
60
28 11 10 h 6 d 2 c 5 3 f
10
对应的哈夫曼编码(左0右1):
符 编码 频率 符 编码 频率
100
a
b
1100
00
0.07
0.19
a
b
000
001
0.07
0.19 0.06
0 b
0 40
1
1
0 60 1 28 1 0 6 d 0 2 c 11 1d Path Length
树的带权路径长度如何计算? WPL = 哈夫曼树则是:WPL 最小的树。
w kl k
k=1
n
经典之例:
4 d
2 c 7 a (b) 5 b
Huffman树
7 a
7 a
5
2 b c
4 d
5 b
2 c (c)
4 d
(a)
WPL=36
WPL=46
WPL= 35
3
构造霍夫曼树的基本思想: 权值大的结点用短路径,权值小的结点用长路径。 构造Huffman树的步骤(即Huffman算法):
(1) 由给定的 n 个权值{w0, w1, w2, …, wn-1},构造具有 n 棵扩充 二叉树的森林F = { T0, T1, T2, …, Tn-1 },其中每一棵扩充二叉树 Ti 只有一个带有权值 wi 的根结点,其左、右子树均为空。 (2) 重复以下步骤, 直到 F 中仅剩下一棵树为止: ① 在 F 中选取两棵根结点的权值最小的扩充二叉树, 做为左、 右子树构造一棵新的二叉树。置新的二叉树的根结点的权值为 其左、右子树上根结点的权值之和。 ② 在 F 中删去这两棵二叉树。 ③ 把新的二叉树加入 F。
哈夫曼树

哈夫曼树及其应用一、基本术语1.路径和路径长度在一棵树中,从一个结点往下可以达到的孩子或子孙结点之间的通路,称为路径。
通路中分支的数目称为路径长度。
若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2.结点的权及带权路径长度若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3.树的带权路径长度树的带权路径长度(Weighted Path Length of Tree):也称为树的代价,定义为树中所有叶结点的带权路径长度之和,通常记为:其中:n表示叶子结点的数目wi和li分别表示叶结点ki的权值和根到结点ki之间的路径长度。
二、哈夫曼树构造1.哈夫曼树的定义在权为w l,w2,…,w n的n个叶子所构成的所有二叉树中,带权路径长度最小(即代价最小)的二叉树称为最优二叉树或哈夫曼树。
【例】给定4个叶子结点a,b,c和d,分别带权7,5,2和4。
构造如下图所示的三棵二叉树(还有许多棵),它们的带权路径长度分别为:(a)WPL=7*2+5*2+2*2+4*2=36(b)WPL=7*3+5*3+2*1+4*2=46(c)WPL=7*1+5*2+2*3+4*3=35其中(c)树的WPL最小,可以验证,它就是哈夫曼树。
2.哈夫曼树的构造假设有n个权值,则构造出的哈夫曼树有n个叶子结点。
n 个权值分别设为w1,w2,…,wn,则哈夫曼树的构造规则为:(1) 将w1,w2,…,wn看成是有n 棵树的森林(每棵树仅有一个结点);(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;(3)从森林中删除选取的两棵树,并将新树加入森林;(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为我们所求得的哈夫曼树。
下面给出哈夫曼树的构造过程,假设给定的叶子结点的权分别为1,5,7,3,则构造哈夫曼树过程如下图所示。
数据结构第六章 哈夫曼树
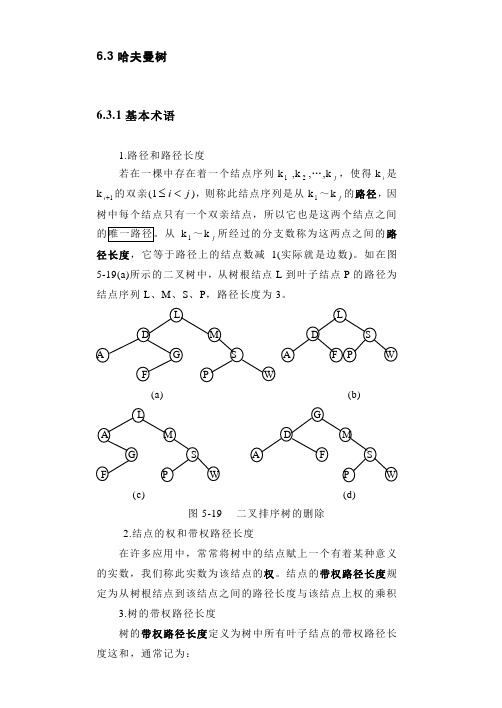
6.3哈夫曼树6.3.1基本术语1.路径和路径长度若在一棵中存在着一个结点序列k1 ,k2,…,kj,使得ki是k1+i 的双亲(1ji<≤),则称此结点序列是从k1~kj的路径,因树中每个结点只有一个双亲结点,所以它也是这两个结点之间k 1~kj所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1(实际就是边数)。
如在图5-19(a)所示的二叉树中,从树根结点L到叶子结点P的路径为结点序列L、M、S、P,路径长度为3。
(a) (b)(c) (d)图5-19 二叉排序树的删除2.结点的权和带权路径长度在许多应用中,常常将树中的结点赋上一个有着某种意义的实数,我们称此实数为该结点的权。
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积3.树的带权路径长度树的带权路径长度定义为树中所有叶子结点的带权路径长度这和,通常记为:2 WPL = ∑=n i i i lw 1其中n 表示叶子结点的数目,i w 和i l 分别表示叶子结点i k 的权值和根到i k 之间的路径长度 。
4.哈夫曼树哈夫曼(Huffman)树又称最优二叉树。
它是n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
因为构造这种树的算法是最早由哈夫曼于1952年提出的,所以被称之为哈夫曼树。
例如,有四个叶子结点a 、b 、c 、d ,分别带权为9、4、5、2,由它们构成的三棵不同的二叉树(当然还有其它许多种)分别如图5-20(a)到图5-20(c)所示。
b ac a b cd d c a b d(a) (b) (c)图5-20 由四个叶子结点构成的三棵不同的带权二叉树 每一棵二叉树的带权路径长度WPL 分别为:(a) WPL = 9×2 + 4×2 + 5×2 + 2×2 = 40(b) WPL = 4×1 + 2×2 + 5×3 + 9×3 = 50(c) WPL = 9×1 + 5×2 + 4×3 + 2×3 = 37其中图5-20(c)树的WPL 最小,稍后便知,此树就是哈夫曼树。
哈夫曼树.ppt
n
w i pi
最小,其中
i 1
Wi是第i个字符的使用频度,而Pi是第i个字符的编码长度, 这正是度量报文的平均长度的式子。
2020/3/5
21
例2:要传输的电文是{CAS;CAT;SAT;AT}
要传输的字符集是 D={C,A,S,T, ;}
每个字符出现的频率是W={ 2,4, 2,3, 3 }
PL=0+1+1+2+2=6
2020/3/5
9
问题2:什么样的带权树路径长度最小?
例如:给定一个权值序列{2,3,4,7},可构造的多种 二叉树的形态。
2
3
4
7
2 34 7
(a) WPL=2×2+2×3+2×4+2×7=32 (b) WPL=1×2+2×3+3×4+3×7=41
2020/3/5
7
4
3
2
(c) WPL=1×7+2×4+3×3+3×2=30
10
哈夫曼树的构造
例:给定权值{7,5,2,4},构造哈夫曼树。
6
方法: 75 2 4
75
(1)a 初始b化:由c 原始d数据生成森林a ; b c
d
(次2小)的找二最叉小(树a树) 作:为在左森右林子中树选构取造两一棵棵根新结的点二权叉值树最(,小b)其的根和
A)先序遍历
B)中序遍历
C)后序遍历
D)从根开始进行层次遍历
2、某二叉树的先序序列和后序序列正好相反,则该二叉
树一定是( B )的二叉树。
A)空或只有一个结点
B)高度等于其结点数
C)任一结点无左孩子
D)任一结点无右孩子
名词解释哈夫曼树
名词解释哈夫曼树哈夫曼树是最早的陆地植物之一,它能很快适应各种不同的生活环境,还能改变自己。
由于陆地变化快,各种动物如食草类、肉食类等,都被迫来到了陆地上,为了适应这些环境,有一些动物就发生了很大的变化,如熊从熊变成了能走路的猿,就是因为长期没在水中生活,他的后腿已经完全退化了;长臂猿的前肢已经退化了;海龟和海豹能爬到陆地上,就是因为生活环境发生了改变。
人们可以用种子繁殖也可以进行无性繁殖。
种子有翅膀的属于子叶植物,像杨、柳、榆树,它们的种子都是靠风力来传播的,因此它们是不需要嫁接的。
种子外面都包着果皮,而且种子外面还有一层厚厚的果肉。
吃过苹果的人都知道,苹果的表皮就像小刀一样会刮得手很疼。
这就是种子的作用。
种子的里面还有胚芽,胚芽才是种子的主体,它决定了种子以后是长出幼苗还是发育成一棵树。
有些植物的种子没有胚芽,有些植物的种子有胚芽。
像竹子的种子就没有胚芽。
而松树的种子有胚芽。
在野外的时候,可以见到许多树木的种子,如松树、红豆杉等。
它们看起来好像没有什么区别,其实它们是有区别的,你仔细观察一下就会发现,松树种子外面有一层薄薄的膜,把种子紧紧的裹住,红豆杉的种子也是用一层薄薄的膜包着的,而竹子的种子没有这层膜。
竹子的种子是要在水中才能发芽的,所以在竹林里你几乎看不到竹笋,但有一些植物的种子可以在干燥的土壤里也可以发芽,例如玉米的种子。
玉米的种子虽然在干燥的土壤里也能发芽,但它要经过一个漫长的过程。
这个过程叫做“吐丝”,种子在慢慢长大的过程中,要不断的吸收营养物质来壮大自己。
哈夫曼树不仅仅分布在北美洲,在世界各地都有。
其中松柏类的常青树比较多,如松树、柏树等,它们的树冠特别庞大,覆盖面积也很广。
其次是阔叶林,有很多乔木树种,如桉树、樟树等,它们的叶子非常茂盛。
再次是针叶林,有很多常绿的针叶树,如山茶、油茶、梧桐等。
灌木、藤本和草本植物更是数不胜数。
还有些落叶林,常绿树种比较少,以竹类居多。
但每种树都有自己的特点,就像人的特点各有不同一样,这样才能构成了这美丽的大千世界!其中松、柏、杉都是我国比较常见的乔木树种。
哈夫曼树及其应用
A
B
C
DE
FG
40% 30% 10%
HI
5% 15%
n
WPL= wi*li i=1
n为叶子结 点的数目
wi和li分别表示叶结点ki的权 值和根到ki的路径长6度
哈夫曼树概念
哈夫曼树(最优二叉树) 在权为w1,w2,……,wn的n个叶结点的所有二叉
树中,WPL最小的二叉树称为最优二叉树或哈夫曼树。 例:给定4个叶结点a,b,c,d,分别带权7,5,2,4,我们来构造3棵二叉树:
17
哈夫曼树构造
哈夫曼树的构造算法实现
Void CreateHT (hufmtree Tree)
{
int i,p1,p2;
InitHT(Tree);
// 初始化
InputW(Tree);
// 输入权值
for (i = n;i<2n-1;i++){ // n-1次合并 SelectMin(Tree,i-1,&p1,&p2);
Tree[p1].parent=Tree[p2].parent=i; Tree[i].lchild = p1; Tree[i].rchild = p2; Tree[i].weight = Tree[p1].weight +Tree[p2].weight; } }
18
哈夫曼编码
哈夫曼树的应用—哈夫曼编码
N
中等
A<90
Y
N
良好
优秀
70-79 中等 40%
80-89 良好 30%
90-100 优秀 10%
A<80
Y
N
A<70
Y A<60
哈夫曼树
字符序列:DATA TRERTER ARE AREA ART 用0、1组合进行编码,希望01串长度最短。 字符集为{A,D,T,R,E},各字母出现的次 数为{6,1,4,6,4} 高频字符,译码尽可能短
一个方案
– – – – – A:10 D:010 T:011 R:11 E:00
基本术语
结点的权
– 在许多实际应用中,常常将树中的某些结 点赋上一个具有一定意义的实数,这个实 数称为该结点的权
结点的带权路径
– 从根结点到结点的路径长度*结点的权
树的带权路径WPL
– 树中所有叶子结点的带权路径长度之和
基本术语
对所有叶子结点i计算 Wi Li
计算WPL
哈夫曼树
最优树/哈夫曼树
(1)与n个权对应的结点构成具有n棵二叉 树的森林F={T1,T2,…,Tn},其中每棵二叉 树Ti都只有一个根结点,左右子树均空 (2)从F中选出根结点权值最小的两棵树 作为一棵树的左右子树,且置新树的根 结点权值为左右子树根结点权值之和 (3)从F中删除这两棵树,将新树加入F (4)重复(2)、(3),直到F中只含一棵树
哈夫曼树
哈夫曼(haffman)树又称为最优二叉树, 它是n个带权叶子结点构成的二叉树中 WPL最小的二叉树。 ??
ቤተ መጻሕፍቲ ባይዱ
– 所有叶子结点的权值均为1(或相等),构 成的二叉树形式? – 在哈夫曼树中叶子结点的权与路径长度的关 系? – 叶子数目已知,结点总数=? – 唯一性?
哈夫曼树—构造(贪心)
ht[m].codify:=“”; for i:=m downto n+1 do begin p:=ht[i].lchild; if p<>0 then ht[p].codify:=ht[i].codify+”0” p:=ht[i].rchild; if p<>0 then ht[p].codify:=ht[i].codify+”1” end;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录一、程序设计目的与要求 (3)1.1程序设计目的 (3)1.2程序设计要求 (3)二、需求分析 (4)三、概要设计 (4)3.1哈夫曼树的构造过程 (4)3.2译码过程是编码过程的逆过程 (5)3.3 构造哈夫曼树和哈夫曼编码类的描述 (5)四、详细设计 (6)五、调试分析 (11)5.1程序编译界面 (11)5.2程序运行界面 (12)六、测试结果 (13)七、附录 (15)7.1设计心得 (15)7.2参考文献 (15)一、程序设计的目的与要求1.1程序设计目的课程设计是《数据结构》课程教学必不可缺的一个重要环节,通过课程设计,使学生对整个课程的知识体系有较深入的理解,在运用本课程的知识解决实际问题方面得到锻炼,对锻炼学生的实践能力以及运用本课程的知识、方法解决更为复杂的实际问题有较好的启发和指导作用,从而为后续课程的学习,毕业设计环节以及将来的实际工作打好坚实的基础。
本课程设计的目是:1.培养学生将所学的算法知识应用于程序设计过程中,设计出运行效率更高的程序;2.了解数据的三种逻辑结构(线性结构、树结构、图结构)和四种存储结构(顺序、链接、索引、散列)的基本特性和相互关系;3.掌握算法知识,学会设计算法并对算法进行分析和评价。
1.2程序设计要求在设计时严格按照题意独立进行设计,不得随意更改。
要求熟悉C、C++等某一种高级程序设计语言。
通过本课程的学习与实践,学生应做到:1.掌握数据结构的基本概念和基本理论。
2.熟练掌握顺序表、链表、队列、栈、树以及二叉树、图等基本数据结构的设计和分析。
3.熟练地掌握常用算法(递归、遍历、查找、排序)的知识。
4.能对所求解的问题进行分析,抽象出逻辑结构,选择合适的存储结构,定义所需的运算,设计相应的算法。
5.对算法进行分析和评价。
二、需求分析在当今信息爆炸时代,如何采用有效的数据压缩技术节省数据文件的存储空间和计算机网络的传送时间已越来越引起人们的重视,哈夫曼编码正是一种应用广泛且非常有效的数据压缩技术。
哈夫曼编码是一种编码方式,以哈夫曼树—即最优二叉树,带权路径长度最小的二叉树,经常应用于数据压缩。
哈弗曼编码使用一张特殊的编码表将源字符(例如某文件中的一个符号)进行编码。
这张编码表的特殊之处在于,它是根据每一个源字符出现的估算概率而建立起来的(出现概率高的字符使用较短的编码,反之出现概率低的则使用较长的编码,这便使编码之后的字符串的平均期望长度降低,从而达到无损压缩数据的目的)。
哈夫曼编码的应用很广泛,利用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。
树中从根到每个叶子都有一条路径,对路径上的各分支约定:指向左子树的分支表示“0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为和各个叶子对应的字符的编码,这就是哈夫曼编码。
哈弗曼译码输入字符串可以把它编译成二进制代码,输入二进制代码时可以编译成字符串。
三、概要设计3.1哈夫曼树的构造过程:用电文中各个字符使用的频度作为叶结点的权,构造一颗具有最小带权路径长度的哈夫曼树,若对树中的每个左分支赋予标记0右标记赋予1,则从根结点到每个叶结点的路径上的标记连接起来就构成一个二进制串,该二进制被称为哈夫曼编码。
3.2译码过程是编码过程的逆过程:从哈夫曼树的根开始,从左到右把二进制编码的每一位进行判别,若遇到0,则选择左分支走向下一个结点;若遇到1,则选择右分支走向下一个结点,直至到达一个树叶结点,便求得相应字符。
3.3构造哈夫曼树和哈夫曼编码类的描述:在构造哈夫曼树时要能方便地实现从双亲结点到左、右孩子结点的操作,而在进行哈夫曼树编码时又要求能方便地从结点到双亲结点的操作,因此,需要将哈夫曼树的结点存储结构设计为三叉链式存储结构。
此外,每一个结点还要设置全值域。
为了判断一个结点是否已加入到哈夫曼树中,每一个结点还要设置一个标志域flag,当flag=0时,表示该结点尚未加入到哈夫曼树中;当flag=1时,表示该结点已加入到哈夫曼树中。
这样,每一个结点应包含五个域,其存储结构示意图如图3.1 1所示。
weight flag parent rchild lchild图3.1 1哈夫曼树的结点存储结构示意图其中,weight域存放结点的权值;flag域存放结点是否加入哈夫曼树的标志值,等于1时表示已加入,否则没加入;parent、rchild、lchild域分别存放父结点,左、右孩子结点的地址。
四、详细设计#include <stdio.h>#include <stdlib.h>/*哈夫曼树建立、哈夫曼编码算法的实现所需头文件*/ #include <string.h>typedef char* HuffmanCode;/*动态分配数组,存储哈夫曼编码*/typedef struct{unsigned int weight ; /* 用来存放各个结点的权值*/unsigned int parent, LChild,RChild ; /*指向双亲、孩子结点的指针*/}HTNode, * HuffmanTree; /*动态分配数组,存储哈夫曼树*/void select(HuffmanTree *ht,int n, int *s1, int *s2){int i;int min;for(i=1; i<=n; i++){if((*ht)[i].parent == 0){min = i;i = n+1;}}for(i=1; i<=n; i++){if((*ht)[i].parent == 0){if((*ht)[i].weight < (*ht)[min].weight)min = i;}}*s1 = min;for(i=1; i<=n; i++){if((*ht)[i].parent == 0 && i!=(*s1)){min = i;i = n+1;}}for(i=1; i<=n; i++){if((*ht)[i].parent == 0 && i!=(*s1)){if((*ht)[i].weight < (*ht)[min].weight)min = i;}}*s2 = min;}void CrtHuffmanTree(HuffmanTree *ht , int *w, int n){ /* w存放已知的n个权值,构造哈夫曼树ht */int m,i;int s1,s2;m=2*n-1;*ht=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); /*0号单元未使用*/ for(i=1;i<=n;i++){/*1-n号放叶子结点,初始化*/(*ht)[i].weight = w[i];(*ht)[i].LChild = 0;(*ht)[i].parent = 0;(*ht)[i].RChild = 0;}for(i=n+1;i<=m;i++){(*ht)[i].weight = 0;(*ht)[i].LChild = 0;(*ht)[i].parent = 0;(*ht)[i].RChild = 0;} /*非叶子结点初始化*//* ------------初始化完毕!对应算法步骤1---------*/for(i=n+1;i<=m;i++) /*创建非叶子结点,建哈夫曼树*/{ /*在(*ht)[1]~(*ht)[i-1]的范围内选择两个parent为0且weight最小的结点,其序号分别赋值给s1、s2返回*/select(ht,i-1,&s1,&s2);(*ht)[s1].parent=i;(*ht)[s2].parent=i;(*ht)[i].LChild=s1;(*ht)[i].RChild=s2;(*ht)[i].weight=(*ht)[s1].weight+(*ht)[s2].weight;}}/*哈夫曼树建立完毕*/void outputHuffman(HuffmanTree HT, int m){if(m!=0){printf("%d ", HT[m].weight);outputHuffman(HT,HT[m].LChild);outputHuffman(HT,HT[m].RChild);}void CrtHuffmanCode(HuffmanTree *ht, HuffmanCode *hc, int n)/*从叶子结点到根,逆向求每个叶子结点对应的哈夫曼编码*/{char *cd;int i;unsigned int c;int start;int p;hc=(HuffmanCode *)malloc((n+1)*sizeof(char *)); /*分配n个编码的头指针*/ cd=(char * )malloc(n * sizeof(char )); /*分配求当前编码的工作空间*/cd[n-1]='\0'; /*从右向左逐位存放编码,首先存放编码结束符*/for(i=1;i<=n;i++) /*求n个叶子结点对应的哈夫曼编码*/{start=n-1; /*初始化编码起始指针*/for(c=i,p=(*ht)[i].parent; p!=0; c=p,p=(*ht)[p].parent) /*从叶子到根结点求编码*/ if( (*ht)[p].LChild == c)cd[--start]='0'; /*左分支标0*/elsecd[--start]='1'; /*右分支标1*/hc[i]=(char *)malloc((n-start)*sizeof(char)); /*为第i个编码分配空间*/strcpy(hc[i],&cd[start]);}free(cd);for(i=1;i<=n;i++)printf("%d编码为%s\n",(*ht)[i].weight,hc[i]);}int main()HuffmanTree HT;HuffmanCode HC;int *w;int i,n; // the number of elements;int wei; // the weight of a element;int m;printf("input the total number of the Huffman Tree:" ); scanf("%d",&n);w=(int *)malloc((n+1)*sizeof(int));for(i=1;i<=n;i++){printf("input the %d element's weight:",i);fflush(stdin);scanf("%d",&wei);w[i]=wei;}CrtHuffmanTree(&HT,w,n);m = 2*n-1;outputHuffman(HT,m);printf("\n");CrtHuffmanCode(&HT,&HC,n);getchar();getchar();}五、调试分析5.1程序编译界面5.2程序运行界面程序敲完了,发现运行后速度很快,还没看清结果就结束了。
