5.1 认识二元一次方程组(1)
北师大数学八年级上册第五章5.1认识二元一次方程

5.1认识二元一次方程组(解析)知识精讲定义含有两个未知数,并且所含未知数项的次数都是1的方程.判定1.方程两边的代数式都是整式——分母中不能含有字母;2.有两个未知数——“二元”;3.含有未知数的项的最高次数为1——“一次”.4.未知数的系数不为0解使二元一次方程两边的值相等的两个未知数的一组取值叫做二元一次方程的解.在写二元一次方程解的时候我们用大括号联立表示.定义由几个一次方程组成并且一共含有两个未知数的方程组叫做二元一次方程组.解二元一次方程组中所有方程(一般为两个)的公共解叫做二元一次方程组的解.三.易错点1.134xy x+=⎧⎨-=⎩和31xy=⎧⎨=-⎩也是二元一次方程组.2.二元一次方程左右两边必须都是整式,如:1=3yx+不是二元一次方程3.二元一次方程组的解一定要写成联立的形式4.二元一次方程组的解必须同时满足所有方程,即将解代入方程组的每一个方程时,等号两边的值都相等.5.组成二元一次方程组的两个一次方程,不一定都是二元一次方程,但两个方程必须一共含有两个未知数三点剖析一.考点:二元一次方程的概念和解,二元一次方程组的概念和解.二.重难点:判断是否为二元一次方程,注意一定满足三个条件.三.易错点:1.134xy x+=⎧⎨-=⎩和31xy=⎧⎨=-⎩也是二元一次方程组.2.二元一次方程组的解一定要写成联立的形式,如方程组2397x yx y-=⎧⎨+=⎩的解是61xy=⎧⎨=⎩.3.二元一次方程组的解必须同时满足所有方程,即将解代入方程组的每一个方程时,等号两边的值都相等.二元一次方程的概念和解例题1、若方程(a﹣2)x|a|﹣1+y=1是关于x、y的二元一次方程,则a的值是()A.﹣1B.﹣2C.1D.2【答案】 B【解析】 ∵方程(a ﹣2)x |a|﹣1+y=1是关于x 、y 的二元一次方程,∴a ﹣2≠0且|a|﹣1=1,解得:a=﹣2。
例题2、 下列各组值中,哪组是二元一次方程2x -y =5的解( )A.26x y =-⎧⎨=⎩B.34x y =⎧⎨=⎩C.43x y =⎧⎨=⎩D.62x y =⎧⎨=⎩【答案】 C【解析】 A 、x =-2、y =6时,左边=-4-6=-10≠5,此选项不符合题意;B 、x =3、y =4时,左边=6-4=2≠5,不符合题意;C 、x =4、y =3时,左边=8-3=5=右边,此选项符合题意;D 、x =6、y =2时,左边=12-2=10≠5,不符合题意.随练1、 已知方程()21320m n m x y ---+=是关于x 、y 的二元一次方程,则m =______,n =______【答案】 1;2【解析】 注意考虑未知数x 的系数,需满足30m -≠随练2、 下列方程中,是二元一次方程的是( )A.xy ﹣1=0B.x 2+y=3C.4x =3y ﹣1D.x ﹣1y=2 【答案】 C【解析】 A 、未知数的项的最高次数是2,不符合二元一次方程的定义;B 、未知数的项的最高次数是2,不符合二元一次方程的定义;C 、符合二元一次方程的定义;D 、是分式方程,不符合二元一次方程的定义.随练3、 在二元一次方程x +4y =13中,当x =5时,y =________.【答案】 2【解析】 方程x +4y =13,当x =5时,5+4y =13,解得:y =2,二元一次方程组的概念和解例题1、 下列方程组中,是二元一次方程组的有( )①⎩⎨⎧-==-1z 2y 37y x 2②⎩⎨⎧==+2xy 3y x ③⎩⎨⎧==-3y 3y x 2④⎪⎩⎪⎨⎧=+=-5y 3x 2213y 2x ⑤⎪⎪⎩⎪⎪⎨⎧=+=+1x1632y x ⑥⎩⎨⎧=+=+7y 5x 24y 3x 2 A.①③⑤B.①③④C.①②③D.③④ 【答案】 D【解析】 ①⎩⎨⎧-==-1z 2y 37y x 2中有3个未知数x ,y ,z 。
北师大出版社初中八年级数学上册--第五章 认识二元一次方程组

根据二元一次方程的定义求字母的值
方法小结:由方程是二元一次方程可知: (1)未知数的系数不为0; (2)未知数的次数都是1.
1.若x2m-1+5y3n-2m =7是二元一次方程,则m=____,n=___.
2m-1=1
1
3n-2m=1
1
2.如果 是二元一次方程,那么k的值是 ( ) A. 2 B. 3 C. 1 D. 0
作业内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
不是
例1 判断下列方程是否为二元一次方程:
(7) 4x+ π =0
(8) 2x=1-3y
不是
是
二元一次方程的判断
判断一个方程是否为二元一次方程的方法: 一看原方程是否是整式方程且只含有两个未知数;二看整理化简后的方程是否具备两个未知数的系数都不为0,且含未知数的项的次数都是1.
(8)4xy+5=0
都是一次方程
观察思考
x-y=2
x+1=2(y-1)
x+y=8
5x+3y=34
只含有1个未知数(元),未知数的次数为1;
x + y = 45.
x + 15 = 60
含有2个未知数(元),未知数的次数为1.
一元一次方程
都是含未知数的等式方程
二元一次方程
观察比较
(3)
是
不是
不是
不是
不是
根据实际问题列二元一次方程组
分析:第一道工序的人数+ _______________ =总人数;第一道工序的件数=________________.设安排第一道工序x人,第二道工序y人,用方程把这些条件表示出来: ___________.
北师版八年级数学上册第五章 二元一次方程组1 认识二元一次方程组

条件
①整式方程;②含有两个未知数; ③含有未知数的项的次数是 1
一般 形式
ax+by=c( a, b, c 为常数,且 ab ≠ 0)
示例 x-2y+1=0, x+y=5
知1-讲
特别提醒 “所含未知数的项的次数都是1”不可理解为
两个未知数的次数都是1, 例如2xy+1=0 不是二 元一次方程.
知1-练
(1) ቊy=x-=3,5; (2) ቊxy==20,.
感悟新知
解题秘方:将每组数值分别代入二元一次方程组 中的每个方程检验,既满足方程①, 又满足方程②的就是此二元一次方程 组的解,否则就不是此方程组的解.
知4-练
感悟新知
知4-练
解:把ቊy=x-=3,5; 代入方程组,发现不满足方程 ②,所以ቊy=x-=3,5; 不是原方程组的解; 把ቊxy==20,. 代入方程组,发现满足方程①②,所以 ቊx=2,是原方程组的解.
③ቐx1x++2yy==24;,④ቊ2xx2+-yy==35,.
感悟新知
知识点 3 二元一次方程的解
知3-讲
定义 适合一个二元一次方程的一组未知数的值,叫做 这个二元一次方程的一个解
示例 x=6, y=2 是方程 x+y=8 的一个解,记作ቊx=y=62,
判断 判断一对数值是不是二元一次方程的解,只需将 方法 这对数值代入方程,看等式是否成的项xy 的次数不是1; ②方程组中第二个方程不是整式方程;③方程组中共有 3个未知数. 只有④满足,④中的π是常数. ⑤方程组中第 二个方程含未知数的项 x2, y2 的次数都为 2. 所以二元 一次方程组有 1 个 .
答案:A
知2-练
2-1. 下列方程组不是二元一次方程组的是_②__③__④__.(填序号) ①ቊ4xx+-yy==1205,;②ቊxy+-yz==35;,
北师大版八年级上册:5.1认识二元一次方程组
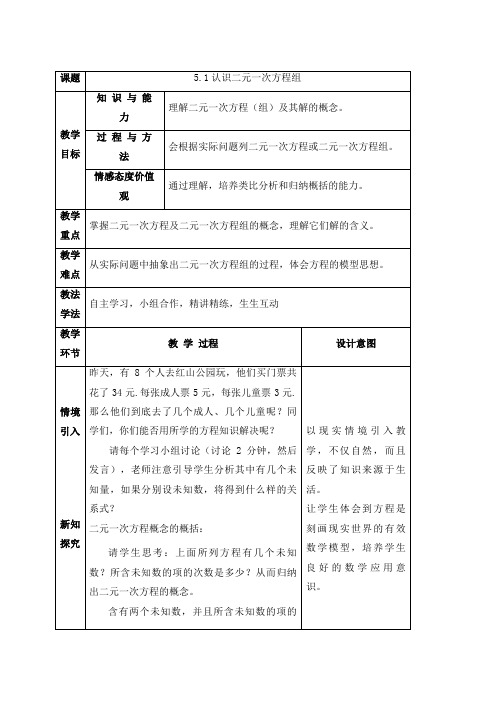
次数都是1的方程。
要求学生注意:这个定义有两个要求:
①含有两个未知数;
②所含未知数的项的最高次数是一次。
引导学生关注两个未
知数的方程。
激发学
生学习的兴趣。
巩固
训练
呈现关于二元一次方程概念的辨析题,进行巩固
练习:
1.下列方程有哪些是二元一次方程:
(1),(2),
(3),(4),(5)。
2.如果方程是二元一次方程,
那么m=,n=。
二元一次方程组的概念:
上面的方程中的x含义
相同吗?y呢?由于x、y的含义分别相同,因而
必同时满足和,我们把这
两个方程用大括号联立起来,写成
二元一次方程组的概念:像这样共含有两个未知
数的两个一次方程所组成的一组方程。
适合一个二元一次方程的一组未知数的值,
叫做这个二元一次方程的解。
二元一次方程组中各个方程的公共解,叫做
做到讲练结合,让学
生更好巩固新知识。
通过讲解与训练,让
学生对利用新知识解
决一些简单问题有更
加明确的认识。
尽量让学生明白
知识点不是孤立的,
需要前后联系,才能
更好地处理一些新问
题。
八年级数学北师大版(上册)5.1_认识二元一次方程组课件

,得4(3m+1)
-3(2m-2)=10. 解这个方程,得m=0.
总结
已知二元一次方程的解求字母的值的方法:将方程 的解代入方程中,得到一个关于这个字母的新方程,解 这个方程即可求出这个字母的值.
探究二:二元一次方程组
红山公园 成人人数+儿童人数=8 成人票数+儿童票数=34
昨天我们8个 人去红山公园 玩,买门票花
预习反馈
问题1: 我们已经知道了方程的定义,学习了最基本的一类方
程,即一元一次方程,你能举出几个例子,并说说它的 定义吗? 问题2:
哪位同学能举例说说你对一元一次方程概念中“元″ 和“次”含义的理解?
元的历史
相传,用“元”这个字表示未知数 ◆源于我国宋元时期的天元术; ◆朱世杰在《四元玉鉴》中将天元术拓广为四元术 ◆清末,李善兰用“天、地、人、物”分别代替英文字母x、y、z、w,于是, “天、地、人、物”成表示未知数的符号,而“元”,即为未知数的统称。
预习反馈 问题3:类比一元一次方程这个概念,你认为我们还有可能学习哪些方程?
第五章 二元一次方程组
5.1 认识二元一次方程组
学习目标
1.通过概念的正反例辨析,能准确识别出二元一次方程(组),并会判 断一组数是否是某二元一次方程(组)的解.
2.通过类比学习和合作交流,归纳总结出二元一次方程(组)及其解的 概念,提高类比分析和归纳概括的能力.
二元一次方程组中各个方程的公共 解,叫做这个二元一次方程组的解.
从历史上看,二元一次方程组问题和一元一次方程问题几乎 出现得一样早. 对于二元问题,我们既可以选择一个量作为未知量也可以选择 两个量作为未知量,前者得到的是一元一次方程,后者得到的 则是二元一次方程组. 《九章算术》中的“三禾”问题 《四元玉鉴》中的“二果问价”
5.1认识二元一次方程组课件ppt

x+1=2(y-1)
解决这个问题:
设他们中有X个成人,Y个儿童。可得到怎 样的方程?
x+y=8 5x+3y=34
想一想
上面的两个问题中,我们分别得到了方程 x-y=2 x+1=2(y-1) x+y=8 5x+3y=34 这些方程各含有几个未知数?含未知数的 项的次数是多少? 这些方程各含有2个未知数,含未知数的项 的次数是1。
二元一次方程组
1.认识二元一次方程组
鸡兔同笼
今有鸡兔同笼, 上有三十五头, 下有九十四足, 问鸡兔各几何?
你能解决上面“鸡兔同笼”的问题吗?
事实上,利用方程(组)可以很简单地解决这一问题, 方程(组)是刻画现实世界中等量关系的有效模型,许 多现实问题都可归结为方程问题。
本章将学习二元一次方程组及其解法,并利用二元一次 方程组解决一些有趣的现实问题。 你————
二元一次方程组的解
(3)有同时适合方程x+y=8、方程 5x+3y=34的x、y的值吗?
二元一次方程组中各个方程的公共解, 叫做这个二元一次方程组的解。 例: x=5 就是二元一次方程组 x+y=8, 的解 y=3 5x+3y=34
作业
随堂练习 书上: 1.2.3.4.5
作好准备了吗?
本章学习目标
感受二元一次方程组是刻画现实世界中等量 关系的有效模型
会解二元一次方程组,体会“消元”的思想
能应用二元一次方程组解决现实生活中的实 际问题
感受二元一次方程组和一次函数的关系
认识二元一次方程组
累死 了!
哼!我从你背上 你还累? 拿来一个,我的 这么大 包裹数就是你 个才比 真的?! 的2倍! 我多驮2 个。
认识二元一次方程组备课

课题:5.1认识二元一次方程组一.备课标:(一)内容标准:能根据具体问题中的数量关系列出方程,体会方程是刻画现实世界数量关系的有效模型。
(二)核心概念:初步学会在具体情境中从数学的角度发现和提出问题,探索具体问题中的数量关系并能根据数量关系列出方程,发展灵活运用数学知识解决实际问题能力。
十大核心概念在本节课中突出培养的是模型思想、应用意识。
二. 备重点、难点:(一)教材分析:本节课是八年级上册第五章《二元一次方程组》第一节“认识二元一次方程组”,属于“数与代数”领域中的“方程”。
本章的学习将使学生进一步体会方程的模型思想,感受代数方法的优越性,也将有助于巩固有理数、整式运算、一元一次方程等知识,方程作为数学的一个重要分支,是刻画现实世界数量关系的一个有效数学模型,它既是一元一次方程的继续和发展,同时又是今后学习线性方程组及平面解析几何等知识的基础,具有承上启下的作用. 本节的重点是通过丰富的实例学习二元一次方程、二元一次方程组、二元一次方程(组)的解的概念,体会二元一次方程组的模型思想,学习列方程解应用题的方法。
(二)重点、难点分析:本节通过丰富的实例,归纳建立二元一次方程和二元一次方程组的概念,并从中体会方程的模型思想。
基于学生对一元一次方程理解的基础上,教材从实际问题出发,通过引导学生经历自主探索和合作交流的活动,学习二元一次方程、二元一次方程组及其解等基本概念,所以确定:重点:1.理解二元一次方程(组)及其解的含义.2.体会方程的模型思想,培养学生良好的数学应用意识.难点:准确分析确定具体情境的等量关系,从实际问题中抽象出二元一次方程的过程.三.备学情:(一)学习条件和起点能力分析:1.学习条件分析:(1)必要条件:学生了解方程、一元一次方程及其解的概念,具备了列一元一次方程解决实际问题的基础经验。
(2)支持性条件:学生初步体会了方程的模型思想,具备了用类比方法学习二元一次方程(组)概念的基本能力.此处表现为类比一元一次方程的形成过程学习二元一次方程。
5.1 认识二元一次方程组 课件 2024-2025学年北师大版 八年级数学上册

0.2
0.3
0.4
…
第一个方程中y的值
…
第二个方程中y的值
…
请你帮她完成表格,并找出符合该问题的解.
解:完成表格如下:
x/kg
0.1
0.2
0.3
0.4
…
第一个方程中y的值
0.4
0.3
0.2
0.1
…
第二个方程中y的值
0.2
…
当x=0.3时,发现两个方程中y值相等,
= . ,
所以可得方程组的解为
= ,
将y=4代入2x+y=8中,得x=2,所以这个方程组的解为
= ,
= ,
将
代入7x-ay=2中,得14-4a=2,解得a=3,
=
所以a的值为3.
14.小颖自己在家制作南瓜芋圆,她准备了1块南瓜和1包木薯粉共0.5
kg,混合后发现芋圆太软,于是又加了1块与第一次等质量的南瓜和2包木
那么能否满足门票花费34元?
x+y=8
5x + 3y = 34
定义: 二元一次方程组中各个方程的公共解,叫做这个
二元一次方程组的解.
x=5
y=3
就是二元一次方程组
x+y=8
5x + 3y = 34
的解
温馨提示
1. 二元一次方程的解是成对出现的;
2. 二元一次方程的解有无数多个,与一元一次方程有
显著区别.而二元一次方程组的解一般只有一个.
买了两种邮票各多少枚?
解:设面值50分的邮票x枚,面值80分的邮
票y枚,由题意得:
x+y=9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新课讲解
方程 x+y=8 和 5x+3y=34中,x的含义相同吗?y呢? x,y所代表的对象分别相同,因而x,y必须同时满足方程
x+y=8和5x+3y=34 ,把它们联立起来, x+y=8
得 5x+3y=34
像这样共含有两个未知数的两个一次方程所组成的一组方 程,叫做二元一次方程组.
【注意】方程组各方程中同一字母必须代表同一个量.
BS八(上) 教学课件
第五章 二元一次方程组
5.1 认识二元一次方程组
累死我了!
新课引入
你还累?这么大 的个,才比我 多驮了2个.
哼,我从你背上拿来 1个,我的包裹数就 是你的2倍!
真的?!
新课引入
思考:听完它们的对 话,你能猜出它们各 驮了多少包裹吗?
1 二元一次方程组的定义
新课讲解
【问题1】设老牛驮了x个包裹 , 小马驮了y个包裹. 你能根据它们的对话列出方程吗?
新课讲解
x-y=2
x+y=8
x+1=2(y-1) 5x+3y=34 上面所列方程各含有几个未知数? 2个未知数
含有未知数的项的次数是多少? 次数是1
【定义】 含有两个未知数,并且所含未知数的项的次数
都是1的方程叫做二元一次方程.
新课讲解
都是含未知数的等式方程
x + 15 = 60
x + y = 45.
x+y=3 A.
x-y=1
x+ 1 =1
B.
y y+x=2
x=1 C.
y=1
6x+4y=9 D.
y=3x+4
新课讲解
2 二元一次方程组的解
【问题】(1)x=6 , y=2适合方程 x+y=8吗 ? x=5 , y=3呢? x=4 , y=4呢?
你还能找到其他x , y的值适合方程x+y=8吗 ?
(2) x=5 , y=3适合方程5x+3y=34吗? x=2 , y=8呢?
别为x元和y元,可列
5x 10y 10x 5y
42, 30
y
2
为解的二元一次方程组是( D) )
(A)
x y 3 3x y 1
(B)3xxyy15
(C)3xx25yy35
(D)3xxyy51
练一练:
5.二元一次方程 x y 6 的正整数
x 1, x 2, x 3, x 4, x 5,
解是__y___5;__y__4_; __y __3;__y__2_;__y__1_. ___ .
1;
(D)
x 5,
y
2.
答案:B,C,D
练一练:
2.二元一次方程 2x 3y 28 的解有:
x 5,
(1)y ___; 6
x ___, (2)y 2;
17
(3)
x 2.5,
y
___;
x ___,
11
(4)
y
7 3
.
10.5
新课讲解
x=5 ,y =3是否为方程 x+y=8的一个解? x=5 , y =3是否为方程 5x +3y=34的一个解?
新课讲解
【例2】 下列方程组是二元一次方程组的是(C )
xy 1, A.x y 1
x z 1, B. x y 1
C. x y 1,
2 2 x y 1
D.
x y 1,
1 x
y
1
紧扣相关概念
新课讲解
【练习】请问下列方程组是二元一次方程组吗?
三个未知数
(1)3yx52xy09 √
老牛的包裹数比小马的多2个; x-y=2
老牛从小马的背上拿来1个包裹,就是小马的2倍.
x+1=2(y-1)
昨天,我们8个人 去红山公园玩,买 门票花了34元
【问题2】他们到底去了 几个成人,几个儿童呢? 设他们中有x个成人,y个儿童. 你能得到怎样的方程?
x+y=8 5x+3y=34
新课讲解
每张成人票 5 元, 每张儿童票 3 元,
二元一次方程组中各个方程的公共解,叫 做这个二元一次方程组的解.
{ 例如,
x=5 y=3
就是二元一次方程组
{x+y=8 5x+3y=34
的解.
随堂即练
1.二元一次方程组 x+2y=10的解是( C )
y=2x
x=4 A.
y=3
x=3 B.
y=6
x=2 C.
y=4
x=4 D.
y=2
练一练:
4.以
x 1
新课讲解
适合一个二元一次方程的一组未知 数的值,叫做这个二元一次方程的一个解.
【例如】x=6 , y=2 是方程x+y=8 的一个解,记作 x=6 y=2
练一练:
1.在下列四组数值中,哪些是二元一次方
程 x 3y 1 的解?
(A)
x 2,
y
3;
(C)
x 10,
y
3;
(B)ቤተ መጻሕፍቲ ባይዱ
x 4,
y
6.如果
x
y
1 2
是方程组
x 2y m 3x y n
的解,
那么m=___5__,n= 1 ________.
7.写出一个以
_____2__x____y____1_____.
x 2
y
3
为解的二元一次方程为
(答案不唯一)
新课讲解
【例3 】 根据以下对话,可以求得小红所买的笔
和笔记本的价格分别是D( )
不是,最高项次数为2.
6x 1 z 1; 2
x y a; 2x 1 0.
y
是. 不是,含有3个未知数. 方程左边的式子不是整式.
练一练:
如果方程 2xm1 3y2mn 1 是二元一
次方程,那么m= 2 ,n= -3 .
【例1】 已知|m-1|x|m|+y2n-1=3是二元一次 方程,则m+n=____0____.
(2)xy
3y 3z
9z 5
8
(3) xy
2 1
√
(5)
x x
1 y
5
√
(4)
3 x
5 y
4
x y 0
未知数出现 在分母中
随堂即练
2.下列各式是二元一次方程的是( A ) A.x=3y B.2x+y=3z C.x²+x-y=0 D.3x+2=5
3.下列不是二元一次方程组的是( B )
小红,你上周买的笔和笔
记本的价格是多少啊?
A.0.8元/支,2.6元/本
哦……我忘了!只记得 先后买了两次,第一次 买了5支笔和10本笔记 本花了42元钱,第二次 买了10支笔和5本笔记 本花了30元钱.
B.0.8元/支,3.6元/本 C.1.2元/支,2.6元/本 D.1.2元/支,3.6元/本
设小红所买的笔和笔记本的价格分
只含有1个未知(元),含有2个未知数(元), 未知数的次数为1. 未知数的次数为1.
一元一次方程
二元一次方程
新课讲解
注意:二元一次方程是整式方
程;所含未知数有2个,所含未
判断下面哪些方程是二元一次方程.
知数项的最高次数是“1”,这
x 3 6;
不是,是一元里一要次特方别注程意. 项的次数.
xy 3;
