西安铁一中滨河学校八年级数学下册第三单元《平行四边形》检测卷(含答案解析)
八年级数学下册《平行四边形》单元测试卷(附答案)

八年级数学下册《平行四边形》单元测试卷(附答案)一.选择题(共10小题,满分40分)1.如图,在▱ABCD中,DE平分∠ADC,AD=8,BE=3,则CD=()A.4B.5C.6D.72.如图,在平行四边形ABCD中,AC、BD相交于点O,∠ODA=90°,AC=10cm,BD=6cm,则BC的长为()A.4cm B.5cm C.6cm D.8cm3.下面关于平行四边形的说法中,不正确的是()A.对角线互相平分的四边形是平行四边形B.有一组对边平行,一组对角相等的四边形是平行四边形C.有一组对边相等,一组对角相等的四边形是平行四边形D.有两组对角相等的四边形是平行四边形4.如图,在▱ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有()A.9个B.8个C.6个D.4个5.如图,▱ABCD中,CE平分∠BCD,交AB于点E,AE=3,BE=5,DE=4,则CE的长为()A.B.C.D.6.如图,在▱ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若▱ABCD的周长为30,则△ABE的周长为()A.30B.26C.20D.157.如图,平行四边形ABCD的周长为16,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为()A.4B.6C.8D.108.如图,将▱DEBF的对角线EF向两端延长,分别至点A和点C,且使AE=CF,连接AB,BC,AD,CD.求证:四边形ABCD为平行四边形.以下是证明过程,其顺序已被打乱,①∴四边形ABCD为平行四边形;②∵四边形DEBF为平行四边形,∴OD=OB,OE=OF;③连接BD,交AC于点O;④又∵AE=CF,∴AE+OE=CF+OF,即OA=OC.正确的证明步骤是()A.①②③④B.③④②①C.③②④①D.④③②①9.如图,在▱ABCD中,点M,N分别是AD、BC的中点,点O是CM,DN的交点,直线AB分别与CM,DN的延长线交于点P、Q.若▱ABCD的面积为192,则△POQ的面积为()A.72B.144C.208D.21610.如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,,则下列结论:①∠CAD=30°②③S平行四边形ABCD=AB•AC④,正确的个数是()A.1B.2C.3D.4二.填空题(共8小题,满分32分)11.如图,已知▱ABCD中,AD⊥BD,AC=10,AD=4,则BD的长是.12.下列条件能判定四边形ABCD是平行四边形的是.A.AB∥CD,AD∥BC B.AD=BC,AB=CDC.AB∥CD,AD=BC D.∠A=∠C,∠B=∠D13.如图,平行四边形ABCD中,对角线AC、BD相交于点O,若AB=2,BC=3,∠ABC=60°,则图中阴影部分的面积是.14.如图,平行四边形ABCD的顶点A,B,C的位置用数对分别表示为(4,6),(1,3),(5,3),则顶点D的位置用数对表示为.15.如图,▱ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则▱ABCD的两条对角线长的和.16.如图,在▱ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E、F,若BE=6,则CF=.17.如图,在平行四边形ABCD中,BD是对角线,E,F分别是边AD,BC上不与端点重合的两点,连接EF,下列条件中使得四边形BFDE是平行四边形的是.(多选)A.AE=CFB.EF经过BD的中点C.BE∥DFD.EF⊥AD18.在如图的网格中,以格点A、B、C、D、E、F中的4个点为顶点,你能画出平行四边形的个数为个.三.解答题(共6小题,满分48分)19.如图,在▱ABCD中,AE平分∠BAD交BD于点E,交BC于点M,CF平分∠BCD交BD于点F.(1)求证:AE=CF;(2)若∠ABC=70°,求∠AMB的度数.20.在▱ABCD中,对角线AC⊥AB,BE平分∠ABC交AD于点E,交AC于点F.(1)求证:AE=AB;(2)若AB=3,BC=5,求AF的长.21.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.(1)求证:AB=AE.(2)若BC=2AE,∠E=31°,求∠DAB的度数.22.如图,点B、C、E、F在同一直线上,BE=CF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:(1)△ABC≌△DEF;(2)四边形ABED是平行四边形.23.如图,在等边△ABC中,D是BC的中点,以AD为边向左侧作等边△ADE,边ED与AB交于点G.(1)求∠CAE的度数;(2)取AB的中点F,连接CF,EF,求证:四边形CDEF是平行四边形.24.在▱ABCD中,点O是对角线BD的中点,点E在边BC上,EO的延长线与边AD交于点F,连接BF、DE如图1.(1)求证:四边形BEDF是平行四边形;(2)若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、P如图2.①当CD=6.CE=4时,求BE的长;②求证:CD=CH.参考答案与解析一.选择题(共10小题,满分40分)1.解:在▱ABCD中,AD=8;∴BC=AD=8,AD∥BC;∴CE=BC﹣BE=8﹣3=5,∠ADE=∠CED;∵DE平分∠ADC;∴∠ADE=∠CDE;∴∠CDE=∠CED;∴CD=CE=5;故选:B.2.解:∵四边形ABCD是平行四边形,AC=10cm,BD=6cm;∴OA=OC=AC=5(cm),OB=OD=BD=3(cm);∵∠ODA=90°;∴AD===4(cm);∴BC=AD=4(cm);故选:A.3.解:A、∵对角线互相平分的四边形是平行四边形;∴选项A不符合题意;B、∵有一组对边平行,一组对角相等的四边形是平行四边形;∴选项B不符合题意;C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形;∴选项C符合题意;D、∵有两组对角相等的四边形是平行四边形;∴选项D不符合题意;故选:C.4.解:设EF与NH交于点O;∵在▱ABCD中,EF∥AD,HN∥AB;∴AD∥EF∥BC,AB∥NH∥CD;则图中的四边BEON、DFOH、DHNC、BEFC、BAHN、AEOH、AEFD、ONCF都是平行四边形,共8个.故选:B.5.解:∵AE=3,BE=5;∴AB=8;∵四边形ABCD是平行四边形;∴CD=AB=8,AB∥CD,AD=BC;∴∠DCE=∠CEB;∵CE平分∠BCD;∴∠DCE=∠BCE;∴∠BCE=∠BEC;∴BC=BE=5=AD;∵AE2+DE2=9+16=25,AD2=25;∴AE2+DE2=AD2;∴∠AED=90°;∵DC∥CD;∴∠CDE=90°;在△DCE中,由勾股定理可得:CE===4;故选:A.6.解:∵四边形ABCD是平行四边形;∴AB=CD,AD=BC,OB=OD;又∵OE⊥BD;∴OE是线段BD的中垂线;∴BE=DE;∴AE+ED=AE+BE;∵▱ABCD的周长为30;∴AB+AD=15;∴△ABE的周长=AB+AE+BE=AB+AD=15;故选:D.7.解:∵平行四边形ABCD;∴AD=BC,AB=CD,OA=OC;∵EO⊥AC;∴AE=EC;∵AB+BC+CD+AD=16;∴AD+DC=8;∴△DCE的周长是:CD+DE+CE=AE+DE+CD=AD+CD=8;故选:C.8.解:连接BD,交AC于点O,如图所示:∵四边形DEBF为平行四边形;∴OD=OB,OE=OF;又∵AE=CF;∴AE+OE=CF+OF;即OA=OC;∴四边形ABCD为平行四边形;即正确的证明步骤是③②④①;故选:C.9.解:连接MN,如图所示:∵四边形ABCD是平行四边形;∴CD∥AB,AD∥BC,AD=BC;∴∠CDQ=∠Q,∠DCB=∠CBQ;∵点M,N分别是AD、BC的中点;∴DM=CN,CN=BN;∴四边形CDMN是平行四边形;在△CDN和△BQN中;;∴△CDN≌△BQN(AAS);同理可得:△CDM≌△P AM;∴△POQ的面积=四边形ABCD的面积+△COD的面积,O是CM的中点;∵▱ABCD的面积为192;∴四边形CDMN的面积是96;∴△CDM的面积为四边形CDMN的面积的一半,即48;∴△COD的面积为24;∴△POQ的面积=四边形ABCD的面积+△COD的面积=192+24=216.故选:D.10.解:①∵AE平分∠BAD;∴∠BAE=∠DAE;∵四边形ABCD是平行四边形;∴AD∥BC,∠ABC=∠ADC=60°;∴∠DAE=∠BEA;∴∠BAE=∠BEA;∴AB=BE=1;∴△ABE是等边三角形;∴AE=BE=1;∵BC=2;∴EC=1;∴AE=EC;∴∠EAC=∠ACE;∵∠AEB=∠EAC+∠ACE=60°;∴∠ACE=30°;∵AD∥BC;∴∠CAD=∠ACE=30°;故①正确;②∵BE=EC,OA=OC;∴OE=AB=,OE∥AB;∴∠EOC=∠BAC=60°+30°=90°;Rt△EOC中,OC=;∵四边形ABCD是平行四边形;∴∠BCD=∠BAD=120°;∴∠ACB=30°;∴∠ACD=90°;Rt△OCD中,OD=;∴BD=2OD=;故②正确;③由②知:∠BAC=90°;∴S平行四边形ABCD=AB•AC;故③正确;④由②知:OE是△ABC的中位线;∴OE=AB;∵AB=BC;∴OE=BC=AD;故④正确;故选:D.二.填空题(共8小题,满分32分)11.解:∵四边形ABCD是平行四边形;∴AO=CO=AC,DO=BO;∵AC=10;∴AO=5;∵AD⊥DB;∴∠ADB=90°,AD=4;∴DO==3;∴BD=6;故答案为:6.12.解:A.根据AB∥CD,AD∥BC能推出四边形ABCD是平行四边形;B.根据AD=BC,AB=CD能推出四边形ABCD是平行四边形;C.根据AB∥CD,AD=BC能得出四边形是等腰梯形,不能推出四边形ABCD是平行四边形D.根据∠A=∠C,∠B=∠D能推出四边形ABCD是平行四边形;故答案为:ABD.13.解:作AM⊥BC于M,如图所示:则∠AMB=90°;∵∠ABC=60°;∴∠BAM=30°;∴BM=AB=×2=1;在Rt△ABM中,AB2=AM2+BM2;∴AM===;∴S平行四边形ABCD=BC•AM=3;∵四边形ABCD是平行四边形;∴AD∥BC,BO=DO;∴∠OBE=∠ODF;在△BOE和△DOF中;;∴△BOE≌△DOF(ASA);∴S△BOE=S△DOF;∴图中阴影部分的面积=▱ABCD的面积=;故答案为:.14.解:∵平行四边形ABCD的顶点A,B,C的位置用数对分别表示为(4,6),(1,3),(5,3);∴点D坐标为(8,6);故答案为:(8,6).15.解:∵四边形ABCD是平行四边形;∴AB=CD=5;∵△OCD的周长为23;∴OD+OC=23﹣5=18;∵BD=2DO,AC=2OC;∴平行四边形ABCD的两条对角线的和=BD+AC=2(DO+OC)=36;故答案为:36.16.解:如图,设BE与FC的交点为H,过点A作AM∥FC,交BE与点O;∵四边形ABCD是平行四边形;∴AD∥BC,AB∥CD;∴∠ABC+∠DCB+180°;∵BE平分∠ABC,CF平分∠BCD;∴∠ABE=∠EBC,∠BCF=∠DCF;∴∠CBE+∠BCF=90°;∴∠BHC=90°;∵AM∥CF;∴∠AOE=∠BHC=90°;∵AD∥BC;∴∠AEB=∠EBC=∠ABE;∴AB=AE=5;又∵∠AOE=90°;∴BO=OE=3;∴AO===4;在△ABO和△MBO中;;∴△ABO≌△MBO(ASA);∴AO=OM=4;∴AM=8;∵AD∥BC,AM∥CF;∴四边形AMCF是平行四边形;∴CF=AM=8;故答案为:8.17.解:∵四边形ABCD是平行四边形;∴AD∥BC;∵AE=CF,AD=BC;∴DE=BF;∴四边形BFDE是平行四边形;故A选项符合题意;若EF经过BD的中点O;∵AD∥BC;∴∠EDO=∠FBO;在△BOF和△DOE中;;∴△BOF≌△DOE(ASA);∴BF=DE;∴四边形BFDE是平行四边形;故B选项符合题意;∵DE∥BF,BE∥DF;∴四边形BFDE是平行四边形;故C选项符合题意;由EF⊥AD不能判定四边形BFDE是平行四边形;故D选项不符合题意;故答案为:A,B,C.18.解:如图所示:图中平行四边形有▱ABEC,▱BDEC,▱BEFC共3个.故答案为:3.三.解答题(共6小题,满分48分)19.(1)证明:∵四边形ABCD是平行四边形;∴AB∥CD,AB=CD,∠BAD=∠BCD∴∠ABE=∠CDF;∵AE平分∠BAD,CF平分∠BCD;∴∠BAE=∠DCF;∴△ABE≌△CDF(ASA);∴AE=CF;(2)∵四边形ABCD是平行四边形;∴AD∥BC,∠BAD+∠ABC=180°;∵∠ABC=70°;∴∠BAD=110°;∵AM平分∠BAD,AD∥BC;∴∠AMB=∠DAM=55°.20.(1)证明:∵四边形ABCD为平行四边形;∴∠AEB=∠EBC;∵BE平分∠ABC;∴∠ABE=∠EBC;∴∠ABE=∠AEB;∴AE=AB;(2)解:AC⊥AB,AB=3,BC=5;∴AC=;过F点作FH⊥BC,垂足为H;∵BE平分∠ABC,AC⊥AB;∴AF=FH;∵S△ABC=S△ABF+S△BFC;∴AB•AC=AB•AF+BC•FH;即;∴AF=.21.(1)证明:∵四边形ABCD是平行四边形;∴AB=CD,AB∥CD,BC=AD;∴∠E=∠DCF;∵点F是AD中点;∴AF=DF;∵∠EF A=∠CFD;∴△AFE≌△DFC(AAS);∴CD=AE;∴AB=AE;(2)解:由(1)可得AF=DF,BC=AD;∵BC=2AE;∵∠E=31°;∴∠AFE=∠E=31°;∴∠DAB=2∠E=62°.22.证明:(1)∵BE=CF;∴BE﹣CE=CF﹣CE;即BC=EF;又∵AC⊥BC于点C,DF⊥EF于点F;∴∠ACB=∠DFE=90°;在△ABC和△DEF中;;∴△ABC≌△DEF(SAS);(2)由(1)知△ABC≌△DEF;∴AB=DE,∠ABC=∠DEF;∴AB∥DE;∴四边形ABED是平行四边形.23.(1)解:∵△ABC是等边三角形,D是BC的中点;∴AD⊥BC,∠BAC=60°;∴∠DAC=∠BAC=30°;∵△AED是等边三角形;∴∠EAD=60°;∴∠CAE=∠EAD+∠DAC=90°;(2)证明:∵F是等边△ABC边AB的中点,D是边BC的中点;∴CF=AD,CF⊥AB;∵△AED是等边三角形;∴AD=ED;∴CF=ED;∵∠BAD=∠BAC=30°,∠EAG=∠EAD=30°;∴ED⊥AB;∴CF∥ED;∵CF=ED;∴四边形CDEF是平行四边形.24.(1)证明:∵在平行四边形ABCD中,点O是对角线BD的中点;∴AD∥BC,BO=DO;∴∠ADB=∠CBD;在△BOE与△DOF中;;∴△BOE≌△DOF(ASA);∴DF=BE且DF∥BE;∴四边形BEDF是平行四边形;(2)①解:如图,过点D作DN⊥EC于点N;∵DE=DC=6,DN⊥EC,CE=4;∴EN=CN=2;∴DN===4;∵∠DBC=45°,DN⊥BC;∴∠DBC=∠BDN=45°;∴DN=BN=4;∴BE=BN﹣EN=4;②证明:∵DN⊥EC,CG⊥DE;∴∠CEG+∠ECG=90°,∠DEN+∠EDN=90°;∴∠EDN=∠ECG;∵DE=DC,DN⊥EC;∴∠EDN=∠CDN;∵∠DHC=∠DBC+∠BCH=45°+∠BCH,∠CDB=∠BDN+∠CDN=45°+∠CDN;∴∠CDB=∠DHC;∴CD=CH.。
新人教版初中数学八年级数学下册第三单元《平行四边形》测试卷(有答案解析)(3)
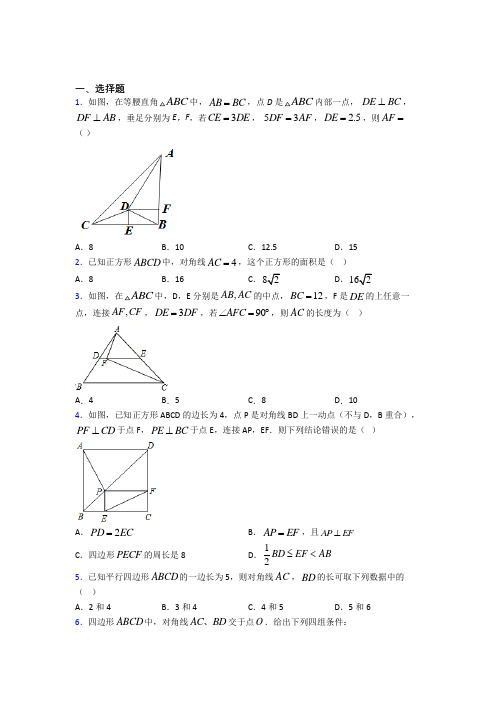
一、选择题1.如图,在等腰直角ABC 中,AB BC =,点D 是ABC 内部一点, DE BC ⊥,DF AB ⊥,垂足分别为E ,F ,若3CE DE =, 53DF AF =, 2.5DE =,则AF =( )A .8B .10C .12.5D .15 2.已知正方形ABCD 中,对角线4AC =,这个正方形的面积是( ) A .8 B .16 C .82 D .162 3.如图,在ABC 中,D ,E 分别是,AB AC 的中点,12BC =,F 是DE 的上任意一点,连接,AF CF ,3DE DF =,若90AFC ∠=︒,则AC 的长度为( )A .4B .5C .8D .104.如图,已知正方形ABCD 的边长为4,点Р是对角线BD 上一动点(不与D ,B 重合),PF CD ⊥于点F ,PE BC ⊥于点E ,连接AP ,EF .则下列结论错误的是( )A .2PD EC =B .AP EF =,且AP EF ⊥C .四边形PECF 的周长是8D .12BD EF AB ≤< 5.已知平行四边形ABCD 的一边长为5,则对角线AC ,BD 的长可取下列数据中的( )A .2和4B .3和4C .4和5D .5和6 6.四边形ABCD 中,对角线AC BD 、交于点O .给出下列四组条件:①AB ∥CD ,AD ∥BC ;②AB CD =,AD BC =;③AO CO =,BO DO =;④AB ∥CD ,AD BC =.其中一定能判定这个四边形是平行四边形的条件共有( )A .1组;B .2组;C .3组;D .4组.7.如图,ABCD 的对角线AC BD 、交于点,O DE 平分ADC ∠交AB 于点,60,E BCD ∠=︒12AD AB =,连接OE .下列结论:①ABCD S AD BD =⋅;②DB 平分CDE ∠;③AO DE =;④OE 垂直平分BD .其中正确的个数有( )A .1个B .2个C .3个D .4个8.如图,在123A A A △中,160A ∠=︒,230A ∠=︒,131A A =,3+n A 是1(1,2,3)n n A A n +=⋅⋅⋅的中点,则202120222023A A A △中最短边的长为( )A .100912 B .101012 C .101112 D .1021129.如图,直线L 上有三个正方形,,a b c ,若,a c 的边长分别为1和3,则b 的面积为( )A .8B .9C .10D .1110.如图,在直角三角形ABC 中,∠ACB =90°,AC =3,BC =4,点M 是边AB 上一点(不与点A ,B 重合),作ME ⊥AC 于点E ,MF ⊥BC 于点F ,若点P 是EF 的中点,则CP 的最小值是( )A .1.2B .1.5C .2.4D .2.5 11.如图,将矩形ABCD 折叠,使点C 和点A 重合,折痕为EF .若5AF =,3BE =,则EF 的长为( )A .23B .17C .25D .3512.如图在ABCD 中,对角线,AC BD 相交于点O ,AOD △与AOB 的周长相差3,8AB =,那么AD 为( )A .5B .8C .11或5D .11或14二、填空题13.如图,正方形ABCD 中,5AD =,点E 、F 是正方形ABCD 内的两点,且4AE FC ==,3BE DF ==,则EF 的平方为________.14.如图,在ABCD 中,AC 与BD 相交于点O ,(1)若18cm,24cm AC BD ==,则AO =_______,BO =_______.又若13AB =厘米,则COD △的周长为________.(2)若AOB 的周长为30cm ,12cm AB =,则对角线AC 与BD 的和是________. 15.如图,B ,E ,F ,D 四点在一条直线上,菱形ABCD 的面积为2120cm ,正方形AECF 的面积为250cm ,则菱形的边长为___cm .16.已知Rt ABC ,90C ∠=︒,4cm AC =,3cm BC =,若PAB △与ABC 全等,PC ________.17.如图,BD 是矩形ABCD 的对角线,在BA 和BD 上分别截取BE ,BF ,使BE =BF ;分别以E ,F 为圆心,以大于12EF 的长为半径作弧,两弧在∠ABD 内交于点G ,作射线BG 交AD 于点P ,若AP =3,则点P 到BD 的距离为_______.18.如图,在平行四边形ABCD 中,BF 平分∠ABC ,交AD 于点F ,CE 平分∠BCD ,交AD 于点E ,AB =8,EF =1,则BC 长为__________.19.在长方形ABCD 中,52AB =,4BC =,CE CF =,CF 平分ECD ∠,则BE =_________.20.如图,将Rt △ABC 沿着点B 到A 的方向平移到△DEF 的位置,BC =8,FO =2,平移距离为4,则四边形AOFD 的面积为__.三、解答题21.综合与实践:问题情境:数学活动课上,老师和同学们一起以“矩形的旋转”开展数学活动.具体操作如下:第一步:如图1,将长与宽都相等的两个矩形纸片ABCD 和EFGH 叠放在一起,这时对角线AC 和EG 互相重合.第二步:固定矩形ABCD ,将矩形EFGH 绕AC 的中点O 逆时针方向旋转,直到点E 与点B 重合时停止.问题解决:(1)奋进小组发现:在旋转过程中,当边AB 与EF 交于点M ,边CD 与GH 交于点N ,如图2、图3所示,请写出线段AM 与CN 始终存在的数量关系,并利用图2说明理由.(2)奋进小组继续探究发现:在旋转开始后,当两个矩形纸片重叠部分为四边形MRNQ 时,如图3所示,请你猜测四边形MRNQ 的形状,并试着证明你的猜想.探索发现:(3)奋进小组还发现在问题(2)中的四边形MRNQ 中MQN ∠与旋转角AOE ∠存在着特定的数量关系,请你写出这一关系,无需说明理由.22.如图,平行四边形ABCD 中,,AP BP 分别平分DAB ∠和CBA ∠,交于DC 边上点P , 2.5AD =.(1)求线段AB 的长.(2)若3BP =,求ABP △的面积.23.如图,四边形ABCD ,//BC AD ,P 为CD 上一点,PA 平分BAD ∠且BP AP ⊥. (1)若80BAD ︒∠=,求ABP ∠的度数;(2)求证:=+BA BC AD ;(3)设3BP a =,4AP a =,过点P 作一条直线,分别与AD ,BC 所在直线交于点E 点F .若AB EF =,求AE 的长(用含a 的代数式表示).24.如图,菱形ABCD 中,60B ∠=︒,点E ,F 分别在BC 和CD 上,BE CF =,求证:AE AF =.25.如图,已知点D 在ABC 的BC 边上,//DE AC 交AB 于E ,//DF AB 交AC 于F .(1)求证:AE DF =;(2)若AD 平分BAC ∠,试判断四边形AEDF 的形状,并说明理由.26.如图,点E 在正方形ABCD 的边AB 上,点F 在边BC 的延长线上,且90EDF ∠=︒.求证:DE DF =.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据比例关系设DF=x ,可判断四边形DEBF 为矩形,根据矩形的性质和比例关系分别表示CB 和AB ,再根据AB BC =,列出方程,求解即可得出x ,从而得出AF .【详解】,DE BC DF AB ⊥⊥,90DEB DFB ∴∠=∠=︒,∵△ABC 为等腰直角三角形,∴∠ABC=90°,∴四边形DEBF 为矩形,∴BF=DE=2.5,DF=EB ,设DF=3x ,则EB=3x ,∵53DF AF =,∴AF=5x ,AB=5x+2.5,∵3CE DE =,∴CE=7.5,∴CB=7.5+3x ,∵AB=CB ,∴5x+2.5=7.5+3x ,解得x=2.5,∴512.5AF x ==,故选:C .【点睛】本题考查矩形的性质和判定,等腰三角形的定义,一元一次方程的应用.能借助相关性质表示对应线段的长度是解题关键.本题主要用到方程思想.2.A解析:A根据勾股定理,可得正方形的边长,进而可得正方形的面积.【详解】∵正方形ABCD 中,对角线4AC =,∴AB 2+BC 2=AC 2,∴2AB 2=42,∴AB 2=8.故选:A .【点睛】本题主要考查的是正方形的性质,勾股定理,熟练掌握勾股定理是解题的关键. 3.C解析:C【分析】根据三角形中位线定理求出DE ,根据题意求出EF ,根据直角三角形的性质计算即可.【详解】解:∵D 、E 分别是AB 、AC 的中点,∴DE 是△ABC 的中位线,∴DE=12BC=6, ∵DE=3DF ,∴EF=4,∵∠AFC=90°,E 是AC 的中点,∴AC=2EF=8,故选:C .【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.4.A解析:A【分析】由三个直角的四边形是矩形,由此判断四边形PECF 是矩形,得到EC PF =,再结合正方形的性质,解得PD =,由此判断A ;过点P 作PN AB ⊥垂足为N ,过P 作//PM EF 交DC 于点M ,连接AM ,由角平分线的性质得到PN PE =,继而结合勾股定理证明AP EF =、证明四边形PEFM 是平行四边形,即可得到EF PM AP ==,设BE x =,结合勾股定理证明222PM A M P A +=,即可判断B ;根据等腰直角三角形的性质计算四边形PECF 的周长即可判断C ;设BE x =,由勾股定理解得EF 的长,再结合04x ≤≤,解得EF 与BD AB 、的数量关系即可判断D .解:A. ,PE BC PF CD ⊥⊥90PEC PFC ∴∠=∠=︒90C ∠=︒∴四边形PECF 是矩形EC PF ∴=正方形ABCD 中45PDF ∠=︒ 22PD PF EC ∴==故A 错误;B.过点P 作PN AB ⊥垂足为N ,过P 作//PM EF 交DC 于点M ,连接AM ,BD 平分ABC ∠,PN AB ⊥,PE BC ⊥PN PE ∴=222222,AP AN PN EF EC PE =+=+且,AN EC PN PE ==AP EF ∴=//,//PM EF PE CD∴四边形PEFM 是平行四边形EF PM AP ∴==设BE x =,则,42PE FC MF x DM x ====-,4EC PF x ==-22(4)AP EF PM x x ===+-222216(42)AD MD AM x +==+-222AP PM AM +=AP PM ∴⊥AP EF ∴⊥故B 正确;C.BPE 为等腰直角三角形PE BE ∴=4PE PF BE EC BC ∴+=+==故四边形PECF 的周长为2()8PE PF +=, 故C 正确;D.设BE x =EF ∴==04x ≤≤EF ∴≥12EF BD ∴≥ 4EF <EF AB ∴<12BD EF AB ∴≤< 故D 正确,故选:A .【点睛】本题考查四边形的综合题,涉及勾股定理、矩形的判定与性质、正方形的判定与性质、平行四边形的判定与性质等知识,是重要考点,难度一般,掌握相关知识是解题关键. 5.D解析:D【分析】由三角形三边关系可得三角形两边之和大于第三边,两边之差小于第三边.【详解】解:由于两条对角线的一半与平行四边形的一边组成一个三角形, 所以12(AC-BD )<5<12(AC+BD ), 由题中数据可得,AC 和BD 的长可取5和6,故选D .【点睛】本题考查了平行四边形对角线互相平分及三角形三边关系问题,能够熟练求解此类问题. 6.C解析:C【分析】根据平行四边形的判定方法对①②③④分别作出判断即可求解.【详解】解:①AB ∥CD ,AD ∥BC ,根据两组对边分别平行的四边形是平行四边形即可得到四边形是平行四边形;②AB CD =,AD BC =,根据两组对边分别相等的四边形是平行四边形即可得到四边形是平行四边形;;③AO CO =,BO DO =,根据对角线互相平分的四边形是平行四边形即可得到四边形是平行四边形;④AB ∥CD ,AD BC =,无法判定四边形是平行四边形.故选:C【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的定义和判定定理是解题关键. 7.C解析:C【分析】求得∠ADB=90°,即AD ⊥BD ,即可得到S ▱ABCD =AD•BD ;依据∠CDE=60°,∠BDE=30°,可得∠CDB=∠BDE ,进而得出DB 平分∠CDE ;依据Rt △AOD 中,AO >AD ,即可得到AO >DE ;依据O 是BD 中点,E 为AB 中点,可得BE=DE ,利用三角形全等即可得OE ⊥BD 且OB=OD .【详解】解:在ABCD 中,∵∠BAD=∠BCD=60°,∠ADC=120°,DE 平分∠ADC ,∴∠ADE=∠DAE=60°=∠AED ,∴△ADE 是等边三角形,12AD AE AB ∴==, ∴E 是AB 的中点,∴DE=BE ,1302BDE AED ︒∴∠=∠=, ∴∠ADB=90°,即AD ⊥BD ,∴S ▱ABCD =AD•BD ,故①正确;∵∠CDE=60°,∠BDE=30°,∴∠CDB=∠CDE-∠BDE=60°-30°=30°,∴∠CDB=∠BDE ,∴DB 平分∠CDE ,故②正确;∵Rt △AOD 中,AO >AD ,∵AD=DE ,∴AO >DE ,故③错误;∵O 是BD 的中点,∴DO=BO,∵E 是AB 的中点,∴BE=AE=DE∵OE =OE∴△DOE ≌△BOE(SSS)∴∠EOD=∠EOB∵∠EOD+∠EOB=180°∴∠BOE=90°∴OE 垂直平分BD ,故④正确;正确的有3个,故选择:C .【点睛】本题考查了平行四边形的性质,等边三角形的判定和性质,直角三角形的性质,平行四边形的面积公式的综合运用,三角形全等判定与性质,熟练掌握平行四边形的性质,等边三角形的性质,直角三角形的性质定理和等边三角形判定定理,三角形全等判定方法和性质是解题的关键.8.B解析:B【分析】根据已知条件和图形的变化可得前几个图形的最短边的长度,进而可得结论.【详解】解:在△A 1A 2A 3中,∠A 1A 3A 2=90°,∠A 2=30°,A 1A 3=1,A n+3是A n A n+1(n=1、2、3…)的中点,可知:A 4A 5//A 1A 3,A 3A 4=A 2A 4,∴∠A 3A 5A 4=90°,∠A 4A 3A 2=∠A 2=30°,∴△A 1A 2A 3是含30°角的直角三角形,同理可证△A n A n+1A n+2是含30°角的直角三角形.△A 1A 2A 3中最短边的长度为A 1A 3=1=012, △A 3A 4A 5中最短边的长度为A 4A 5=12=112, △A 5A 6A 7中最短边的长度为A 5A 7=21142=, …, 所以△A n A n+1A n+2中最短边的长度为1212n -,则△A 2019A 2020A 2021中最短边的长度为120211221122n --==101012. 故选:B .【点睛】 本题考查了规律型:图形的变化类,解决本题的关键是观察图形的变化寻找规律.也考查了直角三角形斜边的中线,三角形的中位线,平行线的性质,含30°角的直角三角形的性质,以及等腰三角形的性质等知识.9.C解析:C【分析】运用正方形边长相等,再根据同角的余角相等可得BAC DCE ∠=∠,然后证明ACB DCE ∆≅∆,再结合全等三角形的性质和勾股定理来求解即可.【详解】解:如图:由于a 、b 、c 都是正方形,所以AC CD =,90ACD ∠=︒;90ACB DCE ACB BAC ,即BAC ECD ∠=∠,在ABC ∆和CED ∆中,90ABC CED ACB CDEAC DC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ()ACB CDE AAS ,AB CE ∴=,BC DE =; 在Rt ABC ∆中,由勾股定理得:22222221310AC AB BC AB DE , 即10b S , 则b 的面积为10,故选:C .【点睛】本题主要考查对全等三角形和勾股定理的综合运用,证明ACB DCE ∆≅∆是解题的关键. 10.A解析:A【分析】先由勾股定理求出AB=5,再证四边形CEMF 是矩形,得EF=CM ,当CM ⊥AB 时,CM 最短,此时EF 也最小,则CP 最小,然后由三角形面积求出CM=2.4,即可得出答案.【详解】解:连接CM ,如图所示:∵∠ACB=90°,AC=3,BC=4,∴2222345AC BC ++=,∵ME ⊥AC ,MF ⊥BC ,∠ACB=90°,∴四边形CEMF 是矩形,∴EF=CM ,∵点P 是EF 的中点,∴CP=12EF , 当CM ⊥AB 时,CM 最短,此时EF 也最小,则CP 最小,∵△ABC 的面积=12AB×CM=12AC×BC , ∴CM=•AC BC AB =34 2.45⨯=, ∴CP=12EF=12CM=1.2, 故选:A .【点睛】本题考查了矩形的判定与性质、勾股定理、三角形面积以及最小值等知识;熟练掌握矩形的判定与性质是解题的关键.11.C解析:C【分析】如图,过E 作EM AD ⊥于M ,证明//,AD BC 90B ∠=︒,四边形ABEM 为矩形,再证明5AE AF ==,求解43ME AB AM BE ====,,可得:2MF =,再利用勾股定理可得答案.【详解】解:如图,过E 作EM AD ⊥于M ,矩形ABCD ,53AF BE ==,,//,AD BC ∴ 90B ∠=︒, 四边形ABEM 为矩形,,AFE CEF ∴∠=∠由对折可知:,AEF CEF ∠=∠∴∠=∠AFE AEF,∴==,AE AF5224∴=-=,AB AE BE四边形ABEM为矩形,,,43∴====ME AB AM BE∴=,MF222∴=+2 5.EF ME MF故选:.C【点睛】本题考查的是轴对称的性质,矩形的判定与性质,等腰三角形的判定,勾股定理的应用,掌握以上知识是解题的关键.12.C解析:C【分析】△与AOB的周长相差3,可分情况得根据平行四边形的性质可得BO=DO,再根据AOD出结果.【详解】解:∵四边形ABCD是平行四边形,∴BO=DO,AO=AO,△与AOB的周长相差3,∵AOD∴AB-AD=3,或AD-AB=3,∵AB=8,∴AD的长为5或11,故选C.【点睛】本题考查平行四边形的性质,解题的关键是掌握平行四边形对角线互相平分.二、填空题13.2【分析】延长BE交CF于G再根据全等三角形的判定得出△BCG与△ABE 全等得出AE=BG=4由BE=3得出EG=1同理得出GF=1再根据勾股定理得出EF的平方【详解】解:延长BE 交CF 于G 如图:∵解析:2【分析】延长BE 交CF 于G ,再根据全等三角形的判定得出△BCG 与△ABE 全等,得出AE=BG=4,由BE=3,得出EG=1,同理得出GF=1,再根据勾股定理得出EF 的平方.【详解】解:延长BE 交CF 于G ,如图:∵AB=5,AE=4,BE=3,222345+=,∴△ABE 是直角三角形,∴同理可得△DFC 是直角三角形,在Rt △ABE 和Rt △CDF 中,543AB CD AE CF BE DF ==⎧⎪==⎨⎪==⎩,∴Rt △ABE ≅Rt △CDF ,∴∠1=∠5,∵四边形ABCD 是正方形,∴∠ABC=∠BCD=90︒,∴∠4+∠5=90︒,∠4+∠3=90︒,∠1+∠2=90︒,∴∠3=∠5,∠4=∠2,在△CBG 和△BAE 中,3524AB BC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△CBG ≌△BAE (ASA ),∴AE=BG=4,CG=BE=3,∴EG=4-3=1,同理可得:GF=1,∴EF 2=EG 2+GF 2=2,故答案为:2.【点睛】本题考查了正方形的性质及全等三角形的判定与性质,关键是根据全等三角形的判定和性质得出EG=FG=1,再利用勾股定理计算.14.9cm12cm34cm36cm【分析】(1)根据平行四边形对角线互相平分对边相等可得结果;(2)根据△AOB的周长和AB的长度得到AO+BO从而得到AC+BD【详解】解:(1)在平行四边形ABCD中解析:9cm 12cm 34cm 36cm【分析】(1)根据平行四边形对角线互相平分,对边相等可得结果;(2)根据△AOB的周长和AB的长度,得到AO+BO,从而得到AC+BD.【详解】解:(1)在平行四边形ABCD中,∵AC=18cm,BD=24cm,∴AO=12AC=9cm=CO,BO=12BD=12cm=DO,∵AB=13cm,∴CD=13cm,∴COD△的周长为CO+DO+CD=9+12+13=34cm,故答案为:9cm,12cm,34cm;(2)∵△AOB的周长为30cm,∴AB+AO+BO=30cm,∵AB=12cm,∴AO+BO=30-12=18cm,∴AC+BD=2AO+2BO=36cm.【点睛】此题考查了平行四边形的性质:平行四边形的对角线互相平分,平行四边形的对边相等.15.13【分析】根据正方形的面积可用对角线进行计算解答即可【详解】解:连接ACBD交于点O∵四边形ABCD是菱形∴AC⊥BDAO=COBO=DO∵正方形AECF的面积为50cm2∴AC2=50∴AC=1解析:13【分析】根据正方形的面积可用对角线进行计算解答即可.【详解】解:连接AC,BD交于点O,∵四边形ABCD是菱形,∴AC ⊥BD ,AO=CO ,BO=DO ,∵正方形AECF 的面积为50cm 2, ∴12AC 2=50, ∴AC=10cm ,∴AO=CO=5cm ,∵菱形ABCD 的面积为120cm 2,∴12×AC×BD=120, ∴BD=24cm ,∴BO=DO=12cm ,∴22AB AO BO =+=25144+=13cm , 故答案为13. 【点睛】本题考查正方形的性质,菱形的性质,关键是根据正方形和菱形的面积进行解答. 16.5cm 或cm 或cm 【分析】利用勾股定理列式求出AB 然后分①点P 与点C 在AB 的两侧时AP 与BC 是对应边时四边形ACBP 是矩形然后利用勾股定理列式计算即可得解;AP 与AC 是对应边时根据对称性可知AB ⊥P解析:5cm 或245cm 或75cm . 【分析】利用勾股定理列式求出AB ,然后分①点P 与点C 在AB 的两侧时,AP 与BC 是对应边时,四边形ACBP 是矩形,然后利用勾股定理列式计算即可得解;AP 与AC 是对应边时,根据对称性可知AB ⊥PC ,再利用三角形的面积列式计算即可得解;②点P 与点C 在AB 的同侧时,利用勾股定理求出BD ,再根据PC=AB-2BD 计算即可得解.【详解】解:在Rt ABC 中,90C ∠=︒,4cm AC =,3cm BC =,由勾股定理得,2222435AB AC BC cm =+=+=,如图,①点P 与点C 在AB 的两侧时,若AP 与BC 是对应边,则四边形ACBP 1是矩形, ∴P 1C=AB=5cm ,若AP 与AC 是对应边,则△ABC 和△ABP 关于直线AB 对称,∴AB ⊥PC设AB 与P 2C 相交于点D ,则S △ABC =12×5•CD=12×3×4, 解得CD=125, ∴P 2C=2CD=2×125=245, ②点P 3与点C 在AB 的同侧时,由勾股定理得,22221293()55BD BC CD =-=-=, 过点P 3作P 3E ⊥AB ,垂足E ,连接P 3C ,如图,则有12×5•P 3E=12×3×4, ∴P 3E=125∴P 3E=CD 又P 3E ⊥AB ,CD ⊥AB ,∴P 3E//CD ,∴四边形P 3CDE 是平行四边形,又∠CDE=90°∴四边形P 3CDE 是矩形,∴P 3C=DE∵3P AB △≌ABC∴P 3A=BC ,∠P 3AB=∠CBA又∠P 3EA=∠CDB=90°∴△P 3AE ≌△CBD∴AE=BD∴P 3C=AB-2BD=5-2×95=75, 综上所述,PC 的长为5cm 或245cm 或75cm . 故答案为:5cm 或245cm 或75cm . 【点睛】 本题考查了全等三角形的对应边相等的性质,勾股定理,轴对称性,难点在于分情况讨论,作出图形更形象直观.17.3【分析】首先结合作图的过程确定BP是∠ABD的平分线然后根据角平分线的性质求得点P到BD的距离即可【详解】结合作图的过程知:BP平分∠ABD∵∠A=90°AP=3∴点P到BD的距离等于AP的长为3解析:3【分析】首先结合作图的过程确定BP是∠ABD的平分线,然后根据角平分线的性质求得点P到BD 的距离即可.【详解】结合作图的过程知:BP平分∠ABD,∵∠A=90°,AP=3,∴点P到BD的距离等于AP的长,为3,故答案为:3.【点睛】考查了尺规作图的知识及角平分线的性质、矩形的性质等知识,解题的关键是根据图形确定BP平分∠ABD.18.15【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB得出AF=AB=8同理可得DE=DC=8再由EF的长即可求出BC的长【详解】解:∵四边形ABCD是平行四边形∴AD∥BCDC=AB=8A解析:15【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB,得出AF=AB=8,同理可得DE=DC=8,再由EF的长,即可求出BC的长.【详解】解:∵四边形ABCD是平行四边形,∴AD∥BC,DC=AB=8,AD=BC,∴∠AFB=∠FBC,∵BF平分∠ABC,∴∠ABF=∠FBC,则∠ABF=∠AFB,∴AF=AB=8,同理可证:DE=DC=8,∵EF=AF+DE-AD=1,即8+8-AD=1,解得:AD=15;故答案为:15.【点睛】本题主要考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证出AF=AB 是解决问题的关键.19.【分析】延长CF 交EA 的延长线于点G 连接EF 过点F 作FH ⊥CE 于点H 过点E 作EM ⊥CF 于点M 由题意易得FH=FDFH=EMEC=EG 进而可得△CDF ≌△CME 然后可得CM=CD=由勾股定理可得BG= 解析:76【分析】延长CF ,交EA 的延长线于点G ,连接EF ,过点F 作FH ⊥CE 于点H ,过点E 作EM ⊥CF 于点M ,由题意易得FH=FD ,FH=EM ,EC=EG ,进而可得△CDF ≌△CME ,然后可得CM=CD=52,由勾股定理可得BG=3,设BE=x ,则有EC=EG=3+x ,最后利用勾股定理可求解.【详解】解:延长CF ,交EA 的延长线于点G ,连接EF ,过点F 作FH ⊥CE 于点H ,过点E 作EM ⊥CF 于点M ,如图所示:∵四边形ABCD 是矩形,4BC =,52AB =∴BC=AD ,52AB DC ==,AB ∥DC ,∠D=∠ABC=∠CBE=90° ∴∠DCF=∠G ,∵CF 平分∠ECD ,∴∠DCF=∠ECF ,DF=FH ,∴∠G=∠ECF ,∴EC=EG ,∴△ECG 是等腰三角形,∴CM=MG ,∵CE=CF ,∴△ECF 是等腰三角形, ∵EM 、FH 分别是等腰三角形ECF 腰上的高线,∴FH=EM=DF ,∴Rt △CDF ≌Rt △CME (HL ),∴52CM DC ==, ∴CG=5, ∴在Rt △CBG 中,3BG =,设BE=x ,则有EC=EG=3+x ,在Rt △CBE 中,222BC BE CE +=,∴()22243x x +=+, 解得:76x =, ∴76BE =; 故答案为76. 【点睛】本题主要考查等腰三角形的性质与判定、矩形的性质及勾股定理,熟练掌握等腰三角形的性质与判定、矩形的性质及勾股定理是解题的关键.20.【分析】根据平移的性质判断AD =CF =BE =4AD ∥CF 再根据平行四边形的面积和三角形面积公式解答即可【详解】如图连接CF 由平移的性质知AD =CF =BE =4AD ∥CF ∴四边形ACFD 为平行四边形∴=解析:28【分析】根据平移的性质,判断AD =CF =BE =4,AD ∥CF ,再根据平行四边形的面积和三角形面积公式解答即可.【详解】如图,连接CF .由平移的性质知,AD =CF =BE =4,AD ∥CF ,∴四边形ACFD 为平行四边形.∴ACFD S =AD •BC =4×8=32,∵FO =2,∴S △FOC =12OF •BE =1242⨯⨯=4, ∴AOFD S 四边形=ACFD FOC S S -=32-4=28.故答案为28.【点睛】本题考查图形的平移以及平行四边形的判定.根据题意得出AOFD S 四边形=ACFD FOC SS -是解答本题的关键. 三、解答题21.(1)AM CN =,理由见解析;(2)四边形MRNQ 为菱形,证明见解析;(3)MQN ∠=AOE ∠【分析】(1)结论:AM=CN .先证明(AAS)AOS COT ≌△△,推出AS CT =,OS OT =,34∠=∠,再证明(ASA)ESM GTN ≌△△即可解决问题.(2)过点Q 作QK ⊥EF ,QL ⊥CD ,垂足分别为点K ,L .首先证明四边形QMRN 是平行四边形,再证明QM=QN 即可.(3)结论:∠MQN=∠AOE .理由三角形的外角的性质以及平行线的性质即可解决问题.【详解】(1)关系:AM CN =理由:如图:设EG 分别与AB 、CD 相交于点S 、T ;∵四边形ABCD 与EFGH 都是矩形,且点O 为对角线的中点;∴//AB CD ,//EF GH ,OA OC =,OE OG =;∴12∠=∠;又AOS COT ∠=∠∴(AAS)AOS COT ≌△△ ∴AS CT =,OS OT =;∴ES GT =;又//EF GH ,∴56∠=∠;又12∠=∠;∴34∠=∠∴(ASA)ESM GTN ≌△△ ∴SM TN =,则AS SM CT TN +=+即AM CN =(2)四边形MRNQ 为菱形.证明:过点Q 作QK ⊥EF ,QL ⊥CD ,垂足分别为点K ,L .由题可知:矩形ABCD ≌矩形EFGH∴AD=EH ,AB ∥CD ,EF ∥HG∴四边形QMRN 为平行四边形,∵QK ⊥EF ,QL ⊥CD ,∴QK=EH ,QL=AD ,∠QKM=∠QLN=90°∴QK=QL ,又∵AB ∥CD ,EF ∥HG ,∴∠KMQ=∠MQN ,∠MQN=∠LNQ ,∴∠KMQ=∠LNQ ,∴△QKM ≌△QLN (AAS )∴MQ=NQ∴四边形MRNQ 为菱形.(3)结论:∠MQN=∠AOE .理由:如图中,∵∠QND=∠1+∠2,∠AOE=∠1+∠3,又由题意可知旋转前∠2与∠3重合,∴∠2=∠3,∴∠QND═∠AOE,∵AB∥CD,∴∠MQN=∠QND,∴∠MQN=∠AOE.【点睛】本题属于四边形综合题,考查了矩形的性质,菱形的判定和性质,全等三角形的判定和性质等知识,解题的关键是正确寻找确定的三角形解决问题,属于中考压轴题.22.(1)5;(2)6【分析】(1)证出AD=DP=2.5,BC=PC=2.5,得出DC=5=AB,即可求出答案;(2)根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB=90°,由勾股定理求出AP,从而求得△ABP的面积.【详解】解:(1)∵AP平分∠DAB,∴∠DAP=∠PAB,∵四边形ABCD是平行四边形,∵AB∥CD,∴∠PAB=∠DPA∴∠DAP=∠DPA∴△ADP是等腰三角形,∴AD=DP=2.5,同理:PC=CB=2.5,即AB=DC=DP+PC=5;(2)∵四边形ABCD是平行四边形,∴AD∥CB,AB∥CD,∴∠DAB+∠CBA=180°,又∵AP 和BP 分别平分∠DAB 和∠CBA ,∴∠PAB+∠PBA=12(∠DAB+∠CBA )=90°, 在△APB 中,∠APB=180°-(∠PAB+∠PBA )=90°;在Rt △APB 中,AB=5,BP=3,∴,∴△APB 的面积=4×3÷2=6.【点睛】本题考查了平行四边形的性质,平行线的性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.23.(1)50︒;(2)证明见解析;(3)52a 或3910a 【分析】(1)根据已知条件PA 平分BAD ∠且BP AP ⊥以及三角形内角和,即可求得ABP ∠的度数;(2)延长BP 交AD 的延长线于点G ,由已知条件即可证明ABP AGP ≌,即可得到BA GA =,BP GP =,进而即可证明BCP GDP △≌△,即可得到=BC GD ,通过相等关系,即可证明=+BA BC AD ;(3)根据题意可知,可以分两种情况进行讨论,分别为:①当//AB EF 时,延长BP 交AD 的延长线于点G ,可知此时四边形ABFE 是平行四边形,可以求得AB 的长度,由(2)中证明的ABP AGP ≌,BCP GDP △≌△,可得BA GA =,BP GP =,=CP DP ,=BC GD ,进而可以证明CFP ≌DEP ,可得CF DE =,进而通过线段的等量关系求得AE 的长;②如图3,过B 作BH AD ⊥交AD 于H ,过F 作FI AD ⊥交AD 于I ,同①可得PFC PED △≌△,则CF DE =,则可得5BF AE BC AD AB a +=+==,由ABP △和梯形ABCD 的面积关系可得BH 的长度,通过勾股定理即可得到AH 的长度,通过证明Rt BHA △≌Rt FIE △,可得75AH EI a ==,进而通过等量关系即可得到AE 的长.【详解】(1)∵PA 平分BAD ∠,BP AP ⊥, ∴11804022BAP DAP BAD ∠=∠=∠=⨯︒=︒,90APB ∠=︒, ∴在Rt ABP 中,180180409050ABP BAP APB ∠=︒-∠-∠=-︒-︒=︒; (2)如图1,延长BP 交AD 的延长线于点G ,∵BP AP ⊥,PA 平分BAD ∠,∴90APB APG ∠=∠=︒,BAP GAP ∠=∠,在ABP △和AGP 中,BAP GAP ∠=∠,AP AP =,APB APG ∠=∠,∴ABP AGP ≌,∴BA GA =,BP GP =, ∵//BC AD ,∴CBP DGP ∠=∠,在BCP 和GDP △中,CBP DGP ∠=∠,BP GP =,CPB DPG ∠=∠,∴BCP GDP △≌△,∴=BC GD ,∴BA GA AD GD AD BC ==+=+;(3)分两种情况讨论,①当//AB EF 时,如图2,延长BP 交AD 的延长线于点G ,∴由已知条件可知,此时四边形ABFE 是平行四边形,∴AE BF =,∵3BP a =,4AP a =,BP AP ⊥,∴在Rt ABP 中,222AB BP AP =+,解得,5AB a =,由(2)可知,ABP AGP ≌,∴5BA GA a ==,3BP GP a ==,由(2)可知,BCP GDP △≌△,∴=CP DP ,=BC GD ,∵//BC AD ,∴BFP GEP ∠=∠,在CFP 和DEP 中,CFP DEP ∠=∠,=CP DP ,CPF DPE ∠=∠,∴CFP ≌DEP ,∴CF DE =,∵=BC GD ,∴BC CF GD DE +=+,∴BF EG =,又∵四边形ABFE 是平行四边形,∴BF AE =,∴BF AE EG ==,∴25AG AE a ==, ∴52AE a =;图2②如图3,过B 作BH AD ⊥交AD 于H ,过F 作FI AD ⊥交AD 于I ,同①可得PFC PED △≌△,∴CF DE =,∴BF AE BF AD DE BF AD CF BC AD +=++=++=+,∴5BF AE BC AD AB a +=+==,在Rt ABP 中,2162ABP S BP AP a =⋅=△, 由(2)可知,梯形ABCD 的面积2212ABP S a ==△,梯形ABCD 的面积2122BC AD BH a +=⨯=, 解得,245BH a =, 在Rt ABH 中,2275AH AB BH a =-=, ∵//BC AD ,∴BH FI =,BF HI =,∵在Rt BHA △和Rt FIE △中,BH FI =,AB EF =,∴Rt BHA △≌Rt FIE △,∴75AH EI a ==, ∴2()BF AE BF AH EI HI BF AH +=+++=+,∴2()BF AE BF AH +=+,∴1110BF a =,∴3910AE AB BF a =-=.图3【点睛】本题考查了平行线的性质、角平分线的性质、勾股定理、全等三角形的证明和性质、三角形面积、梯形面积、线段的和差、三角形内角和等知识,解答本题的关键是正确的作出辅助线,证明三角形全等. 24.证明见解析.【分析】连接AC ,证ABE ACF ≌即可【详解】证明:连接AC ,∵四边形ABCD 是菱形,∴AB BC CD AD ===,AC 平分BCD ∠.∵60B ∠=︒,∴ABC 是等边三角形,∴AB AC =,60∠=∠=∠︒=B BCA ACF . ∴在ABE △与ACF 中,AB AC B ACF BE CF =⎧⎪∠=∠⎨⎪=⎩.∴ABE ACF ≌.∴AE AF =.【点睛】本题考查了菱形的性质,全等三角形的判定和性质,证明三角形全等是解此题的关键. 25.(1)见解析;(2)菱形,见解析【分析】(1)由DE ∥AC 交AB 于E ,DF ∥AB 交AC 于F ,可证得四边形AEDF 是平行四边形,即可证得结论;(2)由AD 平分∠BAC ,DE ∥AC ,易证得△ADE 是等腰三角形,又由四边形AEDF 是平行四边形,即可证得四边形AEDF 是菱形.【详解】(1)证明:∵DE ∥AC ,DF ∥ AB ,∴四边形AEDF 是平行四边形,∴DE=AF ;(2)若AD 平分∠BAC ,则四边形AEDF 是菱形;理由:∵AD 平分∠BAC ,∴∠EAD=∠FAD ,∵DE ∥AC ,∴∠ADE=∠FAD ,∴∠EAD=∠ADE ,∴AE=DE ,∵四边形AEDF 是平行四边形,∴四边形AEDF 是菱形.【点睛】此题考查了等腰三角形的判定与性质,菱形的判定与性质.注意熟练掌握菱形的判定方法是解此题的关键.26.见解析【分析】利用ASA 证明△ADE ≌△CDF 即可得到结论.【详解】 证明:四边形ABCD 是正方形,AD CD ∴=,90A DCF ADC ∠=∠=∠=︒,又90EDF ∠=︒,ADC EDC EDF EDC ∴∠-∠=∠-∠.ADE CDF .在ADE 与CDF 中,ADE CDF AD CDA DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ADE CDF ASA ∴△≌△.DE DF ∴=.【点睛】此题考查全等三角形的判定及性质,正方形的性质,熟记正方形的性质是解题的关键.。
(常考题)人教版初中数学八年级数学下册第三单元《平行四边形》检测(答案解析)(4)

一、选择题1.如图为某城市部分街道示意图,四边形ABCD 为正方形,点G 在对角线BD 上,GE CD ⊥,GF BC ⊥,1500m AD =,小敏行走的路线为B A G E →→→,小聪行走的路线为B A D E F →→→→.若小敏行走的路程为3100m ,则小聪行走的路程为( )A .3100mB .4600mC .5500mD .6100m 2.如图,点E 、F 分别在正方形ABCD 的边BC 、CD 上,45EAF ∠=︒,已知6AD =(正方形的四条边都相等,四个内角都是直角),2DF =.则AEF 的面积AEF S =( )A .6B .12C .15D .30 3.如图,将长方形纸片沿对角线折叠,重叠部分为BDE ,则图中全等三角形共有( )A .0对B .1对C .2对D .3对4.下列命题是真命题的是( )A .三角形的三条高线相交于三角形内一点B .一组对边平行,另一组对边相等的四边形是平行四边形C .对于所有自然数n ,237n n -+的值都是质数D .三角形一条边的两个顶点到这条边上的中线所在直线的距离相等5.已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A .当AB BC =时,四边形ABCD 是菱形B .当AC BD ⊥时,四边形ABCD 是菱形C .当90ABC ∠=时,四边形ABCD 是矩形D .当AC BD =时,四边形ABCD 是正方形6.已知点()0,0A ,()0,4B ,()3,4C t +,()3,D t .记()N t 为ABCD 内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则()N t 所有可能的值为( )A .6、7B .7、8C .6、7、8D .6、8、9 7.如图,在ABC 中,90A ∠=,D 是AB 的中点,过点D 作BC 的平行线,交AC 于点E ,作BC 的垂线交BC 于点F ,若AB CE =,且DFE △的面积为1,则BC 的长为( )A .25B .5C .45D .108.如图1,平行四边形纸片ABCD 的面积为120,20AD =.今沿两对角线将四边形ABCD 剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD 、CB 重合)形成一轴对称图形(戊),如图2所示,则图形戊的两对角线长度和为( )A .26B .29C .2243 D .12539.顺次连接矩形ABCD 各边的中点,所得四边形是( )A .平行四边形B .正方形C .矩形D .菱形10.如图,在直角三角形ABC 中,∠ACB =90°,AC =3,BC =4,点M 是边AB 上一点(不与点A ,B 重合),作ME ⊥AC 于点E ,MF ⊥BC 于点F ,若点P 是EF 的中点,则CP 的最小值是( )A .1.2B .1.5C .2.4D .2.511.如图,已知在正方形ABCD 中,E 是BC 上一点,将正方形的边CD 沿DE 折叠到DF ,延长EF 交AB 于点G ,连接DG .现有如下4个结论:①AG =GF ;②AG 与EC 一定不相等;③45GDE ∠=︒;④BGE △的周长是一个定值.其中正确的个数为( )A .1B .2C .3D .4 12.如图,将矩形ABCD 折叠,使点C 和点A 重合,折痕为EF .若5AF =,3BE =,则EF 的长为( )A .23B .17C .25D .35二、填空题13.在正方形ABCD 中,点E 在对角线BD 上,点P 在正方形的边上,若∠AEB=105°,AE=EP ,则∠AEP 的度数为_________.14.如图,EF 过ABCD 对角线的交点O ,交AD 于E ,交BC 于F ,若ABCD 的周长为19, 2.5OE =,则四边形EFCD 的周长为_____.15.如图,在ABC ∆中,点,D E 分别在边,AB AC 上,且BD CE =,连接,CD DE ,点,,M N P 分别是,,DE BC CD 的中点,34PMN ∠=,则MPN ∠的度数是_______.16.如图,在ABCD 中,AC 与BD 相交于点O ,(1)若18cm,24cm AC BD ==,则AO =_______,BO =_______.又若13AB =厘米,则COD △的周长为________.(2)若AOB 的周长为30cm ,12cm AB =,则对角线AC 与BD 的和是________. 17.已知:如图,把长方形纸片ABCD 沿EF 折叠,使D C 、分别落在D C ''、的位置,若65EFB ︒∠=,则AED '∠的度数为_________.18.如图,A B 、两点分别位于山脚的两端,小明想测量A B 、两点间的距离,于是想了个主意,先在地上取一个可以直接达到A B 、两点的点C ,找到AC BC 、的中点D 、E ,并且测出DE 的长为15m ,则A B 、两点间的距离为_________m .19.如图,矩形ABCD 全等于矩形BEFG ,点C 在BG 上,连接DF ,点H 为DF 的中点,若20AB =,12BC =,则CH 的长为__________.20.如图所示,在ABCD 中,AC 与BD 相交于点O ,若DAC EAC ∠=∠,4AE =,3AO =,则AEC S ∆的面积为____.三、解答题21.如图,过ABCD 对角线AC 与BD 的交点E 作两条互相垂直的直线,分别交边AB 、BC .CD 、DA 于点P 、M 、Q 、N .(1)求证:PBE QDE ≅△△;(2)顺次连接点P 、M 、Q 、N ,求证:四边形PMQN 是菱形.22.如图,四边形ABCD 中,//AD BC ,90A D ∠=∠=︒,点E 是AD 的中点,连接BE ,将ABE △沿BE 折叠后得到GBE ,且点G 在四边形ABCD 内部,延长BG 交DC 于点F ,连接EF .(1)求证:EGF EDF △△≌;(2)求证:BG CD =;(3)若点F 是CD 的中点,8BC =,求CD 的长.23.已知:如图,在梯形ABCD 中,AD ∥BC ,点E 、F 在边BC 上,DE ∥AB ,AF ∥CD ,且四边形AEFD 是平行四边形.(1)试判断线段AD 与BC 的长度之间有怎样的数量关系?并证明你的结论; (2)现有三个论断:①AD AB =;②=B C +∠∠90°;③=2B C ∠∠.请从上述三个论断中选择一个论断作为条件,证明四边形AEFD 是菱形.24.如图,将长方形ABCD 沿着对角线BD 折叠,使点C 落在C '处,BC '交AD 于点E .(1)试判断BDE 的形状,并说明理由.(2)若4AB =,8AD =,求AE 的长.参考答案25.如图1,正方形ABCD ,E 为平面内一点,且90BEC ∠=︒,把BCE 绕点B 逆时针旋转90︒得BAG ,直线AG 和直线CE 交于点F .(1)证明:四边形BEFG 是正方形;(2)若135AGD ∠=︒,猜测CE 和CF 的数量关系,并说明理由;(3)如图2,连接DF ,若13AB =,17CF =,求DF 的长.26.“半角型”问题探究:如图1,在四边形ABCD 中,AB =AD ,∠BAD =120°,∠B =∠ADC =90°,且∠EAF =60°,探究图中线段BE ,EF ,FD 之间的数量关系.(1)小明同学的方法是将△ABE 绕点A 逆时针旋转120°到△ADG 的位置,然后再证明△AFE ≌△AFG ,从而得出结论:(2)如图2,在四边形ABCD 中,AB =AD ,∠B+∠D =180°,E ,F 分别是边BC ,CD 上的点,且∠EAF =12∠BAD ,上述结论是否仍然成立,并说明理由. (3)如图3,边长为4的正方形ABCD 中,点E 、F 分别在AB 、CD 上,AE =CF =1,O 为EF 的中点,动点G 、H 分别在边AD 、BC 上,EF 与GH 的交点P 在O 、F 之间(与O 、F 不重合),且∠GPE =45°,设AG =m ,求m 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】连接CG ,由正方形的对称性,易知AG=CG ,由正方形的对角线互相平分一组对角,GE ⊥DC ,易得DE=GE .在矩形GECF 中,EF=CG .要计算小聪走的路程,只要得到小聪比小敏多走了多少就行.【详解】解:连接GC ,∵四边形ABCD 为正方形,所以AD=DC ,∠ADB=∠CDB=45°,∵∠CDB=45°,GE ⊥DC ,∴△DEG 是等腰直角三角形,∴DE=GE .在△AGD 和△GDC 中,AD CD ADG CDG DG DG ⎧⎪∠∠⎨⎪⎩===,∴△AGD ≌△GDC (SAS )∴AG=CG ,在矩形GECF 中,EF=CG ,∴EF=AG .∵BA+AD+DE+EF-BA-AG-GE ,=AD=1500m .∵小敏共走了3100m ,∴小聪行走的路程为3100+1500=4600(m ),故选:B .【点睛】本题考查了正方形的性质、全等三角形的性质和判定、矩形的性质及等腰三角形的性质.解决本题的关键是证明AG=EF ,DE=GE .2.C解析:C【分析】延长CD 到G ,使DG=BE ,连接AG ,易证ADG ABE △≌△所以AE=AG ,BAE=DAG ∠∠ , 证AFG AEG △≌△,所以 GF=EF ,设BE=DG=x ,则EF=FG=x+2,在ECF Rt △中,利用勾股定理得222462x x 解得求出x ,最后求AGF S △问题即可求解.【详解】 解:延长CD 到G ,使DG=BE ,连接AG ,在正方形ABCD 中,AB=AD ,90ADB B C ADC ∠=∠=∠=∠=︒90ADG B ∴∠=∠=︒,ADG ABE(SAS)∴△≌△,,AG AE BAE DAG ∴=∠=∠,45EAF ∠=︒ ,45DAF BAE ∴∠+∠=︒ ,GAF=45DAG DAF ∴∠∠+∠=︒,GAF=EAF ∴∠∠,又AF=AF ,AFG AEG ∴△≌△(SAS),EF=FG ∴,设BE=DG=x ,则EC=6-x ,FC=4,EF=FG=x+2,在ECF Rt △中,222=FC CE EF +,()()22246=2x x ∴+-+,解得,x=3, GF=DG DF=2+3=5∴+,AEF AGF 11S =S =GF AD=56=1522∴⨯⨯△△, 故选:C .【点睛】本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,正确构造辅助线,证三角形全等是解决本题的关键.3.C解析:C【分析】因为图形对折,所以首先△CDB≌△ABD,由于四边形是长方形,进而可得△ABE≌△CDE,如此答案可得.【详解】解:∵△BDC是将长方形纸片ABCD沿BD折叠得到的,∴CD=AB,AD=BC,∵BD=BD,∴△CDB≌△ABD(SSS),∴∠CBD=∠ADB∴EB=ED∴CE=AE又AB=CD∴△ABE≌△CDE,∴图中全等三角形共有2对故选:C【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要由易到难,循序渐进.4.D解析:D【分析】根据钝角三角形的高的交点在三角形外部可对A进行判断;根据平行四边形的判定对B进行判断;取n=6可对C进行判断;根据三角形全等的知识可对D进行判断.【详解】解:A、钝角三角形的三条高线相交于三角形外一点,所以A选项错误;B、一组对边平行,另一组对边也平行的四边形是平行四边形,所以B选项错误;C、当n=6时,n2-3n+7=25,25不是质数,所以C选项错误;D、通过证明三角形全等,可以证明三角形一条边的两个顶点到这条边上的中线所在直线的距离相等,所以D选项准确.故选:D.【点睛】本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题;错误的命题称为假命题.也考查了平行四边形的判定及全等三角形的判定和性质.5.D解析:D【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.【详解】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB BC=时,它是菱形,故本选项不符合题意;B、根据对角线互相垂直的平行四边形是菱形知:当AC BD⊥时,四边形ABCD是菱形,故本选项不符合题意;C、根据有一个角是直角的平行四边形是矩形知:当90ABC∠=时,四边形ABCD是矩形,故本选项不符合题意;D、根据对角线相等的平行四边形是矩形可知:当AC BD=时,它是矩形,不是正方形,故本选项符合题意;综上所述,符合题意是D选项;故选:D.【点睛】本题考查了对矩形的判定、菱形的判定,正方形的判定的应用,能正确运用判定定理进行判断是解此题的关键,难度适中.6.C解析:C【分析】分别求出t=1,t=1.5,t=2,t=0时的整数点,根据答案即可求出答案.【详解】解:当t=0时,A(0,0),B(0,4),C(3,4),D(3,0),此时整数点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),共6个点;当t=1时,A(0,0),B(0,4),C(3,5),D(3,1),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),共8个点;当t=1.5时,A(0,0),B(0,4),C(3,5.5),D(3,1.5),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),共7个点;当t=2时,A(0,0),B(0,4),C(3,6),D(3,2),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(2,5),共8个点;故选项A错误,选项B错误;选项D错误,选项C正确;故选:C.【点睛】本题考查了平行四边形的性质.主要考查学生的理解能力和归纳能力.7.A解析:A【分析】过A作AH⊥BC于H,根据已知条件得到AE=CE,求得DE=12BC,求得DF=12AH,根据三角形的面积公式得到DE•DF=2,得到AB•AC=8,求得AB=2(负值舍去),根据勾股定理即可得到结论.【详解】解:过A作AH⊥BC于H,∵D是AB的中点,∴AD=BD,∵DE∥BC,∴AE=CE,∴DE=1BC,2∵DF⊥BC,∴DF∥AH,DF⊥DE,∴BF=HF,∴DF=1AH,2∵△DFE的面积为1,∴1DE•DF=1,2∴DE•DF=2,∴BC•AH=2DE•2DF=4×2=8,∴AB•AC=8,∵AB=CE,∴AB=AE=CE=1AC,2∴AB•2AB=8,∴AB=2(负值舍去),∴AC=4,∴2222+=+=2425AB AC故选:A.【点睛】本题考查了三角形中位线定理,三角形的面积的计算,勾股定理,平行线的判定和性质,正确的识别图形是解题的关键.8.A解析:A【分析】由题意可得对角线EF⊥AD,且EF与平行四边形的高相等,进而利用面积与边的关系求出BC边的高即可.【详解】解:如图,连接AD、EF,则可得对角线EF⊥AD,且EF与平行四边形的高相等.∵平行四边形纸片ABCD的面积为120,AD=20,∴BC=AD=20,12EF×AD=12×120,∴EF=6,又AD=20,∴则图形戊中的四边形两对角线之和为20+6=26,故选:A.【点睛】本题考查了平行四边形的性质以及图形的对称问题,熟练掌握平行四边形的性质是解题的关键.9.D解析:D【分析】利用三角形中位线定理,矩形对角线的性质,菱形的判定判断即可.【详解】如图,设矩形ABCD各边的中点依次为E,F,G,H,∴EF,FG,GH,HE分别是△ABC,△BCD,△CDA,△DAB的中位线,∴EF=12AC,FG=12BD,GH=12AC,EH=12BD,∵四边形ABCD是矩形,∴AC=BD,∴EF=FG=GH=HE,∴四边形EFGH是菱形,故选D.【点睛】本题在矩形背景考查了三角形中位线定理,菱形的判定,矩形的性质,熟练运用三角形中位线定理,矩形的性质,菱形的判定是解题的关键.10.A解析:A【分析】先由勾股定理求出AB=5,再证四边形CEMF是矩形,得EF=CM,当CM⊥AB时,CM最短,此时EF也最小,则CP最小,然后由三角形面积求出CM=2.4,即可得出答案.【详解】解:连接CM,如图所示:∵∠ACB=90°,AC=3,BC=4,∴2222345AC BC++=,∵ME⊥AC,MF⊥BC,∠ACB=90°,∴四边形CEMF是矩形,∴EF=CM,∵点P是EF的中点,∴CP=12EF,当CM⊥AB时,CM最短,此时EF也最小,则CP最小,∵△ABC的面积=12AB×CM=12AC×BC,∴CM=•AC BCAB=342.45⨯=,∴CP=12EF=12CM=1.2,故选:A .【点睛】本题考查了矩形的判定与性质、勾股定理、三角形面积以及最小值等知识;熟练掌握矩形的判定与性质是解题的关键.11.C解析:C【分析】根据HL 证明△ADG ≌△FDG ,根据角的平分线的意义求∠GDE ,根据GE=GF+EF=EC+AG ,确定△BGE 的周长为AB+AC.【详解】根据折叠的意义,得△DEC ≌△DEF ,∴EF=EC ,DF=DC ,∠CDE=∠FDE ,∵DA=DF ,DG=DG ,∴Rt △ADG ≌Rt △FDG ,∴AG=FG ,∠ADG=∠FDG ,∴∠GDE=∠FDG+∠FDE =12(∠ADF+∠CDF ) =45°,∵△BGE 的周长=BG+BE+GE ,GE=GF+EF=EC+AG ,∴△BGE 的周长=BG+BE+ EC+AG=AB+AC ,是定值,∴正确的结论有①③④,故选C.【点睛】本题考查了正方形中的折叠变化,直角三角形的全等及其性质,角的平分线,三角形的周长,熟练掌握折叠的全等性是解题的关键.12.C解析:C【分析】如图,过E 作EM AD ⊥于M ,证明//,AD BC 90B ∠=︒,四边形ABEM 为矩形,再证明5AE AF ==,求解43ME AB AM BE ====,,可得:2MF =,再利用勾股定理可得答案.【详解】解:如图,过E 作EM AD ⊥于M ,矩形ABCD ,53AF BE ==,,//,AD BC ∴ 90B ∠=︒, 四边形ABEM 为矩形,,AFE CEF ∴∠=∠由对折可知:,AEF CEF ∠=∠,AFE AEF ∴∠=∠5AE AF ∴==,224AB AE BE ∴=-=,四边形ABEM 为矩形,43ME AB AM BE ∴====,, 2MF ∴=,22+2 5.EF ME MF ∴=故选:.C【点睛】本题考查的是轴对称的性质,矩形的判定与性质,等腰三角形的判定,勾股定理的应用,掌握以上知识是解题的关键.二、填空题13.60°或90°或150°【分析】首先根据题意作出正方形以及∠AEB 再以E 为圆心EA 为半径作圆与正方形的交点即为满足条件的P 点分类讨论即可【详解】如图所示在正方形ABCD 中∠AEB=105°∵点P 在正解析:60°或90°或150°【分析】首先根据题意作出正方形以及∠AEB ,再以E 为圆心,EA 为半径作圆,与正方形的交点即为满足条件的P 点,分类讨论即可.【详解】如图所示,在正方形ABCD 中,∠AEB=105°,∵点P 在正方形的边上,且AE=EP ,∴可以E 为圆心,EA 为半径作圆,与正方形的交点即为满足条件的P 点,①当P 在AD 上时,如图,AE=EP 1,∵∠EBA=45°,∴∠EAB=180°-45°-105°=30°,∠EAP 1=60°,△EAP 1为等边三角形,∴此时∠AEP 1=60°;②当P 在CD 上时,如图,AE=EP 2,AE=EP 3,由①可知∠DEP1=180°-105°-60°=15°,∴此时∠DEP1=∠DEP2=15°,∠CEP2=∠AEP1=60°,∴此时∠AEP2=60°+15°+15°=90°;∠AEP3=2∠AED=2×(180°-105°)=150°,故答案为:60°或90°或150°.【点睛】本题考查正方形的性质以及等腰三角形的判定,熟练运用尺规作图的方式进行等腰三角形的确定是解题关键.14.145【分析】根据平行四边形的性质易证三角形全等进而易得AE=CF故四边形的周长=AD+CD+EF根据已知求解即可【详解】解:在平行四边形ABCD中AD∥BCAC与BD互相平分∴AO=OC∠DAC=解析:14.5【分析】根据平行四边形的性质易证三角形全等,进而易得AE=CF,故四边形EFCD的周长=AD+CD+EF,根据已知求解即可.【详解】解:在平行四边形ABCD中,AD∥BC,AC与BD互相平分∴AO=OC,∠DAC=∠ACB,∠AOE=∠COF∴△AOE≌△COF∴AE=CF,OF=OE=2.5∴四边形EFCD的周长=CF+DE+CD+EF=AE+DE+CD+EF=AD+CD+EF=192.5 2×2=14.5.故答案为:14.5.【点睛】本题考查了平行四边形的性质以及三角形全等的证明,将所求线段转化为已知线段是解题的关键.15.【分析】根据点MNP分别是DEBCCD的中点可以证明MP是ΔDEC的中位线NP是ΔDBC的中位线根据中位线定理可得到MP=NP再根据等腰三角形的性质得到∠PMN=∠PNM最后根据三角形的内角和定理可解析:112【分析】根据点 M,N,P 分别是 DE,BC,CD 的中点,可以证明MP是ΔDEC的中位线,NP是ΔDBC的中位线,根据中位线定理可得到MP=NP,再根据等腰三角形的性质得到∠PMN=∠PNM,最后根据三角形的内角和定理可以得到∠MPN.【详解】解:如图∵点 M,N,P 分别是 DE,BC,CD 的中点∴MP是ΔDEC的中位线,∴MP=1EC,2NP是ΔDBC的中位线∴NP=1BD,2又∵BD=CE∴MP=NP∴∠PMN=∠PNM=34∘∴∠MPN=180∘-∠PMN-∠PNM=180∘-34∘-34∘=112∘故答案位:112°【点睛】本题考查了三角形的中位线定理,等腰三角形的性质和判定,以及三角形的内角和定理,解题的关键是灵活运用三角形的中位线定理求线段的长度.16.9cm12cm34cm36cm【分析】(1)根据平行四边形对角线互相平分对边相等可得结果;(2)根据△AOB的周长和AB的长度得到AO+BO从而得到AC+BD【详解】解:(1)在平行四边形ABCD中解析:9cm 12cm 34cm 36cm【分析】(1)根据平行四边形对角线互相平分,对边相等可得结果;(2)根据△AOB的周长和AB的长度,得到AO+BO,从而得到AC+BD.解:(1)在平行四边形ABCD 中,∵AC=18cm ,BD=24cm ,∴AO=12AC=9cm=CO ,BO=12BD=12cm=DO , ∵AB=13cm ,∴CD=13cm ,∴COD △的周长为CO+DO+CD=9+12+13=34cm ,故答案为:9cm ,12cm ,34cm ;(2)∵△AOB 的周长为30cm ,∴AB+AO+BO=30cm ,∵AB=12cm ,∴AO+BO=30-12=18cm ,∴AC+BD=2AO+2BO=36cm .【点睛】此题考查了平行四边形的性质:平行四边形的对角线互相平分,平行四边形的对边相等. 17.【分析】由长方形纸片可得再求解由折叠的性质求解结合平角的定义可得答案【详解】解:长方形纸片由折叠可得:故答案为:【点睛】本题考查的是矩形与折叠平行线的性质简单题解题的关键是理解折叠的性质解析:50︒【分析】由长方形纸片ABCD ,65EFB ∠=︒可得//,AD BC 再求解,DEF ∠ 由折叠的性质求解,D EF '∠ 结合平角的定义可得答案.【详解】 解: 长方形纸片ABCD ,65EFB ∠=︒,//,AD BC ∴65DEF EFB ∴∠=∠=︒,由折叠可得:65D EF DEF '∠=∠=︒,180180656550.AED D EF DEF ''∴∠=︒-∠-∠=︒-︒-︒=︒故答案为:50.︒【点睛】本题考查的是矩形与折叠,平行线的性质,简单题,解题的关键是理解折叠的性质. 18.30【分析】由DE 分别是边ACAB 的中点首先判定DE 是三角形的中位线然后根据三角形的中位线定理求得AB 的长即可【详解】解:∵DE 分别是ACBC 的中点∴DE 是△ABC 的中位线根据三角形的中位线定理得:解析:30【分析】由D ,E 分别是边AC ,AB 的中点,首先判定DE 是三角形的中位线,然后根据三角形的中位线定理求得AB 的长即可.解:∵D、E分别是AC、BC的中点,∴DE是△ABC的中位线,根据三角形的中位线定理,得:AB=2DE=30m.故答案为:30.【点睛】本题考查了三角形中位线定理的运用;熟记三角形中位线定理是解决问题的关键.19.【分析】连接并延长交于Q由矩形的性质得出由平行线的性质得出由证得得出则是等腰直角三角形得出由直角三角形斜边上的中线性质即可得出结果【详解】如图所示:连接并延长交于Q∵矩形全等于矩形∴∴∵点H为的中点解析:42【分析】连接GH并延长GH交CD于Q,由矩形的性质得出20AB CD BG===,12BC FG==,////,90FG AE CD GCQ∠=,由平行线的性质得出HFG HDQ∠=∠,由ASA证得HFG HDQ≌,得出12DQ FG==,HG HQ=,8CG BG BC=-=,8CQ CD DQ=-=,则GCQ是等腰直角三角形,得出282GQ CQ==,由直角三角形斜边上的中线性质即可得出结果.【详解】如图所示:连接GH并延长GH交CD于Q,∵矩形ABCD全等于矩形BEFG,∴20AB CD BG===,12BC FG==,////FG AE CD,90GCQ∠=,∴HFG HDQ∠=∠,∵点H为DF的中点,∴HF HD=,在HFG和HDQ中,HFG HDQHF HDGHF QHD∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()HFG HDQ ASA≌,∴12DQ FG==,HG HQ=,20128CG BG BC =-=-=,20128CQ CD DQ =-=-=,∴GCQ 是等腰直角三角形, ∴282GQ CQ ==, 在Rt GCQ 中,HG HQ =,∴11824222CH GQ ==⨯=, 故答案为:42.【点睛】本题考查了矩形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识;熟练掌握矩形的性质,通过作辅助线构建全等三角形是解题的关键.20.【分析】先证明△AEC 是等腰三角形再证OE ⊥AC 然后用勾股定理求出OE 即可求【详解】解:如图1连接OE ∵四边形ABCD 是平行四边形∴OA=OC=3AD ∥BC ∴∠DAC=∠ACB 又∵∴∠ACB=∠EA 解析:37【分析】先证明△AEC 是等腰三角形,再证OE ⊥AC ,然后用勾股定理求出OE ,即可求AEC S ∆.【详解】解:如图1,连接OE ,∵四边形ABCD 是平行四边形,∴OA=OC=3,AD ∥BC ,∴∠DAC=∠ACB ,又∵DAC EAC ∠=∠,∴∠ACB=∠EAC ,∴AE=EC=4,∴△AEC 是等腰三角形,∴OE ⊥AC ,在Rt △AOE 中,由勾股定理得,AO 2+OE 2=AE 2,∴32+OE 2=42,∴7∴167372AEC s =⨯= 故答案是:37本题综合考查了平行四边形的性质,等腰三角形的判定与性质和勾股定理等相关知识,证明△AEC 是等腰三角形是解本题的关键.三、解答题21.(1)见解析;(2)见解析.【分析】(1)由ASA 证PBE QDE ≅△△即可;(2)由全等三角形的性质得出EP EQ =,同理可得EM EN =,根据对角线互相平分的四边形是平行四边形得四边形PMQN 是平行四边形,再由对角线互相垂直的平行四边形是菱形,即可得出结论.【详解】(1)证明:四边形ABCD 是平行四边形,EB ED ∴=,//AB CD ,EBP EDQ ∴∠=∠,在PBE △和QDE △中,EBP EDQ EB ED BEP DEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩,()PBE QDE ASA ∴≅△△;(2)证明:如图所示:PBE QDE ≅△△,EP EQ ∴=,同理可得EM EN =,∴四边形PMQN 是平行四边形,PQ MN ⊥,∴四边形PMQN 是菱形.【点睛】本题考查了平行四边形的判定与性质,菱形的判定,全等三角形的判定与性质;熟练掌握菱形的判定和平行四边形的判定与性质,证明三角形全等是解题的关键.22.(1)见解析;(2)见解析;(3)2(1)根据HL 证明Rt △EGF ≌Rt △EOF 即可;(2)证明四边形ABCD 为矩形,可得BG=CD ;(3)设CD=x ,分别表示出BE 2,EF 2,BF 2,证明∠BEF=90°,利用勾股定理得到方程,解之即可.【详解】解:(1)∵E 是AD 中点,∴AE=DE ,由折叠可知:AE=EG ,∠EGB=∠EGF=∠D=∠A=90°,∴EG=ED ,又EF=EF ,∴Rt △EGF ≌Rt △EOF (HL );(2)△ABE 折叠得到△GBE ,∴AB=BG ,∵AD ∥BC ,∠A=∠D=90°,∴∠ABC=90°,∠C=90°,∴四边形ABCD 为矩形,∴AB=DC ,∴BG=CD ;(3)∵点E 是AD 中点,AD=BC=8,∴AE=DE=4,∵点F 是CD 中点,∴设CD=x ,则DF=12x , 则BE 2=BG 2+EG 2,即BE 2=CD 2+AE 2,即BE 2=x 2+42,且EF 2=DE 2+DF 2,即EF 2=42+(12x )2, 且BF 2=BC 2+CF 2,即BF 2=82+(12x )2, ∵∠AEB=∠GEB ,∠DEF=∠GEF ,∴∠BEF=∠GEB+∠GEF=90°,∴BF 2=BE 2+EF 2,∴82+(12x )2= x 2+42+42+(12x )2,解得:x=,即CD=【点睛】本题考查了矩形的判定和性质,勾股定理,折叠的性质,全等三角形的判定和性质,熟记性质,找出三角形全等的条件,合理利用勾股定理得到方程是解题的关键.23.(1)3BC AD ,见解析;(2)见解析【分析】(1)先证明四边形ABED 是平行四边形,得到AD BE =,同理得到AD FC =,根据四边形AEFD 是平行四边形,得到AD EF =,从而得到AD BE EF FC ===,进而得到3BC AD =;(2)选择论断②作为条件.根据DE ∥AB ,得到B DEC ∠=∠,从而证明90DEC C ∠+∠=,得到90EDC ∠=,根据EF FC =,得到DF EF =,从而证明平行四边形AEFD 是菱形.【详解】解:(1)线段AD 与BC 的长度之间的数量为:3BC AD =.证明:∵AD ∥BC ,DE ∥AB ,∴四边形ABED 是平行四边形.∴AD BE =.同理可证,四边形AFCD 是平行四边形.∴AD FC =.又∵四边形AEFD 是平行四边形,∴AD EF =.∴AD BE EF FC ===.∴3BC AD =.(2)选择论断②作为条件.证明:∵DE ∥AB ,∴B DEC ∠=∠.∵90B C ∠+∠=,∴90DEC C ∠+∠=.即得90EDC ∠=.又∵EF FC =,∴DF EF =.∵四边形AEFD 是平行四边形,∴平行四边形AEFD 是菱形.【点睛】本题考查平行四边形的判定与性质,菱形的判定,直角三角形斜边上的中线等于斜边的一半等知识,熟知相关定理并根据题意灵活应用是解题关键.24.(1)BDE 是等腰三角形,证明见解析;(2)3AE =.【分析】(1)根据折叠的性质可知EBD DBC ∠=∠,又因为//AD BC ,可知ADB DBC ∠=∠,即推出ADB EBD ∠=∠,所以BE DE =,BDE 为等腰三角形.(2)设AE x =,则8BE DE x ==-,在Rt ABE △中根据勾股定理列出等式,解出x 即可.【详解】(1)BDE 是等腰三角形,理由是:由折叠得:EBD DBC ∠=∠,∵四边形ABCD 是矩形,∴//AD BC ,∴ADB DBC ∠=∠,∴ADB EBD ∠=∠,∴BE DE =,∴BDE 是等腰三角形.(2)设AE x =,则8BE DE x ==-,∵四边形ABCD 是矩形,∴90A ∠=︒,∴在Rt ABE △中,222AB AE BE +=,即2224(8)x x +=-,解得:3x =,∴3AE =.【点睛】本题考查翻折的性质,矩形的性质,等腰三角形的判定以及勾股定理.根据翻折的性质间接证明出BE DE =是解答本题的关键.25.(1)见解析;(2)CE=CF ,理由见解析;(3)【分析】(1)根据正方形的判定定理进行证明即可;(2)证明Rt ADH ≌Rt BAG 得DH AG =,AH=BG ,再证明△DHG 是等腰直角三角形,可得DH=BH=AG ,最后由BEFG 是正方形可得结论;(3)分点F 在AB 右侧和左侧两种情况求解即可.【详解】解:(1)证明:90BEC =︒∠,把BCE 绕点B 逆时针旋转90︒得BAG , BE BG ∴=,90EBG ∠=︒,90BGA ∠=︒,则90BGF ∠=︒,90BEC EBG BGF ∴∠=∠=∠=︒,∴四边形BEFG 是正方形;(2)CE CF =,理由如下:过D 点作DH AF ⊥,垂足为H ,如图,四边形ABCD 是正方形,90BAD ∴∠=︒,AB AD =,90BGA ∠=︒,90DAH BAG ∴∠+∠=︒,90BAG ABG ∠+∠=︒,DAH ABG ∴∠=∠,在Rt ADH 和Rt BAG 中,90,DAH ABG BGA AHD AD AB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩Rt ADH ∴≌()Rt BAG AAS ,DH AG ∴=,∵∠DGH =180°-∠AGD =45°∴在Rt △DHG 中,∠GDH =45°∴DH =GH =AG ∴1122AG GH AH BG === 又AG CE =,EF BG =,2EF CE ∴=,CE CF ∴=;(3)①点F 在AB 右侧时,如图,过D 作DK ⊥AG ,交其延长线于K .设正方形BEFG 的边长为x ,则BE x =,17CE x =-,在Rt BEC △中,13BC =,根据勾股定理可得,222BE CE BC +=,即222(17)13x x +-=,解得112x =,25(x =不符合条件,舍去),即12BG BE ==,17125AG CE ==-=,∵四边形BEFG 是正方形,∴∠BAD =90°.∵DK ⊥AG ,∴∠K =90°.∵∠BAG +∠KAD =180°—∠BAD =90°∠ADK +∠KAD =90°∴∠BAG =∠ADK在Rt △ABG 和Rt △DAK 中,90G K AB ADBAG ADK ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩所以Rt △ADK ≌Rt BAG ,则AK =BG =12,DK =AG =5,∵AF +FK =AK =BG=GF=AG +AF∴FK =AG =5在R t △DFK 中,根据勾股定理可得,DF 2252DK FK +=②点F 在AB 左侧时,如图,过D 作DK ⊥AG ,交其延长线于K .方法同①,可得FK =AG =12,在R t △DFK 中,根据勾股定理可得,DF 22122DK FK +=综上所述,DF 的长为522【点睛】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,正方形的性质,勾股定理,熟练掌握相关性质和定理是解本题的关键.26.(1)见详解;(2)见详解;(3)4833m <≤ 【分析】(1)根据旋转变换及三角形全等即可得解;(2)延长FD 到点G ,使DG=BE ,连接AG ,通过,ABE ADG △≌△AEF AGF ≌即可得解;(3)根据题意分两种情况∶P 与O 重合,H 与C 重合,通过构造全等三角形,求得MN=NQ ,再设BM=a ,则CM=4-a ,MN=QN=a+2,根据222MN CM CN =+,得出222(2)(4)2a a +=-+,进而得到a=43,求得AG 的长为于43;根据BM=43,可得48'433AG CM ==-=,进而分析计算即可得出m 的取值范围 . 【详解】解∶(1)结论∶ EF=BE+FD .理由如下 ∶由旋转及题意知,F ,D ,G 三点共线,BE=DG ,AE=AG ,∠BAE=∠DAG ,∠EAF=12∠BAD, ∴∠GAF=∠DAF+∠DAG=∠DAF+∠BAE=∠BAD-∠EAF=∠EAF ,∴∠EAF=∠GAF ,在△AEF 和△AGF 中, AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩, ∴AEF AGF ≌∴.EF=FG , 又∵FG=DG+DF=BE+DF ,∴EF=BE+DF.(2)结论EF=BE+DF 仍然成立.理由如下 ∶延长FD 到点G ,使DG=BE ,连接AG ,如图所示∶∵∠B+∠ADC =180°,180ADF ADG ∠+∠=︒ ,∴B ADG ∠=∠,在△ABE 和△ADG 中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,,ABE ADG ∴△≌△∴AE=AG ,∠BAE=∠DAG ,12EAF BAD ∠=∠ GAF DAF DAG FAD BAE BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠ , ∴∠EAF=∠GAF ,在△AEF 和△AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩, ∴,AEF AGF △≌△∴.EF=FG.又 ∴FG=DG+DF=BE+DF ,∴EF=BE+DF .(3)①假设P 与O 重合, 如图,∵O 为EF 的中点,∴O 为正方形ABCD 的对称中心,过A 作AN //EF 交CD 于N ,则NF=AE=1, ∴DN=CN=2,过O 作''//G H GH 交AD 于'G ,交BC 于'H ,''AG CH ∴=,''DG BH = ,过A 作//''AM G H 交BC 于M ,∴''AG MH = ,'45G OE ∠=︒ ,∴∠MAN=45°,延长CD 到Q ,使DQ=BM ,由AB=AD ,∠B=∠ADQ ,BM=DQ ,可得△ABM ≌△ADQ ,∴AM=AQ,∠BAM=∠DAQ∵∠MAN=45°,∠BAD=90°,∴∠BAM+∠DAN=45°=∠DAQ+∠DAN=∠QAN,∴∠MAN= ∠QAN由AM=AQ ,∠MAN=∠QAN ,AN=AN ,可得△MAN ≌△QAN ,∴MN=NQ设BM=a ,则CM=4-a ,MN=QN=a+2,∵222MN CM CN =+,()()222242a a ∴+=-+ ,解得∶a=43, ∴ BM=43, CM=83又∵'''AG CH MH ==,814'323AG ∴=⨯=, ②当H 与C 重合时,如图由①知BM=4348''433AG CM ==-=∴,∴m 的取值范围为∶4833m <≤ . 【点睛】 本题考查了全等三角形的判定和性质,旋转变换以及正方形的性质,熟练掌握相关各个性质并作辅助线构造出全等三角形是解题的关键.。
八年级数学下册《平行四边形的判定》单元测试卷(附带答案)

八年级数学下册《平行四边形的判定》单元测试卷(附带答案)一.选择题1.四边形ABCD中,AD∥BC.要判别四边形ABCD是平行四边形,还需满足条件()A.∠A+∠C=180°B.∠B+∠A=180°C.∠A=∠D D.∠B=∠D2.四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是()A.AB∥DC,AD∥BC B.AB=DC,AD=BCC.AO=CO,BO=DO D.AB=DC,AD∥BC3.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是()A.∠ABC=∠ADC,AD∥BC B.∠ABD=∠BDC,∠BAD=∠DCBC.∠ABD=∠BDC,OA=OC D.∠ABC=∠ADC,AB=CD4.下列说法不正确的是()A.两组对边分别平行的四边形是平行四边形B.一组对边平行,另一组对边相等的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形D.一组对边平行,一组对角相等的四边形是平行四边形5.如图,在▱ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于()A.2B.3C.4D.66.如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为()A.66°B.104°C.114°D.124°7.已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB =CD;④∠BAD=∠DCB;⑤AD∥BC,从以上5个条件中任选2个条件为一组,能判定四边形ABCD 是平行四边形的有()组.A.4B.5C.6D.78.如图,在平行四边形ABCD中,E,F是对角线BD上不同的两点,连接AE,CE,AF,CF.下列条件中,不能得出四边形AECF一定是平行四边形的为()A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF9.如图,在▱ABCD中,点E,F分别在边BC,AD上,有下列条件:①BE=DF;②AE∥CF;③AE=CF;④∠BAE=∠DCF.其中,能使四边形AECF是平行四边形的条件有()A.1个B.2个C.3个D.4个10.如图,在▱ABCD中,∠ABC=45°,BC=4,点F是CD上一个动点,以F A、FB为邻边作另一个▱AEBF,当F点由D点向C点运动时,下列说法正确的选项是()①▱AEBF的面积先由小变大,再由大变小②▱AEBF的面积始终不变③线段EF最小值为4A.①B.②C.①③D.②③二.填空题11.如图,BD是▱ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是.12.如图,在▱ABCD中,AB=2cm,AD=4cm,AC⊥BC,则△DBC比△ABC的周长长cm.13.如图,在四边形ABCD中,若AB=CD,则添加一个条件,能得到平行四边形ABCD.(不添加辅助线,任意添加一个符合题意的条件即可)14.在平面直角坐标系中,A(﹣1,1),B(2,3),C(3m,4m+1),D在x轴上,若以A,B,C,D四点为顶点的四边形是平行四边形,求点D的坐标.15.如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发秒后其中一个新四边形为平行四边形.16.如图,在平面直角坐标系中,有一Rt△ABC,∠C=90°且A(﹣1,3)、B(﹣3,﹣1)、C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.若点Q在x轴上,点P在直线AB上,要使以Q、P、A1、C1为顶点的四边形是平行四边形,满足条件的点Q的坐标为.17.在平面直角坐标系里,A(1,0),B(0,2),C(﹣4,2),若以A、B、C、D为顶点的四边形是平行四边形,则点D的坐标为.18.如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为.三.解答题19.如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,BE=CF.(1)求证:△ABC≌△DEF;(2)连接AD,求证:四边形ACFD是平行四边形.20.E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.(1)根据题意,画出图形;(2)求证:①△AFD≌△CEB;②四边形ABCD是平行四边形.21.已知,如图所示,AB∥CD,AB=CD,点E、F在BD上.∠BAE=∠DCF,连接AF、EC,求证:(1)AE=FC;(2)四边形AECF是平行四边形.22.如图,四边形ABCD中AC、BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠E=∠F,AD=BC.(1)求证:O是线段AC的中点:(2)连接AF、EC,证明四边形AFCE是平行四边形.23.如图,AB=CD,E,F分别为AB、CD上的点,连接BC,分别与AF、ED相交于点G,H.∠B=∠C,BH=CG.(1)求证:AG=DH;(2)求证:四边形AFDE是平行四边形.24.已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.参考答案一.选择题1.解:∵AD∥BC∴∠A+∠B=180°,∠D+∠C=180°∴A.∠A+∠C=180°,可得∠B=∠C,这样的四边形是等腰梯形,不是平行四边形,故此选项错误;B.∠A+∠B从题目已知条件即可得出,无法证明四边形为平行四边形,此选项错误;C.同理A,这样的四边形是等腰梯形,故此选项错误;D.∠B=∠D,可得∠A+∠D=180°,则BA∥CD,故四边形ABCD是平行四边形,此选项正确;故选:D.2.解:∵AB∥DC,AD∥BC∴四边形ABCD是平行四边形,故选项A不合题意;∵AB=CD,AD=BC∴四边形ABCD是平行四边形,故选项B不合题意;∵AO=CO,BO=DO∴四边形ABCD是平行四边形,故选项C不合题意;∵AB=CD,AD∥BC∴四边形ABCD不一定是平行四边形,故选项D符合题意;故选:D.3.解:A、∵AD∥BC∴∠ABC+∠BAD=180°∵∠ABC=∠ADC∴∠ADC+∠BAD=180°∴AB∥CD∴四边形ABCD是平行四边形,故此选项不合题意;B、∵∠ABD=∠BDC,∠BAD=∠DCB∴∠ADB=∠CBD∴AD∥CB∵∠ABD=∠BDC∴AB∥CD∴四边形ABCD是平行四边形,故此选项不合题意;C、∵∠ABD=∠BDC,OA=OC又∠AOB=∠COD∴△AOB≌△COD(AAS)∴四边形ABCD是平行四边形,故此选项不合题意;D、∠ABC=∠ADC,AB=CD不能判断四边形ABCD是平行四边形,故此选项符合题意;故选:D.4.解:A、∵两组对边分别平行的四边形是平行四边形∴选项A不符合题意;B、∵一组对边平行,另一组对边相等的四边形不一定是平行四边形∴选项B符合题意;C、∵一组对边平行且相等的四边形是平行四边形∴选项C不符合题意;D、∵一组对边平行,一组对角相等的四边形是平行四边形∴选项D不符合题意;故选:B.5.解:∵四边形ABCD是平行四边形∴AB∥CD,AD=BC=8,CD=AB=6∴∠F=∠DCF∵CF平分∠BCD∴∠FCB=∠DCF∴∠F=∠FCB∴BF=BC=8同理:DE=CD=6∴AF=BF﹣AB=2,AE=AD﹣DE=2∴AE+AF=4;故选:C.6.解:∵四边形ABCD是平行四边形∴AB∥CD∴∠ACD=∠BAC由折叠的性质得:∠BAC=∠B′AC∴∠BAC=∠ACD=∠B′AC=∠1=22°∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°;7.解:①与⑤根据两组对边分别平行的四边形是平行四边形,能推出四边形ABCD为平行四边形;①与③根据一组对边平行且相等的四边形是平行四边形,能推出四边形ABCD为平行四边形;①与④,⑤与④根据两组对角分别相等的四边形是平行四边形,能推出四边形ABCD为平行四边形;①与②,②与⑤根据对角线互相平分的四边形是平行四边形,能推出四边形ABCD为平行四边形.所以能推出四边形ABCD为平行四边形的有6组.故选:C.8.解:如图,连接AC与BD相交于O在▱ABCD中,OA=OC,OB=OD要使四边形AECF为平行四边形,只需证明得到OE=OF即可;A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;B、若AE=CF,则无法判断OE=OE,故本选项符合题意;C、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;D、由∠BAE=∠DCF,从而推出△DFC≌△BEA,然后得出∠DFC=∠BEA,∴∠CFE=∠AEF,∴FC∥AE,由全等可知FC=AE,所以四边形AECF是平行四边形;故本选项不符合题意;故选:B.9.解:①正确,理由如下:∵四边形ABCD平行四边形∴AD=BC,AD∥BC又∵BE=DF∴AF=EC.又∵AF∥EC∴四边形AECF是平行四边形.②正确,理由如下:∵AF∥EC,AE∥CF∴四边形AECF是平行四边形;④正确;理由如下:∵四边形ABCD是平行四边形∴∠B=∠D∵∠BAE=∠DCF∴∠AEB=∠CFD.∵AD∥BC∴∠AEB=∠EAD.∴∠CFD=∠EAD.∴AE∥CF.∵AF∥CE∴四边形AECF是平行四边形.∵AE=CF不能得出四边形AECF是平行四边形∴③不正确;能使四边形AECF是平行四边形的条件有3个.故选:C.10.解:过点C作CG⊥AB于点G则∵AB与CG的值始终不变化∴△ABF的面积始终不变化∵▱AEBF的面积=2×△ABF的面积∴▱AEBF的面积始终不变∴①错误,②正确;连接EF,与AB交于点H∵四边形AEBF是平行四边形∴AH=BH,EH=FH当FH⊥AB时,FH的值最小,EF=2FH的值也最小此时,FH=CG∵∠ABC=45°,CG⊥AB∴BG=CG∵BG2+CG2=BC2=16∴∴FH=∴线段EF最小值为EF=2FH=4.∴③正确故选:D.二.填空题(共8小题)11.解:如图,连接AC交BD于点O∵四边形ABCD为平行四边形∴AO=CO,BO=DO∴当BE=DF时,可得OE=OF,则四边形AECF为平行四边形∴可增加BE=DF故答案为:BE=DF(答案不唯一).12.解:在▱ABCD中,∵AB=CD=2cm,AD=BC=4cm,AO=CO,BO=DO ∵AC⊥BC∴AC==6cm∴OC=3cm∴BO==5cm∴BD=10cm∴△DBC的周长﹣△ABC的周长=BC+CD+BD﹣(AB+BC+AC)=BD﹣AC=10﹣6=4cm 故答案为:4.13.解:根据平行四边形的判定,可再添加一个条件:AD=BC.故答案为:AD=BC(答案不唯一).14.解:由点C的坐标可以判断出点C在直线y=上已知A、B两点,所以以AB为边和对角线分类讨论当AB为边时,AB∥CD,AB=CD,如图可证得△ABE≌△CDF∴FC=BE=2,AE=DF=3若点D在x轴正半轴时∴点C坐标为(,﹣2)∴点D坐标为(,0)若点D在x轴负半轴时点C坐标为(,2)点D坐标为(﹣,0)当AB为对角线时AB与CD相交于AB的中点(,2)设点D(m,0)可得点C坐标为(1﹣m,4)将点C坐标代入解析式可得m=点D坐标为(,0)故点D的坐标为(,0)或(,0)或(﹣,0).15.解:根据题意有AP=tcm,CQ=2tcm,PD=(12﹣t)cm,BQ=(15﹣2t)cm.①∵AD∥BC∴当AP=BQ时,四边形APQB是平行四边形.∴t=15﹣2t解得t=5.∴t=5s时四边形APQB是平行四边形;②AP=tcm,CQ=2tcm∵AD=12cm,BC=15cm∴PD=AD﹣AP=(12﹣t)cm∵AD∥BC∴当PD=QC时,四边形PDCQ是平行四边形.即:12﹣t=2t解得t=4s∴当t=4s时,四边形PDCQ是平行四边形.综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.故答案是:4或5.16.解:∵点Q在x轴上,点P在直线AB上,以Q、P、A1、C1为顶点的四边形是平行四边形当A1C1为平行四边形的边时∴PQ=A1C1=2∵P点在直线y=2x+5上∴令y=2时,2x+5=2,解得x=﹣1.5令y=﹣2时,2x+5=﹣2,解得x=﹣3.5∴点Q的坐标为(﹣1.5,0),(﹣3.5,0)当A1C1为平行四边形的对角线时∵A1C1的中点坐标为(3,2)∴P的纵坐标为4代入y=2x+5得,4=2x+5解得x=﹣0.5∴P(﹣0.5,4)∵A1C1的中点坐标为:(3,2)∴直线PQ的解析式为:y=﹣x+当y=0时,即0=﹣x+解得:x=6.5故Q为(﹣1.5,0)或(﹣3.5,0)或(6.5,0).故答案为(﹣1.5,0)或(﹣3.5,0)或(6.5,0).17.解:如图有三种情况:①平行四边形AD1CB∵A(1,0),B(0,2),C(﹣4,2)∴AD1=BC=4,OD1=3则D的坐标是(﹣3,0);②平行四边形AD2BC∵A(1,0),B(0,2),C(﹣4,2)∴AD2=BC=4,OD2=1+4=5则D的坐标是(5,0);③平行四边形ACD3B∵A(1,0),B(0,2),C(﹣4,2)∴D3的纵坐标是2+2=4,横坐标是﹣(4+1)=﹣5则D的坐标是(﹣5,4)故答案为:(﹣3,0)或(5,0)或(﹣5,4).18.解:如图,①当BC为对角线时,易求M1(3,2);②当AC为对角线时,CM∥AB,且CM=AB.所以M2(﹣3,2);③当AB为对角线时,AC∥BM,且AC=BM.则|M y|=OC=2,|M x|=OB+OA=5,所以M3(5,﹣2).综上所述,符合条件的点D的坐标是M1(3,2),M2(﹣3,2),M3(5,﹣2).故答案为:(3,2)(﹣3,2)(5,﹣2).三.解答题19.证明:(1)∵AB∥DE∴∠B=∠DEF∵BE=CF∴BE+CE=CF+CE即BC=EF在△ABC和△DEF中∴△ABC≌△DEF(SAS);(2)由(1)得:△ABC≌△DEF∴AC=DF,∠ACB=∠F∴AC∥DF∴四边形ACFD是平行四边形.20.(1)解:如图,即为所画的图形;(2)证明:①如图,∵AD∥BC,DF∥BE∴∠DAF=∠BCE,∠DF A=∠BEC又AE=CF∴AE+EF=CF+EF即AF=CE在△AFD与△CEB中∴△AFD≌△CEB(ASA);②由①知,△AFD≌△CEB则AD=CB又∵AD∥BC∴四边形ABCD是平行四边形.21.证明:(1)∵AB∥CD∴∠B=∠D.在△ABE和△CDF中∴△ABE≌△CDF(ASA).∴AE=CF.(2)由(1)△ABE≌△CDF得AE=CF,∠AEB=∠CFD ∴180°﹣∠AEB=180°﹣∠CFD即∠AEF=∠CFE.∴AE∥CF.∵AE=CF∴四边形AECF是平行四边形.22.证明:(1)∵∠E=∠F∴AD∥BC∵AD=BC∴四边形ABCD是平行四边形∴AC,BD互相平分;即O是线段AC的中点.(2)∵AD∥BC∴∠EAC=∠FCA在△OAE和△OCF中∴△OAE≌△OCF(ASA).∴OE=OF又∵OA=OC∴四边形AFCE是平行四边形.23.证明:(1)∵BH=CG∴BH+HG=CG+HG∴BG=CH在△ABG与△CDH中∴△ABG≌△CDH(SAS)∴AG=DH;(2)∵△ABG≌△CDH∴∠AGB=∠CHD∴AF∥DE∵∠B=∠C∴AB∥CD∴四边形AFDE是平行四边形.24.证明:(1)四边形ABCD是平行四边形∴∠DAB=∠BCD∴∠EAM=∠FCN又∵AD∥BC∴∠E=∠F.∵在△AEM与△CFN中∴△AEM≌△CFN(ASA);(2)∵四边形ABCD是平行四边形∴AB=CD,AB∥CD又由(1)得AM=CN∴BM=DN,BM∥DN∴四边形BMDN是平行四边形.。
(常考题)人教版初中数学八年级数学下册第三单元《平行四边形》测试(含答案解析)

一、选择题1.如图,在等腰直角ABC 中,AB BC =,点D 是ABC 内部一点, DE BC ⊥,DF AB ⊥,垂足分别为E ,F ,若3CE DE =, 53DF AF =, 2.5DE =,则AF =( )A .8B .10C .12.5D .15 2.已知正方形ABCD 中,对角线4AC =,这个正方形的面积是( ) A .8B .16C .82D .162 3.如图,将长方形纸片沿对角线折叠,重叠部分为BDE ,则图中全等三角形共有( )A .0对B .1对C .2对D .3对4.如图,在平行四边形ABCD 中,90B ∠<︒,BC AB >.作AE BC ⊥于点E ,AF CD ⊥于点F ,记EAF ∠的度数为α,AE a =,AF b =.则以下选项错误的是( )A .::a b CD BC =B .D ∠的度数为αC .若60α=︒,则四边形AECF 的面积为平行四边形ABCD 面积的一半D .若60α=︒,则平行四边形ABCD )433a b + 5.已知四边形ABCD 中,90A B C ∠=∠=∠=,如果添加一个条件,即可判定该四边形是正方形,那么所添加的这个条件可以是( )A .90D ∠=;B .AB CD =;C .AD BC =; D .BC CD =. 6.如图,在四边形ABCD 中,对角线AC 、BD 相交于点O ,下列条件不能判定四边形ABCD 为平行四边形的是( )A .AB ∥CD ,AD ∥BCB .AD ∥BC ,AB =CD C .OA =OC ,OB =OD D .AB =CD ,AD =BC7.如图,点D 和点E 分别是BC 和BA 的中点,已知AC =4,则DE 为( )A .1B .2C .4D .88.如图1,平行四边形纸片ABCD 的面积为120,20AD =.今沿两对角线将四边形ABCD 剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD 、CB 重合)形成一轴对称图形(戊),如图2所示,则图形戊的两对角线长度和为( )A .26B .29C .2243D .1253 9.在菱形ABCD 中,∠ABC=60゜,AC=4,则BD=( )A 3B .3C .3D .310.如图,在直角三角形ABC 中,∠ACB =90°,AC =3,BC =4,点M 是边AB 上一点(不与点A ,B 重合),作ME ⊥AC 于点E ,MF ⊥BC 于点F ,若点P 是EF 的中点,则CP 的最小值是( )A .1.2B .1.5C .2.4D .2.511.如图,在矩形ABCD 中,3AB =,4=AD ,ABC ∠的平分线BE 交AD 于点E .点F ,G 分别是BC ,BE 的中点,则FG 的长为( )A .2B .52C .102D .32212.如图,矩形纸片ABCD 中,4AB =,3AD =,折叠纸片使AD 边与对角线BD 重合,则折痕为DG 的长为( )A .3B .423C .2D .352二、填空题13.如图,在平行四边形ABCD 中,2AD CD =,F 是AD 的中点,CE AB ⊥,垂足E 在线段AB 上.下列结论①DCF ECF ∠=∠;②EF CF =;③3DFE AEF ∠=∠;④2BEC CEF S S <中,一定成立的是_________.(请填序号)14.如图,在边长为8厘米的正方形ABCD 中,动点P 在线段AB 上以2厘米/秒的速度由A 点向B 点运动,同时动点Q 在线段BC 上以1厘米/秒的速度由C 点向B 点运动,当点P 到达点B 时整个运动过程立即停止.设运动时间为1秒,当AQ DP ⊥时,t 的值为______.15.己知菱形ABCD 的边长是3,点E 在直线AD 上,DE =1,联结BE 与对角线AC 相交于点M ,则AM MC的值是______. 16.如图,在平行四边形ABCD 中,BE 平分ABC ∠,CF BE ⊥,连接AE ,G 是AB 的中点,连接GF ,若4AE =,则GF =_____.17.如图,在平行四边形ABCD 中,过点C 的直线CE ⊥AB ,垂足为E ,若∠BAD =127°,则∠BCE =____.18.在△ABC 中, AD 是BC 边上的高线,CE 是AB 边上的中线,CD =AE ,且CE <AC .若AD =6,AB =10,则CE =___________19.如图,B ,E ,F ,D 四点在一条直线上,菱形ABCD 的面积为2120cm ,正方形AECF 的面积为250cm ,则菱形的边长为___cm .20.如图,矩形ABCD 中,2AB =,4=AD ,点E 是边AD 上的一个动点;把BAE △沿BE 折叠,点A 落在A '处,如果A '恰在矩形的对称轴上,则AE 的长为______.三、解答题21.如图,BD 为ABC 的角平分线,E 为AB 上一点,BE BC =,连结DE . (1)求证:BDC BDE ≅△△;(2)若7AB =,2CD =,90︒∠=C ,求ABD △的面积.22.如图,在菱形ABCD 中,过点D 分别作DE ⊥AB 于点E ,作DF ⊥BC 于点F .求证:AE =CF .23.如图,在正方形ABCD 中,点P 是对角线AC 上的一点,点E 在BA 的延长线上,且PB PE =,连结DE .(1)求证:PD PE =.(2)试判断DE 和BP 的数量关系,并说明理由.24.下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.已知:四边形ABCD 是平行四边形,且,AB BC <求作:菱形ABEF ,使点E 在BC 上,点F 在AD 上.作法:①作BAD ∠的角平分线,交BC 于点E ;②以A 为圆心,AB 长为半径作弧,交AD 于点F ;③连接EF .则四边形ABEF 为所求作的菱形.根据小明设计的尺规作图过程(1)使用直尺和圆规,补全图形(保留作图痕迹);(2)求证四边形ABEF 为菱形.25.如图,在▱ABCD 中,AB =12cm ,BC =6cm ,∠A =60°,点P 沿AB 边从点A 开始以2cm/秒的速度向点B 移动,同时点Q 沿DA 边从点D 开始以1cm/秒的速度向点A 移动,用t 表示移动的时间(0≤t ≤6).(1)当t 为何值时,△PAQ 是等边三角形?(2)当t 为何值时,△PAQ 为直角三角形?26.如图,在正方形中ABCD ,E 是AB 上一点,F 是AD 延长线上一点,且DF BE =.(1)求证:CE CF =;(2)若点G 在AD 上,且45GCE ︒∠=,判断线段GE BE GD 、、之间的数量关系,并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据比例关系设DF=x ,可判断四边形DEBF 为矩形,根据矩形的性质和比例关系分别表示CB 和AB ,再根据AB BC =,列出方程,求解即可得出x ,从而得出AF .【详解】,DE BC DF AB ⊥⊥,90DEB DFB ∴∠=∠=︒,∵△ABC 为等腰直角三角形,∴∠ABC=90°,∴四边形DEBF 为矩形,∴BF=DE=2.5,DF=EB ,设DF=3x ,则EB=3x ,∵53DF AF =,∴AF=5x ,AB=5x+2.5,∵3CE DE =,∴CE=7.5,∴CB=7.5+3x ,∵AB=CB ,∴5x+2.5=7.5+3x ,解得x=2.5,∴512.5AF x ==,故选:C .【点睛】本题考查矩形的性质和判定,等腰三角形的定义,一元一次方程的应用.能借助相关性质表示对应线段的长度是解题关键.本题主要用到方程思想.2.A解析:A【分析】根据勾股定理,可得正方形的边长,进而可得正方形的面积.【详解】∵正方形ABCD 中,对角线4AC =,∴AB 2+BC 2=AC 2,∴2AB 2=42,∴AB 2=8.故选:A .【点睛】本题主要考查的是正方形的性质,勾股定理,熟练掌握勾股定理是解题的关键. 3.C解析:C【分析】因为图形对折,所以首先△CDB ≌△ABD ,由于四边形是长方形,进而可得△ABE ≌△CDE ,如此答案可得.【详解】解:∵△BDC 是将长方形纸片ABCD 沿BD 折叠得到的,∴CD=AB ,AD=BC ,∵BD=BD ,∴△CDB ≌△ABD (SSS ),∴∠CBD=∠ADB∴EB=ED∴CE=AE又AB=CD∴△ABE ≌△CDE ,∴图中全等三角形共有2对故选:C【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、SSA 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要由易到难,循序渐进. 4.C解析:C【分析】由平行四边形的性质得出//AD BC ,AD BC =,AB CD =,B D ∠=∠,得出180D C ∠+∠=︒,求出180EAF C ∠+∠=︒,得出B D EAF α∠=∠=∠=;由平行四边形ABCD 的面积得出::a b CD BC =;若60α=︒,则60B D ∠=∠=︒,求出30BAE DAF ∠=∠=︒,由直角三角形的性质得出BE AE ==,DF ,得出2AB BE =,2AD DF ==,求出平行四边形ABCD 的周长2())AB AD a b =+=+;求出ABE ∆的面积212BE AE =⨯=,ADF ∆的面积2=,平行四边形ABCD 的面积BC AE a =⨯=⨯=,得出四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22)a b =+≠平行四边形ABCD 面积的一半;即可得出结论.解:四边形ABCD 是平行四边形,//AD BC ∴,AD BC =,AB CD =,B D ∠=∠,180D C ∴∠+∠=︒,AE BC ⊥于点E ,AF CD ⊥于点F ,360290180EAF C ∴∠+∠=︒-⨯︒=︒,B D EAF α∴∠=∠=∠=;平行四边形ABCD 的面积BC AE CD AF =⨯=⨯,AE a =,AF b =,BC a CD b ∴⨯=⨯,::a b CD BC ∴=;若60α=︒,则60B D ∠=∠=︒,30BAE DAF ∴∠=∠=︒,BE AE ∴==,DF =,2AB BE ∴==,2AD DF ==,∴平行四边形ABCD 的周长2())AB AD a b =+=+;ABE ∆的面积21122BE AE a =⨯=⨯=,ADF ∆的面积21122DF AF b =⨯=⨯,平行四边形ABCD 的面积BC AE a =⨯=⨯=, ∴四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22)a b =+≠平行四边形ABCD 面积的一半; 综上所述,选项A 、B 、D 不符合题意,选项C 符合题意;故选:C .【点睛】本题考查了平行四边形的性质、直角三角形的性质、三角形面积等知识;熟练掌握平行四边形的性质和直角三角形的性质是解题的关键.5.D解析:D【分析】由已知可得该四边形为矩形,再添加条件:一组邻边相等,即可判定为正方形.【详解】解:由∠A=∠B=∠C=90°可判定四边形ABCD 为矩形,因此再添加条件:一组邻边相等,即可判定四边形ABCD 为正方形,【点睛】本题考查正方形的判定.掌握相关判定定理正确推理论证是解题关键.6.B解析:B【分析】根据平行四边形的判定方法即可判断.【详解】A、根据两组对边分别平行的四边形是平行四边形,可以判定;B、无法判定,四边形可能是等腰梯形,也可能是平行四边形;C、根据对角线互相平分的四边形是平行四边形,可以判定;D、根据两组对边分别相等的四边形是平行四边形,可以判定;故选:B.【点睛】本题考查平行四边形的判定,解题的关键是掌握平行四边形的判定定理.7.B解析:B【分析】根据三角形中位线定理解答即可.【详解】解:∵点D和点E分别是BC和BA的中点,∴DE是△ABC的中位线,∴DE=12AC=124=2,故选:B.【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.8.A解析:A【分析】由题意可得对角线EF⊥AD,且EF与平行四边形的高相等,进而利用面积与边的关系求出BC边的高即可.【详解】解:如图,连接AD、EF,则可得对角线EF⊥AD,且EF与平行四边形的高相等.∵平行四边形纸片ABCD的面积为120,AD=20,∴BC=AD=20,12EF×AD=12×120,∴EF=6,又AD=20,∴则图形戊中的四边形两对角线之和为20+6=26,故选:A .【点睛】本题考查了平行四边形的性质以及图形的对称问题,熟练掌握平行四边形的性质是解题的关键.9.D解析:D【分析】根据菱形的性质可得到直角三角形,利用勾股定理计算即可;【详解】如图,AC 与BD 相较于点O ,∵四边形ABCD 是菱形,4AC =,∴AC BD ⊥,2AO =,又∵∠ABC=60゜,∴30ABO ∠=︒,∴24AB AO ==, ∴224223BO =-= ∴243BD BO ==;故选D .【点睛】本题主要考查了菱形的性质,结合勾股定理计算是解题的关键.10.A解析:A【分析】先由勾股定理求出AB=5,再证四边形CEMF 是矩形,得EF=CM ,当CM ⊥AB 时,CM 最短,此时EF 也最小,则CP 最小,然后由三角形面积求出CM=2.4,即可得出答案.【详解】解:连接CM,如图所示:∵∠ACB=90°,AC=3,BC=4,∴AB=2222345AC BC+=+=,∵ME⊥AC,MF⊥BC,∠ACB=90°,∴四边形CEMF是矩形,∴EF=CM,∵点P是EF的中点,∴CP=12EF,当CM⊥AB时,CM最短,此时EF也最小,则CP最小,∵△ABC的面积=12AB×CM=12AC×BC,∴CM=•AC BCAB=342.45⨯=,∴CP=12EF=12CM=1.2,故选:A.【点睛】本题考查了矩形的判定与性质、勾股定理、三角形面积以及最小值等知识;熟练掌握矩形的判定与性质是解题的关键.11.C解析:C【分析】连接CE,由矩形的性质和角平分线的性质可得AB=AE=3,可得ED=1,由勾股定理可求CE 的长,由三角形中位线定理可求FG的长;【详解】连接CE,如图所示:∵四边形ABCD是矩形,∴∠BAD=∠ABC=∠D=90°,AB=CD=3,AD=BC=4,AD∥BC,∴∠CBE=∠AEB,∵BE平分∠ABC.∴∠ABE=∠CBE=45°,∴∠ABE=∠AEB=45°,∴AB=AE=3,∴ED=AD-AE=4-3=1,在Rt△CDE中=∵点F、G分别为BC、BE的中点,∴FG是△CBE的中位线,FG=12故选:C【点睛】本题考查了矩形的性质,勾股定理,等腰直角三角形的判定与性质,三角形中位线的定理等知识;熟练掌握矩形的性质和三角形中位线定理,求出EC的长度是解题的关键. 12.D解析:D【分析】首先设AG=x,由矩形纸片ABCD中,AB=4,AD=3,可求得BD的长,又由折叠的性质,可求得A′B的长,然后由勾股定理可得方程:x2+22=(4-x)2,解此方程即可求得AG 的长,继而求得答案.【详解】解:设AG=x,∵四边形ABCD是矩形,∴∠A=90°,∵AB=4,AD=3,∴BD5,由折叠的性质可得:A′D=AD=3,A′G=AG=x,∠DA′G=∠A=90°,∴∠BA′G=90°,BG=AB-AG=4-x,A′B=BD-A′D=5-3=2,∵在Rt△A′BG中,A′G2+A′B2=BG2,∴x2+22=(4-x)2,解得:x=32,∴AG=32,∴在Rt △ADG 中,DG=. 故选:D .【点睛】 此题考查了折叠的性质、矩形的性质以及勾股定理.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想与方程思想的应用.二、填空题13.②③④【分析】如图延长EF 交CD 的延长线于H 作EN ∥BC 交CD 于NFK ∥AB 交BC 于K 利用平行四边形的性质全等三角形的判定和性质一一判断即可解决问题【详解】解:如图延长EF 交CD 的延长线于H 作EN ∥解析:②③④【分析】如图延长EF 交CD 的延长线于H .作EN ∥BC 交CD 于N ,FK ∥AB 交BC 于K .利用平行四边形的性质,全等三角形的判定和性质一一判断即可解决问题.【详解】解:如图,延长EF 交CD 的延长线于H .作EN ∥BC 交CD 于N ,FK ∥AB 交BC 于K . ∵四边形ABCD 是平行四边形,∴AB ∥CH ,∴∠A=∠FDH ,在△AFE 和△DFH 中,A FDH AFE HFD AF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AFE ≌△DFH ,∴EF=FH ,∵CE ⊥AB ,AB ∥CH ,∴CE ⊥CD ,∴∠ECH=90°,∴CF=EF=FH ,故②正确,∵DF=CD=AF ,∴∠DFC=∠DCF=∠FCB ,∵∠FCB >∠ECF ,∴∠DCF >∠ECF ,故①错误,∵FK ∥AB ,FD ∥CK ,∴四边形DFKC 是平行四边形,∵AD=2CD ,F 是AD 中点,∴DF=CD ,∴四边形DFKC是菱形,∴∠DFC=∠KFC,∵AE∥FK,∴∠AEF=∠EFK,∵FE=FC,FK⊥EC,∴∠EFK=∠KFC,∴∠DFE=3∠AEF,故③正确,∵四边形EBCN是平行四边形,∴S△BEC=S△ENC,∵S△EHC=2S△EFC,S△EHC>S△ENC,∴S△BEC<2S△CEF,故④正确,故正确的有②③④.故答案为②③④.【点睛】本题考查平行四边形的性质、全等三角形的判定和性质、直角三角形斜边的中线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.14.【分析】由ASA可证△ABQ≌△DAP可得AP=BQ列出方程可求t的值【详解】∵四边形ABCD是正方形∴AD=AB∠B=∠BAD=90°∵AQ⊥DP∴∠QAD+∠ADP=90°且∠DAQ+∠BAQ=解析:8 3【分析】由“ASA”可证△ABQ≌△DAP,可得AP=BQ,列出方程可求t的值.【详解】∵四边形ABCD是正方形∴AD=AB,∠B=∠BAD=90°∵AQ⊥DP∴∠QAD+∠ADP=90°,且∠DAQ+∠BAQ=90°,∴∠BAQ=∠ADP,且∠B=∠BAD=90°,AD=AB∴△ABQ≌△DAP(ASA)∴AP=BQ∴2t=8−t∴t =83, 故答案为:83. 【点睛】本题考查了全等三角形判定和性质,正方形的性质,一元一次方程的应用,证明△ABQ ≌△DAP 是本题的关键.15.或【分析】首先根据题意作图注意分为E 在线段AD 上与E 在AD 的延长线上然后由菱形的性质可得AD ∥BC 则可证得△MAE ∽△MCB 根据相似三角形的对应边成比例即可求得答案【详解】解:∵菱形ABCD 的边长是 解析:23或43【分析】 首先根据题意作图,注意分为E 在线段AD 上与E 在AD 的延长线上,然后由菱形的性质可得AD ∥BC ,则可证得△MAE ∽△MCB ,根据相似三角形的对应边成比例即可求得答案.【详解】解:∵菱形ABCD 的边长是3,∴AD=BC=3,AD ∥BC ,如图①:当E 在线段AD 上时,∴AE=AD -DE=3-1=2,∴△MAE ∽△MCB , ∴23MA AE MC BC ==; 如图②,当E 在AD 的延长线上时,∴AE=AD+DE=3+1=4,∴△MAE ∽△MCB , ∴43MA AE MC BC ==. ∴MA MC 的值是23或43. 故答案为23或43.【点睛】此题考查了菱形的性质,相似三角形的判定与性质等知识.解题的关键是注意此题分为E 在线段AD 上与E 在AD 的延长线上两种情况,小心不要漏解.16.2【分析】根据平行四边形的性质结合角平分线的定义可求解即可得利用等腰三角形的性质得到进而可得是的中位线根据三角形的中位线的性质可求解【详解】解:在平行四边形中∴∵平分∴∴∴∵∴∵是的中点∴是的中位线 解析:2【分析】根据平行四边形的性质结合角平分线的定义可求解CBE BEC ∠=∠,即可得CB CE =,利用等腰三角形的性质得到BF EF =,进而可得GF 是ABE △的中位线,根据三角形的中位线的性质可求解.【详解】解:在平行四边形ABCD 中,//AB CD ,∴ABE BEC ∠=∠,∵BE 平分ABC ∠,∴ABE CBE ∠=∠,∴CBE BEC ∠=∠,∴CB CE =,∵CF BE ⊥,∴BF EF =,∵G 是AB 的中点,∴GF 是ABE △的中位线, ∴12GF AE =∵4AE =,∴2GF =; 故答案为:2.【点睛】本题主要考查了平行四边形的性质,等腰三角形的性质与判定,三角形中位线的性质,证明GF 是ABE △的中位线是解题的关键.17.37°【分析】由平行四边形的性质得出∠B+∠BAD=180°可得∠B 的度数由直角三角形的两上锐角互余得出∠BCE=90°-∠B 即可【详解】解:∵四边形ABCD 是平行四边形∴AD ∥BC ∴∠B+∠BAD解析:37°【分析】由平行四边形的性质得出∠B+∠BAD=180°,可得∠B 的度数,由直角三角形的两上锐角互余得出∠BCE=90°-∠B 即可.【详解】解:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠B+∠BAD=180°,∵∠BAD=127°∴∠B=53°,∵CE ⊥AB ,∴∠E=90°,∴∠BCE=90°-∠B=90°-53°=37°,故答案为:37°.【点睛】本题考查了平行四边形的性质、直角三角形两锐角互余.熟练掌握平行四边形的性质,求出∠B 的度数是解决问题的关键.18.【分析】先根据勾股定理求得AB 再做△ABD 的中位线EF 可得EF=3BF=DF=4从而可得CF=1再次利用勾股定理即可求得CE 【详解】解:∵AD 是BC 边上的高线AD=6AB=10∴∠D=90°∵CE 是【分析】先根据勾股定理求得AB ,再做△ABD 的中位线EF ,可得EF=3,BF=DF=4,从而可得CF=1,再次利用勾股定理即可求得CE .【详解】解:∵AD 是BC 边上的高线,AD =6,AB =10,∴∠D=90°,BD 8==,∵CE 是AB 边上的中线,CD =AE , ∴152CD AE BE AB ====, 取BD 的中点F,连接CF ,∴EF 为△ABD 的中位线, ∴132EF AD ==,EF//AD , ∴∠EFB=∠D=90°, 在Rt △BEF 中,根据勾股定理,2222534BF BE EF =-=-=,∴DF=BD-BF=8-4=4,∴CF=CD-DF=5-4=1,在Rt △CEF 中,根据勾股定理,22221310CE CF EF =+=+=,故答案为:10.【点睛】本题考查三角形中位线的定理,勾股定理.能正确作出辅助线,构造直角三角形是解题关键.19.13【分析】根据正方形的面积可用对角线进行计算解答即可【详解】解:连接ACBD 交于点O ∵四边形ABCD 是菱形∴AC ⊥BDAO=COBO=DO ∵正方形AECF 的面积为50cm2∴AC2=50∴AC=1解析:13【分析】根据正方形的面积可用对角线进行计算解答即可.【详解】解:连接AC ,BD 交于点O ,∵四边形ABCD 是菱形,∴AC ⊥BD ,AO=CO ,BO=DO ,∵正方形AECF的面积为50cm2,∴12AC2=50,∴AC=10cm,∴AO=CO=5cm,∵菱形ABCD的面积为120cm2,∴12×AC×BD=120,∴BD=24cm,∴BO=DO=12cm,∴AB,故答案为13.【点睛】本题考查正方形的性质,菱形的性质,关键是根据正方形和菱形的面积进行解答.20.2或【分析】分两种情况:①过A′作MN∥CD交AD于M交BC于N则直线MN是矩形ABCD的对称轴得出AM=BN=AD=2由勾股定理得到A′N=0求得A′M=2再得到A′E即可;②过A′作PQ∥AD交解析:2【分析】分两种情况:①过A′作MN∥CD交AD于M,交BC于N,则直线MN是矩形ABCD 的对称轴,得出AM=BN=12AD=2,由勾股定理得到A′N=0,求得A′M=2,再得到A′E即可;②过A′作PQ∥AD交AB于P,交CD于Q;求出∠EBA′=30°,再利用勾股定理求出A′E,即可得出结果.【详解】解:分两种情况:①如图1,过A′作MN∥CD交AD于M,交BC于N,则直线MN是矩形ABCD 的对称轴,∴AM=BN=12AD=2,∵△ABE沿BE折叠得到△A′BE,∴A′E=AE,A′B=AB=2,∴,即A′与N重合,∴A′M=2= A′E,∴AE=2;②如图2,过A′作PQ ∥AD 交AB 于P ,交CD 于Q ,则直线PQ 是矩形ABCD 的对称轴,∴PQ ⊥AB ,AP=PB ,AD ∥PQ ∥BC ,∴A′B=2PB ,∴∠PA′B=30°,∴∠A′BC=30°,∴∠EBA′=30°,设A′E=x ,则BE=2x ,在△A′EB 中,()22222x x =+,解得:x=23, ∴AE=A′E=23;综上所述:AE 的长为223, 故答案为:2或33. 【点睛】 本题考查了翻折变换—折叠问题,矩形的性质,勾股定理;正确理解折叠的性质是解题的关键.三、解答题21.(1)证明见解析;(2)7【分析】(1)根据角平分线的性质可得DBC DBE ∠=∠,再根据已知条件BE BC =,BD BD =,即可证明;(2)根据(1)中结果,得2DE CD ==,90DEB C ∠=∠=︒,即可求得ABD △的面积.【详解】(1)∵BD 平分ABC ∠,∴DBC DBE ∠=∠,∴在BDC 和BDE 中,BD BD =,DBC DBE ∠=∠,BE BC =,∴BDC ≌BDE ;(2)∵BDC ≌BDE ,∴2DE CD ==,90DEB C ∠=∠=︒, ∴1172722ABD S AB DE =⋅=⨯⨯=△. 【点睛】本题考查了角平分线的性质、全等三角形的证明和性质、三角形面积等知识,解题的关键是熟练掌握运用以上知识点.22.见解析【分析】先由菱形的性质得到AD CD =,A C ∠=∠,再由AAS 证得ADE CDF ∆≅∆,即可得出结论.【详解】解:证明:∵四边形ABCD 是菱形, AD CD ∴=,A C ∠=∠,DE AB ∵⊥,DF BC ⊥,90AED CFD ∴∠=∠=︒,在ADE ∆和CDF ∆中,AED CFD A CAD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ADE CDF AAS ∴∆≅∆,AE CF ∴=.【点睛】本题考查了菱形的性质、全等三角形的判定与性质等知识;熟练掌握菱形的性质和全等三角形的判定与性质是解题的关键.23.(1)见解析;(2)DE =,见解析【分析】(1)根据SAS 证明APD APB ≌△△可得PD=PB ,再结合PD=PE 即可得出结论; (2)证明DPE 是等腰直角三角形即可得出结论.【详解】解:(1)证明:∵四边形ABCD 是正方形,∴AB AD =,∵AC 是正方形ABCD 的对角线,∴=45CAD CAB ∠=∠︒∵AP AP =,∴()APD APB SAS ≌, ∴PD PB =, ∵PB PE =,∴PD PE =. (2)2DE BP =.理由如下: ∵由(1)知,APD APB ≌△△,PD PB PE ==,∴设PEB PBE PDA x ∠=∠=∠=︒,∴1802EPB x ∠=︒-︒,∵45DAP ∠=︒,∴18045135DPA BPA x x ∠=∠=︒-︒-=︒-︒,∴1802(135)45APE EPB BPA x x x ∠=∠-∠=︒-︒-︒-︒=︒-︒,∴135(45)90DPE DPA APE x x ∠=∠-∠=︒-︒-︒-︒=︒.∴DPE 是等腰直角三角形,∴22DE DP BP ==. 【点睛】本题是四边形综合题目,考查了正方形的性质,全等三角形的判定与性质,熟记正方形的性质,证明三角形全等是解决问题的关键.24.(1)见解析;(2)见解析【分析】(1)根据要求画出图形即可.(2)利用平行四边形的判定,菱形的判定解决问题即可.【详解】解:解:()1如图所示.()2证明:AE ∵平分,BAD ∠13,∴∠=∠在ABCD 中,//,AD BC23,∴∠=∠12,∴∠=∠,AB BE ∴=,AF BE ∴=又//,AF BE∴四边形ABEF 为平行四边形.,AF AB = ∴四边形ABEF 为菱形.【点睛】本题考查作图-复杂作图,平行四边形的判定和性质,菱形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.25.(1)t =2;(2)t =3或65t =. 【分析】(1)根据等边三角形的性质,列出关于t 的方程,进而即可求解.(2)根据△PAQ 是直角三角形,分两类讨论,分别列出方程,进而即可求解.【详解】解:(1)由题意得:AP =2t (米),AQ =6-t (米).∵∠A =60°,∴当△PAQ 是等边三角形时,AQ =AP ,即2t =6-t ,解得:t =2,∴当t =2时,△PAQ 是等边三角形.(2)∵△PAQ 是直角三角形,∴当∠AQP =90°时,有∠APQ =30°,即AP =2AQ ,∴2t =2(6-t ),解得:t =3(秒),当∠APQ =90°时,有∠AQP =30°,即AQ =2AP ,∴6-t =2·2t ,解得65t =(秒), ∴当t =3或65t =时,△PAQ 是直角三角形. 【定睛】本题主要考查等边三角形的性质,直角三角形的定义以及平行四边形的定义,熟练掌握等边三角形的性质,直角三角形的定义,列出方程,是解题的关键.26.(1)见解析;(2)GE=BE+GD ,理由见解析【分析】(1)由DF=BE ,四边形ABCD 为正方形可证△CEB ≌△CFD ,从而证出CE=CF ;(2)由(1)得,CE=CF ,∠BCE+∠ECD=∠DCF+∠ECD 即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF ,故可证得△ECG ≌△FCG ,即EG=FG=GD+DF .又因为DF=BE ,所以可证出GE=BE+GD .【详解】解:(1)证明:∵四边形ABCD 是正方形,∴BC=CD ,∠B=∠CDA ,∴∠B=∠CDF ,在△CBE 与△CDF 中,B CDF BE DF ⎪∠∠⎨⎪⎩==,∴△CBE ≌△CDF (SAS ),∴CE=CF ;(2)GE=BE+GD ,理由:由(1)得△CBE ≌△CDF ,∴∠BCE=∠DCF ,CE=CF .∵∠GCE=45°,∴∠BCE+∠DCG=45°,∴∠GCF=∠DCF+∠DCG=45°,在△ECG 与△FCG 中,CE CF GCE GCF GC GC ⎧⎪∠∠⎨⎪⎩===,∴△ECG ≌△FCG (SAS ),∴GE=GF ,∴GE=DF+GD=BE+GD .【点睛】本题主要考查正方形的性质以及全等三角形的判定和性质,证两条线段相等往往转化为证明这两条线段所在三角形全等,在第二问中也考查了通过全等找出和GE 相等的线段,从而得出线段GE ,BE ,GD 之间的数量关系.。
(常考题)人教版初中数学八年级数学下册第三单元《平行四边形》测试(包含答案解析)

一、选择题1.如图为某城市部分街道示意图,四边形ABCD 为正方形,点G 在对角线BD 上,GE CD ⊥,GF BC ⊥,1500m AD =,小敏行走的路线为B A G E →→→,小聪行走的路线为B A D E F →→→→.若小敏行走的路程为3100m ,则小聪行走的路程为( )A .3100mB .4600mC .5500mD .6100m 2.如图,在ABC 中,D ,E 分别是,AB AC 的中点,12BC =,F 是DE 的上任意一点,连接,AF CF ,3DE DF =,若90AFC ∠=︒,则AC 的长度为( )A .4B .5C .8D .103.在平面直角坐标系中,长方形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点,若E 为x 轴上的一个动点,当△CDE 的周长最小时,求点E 的坐标( )A .(一3,0)B .(3,0)C .(0,0)D .(1,0) 4.下列条件中不能判定一定是平行四边形的有( )A .一组对角相等,一组邻角互补B .一组对边平行,另一组对边相等C .两组对边相等D .一组对边平行,且另一组对边也平行5.下列命题中,错误的是 ( )A .有一个角是直角的平行四边形是正方形;B .对角线相等的菱形是正方形;C .对角线互相垂直的矩形是正方形;D .一组邻边相等的矩形是正方形. 6.如果平行四边形ABCD 的对角线相交于点O ,那么在下列条件中,能判断平行四边形ABCD 为菱形的是( )A .OAB OBA ∠=∠;B .OAB OBC ∠=∠; C .OAB OCD ∠=∠; D .OAB OAD ∠=∠.7.如图,在ABC 中,90A ∠=,D 是AB 的中点,过点D 作BC 的平行线,交AC 于点E ,作BC 的垂线交BC 于点F ,若AB CE =,且DFE △的面积为1,则BC 的长为( )A .25B .5C .45D .108.菱形的一个内角是60︒,边长是3cm ,则这个菱形的较短的对角线长是( ) A .3cm 2 B .33cm 2 C .3cm D .33cm 9.如图,在矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB ,CD 交于点E 、F ,连接BF 交AC 于点M ,连接DE ,BO .若60COB ∠=︒,FO FC =.则下列结论:①FB 垂直平分OC ;②四边形DEBF 为菱形;③OC FB =;④2AM BM =;⑤:3:2BOM AOE S S =.其中正确结论的个数是( )A .5个B .4个C .3个D .2个10.如图,把一张长方形纸片沿对角线折叠,若△EDF 是等腰三角形,则∠BDC ( )A .45ºB .60ºC .67.5ºD .75º11.如图,已知在正方形ABCD 中,E 是BC 上一点,将正方形的边CD 沿DE 折叠到DF ,延长EF 交AB 于点G ,连接DG .现有如下4个结论:①AG =GF ;②AG 与EC 一定不相等;③45GDE ∠=︒;④BGE △的周长是一个定值.其中正确的个数为( )A .1B .2C .3D .412.如图,菱形ABCD 中,4AB =,60A ∠=︒,点E 是线段AB 上一点(不与A ,B 重合),作EDF ∠交BC 于点F ,且60EDF ∠=︒,则BEF 周长的最小值是( )A .6B .43C .43+D .423+二、填空题13.如图,在菱形ABCD 中,13cm AB =,24cm AC =,E ,F 分别是CD 和BC 的中点,连接EF 并延长与AB 的延长线相交于点G ,则EG 的长度为________cm .14.如图,四边形ABCD 是长方形,F 是DA 延长线上一点,CF 交AB 于点E ,G 是CF 上一点,且∠ACG =∠AGC ,∠GAF =∠F .若∠ECB =20°,则∠ACD 的度数是______________.15.如图,,E F 分别是ABCD 的边,AD BC 上的点.8,60,EF DEF =∠=︒将EFCD 四边形沿EF 翻折,得到四边形',EFCD ED '交BC 于点,G 则GEF △的周长为________.16.己知菱形ABCD 的边长是3,点E 在直线AD 上,DE =1,联结BE 与对角线AC 相交于点M ,则AM MC的值是______. 17.在平面直角坐标系xOy 中,OABC 的三个顶点的坐标分别为()()()0,0,3,0,4,3O A B ,则其第四个顶点C 的坐标为______.18.已知Rt ABC ,90C ∠=︒,4cm AC =,3cm BC =,若PAB △与ABC 全等,PC ________.19.如图,矩形ABCD 中,2AB =,4=AD ,点E 是边AD 上的一个动点;把BAE △沿BE 折叠,点A 落在A '处,如果A '恰在矩形的对称轴上,则AE 的长为______.20.如图,长方形ABCD 中,4=AD ,3AB =,点P 是AB 上一点,1AP =,点E 是BC 上一动点,连接PE ,将BPE 沿PE 折叠,使点B 落在B ',连接DB ',则PB DB ''+的最小值是________.三、解答题21.如图,在ABCD 中,对角线AC 与BD 相交于点O ,点M ,N 分别为OB ,OD 的中点,连接AM 并延长至点E ,使EM AM =,连接CE ,CN .(1)求证:ABM CDN ≌;(2)当AB 与AC 满足什么数量关系时,四边形MECN 是矩形?请说明理由;(3)连接AN ,EN .当ANE 满足什么条件时,四边形MECN 是正方形?请说明理由.22.综合与实践——探究正方形旋转中的数学问题问程情境:已知正方形ABCD 中,点O 是线段BC 的中点,将将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''(点A ',B ',C ',D 分别是点A ,B ,C ,D 的对应点).同学们通过小组合作,提出下列数学问题,请你解答.特例分析:(1)“乐思”小组提出问题:如图1,在正方形绕点O 旋转过程中,顺次连接点B ,B ',C ,C '得到四边形''BB CC ,求证:四边形''BB CC 是矩形;(2)“善学”小组提出问题:如图2.在旋转过程中,当点B '落在对角线BD 上时,设A B ''与CD 交于点M .求证:四边形OB MC '是正方形.深入探究:(3)“好问”小组提出问题:如图3.若点O 是线段BC 的三等分点且2OB OC =,在正方形ABCD 旋转的过程中当线段A D ''经过点D 时,请直接写出''DD OC 的值. 23.如图,在四边形ABCD 中,,E F 分别是,AD BC 的中点,,G H 分别是对角线,BD AC 的中点,依次连接,,,E G F H 连接,EF GH .(1)求证:四边形EGFH 是平行四边形;(2)当AB CD =时,EF 与GH 有怎样的位置关系?请说明理由;(3)若,20,70AB CD ABD BDC =∠=︒∠=︒,则GEF ∠= ︒.24.如图,四边形ABCD 的对角线AC 、BD 相交于点O ,∠ACB =∠ADB =90°,M 为边AB 的中点,连接MC ,MD .(1)求证:MC =MD :(2)若△MCD 是等边三角形,求∠AOB 的度数.25.如图,菱形EFGH 的三个顶点E 、G 、H 分别在正方形ABCD 的边AB 、CD 、DA 上,连接CF .(1)求证:∠HEA =∠CGF ;(2)当AH =DG 时,求证:菱形EFGH 为正方形.26.如图,已知四边形ABCD 是平行四边形,E 是AB 延长线上一点且BE AB =,连接CE ,BD .(1)求证:四边形BECD 是平行四边形(2)连接DE ,若4AB BD ==,22DE =,求BECD 的面积.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】连接CG ,由正方形的对称性,易知AG=CG ,由正方形的对角线互相平分一组对角,GE ⊥DC ,易得DE=GE .在矩形GECF 中,EF=CG .要计算小聪走的路程,只要得到小聪比小敏多走了多少就行.【详解】解:连接GC ,∵四边形ABCD 为正方形,所以AD=DC ,∠ADB=∠CDB=45°,∵∠CDB=45°,GE ⊥DC ,∴△DEG 是等腰直角三角形,∴DE=GE .在△AGD 和△GDC 中,AD CD ADG CDG DG DG ⎧⎪∠∠⎨⎪⎩===,∴△AGD ≌△GDC (SAS )∴AG=CG ,在矩形GECF 中,EF=CG ,∴EF=AG .∵BA+AD+DE+EF-BA-AG-GE ,=AD=1500m .∵小敏共走了3100m ,∴小聪行走的路程为3100+1500=4600(m ),故选:B .【点睛】本题考查了正方形的性质、全等三角形的性质和判定、矩形的性质及等腰三角形的性质.解决本题的关键是证明AG=EF ,DE=GE .2.C解析:C【分析】根据三角形中位线定理求出DE ,根据题意求出EF ,根据直角三角形的性质计算即可.【详解】解:∵D 、E 分别是AB 、AC 的中点,∴DE 是△ABC 的中位线,∴DE=12BC=6, ∵DE=3DF ,∴EF=4,∵∠AFC=90°,E 是AC 的中点,∴AC=2EF=8,故选:C .【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.3.D解析:D【分析】由于C 、D 是定点,则CD 是定值,如果△CDE 的周长最小,即DE +CE 有最小值.为此,作点D 关于x 轴的对称点D′,当点E 在线段CD′上时,△CDE 的周长最小.【详解】如图,作点D 关于x 轴的对称点D′,连接CD′与x 轴交于点E ,连接DE .若在边OA 上任取点E′与点E 不重合,连接CE′、DE′、D′E′由DE′+CE′=D′E′+CE′>CD′=D′E +CE =DE +CE ,∴△CDE 的周长最小.∵OB =4,D 为边OB 的中点,∴OD =2,∴D (0,2),∵在长方形OACB 中,OA =3,OB =4,D 为OB 的中点,∴BC =3,D′O =DO =2,D′B =6,∵OE ∥BC ,∴Rt △D′OE ∽Rt △D′BC , ∴OE D O BC D B='', 即:623OE =,即:OE =1, ∴点E 的坐标为(1,0)故选:D .【点睛】此题主要考查轴对称−−最短路线问题,解决此类问题,一般都是运用轴对称的性质,将求折线问题转化为求线段问题,其说明最短的依据是:两点之间线段最短.4.B解析:B【分析】平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定逐一验证.【详解】A、能用两组对角相等的四边形是平行四边形判定平行四边形;B、不能判定平行四边形,如等腰梯形;C、能用两组对边相等的四边形是平行四边形判定平行四边形;D、能用两组对边分别平行的四边形是平行四边形判定平行四边形;故选:B.【点睛】本题考查平行四边形的判定,解题的关键是掌握平行四边形的判定定理.5.A解析:A【分析】根据正方形的判定逐项作出判断即可求解.【详解】解:A. 有一个角是直角的平行四边形是正方形,判断错误,应该是矩形,符合题意;B. 对角线相等的菱形是正方形,判断正确,不合题意;C. 对角线互相垂直的矩形是正方形,判断正确,不合题意;D. 一组邻边相等的矩形是正方形,判断正确,不合题意.故选:A【点睛】本题考查了正方形的判定,熟练掌握正方形的判定方法是解题关键.6.D解析:D【分析】根据菱形的判定方法判断即可.【详解】解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠OAB=∠ACD,∵∠OAB=∠OAD,∴∠DAC=∠DCA,∴AD=CD,∴四边形ABCD是菱形(邻边相等的平行四边形是菱形)故选:D.【点睛】本题考查菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.7.A解析:A【分析】过A作AH⊥BC于H,根据已知条件得到AE=CE,求得DE=12BC,求得DF=12AH,根据三角形的面积公式得到DE•DF=2,得到AB•AC=8,求得AB=2(负值舍去),根据勾股定理即可得到结论.【详解】解:过A作AH⊥BC于H,∵D是AB的中点,∴AD=BD,∵DE∥BC,∴AE=CE,∴DE=12BC,∵DF⊥BC,∴DF∥AH,DF⊥DE,∴BF=HF,∴DF=12AH,∵△DFE的面积为1,∴12DE•DF=1,∴DE•DF=2,∴BC•AH=2DE•2DF=4×2=8,∴AB•AC=8,∵AB=CE,∴AB=AE=CE=1AC,2∴AB•2AB=8,∴AB=2(负值舍去),∴AC=4,∴==故选:A.【点睛】本题考查了三角形中位线定理,三角形的面积的计算,勾股定理,平行线的判定和性质,正确的识别图形是解题的关键.8.C解析:C【分析】根据菱形的四边相等和一个内角是60°,可判断较短对角线与两边组成等边三角形,根据等边三角形的性质可求较短的对角线长.【详解】解:因为菱形的四边相等,当一个内角是60°,则较短对角线与两边组成等边三角形.∵菱形的边长是3cm,∴这个菱形的较短的对角线长是3cm.故选:C.【点睛】此题考查了菱形四边都相等的性质及等边三角形的判定,解题关键是判断出较短对角线与两边构成等边三角形.9.C解析:C【分析】证明△OFB≌△CFB,可判断结论①正确;利用菱形的定义,可判断结论②正确;根据OC=OB,斜边大于直角边,可判断结论③错误;根据30度角的性质,可判断AB=2BM,故结论④是错误的;证NE∥BM,AN=NO=OM,所以BM=3NE,AO=2OM,利用三角形面积公式计算判断,结论⑤正确.【详解】连接BD,∵四边形ABCD是矩形,∴AC=BD,AC、BD互相平分,∵O为AC中点,∴BD也过O点,∴OB=OC,∵∠COB=60°,OB=OC,∴△OBC是等边三角形,∴OB=BC=OC,∠OBC=60°,∵FO=FC,BF=BF∴△OBF≌△CBF(SSS),∴△OBF与△CBF关于直线BF对称,∴FB⊥OC,OM=CM;∴①正确,∵AB∥CD,∴∠OCF=∠OAE,∵OA=OC,∴△AOE≌△COF,∴OE=OF,FC=AE,∴DF=BE,DF∥BE,∴四边形EBFD是平行四边形,∵OA=OB,∴∠OAB=∠OBA=30°,∵FO=OE=FC=AE,∴∠AOE=∠FOM=30°,∴∠BOF=90°,∴BE=BF,∴四边形EBFD是菱形,∴结论②正确;∵OA=OB,∴∠OAB=∠OBA=30°,∵FO=OE=FC=AE,∴∠AOE=∠FOM=30°,∴∠BOF=90°,∴FB>OB,∵OB=OC,∴FB>OC,∴③错误,在直角三角形AMB中,∵∠BAM=30°,∠AMB=90°,∴AB=2BM,∴④错误,设ED与AC的交点为N,设AE=OE=2x,则NE=x,BE=4x,∴AB=6x ,∴BM=3x , ∴11::22BOM AOE S SOM BM AO NE =⋅⋅ =3:2OM x OM x ⋅⋅=3:2,结论⑤正确.故选C .【点睛】本题考查了矩形的性质,等腰三角形三线合一性质,全等三角形,直角三角形30°角的性质,菱形的判定,熟练掌握,灵活运用是解题的关键.10.C解析:C【分析】由翻折可知:△BDF ≌△BCD ,所以∠EBD=∠CBD ,∠E=∠C=90°,由于△EDF 是等腰三角形,易证∠ABF=45°,所以∠CBD=12∠CBE=22.5°,从而可求出∠BDC=67.5°. 【详解】解:由翻折的性质得,∠DBC=∠EBD ,∵矩形的对边AD ∥BC ,∠E=∠C=90°,∴∠DBC=∠ADB ,∴∠EBD=∠ADB ,∵△EDF 是等腰三角形,∠E=90°,∴△EDF 是等腰直角三角形,∴∠DFE=45°,∵∠EBD+∠ADB=∠DFE ,∴∠DBF=12∠DFE=22.5°, ∴∠CBD =22.5°,∴∠BDC=67.5°,故选:C .【点睛】本题考查等腰三角形,涉及矩形的性质,全等三角形的判定与性质等知识,需要学生灵活运用所学知识.11.C解析:C【分析】根据HL 证明△ADG ≌△FDG ,根据角的平分线的意义求∠GDE ,根据GE=GF+EF=EC+AG ,确定△BGE 的周长为AB+AC.【详解】根据折叠的意义,得△DEC ≌△DEF ,∴EF=EC ,DF=DC ,∠CDE=∠FDE ,∵DA=DF ,DG=DG ,∴Rt △ADG ≌Rt △FDG ,∴AG=FG ,∠ADG=∠FDG ,∴∠GDE=∠FDG+∠FDE =12(∠ADF+∠CDF ) =45°,∵△BGE 的周长=BG+BE+GE ,GE=GF+EF=EC+AG ,∴△BGE 的周长=BG+BE+ EC+AG=AB+AC ,是定值,∴正确的结论有①③④,故选C.【点睛】本题考查了正方形中的折叠变化,直角三角形的全等及其性质,角的平分线,三角形的周长,熟练掌握折叠的全等性是解题的关键.12.D解析:D【分析】只要证明DBE DCF ∆≅∆得出DEF ∆是等边三角形,因为BEF ∆的周长4BE BF EF BF CF EF BC EF EF =++=++=+=+,所以等边三角形DEF ∆的边长最小时,BEF ∆的周长最小,只要求出DEF ∆的边长最小值即可.【详解】解:连接BD ,菱形ABCD 中,60A ∠=︒,ADB ∴∆与CDB ∆是等边三角形,60DBE C ∴∠=∠=∠︒,BD DC =,60EDF ∠=︒,BDE CDF ∴∠=∠,在BDE ∆和CDF ∆中,DBE C BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,DBE DCF ∴∆≅∆,DE DF ∴=,BDE CDF ∠=∠,BE CF =,60EDF BDC ∴∠=∠=︒,DEF ∴∆是等边三角形,BEF ∆的周长4BE BF EF BF CF EF BC EF EF =++=++=+=+,∴等边三角形DEF ∆的边长最小时,BEF ∆的周长最小,当DE AB ⊥时,DE 最小23=,BEF ∴∆的周长最小值为423+,故选:D .【点睛】本题考查菱形的性质、全等三角形的判定和性质、等边三角形的判定和性质、最小值问题等知识,解题的关键是正确寻找全等三角形,利用全等三角形的性质解决问题,学会转化的思想解决问题,所以中考常考题型.二、填空题13.10【分析】连接对角线BD 交AC 于点O 证四边形BDEG 是平行四边形得EG =BD 利用勾股定理求出OD 的长BD =2OD 即可求出EG 【详解】解:连接BD 交AC 于点O 如图:∵菱形ABCD 的边长为13cm ∴A解析:10【分析】连接对角线BD ,交AC 于点O ,证四边形BDEG 是平行四边形,得EG =BD ,利用勾股定理求出OD 的长,BD =2OD ,即可求出EG .【详解】解:连接BD ,交AC 于点O ,如图:∵菱形ABCD 的边长为13cm ,∴AB//CD,AB=BC=CD=DA=13cm,∵点E、F分别是边CD、BC的中点,∴ EF//BD,∵AC、BD是菱形的对角线,AC=24cm,∴AC⊥BD,AO=CO=1AC=12cm,OB=OD,2又∵AB//CD,EF//BD,∴DE//BG,BD//EG,∴四边形BDEG是平行四边形,∴BD=EG,在△COD中,∵OC⊥OD,CD=13cm,CO=12cm,∴OB=OD5=cm,∴BD=2OD=10cm,∴EG=BD=10cm;故答案为:10.【点睛】本题主要考查了菱形的性质,平行四边形的判定与性质及勾股定理等知识;熟练掌握菱形、平行四边形的性质和勾股定理是解题的关键.14.30°【分析】根据矩形的性质得到AD∥BC∠DCB=90°根据平行线的性质得到∠F=∠ECB=20°根据三角形的外角的性质得到∠ACG=∠AGC=∠GAF+∠F=2∠F=40°于是得到结论【详解】解解析:30°【分析】根据矩形的性质得到AD∥BC,∠DCB=90°,根据平行线的性质得到∠F=∠ECB=20°,根据三角形的外角的性质得到∠ACG=∠AGC=∠GAF+∠F=2∠F=40°,于是得到结论.【详解】解:∵四边形ABCD是矩形,∴AD∥BC,∠DCB=90°,∴∠F=∠ECB∵∠ECB=20°,∴∠F=∠ECB=20°,∵∠GAF=∠F,∴∠GAF=∠F=20°,∴∠ACG=∠AGC=∠GAF+∠F=2∠F=40°,∴∠ACB=∠ACG+∠ECB=60°,∴∠ACD=90°﹣∠ACB=90°﹣60°=30°,故答案为:30°.【点睛】本题考查了矩形的性质,用到的知识点为:矩形的对边平行;两直线平行,内错角相等;三角形的一个外角等于和它不相邻的两个内角的和.15.24【分析】根据平行四边形的性质得到AD ∥BC 由平行线的性质得到∠AEG=∠EGF 根据折叠的性质得到推出△GEF 是等边三角形于是得到结论【详解】解:∵四边形ABCD 是平行四边形∴AD ∥BC ∴∠AEG解析:24【分析】根据平行四边形的性质得到AD ∥BC ,由平行线的性质得到∠AEG=∠EGF ,根据折叠的性质得到60GEF DEF ∠=∠=︒,推出△GEF 是等边三角形,于是得到结论.【详解】解:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠AEG=∠EGF ,∵将四边形EFCD 沿EF 翻折,得到EFC D '',∴60GEF DEF ∠=∠=︒,∴∠AEG=60°,∴∠EGF=60°,∴△EGF 是等边三角形,∵EF=8,∴△GEF 的周长=24,故答案为:24.【点睛】此题考查平行四边形的性质,折叠的性质,等边三角形的判定及性质,熟练掌握基本性质是解题关键.16.或【分析】首先根据题意作图注意分为E 在线段AD 上与E 在AD 的延长线上然后由菱形的性质可得AD ∥BC 则可证得△MAE ∽△MCB 根据相似三角形的对应边成比例即可求得答案【详解】解:∵菱形ABCD 的边长是 解析:23或43【分析】 首先根据题意作图,注意分为E 在线段AD 上与E 在AD 的延长线上,然后由菱形的性质可得AD ∥BC ,则可证得△MAE ∽△MCB ,根据相似三角形的对应边成比例即可求得答案.【详解】解:∵菱形ABCD 的边长是3,∴AD=BC=3,AD ∥BC ,如图①:当E 在线段AD 上时,∴AE=AD -DE=3-1=2,∴△MAE ∽△MCB , ∴23MA AE MC BC ==; 如图②,当E 在AD 的延长线上时,∴AE=AD+DE=3+1=4,∴△MAE ∽△MCB ,∴43MA AE MC BC ==. ∴MA MC的值是23或43. 故答案为23或43.【点睛】此题考查了菱形的性质,相似三角形的判定与性质等知识.解题的关键是注意此题分为E 在线段AD 上与E 在AD 的延长线上两种情况,小心不要漏解.17.【分析】由题意得出OA=3由平行四边形的性质得出BC ∥OABC=OA=3即可得出结果【详解】解:∵O (00)A (30)∴OA=3∵四边形OABC 是平行四边形∴BC ∥OABC=OA=3∵B (43)∴点解析:()1,3【分析】由题意得出OA=3,由平行四边形的性质得出BC ∥OA ,BC=OA=3,即可得出结果.【详解】解:∵O (0,0)、A (3,0),∴OA=3,∵四边形OABC 是平行四边形,∴BC ∥OA ,BC=OA=3,∵B (4,3),∴点C 的坐标为(4-3,3),即C (1,3);故答案为:(1,3).【点睛】本题考查了平行四边形的性质、坐标与图形性质;熟练掌握平行四边形的性质是解题的关键.18.5cm 或cm 或cm 【分析】利用勾股定理列式求出AB 然后分①点P 与点C 在AB 的两侧时AP 与BC 是对应边时四边形ACBP 是矩形然后利用勾股定理列式计算即可得解;AP 与AC 是对应边时根据对称性可知AB ⊥P解析:5cm 或245cm 或75cm . 【分析】利用勾股定理列式求出AB ,然后分①点P 与点C 在AB 的两侧时,AP 与BC 是对应边时,四边形ACBP 是矩形,然后利用勾股定理列式计算即可得解;AP 与AC 是对应边时,根据对称性可知AB ⊥PC ,再利用三角形的面积列式计算即可得解;②点P 与点C 在AB 的同侧时,利用勾股定理求出BD ,再根据PC=AB-2BD 计算即可得解.【详解】解:在Rt ABC 中,90C ∠=︒,4cm AC =,3cm BC =,由勾股定理得,2222435AB AC BC cm =+=+=,如图,①点P 与点C 在AB 的两侧时,若AP 与BC 是对应边,则四边形ACBP 1是矩形, ∴P 1C=AB=5cm ,若AP 与AC 是对应边,则△ABC 和△ABP 关于直线AB 对称,∴AB ⊥PC设AB 与P 2C 相交于点D ,则S △ABC =12×5•CD=12×3×4, 解得CD=125, ∴P 2C=2CD=2×125=245, ②点P 3与点C 在AB 的同侧时,由勾股定理得,22221293()55BD BC CD =-=-=, 过点P 3作P 3E ⊥AB ,垂足E ,连接P 3C ,如图,则有12×5•P 3E=12×3×4, ∴P 3E=125∴P 3E=CD 又P 3E ⊥AB ,CD ⊥AB ,∴P 3E//CD ,∴四边形P 3CDE 是平行四边形,又∠CDE=90°∴四边形P 3CDE 是矩形,∴P 3C=DE∵3P AB △≌ABC∴P 3A=BC ,∠P 3AB=∠CBA又∠P 3EA=∠CDB=90°∴△P 3AE ≌△CBD∴AE=BD∴P 3C=AB-2BD=5-2×95=75, 综上所述,PC 的长为5cm 或245cm 或75cm . 故答案为:5cm 或245cm 或75cm . 【点睛】 本题考查了全等三角形的对应边相等的性质,勾股定理,轴对称性,难点在于分情况讨论,作出图形更形象直观.19.2或【分析】分两种情况:①过A′作MN ∥CD 交AD 于M 交BC 于N 则直线MN 是矩形ABCD 的对称轴得出AM=BN=AD=2由勾股定理得到A′N=0求得A′M=2再得到A′E 即可;②过A′作PQ ∥AD 交解析:2 【分析】分两种情况:①过A′作MN ∥CD 交AD 于M ,交BC 于N ,则直线MN 是矩形ABCD 的对称轴,得出AM=BN=12AD=2,由勾股定理得到A′N=0,求得A′M=2,再得到A′E 即可;②过A′作PQ ∥AD 交AB 于P ,交CD 于Q ;求出∠EBA′=30°,再利用勾股定理求出A′E ,即可得出结果.【详解】解:分两种情况:①如图1,过A′作MN ∥CD 交AD 于M ,交BC 于N ,则直线MN 是矩形ABCD 的对称轴,∴AM=BN=12AD=2, ∵△ABE 沿BE 折叠得到△A′BE , ∴A′E=AE ,A′B=AB=2,∴A′N=22A B BN '-=0,即A′与N 重合,∴A′M=2= A′E ,∴AE=2;②如图2,过A′作PQ ∥AD 交AB 于P ,交CD 于Q ,则直线PQ 是矩形ABCD 的对称轴,∴PQ ⊥AB ,AP=PB ,AD ∥PQ ∥BC ,∴A′B=2PB ,∴∠PA′B=30°,∴∠A′BC=30°,∴∠EBA′=30°,设A′E=x ,则BE=2x ,在△A′EB 中,()22222x x =+,解得:x=23, ∴AE=A′E=23;综上所述:AE 的长为223, 故答案为:2或33. 【点睛】 本题考查了翻折变换—折叠问题,矩形的性质,勾股定理;正确理解折叠的性质是解题的关键.20.【分析】根据题意可知最小时落在线段PD 上利用勾股定理求出PD 即可【详解】如图连接PD 根据题意可知当落在线段PD 上时最小且最小值为PD 长在中综上可知最小值为故答案为:【点睛】本题考查翻折的性质结合题意 解析:17 【分析】 根据题意可知PB DB ''+最小时,B '落在线段PD 上,利用勾股定理求出PD 即可.【详解】如图,连接PD ,根据题意可知当B '落在线段PD 上时,PB DB ''+最小,且最小值为PD 长.在Rt APD 中,2211617PD AP AD =+=+=.综上可知PB DB ''+最小值为17.17【点睛】本题考查翻折的性质,结合题意根据两点之间线段最短得出当B '落在线段PD 上时,PB DB ''+最小是解答本题的关键.三、解答题21.(1)见解析;(2)AC=2AB ,理由见解析;(3)当AN=EN 且∠ENA=90°时,四边形MECN 是正方形.【分析】(1)根据SAS 证明三角形全等即可.(2)先根据等腰三角形的性质可得∠NMA=90°,再根据有一个角是直角的平行四边形是矩形证明即可.(3)先根据直角三角形斜边上的中线等于斜边的一半得出MN=EM ,再根据有一个角是直角的菱形是正方形证明即可.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AB=CD ,AB ∥CD ,OB=OD ,OA=OC ,∴∠ABM=∠CDN ,∵点M ,N 分别为OB ,OD 的中点,∴11,22==BM OB DN OD ∴BM=DN ,在△ABM 和△CDN 中, AB CD ABM CDN BM DN =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△CDN .(2)当AC=2AB 时,四边形MECN 是矩形,理由如下:∵△ABM ≌△CDN ,∴AM=CN ,∠AMB=∠CND ,∴∠AMN=∠CNM ,∴AM ∥CN ,∵EM AM =,∴EM CN =,∴四边形EMNC 是平行四边形,∵四边形ABCD 是平行四边形,∴AC=2OA ,∵AC=2AB ,∴AB=OA ,∵M 是OB 的中点,∴AM ⊥OB ,∴∠NMA=90°,∴∠NME=90°,∴平行四边形MECN 是矩形.(3)当AN=EN 且∠ENA=90°时,四边形MECN 是正方形;理由如下:连接AN 、EN∵△ABM ≌△CDN ,∴AM=CN ,∠AMB=∠CND ,∴∠AMN=∠CNM ,∴AM ∥CN ,∵EM AM =,∴EM CN =,∴四边形EMNC 是平行四边形,∵EM AM =,∠ENA=90°∴MN=EM ,∴平行四边形EMNC 是菱形,∵AN=EN ,AM=EM∴∠NME=90°,∴四边形EMNC 是正方形.【点睛】本题考查了正方形的判定、平行四边形的性质和判定、全等三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.22.(1)证明见解析;(2)证明见解析;(3)2'='DD OC . 【分析】(1)由旋转性质可得 OB=OB′ ,OC=OC′ ,得到四边形BB′CC′是平行四边形,又 BC=B′ C′ ,得到平行四边形BB′CC′是矩形.(2)先由∠C=∠OB′M=∠B′OC=90°,证明四边形 OB′MC 是矩形 ,再由OC=OB′ 得到四边形 OB′MC 是正方形.(3)过D 作DN ⊥B′C′,证Rt △DNO ≌Rt △DCO(HL),设OC=a ,得到OC′=a ,DD′=2a ,即可求解.【详解】解:(1)由旋转性质可得OB OB '=,OC OC '=.点O 是线段BC 的中点 OB OC ∴=,''∴=OB OC ,OB OC =.∴四边形''BB CC 是平行四边形.又BC B C ''=,∴平行四边形''BB CC 是矩形. (2)证明:四边形ABCD 是正方形,BC CD ∴=,90C ∠=︒.180180904522-∠︒-∴︒∠=∠===︒︒C CBD CDB 由旋转可知,OB OB '=,45''∴∠=∠=︒OB B OBB454590'''∴∠=∠+∠=︒+︒=︒B OC OB B OBB .四边形A B C D ''''是正方形,90'∴∠=︒OB M∴四边形OB MC '是矩形OB OC =,OC=OC′ ,OB′=OB ,∴OC=OB′∴矩形OB MC '是正方形,(3)2'='DD OC . 如图,过D 作DN ⊥B′C′可知,∠A′=∠B′=∠B′ND=90°,∠D′=∠C′=∠C′ND=90°,∴四边形DNC′D′为矩形,四边形DNB′A′为矩形,在Rt △DNO 与Rt △DCO 中,∵OD=OD ,DN=DC ,∴Rt △DNO ≌Rt △DCO(HL)设OC=a ,则OB=2OC=2a ,∴ON=OC=OC′=a∴BC=OB+OC=3a ,DD′=NC′=ON+OC′=2a ,∴2DD a OC a'='=2. 【点睛】 本题考查了特殊的四边形,平行四边形,矩形,正方形的性质和判定,解题的关键是熟练掌握特殊的四边形的性质和判定.23.(1)见解析;(2)GH EF ⊥,见解析;(3)25︒【分析】(1)利用中位线性质得//EG AB ,且12GE AB =,//HF AB ,且12HF AB =,可推出//EG HF ,且EG HF =,可证四边形EGFH 是平行四边形;(2由G F 、分别是BD BC 、的中点,可得12GF CD =,由(1)知12GE AB =,由AB CD =,可证GE GF =,由(1)知四边形EGFH 是平行四边形,可证四边形EGFH 是菱形即可;(3)先证四边形EGFH 是平行四边形;再证四边形EGFH 是菱形,由EG ∥AB ,GF ∥CD ,可求∠EGD=∠ABD=20°,∠BGF=∠BDC=70°利用平角可求∠DGF=180°-∠BGF=110°,利用两角和求∠EGF=130°利用菱形性质求∠GEH=180°-∠EGF=50º,由FE 平分∠GEH ,∠GEF=25︒即可.【详解】证明:(1)E G 、分别是AD BD 、的中点,//EG AB ∴,且12GE AB =, 同理可证://HF AB ,且12HF AB =, //EG HF ∴,且EG HF =,∴四边形EGFH 是平行四边形;(2)GH EF ⊥,理由:G F 、分别是BD BC 、的中点,12GF CD ∴=, 由(1)知12GE AB =, 又AB CD =,GE GF ∴=, 又四边形EGFH 是平行四边形,∴四边形EGFH 是菱形,GH EF ∴⊥;(3)E G 、分别是AD BD 、的中点,F H 、分别是BC AC 、的中点,//EG AB ∴,//HF AB ,12GE AB =, //EG HF ∴,同理可证//EH GF ,12GF CD =, ∴四边形EGFH 是平行四边形,∵AB CD =,GE GF ∴=,∴四边形EGFH 是菱形,20,70ABD BDC ∠=︒∠=︒,EG ∥AB ,GF ∥CD ,∴∠EGD=∠ABD=20°,∠BGF=∠BDC=70°,∴∠DGF=180°-∠BGF=110°,∴∠EGF=∠EGD+∠DGF=20°+110°=130°,∴∠GEH=180°-∠EGF=50º,∵FE 平分∠GEH ,∴∠GEF=11502522GEH ∠=⨯︒=︒.故答案为:25︒.【点睛】本题考查平行四边形,菱形判断与性质,求菱形内角,掌握平行四边形的判定方法,菱形的判定与性质,会利用菱形的性质求角度是解题关键.24.(1)见解析;(2)120°【分析】(1)根据直角三角形斜边上的中线等于斜边的一半求证;(2)根据补角定义和直角三角形性质可得∠MDA+∠MCB=120°,∠MDB+∠MCA=60°,再由等边三角形的性质得到∠BDC+∠ACD=60°,最后由对顶角相等和三角形内角和定理可得∠AOB=120°.【详解】(1)证明:由已知可得:1122MC AB MD AB ==,,∴MC=MD;(2)∵△MCD是等边三角形,∴∠DMC=60°,∴∠AMD+∠BMC=180°-60°=120°,与(1)同理有:MA=MD,MC=MB,∴∠MAD=∠MDA,∠MCB=∠MBC,∴2(∠MDA+∠MCB)=360°-(∠AMD+∠BMC)=360°-120°=240°,∴∠MDA+∠MCB=120°,∵∠ADB+∠BCA=180°,∴∠MDB+∠MCA=(∠ADB+∠BCA)-(∠MDA+∠MCB)=180°-120°=60°,∴∠BDC+∠ACD=(∠MDC+∠MCD)-(∠MDB+∠MCA)=120°-60°=60°,∴∠AOB=∠DOC=180°-(∠BDC+∠ACD)=180°-60°=120°.【点睛】本题考查等边三角形和直角三角形的综合应用,熟练掌握等边三角形和直角三角形的性质、补角定义、三角形内角和定理是解题关键.25.(1)见解析;(2)见解析.【分析】(1)连接GE,根据正方形对边平行,得∠AEG=∠CGE,根据菱形的对边平行,得∠HEG=∠FGE,利用两个角的差求解即可;(2)根据正方形的判定定理,证明∠GHE=90°即可.【详解】证明:(1)连接GE,∵AB∥CD,∴∠AEG=∠CGE,∵GF∥HE,∴∠HEG=∠FGE,∴∠HEA=∠CGF ;(2)∵四边形ABCD 是正方形,∴∠D=∠A=90°,∵四边形EFGH 是菱形,∴HG=HE ,在Rt △HAE 和Rt △GDH 中,AH DG HE HG=⎧⎨=⎩, ∴Rt △HAE ≌Rt △GDH ,∴∠AHE=∠DGH ,∵∠DHG+∠DGH=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∴菱形EFGH 为正方形.【点睛】本题考查了正方形的性质和判定,菱形的性质,平行线的性质,熟记正方形的性质和判定是解题的关键.26.(1)见解析;(2)47BECD S =菱形【分析】(1)根据四边形ABCD 是平行四边形,得到AB CD =,//AB CD ,再根据BE AB =,得到BE CD =,利用一组对边平行且相等的四边形BECD 是平行四边形去判定.(2)先利用已知条件证四边形BECD 是菱形,再在Rt BOE △中,利用勾股定理求BO ,进而求BC ,则可求菱形面积.【详解】解:(1)∵四边形ABCD 是平行四边形,∴AB CD =,//AB CD ,又∵BE AB =,∴BE CD =,//BE CD ,∴四边形BECD 是平行四边形.(2)如图,连接DE ,交BC 于点O ,∵4AB BD ==,BE AB =,∴4BD BE ==,由(1)得四边形BECD 是平行四边形,∴BECD 是菱形,∴DE BC ⊥, ∵22DE = ∴122OE DE ==, 在Rt BOE △中,22224(2)14BO BE OE =-=-= ∴2214BC BO == ∴11214224722BECD S BC DE =⋅=⨯=菱形 【点睛】 本题考查了平行四边形、菱形性质和判定的综合应用,熟练掌握相关知识是解答此题的关键.。
(常考题)人教版初中数学八年级数学下册第三单元《平行四边形》测试卷(包含答案解析)(1)
一、选择题1.已知正方形ABCD 中,对角线4AC =,这个正方形的面积是( )A .8B .16C .82D .162 2.在平面直角坐标系中,长方形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点,若E 为x 轴上的一个动点,当△CDE 的周长最小时,求点E 的坐标( )A .(一3,0)B .(3,0)C .(0,0)D .(1,0) 3.下列命题为假命题的是( )A .直角三角形斜边上的中线等于斜边的一半.B .两边及其一边的对角对应相等的两个三角形全等.C .等边三角形一边上的高线与这边上的中线互相重合.D .到线段两端点距离相等的点在这条线段的垂直平分线上.4.四边形ABCD 中,对角线AC BD 、交于点O .给出下列四组条件:①AB ∥CD ,AD ∥BC ;②AB CD =,AD BC =;③AO CO =,BO DO =;④AB ∥CD ,AD BC =.其中一定能判定这个四边形是平行四边形的条件共有( )A .1组;B .2组;C .3组;D .4组. 5.如图,点D 和点E 分别是BC 和BA 的中点,已知AC =4,则DE 为( )A .1B .2C .4D .86.下列命题中,错误的是( )A .一组对边平行的四边形是梯形;B .两组对边分别相等的四边形是平行四边形;C .对角线相等的平行四边形是矩形;D .一组邻边相等的平行四边形是菱形.7.如图,以平行四边形ABCD 的边AB 、BC 、CD 、DA 为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH ,当()090ADC αα∠=︒<<︒时,有以下结论:①180GCF α∠=︒-;②90HAE α∠=︒+;③HE HG =;④ EH GH ⊥;⑤四边形EFGH 是平行四边形.则结论正确的是( )A .①③④B .②③⑤C .①③④⑤D .②③④⑤ 8.在菱形ABCD 中,∠ABC=60゜,AC=4,则BD=( )A .3B .23C .33D .439.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,30ACD ∠=︒,若ABC 的周长比AOB 的周长大10,则AB 的长为( ).A .103B .53C .10D .2010.如图,Rt Rt ABC BAD △≌△,BC 、AD 交于点E ,M 为斜边的中点,若CMD α∠=,AEB β∠=.则α和β之间的数量关系为( )A .2180βα-=︒B .60βα-=︒C .180αβ+=︒D .2βα=11.如图,在矩形ABCD 中,3AB =,4=AD ,ABC ∠的平分线BE 交AD 于点E .点F ,G 分别是BC ,BE 的中点,则FG 的长为( )A .2B .52C .102D .32212.如图所示,已知Rt ABC 中,90B ︒∠=,3AB =,4BC =,D F 、分别为AB AC 、的中点,E 是BC 上动点,则DEF 周长的最小值为( )A .240+B .213+C .13D .6二、填空题13.如图,正方形ABCD 的边长为2,O 是对角线BD 上一动点(点O 与端点B ,D 不重合),OM ⊥AD 于点M ,ON ⊥AB 于点N ,连接MN ,则MN 长的最小值为_____.14.己知菱形ABCD 的边长是3,点E 在直线AD 上,DE =1,联结BE 与对角线AC 相交于点M ,则AM MC的值是______. 15.如图,矩形纸片ABCD 的长AD =6cm ,宽AB =2cm ,将其折叠,使点D 与点B 重合,那么折叠后DE 的长______cm .16.如图,点E 是长方形纸片DC 上的中点,将C ∠过E 点折起一个角,折痕为EF ,再将D ∠过点E 折起,折痕为GE ,且C ,D 均落在GF 上的一点H 处.若1649'∠=︒,则CEF ∠=_______.17.如图,在Rt ABC ∆中,90,6,10ACB AC AB ∠===,过点A 作//,AM CB CE 平分ACB ∠交AM 于点,E Q 是线段CE 上的点,连接BQ ,过点B 作BP BQ ⊥交AM 于点P ,当PBQ ∆为等腰三角形时,AP =________________________.18.如图,在正方形纸片ABCD 中,E 是CD 的中点,将正方形纸片折叠,点B 落在线段AE 上的点G 处,折痕为AF .若1DE =,则BF 的长为__________.19.如图,边长分别为4和2的两个正方形ABCD 和CEFG 并排放在一起,连结EG 并延长交BD 于点N ,交AD 于点M .则线段MN 的长是__________.20.在长方形ABCD 中,52AB =,4BC =,CE CF =,CF 平分ECD ∠,则BE =_________.三、解答题∠、21.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分BCD CF平分GCDEF BC交CD于点O.∠,//=;(1)求证:OE OF(2)若点O为CD的中点,求证:四边形DECF是矩形.22.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且=.∠=∠,BE CF=,EBC FCBAC BD求证:四边形AFDE是平行四边形;23.如图,在ABCD中,对角线AC与BD相交于点O,点E,F在BD上,且=,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.BE DF=;(1)求证:AE CF∠,判断四边形AGCH的形状,并证明你的结论.(2)若AC平分HAG∠∠均为直角,则称这样的四边形为“美妙四边24.如图1,在四边形ABCD中,若,A C形”.(1)概念理解:长方形__________________美妙四边形(填“是”或“不是”); (2)性质探究:如图l ,试证明:2222CD AB AD BC -=-;(3)概念运用:如图2,在等腰直角三角形ABC 中,,90AB AC A =∠=︒,点D 为BC 的中点,点E ,点F 分别在,AB AC 上,连接,DE DF ,如果四边形AEDF 是美妙四边形,试证明:AE AF AB +=.25.已知:如图所示,在平行四边形ABCD 中,DE 、BF 分别是∠ADC 和∠ABC 的角平分线,交AB 、CD 于点E 、F ,连接BD 、EF .(1)求证:BD 、EF 互相平分;(2)若∠A =60°,AE =2EB ,AD =4,求线段BD 的长.26.正方形ABCD 中,对角线AC 、BD 交于点O ,E 为BD 上一点,延长AE 到点N ,使AE EN =,连接CN 、CE .(1)求证:CAN △为直角三角形.(2)若45AN =6,求BE 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】根据勾股定理,可得正方形的边长,进而可得正方形的面积.【详解】∵正方形ABCD 中,对角线4AC =,∴AB 2+BC 2=AC 2,∴2AB 2=42,∴AB 2=8.故选:A .【点睛】本题主要考查的是正方形的性质,勾股定理,熟练掌握勾股定理是解题的关键. 2.D解析:D【分析】由于C 、D 是定点,则CD 是定值,如果△CDE 的周长最小,即DE +CE 有最小值.为此,作点D 关于x 轴的对称点D′,当点E 在线段CD′上时,△CDE 的周长最小.【详解】如图,作点D 关于x 轴的对称点D′,连接CD′与x 轴交于点E ,连接DE .若在边OA 上任取点E′与点E 不重合,连接CE′、DE′、D′E′由DE′+CE′=D′E′+CE′>CD′=D′E +CE =DE +CE ,∴△CDE 的周长最小.∵OB =4,D 为边OB 的中点,∴OD =2,∴D (0,2),∵在长方形OACB 中,OA =3,OB =4,D 为OB 的中点,∴BC =3,D′O =DO =2,D′B =6,∵OE ∥BC ,∴Rt △D′OE ∽Rt △D′BC , ∴OE D O BC D B='', 即:623OE =,即:OE =1,∴点E 的坐标为(1,0)故选:D .【点睛】此题主要考查轴对称−−最短路线问题,解决此类问题,一般都是运用轴对称的性质,将求折线问题转化为求线段问题,其说明最短的依据是:两点之间线段最短.3.B解析:B【分析】根据直角三角形斜边的中线的性质,三角形全等的判定,等边三角形的性质以及线段垂直平分线的性质对各选项分析判断即可得解.【详解】A 、直角三角形斜边上的中线等于斜边的一半,是真命题,不符合题意;B 、两边及其一边的对角对应相等的两个三角形全等,是假命题,符合题意.C 、等边三角形一边上的高线与这边上的中线互相重合,是真命题,不符合题意;D 、到线段两端点距离相等的点在这条线段的垂直平分线上,是真命题,不符合题意; 故选:B .【点睛】本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.4.C解析:C【分析】根据平行四边形的判定方法对①②③④分别作出判断即可求解.【详解】解:①AB ∥CD ,AD ∥BC ,根据两组对边分别平行的四边形是平行四边形即可得到四边形是平行四边形;②AB CD =,AD BC =,根据两组对边分别相等的四边形是平行四边形即可得到四边形是平行四边形;;③AO CO =,BO DO =,根据对角线互相平分的四边形是平行四边形即可得到四边形是平行四边形;④AB∥CD,AD BC=,无法判定四边形是平行四边形.故选:C【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的定义和判定定理是解题关键.5.B解析:B【分析】根据三角形中位线定理解答即可.【详解】解:∵点D和点E分别是BC和BA的中点,∴DE是△ABC的中位线,∴DE=12AC=12⨯4=2,故选:B.【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.6.A解析:A【分析】根据梯形,平行四边形,矩形,菱形的判定进行判断即可.【详解】解:A、一组对边平行,另一组对边不平行的四边形是梯形,故错误,符合题意;B、两组对边分别相等的四边形是平行四边形,正确,不符合题意;C、对角线相等的平行四边形是矩形,正确,不符合题意;D、一组邻边相等的平行四边形是菱形,正确,不符合题意;故选:A.【点睛】主要考查梯形,平行四边形,矩形,菱形的判定,注意梯形的定义应从两组对边的不同位置关系分别考虑.7.D解析:D【分析】根据平行四边形性质得出∠ABC=∠ADC=α,∠BAD=∠BCD,AB=CD,AD=BC,AD∥BC,AB∥CD,根据等腰直角三角形得出BE=AE=CG=DG,AH=DH=BF=CF,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠EDA=45°,求出∠HAE=∠HDG=∠FCG=∠FBE=90°+α,证△FBE≌△HAE≌△HDG≌△FCG,推出∠BFE=∠GFC,EF=EH=HG=GF,求出∠EFG=90°,根据正方形性质得出即可.【详解】解:∵四边形ABCD 是平行四边形,∴∠ABC=∠ADC=α,∠BAD=∠BCD ,AB=CD ,AD=BC ,AD ∥BC ,AB ∥CD ,∵平行四边形ABCD 的边AB 、BC 、CD 、DA 为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,∴BE=AE=CG=DG ,AH=DH=BF=CF ,∠ABE=∠EAB=∠FBC=∠FCB=∠GCD=∠GDC=∠HAD=∠EDA=45°,∵AB ∥CD ,∴∠BAD=∠BCD=180°-α,∴∠EAH=360°-45°-45°-(180°-α)=90°+α,∠GCF=360°-45°-45°-(180°-α)=90°+α, ∴①错误;②正确;∠HDG=45°+45°+α=90°+α,∠FBE=45°+45°+α=90°+α,∴∠HAE=∠HDG=∠FCG=∠FBE ,在△FBE 、△HAE 、△HDG 、△FCG 中,BF AH DH CF FBE HAE HDG FCG BE AE DG CG ===⎧⎪∠=∠=∠=∠⎨⎪===⎩,∴△FBE ≌△HAE ≌△HDG ≌△FCG (SAS ),∴∠BFE=∠GFC ,EF=EH=HG=GF ,③正确;∴四边形EFGH 是菱形,∵∠BFC=90°=∠BFE+∠EFC=∠GFC+∠CFE ,∴∠EFG=90°,∴四边形EFGH 是正方形,⑤正确;∴EH ⊥GH ,④正确;故选:D .【点睛】本题考查了等腰直角三角形,全等三角形的性质和判定,正方形的判定,平行四边形的性质,菱形的判定的应用,主要考查学生的推理能力.8.D解析:D【分析】根据菱形的性质可得到直角三角形,利用勾股定理计算即可;【详解】如图,AC 与BD 相较于点O ,∵四边形ABCD 是菱形,4AC =,∴AC BD ⊥,2AO =,又∵∠ABC=60゜,∴30ABO ∠=︒,∴24AB AO ==, ∴224223BO =-= ∴243BD BO ==;故选D .【点睛】本题主要考查了菱形的性质,结合勾股定理计算是解题的关键.9.A解析:A【分析】由矩形的性质和已知条件求出3,BC=10,即可得出答案.【详解】解:∵四边形ABCD 是矩形,∴AO=CO=DO=BO ,AD=BC ,∠ABC=90°,AB ∥CD ,∴∠BAC=∠ACD=30°,∴3,∵△ABC 的周长=AB+AC+BC=AB+AO+OC+BC ,△AOB 的周长=AB +AO +BO ,又∵ABC 的周长比△AOB 的周长长10,∴AB+AC+BC-(AB +AO +BO )=BC=10,∴3103故选:A .【点睛】本题考查了矩形的性质、含30°角的直角三角形的性质等知识,熟练掌握矩形的性质,求出BC 的长是解题的关键.10.A解析:A【分析】根据题意可得,CAB DBA ABC BAD ∠=∠∠=∠,再由直角三角形斜边的中线等于斜边的一半,可证CM DM AM BM ===,继而证明()AMC BMD SSS △≌△,解得1802AMC BMD CAM ∠=∠=︒-∠,最后根据三角形内角和180°定理,分别解得αβ、与CAM ∠的关系,整理即可解题.【详解】Rt Rt ABC BAD △≌△,CAB DBA ABC BAD ∴∠=∠∠=∠ M 是AB 的中点,11,22CM AB DM AB ∴== CM DM AM BM ∴===∴∠CAM=∠MCA ,Rt Rt ABC BAD △≌△AC BD ∴=()AMC BMD SSS △≌△1802AMC BMD CAM ∴∠=∠=︒-∠CMD α∴=∠180AMC BMD =︒-∠-∠1802(1802)CAM =︒-⨯︒-∠4180CAM =∠-︒90ABC BAD CAM ∠=∠=︒-∠,AEB β=∠=180BAD ABC ︒-∠-∠180(90)(90)CAM CAM =︒-︒-∠-︒-∠2CAM =∠2180βα∴-=︒故选:A .【点睛】本题考查全等三角形的判定与性质、直角三角形斜边中线的性质、等腰三角形的性质、三角形内角和180°等知识,是重要考点,难度较易,掌握相关知识是解题关键.11.C解析:C【分析】连接CE ,由矩形的性质和角平分线的性质可得AB=AE=3,可得ED=1,由勾股定理可求CE 的长,由三角形中位线定理可求FG 的长;【详解】连接CE ,如图所示:∵四边形ABCD是矩形,∴∠BAD=∠ABC=∠D=90°,AB=CD=3,AD=BC=4,AD∥BC,∴∠CBE=∠AEB,∵BE平分∠ABC.∴∠ABE=∠CBE=45°,∴∠ABE=∠AEB=45°,∴AB=AE=3,∴ED=AD-AE=4-3=1,在Rt△CDE中EC=22221310DE CD+=+=∵点F、G分别为BC、BE的中点,∴FG是△CBE的中位线,FG=12CE=10故选:C【点睛】本题考查了矩形的性质,勾股定理,等腰直角三角形的判定与性质,三角形中位线的定理等知识;熟练掌握矩形的性质和三角形中位线定理,求出EC的长度是解题的关键. 12.B解析:B【分析】先根据三角形的中位线定理可求得DF的长为2,然后作出点F关于BC的对称点F′,连接DF′交BC于点E,此时DEF周长的最小,由轴对称图形的性质可知EF=EF′,从而可得到ED+EF=DF′,再证明四边形DBMF为矩形,得出FF′=3,然后在Rt△DFF′中,由勾股定理可求得DF′的长度,从而可求得三角形DEF周长的最小值.【详解】解:如图,作点F关于BC的对称点F′,连接DF′交BC于点E.此时DE+EF最小∵点D 、F 分别是AB 和AC 的中点,BC=4,3AB =,∴DF=12BC=2,DF//BC ,BD=1.5, ∵点F 与点F′关于BC 对称,∴EF=EF′,FF′⊥BC ,FM= F′M , ∴DE+EF 最小值为DE+ EF′=DF′,90DFF ∠'=︒,∵DF//BC ,90B ∠=︒,∴90B BDF FMB ∠=∠=∠=︒,∴四边形DBMF 为矩形,∴BD=FM=1.5,∴FF′=3,在Rt △DFF′中,2'2222313DF DF FF =+=+=',∴△DEF 周长的最小值=DF+DE+EF=DF+DF′=2+13.故选:B【点睛】本题主要考查的是轴对称路径最短问题,以及勾股定理,矩形的判定,作出点F 关于BC 的对称点,将DE+EF 转化为DF′的长是解题的关键.二、填空题13.1【分析】连接AO 可证四边形AMON 是矩形可得AO =MN 当AO ⊥BD 时AO 有最小值即MN 有最小值由等腰直角三角形的性质可求解【详解】解:如图连接AO ∵四边形ABCD 是正方形∴AB =AD =BD =AB =解析:1.【分析】连接AO ,可证四边形AMON 是矩形,可得AO =MN ,当AO ⊥BD 时,AO 有最小值,即MN 有最小值,由等腰直角三角形的性质可求解.【详解】解:如图,连接AO ,∵四边形ABCD 是正方形,∴AB =AD 2BD 2=2,∠DAB =90°,又∵OM ⊥AD ,ON ⊥AB ,∴四边形AMON 是矩形,∴AO=MN,∵当AO⊥BD时,AO有最小值,∴当AO⊥BD时,MN有最小值,此时AB=AD,∠BAD=90°,AO⊥BD,∴AO=12BD=1,∴MN的最小值为1,故答案为:1.【点睛】本题考查了正方形的性质,矩形的判定和性质,垂线段最短,等腰直角三角形的性质,利用矩形的对角线相等,把线段MN的最小值转化为线段AO的最小值是解题的关键. 14.或【分析】首先根据题意作图注意分为E在线段AD上与E在AD的延长线上然后由菱形的性质可得AD∥BC则可证得△MAE∽△MCB根据相似三角形的对应边成比例即可求得答案【详解】解:∵菱形ABCD的边长是解析:23或43【分析】首先根据题意作图,注意分为E在线段AD上与E在AD的延长线上,然后由菱形的性质可得AD∥BC,则可证得△MAE∽△MCB,根据相似三角形的对应边成比例即可求得答案.【详解】解:∵菱形ABCD的边长是3,∴AD=BC=3,AD∥BC,如图①:当E在线段AD上时,∴AE=AD-DE=3-1=2,∴△MAE∽△MCB,∴23 MA AEMC BC==;如图②,当E在AD的延长线上时,∴AE=AD+DE=3+1=4,∴△MAE∽△MCB,∴43 MA AEMC BC==.∴MAMC 的值是23或43.故答案为23或43.【点睛】此题考查了菱形的性质,相似三角形的判定与性质等知识.解题的关键是注意此题分为E 在线段AD上与E在AD的延长线上两种情况,小心不要漏解.15.【分析】由矩形的性质和折叠的性质以及勾股定理得出方程解方程即可【详解】由折叠的性质得:BE=DE设DE长为xcm则AE=(6−x)cmBE=xcm∵四边形ABCD是矩形∴∠A=90°根据勾股定理得:解析:10 3【分析】由矩形的性质和折叠的性质以及勾股定理得出方程,解方程即可.【详解】由折叠的性质得:BE=DE,设DE长为xcm,则AE=(6−x)cm,BE=xcm,∵四边形ABCD是矩形,∴∠A=90°,根据勾股定理得:AE2+AB2=BE2,即(6−x)2+22=x2,解得:x=103,即DE长为103cm,故答案为:103.【点睛】本题考查了矩形的性质、翻折变换、勾股定理等知识;熟练掌握矩形和翻折变换的性质,运用勾股定理进行计算是解决问题的关键.16.【分析】根据翻折的性质可得∠GEH=∠1∠HEF=∠CEF从而可求出∠DEH∠CEF的度数【详解】解:∵∠GEH=∠1∴∠GEH=∴∠DEH=+=∴∠HEF=∠CEF=×(180°-)=故答案为:【解析:2551'︒【分析】根据翻折的性质可得∠GEH=∠1,∠HEF=∠CEF,从而可求出∠DEH,∠CEF的度数.【详解】解:∵1649'∠=︒,∠GEH=∠1,∴∠GEH=649'︒,∴∠DEH =649'︒+649'︒=12818'︒,∴∠HEF=∠CEF=12×(180°-12818'︒)=2551'︒,故答案为:2551'︒.【点睛】本题考查了翻折变换的性质,熟练掌握折叠的性质找出相等的角是解题的关键.17.【分析】过点P作PG⊥CB交CB的延长线于点G过点Q作QF⊥CB运用AAS定理证明△QBF≌△BPG根据平行线的性质和角平分线的定义求得△AEC为等腰直角三角形利用勾股定理求得线段BC的长然后结合全解析:10【分析】过点P作PG⊥CB,交CB的延长线于点G,过点Q作QF⊥CB,运用AAS定理证明△QBF≌△BPG,根据平行线的性质和角平分线的定义求得△AEC为等腰直角三角形,利用勾股定理求得线段BC的长,然后结合全等三角形和矩形的性质求解.【详解】解:过点P作PG⊥CB,交CB的延长线于点G,过点Q作QF⊥CB∵BP BQ⊥,PG⊥CB∴∠1+∠2=90°,∠2+∠3=90°∴∠1=∠3∵QF⊥CB,BP BQ⊥∴∠QFB=∠PGB=90°又∵PBQ∆为等腰三角形∴QB=PB在△QBF和△BPG中1=3QFB PGB QB PB∠∠⎧⎪∠=∠⎨⎪=⎩∴△QBF≌△BPG∴PG=BF,BG=QF∵∠ACB=90°,CE平分ACB∠∴∠ACE=∠ECB=45°又∵AM∥CB,∴∠AEC=∠ECB=45°∴∠AEC=∠ACE=45°∴△AEC为等腰直角三角形∵AM∥BC,∠ACB=90°∴∠CAM+∠ACB=180°,即∠CAM=90°∴∠CAM=∠ACB=∠PGB=90°∴四边形ACGP为矩形,∴PG=AC=6,AP=CG在Rt△ABC中,BC=228-=AB AC∴CF=BC-BF=BC-PG=8-6=2∵QF⊥BC,∠ECB=45°∴△CQF是等腰直角三角形,即CF=QF=2∴AP=CG=BC+BG=BC+QF=8+2=10【点睛】本题考查矩形的判定和性质、全等三角形的判定和性质以及勾股定理,掌握相关性质定理正确推理论证是解题关键18.【分析】连接FE根据题意得CD=2AE=设BF=x则FG=xCF=2-x在Rt△GEF中利用勾股定理可得EF2=(-2)2+x2在Rt△FCE中利用勾股定理可得EF2=(2-x)2+12从而得到关于解析:51-【分析】连接FE,根据题意得CD=2,AE=5,设BF=x,则FG=x,CF=2-x,在Rt△GEF中,利用勾股定理可得EF2=(5-2)2+x2,在Rt△FCE中,利用勾股定理可得EF2=(2-x)2+12,从而得到关于x方程,求解x即可.【详解】解:连接EF,如图,∵E是CD的中点,且CE=1∴CD=2,DE=1∵四边形ABCD是正方形,∴AB=BC=CD=DA=2∴=设BF=x ,由折叠得,AG=AB=2,FG=BF=x ,∴2,在Rt △GFE 中,222222)EF FG GE x =+=+在Rt △CFE 中,CF=BC-BF=2-x ,CE=1∴22222(2)1EF FC CE x =+=-+∴22222)(2)1x x +=-+解得:1x ,即1,1【点睛】本题主要考查了折叠的性质、勾股定理.折叠问题主要是抓住折叠的不变量,在直角三角形中利用勾股定理求解是解题的关键.19.【分析】根据题意易证明和是等腰直角三角形再根据勾股定理即可求出MN 【详解】∵四边形ABCD 和CEFG 为正方形∴∴和是等腰直角三角形∴∴在中故答案为:【点睛】本题考查正方形和平行线的性质等腰直角三角形【分析】根据题意易证明MND 和MDG 是等腰直角三角形,2DM DC GC =-=.再根据勾股定理即可求出MN .【详解】∵四边形ABCD 和CEFG 为正方形,//AD BE .∴45DMG BEM MDN DGM ∠=∠=∠=∠=︒,∴MND 和MDG 是等腰直角三角形,∴422DG DM DC GC ==-=-=.∴在Rt MND △中,222MN MD ===【点睛】本题考查正方形和平行线的性质,等腰直角三角形的判定和性质以及勾股定理.根据题意证明MND 是等腰直角三角形在结合勾股定理求解是解答本题的关键. 20.【分析】延长CF 交EA 的延长线于点G 连接EF 过点F 作FH ⊥CE 于点H 过点E 作EM ⊥CF 于点M 由题意易得FH=FDFH=EMEC=EG 进而可得△CDF ≌△CME 然后可得CM=CD=由勾股定理可得BG= 解析:76【分析】延长CF ,交EA 的延长线于点G ,连接EF ,过点F 作FH ⊥CE 于点H ,过点E 作EM ⊥CF 于点M ,由题意易得FH=FD ,FH=EM ,EC=EG ,进而可得△CDF ≌△CME ,然后可得CM=CD=52,由勾股定理可得BG=3,设BE=x ,则有EC=EG=3+x ,最后利用勾股定理可求解.【详解】解:延长CF ,交EA 的延长线于点G ,连接EF ,过点F 作FH ⊥CE 于点H ,过点E 作EM ⊥CF 于点M ,如图所示:∵四边形ABCD 是矩形,4BC =,52AB =∴BC=AD ,52AB DC ==,AB ∥DC ,∠D=∠ABC=∠CBE=90° ∴∠DCF=∠G ,∵CF 平分∠ECD ,∴∠DCF=∠ECF ,DF=FH ,∴∠G=∠ECF ,∴EC=EG ,∴△ECG 是等腰三角形,∴CM=MG ,∵CE=CF ,∴△ECF 是等腰三角形, ∵EM 、FH 分别是等腰三角形ECF 腰上的高线, ∴FH=EM=DF ,∴Rt △CDF ≌Rt △CME (HL ),∴52CM DC ==, ∴CG=5,∴在Rt △CBG 中,223BG CG CB -=,设BE=x ,则有EC=EG=3+x ,在Rt △CBE 中,222BC BE CE +=,∴()22243x x +=+, 解得:76x =, ∴76BE =; 故答案为76. 【点睛】本题主要考查等腰三角形的性质与判定、矩形的性质及勾股定理,熟练掌握等腰三角形的性质与判定、矩形的性质及勾股定理是解题的关键.三、解答题21.(1)见解析;(2)见解析【分析】(1)由角平分线的定义及平行线的性质可证得DCE FEC ∠=∠,EFC DCF ∠=∠,得OE OC =,OF OC =,即可得出结论;(2)先证得四边形DECF 是平行四边形,再利用角平分线的定义可求得90ECF ∠=︒,则可证得四边形DECF 为矩形.【详解】证明:(1)∵CE 平分BCD ∠、CF 平分GCD ∠∴BCE DCE ∠=∠,DCF GCF ∠=∠∵EF ∥BC ,∴BCE FEC ∠=∠,EFC GCF ∠=∠∴DCE FEC ∠=∠,EFC DCF ∠=∠∴OE OC =,OF OC =,∴OE OF =.(2)∵点O 为CD 的中点,∴OD OC =,又OE OF =,∴四边形DECF 是平行四边形∵CE 平分BCD ∠、CF 平分GCD ∠, ∴12DCE BCD ∠=∠,12DCF DCG ∠=∠ ∴()11=9022DCE DCF BCD DCG BCG ∠+∠=∠+∠∠=︒ ∵DCE DCF ECF ∠+∠=∠, ∴90ECF ∠=︒∵四边形DECF 是平行四边形,∴平行四边形DECF 是矩形.【点睛】本题主要考查了矩形的判定、平行四边形的判定与性质、等腰三角形的判定以及平行线的性质等知识,掌握相关性质定理正确推理论证是解题关键.22.见解析【分析】证明△ABE ≌△DCF ,得到AE=DF ,∠EAB=∠FDC ,推出AE ∥DF ,即可证明结论.【详解】解:∵AC=BD ,即AB+BC=CD+CB ,∴AB=CD ,∵∠EBC=∠FCB ,∴∠ABE=∠DCF ,在△ABE 和△DCF 中,AB CD ABE DCF BE CF =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△DCF (SAS ),∴AE=DF ,∠EAB=∠FDC ,∴AE ∥DF ,∴四边形AFDE 是平行四边形.【点睛】本题考查了全等三角形的判定和性质,平行四边形的判定,解题的关键是根据全等得到对应角和对应边相等.23.(1)见解析;(2)四边形AGCH 是菱形,见解析【分析】(1)利用SAS 证明△AOE ≌△COF 即可得到结论;(2)四边形AGCH 是菱形.根据△AOE ≌△COF 得∠EAO=∠FCO ,推出AG ∥CH ,证得四边形AGCH 是平行四边形,再根据AD ∥BC ,AC 平分HAG ∠,得到GAC ACB ∠=∠,证得GA=GC ,即可得到结论.【详解】证明:(1)四边形ABCD 是平行四边形,OA OC ∴=,OB OD =,BE DF =,OB BE OD DF ∴-=-,即OE OF =,又AOE COF ∠=∠,AOE COF ∴≌,AE CF ∴=.(2)四边形AGCH 是菱形.理由:AOE COF ≌,EAO FCO ∴∠=∠,//AG CH ∴,四边形ABCD 是平行四边形,//AD BC ∴,∴四边形AGCH 是平行四边形,//AD BC ,HAC ACB ∠∠∴=,AC 平分HAG ∠,HAC GAC ∠∠∴=,∴GAC ACB ∠=∠,GA GC ∴=,∴平行四边形AGCH 是菱形.【点睛】此题考查平行四边形的性质,全等三角形的判定及性质,菱形的判定定理,等角对等边证明边相等,熟记平行四边形的判定定理是解题的关键.24.(1)是;(2)见解析;(3)见解析【分析】(1)因为长方形的四个角都是直角,所以长方形是美妙四边形;(2)连接BD ,在Rt △ABD 和Rt △CBD 中,根据勾股定理可以解决;(3)连接AD ,利用等腰直角三角形的性质证明90ADB ∠=︒,45DAF EBD ∠=∠=︒,AD BD =,于是可证ADF BDE ∠=∠,继而证明用ASA 证明BED AFD ∆≅∆,根据全等三角形的性质得BE AF =,据此可得AE AF AB +=.【详解】解:(1)∵长方形的四个角都是直角,∴长方形是美妙四边形;故答案是:是;(2)如图1,连接BD ,在Rt △ABD 中,222BD AB AD =+,在Rt △CBD 中,222BD BC CD =+,∴2222CD CB AD AB +=+,∴2222CD AB AD BC -=-;(3)如图2,连接AD ,∵四边形AEDF 是美妙四边形,90A ∠=︒,∴90EDF ∠=︒,∵,90AB AC A =∠=︒,点D 为BC 的中点,∴90ADB ∠=︒,45DAF EBD ∠=∠=︒,AD BD =,∴ADF BDE ∠=∠,在Rt △ADF 和Rt △BDE 中,DAF DBE AD BDADF BDE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()BED AFD ASA ∆≅∆BE AF ∴=,AE AF AE BE AB ∴+=+=【点睛】本题考查了四边形综合问题,等腰直角三角形的性质及全等三角形的判定和性质,勾股定理,作辅助线构造直角三角形或全等三角形是解题关键.25.(1)证明见解析;(2)7【分析】(1)证明EF 、BD 互相平分,只要证DEBF 是平行四边形,利用两组对边分别平行来证明;(2)过D 点作DG ⊥AB 于点G ,通过已知可证△ADE 是等边三角形,所以CE=2,DE=4,由勾股定理可求DG ,继而可求得BD .【详解】(1)证明:∵四边形ABCD 是平行四边形,∴CD ∥AB ,CD=AB ,AD=BC ,∵DE 、BF 分别是∠ADC 和∠ABC 的角平分线,∴∠ADE=∠CDE ,∠CBF=∠ABF ,∵CD ∥AB ,∴∠AED=∠CDE ,∠CFB=∠ABF ,∴∠AED=∠ADE ,∠CFB=∠CBF ,∴AE=AD ,CF=CB ,∴AE=CF ,∴AB-AE=CD-CF ,即BE=DF ,∵DF ∥BE ,∴四边形DEBF 是平行四边形,∴BD 、EF 互相平分;(2)如图,过D 点作DG ⊥AB 于点G ,∵∠A=60︒,AE=AD ,∴△ADE 是等边三角形,∵AD=4,∴DE=AE=4,∵AE=2EB ,∴BE=2,在Rt △ADG 中,AD=4,∠A=60︒, ∴122AG AD ==, ∴2223AD AG -= ∴()222242327BD DG BG =+=+=【点睛】本题考查平行四边形的判定和性质、等边三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用所学知识解决问题.26.(1)见解析;(2)42BE =.【分析】(1)由四边形ABCD 是正方形,易证得△ABE ≌△CBE ,继而证得AE=CE ,再由AE=CE ,AE=EN ,即可证得∠ACN=90°,则可判定△CAN 为直角三角形;(2)由56,易求得CN 的长,然后由三角形中位线的性质,求得OE 的长,继而求得答案.【详解】解:(1)证明:∵四边形ABCD 是正方形,∴∠ABD=∠CBD=45°,AB=CB ,在△ABE 和△CBE 中, AB CB ABE CBE BE BE ⎧⎪∠∠⎨⎪⎩===,∴△ABE ≌△CBE (SAS ),∴AE=CE ;∵AE=CE ,AE=EN ,∴∠EAC=∠ECA ,CE=EN ,∴∠ECN=∠N ,∵∠EAC+∠ECA+∠ECN+∠N=180°,∴∠ACE+∠ECN=90°,即∠ACN=90°,∴△CAN 为直角三角形;(2)∵正方形的边长为6, ∴AC BD == ∵90,ACN AN ∠=︒=∴CN ==∵,OA OC AE EN ==,∴12OE CN ==∵12OB BD == ∴BE OB OE =+=【点睛】此题考查了正方形的性质、全等三角形的判定与性质、直角三角形的判定以及勾股定理等知识.注意利用勾股定理求得各线段的长是关键.。
新人教版初中数学八年级数学下册第三单元《平行四边形》测试卷(答案解析)(5)
一、选择题1.如图,菱形ABCD 中,50A ∠=︒,则ADB ∠的度数为( )A .65︒B .55︒C .45︒D .25︒ 2.如图,在平行四边形ABCD 中,DE 平分,6,2ADC AD BE ∠==,则平行四边形ABCD 的周长是( )A .16B .18C .20D .243.如图,在ABC 中,90ACB ∠=︒,点D 在AC 边上且AD BD =,M 是BD 的中点.若16AC =,8BC =,则CM 等于( )A .5B .6C .8D .10 4.如图,将长方形纸片沿对角线折叠,重叠部分为BDE ,则图中全等三角形共有( )A .0对B .1对C .2对D .3对 5.如图,把长方形纸片ABCD 沿对角线折叠,设重叠部分为EBD △.下列说法错误的是( )A .AE CE =B .12AE BE =C .EBD EDB ∠=∠ D .△ABE ≌△CDE 6.已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A .当AB BC =时,四边形ABCD 是菱形B .当AC BD ⊥时,四边形ABCD 是菱形C .当90ABC ∠=时,四边形ABCD 是矩形D .当AC BD =时,四边形ABCD 是正方形7.如图,ABE 、BCF 、CDG 、DAH 是四个全等的直角三角形,其中,AE =5,AB =13,则EG 的长是( )A .72B .62C .7D .73 8.如图,在四边形ABCD 中,对角线AC 、BD 相交于点O ,下列条件不能判定四边形ABCD 为平行四边形的是( )A .AB ∥CD ,AD ∥BCB .AD ∥BC ,AB =CD C .OA =OC ,OB =OD D .AB =CD ,AD =BC9.如图,ABCD 的对角线AC BD 、交于点,O DE 平分ADC ∠交AB 于点,60,E BCD ∠=︒12AD AB =,连接OE .下列结论:①ABCD S AD BD =⋅;②DB 平分CDE ∠;③AO DE =;④OE 垂直平分BD .其中正确的个数有( )A .1个B .2个C .3个D .4个10.在菱形ABCD 中,∠ABC=60゜,AC=4,则BD=( )A .3B .23C .33D .43 11.下列结论中,菱形具有而矩形不一定具有的性质是( ) A .对角线相等 B .对角线互相平分 C .对角线互相垂直 D .对边相等且平行 12.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,30ACD ∠=︒,若ABC 的周长比AOB 的周长大10,则AB 的长为( ).A .103B .53C .10D .20二、填空题13.如图,在平行四边形ABCD 中,2AD CD =,F 是AD 的中点,CE AB ⊥,垂足E 在线段AB 上.下列结论①DCF ECF ∠=∠;②EF CF =;③3DFE AEF ∠=∠;④2BEC CEF S S <中,一定成立的是_________.(请填序号)14.如图所示,在平行四边形ABCD 中2=AD AB ,CE 平分BCD ∠交AD 边于点E ,且4AE =,则AB 的长为______.15.如图,在Rt △ABC 中,∠ACB =90°,CD 是斜边AB 上的中线,E 、F 分别为DB 、BC 的中点,若AB =8,则EF =_____.16.在Rt ABC 中,∠C =90°,点D 是AB 边的中点,若AB =8,则CD =______. 17.如图,在平面直角坐标系xOy 中,点A 的坐标为(10,8),过点A 作AB x ⊥轴于点B ,AC y ⊥轴于点C ,点D 在AB 上.将△CAD 沿直线CD 翻折,点A 恰好落在x 轴上的点E 处,则点D 的坐标为_______.18.如图,90MON ∠=︒,矩形ABCD 的顶点A ,B 分别在边OM ,ON 上,当点B 在边ON 上移动时,点A 随之在边OM 上移动,2AB =,1BC =,运动过程中,点D 到点O 的最大距离为______.19.已知:如图,把长方形纸片ABCD 沿EF 折叠,使D C 、分别落在D C ''、的位置,若65EFB ︒∠=,则AED '∠的度数为_________.20.如图(1)所示为长方形纸带,将纸带沿EF 折叠成图(2),再沿BF 折叠成图(3),继续沿EF 折叠成图(4),按此操作,最后一次折叠后恰好完全盖住EFG ;整个过程共折叠了8次,问图(1)中DEF ∠的度数是_________.三、解答题21.如图所示,小明在测量旗杆AB 的高度时发现,国旗的升降绳自然下垂到地面时,还剩余0.3米,小明走到距离国旗底部6米的C 处,把绳子拉直,绳子末端恰好位于他的头顶D 处,假设小明的身高为1.5米,求旗杆AB 的高度是多少米?22.已知:线段,a b ,α∠(如图),用直尺和圆规作一个平行四边形,使它的两条对角线长分别等于线段,a b ,且两条对角线所成的一个角等于α∠.23.已知:如图,ABCD 中,AE 、CF 分别是BAD ∠和BCD ∠的角平分线,分别交边DC 、AB 于点E 、F ,求证:AE CF =.24.已知:平行四边形ABCD 中,点M 为边CD 的中点,点N 为边AB 的中点,联结AM 、CN .(1)求证:AM ∥CN ;(2)过点B 作BH AM ⊥,垂足为H ,联结CH .求证:△BCH 是等腰三角形.25.如图,已知点D 在ABC 的BC 边上,//DE AC 交AB 于E ,//DF AB 交AC 于F .(1)求证:AE DF =;,试判断四边形AEDF的形状,并说明理由.(2)若AD平分BAC26.下图所示的三种拼块A,B,C,每个拼块都是由一些大小相同、面积为1个单位的小正方形组成,如编号为A的拼块的面积为3个单位.现用若干个这三种拼块拼正方形,拼图时每种拼块都要用到,且这三种拼块拼图时可平移、旋转,或翻转.(1)若用1个A种拼块,2个B种拼块,4个C种拼块,则拼出的正方形的面积为个单位;(2)在图1和图2中,各画出了一个正方形拼图中1个A种拼块和1个B种拼块,请分别用不同的拼法将图1和图2中的正方形拼图补充完整.要求:所用的A,B,C三种拼块的个数与(1)不同,用实线画出边界线,拼块之间无缝隙,且不重叠.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】由菱形得到AB=AD,进而得到∠ADB=∠ABD,再由三角形内角和定理即可求解.【详解】解:∵四边形ABCD为菱形,∴AD=AB,∴∠ADB=∠ABD=(180°-∠A)÷2=(180°-50°)÷2=65°,故选:A.【点睛】本题考查了菱形的性质,菱形的邻边相等,属于基础题,熟练掌握菱形的性质是解决本题的关键.2.C解析:C【分析】根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CD、BC的长度,再求出▱ABCD的周长.【详解】解:∵DE平分∠ADC,∴∠ADE=∠CDE,∵四边形ABCD是平行四边形,∴AD∥BC,BC=AD=6,AB=CD,∴∠ADE=∠CED,∴∠CDE=∠CED,∴CE=CD,∵AD=6,BE=2,∴CE=BC-BE=6-2=4,∴CD=AB=4,∴▱ABCD的周长=6+6+4+4=20.故选:C.【点睛】本题考查了平行四边形对边平行,对边相等的性质,角平分线的定义,等角对等边的性质,熟练掌握平行四边形的性质,证明CE=CD是解题的关键.3.A解析:A【分析】根据直角三角形斜边的中线等于斜边的一半,得出12CM BD=,设CM x=,则2BD AD x ==,再根据勾股定理列方程求解即可得出答案.【详解】 解:90ACB ∠=︒,M 是BD 的中点,12CM BD ∴= 设CM x =,则2BD AD x ==16AC =162CD AC AD x ∴=-=-在Rt BCD △中,根据勾股定理得222BC CD BD +=即()()22281622x x +-=解得:5x =,故选A .【点睛】本题考查了直角三角形斜边的中线性质、勾股定理,熟练掌握性质定理是解题的关键. 4.C解析:C【分析】因为图形对折,所以首先△CDB ≌△ABD ,由于四边形是长方形,进而可得△ABE ≌△CDE ,如此答案可得.【详解】解:∵△BDC 是将长方形纸片ABCD 沿BD 折叠得到的,∴CD=AB ,AD=BC ,∵BD=BD ,∴△CDB ≌△ABD (SSS ),∴∠CBD=∠ADB∴EB=ED∴CE=AE又AB=CD∴△ABE ≌△CDE ,∴图中全等三角形共有2对故选:C【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、SSA 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要由易到难,循序渐进. 5.B解析:B【分析】由折叠的性质和平行线的性质可得∠ADB=∠CBD ,可得BE=DE ,可证AE=CE ,由“SAS”可证△ABE ≌△CDE ,即可求解.【详解】解:如图,∵把矩形纸片ABC'D 沿对角线折叠,∴∠CBD=∠DBC',CD=C'D=AB ,AD=BC=BC',∵AD ∥BC',∴∠EDB=∠DBC',∴∠EDB=∠EBD ,故选项C 正确;∴BE=DE ,∵AD=BC ,∴AE=CE ,故选项A 正确;在△ABE 和△CDE 中,AB CD A C AE CE =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△CDE (SAS ),故选项D 正确; 没有条件能够证明12AE BE =, 故选:B .【点睛】本题考查了翻折变换,全等三角形的判定和性质,矩形的性质,掌握折叠的性质是本题的关键. 6.D解析:D【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.【详解】解:A 、根据邻边相等的平行四边形是菱形可知:四边形ABCD 是平行四边形,当AB BC =时,它是菱形,故本选项不符合题意;B 、根据对角线互相垂直的平行四边形是菱形知:当AC BD ⊥时,四边形ABCD 是菱形,故本选项不符合题意;C、根据有一个角是直角的平行四边形是矩形知:当90∠=时,四边形ABCD是ABC矩形,故本选项不符合题意;=时,它是矩形,不是正方D、根据对角线相等的平行四边形是矩形可知:当AC BD形,故本选项符合题意;综上所述,符合题意是D选项;故选:D.【点睛】本题考查了对矩形的判定、菱形的判定,正方形的判定的应用,能正确运用判定定理进行判断是解此题的关键,难度适中.7.A解析:A【分析】根据勾股定理求出BE,证明四边形EFGH为正方形,根据正方形的性质、勾股定理计算,得到答案.【详解】解:在Rt△ABE中,AE=5,AB=13,由勾股定理得,BE12,∵△ABE、△BCF、△CDG、△DAH是四个全等的直角三角形,∴∠AEB=∠BFC=∠CGD=90°,BF=CG=DH=AE=5,∴∠FEB=∠EFC=∠FGD=90°,EF=EH=12﹣5=7,∴四边形EFGH为正方形,∴EG,故选:A.【点睛】本题考查的是全等三角形的应用,掌握全等三角形的对应边相等、对应角相等是解题的关键.8.B解析:B【分析】根据平行四边形的判定方法即可判断.【详解】A、根据两组对边分别平行的四边形是平行四边形,可以判定;B、无法判定,四边形可能是等腰梯形,也可能是平行四边形;C、根据对角线互相平分的四边形是平行四边形,可以判定;D、根据两组对边分别相等的四边形是平行四边形,可以判定;故选:B.【点睛】本题考查平行四边形的判定,解题的关键是掌握平行四边形的判定定理.9.C解析:C【分析】求得∠ADB=90°,即AD ⊥BD ,即可得到S ▱ABCD =AD•BD ;依据∠CDE=60°,∠BDE=30°,可得∠CDB=∠BDE ,进而得出DB 平分∠CDE ;依据Rt △AOD 中,AO >AD ,即可得到AO >DE ;依据O 是BD 中点,E 为AB 中点,可得BE=DE ,利用三角形全等即可得OE ⊥BD 且OB=OD .【详解】解:在ABCD 中,∵∠BAD=∠BCD=60°,∠ADC=120°,DE 平分∠ADC ,∴∠ADE=∠DAE=60°=∠AED ,∴△ADE 是等边三角形,12AD AE AB ∴==, ∴E 是AB 的中点,∴DE=BE ,1302BDE AED ︒∴∠=∠=, ∴∠ADB=90°,即AD ⊥BD ,∴S ▱ABCD =AD•BD ,故①正确;∵∠CDE=60°,∠BDE=30°,∴∠CDB=∠CDE-∠BDE=60°-30°=30°,∴∠CDB=∠BDE ,∴DB 平分∠CDE ,故②正确;∵Rt △AOD 中,AO >AD ,∵AD=DE ,∴AO >DE ,故③错误;∵O 是BD 的中点,∴DO=BO,∵E 是AB 的中点,∴BE=AE=DE∵OE =OE∴△DOE ≌△BOE(SSS)∴∠EOD=∠EOB∵∠EOD+∠EOB=180°∴∠BOE=90°∴OE 垂直平分BD ,故④正确;正确的有3个,故选择:C .【点睛】本题考查了平行四边形的性质,等边三角形的判定和性质,直角三角形的性质,平行四边形的面积公式的综合运用,三角形全等判定与性质,熟练掌握平行四边形的性质,等边三角形的性质,直角三角形的性质定理和等边三角形判定定理,三角形全等判定方法和性质是解题的关键.10.D解析:D【分析】根据菱形的性质可得到直角三角形,利用勾股定理计算即可;【详解】如图,AC 与BD 相较于点O ,∵四边形ABCD 是菱形,4AC =,∴AC BD ⊥,2AO =,又∵∠ABC=60゜,∴30ABO ∠=︒,∴24AB AO ==, ∴224223BO =-= ∴243BD BO ==;故选D .【点睛】本题主要考查了菱形的性质,结合勾股定理计算是解题的关键.11.C解析:C【分析】根据矩形和菱形的性质即可得出答案.【详解】解:A : 因为矩形的对角线相等,故此选项不符合题意;B :因为菱形和矩形的对角线都互相平分,故此选项不符合题意;C:因为对角线互相垂直是菱形具有的性质,故此选项符合题意;D:因为矩形和菱形的对边都相等且平分,故此选项不符合题意;故选:C.【点睛】本题考查矩形和菱形的性质,掌握矩形和菱形性质的区别是解题关键.12.A解析:A【分析】由矩形的性质和已知条件求出,BC=10,即可得出答案.【详解】解:∵四边形ABCD是矩形,∴AO=CO=DO=BO,AD=BC,∠ABC=90°,AB∥CD,∴∠BAC=∠ACD=30°,∴,∵△ABC的周长=AB+AC+BC=AB+AO+OC+BC,△AOB的周长=AB+AO+BO,又∵ABC的周长比△AOB的周长长10,∴AB+AC+BC-(AB+AO+BO)=BC=10,∴故选:A.【点睛】本题考查了矩形的性质、含30°角的直角三角形的性质等知识,熟练掌握矩形的性质,求出BC的长是解题的关键.二、填空题13.②③④【分析】如图延长EF交CD的延长线于H作EN∥BC交CD于NFK∥AB交BC于K利用平行四边形的性质全等三角形的判定和性质一一判断即可解决问题【详解】解:如图延长EF交CD的延长线于H作EN∥解析:②③④【分析】如图延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.利用平行四边形的性质,全等三角形的判定和性质一一判断即可解决问题.【详解】解:如图,延长EF交CD的延长线于H.作EN∥BC交CD于N,FK∥AB交BC于K.∵四边形ABCD是平行四边形,∴AB∥CH,∴∠A=∠FDH,在△AFE和△DFH中,A FDH AFE HFD AF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AFE ≌△DFH ,∴EF=FH ,∵CE ⊥AB ,AB ∥CH ,∴CE ⊥CD ,∴∠ECH=90°,∴CF=EF=FH ,故②正确,∵DF=CD=AF ,∴∠DFC=∠DCF=∠FCB ,∵∠FCB >∠ECF ,∴∠DCF >∠ECF ,故①错误,∵FK ∥AB ,FD ∥CK ,∴四边形DFKC 是平行四边形,∵AD=2CD ,F 是AD 中点,∴DF=CD ,∴四边形DFKC 是菱形,∴∠DFC=∠KFC ,∵AE ∥FK ,∴∠AEF=∠EFK ,∵FE=FC ,FK ⊥EC ,∴∠EFK=∠KFC ,∴∠DFE=3∠AEF ,故③正确,∵四边形EBCN 是平行四边形,∴S △BEC =S △ENC ,∵S △EHC =2S △EFC ,S △EHC >S △ENC ,∴S △BEC <2S △CEF ,故④正确,故正确的有②③④.故答案为②③④.【点睛】本题考查平行四边形的性质、全等三角形的判定和性质、直角三角形斜边的中线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.14.4【分析】根据平行四边形性质得出AB=DCAD ∥BC 推出∠DEC=∠BCE 求出∠DEC=∠DCE 推出DE=DC=AB 得出AD=2DE 即可求出AB 的长【详解】解:∵四边形ABCD 是平行四边形∴AB=D解析:4【分析】根据平行四边形性质得出AB=DC ,AD ∥BC ,推出∠DEC=∠BCE ,求出∠DEC=∠DCE ,推出DE=DC=AB ,得出AD=2DE ,即可求出AB 的长.【详解】解:∵四边形ABCD 是平行四边形,∴AB=DC ,AD ∥BC ,∴∠DEC=∠BCE ,∵CE 平分∠DCB ,∴∠DCE=∠BCE ,∴∠DEC=∠DCE ,∴DE=DC=AB ,∵AD=2AB=2CD ,CD=DE ,∴AD=2DE ,∴AE=DE=4,∴DC=AB=DE=4,故答案为:4.【点睛】本题考查了平行四边形性质,平行线性质,角平分线定义,等腰三角形的性质和判定的应用;熟练掌握平行四边形的性质,证出DE=AE=DC 是解决问题的关键.15.2【分析】根据直角三角形的性质求出再根据三角形中位线定理计算即可【详解】解:在中是斜边上的中线分别为的中点是的中位线故答案为:2【点睛】本题考查的是直角三角形的性质三角形中位线定理掌握三角形的中位线 解析:2【分析】根据直角三角形的性质求出CD ,再根据三角形中位线定理计算即可.【详解】解:在Rt ABC ∆中,90ACB ∠=︒,CD 是斜边AB 上的中线,8AB =,118422CD AB ∴==⨯=, E 、F 分别为DB 、BC 的中点,EF ∴是BCD ∆的中位线,114222EF CD ∴==⨯=,故答案为:2.【点睛】本题考查的是直角三角形的性质、三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.16.4【分析】根据直角三角形斜边上的中线等于斜边的一半可以得【详解】∵D 是AB 的中点∴∴故答案为:4【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质熟记性质是解题的关键解析:4.【分析】根据直角三角形斜边上的中线等于斜边的一半可以得2AB CD =.【详解】∵90C ∠=︒,D 是AB 的中点,∴2AB CD =, ∴118422CD AB ==⨯=. 故答案为:4.【点睛】 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键. 17.【分析】如详解中图先作出△CDE ;再由折叠性质得到CE=CA=10DE=DA=8-m 利用勾股定理计算出OE=6则EB=4在Rt △DBE 中利用勾股定理得到(8-m )2=m2+42然后解方程求出m 即可得解析:(10,3)【分析】如详解中图,先作出△CDE ;再由折叠性质得到CE=CA=10,DE=DA=8-m ,利用勾股定理计算出OE=6,则EB=4.在Rt △DBE 中利用勾股定理得到(8-m )2=m 2+42.然后解方程求出m 即可得到点D 的坐标.【详解】解:如图,作△CDE .设DB=m .由题意可得,OB=CA=10,OC=AB=8,∵△CED 与△CAD 关于直线CD 对称,∴CE=CA=10,DE=DA=8-m ,在Rt△COE中,OE=22-=6,108∴EB=10-6=4.在Rt△DBE中,∠DBE=90°,∴DE2=DB2+EB2.即(8-m)2=m2+42.解得m=3,∴点D的坐标是(10,3).故答案为(10,3).【点睛】本题考查了作图以及利用折叠的性质和勾股定理解直角三角形,掌握相关性质是解答此题的关键.18.【分析】取AB的中点E则OE=1DE=利用三角形原理可确定最大值【详解】如图取AB的中点E连接OEDE∵OE是直角三角形ABO斜边上的中线AB=2∴OE=1在直角三角形DAE中根据勾股定理得DE==解析:21+【分析】取AB的中点E,则OE=1,DE=2,利用三角形原理可确定最大值.【详解】如图,取AB的中点E,连接OE,DE,∵OE是直角三角形ABO斜边上的中线,AB=2,∴OE=1,在直角三角形DAE中,根据勾股定理,得DE=22+=2,DA AE∴当O,D,E三点共线时,DO最大,且最大值为2+1,故应该填21+.【点睛】本题考查了线段的最值,构造斜边上的中线,灵活运用三角形原理是解题的关键. 19.【分析】由长方形纸片可得再求解由折叠的性质求解结合平角的定义可得答案【详解】解:长方形纸片由折叠可得:故答案为:【点睛】本题考查的是矩形与折叠平行线的性质简单题解题的关键是理解折叠的性质解析:50︒【分析】由长方形纸片ABCD ,65EFB ∠=︒可得//,AD BC 再求解,DEF ∠ 由折叠的性质求解,D EF '∠ 结合平角的定义可得答案.【详解】 解: 长方形纸片ABCD ,65EFB ∠=︒,//,AD BC ∴65DEF EFB ∴∠=∠=︒,由折叠可得:65D EF DEF '∠=∠=︒,180180656550.AED D EF DEF ''∴∠=︒-∠-∠=︒-︒-︒=︒故答案为:50.︒【点睛】本题考查的是矩形与折叠,平行线的性质,简单题,解题的关键是理解折叠的性质. 20.20°【分析】根据最后一次折叠后恰好完全盖住∠EFG ;整个过程共折叠了8次可得CF 与GF 重合依据平行线的性质即可得到∠DEF 的度数【详解】解:设∠DEF=α在图(1)中∵是长方形纸带∴AD//BC ∴解析:20°【分析】根据最后一次折叠后恰好完全盖住∠EFG ;整个过程共折叠了8次,可得CF 与GF 重合,依据平行线的性质,即可得到∠DEF 的度数.【详解】解:设∠DEF=α,在图(1)中∵是长方形纸带,∴AD//BC ,∴∠EFB=∠DEF =α,∵折叠8次后CF 与GF 重合,∴∠CFE=8∠EFB=8α,∵CF ∥DE ,∴∠DEF+∠CFE=180°,∴α+8α=180°,∴α=20°,即∠DEF=20°.故答案为:20°.【点睛】本题考查了翻折变换以及矩形的性质.在本题中应理解∠DEF+∠CFE=180°.解决该题型题目时,根据翻折变换找出相等的边角关系是关键.三、解答题21.旗杆AB 的高度为10.6米【分析】过点D 作DE AB ⊥,垂足为E ,可证四边形BCDE 为长方形,可知 1.5BE CD ==米,设旗杆高度为x 米,则绳子长度为(0.3)AD x =+米,( 1.5)AE x =-米,在Rt ADE △中,由勾股定理,得222AE DE AD +=,222( 1.5)6(0.3)x x -+=+,解方程即可.【详解】解:过点D 作DE AB ⊥,垂足为E ,∵AB ⊥BC ,CD ⊥BC∴∠EBC=∠BCD=∠BED=90°,∴四边形BCDE 为长方形,∴ 1.5BE CD ==米,设旗杆高度为x 米,则绳子长度为(0.3)AD x =+米,( 1.5)AE AB BE x =-=-米, 在Rt ADE △中,由勾股定理,得222AE DE AD +=,∴222( 1.5)6(0.3)x x -+=+,整理得223 2.25360.60.09x x x x -++=++,即3.638.16x =,解得10.6x =.答:旗杆AB 的高度为10.6米.【点睛】本题考查勾股定理,矩形的判定与性质,一元一次方程的解法,掌握勾股定理,矩形的判定与性质,一元一次方程的解法,利用勾股定理结合旗杆与绳长的关系构造方程是解题关键.22.见解析【分析】先作线段a 、b 的垂直平分线得到12a 和12b ,再作∠AOB=∠α,且OA=12a ,OB=12b ,然后在OA 的反向延长线上截取OD=12a ,在OB 的反向延长线上截取OC=12b ,则利用平行四边形的判定方法可判断四边形ABCD 为平行四边形.【详解】解:如图,四边形ABCD 为所作.【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.23.见解析【分析】根据平行四边形的性质及角平分线的定义,证明ADE CBF ∆≅∆即可判断AE CF =.【详解】解:四边形ABCD 是平行四边形,DAB DCB ∴∠=∠,D B ∠=∠,AD BC =.AE ∵、CF 分别是BAD ∠和BCD ∠的角平分线,DAE BCF ∴∠=∠.()ADE CBF ASA ∴∆≅∆.AE CF ∴=.【点睛】本题主要考查了平行四边形的性质、全等三角形的判定和性质.证明线段相等的技巧一般是找到两个线段的相关三角形,通过全等求解.24.(1)见解析;(2)见解析【分析】(1)由四边形ABCD 是平行四边形,根据平行四边形的性质,可得AB ∥CD ,AB=CD ,又由点M 为边CD 的中点,点N 为边AB 的中点,即可得CM=AN ,继而可判定四边形ANCM 是平行四边形,则可证得AM ∥CN .(2)由AM ∥CN ,BH ⊥AM ,点N 为边AB 的中点,可证得BH ⊥CN ,ME 是△BAH 的中位线,则可得CN 是BH 的垂直平分线,继而证得△BCH 是等腰三角形.【详解】解:(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD 且AB CD =.∵点M 、N 分别是边CD 、AB 的中点, ∴12CM CD =,1AN AB 2=. ∴CM AN =.又∵AB ∥CD ,∴四边形ANCM 是平行四边形∴AM ∥CN .(2)设BH 与CN 交于点E ,∵AM ∥CN ,BH ⊥AM ,∴BH ⊥CN ,∵N 是AB 的中点,∴EN 是△BAH 的中位线,∴BE=EH ,∴CN 是BH 的垂直平分线,∴CH=CB ,∴△BCH 是等腰三角形.【点睛】此题考查了平行四边形的判定与性质、线段垂直平分线的性质以及等腰三角形的判定.此题难度适中,注意掌握数形结合思想的应用.25.(1)见解析;(2)菱形,见解析【分析】(1)由DE ∥AC 交AB 于E ,DF ∥AB 交AC 于F ,可证得四边形AEDF 是平行四边形,即可证得结论;(2)由AD 平分∠BAC ,DE ∥AC ,易证得△ADE 是等腰三角形,又由四边形AEDF 是平行四边形,即可证得四边形AEDF 是菱形.【详解】(1)证明:∵DE ∥AC ,DF ∥ AB ,∴四边形AEDF 是平行四边形,∴DE=AF ;(2)若AD 平分∠BAC ,则四边形AEDF 是菱形;理由:∵AD 平分∠BAC ,∴∠EAD=∠FAD ,∵DE ∥AC ,∴∠ADE=∠FAD,∴∠EAD=∠ADE,∴AE=DE,∵四边形AEDF是平行四边形,∴四边形AEDF是菱形.【点睛】此题考查了等腰三角形的判定与性质,菱形的判定与性质.注意熟练掌握菱形的判定方法是解此题的关键.26.(1)25;(2)补图见解析.【分析】(1)根据题意,知A 的拼块的面积为 3 个单位,B的面积为3个单位,C的面积为4个单位,即可得出;(2)图1用了3个A,2个B,1个C,图2用了4个A,1个B,1个C,和(1)不同即可.【详解】⨯+⨯+⨯=,(1)13234425∴正方形的面积为25;(2)答案不唯一,如:【点睛】本题主要考查了正方形的面积组合,读懂题意是解题的关键.。
新人教版初中数学八年级数学下册第三单元《平行四边形》测试卷(答案解析)(3)
一、选择题1.下列命题中,其逆命题是真命题的有( )个①全等三角形的对应角相等,② 两直线平行,同位角相等,③等腰三角形的两个底角相等,④正方形的四个角相等.A .1B .2C .3D .42.图1中甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD .已知图甲中,45F ∠=︒,15H ∠=︒,图乙中 2MN =,则图2中正方形的对角线AC 长为( )A .22B .23C .231+D .232+ 3.如图,正方形ABCD 中,6AB =,点E 在边CD 上,且2CE DE =.将ADE 沿AE 对折至AFE △,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①ABG AFG △≌△;②BG GC =;③//AG CF ;④3FGC S=.其中正确结论的个数是( )A .1B .2C .3D .44.在平面直角坐标系中,长方形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点,若E 为x 轴上的一个动点,当△CDE 的周长最小时,求点E 的坐标( )A .(一3,0)B .(3,0)C .(0,0)D .(1,0) 5.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF .若菱形ABCD 的边长为4,120B ∠=︒,则EF 的值是( )A .3B .2C .23D .46.已知点()0,0A ,()0,4B ,()3,4C t +,()3,D t .记()N t 为ABCD 内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则()N t 所有可能的值为( )A .6、7B .7、8C .6、7、8D .6、8、9 7.如图,己知四边形ABCD 是平行四边形,下列说法正确..的是( )A .若AB AD =,则平行四边形ABCD 是矩形B .若AB AD =,则平行四边形ABCD 是正方形C .若AB BC ⊥,则平行四边形ABCD 是矩形D .若AC BD ⊥,则平行四边形ABCD 是正方形8.如图,在123A A A △中,160A ∠=︒,230A ∠=︒,131A A =,3+n A 是1(1,2,3)n n A A n +=⋅⋅⋅的中点,则202120222023A A A △中最短边的长为( )A .100912B .101012 C .101112 D .1021129.如图,在矩形ABCD 中,O 为AC 中点,过点O 的直线分别与AB ,CD 交于点E 、F ,连接BF 交AC 于点M ,连接DE ,BO .若60COB ∠=︒,FO FC =.则下列结论:①FB 垂直平分OC ;②四边形DEBF 为菱形;③OC FB =;④2AM BM =;⑤:3:2BOM AOE S S =.其中正确结论的个数是( )A .5个B .4个C .3个D .2个10.如图,菱形ABCD 中,∠ABC=60°,AB=4,E 是边AD 上一动点,将△CDE 沿CE 折叠,得到△CFE ,则△BCF 面积的最大值是( )A .8B .83C .16D .163 11.如图,Rt Rt ABC BAD △≌△,BC 、AD 交于点E ,M 为斜边的中点,若CMD α∠=,AEB β∠=.则α和β之间的数量关系为( )A .2180βα-=︒B .60βα-=︒C .180αβ+=︒D .2βα=12.如图,已知平行四边形ABCD 中,4B A ∠=∠,则C ∠=( )A .18°B .36°C .72°D .144°二、填空题13.如图,平行四边形ABCD 中,CE AD ⊥于点E ,点F 为边AB 的中点,连接EF ,CF ,若12AD CD =,38CEF ∠=︒,则AFE ∠=_____________.14.如图所示,在平行四边形ABCD 中2=AD AB ,CE 平分BCD ∠交AD 边于点E ,且4AE =,则AB 的长为______.15.如图,在菱形纸片ABCD 中,4AB =,60A ∠=︒,将菱形纸片翻折,使点A 落在CD 边的中点E 处,折痕为FG ,点F 、G 分别在边AB 、AD 上,则GE =_______.16.如图,在平面直角坐标系中,点A 、点B 分别在x 轴和y 轴的正半轴上运动,且AB =4,若AC =BC =5,△ABC 的形状始终保持不变,则在运动的过程中,点C 到原点O 的最小距离为____________.17.如图,在平面直角坐标系xOy 中,点A 的坐标为(10,8),过点A 作AB x ⊥轴于点B ,AC y ⊥轴于点C ,点D 在AB 上.将△CAD 沿直线CD 翻折,点A 恰好落在x 轴上的点E 处,则点D 的坐标为_______.18.在四边形ABCD 中,AD ∥BC ,要使四边形ABCD 是平行四边形,还需添加一个条件,这个条件可以是__________.(只要填写一种情况)19.如图,EF 过ABCD 对角线的交点O ,交AD 于E ,交BC 于F ,若ABCD 的周长为19, 2.5OE =,则四边形EFCD 的周长为_____.20.已知Rt ABC ,90C ∠=︒,4cm AC =,3cm BC =,若PAB △与ABC 全等,PC ________.三、解答题21.如图,在平行四边形ABCD 中,点E 是边AD 的中点,连接CE 并延长交BA 的延长线于点F ,连接AC ,DF .(1)求证:AEF ≌DEC ;(2)求证:四边形ACDF 是平行四边形.22.如图,在长方形ABCD 中,DC =6cm ,在DC 上存在一点E ,沿直线AE 把△ADE 折叠,使点D 恰好落在BC 边上的点F 处,若△ABF 的面积为24cm 2,那么折叠的△ADE 的面积为多少?23.如图,在正方形中ABCD ,E 是AB 上一点,F 是AD 延长线上一点,且DF BE =.(1)求证:CE CF =;(2)若点G 在AD 上,且45GCE ︒∠=,判断线段GE BE GD 、、之间的数量关系,并说明理由.24.在ABC 中,23,AB CD AB =⊥于点,2D CD =.(1)如图1,当点D 是线段AB 的中点时,①AC 的长为________;②延长AC 至点E ,使得CE AC =,此时CE 与CB 的数量关系是_______,BCE ∠与A ∠的数量关系是_______;(2)如图2,当点D 不是线段AB 的中点时,画BCE ∠(点E 与点D 在直线BC 的异侧),使2BCE ∠=,A CE CB ∠=,连接AE .①按要求补全图形;②求AE 的长.25.已知:如图,在ABCD 中,AE 是BC 边上的高,将ABE △沿BC 方向平移,使点E 与点C 重合,得到GFC .(1)求证:BE DG =(2)若四边形ABFG 是菱形,且60B ︒∠=,求:AB BC 的值.26.正方形ABCD 中,对角线AC 、BD 交于点O ,E 为BD 上一点,延长AE 到点N ,使AE EN =,连接CN 、CE .(1)求证:CAN △为直角三角形.(2)若45AN =6,求BE 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】先把每一个命题的条件和结论互换就得到它的逆命题,再进行判断即可.【详解】解:“全等三角形的对应角相等”的逆命题是“三组角分别对应相等的两个三角形全等”,逆命题是假命题,故①不符合题意;“两直线平行,同位角相等”的逆命题是“同位角相等,两直线平行”,逆命题是真命题,故②符合题意;“等腰三角形的两个底角相等”的逆命题是“在一个三角形中,有两个角相等的三角形是等腰三角形”,逆命题是真命题,故③符合题意;“正方形的四个角相等”的逆命题是“四个角相等的四边形是正方形”,逆命题是假命题,故④不符合题意;综上:符合题意的有②③.故选:.B【点睛】本题考查的是命题与逆命题,命题真假的判断,正方形的判定方法,掌握由原命题得到逆命题,以及判断命题的真假是解题的关键.2.D解析:D【分析】连接HF ,过点G 作GI HF 交HF 于点I ,根据甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD ,可得EFH △是等腰直角三角形,则可求得45GFI ,30GHI ,根据勾股定理,可得:1GI =,3HI,则有1FI GI ,31EF HF HI FI ,根据正方形的对角线2AC EF =可求出答案.【详解】解:如图示,连接HF ,过点G 作GI HF 交HF 于点I ,∵甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD .∴根据题意,根据对称性可得EFH △是等腰直角三角形,则有:90EFH,45EHF HEF ∵45GFE ,15EHG , ∴45GFI ,30GHI ,又∵GIHF ,2MN =, ∴根据勾股定理,可得:1GI =,3HI , 则有1FIGI , ∴31EF HF HI FI , ∴正方形的对角线2231232ACEF ,故选:D .【点睛】 本题考查了正方形的性质,勾股定理,直角三角形的性质,熟悉相关性质是解题的关键. 3.C解析:C【分析】由正方形和折叠的性质得出AF =AB ,∠B =∠AFG =90°,由HL 即可证明Rt △ABG ≌Rt △AFG ,得出①正确;设BG =x ,则CG =BC−BG =6−x ,GE =GF +EF =BG +DE =x +2,由勾股定理求出x =3,得出②正确;由等腰三角形的性质和外角关系得出∠AGB =∠FCG ,证出平行线,得出③正确; 根据三角形的特点及面积公式求出△FGC 的面积,即可求证④.【详解】∵四边形ABCD 是正方形,∴AB =AD =DC =6,∠B =D =90°,∵CD =3DE ,∴DE =2,∵△ADE 沿AE 折叠得到△AFE ,∴DE =EF =2,AD =AF ,∠D =∠AFE =∠AFG =90°,∴AF =AB ,∵在Rt △ABG 和Rt △AFG 中,AG AG AB AF =⎧⎨=⎩, ∴Rt △ABG ≌Rt △AFG (HL ),∴①正确;∵Rt △ABG ≌Rt △AFG ,∴BG =FG ,∠AGB =∠AGF ,设BG =x ,则CG =BC−BG =6−x ,GE =GF +EF =BG +DE =x +2,在Rt △ECG 中,由勾股定理得:CG 2+CE 2=EG 2,∵CG =6−x ,CE =4,EG =x +2∴(6−x )2+42=(x +2)2解得:x =3,∴BG =GF =CG =3,∴②正确;∵CG =GF ,∴∠CFG =∠FCG ,∵∠BGF =∠CFG +∠FCG ,又∵∠BGF =∠AGB +∠AGF ,∴∠CFG +∠FCG =∠AGB +∠AGF ,∵∠AGB =∠AGF ,∠CFG =∠FCG ,∴∠AGB =∠FCG ,∴AG ∥CF ,∴③正确;∵△CFG 和△CEG 中,分别把FG 和GE 看作底边,则这两个三角形的高相同. ∴35CFG CEG SFG S GE ==, ∵S △GCE =12×3×4=6, ∴S △CFG =35×6=185, ∴④不正确;正确的结论有3个,故选:C .【点睛】本题考查了正方形性质、折叠性质、全等三角形的性质和判定、等腰三角形的性质和判定、平行线的判定等知识点的运用;主要考查学生综合运用性质进行推理论证与计算的能力,有一定难度.4.D解析:D【分析】由于C 、D 是定点,则CD 是定值,如果△CDE 的周长最小,即DE +CE 有最小值.为此,作点D 关于x 轴的对称点D′,当点E 在线段CD′上时,△CDE 的周长最小.【详解】如图,作点D 关于x 轴的对称点D′,连接CD′与x 轴交于点E ,连接DE .若在边OA 上任取点E′与点E 不重合,连接CE′、DE′、D′E′由DE′+CE′=D′E′+CE′>CD′=D′E +CE =DE +CE ,∴△CDE 的周长最小.∵OB =4,D 为边OB 的中点,∴OD =2,∴D (0,2),∵在长方形OACB 中,OA =3,OB =4,D 为OB 的中点,∴BC =3,D′O =DO =2,D′B =6,∵OE ∥BC ,∴Rt △D′OE ∽Rt △D′BC , ∴OE D O BC D B='', 即:623OE =,即:OE =1, ∴点E 的坐标为(1,0)故选:D .【点睛】此题主要考查轴对称−−最短路线问题,解决此类问题,一般都是运用轴对称的性质,将求折线问题转化为求线段问题,其说明最短的依据是:两点之间线段最短.5.B解析:B【分析】根据菱形的性质证明△ABD 是等边三角形,求得BD=4,再证明EF 是△ABD 的中位线即可得到结论.【详解】解:连接AC ,BD∵四边形ABCD 是菱形,∴AC BD ⊥,BD 平分∠ABC ,4AB BC CD DA ====∴∠111206022ABD ABC ︒=∠=⨯=︒ ∵AB AD =∴△ABD 是等边三角形, ∴ 4.BD =由折叠的性质得:EF AO ⊥,EF 平分AO ,又∵BD AC ⊥,∴//EF BD∴EF 为△ABD 的中位线, ∴122EF BD == 故选:B .【点睛】 本题考查了折叠性质,菱形性质,主要考查学生综合运用定理进行推理和计算的能力. 6.C解析:C【分析】分别求出t=1,t=1.5,t=2,t=0时的整数点,根据答案即可求出答案.【详解】解:当t=0时,A (0,0),B (0,4),C (3,4),D (3,0),此时整数点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),共6个点;当t=1时,A (0,0),B (0,4),C (3,5),D (3,1),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),共8个点;当t=1.5时,A (0,0),B (0,4),C (3,5.5),D (3,1.5),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),共7个点; 当t=2时,A (0,0),B (0,4),C (3,6),D (3,2),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(2,5),共8个点;故选项A 错误,选项B 错误;选项D 错误,选项C 正确;故选:C .【点睛】本题考查了平行四边形的性质.主要考查学生的理解能力和归纳能力.7.C解析:C【分析】根据已知及各个特殊四边形的判定方法对各个选项进行分析从而得到最后答案.【详解】解:A 、若AB=AD ,则▱ABCD 是菱形,选项说法错误;B 、若AB=AD ,则▱ABCD 是菱形,选项说法错误;C 、若AB ⊥BC ,则▱ABCD 是矩形,选项说法正确;D 、若AC ⊥BD ,则▱ABCD 是菱形,选项说法错误;故选:C .【点睛】此题考查了菱形,矩形,正方形的判定方法,对角线互相垂直平分且相等的四边形是正方形.8.B解析:B【分析】根据已知条件和图形的变化可得前几个图形的最短边的长度,进而可得结论.【详解】解:在△A 1A 2A 3中,∠A 1A 3A 2=90°,∠A 2=30°,A 1A 3=1,A n+3是A n A n+1(n=1、2、3…)的中点,可知:A 4A 5//A 1A 3,A 3A 4=A 2A 4,∴∠A 3A 5A 4=90°,∠A 4A 3A 2=∠A 2=30°,∴△A 1A 2A 3是含30°角的直角三角形,同理可证△A n A n+1A n+2是含30°角的直角三角形.△A 1A 2A 3中最短边的长度为A 1A 3=1=012, △A 3A 4A 5中最短边的长度为A 4A 5=12=112,△A 5A 6A 7中最短边的长度为A 5A 7=21142=, …, 所以△A n A n+1A n+2中最短边的长度为1212n -,则△A 2019A 2020A 2021中最短边的长度为120211221122n --==101012. 故选:B .【点睛】 本题考查了规律型:图形的变化类,解决本题的关键是观察图形的变化寻找规律.也考查了直角三角形斜边的中线,三角形的中位线,平行线的性质,含30°角的直角三角形的性质,以及等腰三角形的性质等知识.9.C解析:C【分析】证明△OFB ≌△CFB ,可判断结论①正确;利用菱形的定义,可判断结论②正确; 根据OC=OB ,斜边大于直角边,可判断结论③错误;根据30度角的性质,可判断AB=2BM ,故结论④是错误的;证NE ∥BM ,AN=NO=OM ,所以BM=3NE ,AO=2OM ,利用三角形面积公式计算判断,结论⑤正确.【详解】连接BD ,∵四边形ABCD 是矩形,∴AC=BD ,AC 、BD 互相平分,∵O 为AC 中点,∴BD 也过O 点,∴OB=OC ,∵∠COB=60°,OB=OC ,∴△OBC 是等边三角形,∴OB=BC=OC ,∠OBC=60°,∵FO=FC ,BF=BF∴△OBF ≌△CBF (SSS ),∴△OBF 与△CBF 关于直线BF 对称,∴FB ⊥OC ,OM=CM ;∴①正确,∵AB ∥CD ,∴∠OCF=∠OAE ,∵OA=OC ,∴△AOE ≌△COF ,∴OE=OF ,FC=AE ,∴DF=BE ,DF ∥BE ,∴四边形EBFD 是平行四边形,∵OA=OB ,∴∠OAB=∠OBA=30°,∵FO=OE=FC=AE ,∴∠AOE=∠FOM=30°,∴∠BOF=90°,∴BE=BF ,∴四边形EBFD 是菱形,∴结论②正确;∵OA=OB ,∴∠OAB=∠OBA=30°,∵FO=OE=FC=AE ,∴∠AOE=∠FOM=30°,∴∠BOF=90°,∴FB >OB ,∵OB=OC ,∴FB >OC ,∴③错误,在直角三角形AMB 中,∵∠BAM=30°,∠AMB=90°,∴AB=2BM ,∴④错误,设ED 与AC 的交点为N ,设AE=OE=2x ,则NE=x ,BE=4x ,∴AB=6x ,∴BM=3x , ∴11::22BOM AOE S SOM BM AO NE =⋅⋅ =3:2OM x OM x ⋅⋅=3:2,结论⑤正确.故选C .【点睛】本题考查了矩形的性质,等腰三角形三线合一性质,全等三角形,直角三角形30°角的性质,菱形的判定,熟练掌握,灵活运用是解题的关键.10.A解析:A【分析】由三角形底边BC 是定长,所以当△BCF 的高最大时,△BCF 的面积最大,即当FC ⊥BC 时,三角形有最大面积.【详解】解:在菱形ABCD 中,BC=CD=AB=4又∵将△CDE 沿CE 折叠,得到△CFE ,∴FC=CD=4由此,△BCF 的底边BC 是定长,所以当△BCF 的高最大时,△BCF 的面积最大,即当FC ⊥BC 时,三角形有最大面积∴△BCF 面积的最大值是1144822BC FC =⨯⨯= 故选:A .【点睛】本题考查菱形的性质和折叠的性质,掌握三角形面积的计算方法和菱形的性质正确推理计算是解题关键.11.A解析:A【分析】根据题意可得,CAB DBA ABC BAD ∠=∠∠=∠,再由直角三角形斜边的中线等于斜边的一半,可证CM DM AM BM ===,继而证明()AMC BMD SSS △≌△,解得1802AMC BMD CAM ∠=∠=︒-∠,最后根据三角形内角和180°定理,分别解得αβ、与CAM ∠的关系,整理即可解题.【详解】Rt Rt ABC BAD △≌△,CAB DBA ABC BAD ∴∠=∠∠=∠ M 是AB 的中点, 11,22CM AB DM AB ∴== CM DM AM BM ∴===∴∠CAM=∠MCA ,Rt Rt ABC BAD △≌△AC BD ∴=()AMC BMD SSS △≌△1802AMC BMD CAM ∴∠=∠=︒-∠CMD α∴=∠180AMC BMD =︒-∠-∠1802(1802)CAM =︒-⨯︒-∠4180CAM =∠-︒90ABC BAD CAM ∠=∠=︒-∠,AEB β=∠=180BAD ABC ︒-∠-∠180(90)(90)CAM CAM =︒-︒-∠-︒-∠2CAM =∠2180βα∴-=︒故选:A .【点睛】本题考查全等三角形的判定与性质、直角三角形斜边中线的性质、等腰三角形的性质、三角形内角和180°等知识,是重要考点,难度较易,掌握相关知识是解题关键. 12.B解析:B【分析】利用平行四边形的性质解决问题即可【详解】解:在平行四边形ABCD 中,∵BC ∥AD ,∴∠A+∠B=180°,∵∠B=4∠A ,∴∠A=36°,∴∠C=∠A=36°,故选:B .【点睛】本题考查平行四边形的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.二、填空题13.24°【分析】延长CF 交DA 延长线于点G 证△BCF ≌△AGF 得GF=FC 由垂直得△FEC 是等腰三角形可知△BFC 是等腰三角形求出∠GFE 和∠GFA 即可【详解】解:延长CF 交DA 延长线于点G ∵AG ∥B解析:24°【分析】延长CF 交DA 延长线于点G ,证△BCF ≌△AGF ,得GF=FC ,由垂直得△FEC 是等腰三角形,12AD CD =,可知△BFC 是等腰三角形,求出∠GFE 和∠GFA 即可. 【详解】解:延长CF 交DA 延长线于点G ,∵AG ∥BC ,∴∠G=∠BCF ,∠GAF=∠B ,∵AF=FB ,∴△AGF ≌△BCF ,∴GF=CF ,AG=BC ,∵CE AD ⊥,∴EF=FG=FC ,∠GEC=90°,∵38CEF ∠=︒,∴∠FEG=∠FGE=52°,∠GFE=76°, ∵12AD CD =, ∴BC=BF=AF ,∵AG=BC ,∴AG=AF ,∠G=∠AFG=52°, AFE ∠=76°-52°=24°.【点睛】本题考查了平行四边形的性质,直角三角形的性质,等腰三角形的性质,全等三角形的性质与判定,解题关键是作出适当的辅助线,构造等腰三角形.14.4【分析】根据平行四边形性质得出AB=DCAD∥BC推出∠DEC=∠BCE求出∠DEC=∠DCE推出DE=DC=AB得出AD=2DE即可求出AB的长【详解】解:∵四边形ABCD是平行四边形∴AB=D解析:4【分析】根据平行四边形性质得出AB=DC,AD∥BC,推出∠DEC=∠BCE,求出∠DEC=∠DCE,推出DE=DC=AB,得出AD=2DE,即可求出AB的长.【详解】解:∵四边形ABCD是平行四边形,∴AB=DC,AD∥BC,∴∠DEC=∠BCE,∵CE平分∠DCB,∴∠DCE=∠BCE,∴∠DEC=∠DCE,∴DE=DC=AB,∵AD=2AB=2CD,CD=DE,∴AD=2DE,∴AE=DE=4,∴DC=AB=DE=4,故答案为:4.【点睛】本题考查了平行四边形性质,平行线性质,角平分线定义,等腰三角形的性质和判定的应用;熟练掌握平行四边形的性质,证出DE=AE=DC是解决问题的关键.15.28【分析】过点作于根据菱形的性质得到继而可证再利用含30°角的直角三角形性质解得结合勾股定理解得的长根据折叠的性质得到最后在中利用勾股定理得据此整理解题即可【详解】过点作于是菱形是中点在中折叠在中解析:2.8【分析】过点E 作EH AD ⊥于H , 根据菱形的性质,得到//AB CD ,4AD BC CD AB ====,继而可证60A HDE ∠=∠=︒,再利用含30°角的直角三角形性质,解得12DH DE =,结合勾股定理解得HE 的长,根据折叠的性质,得到,AG GE AF EF ==,最后在Rt HGE 中利用勾股定理得222GE GH HE =+,据此整理解题即可.【详解】过点E 作EH AD ⊥于H ,ABCD 是菱形//AB CD ∴,4AD BC CD AB ====60A HDE ∴∠=∠=︒E 是CD 中点2DE ∴=在Rt DHE △中,2DE =HE DH ⊥60HDE ∠=︒30HED ∴∠=︒221,213DH HE ∴==-=折叠,AG GE AF EF ∴==在Rt HGE 中222GE GH HE =+22(41)3GE GE ∴=-++2.8GE ∴=故答案为:2.8.【点睛】本题考查翻折变换、菱形的性质、含30°角的直角三角形等知识,是重要考点,难度较易,掌握相关知识是解题关键.16.【分析】如图过作于证明求解结合三角形的三边的关系可得:>当三点共线时可得从而可得答案【详解】解:如图过作于由三角形三边的关系可得:>当三点共线时的最小值是:点C 到原点O 的最小距离为故答案为:【点睛】 解析:212- 【分析】 如图,过C 作CG AB ⊥于,G 4AB =,证明2,GB GA ==求解21,2,CG OG == 结合三角形的三边的关系可得:OC >,CG OG - 当,,C O G 三点共线时,,OC CG OG =- 可得212,CO CG OG ≥-=-从而可得答案.【详解】解:如图,过C 作CG AB ⊥于,G 4AB =, 5,CB CA ==2,GB GA ∴==22225221CG CA GA ∴=-=-=,90AOB ∠=︒,122OG AB ∴==, 由三角形三边的关系可得:OC >,CG OG -当,,C O G 三点共线时,,OC CG OG =-212,CO CG OG ∴≥-=-∴ CO 的最小值是:21 2.-∴ 点C 到原点O 的最小距离为21 2.-21 2.【点睛】本题考查的是等腰三角形的性质,勾股定理的应用,直角三角形斜边上的中线等于斜边的一半,三角形三边之间的关系,掌握以上知识是解题的关键.17.【分析】如详解中图先作出△CDE;再由折叠性质得到CE=CA=10DE=DA=8-m利用勾股定理计算出OE=6则EB=4在Rt△DBE中利用勾股定理得到(8-m)2=m2+42然后解方程求出m即可得解析:(10,3)【分析】如详解中图,先作出△CDE;再由折叠性质得到CE=CA=10,DE=DA=8-m,利用勾股定理计算出OE=6,则EB=4.在Rt△DBE中利用勾股定理得到(8-m)2=m2+42.然后解方程求出m即可得到点D的坐标.【详解】解:如图,作△CDE.设DB=m.由题意可得,OB=CA=10,OC=AB=8,∵△CED与△CAD关于直线CD对称,∴CE=CA=10,DE=DA=8-m,在Rt△COE中,22-,108∴EB=10-6=4.在Rt△DBE中,∠DBE=90°,∴DE2=DB2+EB2.即(8-m)2=m2+42.解得m=3,∴点D的坐标是(10,3).故答案为(10,3).【点睛】本题考查了作图以及利用折叠的性质和勾股定理解直角三角形,掌握相关性质是解答此题的关键.18.(答案不唯一)【分析】根据平行四边形的判定定理有一组对边平行且相等的四边形是平行四边形即可填写【详解】解:∵AD∥BCAD=BC∴四边形ABCD 是平行四边形故答案为:AD=BC(答案不唯一)【点睛】=(答案不唯一)解析:AD BC【分析】根据平行四边形的判定定理“有一组对边平行且相等的四边形是平行四边形”即可填写.【详解】解:∵AD∥BC,AD=BC,∴四边形ABCD是平行四边形.故答案为:AD=BC(答案不唯一)【点睛】本题考查了平行四边形的判定,熟知平行四边形的判定定理是解题的关键,本题有多种答案,如可以根据平行四边形的定义填写AB∥CD等.19.145【分析】根据平行四边形的性质易证三角形全等进而易得AE=CF故四边形的周长=AD+CD+EF根据已知求解即可【详解】解:在平行四边形ABCD中AD∥BCAC与BD互相平分∴AO=OC∠DAC=解析:14.5【分析】根据平行四边形的性质易证三角形全等,进而易得AE=CF,故四边形EFCD的周长=AD+CD+EF,根据已知求解即可.【详解】解:在平行四边形ABCD中,AD∥BC,AC与BD互相平分∴AO=OC,∠DAC=∠ACB,∠AOE=∠COF∴△AOE≌△COF∴AE=CF,OF=OE=2.5∴四边形EFCD的周长=CF+DE+CD+EF=AE+DE+CD+EF=AD+CD+EF=192.5 2×2=14.5.故答案为:14.5.【点睛】本题考查了平行四边形的性质以及三角形全等的证明,将所求线段转化为已知线段是解题的关键.20.5cm或cm或cm【分析】利用勾股定理列式求出AB然后分①点P与点C 在AB的两侧时AP与BC是对应边时四边形ACBP是矩形然后利用勾股定理列式计算即可得解;AP与AC是对应边时根据对称性可知AB⊥P解析:5cm或245cm或75cm.【分析】利用勾股定理列式求出AB,然后分①点P与点C在AB的两侧时,AP与BC是对应边时,四边形ACBP是矩形,然后利用勾股定理列式计算即可得解;AP与AC是对应边时,根据对称性可知AB⊥PC,再利用三角形的面积列式计算即可得解;②点P与点C在AB的同侧时,利用勾股定理求出BD,再根据PC=AB-2BD计算即可得解.【详解】解:在Rt ABC 中,90C ∠=︒,4cm AC =,3cm BC =, 由勾股定理得,2222435AB AC BC cm =+=+=,如图,①点P 与点C 在AB 的两侧时,若AP 与BC 是对应边,则四边形ACBP 1是矩形, ∴P 1C=AB=5cm ,若AP 与AC 是对应边,则△ABC 和△ABP 关于直线AB 对称,∴AB ⊥PC设AB 与P 2C 相交于点D ,则S △ABC =12×5•CD=12×3×4, 解得CD=125, ∴P 2C=2CD=2×125=245, ②点P 3与点C 在AB 的同侧时,由勾股定理得,22221293()55BD BC CD =-=-=, 过点P 3作P 3E ⊥AB ,垂足E ,连接P 3C ,如图,则有12×5•P 3E=12×3×4, ∴P 3E=125∴P 3E=CD 又P 3E ⊥AB ,CD ⊥AB ,∴P 3E//CD ,∴四边形P 3CDE 是平行四边形,又∠CDE=90°∴四边形P 3CDE 是矩形,∴P 3C=DE∵3P AB △≌ABC∴P3A=BC,∠P3AB=∠CBA 又∠P3EA=∠CDB=90°∴△P3AE≌△CBD∴AE=BD∴P3C=AB-2BD=5-2×95=75,综上所述,PC的长为5cm或245cm或75cm.故答案为:5cm或245cm或75cm.【点睛】本题考查了全等三角形的对应边相等的性质,勾股定理,轴对称性,难点在于分情况讨论,作出图形更形象直观.三、解答题21.(1)见解析;(2)见解析【分析】(1)根据平行四边形的性质可得AB//CD,根据平行线的性质可得就爱∠FAE=∠CDE,利用ASA即可证明△AEF≌△DEC;(2)根据全等三角形的性质可得AF=DC,根据有一组对边平行且相等的四边形是平行四边形即可得结论.【详解】(1)∵在平行四边形ABCD中,AB∥CD,∴∠FAE=∠CDE,∵点E是边AD的中点,∴AE=DE,在△AEF和△DEC中FAE CDE AE DEAEF DEC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AEF≌△DEC(ASA).(2)∵△AEF≌△DEC,∴AF=DC,∵AF∥DC,∴四边形ACDF是平行四边形.【点睛】本题考查平行四边形的判定与性质,平行四边形的对边互相平行;有一组对边平行且相等的四边形是平行四边形;熟练掌握相关性质与判定定理是解题关键.22.503cm2【分析】由面积法可求BF 的长,由勾股定理可求AF 的长,即可求CF 的长,由勾股定理可求DE 的长,即可求解.【详解】解:∵四边形ABCD 是长方形,∴AB =CD =6cm ,BC =AD ,∵S △ABF =12AB×BF =24cm 2, ∴BF =8cm ,在Rt △ABF 中,AF=10(cm ),∵沿直线AE 把△ADE 折叠,使点D 恰好落在BC 边上的点F 处,∴AD =AF =10cm ,DE =EF ,∴BC =10cm ,∴FC =BC ﹣BF =2cm ,在Rt △EFC 中,EF 2=EC 2+CF 2,∴DE 2=(6﹣DE )2+4,∴DE =103(cm ), ∴S △ADE =12×AD×DE =1101023⨯⨯=503(cm2), 答:折叠的△ADE 的面积为503cm 2. 【点睛】 此题考查矩形的性质,折叠的性质,勾股定理,利用面积法求线段的长度,熟记矩形的性质是解题的关键.23.(1)见解析;(2)GE=BE+GD ,理由见解析【分析】(1)由DF=BE ,四边形ABCD 为正方形可证△CEB ≌△CFD ,从而证出CE=CF ;(2)由(1)得,CE=CF ,∠BCE+∠ECD=∠DCF+∠ECD 即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF ,故可证得△ECG ≌△FCG ,即EG=FG=GD+DF .又因为DF=BE ,所以可证出GE=BE+GD .【详解】解:(1)证明:∵四边形ABCD 是正方形,∴BC=CD ,∠B=∠CDA ,∴∠B=∠CDF ,在△CBE 与△CDF 中,BC CD B CDF BE DF ⎧⎪∠∠⎨⎪⎩===,∴△CBE ≌△CDF (SAS ),∴CE=CF ;(2)GE=BE+GD ,理由:由(1)得△CBE ≌△CDF ,∴∠BCE=∠DCF ,CE=CF .∵∠GCE=45°,∴∠BCE+∠DCG=45°,∴∠GCF=∠DCF+∠DCG=45°,在△ECG 与△FCG 中,CE CF GCE GCF GC GC ⎧⎪∠∠⎨⎪⎩===,∴△ECG ≌△FCG (SAS ),∴GE=GF ,∴GE=DF+GD=BE+GD .【点睛】本题主要考查正方形的性质以及全等三角形的判定和性质,证两条线段相等往往转化为证明这两条线段所在三角形全等,在第二问中也考查了通过全等找出和GE 相等的线段,从而得出线段GE ,BE ,GD 之间的数量关系.24.(1)②CE=CB ;∠BCE=2∠A ;(2)①补全的图形见解析;②【分析】(1)①由D 是BC 的中点及CD ⊥AB ,根据勾股定理即可求解;②证明△ADC ≌△BDC ,继而得到BC=CE ,根据∠BCE=∠CAB+∠CBA ,∠CAB=∠CBA ,即可得到∠BCE=2∠A ; (2)①根据题干补全图形即可;②作∠ACM=∠BCE ,在射线CM 上截取CF=CA ,连接BF 、AF ,过点C 作CG ⊥AF 于点G ,利用已知条件先证△ACE ≌△FCB ,得到AE=BF ,然后再证四边形ADCG 是矩形,可求得AG=CD=2AF ,Rt △BAF 中,利用勾股定理即可求出BF ,继而可得AE 的长.【详解】解:(1)①∵D 是BC 的中点,CD ⊥AB ,∴∠ADC=∠BDC =90°,∴在Rt △ADC中,可得:AC ==②如图,延长AC 至点E ,使CE=AC ,在△ADC 和△BDC 中,DC DC AD BDADC BDC =⎧⎪=⎨⎪∠=∠⎩, ∴△ADC ≌△BDC ,∴AC=BC ,又∵AC=CE ,∴CB=CE ,∵∠BCE=∠CAB+∠CBA ,∠CAB=∠CBA ,∴∠BCE=∠CAB+∠CAB=2∠CAB ,即∠BCE=2∠A ;(2)①补全的图形见下图:②如图,作∠ACM=∠BCE ,在射线CM 上截取CF=CA ,连接BF 、AF ,过点C 作CG ⊥AF 于点G ,∴∠ACM+∠FCE=∠BCE+∠FCE,即∠ACE=∠FCB,∵CE=CB,∴△ACE≌△FCB,∴AE=BF,又∵CG⊥AF,∴∠CGF=90°,∵CF=CA,∴∠ACF=2∠ACG,AF=2AG,又∵∠BCE=2∠BAC,∠ACF=∠BCE,∴∠ACG=∠BAC,∴CG∥AD,∴∠AGC=∠BAF=∠ADC=90°,∴四边形ADCG是矩形,∴2,∴AF=2,在Rt△BAF中,∠BAF=90°,AB=23,AF=2∴222025=+==BF AB AF又∵AE=BF,∴AE=25即AE的长为5【点睛】本题考查全等三角形、等腰三角形、矩形的判定和性质、勾股定理及尺规作图,解题的关键是综合运用这些知识.25.(1)见详解;(2)AB:BC=2:3.【分析】(1)根据平移的性质,可得:AE=CG,再证明Rt△ABE≌Rt△CDG即可得到BE=DG;(2)根据四边形ABFG是菱形,得出AB=BF;根据条件找到满足AB=BF的AB与BC满足的数量关系即可.【详解】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD.∵AE是BC边上的高,且CG是由AE沿BC方向平移而成.∴CG⊥AD.∴∠AEB=∠CGD=90°.∵AE=CG,AB=CD,∴Rt△ABE≌Rt△CDG(HL).∴BE=DG;(2)∵四边形ABFG是菱形∴AB∥GF,AG∥BF,∵Rt△ABE中,∠B=60°,∴∠BAE=30°,∴BE=1AB.(直角三角形中30°所对直角边等于斜边的一半)2∵四边形ABFG是菱形,∴AB=BF.∴BE=CF,∴EF=1AB,2∴BC=3AB,2∴AB:BC=2:3.【点睛】本题考查平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等和平行四边形的性质以及菱形的性质.26.(1)见解析;(2)42BE .【分析】(1)由四边形ABCD是正方形,易证得△ABE≌△CBE,继而证得AE=CE,再由AE=CE,AE=EN,即可证得∠ACN=90°,则可判定△CAN为直角三角形;(2)由6,易求得CN 的长,然后由三角形中位线的性质,求得OE 的长,继而求得答案.【详解】解:(1)证明:∵四边形ABCD 是正方形,∴∠ABD=∠CBD=45°,AB=CB ,在△ABE 和△CBE 中,AB CB ABE CBE BE BE ⎧⎪∠∠⎨⎪⎩===,∴△ABE ≌△CBE (SAS ),∴AE=CE ;∵AE=CE ,AE=EN ,∴∠EAC=∠ECA ,CE=EN ,∴∠ECN=∠N ,∵∠EAC+∠ECA+∠ECN+∠N=180°,∴∠ACE+∠ECN=90°,即∠ACN=90°,∴△CAN 为直角三角形;(2)∵正方形的边长为6,∴AC BD ==∵90,ACN AN ∠=︒=∴CN ==∵,OA OC AE EN ==,∴12OE CN ==∵12OB BD ==∴BE OB OE =+=【点睛】此题考查了正方形的性质、全等三角形的判定与性质、直角三角形的判定以及勾股定理等知识.注意利用勾股定理求得各线段的长是关键.。
新人教版初中数学八年级数学下册第三单元《平行四边形》测试卷(含答案解析)(1)
16.如图,将长方形纸片 沿着对角线 翻折,点 落在点 处, 与 交于点 .若 , ,则 _______ .
17.在△ABC中,AD是BC边上的高线,CE是AB边上的中线,CD=AE,且CE<AC.若AD=6,AB=10,则CE=___________
24.如图,点 在正方形 的边 上,点 在边 的延长线上,且 .求证: .
25.如图,在正方形中 , 是 上一点, 是 延长线上一点,且 .
(1)求证: ;
(2)若点 在 上,且 ,判断线段 之间的数量关系,并说明理由.
26.如图,平行四边形 中, 是它的一条对角线,过 、 两点作 ,垂足分别为 、 ,延长 、 分别交 、 于 、 .
A.(一3,0)B.(3,0)C.(0,0)D.(1,0)
4.如图, 是 的边 的中点 平分 .且 ,垂足为 且 , . ,则 的周长是()
A.24B.25C.26D.28
5.如图,在 中,对角线 , 相交于点 , 、 是对角线 上的两点,给出下列四个条件,其中不能判定四边形 是平行四边形的有()
A. B. C. D.
(1) .求 的长.
【参考答案】***试卷处理标记,请不要删除
一、选择题
1.D
解析:D
【分析】
连接 ,过点 作 交 于点 ,根据甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD,可得 是等腰直角三角形,则可求得 , ,根据勾股定理,可得: , ,则有 , ,根据正方形的对角线 可求出答案.
三、解答题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.如图,在等腰直角ABC 中,AB BC =,点D 是ABC 内部一点, DE BC ⊥,DF AB ⊥,垂足分别为E ,F ,若3CE DE =, 53DF AF =, 2.5DE =,则AF =( )A .8B .10C .12.5D .152.如图,三个正方形围成一个直角三角形,64、400分别为所在正方形的面积,则图中字母M 所代表的正方形面积可表示为( )A .40064-B .2240064-C .2240064-D .40064+ 3.如图,在ABCD 中,对角线AC ,BD 相交于点O ,E 、F 是对角线AC 上的两点,给出下列四个条件,其中不能判定四边形DEBF 是平行四边形的有( )A .AE CF =B .DE BF =C .ADE CBF ∠=∠D .ABE CDF ∠=∠ 4.下列命题是真命题的是( )A .三角形的三条高线相交于三角形内一点B .一组对边平行,另一组对边相等的四边形是平行四边形C .对于所有自然数n ,237n n -+的值都是质数D .三角形一条边的两个顶点到这条边上的中线所在直线的距离相等5.如图,在平行四边形ABCD 中,100B D ︒∠+∠=,则B 等于( )A .50°B .65°C .100°D .130°6.如图,在平行四边形ABCD 中,90B ∠<︒,BC AB >.作AE BC ⊥于点E ,AF CD ⊥于点F ,记EAF ∠的度数为α,AE a =,AF b =.则以下选项错误的是( )A .::a b CD BC =B .D ∠的度数为αC .若60α=︒,则四边形AECF 的面积为平行四边形ABCD 面积的一半D .若60α=︒,则平行四边形ABCD 的周长为()433a b + 7.如图,ABCD 的对角线AC 、BD 交于点O ,顺次连接ABCD 各边中点得到一个新的四边形,如果添加下列四个条件中的一个条件:①AC BD ⊥;②ΔΔABO CBO C C =;③DAO CBO ∠=∠;④DAO BAO ∠=∠,可以使这个新的四边形成为矩形,那么这样的条件个数是( )A .1个B .2个C .3个D .4个8.已知四边形ABCD 中,90A B C ∠=∠=∠=,如果添加一个条件,即可判定该四边形是正方形,那么所添加的这个条件可以是( )A .90D ∠=;B .AB CD =;C .AD BC =; D .BC CD =. 9.如图,点D 和点E 分别是BC 和BA 的中点,已知AC =4,则DE 为( )A .1B .2C .4D .810.如图,已知四边形ABCD 中,R 、P 分别为BC 、CD 上的点,E 、F 分别为AP、RP的中点.当点P在CD上从点C向点D移动而点R不动时,那么下列结论成立的是()A.线段EF的长逐渐增大B.线段EF的长不变C.线段EF的长逐渐减小D.线段EF的长与点P的位置有关11.下列结论中,菱形具有而矩形不一定具有的性质是()A.对角线相等B.对角线互相平分C.对角线互相垂直D.对边相等且平行12.如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边的中线,点D,E分别在边AC 和BC上,DB=DE,EF⊥AC于点F,则以下结论;①∠DBM=∠CDE;②BN=DN;③AC=2DF;④S BDE∆﹤S BMFE四边形其中正确的结论是()A.①②③B.②③④C.①②④D.①③二、填空题13.如图,平行四边形ABCD中,CE AD⊥于点E,点F为边AB的中点,连接EF,CF,若12AD CD=,38CEF∠=︒,则AFE∠=_____________.14.如图,在平面直角坐标系中,点A、点B分别在x轴和y轴的正半轴上运动,且AB=4,若AC=BC=5,△ABC的形状始终保持不变,则在运动的过程中,点C到原点O的最小距离为____________.15.如图,在ABC 中,10AB AC ==,D 为CA 延长线上一点,DE BC ⊥交AB 于点F .若F 为AB 中点,且12BC =,则DF =__________.16.如图,将ABCD 沿对角线AC 进行折叠,折叠后点D 落在点F 处,AF 交BC 于点E ,有下列结论:①ABF CFB ≌;②AE CE =;③//BF AC ;④BE CE =,其中正确结论的是__________.17.如图,在ABCD 中,AC 与BD 相交于点O ,(1)若18cm,24cm AC BD ==,则AO =_______,BO =_______.又若13AB =厘米,则COD △的周长为________.(2)若AOB 的周长为30cm ,12cm AB =,则对角线AC 与BD 的和是________. 18.如图,将两个边长为1的小正方形,沿对角线剪开,重新拼成一个大正方形,则大正方形的边长是______.19.在长方形ABCD 中,52AB =,4BC =,CE CF =,CF 平分ECD ∠,则BE =_________.20.如图,将一张长方形纸片折叠成一个等腰梯形,则这个梯形的面积是_____cm 2.三、解答题 21.如图,四边形ABCD 是矩形,对角线AC 与BD 相交于点O ,∠AOD =60°,AD =2,求AC 的长度.22.如图,在菱形ABCD 中,过点D 分别作DE ⊥AB 于点E ,作DF ⊥BC 于点F .求证:AE =CF .23.如图,在ABCD 中,AE 平分BAD ∠交BD 于点E ,交BC 于点M ,CF 平分BCD ∠交BD 于点F .(1)若70ABC ∠=︒,求AMB ∠的度数;(2)求证:AE CF =.24.在ABC 中,23,AB CD AB =⊥于点,2D CD =.(1)如图1,当点D 是线段AB 的中点时,①AC 的长为________;②延长AC 至点E ,使得CE AC =,此时CE 与CB 的数量关系是_______,BCE ∠与A ∠的数量关系是_______;(2)如图2,当点D 不是线段AB 的中点时,画BCE ∠(点E 与点D 在直线BC 的异侧),使2BCE ∠=,A CE CB ∠=,连接AE .①按要求补全图形; ②求AE 的长.25.如图,在中,,D 为的中点,,,连接交于点O .(1)证明:四边形为菱形; (2)若,,求菱形的高.26.如图,在直角ABC 中,90BAC ∠=︒,点D 是BC 上一点,连接AD ,把AD 绕点A 逆时针旋转90°,得到AE ,连接DE 交AC 于点M .(1)如图1,若2,30,AB C AD BC =∠=︒⊥,求CD 的长;(2)如图2,若45ADB ∠=︒,点N 为ME 上一点,12MN BC =,求证:AN EN CD =+;(3)如图3,若30C ∠=︒,点D 为直线BC 上一动点,直线DE 与直线AC 交于点M ,当ADM △为等腰三角形时,请直接写出此时CDM ∠的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据比例关系设DF=x ,可判断四边形DEBF 为矩形,根据矩形的性质和比例关系分别表示CB 和AB ,再根据AB BC =,列出方程,求解即可得出x ,从而得出AF .【详解】,DE BC DF AB ⊥⊥,90DEB DFB ∴∠=∠=︒,∵△ABC 为等腰直角三角形,∴∠ABC=90°,∴四边形DEBF 为矩形,∴BF=DE=2.5,DF=EB ,设DF=3x ,则EB=3x ,∵53DF AF =,∴AF=5x ,AB=5x+2.5,∵3CE DE =,∴CE=7.5,∴CB=7.5+3x ,∵AB=CB ,∴5x+2.5=7.5+3x ,解得x=2.5,∴512.5AF x ==,故选:C .【点睛】本题考查矩形的性质和判定,等腰三角形的定义,一元一次方程的应用.能借助相关性质表示对应线段的长度是解题关键.本题主要用到方程思想.2.A解析:A【分析】要求图中字母所代表的正方形的面积,根据面积=边长×边长=边长的平方,设M 的边长为a ,直角三角形斜边的长为c ,另一直角边为b ,则2400c =,264b =,已知斜边和一直角边的平方,由勾股定理即可求出2a ,即可得到答案.【详解】设M 的边长为a ,直角三角形斜边的长为c ,另一直角边为b ,则2400c =,264b =,如图所示,在该直角三角形中,由勾股定理得:22240064a c b =-=-,故选:A .【点睛】本题主要考查勾股定理的应用和正方形的面积公式,解题的关键在于熟练运用勾股定理求出正方形的边长的平方.3.B解析:B【分析】根据全等三角形的判定和性质以及平行四边形的判定定理分别判断即可.【详解】解:A 、∵AE CF =,∴AO=CO ,由于四边形ABCD 是平行四边形,则BO=DO ,∴四边形DEBF 是平行四边形;B 、不能证明四边形DEBF 是平行四边形;C 、∵四边形ABCD 是平行四边形,∴AD=BC ,∠DAE=∠BCF ,又∠ADE=∠CBF ,∴△DAE ≌△BCF (ASA ),∴AE=CF ,同A 可证四边形DEBF 是平行四边形;D 、同C 可证:△ABE ≌△CDF (ASA ),∴AE=CF ,同A 可证四边形DEBF 是平行四边形;故选:B .【点睛】本题考查了平行四边形的判定定理,对角线互相平分的四边形是平行四边形,熟练掌握平行四边形的判定定理是解题的关键.4.D解析:D【分析】根据钝角三角形的高的交点在三角形外部可对A 进行判断;根据平行四边形的判定对B 进行判断;取n=6可对C 进行判断;根据三角形全等的知识可对D 进行判断.【详解】解:A 、钝角三角形的三条高线相交于三角形外一点,所以A 选项错误;B 、一组对边平行,另一组对边也平行的四边形是平行四边形,所以B 选项错误;C 、当n=6时,n 2-3n+7=25,25不是质数,所以C 选项错误;D 、通过证明三角形全等,可以证明三角形一条边的两个顶点到这条边上的中线所在直线的距离相等,所以D 选项准确.故选:D .【点睛】本题考查了命题:判断事物的语句叫命题;正确的命题称为真命题;错误的命题称为假命题.也考查了平行四边形的判定及全等三角形的判定和性质.5.A解析:A【分析】根据平行四边形的对角相等求出∠B 即可得解.【详解】解:□ABCD 中,∠B =∠D ,∵∠B +∠D =100°,∴∠B =12×100°=50°, 故选:A .【点睛】本题考查了平行四边形的性质,主要利用了平行四边形的对角相等是基础题. 6.C解析:C【分析】由平行四边形的性质得出//AD BC ,AD BC =,AB CD =,B D ∠=∠,得出180D C ∠+∠=︒,求出180EAF C ∠+∠=︒,得出B D EAF α∠=∠=∠=;由平行四边形ABCD 的面积得出::a b CD BC =;若60α=︒,则60B D ∠=∠=︒,求出30BAE DAF ∠=∠=︒,由直角三角形的性质得出BE AE ==,DF ,得出2AB BE =,2AD DF ==,求出平行四边形ABCD 的周长2())AB AD a b =+=+;求出ABE ∆的面积212BE AE =⨯=,ADF ∆的面积2=,平行四边形ABCD 的面积BC AE a =⨯=⨯=,得出四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22)a b =+≠平行四边形ABCD 面积的一半;即可得出结论. 【详解】 解:四边形ABCD 是平行四边形,//AD BC ∴,AD BC =,AB CD =,B D ∠=∠,180D C ∴∠+∠=︒,AE BC ⊥于点E ,AF CD ⊥于点F ,360290180EAF C ∴∠+∠=︒-⨯︒=︒,B D EAF α∴∠=∠=∠=;平行四边形ABCD 的面积BC AE CD AF =⨯=⨯,AE a =,AF b =, BC a CD b ∴⨯=⨯,::a b CD BC ∴=;若60α=︒,则60B D ∠=∠=︒,30BAE DAF ∴∠=∠=︒,BE AE ∴==,DF =,2AB BE ∴==,2AD DF ==,∴平行四边形ABCD 的周长2())AB AD a b =+=+;ABE ∆的面积21122BE AE a =⨯=⨯=,ADF ∆的面积21122DF AF b =⨯=⨯,平行四边形ABCD 的面积BC AE a =⨯=⨯=, ∴四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22)a b =+≠平行四边形ABCD 面积的一半; 综上所述,选项A 、B 、D 不符合题意,选项C 符合题意; 故选:C .【点睛】本题考查了平行四边形的性质、直角三角形的性质、三角形面积等知识;熟练掌握平行四边形的性质和直角三角形的性质是解题的关键.7.C解析:C【分析】根据顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.逐一对四个条件进行判断.【详解】解:顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.①,AC BD ⊥∴新的四边形成为矩形,符合条件; ②四边形ABCD 是平行四边形,,AO OC BO DO ∴==.ΔΔ,ABO CBO C C AB BC =∴=.根据等腰三角形的性质可知,BO AC BD AC ⊥∴⊥.所以新的四边形成为矩形,符合条件; ③四边形ABCD 是平行四边形,CBO ADO ∠∠∴=.,DAO CBO ADO DAO ∠∠∠∠=∴=.AO OD ∴=.,AC BD ∴=∴四边形ABCD 是矩形,连接各边中点得到的新四边形是菱形,不符合条件;④,DAO BAO BO DO ∠∠==,AO BD ∴⊥,即平行四边形ABCD 的对角线互相垂直,∴新四边形是矩形.符合条件.所以①②④符合条件.故选:C .【点睛】本题考查特殊四边形的判定与性质,掌握矩形、平行四边形的判定与性质是解题的关键. 8.D解析:D【分析】由已知可得该四边形为矩形,再添加条件:一组邻边相等,即可判定为正方形.【详解】解:由∠A=∠B=∠C=90°可判定四边形ABCD 为矩形,因此再添加条件:一组邻边相等,即可判定四边形ABCD 为正方形,故选:D .【点睛】本题考查正方形的判定.掌握相关判定定理正确推理论证是解题关键.9.B解析:B【分析】根据三角形中位线定理解答即可.【详解】解:∵点D和点E分别是BC和BA的中点,∴DE是△ABC的中位线,∴DE=12AC=124=2,故选:B.【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.10.B解析:B【分析】因为AR的长度不变,根据中位线定理可知,线段EF的长不变.【详解】解:因为AR的长度不变,根据中位线定理可知,EF平行与AR,且等于AR的一半.所以当点P在CD上从C向D移动而点R不动时,线段EF的长不变.故选:B.【点睛】主要考查中位线定理.在解决与中位线定理有关的动点问题时,只要中位线所对应的底边不变,则中位线的长度也不变.11.C解析:C【分析】根据矩形和菱形的性质即可得出答案.【详解】解:A:因为矩形的对角线相等,故此选项不符合题意;B:因为菱形和矩形的对角线都互相平分,故此选项不符合题意;C:因为对角线互相垂直是菱形具有的性质,故此选项符合题意;D:因为矩形和菱形的对边都相等且平分,故此选项不符合题意;故选:C .【点睛】本题考查矩形和菱形的性质,掌握矩形和菱形性质的区别是解题关键.12.D解析:D【分析】①设∠EDC=x ,则∠DEF=90°-x 从而可得到∠DBE=∠DEB=180°-(90°-x )-45°=45°+x ,∠DBM=∠DBE-∠MBE=45°+x-45°=x ,从而可得到∠DBM=∠CDE ;③由△BDM ≌△DEF ,可知DF=BM ,由直角三角形斜边上的中线的性质可知BM=12AC ; ④可证明△BDM ≌△DEF ,然后可证明:△DNB 的面积=四边形NMFE 的面积,所以△DNB 的面积+△BNE 的面积=四边形NMFE 的面积+△BNE 的面积;【详解】解:①设∠EDC=x ,则∠DEF=90°-x ,∵BD=DE ,∴∠DBE=∠DEB=∠EDC+∠C=x+45°,∴∠DBM=∠DBE-∠MBE=45°+x-45°=x .∴∠DBM=∠CDE ,故①正确;②由①得∠DBM=∠CDE ,如果BN=DN ,则∠DBM=∠BDN ,∴∠BDN=∠CDE ,∴DE 为∠BDC 的平分线,∴△BDE ≌△FDE ,∴EB ⊥DB ,已知条件∠ABC=90°,∴②错误的;③在△BDM 和△DEF 中,DBM CDE DMB DFE BD DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BDM ≌△DEF (AAS ),∴BM=DF ,∵∠ABC=90°,M 是AC 的中点,∴BM=12AC ,∴DF=12AC , 即AC=2DF ;故③正确.④由③知△BDM ≌△DEF (AAS )∴S △BDM =S △DEF ,∴S △BDM -S △DMN =S △DEF -S △DMN ,即S △DBN =S 四边形MNEF .∴S △DBN +S △BNE =S 四边形MNEF +S △BNE ,∴S △BDE =S 四边形BMFE ,故④错误;故选D .【点睛】本题主要考查了全等三角形的判定与性质、角平分线的性质,利用面积法证明S △BDE =S 四边形BMFE 是解题的关键.二、填空题13.24°【分析】延长CF 交DA 延长线于点G 证△BCF ≌△AGF 得GF=FC 由垂直得△FEC 是等腰三角形可知△BFC 是等腰三角形求出∠GFE 和∠GFA 即可【详解】解:延长CF 交DA 延长线于点G ∵AG ∥B解析:24°【分析】延长CF 交DA 延长线于点G ,证△BCF ≌△AGF ,得GF=FC ,由垂直得△FEC 是等腰三角形,12AD CD =,可知△BFC 是等腰三角形,求出∠GFE 和∠GFA 即可. 【详解】解:延长CF 交DA 延长线于点G ,∵AG ∥BC ,∴∠G=∠BCF ,∠GAF=∠B ,∵AF=FB ,∴△AGF ≌△BCF ,∴GF=CF ,AG=BC ,∵CE AD ⊥,∴EF=FG=FC ,∠GEC=90°,∵38CEF ∠=︒,∴∠FEG=∠FGE=52°,∠GFE=76°, ∵12AD CD =, ∴BC=BF=AF ,∵AG=BC ,∴AG=AF ,∠G=∠AFG=52°,AFE ∠=76°-52°=24°.【点睛】本题考查了平行四边形的性质,直角三角形的性质,等腰三角形的性质,全等三角形的性质与判定,解题关键是作出适当的辅助线,构造等腰三角形.14.【分析】如图过作于证明求解结合三角形的三边的关系可得:>当三点共线时可得从而可得答案【详解】解:如图过作于由三角形三边的关系可得:>当三点共线时的最小值是:点C 到原点O 的最小距离为故答案为:【点睛】 212【分析】如图,过C 作CG AB ⊥于,G 4AB =,证明2,GB GA ==求解21,2,CG OG == 结合三角形的三边的关系可得:OC >,CG OG - 当,,C O G 三点共线时,,OC CG OG =- 可得212,CO CG OG ≥-=从而可得答案.【详解】解:如图,过C 作CG AB ⊥于,G 4AB =, 5,CB CA ==2,GB GA ∴==22225221CG CA GA ∴=-=-,90AOB ∠=︒,122OG AB ∴==, 由三角形三边的关系可得:OC >,CG OG -当,,C O G 三点共线时,,OC CG OG =-212,CO CG OG ∴≥-=∴ CO 21 2.∴ 点C 到原点O 21 2.21 2.【点睛】本题考查的是等腰三角形的性质,勾股定理的应用,直角三角形斜边上的中线等于斜边的一半,三角形三边之间的关系,掌握以上知识是解题的关键.15.8【分析】过点A作AM⊥BC过点A作AN⊥BC交DE于N证明△AFN≌△BFE得出AN=BE=3再利用勾股定理解答即可【详解】解:∵AB=AC∴∠B=∠C∵∴∠C+∠BFE=90∠B+∠BFE=90解析:8【分析】过点A作AM⊥BC,过点A作AN⊥BC交DE于N,证明△AFN≌△BFE,得出AN=BE=3,再利用勾股定理解答即可.【详解】解:∵AB=AC,∴∠B=∠C,∵DE BC⊥,∴∠C+∠BFE=90,∠B+∠BFE=90°,∵∠BFE=∠AFD,∠B=∠C,∴∠BFE=∠AED=∠CDE,∴AD=AF,过点A作AM⊥BC,在△ABC中,∵AB=AC,∴M为BC的中点,∴BM=12BC=6,在Rt△ABM中,2222106AB BM-=-∵F为AB中点,FE⊥BC,∴FE为△ABM的中位线,BF=AF=12AB=5,∴AD=AF=5,BE=13BM=,2过点A作AN⊥BC交DE于N,∵AF=BF,∠AFN=∠BFE,∠ANF=∠BEF=90°,∴△AFN≌△BFE,∴AN=BE=3,在Rt△AND中,DN=2222AD AN-=-=,534∵AD=AF,AN⊥DF,∴DF=2DN=8.故答案为:8.【点睛】本题考查了勾股定理,等腰三角形的性质的运用,平行线的性质的运用,全等三角形的判定及性质的运用,正确作出辅助线是解题的关键.16.①②③【分析】根据SSS即可判定△ABF≌△CFB根据全等三角形的性质以及等式性质即可得到EC=EA根据∠EBF=∠EFB=∠EAC=∠ECA即可得出BF∥AC根据E不一定是BC的中点可得BE=CE解析:①②③【分析】根据SSS即可判定△ABF≌△CFB,根据全等三角形的性质以及等式性质,即可得到EC=EA,根据∠EBF=∠EFB=∠EAC=∠ECA,即可得出BF∥AC.根据E不一定是BC的中点,可得BE=CE不一定成立.【详解】解:由折叠可得,AD=AF,DC=FC,又∵平行四边形ABCD中,AD=BC,AB=CD,∴AF=BC,AB=CF,在△ABF和△CFB中,AB CF AF CB BF FB =⎧⎪=⎨⎪=⎩,∴△ABF ≌△CFB (SSS ),故①正确;∴∠EBF =∠EFB ,∴BE =FE ,∴BC -BE =FA -FE ,即EC =EA ,故②正确;∴∠EAC =∠ECA ,又∵∠AEC =∠BEF ,∴∠EBF =∠EFB =∠EAC =∠ECA ,∴BF ∥AC ,故③正确;∵E 不一定是BC 的中点,∴BE =CE 不一定成立,故④错误;故答案为:①②③.【点睛】本题主要考查了折叠问题,全等三角形的判定与性质以及平行线的判定的运用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.17.9cm12cm34cm36cm 【分析】(1)根据平行四边形对角线互相平分对边相等可得结果;(2)根据△AOB 的周长和AB 的长度得到AO+BO 从而得到AC+BD 【详解】解:(1)在平行四边形ABCD 中解析:9cm 12cm 34cm 36cm【分析】(1)根据平行四边形对角线互相平分,对边相等可得结果;(2)根据△AOB 的周长和AB 的长度,得到AO+BO ,从而得到AC+BD .【详解】解:(1)在平行四边形ABCD 中,∵AC=18cm ,BD=24cm ,∴AO=12AC=9cm=CO ,BO=12BD=12cm=DO , ∵AB=13cm ,∴CD=13cm ,∴COD △的周长为CO+DO+CD=9+12+13=34cm ,故答案为:9cm ,12cm ,34cm ;(2)∵△AOB 的周长为30cm ,∴AB+AO+BO=30cm ,∵AB=12cm ,∴AO+BO=30-12=18cm ,∴AC+BD=2AO+2BO=36cm .【点睛】此题考查了平行四边形的性质:平行四边形的对角线互相平分,平行四边形的对边相等.18.【分析】由题意和图示可知将两个边长为1的正方形沿对角线剪开将所得的四个三角形拼成一个大正方形大正方形的边长恰好是小正方形的对角线的长根据正方形的性质利用勾股定理求出小正方形对角线的长即可【详解】∵如【分析】由题意和图示可知,将两个边长为1的正方形沿对角线剪开,将所得的四个三角形拼成一个大正方形,大正方形的边长恰好是小正方形的对角线的长,根据正方形的性质,利用勾股定理求出小正方形对角线的长即可.【详解】∵如图是两个边长为1的小正方形,∴其对角线的长度==,∴【点睛】本题主要考查正方形的性质和勾股定理,熟练运用和掌握以上两个知识点是解题的关键.19.【分析】延长CF交EA的延长线于点G连接EF过点F作FH⊥CE于点H过点E作EM⊥CF于点M由题意易得FH=FDFH=EMEC=EG进而可得△CDF≌△CME 然后可得CM=CD=由勾股定理可得BG=解析:7 6【分析】延长CF,交EA的延长线于点G,连接EF,过点F作FH⊥CE于点H,过点E作EM⊥CF于点M,由题意易得FH=FD,FH=EM,EC=EG,进而可得△CDF≌△CME,然后可得CM=CD=52,由勾股定理可得BG=3,设BE=x,则有EC=EG=3+x,最后利用勾股定理可求解.【详解】解:延长CF,交EA的延长线于点G,连接EF,过点F作FH⊥CE于点H,过点E作EM⊥CF于点M,如图所示:∵四边形ABCD 是矩形,4BC =,52AB = ∴BC=AD ,52AB DC ==,AB ∥DC ,∠D=∠ABC=∠CBE=90° ∴∠DCF=∠G ,∵CF 平分∠ECD ,∴∠DCF=∠ECF ,DF=FH ,∴∠G=∠ECF ,∴EC=EG ,∴△ECG 是等腰三角形,∴CM=MG ,∵CE=CF ,∴△ECF 是等腰三角形, ∵EM 、FH 分别是等腰三角形ECF 腰上的高线, ∴FH=EM=DF ,∴Rt △CDF ≌Rt △CME (HL ), ∴52CM DC ==, ∴CG=5,∴在Rt △CBG 中,223BG CG CB -=, 设BE=x ,则有EC=EG=3+x ,在Rt △CBE 中,222BC BE CE +=, ∴()22243x x +=+, 解得:76x =, ∴76BE =; 故答案为76. 【点睛】本题主要考查等腰三角形的性质与判定、矩形的性质及勾股定理,熟练掌握等腰三角形的性质与判定、矩形的性质及勾股定理是解题的关键.20.40【分析】先由矩形的性质得AD=BC=13cm∠A=∠D=90°AD∥BC再由折叠的性质得AB=AB=4cmAE=AE=3cmCD=CD=4cmDF=DF=3cm求出EF的长然后由梯形面积公式即可解析:40【分析】先由矩形的性质得AD=BC=13cm,∠A=∠D=90°,AD∥BC,再由折叠的性质得AB=A'B=4cm,AE=A'E=3cm,CD=CD'=4cm,DF=D'F=3cm,求出EF的长,然后由梯形面积公式即可得出答案.【详解】解:如图所示:∵四边形ABCD是矩形,∴AD=BC=13cm,∠A=∠D=90°,AD∥BC,∴EF∥BC,AB⊥AD,由折叠的性质得:AB=A'B=4cm,AE=A'E=3cm,CD=CD'=4cm,DF=D'F=3cm,∴EF=AD-AE-DF=13-3-3=7(cm),∴等腰梯形BCFE的面积=12(EF+BC)×AB=12(7+13)×4=40(cm2),故答案为:40.【点睛】本题考查了翻折变换的性质、矩形的性质、等腰梯形的性质等知识;熟练掌握翻折变换和矩形的性质是解题的关键.三、解答题21.4【分析】根据矩形的性质和等边三角形的性质,可以得到OA的长,从而可以求得AC的长.【详解】解:∵四边形ABCD是矩形,∴OA=OC=OB=OD,∵∠AOD=60°,AD=2,∴△AOD是等边三角形,∴OA=OD=2,∴AC =2OA =4,即AC 的长度为4.【点睛】本题考查了矩形的性质,等边三角形的判定与性质,熟记性质并判断出△AOB 是等边三角形是解题的关键.22.见解析【分析】先由菱形的性质得到AD CD =,A C ∠=∠,再由AAS 证得ADE CDF ∆≅∆,即可得出结论.【详解】解:证明:∵四边形ABCD 是菱形,AD CD ∴=,A C ∠=∠,DE AB ∵⊥,DF BC ⊥,90AED CFD ∴∠=∠=︒,在ADE ∆和CDF ∆中,AED CFD A CAD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ADE CDF AAS ∴∆≅∆,AE CF ∴=.【点睛】本题考查了菱形的性质、全等三角形的判定与性质等知识;熟练掌握菱形的性质和全等三角形的判定与性质是解题的关键.23.(1)55°;(2)见解析【分析】(1)根据平行四边形的性质得到//AD BC ,根据平行线的性质得到180ABC BAD ∠+∠=︒,根据角平分线的定义得到1552DAM BAD ∠=∠=︒,于是得到结论;(2)根据平行四边形的性质得到AB CD =,BAD BCD ∠=∠,//AB CD ,求得ABE CDF ∠=∠,根据角平分线的定义及等量代换得到BAE DCF ∠=∠,根据全等三角形的性质即可得到AE CF =.【详解】(1)解:∵四边形ABCD 是平行四边形,∴//AD BC ,∴ 180ABC BAD ∠+∠=︒.∵70ABC ∠=︒,∴110BAD ∠=︒.∵AE 平分BAD ∠, ∴1552DAM BAD ∠=∠=︒. ∵//AD BC , ∴55AMB DAM ∠=∠=︒.(2)证明:∵四边形ABCD 是平行四边形,∴AB CD =,BAD BCD ∠=∠,//AB CD ,∴ ABE CDF ∠=∠.∵AE 平分BAD ∠, ∴12BAE BAD ∠=∠. ∵CF 平分BCD ∠, ∴12DCF BCD ∠=∠. ∵BAD BCD ∠=∠, ∴BAE DCF ∠=∠.又∵AB CD =,ABE CDF ∠=∠,∴ABE CDF △≌△,∴AE CF =.【点睛】本题考查了平行四边形的性质,全等三角形的判定和性质,正确的识别图形是解题的关键.24.(1)②CE=CB ;∠BCE=2∠A ;(2)①补全的图形见解析;②【分析】(1)①由D 是BC 的中点及CD ⊥AB ,根据勾股定理即可求解;②证明△ADC ≌△BDC ,继而得到BC=CE ,根据∠BCE=∠CAB+∠CBA ,∠CAB=∠CBA ,即可得到∠BCE=2∠A ; (2)①根据题干补全图形即可;②作∠ACM=∠BCE ,在射线CM 上截取CF=CA ,连接BF 、AF ,过点C 作CG ⊥AF 于点G ,利用已知条件先证△ACE ≌△FCB ,得到AE=BF ,然后再证四边形ADCG 是矩形,可求得AG=CD=2AF ,Rt △BAF 中,利用勾股定理即可求出BF ,继而可得AE 的长.【详解】解:(1)①∵D 是BC 的中点,CD ⊥AB ,∴∠ADC=∠BDC =90°,∴在Rt △ADC 中,可得:AC ==②如图,延长AC 至点E ,使CE=AC ,在△ADC 和△BDC 中,DC DC AD BDADC BDC =⎧⎪=⎨⎪∠=∠⎩, ∴△ADC ≌△BDC ,∴AC=BC ,又∵AC=CE ,∴CB=CE ,∵∠BCE=∠CAB+∠CBA ,∠CAB=∠CBA ,∴∠BCE=∠CAB+∠CAB=2∠CAB ,即∠BCE=2∠A ;(2)①补全的图形见下图:②如图,作∠ACM=∠BCE ,在射线CM 上截取CF=CA ,连接BF 、AF ,过点C 作CG ⊥AF 于点G ,∴∠ACM+∠FCE=∠BCE+∠FCE,即∠ACE=∠FCB,∵CE=CB,∴△ACE≌△FCB,∴AE=BF,又∵CG⊥AF,∴∠CGF=90°,∵CF=CA,∴∠ACF=2∠ACG,AF=2AG,又∵∠BCE=2∠BAC,∠ACF=∠BCE,∴∠ACG=∠BAC,∴CG∥AD,∴∠AGC=∠BAF=∠ADC=90°,∴四边形ADCG是矩形,∴AG=CD=2,∴AF=22,在Rt△BAF中,∠BAF=90°,AB=23,AF=22,∴222025=+==BF AB AF又∵AE=BF,∴AE=25,即AE的长为25.【点睛】本题考查全等三角形、等腰三角形、矩形的判定和性质、勾股定理及尺规作图,解题的关键是综合运用这些知识.25.(1)见解析;(2)【分析】(1)先证明四边形ADCE是平行四边形,再由直角三角形斜边上的中线性质得出CD=AB=AD,即可得出四边形ADCE为菱形;(2)过点D作DF⊥CE,垂足为点F;先证明△BCD是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由平行线的性质得出∠DCE=∠BDC=60°,在Rt△CDF中,求出DF即可.【详解】解:(1)证明:∵AE∥CD,CE∥AB,∴四边形ADCE是平行四边形,∵∠ACB=90°,D为AB的中点,∴CD=AB=AD,∴四边形ADCE为菱形;(2)过点D作DF⊥CE,垂足为点F,如图所示:DF即为菱形ADCE的高,∵∠B=60°,CD=BD,∴△BCD是等边三角形,∴∠BDC=∠BCD=60°,CD=BC=6,∵CE∥AB,∴∠DCE=∠BDC=60°,∴∠CDF=30°,又∵CD=BC=6,∴CF=3,∴在Rt△CDF中,DF==.【点睛】本题考查了平行四边形的判定、菱形的判定、等边三角形的判定与性质、平行线的性质,熟练掌握直角三角形的性质,并能进行推理论证与计算是解决问题的关键.26.(1)3;(2)见解析;(3)60︒或15︒或37.5︒【分析】(1)根据含30°角的直角三角形的性质可得BC=2AB=4,BD=12AB=1,即可得出CD的长;(2)在BD 上截取DF=EN ,可证出AEN ADF △≌△,由全等三角形的性质得AN=AF ,,EAN DAF ANE AFD ∠=∠∠=∠,可得出,MAN BAF ANM AFB ∠=∠∠=∠,则AMN ABF △≌△,可得12BF MN BC ==,即F 是BC 的中点,可得出AN=AF=FC=DF+CD=EN+CD ;(3)由题意可得AD=AE ,90EAD ∠=︒,45EDA AED ∠=∠=︒,分三种情况:①AM=MD ,②AM=AD ,③AD=MD ,根据等腰三角形的性质求出AMD ∠的度数,再根据三角形外角的性质即可求解.【详解】解:(1)∵90BAC ∠=︒,2,30AB C =∠=︒,∴BC=2AB=4,60B ∠=︒,∵AD BC ⊥∴90,30ADB BAD ∠=︒∠=︒,∴BD=12AB=1, ∴CD =BC-BD=4-1=3;(2)证明:如图2,在BD 上截取DF=EN ,∵把AD 绕点A 逆时针旋转90°,得到AE ,∴AD=AE ,90EAD ∠=︒,45EDA AED ∠=∠=︒,∵45ADB ∠=︒,∴45ADF AEN ∠=∠=︒,∴AEN ADF △≌△,∴AN=AF ,,EAN DAF ANE AFD ∠=∠∠=∠,∵90EAD ∠=︒,EAN DAF ∠=∠,∴90NAF ∠=︒,∵90BAC ∠=︒,ANE AFD ∠=∠,∴,MAN BAF ANM AFB ∠=∠∠=∠,∵AN=AF ,∴AMN ABF △≌△,∴12BF MN BC ==,即F 是BC 的中点, ∴AF=FC=DF+CD=EN+CD ,∵AN=AF ,∴AN EN CD =+; (3)解:由题意可得AD=AE ,90EAD ∠=︒,∴45EDA AED ∠=∠=︒,分三种情况:①AM=MD 时,∵AM=MD ,∴45EDA MAD ∠=∠=︒,∴90AMD ∠=︒,∵30C ∠=︒,∴CDM AMD C ∠=∠-∠=60︒;②AM=AD 时,∵AM=AD ,∴45EDA AMD ∠=∠=︒,∵30C ∠=︒,∴CDM AMD C ∠=∠-∠=15︒;③AD=MD 时,∵AD=MD ,∴AMD MAD ∠=∠,∴45EDA ∠=︒,∴1804567.52AMD MAD ︒-︒∠=∠==︒, ∵30C ∠=︒,∴CDM AMD C ∠=∠-∠=37.5︒.∴当ADM △为等腰三角形时,CDM ∠的度数为60︒或15︒或37.5︒.【点睛】本题主要考查了几何变换综合题,需要熟练掌握旋转的性质,直角三角形的性质,直角三角形斜边上中线的性质以及全等三角形的判定与性质,等腰三角形的性质,解题的关键是学会添加常用辅助线,正确寻找全等三角形解决问题.。
