大学物理能量守恒定律
大学物理 第三章 动量守恒定律和能量守恒定律 3-5 保守力与非保守力
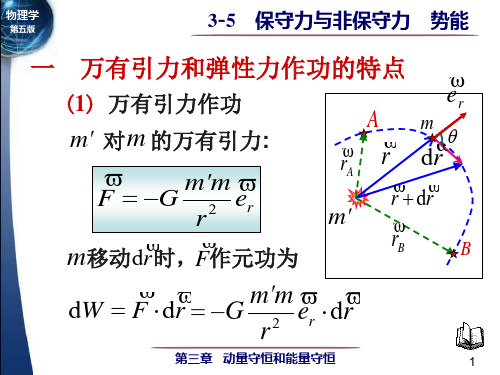
m' m m' m 引力的功 引力的功 WAB = −(−G r ) − (−G r ) B A
A点势能: 点势能: 且令E 设B点为无限远 即rB=∞ 且令 PB=0 点为无限远
m' m WAB = −G rA
= − ( E pB − E pA ) = E pA
功与路径无关,只决定于初末位置。 功与路径无关,只决定于初末位置。 第三章 动量守恒和能量守恒
4
} ⇒ dW
物理学
第五版
3-5 保守力与非保守力 势能 -
F
dW
O
x1
x2
dx
x2 x
W = ∫ Fdx = ∫
x1
x2
x1
1 2 1 2 − kxdx = −( kx2 − kx1 ) 2 2
5
第三章 动量守恒和能量守恒
W p → p0 = −( Ep0 − Ep ) = −∆Ep
E p ( x, y, z) =
∫
E p0 = 0
( x, y,z )
F ⋅ dr
任意一点的势能等于在保守力作用下 从该点到势能零点保守力所作的功
第三章 动量守恒和能量守恒 10
物理学
第五版
3-5 保守力与非保守力 势能 -
W AB = − ( E pB − E pA ) = − ∆ E P
引力的功 引力的功
m' m m' m WAB = −(−G ) − (−G ) rB rA
引力势能 引力势能
m' m Ep = −G r
弹性势能 弹性势能
弹力的功 弹力的功
W AB 1 1 2 2 = − ( kx B − kx A ) 2 2
能量守恒定律

三、能量守恒定律 - 重要意义
能量守恒定律,是自然界最普遍、最重要的基 本定律之一。从物理、化学到地质、生物,大到宇 宙天体。小到原子核内部,只要有能量转化,就一 定服从能量守恒的规律。从日常生活到科学研究、 工程技术,这一规律都发挥着重要的作用。人类对 各种能量,如煤、石油等燃料以及水能、风能、核 能等的利用,都是通过能量转化来实现的。能量守 恒定律是人们认识自然和利用自然的有力武器。 “能量的转化和守恒定律”的三种表述反映了人类 认识这一自然规律的历程。这三种表述一种比一种 更深刻,一种比一种更接近客观真理。人类正是这 样一步一步地认识物质世界的。
(4)永动机的不可能
据说永动机的概念发端于印度,在公元12世纪传入欧洲。 据记载欧洲最早、最著名的一个永动机设计方案是十三 世纪时一个叫亨内考(Villand de Honnecourt)的法国人提 出来的。如图所示:轮子中央有一个转动轴,轮子边缘安装 着12个可活动的短杆,每个短杆的一端装有一个铁球。 随后,研究和发明永动机的人不断涌现。尽管有不少学 者研究指出永动机是不可能的,研究永动机的人还是前赴后 继。 文艺复兴时期意大利伟大学者达 芬奇(Leonardo da vinc,1452-1519)曾经用不少精力研究永动机。可贵的是 他最后得到了永动机不可能的结论。 与达 芬奇同时代还有一位名叫卡丹的意大利人 (Jerome Cardan ,1501-1576),他以最早给出求解三次 方程的根而出名,也认为永动机是不可能的。
1. 能量守恒定律发现的准备
能械能和热能有较深入的研究。我们现在就这 两方面来叙述。
(1)活力与死力的论战
1644年笛卡尔(Rene Descartes,1596-1650)在他所著的《哲学原理》 中讨论碰撞问题时引进了动量的概念,用以度量运动。1687年牛顿(Isac Newton,1642-1727)在他的《自然哲学的数学原理》中把动量的改变来 度量力。与此不同的是莱布尼兹(Gottfried Wilhelm Leibniz,1646- 1716)在1686年的一篇论文中抨击笛卡尔,主张用质量乘速度的平方来 度量运动,莱布尼兹称之为活力。把牛顿由动量所度量的力也称为死力。 莱布尼兹的主张正好和1669年惠更斯关于碰撞问题研究的结论一致,该 结论说“两个物体相互碰撞时,它们的质量与速度平方乘积之和在碰撞 前后保持不变。” 从莱布尼兹挑起争论起,形成了以笛卡尔和莱布尼兹两大派的论争。 这场论战延续了近半个世纪,许多学者都参加了论战,并且各有实验佐 证。一直到1743年法国学者达朗贝尔(Jean le Rond d'Alembert,1717 -1783)在他的《论动力学》中说:“对于量度一个力来说,用它给予 一个受它作用而通过一定距离的物体的活力,或者用它给予受它作用一 定时间的物体的动量同样都是合理的。”在这里,达朗贝尔揭示了活力 是按作用距离力的量度,而动量是按作用时间力的量度。这场争论终于 尘埃落定了。活力才作为一个正式的力学名词为力学家们普遍接受。
大学物理动量守恒定律和能量守恒定律

04
动量守恒定律和能量守恒定 律的意义与影响
在物理学中的地位
基础定律
动量守恒定律和能量守恒定律是物理学中的两个基础定律,它们 在理论物理学和实验物理学中都占据着重要的地位。
理论基石
这两个定律为物理学理论体系提供了基石,许多物理理论和公式都 是基于这两个定律推导出来的。
验证实验
许多实验通过验证动量守恒定律和能量守恒定律的正确性,来检验 实验的准确性和可靠性。
适用条件
系统不受外力或外力合力为零
动量守恒定律只有在系统不受外力或外力合力为零的情况下才成立。如果系统受到外力作 用,则总动量将发生变化。
系统内力的作用相互抵消
系统内力的作用只会改变系统内各物体的速度,而不会改变系统的总动量。如果系统内力 的作用相互抵消,则总动量保持不变。
理想气体和刚体的动量守恒
未来能源利用的发展需要解决环 境问题和能源短缺问题,动量守 恒定律和能量守恒定律将在新能 源技术、节能技术等领域发挥关
键作用。
感谢您的观看
THANKS
在理想气体和刚体的研究中,由于气体分子之间的相互作用力和刚体之间的碰撞力都可以 忽略不计,因此它们的动量守恒。
实例分析
弹性碰撞
当两个小球发生弹性碰撞时,根据动量守恒定律,它们碰撞后 的速度满足m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'。由于弹性碰撞中能 量没有损失,因此碰撞前后两小球的速度变化量相等。
动量与能量的关系
动量是质量与速度的乘积,表 示物体的运动状态;能量是物 体运动状态的度量,包括动能
和势能。
动量和能量都是矢量,具有 方向性,遵循矢量合成法则。
动量和能量可以相互转化,但 总量保持不变,这是动量守恒 和能量守恒定律的内在联系。
大学物理(3.4.2)--功能原理机械能守恒定律能量守恒定律

第四讲功能原理 机械能守恒定律 能量守恒定律k k k i i i i ii e E E E v m v m W W ∆=-=-=+∑122122)2121(系统的外力和内力作功的总和等于系统动能的增量。
回顾前面学过的知识点:1. 质点系动能定理P1p 2p )(E E E W ∆-=--=2. 保守力作功等于势能的减少3. 成对力的功只与作用力和相对位移有关:r d F dW '⋅= 22/16※ 质点系功能原理1、系统的机械能: 动能与势能的总和称为机械能3、由势能的定义,保守内力的功总等于系统势能的减少pin c E W ∆-= 2、内力的功可分为: 保守内力的功和非保守内力功pk E E E +=(保守内力的功由势能代替)第四讲 功能原理 机械能守恒定律 能量守恒定律 in ncin c in in W W W W i i+==∑非保守内力的功将导致机械能与其他形式的能量转换。
inncex p k W W E E E +=∆+∆=∆k in ncp ex in nc in c ex in ex E W E W W W W W W ∆=+∆-=++=+ 4、系统的功能原理 (由质点系动能定理)在选定的质点系内,在任一过程中,质点系总机械能的增量等于所有外力的功与非保守内力的功的代数和。
4/16※ 机械能守恒定律问题1:有非保守内力作功,系统的机械能不守恒 ?例如:摩擦力作功,机械能转变成热能。
0=+in nc ex W W 0=∆+∆=∆p k E E E 常量=+p k E E 由功能原理:则:或:如果: 如果系统内只有保守内力作功,其他内力和一切外力都不作功,或元功之和恒为零,则系统内各物体的动能和势能可以相互转换,但总机械能保持不变。
问题2:有摩擦力作功:机械能守恒?in nc ex p k W W E E E +=∆+∆=∆力 f 作正功,f ' 作负功,总和为零,机械能守恒。
大学物理第三章-动量守恒定律和能量守恒定律-习题及答案

即:作用在两质点组成的系统的合外力的冲量等于系统内两质点动量之和的增 量,即系统动量的增量。 2.推广:n 个质点的情况
t2 t2 n n n n F d t + F d t m v mi vi 0 i外 i内 i i i 1 i 1 i 1 i 1 t1 t1
yv 2
同乘以 ydy,得
y 2 gdty y
积分 得
y
0
y
gdty
yvdt( yv)
0
1 3 1 gy ( yv) 2 3 2
因而链条下落的速度和落下的距离的关系为
2 v gy 3
1/ 2
7
第4讲
动量和冲量
考虑到内力总是成对出现的,且大小相等,方向相反,故其矢量和必为零, 即
F
i 0
n
i内
0
设作用在系统上的合外力用 F外力 表示,且系统的初动量和末动量分别用
5
第4讲
动量和冲量
P0 和 P 表示,则
t2 n n F d t m v mi vi 0 i i 外力 t1
F外 dt=dPFra bibliotek力的效果 关系 适用对象 适用范围 解题分析
*动量定理与牛顿定律的关系 牛顿定律 动量定理 力的瞬时效果 力对时间的积累效果 牛顿定律是动量定理的 动量定理是牛顿定律的 微分形式 积分形式 质点 质点、质点系 惯性系 惯性系 必须研究质点在每时刻 只需研究质点(系)始末 的运动情况 两状态的变化
1
第4讲
动量和冲量
§3-1 质点和质点系的动量定理
实际上,力对物体的作用总要延续一段时间,在这段时间内,力的作用将 积累起来产生一个总效果。下面我们从力对时间的累积效应出发,介绍冲量、 动量的概念以及有关的规律,即动量守恒定律。 一、冲量 质点的动量定理 1.动量:Momentum——表示运动状态的物理量 1)引入:质量相同的物体,速度不同,速度大难停下来,速度小容易停下;速 度相同的物体,质量不同,质量大难停下来,质量小容易停下。 2)定义:物体的质量 m 与速度 v 的乘积叫做物体的动量,用 P 来表示 P=mv 3)说明:动量是矢量,大小为 mv,方向就是速度的方向;动量表征了物体的 运动状态 -1 4)单位:kg.m.s 5)牛顿第二定律的另外一种表示方法 F=dP/dt 2.冲量:Impulse 1)引入:使具有一定动量 P 的物体停下,所用的时间Δt 与所加的外力有关, 外力大,Δt 小;反之外力小,Δt 大。 2)定义: 作用在物体外力与力作用的时间Δt 的乘积叫做力对物体的冲量, 用 I 来表 示 I= FΔt 在一般情况下,冲量定义为
大学物理第三章动量守恒定律和能量守恒定律

动量守恒定律的表述
总结词
动量守恒定律表述为系统不受外力或所 受外力之和为零时,系统总动量保持不 变。
VS
详细描述
动量守恒定律是自然界中最基本的定律之 一,它表述为在一个封闭系统中,如果没 有外力作用或者外力之和为零,则系统总 动量保持不变。也就是说,系统的初始动 量和最终动量是相等的。
动量守恒定律的适用条件
能量守恒定律可以通过电磁学 的基本公式推导出来。
能量守恒定律可以通过相对论 的质能方程推导出来。
能量守恒定律的应用实例
01
02
03
04
机械能守恒
在无外力作用的系统中,动能 和势能可以相互转化,但总和
保持不变。
热能守恒
在一个孤立系统中,热量只能 从高温物体传递到低温物体,
最终达到热平衡状态。
电磁能守恒
详细描述
根据牛顿第三定律,作用力和反作用力大小相等、方向相反。如果将一个物体施加一个力F,则该力会产生一个 加速度a,进而改变物体的速度v。由于力的作用是相互的,反作用力也会对另一个物体产生相同大小、相反方向 的加速度和速度变化。因此,在系统内力的相互作用下,系统总动量保持不变。
02
能量守恒定律
能量守恒定律的表述
感谢观看
01
能量守恒定律表述为:在一个封闭系统中,能量不能被创造或消灭, 只能从一种形式转化为另一种形式。
02
能量守恒定律是自然界的基本定律之一,适用于宇宙中的一切物理过 程。
03
能量守恒定律是定量的,可以用数学公式表示。
04
能量守恒定律是绝对的,不受任何物理定律的限制。
能量守恒定律的适用条件
能量守恒定律适用于孤立系统,即系统与外界没有能量 交换。
(大学物理)第二章守恒定律
这并不是空谈……..今天条件不具备,明天就会创造出来;今天还没有,明天
一定会有!
8
原子城——金银滩草原
9
金银滩草原
10
例 作用
在
质F点(的 2yi力 4x2j)
( N)
,质
点
从
原
点运动
到x坐 ( 2标 m) 为, y( 1 m) 的
点(如图
计算F力 分别沿下列路径 功所 :y作 ( j) 的
3.在所有惯性系中,动能定理形式保持不变。
A1212m2v2 12m1v2
动能定理的量值相对不同惯性系值不相同, 即
(V22-V21)的值不相同。
14
[例]质点m=0.5Kg,运动方程x=5t,y=0.5t2 (SI) , 求从t=2s到t=4s这段时间内外力所作的功.
解法
1:
用功的定义式
r aA f 5 ddmtt2iar2f d0 01r..55 jtj2 j
m1
f1 f2
dr2
m2
F2
m2
A B 2 2 F 2f2d r21 2m 2 v2 2 B 21 2m 2 v2 2 A 2 A1
A2
B1
B2
B1
B2
F1dr1 F2dr2 f1dr1 f2dr2
A1
A2
A1
A2
12m1v12B1
12m2v22B2
12m1v12A1
12m2v22A2
第二章 守恒定律
牛顿运动三定律
动能定理
动量定理
三定理
角动量定理
能量守恒定律 动量守恒定律 角动量守恒定律
三守恒定律
1
Fma ——力与运动状态变化间的瞬时关系
大学物理物质的能量
v
m0v 2 1 2
vdv 1 2
0
m0 v 2 1 2
m0 c 2 1 2
v 0
即 Ek
m0c 2 1 2
m0c 2 (m m0 )c 2 mc2
经典力学中的表达式: Ek
1 m0 v 2 2
在什么情况下,以上两式相当
作泰勒级数展开:
§1.4 物质的能量
一、能量守恒定律
能量守恒定律是物质在运动和相互作用的过程中遵循一个普 遍的原理。即: 能量可在不同的系统之间交换,不同形式的能量是可以相互转化 的,但能量的总量保持不变。
二、实物的质量与能量
由爱因斯坦的相对论可知,运动中实物(质点)的质量为
m m0 v2 1— 2 c
令
v c
Q
式中 为与U 等效的物理量
d (mv ) F 中质量 m 为动质量 dt
因此,不能提到微分号外写成:
dv F m ma dt
只有在实物以低速运动时, 才能近似写成上式的形式。
(1 )
2 1 2
?
1 3 5 1 2 4 6 2 8 16
1 1 v 2 如果 v << c ,则: 1 上式可作近似为: (1 ) 2 1 2 2 c 2 m c 0 则:Ek m0c 2 1 m0 v 2 1 2 2
2 ( m c 0i Ei ) 恒量
或
( m0i c Ei ) 0
2
能量守恒定律和质量守恒原理在爱因斯坦的质能方程中得 到了统一。
三、势能和势能曲线
保守力做功只与路径的起点和终点的位置有关,与路径无 2 关,所以保守力做功必定是空间位置的函数。
大学物理(上册)_能量 能量守恒定律
势能
•做功与路径无关,只与起点、终点位置有关 m b
F
A F dr
a
b
L1
a
a
F dr
b
L2
(路径L1) (路径L2)
•对沿闭合路径运动一周的物体做功为零 F dr 0
L
否则为非保守力(耗散力)
2. 势能
凡保守力的功均可表示为与相互作用物体相对位置 有关的某函数在始末位置的值之差,我们将该函数定 义为此物体系的势能。
保守力 重力 势能(E p ) 势能零点 势能曲线 Ep 0 Ep
mgh
1 kx 2 2
mM G r
h=0 x=0
h
弹力
0 引力
x
r
r=∞
Ep 0
3. 保守力与相关势能的关系:
1)凡保守力都有其相关势能,势能属于物体系, 保守力为该势能系统的内力。 2)保守力的功等于其相关势能增量的负值。
A保 Ep Ep2 Ep1 Ep1 Ep2
弹簧伸长 0.1 m 得
k
M
S
ห้องสมุดไป่ตู้
F
物体上升 0.1 m
缓慢下拉:每时刻物体处于平衡态
k x (0<x≤0.1m) 前0.1m为变力 F= k x0 =Mg (0.1<x≤0.2m) 后0.1m为恒力
0.1
A
F
kxdx Mgdx
0 0.1 .1 0.2 kx 2 |0 Mgx | 0 0.1
F保 grad Ep Ep
Ep Ep Ep x i y j z k
指向势能降低最快的方向
练习2:
大学物理,力学中的守恒定律 1
保守力在 l 方向投影
v F保 = − gradEp = −∇Ep
=−
(
∂Ep ∂x
v ∂Ep v ∂Ep v i + ∂y j + ∂z k
)
第19页 共32页 页 页
大学物理
的质点在外力F的作用下沿 轴运动。 练习3 练习3 质量为 m的质点在外力 的作用下沿 轴运动。 的质点在外力 的作用下沿x轴运动 已知t 时质点位于原点, 已知 = 0时质点位于原点,初速度为零。力F随距离线 时质点位于原点 初速度为零。 随距离线 性减小, 性减小,x = 0处,F=F0; x=L处,F = 0。试求质点在 处 处 。 x=L处的速率。 处的速率。 处的速率
v s
s
b
(1) 变力的功 v v d 元功: 元功: A = F ⋅ d r v = F ⋅ d r ⋅ cos θ 直角坐标系: 直角坐标系:
= F d s cos θ
ds v r θd
b
v v v v v r F = Fx i + Fy j + Fz k r a r r r dr = dxi + dyj + dzk v v dA = F ⋅ dr = Fx dx + Fy dy + Fz dz
P
C
y
R
r F
m
解: v
.
o
v v F = F0 x i + F0 y j
v r
x
0
v v v d r = dx i + dyj
2R
v v v r = xi + yj
v v 2 A= ∫ F ⋅ dr = ∫ F xd x + ∫ F yd y = 2F R 0 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质点动力学
2-4-4 机械能守恒定律
质点系的动能定理: 其中
W内 W外 Ek 2 Ek1
W内 W保内 W非保内
W外 W保内 W非保内 Ek 2 Ek1
W保内 E p 2 E p1
W外 W非保内 Ek 2 Ep 2 Ek1 Ep1
P.10/46
质点动力学
为什么我们可以把动能看作是物体所具有 的一种作功的本领?
利用动能作功的例子
在中国三峡水电站安装
世界最大的水力发电机定子
P.11/46
质点动力学
注意
• 动能是标量,仅是状态量v 的单值函数,也 是状态量; • 功与动能的本质区别:它们的单位和量纲相 同,但功是过程量,能是状态量。功是能量 变化的量度; • 功和能具有普遍意义; • 动能定理由牛顿第二定律导出, 只适用于 惯性参考系,动能也与参考系有关。
所以:
Fx
E p x
Fy
E p y
Fz
E p z
保守力的矢量式:
E p E p E p F x i y j z
结论:
k
保守力沿各坐标方向的分量,在数值上等于系 统的势能沿相应方向的空间变化率的负值,其方向 指向势能降低的方向。
a
a
b b F1 dr F2 dr Fn dr
a a
W W1 W2 Wn
结论:合力对质点所作的功等于每个分力对质点
作功之代数和
。
P.3/46
质点动力学
在直角坐标系Oxyz中
F Fx i Fy j Fz k
质点动力学
§2-4 能量守恒定律
2-4-1 功和功率
功是度量能量转换的基本物理量,它描写了力 对空间积累作用。
物体发生了位移 r ,则 把力在位移方向的分力与 位移 r 的乘积称为功。
功的定义: 在力 F 的作用下,
z
r
O
F
F
r1
x
y
P.1/46
质点动力学
W F r cos F r
解:
F 6t a 3t m 2
v t
dv a dt
dv adt 3t dt
3 2 两边积分: dv 3tdt v t 0 0 2 3 2 dx dx vdt t dt v 2 dt 2 3 2 9 42 A F dx 6t t dt t 36 ( J ) 0 2 4 0
机械能守恒定律
当系统只受保守内力作功时,质点系的总机 械能保持不变。
注意:
(1)机械能守恒定律只适用于惯性系,不适合 于非惯性系。这是因为惯性力可能作功。 (2)在某一惯性系中机械能守恒,但在另一惯 性系中机械能不一定守恒。这是因为外力的功与 参考系的选择有关。对一个参考系外力功为零, 但在另一参考系中外力功也许不为零。
P.30/46
质点动力学
保守力与势能的积分关系: 保守力与势能的微分关系:
W E p
dW dE p
因为:
dW F dr Fx dx Fy dy Fz dz
dE p E p x dx E p y dy E p z dz
P.31/46
质点动力学
说明:(1)势能是一个系统的属性。
(2) 势能的大小只有相对的意义,相对 于势能的零点而言。 (3)势能的零点可以任意选取。 设空间r0点为势能的零点,则空间任意一点 r 的势能为:
E p (r ) E (r ) E p (ro ) F dr
ro r
结论:
势能曲线对照表
势能随位置变化的曲线~势能曲线
保守力 重 力 势能(E p ) mgh
1 2
势能零点 h=0
Ep 0
势能曲线 h
Ep
弹 力
kx
2
x=0
Ep
0 0
x
引 力
mM G r
r=∞
r
P.28/46
质点动力学
锥 体 为 什 么 上 滚 ?
P.29/46
质点动力学
跳高采用那种方式最好,为什么?
设铁锤第二次敲打时能敲入的深度为ΔS ,则有
S1 S 1 1 2 1 2 2 0 mv 0 kxdx k ( S1 S ) kS1 S1 2 2 2
P.16/46
质点动力学
2 ( S1 S ) 2 2S1
化简后
S1 S 2S1
第二次能敲入的深度为:
S 2S1 S1 ( 2 1) 1cm 0.41cm
P.17/46
质点动力学
2-4-3 保守力与非保守力
(1)重力的功
初始位置
势能
z
a( x a , y a , z a )
b( xb , yb , z b )
末了位置
za a
zb
r
Wab
假设物体沿 x 轴运动,外力 在该方向的分 力所做的功可 用右图中曲线 下面的面积表 示
Fx
Fx f ( x)
O
xa
xb
x
P.5/46
功和参考系
功与参考系有关,具有相对性
质点动力学
举 例
f
以车厢为参考系,摩擦力不作功。以地面为 参考系,摩擦力作功。一般情况下,通常约定 以地面为参考系。
P.6/46
弹性力作功只与弹簧的起始和终了位置有关, 而与弹性变形的过程无关。
作功特点:
作功与路径无关,只与始末位置有关的力。
P.21/46
质点动力学
保守力和非保守力的定义:
若
若
A l F dr 0,
A l F dr 0,
F为保守力。
F为非保守力。
物体沿闭合路径绕行一周,这些力所作的功恒 为零,具有这种特性的力统称为保守力。没有这种 特性的力,统称为非保守力。
物体在保守力场中a、b两点的势能Epa与 Epb之差,等 于质点由a点移动到b点过程中保守力所做的功Wab。
E pa E pb
b
a
F dr Wab
Wab ( E pb E pa ) E p
保守力做功在数值上等于 系统势能的减少。
P.25/46
质点动力学
P.33/46
质点动力学
机械能
E Ek Ep
W外 W非保内 E2 E1
质点系的功能原理 质点系机械能的增量等于所有外力和所 有非保守内力所作功的代数和。
如果
W外 W非保内 0
E E k E p 恒量
P.34/46
质点动力学
机械能守恒演示实验
P.35/46
质点动力学
P.12/46
质点动力学
2.质点系的动能定理
一个由n个质点组成的质点系,考察第i个质点。 质点的动能定理:
Wi外 Wi内 E k 2i E k1i
对系统内所有质点求和
i
n
Fi
W
i 1
n
i内
Wi外 E k 2i E k1i
i 1
n
n
fi
i 1
i 1
万有引力作功只与质点的始、末位置有关,而 与具体路径无关。
(3)弹性力的功
m
o x1
F
m
由虎克定律:
F kxi
P.20/46
a x2
x
x b
质点动力学
x2 x2 W F dx kxi dxi kxdx
x1 x1
1 2 1 2 W kx1 kx2 2 2
解 设铁锤敲打钉子前的
速度为v0,
敲打后两者的共同速 度为v。
O
S1 S2
Mv0 ( M m) v Mv 0 v M m
x
P.15/46
质点动力学
铁锤第一次敲打时,克服阻力做功,设钉子所受阻 力大小为:
f kx
M m , v v0
由动能定理, 有:
S1 1 1 2 2 0 mv 0 kxdx kS1 0 2 2
国际单位:焦耳(J )N· m
质点由a点沿曲线运动到b点的过程中,变力F 所
作的功 。
元功: dW F dr
W
b a
dr
F
b
b F dr F cos dr
a
a
P.2/46
质点动力学
合力的功:
W
b
a
b
b F dr F1 F2 Fn dr
P.8/46
质点动力学
2-4-2 动能和动能定理
1.质点动能定理 动能: 质点因有速度而具有的作功本领。 1 2 单位:(J) Ek mv 2
设质点m在力的作用下沿 曲线从a点移动到b点 元功:
dr
a
b
dW F dr F cos ds
F
P.9/46
质点动力学
保守力: 重力、弹性力、万有引力、静电力 非保守力: 摩擦力、爆炸力
Why ?
P.22/46
作功与路径无关
F d r 0
Wacb Wadb
a
质点动力学
证明: 设保守力沿闭合路径acbda作功
作功与路径无关: 因为: 所以:
Wacb Wbda
