三角函数反三角函数积分公式求导公式
三角函数和反三角函数公式

一.三角函数公式1.诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2(90度) - a) = cos(a)cos(π/2(90度) - a) = sin(a)sin(π/2 (90度)+ a) = cos(a)cos(π/2 (90度)+ a) = - sin(a)sin(π(180度)- a) = sin(a)cos(π(180度) - a) = - cos(a)sin(π(180度)+ a) = - sin(a)cos(π(180度)+ a) = - cos(a)2.两角和与差的三角函数sin(a + b) = sin(a)cos(b) + cos(α)sin(b)cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)] tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)]3.和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2]sin(a) sin(b) = 2cos[(a + b)/2]sin[(a - b)/2]cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2]cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2]4.积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)]cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]5.二倍角公式sin(2a) = 2sin(a)cos(b)cos(2a) = cos2(a) - sin2(a) = 2cos2(a) -1=1 - 2sin2(a)6.半角公式sin2(a/2) = [1 - cos(a)] / 2cos2(a/2) = [1 + cos(a)] / 2tan(a/2) = [1 - cos(a)] /sin(a) = sina / [1 + cos(a)]7.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)二.反三角函数公式反三角函数其他公式:cos(arcsinx)=√(1-x^2)arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=xarcsin x = x + x^3/(2*3) + (1*3)x^5/(2*4*5) +1*3*5(x^7)/(2*4*6*7)……+(2k+1)!!*x^(2k-1)/(2k!!*(2k+1))+……(|x|<1) !!表示双阶乘arccos x = π -(x + x^3/(2*3) + (1*3)x^5/(2*4*5) + 1*3*5(x^7)/(2*4*6*7)……)(|x|<1)arctan x = x - x^3/3 + x^5/5 -……举例当x∈[-π/2,π/2] 有arcsin(sinx)=xx∈[0,π],arccos(cosx)=xx∈(-π/2,π/2),arctan(tanx)=xx∈(0,π),arccot(cotx)=xx>0,arctanx=π/2-arctan1/x,arccotx类似若(arctanx+arctany)∈(-π/2,π/2),则arctanx+arctany=arctan((x+y)/(1-xy)) 例如,arcsinχ表示角α,满足α∈[-π/2,π/2]且sinα=χ;arccos(-4/5)表示角β,满足β∈[0,π]且cosβ=-4/5;arctan2表示角φ,满足φ∈(-π/2,π/2)且tanφ=2。
三角函数-反三角函数-积分公式-求导公式
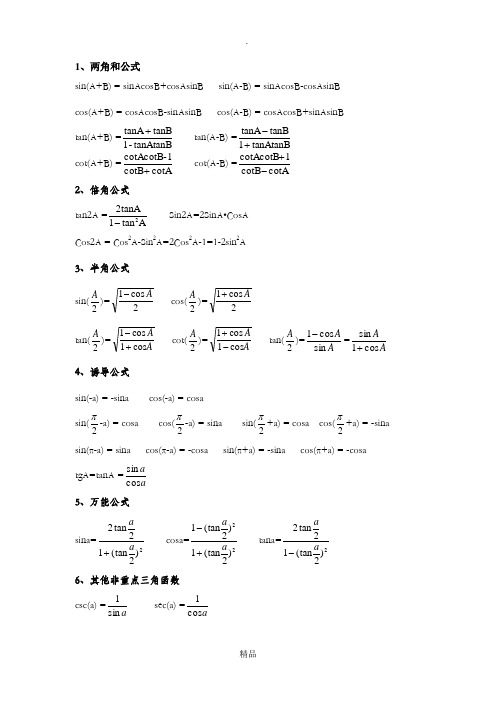
1、两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+ 2、倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A3、半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin 5、万能公式 sina=2)2(tan 12tan2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 6、其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 17、(a+b)的三次方,(a-b)的三次方公式(a+b)^3=a^3+3a^2b+3ab^2+b^3(a-b)^3=a^3-3a^2b+3ab^2-b^3a^3+b^3=(a+b)(a^2-ab+b^2)a^3-b^3=(a-b)(a^2+ab+b^2)8、反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—π/2,π/2〕时,有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2,π/2),arctan(tanx)=xx∈(0,π),arccot(cotx)=xx〉0,arctanx=π/2-arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy) 9、三角函数求导:(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/√(1-x^2)(arccosx)'=-1/√(1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)10、基本求导公式⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。
三角函数与反三角函数公式大全

三角函数与反三角函数公式大全三角函数和反三角函数是高中数学中的重要内容,也是数学和物理学中广泛应用的数学工具。
下面我们将介绍一些常用的三角函数和反三角函数的公式。
1. 正弦函数(sin)和余弦函数(cos)的关系:sin^2x + cos^2x = 12. 正切函数(tan)与正弦函数(sin)和余弦函数(cos)的关系:tanx = sinx / cosx3. 余切函数(cot)和正弦函数(sin)和余弦函数(cos)的关系:cotx = cosx / sinx4. 正弦函数(sin)和余弦函数(cos)的周期性:sin(x + 2π) = sinxcos(x + 2π) = cosx5. 正弦函数(sin)和余弦函数(cos)的奇偶性:sin(-x) = -sinxcos(-x) = cosx6. 正切函数(tan)和余切函数(cot)的奇偶性:tan(-x) = -tanxcot(-x) = -cotx7. 正弦函数(sin)和余弦函数(cos)的对称性:sin(π - x) = sinxcos(π - x) = -cosx8. 正切函数(tan)和余切函数(cot)的对称性:tan(π - x) = -tanxcot(π - x) = -cotx9. 正弦函数(sin)和余弦函数(cos)的双角和差公式:sin(x ± y) = sinxcosy ± cosxsinycos(x ± y) = cosxcosy ∓ sinxsiny10. 正切函数(tan)和余切函数(cot)的双角和差公式:tan(x ± y) = (tanx ± tany) / (1 ∓ tanxtany)cot(x ± y) = (cotxcoty ∓1) / (coty ± cotx)11. 正弦函数(sin)和余弦函数(cos)的和差化积公式:sinx + siny = 2sin[(x + y) / 2]cos[(x - y) / 2]sinx - siny = 2sin[(x - y) / 2]cos[(x + y) / 2]cosx + cosy = 2cos[(x + y) / 2]cos[(x - y) / 2]cosx - cosy = -2sin[(x + y) / 2]sin[(x - y) / 2] 12. 正切函数(tan)和余切函数(cot)的和差化积公式:tanx + tany = (tanx + tany) / (1 - tanxtany)tanx - tany = (tanx - tany) / (1 + tanxtany)cotx + coty = (cotx + coty) / (cotxcoty - 1)cotx - coty = (cotx - coty) / (cotxcoty + 1)13. 正弦函数(sin)和余弦函数(cos)的倍角公式:sin2x = 2sinxcosxcos2x = cos^2x - sin^2x = 2cos^2x - 1 = 1 - 2sin^2x14. 正弦函数(sin)和余弦函数(cos)的半角公式:sin(x/2) = ±√[(1 - cosx) / 2]cos(x/2) = ±√[(1 + cosx) / 2]15. 反正弦函数(arcsin)和反余弦函数(arccos)的范围:-π/2 ≤ arcsinx ≤ π/20 ≤ arccosx ≤ π16. 反正弦函数(arcsin)和反余弦函数(arccos)的负值关系:arcsin(-x) = -arcsinxarccos(-x) = π - arccosx17. 反正弦函数(arcsin)和反余弦函数(arccos)的和、差关系:arcsin(x) ± arccos(x) = π/2这些公式是三角函数和反三角函数的基本关系,掌握它们对于理解和解决三角函数相关的问题非常重要。
三角函数_反三角函数_积分公式_求导公式-反sin三角函数积分之欧阳文创编

1、两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanB tanA +tan(A-B) =tanAtanB1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+2、倍角公式 tan2A =Atan 12tanA 2-Sin2A=2SinA•CosACos2A = Cos2A-Sin2A=2Cos2A-1=1-2sin2A 3、半角公式 sin(2A )=2cos 1A-cos(2A )=2cos 1A+ tan(2A )=AA cos 1cos 1+-cot(2A )=AA cos 1cos 1-+tan(2A )=A A sin cos 1-=AAcos 1sin +4、诱导公式sin(-a) = -sinacos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sinacos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosatgA=tanA =aa cos sin5、万能公式sina=2)2(tan 12tan2aa +cosa=22)2(tan 1)2(tan 1aa+-tana=2)2(tan 12tan2aa - 6、其他非重点三角函数 csc(a) =a sin 1sec(a) =acos 1 7、(a +b )的三次方,(a -b )的三次方公式(a+b)^3=a^3+3a^2b+3ab^2+b^3 (a-b)^3=a^3-3a^2b+3ab^2-b^3 a^3+b^3=(a+b)(a^2-ab+b^2) a^3-b^3=(a-b)(a^2+ab+b^2) 8、反三角函数公式 arcsin(-x)=-arcsinx arccos(-x)=π-arccosx arctan(-x)=-arctanx arccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx )当x∈〔—π/2,π/2〕时,有arcsin(sinx)=x 当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2,π/2),arctan(tanx)=x x∈(0,π),arccot(cotx)=xx 〉0,arctanx=π/2-arctan1/x,arccotx 类似 若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy) 9、三角函数求导: (sinx)'=cosx (cosx)'=-sinx (tanx)'=(secx)^2 (secx)'=secxtanx (cotx)'=-(cscx)^2 (cscx)'=-csxcotx (arcsinx)'=1/√(1-x^2) (arccosx)'=-1/√(1-x^2) (arctanx)'=1/(1+x^2) (arccotx)'=-1/(1+x^2) 10、基本求导公式⑴0)(='C (C 为常数)⑵1)(-='n n nx x ;一般地,1)(-='αααx x 。
三角函数反三角函数积分公式_求导公式

三角函数反三角函数积分公式_求导公式三角函数是高等数学中重要的一类函数,其基本函数包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)以及它们的反函数(反正弦函数、反余弦函数、反正切函数)。
在解决三角函数的一些问题时,反三角函数的积分公式和求导公式是十分重要的。
本文将详细介绍三角函数反三角函数的积分公式和求导公式。
一、反正弦函数的积分公式和求导公式1.反正弦函数的积分公式:∫arcsinxdx = xarcsinx + √(1-x²) + C该公式可以通过对反正弦函数进行求导并使用换元法得到。
2.反正弦函数的求导公式:d(arcsinx)dx = 1/√(1-x²)要证明该公式,可以使用链式法则或利用三角恒等式进行变形。
二、反余弦函数的积分公式和求导公式1.反余弦函数的积分公式:∫arccosxdx = xarccosx - √(1-x²) + C该公式可以通过对反余弦函数进行求导并使用换元法得到。
2.反余弦函数的求导公式:d(arccosx)dx = -1/√(1-x²)同样地,要证明该公式,可以使用链式法则或利用三角恒等式进行变形。
三、反正切函数的积分公式和求导公式1.反正切函数的积分公式:∫arctanxdx = xarctanx - 1/2ln,1+x², + C该公式可以通过对反正切函数进行求导并使用换元法得到。
2.反正切函数的求导公式:d(arctanx)dx = 1/(1+x²)同样地,要证明该公式,可以使用链式法则或利用反函数关系进行推导。
以上就是三角函数反三角函数的积分公式和求导公式的详细介绍。
这些公式在解决一些涉及三角函数的问题时起到了重要的作用,可以帮助我们更好地理解和应用三角函数。
在实际应用中,我们可以根据具体情况选择适当的公式来求解问题。
角函数反三角函数积分公式_求导公式

1、两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cosAsinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB tan(A+B)=tanAtanB -1tanB tanA +tan(A-B)=tanAtanB1tanB tanA +- cot(A+B)=cotA cotB 1-cotAcotB +cot(A-B)=cotAcotB 1cotAcotB -+ 2、倍角公式 tan2A=Atan 12tanA 2-Sin2A=2SinA?CosA Cos2A=Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A3、半角公式 sin(2A )=2cos 1A -cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式sin(-a)=-sinacos(-a)=cosa sin(2π-a)=cosacos(2π-a)=sinasin(2π+a)=cosacos(2π+a)=-sina sin(π-a)=sinacos(π-a)=-cosasin(π+a)=-sinacos(π+a)=-cosa tgA=tanA=aa cos sin 5、万能公式 sina=2)2(tan 12tan 2a a +cosa=22)2(tan 1)2(tan 1a a +-tana=2)2(tan 12tan 2a a - 6、其他非重点三角函数 csc(a)=a sin 1sec(a)=acos 1 7、(a +b )的三次方,(a -b )的三次方公式(a+b)^3=a^3+3a^2b+3ab^2+b^3(a-b)^3=a^3-3a^2b+3ab^2-b^3a^3+b^3=(a+b)(a^2-ab+b^2)a^3-b^3=(a-b)(a^2+ab+b^2)8、反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—π/2,π/2〕时,有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2,π/2),arctan(tanx)=xx∈(0,π),arccot(cotx)=xx 〉0,arctanx=π/2-arctan1/x,arccotx 类似若(arctanx+arctany )∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy)9、三角函数求导:(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/√(1-x^2)(arccosx)'=-1/√(1-x^2)(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)10、基本求导公式⑴0)(='C (C 为常数)⑵1)(-='n n nx x ;一般地,1)(-='αααx x 。
三角函数_反三角函数_积分公式_求导公式(完整资料).doc

【最新整理,下载后即可编辑】1、两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB-1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +-cot(A+B) =cotAcotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+2、倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 3、半角公式 sin(2A )=2cos 1A- cos(2A )=2cos 1A+tan(2A )=AA cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=AA sin cos 1-=AAcos 1sin + 4、诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a)= -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aa cos sin5、万能公式sina=2)2(tan 12tan2aa +cosa=22)2(tan 1)2(tan 1aa+-tana=2)2(tan 12tan2aa -6、其他非重点三角函数 csc(a) =asin 1 sec(a) =acos 1 7、(a +b )的三次方,(a -b )的三次方公式(a+b)^3=a^3+3a^2b+3ab^2+b^3(a-b)^3=a^3-3a^2b+3ab^2-b^3a^3+b^3=(a+b)(a^2-ab+b^2)a^3-b^3=(a-b)(a^2+ab+b^2)8、反三角函数公式arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—π/2,π/2〕时,有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2,π/2),arctan(tanx)=xx∈(0,π),arccot(cotx)=xx〉0,arctanx=π/2-arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy)9、三角函数求导:(sinx)'=cosx(cosx)'=-sinx(tanx)'=(secx)^2(secx)'=secxtanx(cotx)'=-(cscx)^2(cscx)'=-csxcotx(arcsinx)'=1/√(1-x^2)(arccosx)'=-1/√(1-x^2) (arctanx)'=1/(1+x^2) (arccotx)'=-1/(1+x^2)10、基本求导公式 ⑴0)(='C (C为常数)⑵1)(-='n n nx x ;一般地,1)(-='αααx x 。
三角函数的求导公式

三角函数的求导公式是什么?三角函数,(sinx)'= cosx ,(cosx)'=-sinx.反三角函数,(arcsin X)'=1/√(1-x^2)倒数关系: 商的关系:平方关系:tanα·cotα=1sinα·cscα=1cosα·secα=1 sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secαsin2α+cos2α=1 1+tan2α=sec2α1+cot2α=csc2α诱导公式sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=——————1-tanα·tanβtanα-tanβtan(α-β)=——————1+tanα·tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2)cosα=——————1+tan2(α/2)2tan(α/2)tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin—--·cos—-—2 2α+βα-βsinα-sinβ=2cos—--·sin—-—2 2α+βα-βcosα+cosβ=2cos—--·cos—-—2 2α+βα-βcosα-cosβ=-2sin—--·sin—-—2 2 1sinα·cosβ=-[sin(α+β)+sin(α-β)]21cosα·sinβ=-[sin(α+β)-sin(α-β)]21cosα·cosβ=-[cos(α+β)+cos(α-β)]21sinα·sinβ=--[cos(α+β)-cos(α-β)]2化asinα±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)这是公式塞!其实其他公式都是前3个公式推的!式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinα。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数反三角函数积分公式求导公式
集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY-
1、两角和公式
sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB
cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =
tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA
cotB 1cotAcotB -+ 2、倍角公式 tan2A =A
tan 12tanA 2- Sin2A=2SinACosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A
3、半角公式 sin(2A )=2cos 1A - cos(2
A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2
A )=A A sin cos 1-=A A cos 1sin + 4、诱导公式
sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2
π+a) = -sina
sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =a
a cos sin 5、万能公式 sina=2)2(tan 12tan
2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2
)2(tan 12tan 2a a - 6、其他非重点三角函数 csc(a) =a sin 1 sec(a) =a
cos 1 7、(a +b )的三次方,(a -b )的三次方公式
(a+b)^3=a^3+3a^2b+3ab^2+b^3
(a-b)^3=a^3-3a^2b+3ab^2-b^3
a^3+b^3=(a+b)(a^2-ab+b^2)
a^3-b^3=(a-b)(a^2+ab+b^2)
8、反三角函数公式
arcsin(-x)=-arcsinx
arccos(-x)=π-arccosx
arctan(-x)=-arctanx
arccot(-x)=π-arccotx
arcsinx+arccosx=π/2=arctanx+arccotx
sin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)
当x∈〔—π/2,π/2〕时,有arcsin(sinx)=x
当x∈〔0,π〕,arccos(cosx)=x
x∈(—π/2,π/2),arctan(tanx)=x
x∈(0,π),arccot(cotx)=x
x〉0,arctanx=π/2-arctan1/x,arccotx类似
若(arctanx+arctany)∈(—π/2,π/2),则arctanx+arctany=arctan(x+y/1-xy) 9、三角函数求导:
(sinx)'=cosx
(cosx)'=-sinx
(tanx)'=(secx)^2
(secx)'=secxtanx
(cotx)'=-(cscx)^2
(cscx)'=-csxcotx
(arcsinx)'=1/√(1-x^2)
(arccosx)'=-1/√(1-x^2)
(arctanx)'=1/(1+x^2)
(arccotx)'=-1/(1+x^2)
10、基本求导公式
⑴ 0)(='C (C 为常数)⑵ 1)(-='n n nx x ;一般地,1)(-='αααx x 。
特别地:1)(='x ,x x 2)(2=',21)1
(x x -
=',x x 21)(='。
⑶ x x e e =')(;一般地,)1,0( ln )(≠>='a a a a a x x 。
⑷ x x 1)(ln =';一般地,)1,0( ln 1)(log ≠>='a a a
x x a 。
11、求导法则 ⑴ 四则运算法则
设f (x ),g (x )均在点x 可导,则有:(Ⅰ))()())()((x g x f x g x f '±'='±; (Ⅱ))()()()())()((x g x f x g x f x g x f '+'=',特别)())((x f C x Cf '='(C 为常数); (Ⅲ))0)(( ,)()()()()())()((
2≠'-'='x g x g x g x f x g x f x g x f ,特别21()()()()g x g x g x ''=-。
12、微分 函数()y f x =在点x 处的微分:()dy y dx f x dx ''==
13、积分公式
常用的不定积分公式:
(1) ⎰⎰⎰⎰⎰+==+=+=-≠++=+c x dx x x dx x c x xdx c x dx C x dx x 43,2,),1( 11433
221αααα
; (2) C x dx x
+=⎰||ln 1; C e dx e x x +=⎰; )1,0( ln ≠>+=⎰a a C a a dx a x x ; (3)⎰⎰=dx x f k dx x kf )()((k 为常数)
定积分:
⑴ ⎰⎰⎰+=+b
a b a b a dx x g k dx x f k dx x g k x f k )()()]()([2121
分部积分法:
设u (x ),v (x )在[a ,b ]上具有连续导数)(),(x v x u '',则 14、重要的等价无穷小替换: 当x→0时,
sinx~x
tanx~x
arcsinx~x
arctanx~x
1-cosx~1/2*(x^2)
(a^x)-1~x*lna
(e^x)-1~x
ln(1+x)~x
(1+Bx)^a-1~aBx
[(1+x)^1/n]-1~(1/n)*x loga(1+x)~x/lna。
